一級建築士試験の法規は、学科試験を突破するうえで”鬼門”となります。
「法令集から条文を探して言葉を追いかける」ため、解答に時間を要する科目です。
そのような理由から、法規は「いつも時間が足りない」という悩みが絶えません。
さらに計算問題となると、勉強の荷が重くなる方も多いのではないでしょうか?
ここでは、法規の難問である計算問題の攻略ポイントをギュッと絞って解説します。
一級建築士試験合格を目指すために「法規を攻略する」という強い意志を貫きましょう!

「オリジナル解説」

「攻略への執念」

「確実に点を取る」
こんな人におすすめ!
- 法規の計算問題を攻略したい。
- 法規の計算問題の単純ミスを無くしたい。
- 法規の計算問題は何から手を付けて良いか分からない。



法規の計算問題は、
とにかく大変!忙しい💦
計算問題あるある
- 複合的な要素が絡み、条文を読んでも意味が分からない。
- 全力で答えを出したものの、その答えが選択肢に無くてあせる。
- どこで間違えたのか?その謎をめぐって法令集を行ったり来たり。
- ありがちな間違いを予想した選択肢も、しっかりと用意されている。
- たどり着いた答えに自信を持って、落とし穴を踏んでしまい・・ドボン!



また、やってしまった・・
私は一級建築士に向いてない?
このような典型的なミスをしてしまい、私も悔しい思いをしたことがあります。
(同じミスを繰り返してしまうと、戦意喪失することも・・)
しかし、計算問題さえ克服できれば、法規の攻略にかなり近づくとは思いませんか?
法規を”完全武装”することで、一級建築士試験「合格」を引き寄せましょう!



一級建築士を引き寄せる。
合格通知よ、来い!来い!


この動画を YouTube で視聴
一級建築士|法規の計算問題に挑戦して攻略ポイントを紹介!


法規の試験時間は”1時間45分(105 分)/ 出題数30問”。
105分÷30問=3.5分・・・1問当たりに使える時間は3分30秒です。
そのような理由から、計算問題に至っては法令集を探している余裕はありません。


3分30秒/1問です。
カチカチカチ・・・



ペラペラペラ・・
法規はとにかく忙しい!
計算問題の対策
- 答えを導くための手順や工程を確立しておく。
- 数値や公式は覚えておき、自分の知識で対応する。
- ケアレスミスを避けるために、残り時間を明確にする。
計算問題と対峙するときに「残り時間を明確にする」というのは大事なこと。
序盤から計算問題だと、残り時間が読めない不安感から、冷静に対処しきれません。
私の場合は、先に文章問題をすべて片付けておき、計算問題を”最後”に取り掛かります。
(法規と構造、いずれも同じ戦法です。)
解答に使える時間がはっきりすることで、ペース配分も決まりますよね?
法規の計算問題は毎年3問ほど、5分/問と捉えても20分あれば十分な解答ができるでしょう。



さあ、始めましょう!
法令集を準備して下さい。
高さと階数
難易度:★★☆☆☆

インデックス


- 令1条【用語の定義】
- 二号:地階
- 令2条【面積・高さの算定】
- 六号:建築物の高さ
- 八号:階数
- 2項:地盤面の位置
- 法33条:避雷設備



解答するのに必要な条文を
インデックスにまとめてます。
枝1.


枝1.は最後に解説
枝1.は補足が必要なため、枝2.3.4.→枝1.の順に進めて、最後に解説させていただきます。



後でしっかり説明します。
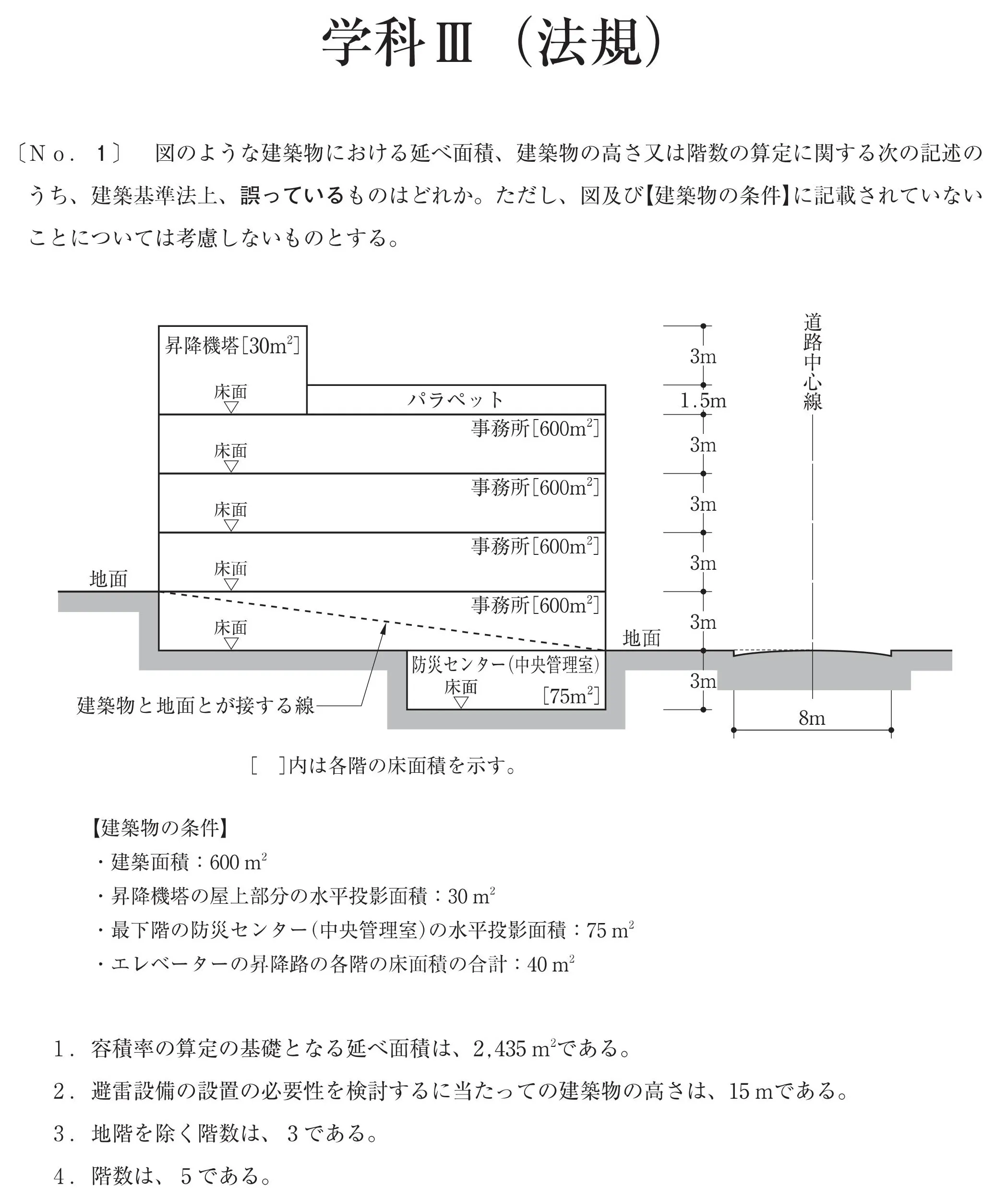
【建築物の高さ】
枝2.建築物の高さ


避雷設備の設置の必要性を検討するに当たっての建築物の高さは、15mである。
条文:建築物の高さ
- 法33条:避雷設備
- 令2条六号:建築物の高さ
- 令2条2項:地盤面の位置
法33条:避雷設備
キーワードは「避雷設備」、条文を読むときに「避雷設備=法33条」を知っておくことが必要です。
その準備として、「避雷設備」のところに「33条」とメモ書き⇩しておきましょう。
避雷設備(法33条)の設置の必要性を検討するに当たっての建築物の高さは、15mである。



「避雷設備」=法33条!
攻略ポイント!
文章のキーワードには、「法○○条」「令○○条」をメモ書きしておくこと。



これは大事なこと!
高さの起点はどっち?
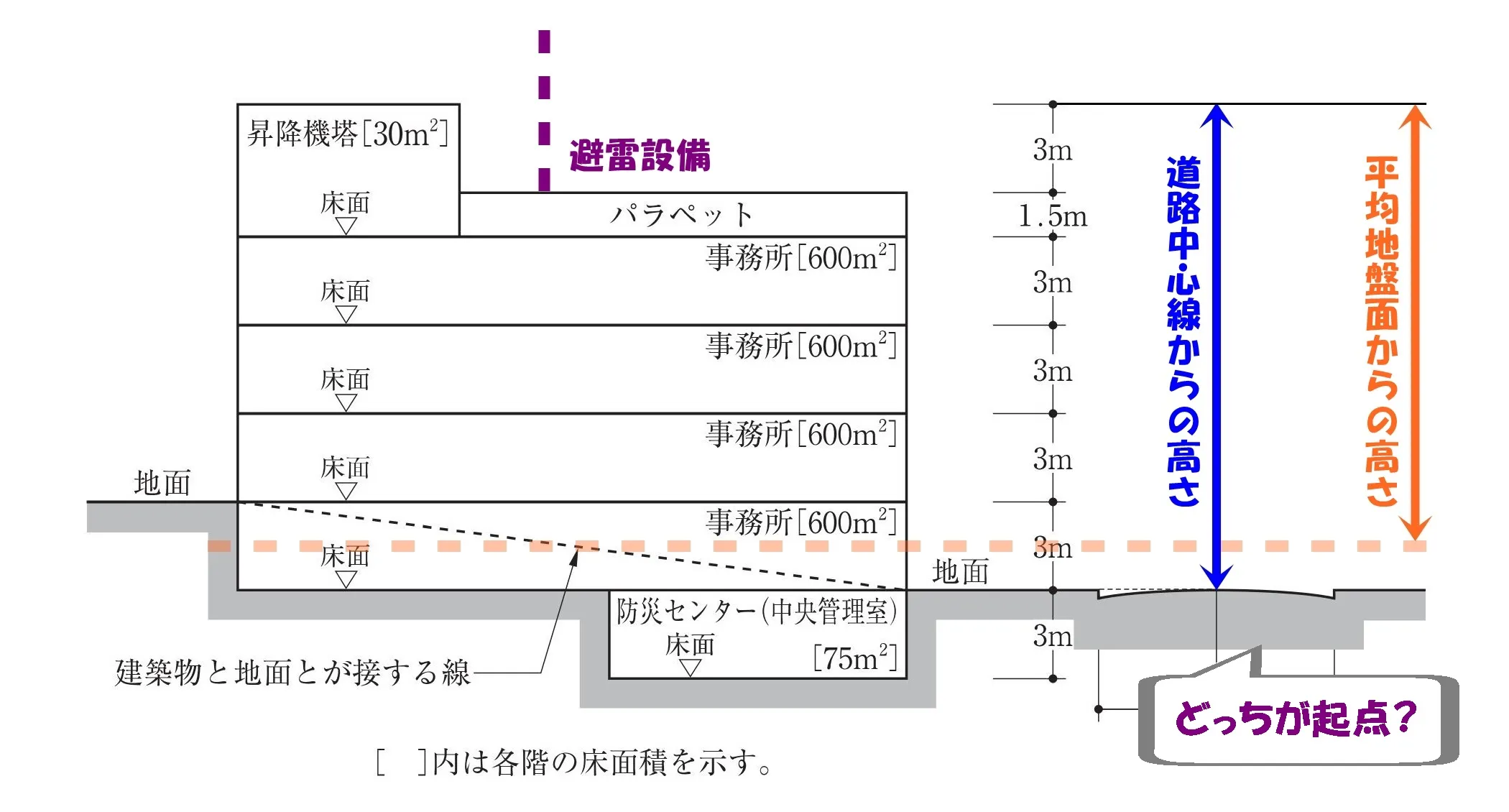

条文にある「建築物の高さ」とは?
- 地盤面からの高さ
- 道路中心線からの高さ
この2つのどちらを”高さの起点”とするか?によって、解答は異なります。



どっち?
チェックポイント
- 法33条:避雷設備
- 令2条六号:建築物の高さ
法56条1項一号の規定並びに令130条の12及び令135条の19の規定による高さの算定は「路面の中心」からの高さによる。
法33条及び~を算定する場合を除き、昇降機塔~屋上部分の水平投影面積の合計が、建築面積の1/8以内の場合においては、当該建築物の高さに算入しない。
建築基準法(一部省略)



「避雷設備」=法33条!
「避雷設備=法33条」ということから、建築物の高さは路面の中心からではありませんよね?
「昇降機塔は建築面積の1/8以内まで建築物の高さに算入しない」についても、法33条を算定する場合は除かれているため、建築物の高さは”昇降機塔の頂部まで”ということになります。



なるほど・・
平均地盤面からの高さ
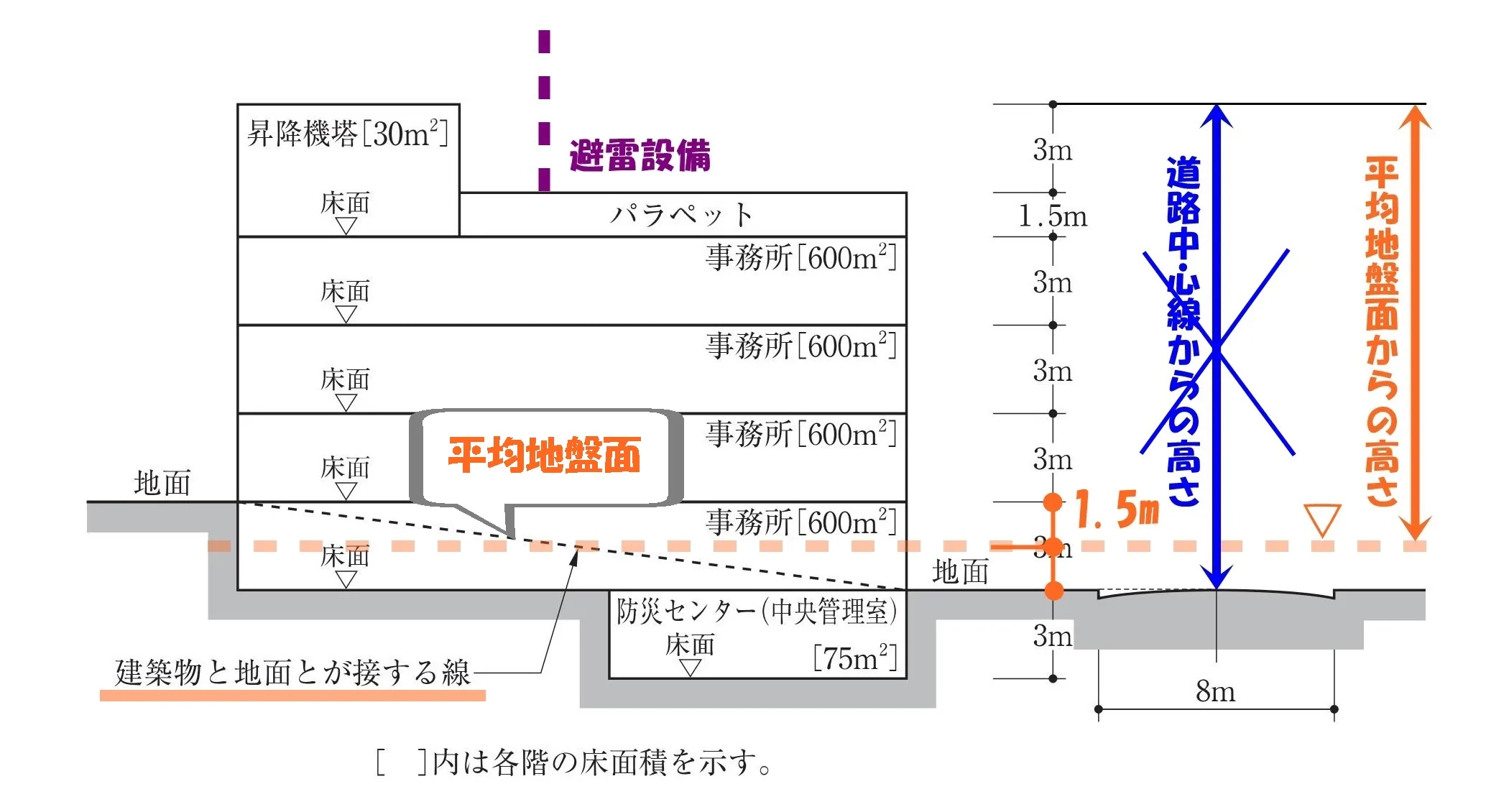

令2条六号:建築物の高さ
- 建築物の高さは、地盤面からの高さとする。
- 建築物の高さは、昇降機塔の頂部まで含める。
そして、令2条2項により「地盤面の高さ」=「平均地盤面からの高さ」ということになります。


地盤面とは?
令2条2項:地盤面の位置
地盤面とは、建築物が周囲の地面と接する位置の平均の高さにおける水平面をいう。
建築基準法(一部省略)


建築物の高さ:1.5(平均地盤面)+3.0+3.0+3.0+1.5+3.0(昇降機塔)=15m。
枝2.(正)
避雷設備(法33条)の設置の必要性を検討するに当たっての建築物の高さは、15mである。



〇
【地階を除く階数】
枝3.地階を除く階数


「地階を除く階数」を数えるためには、「地階」についての定義を知る必要があります。
条文:地階を除く階数
- 令1条二号:地階
- 令2条八号:階数
- 令2条2項:地盤面の位置
地階はどこから?
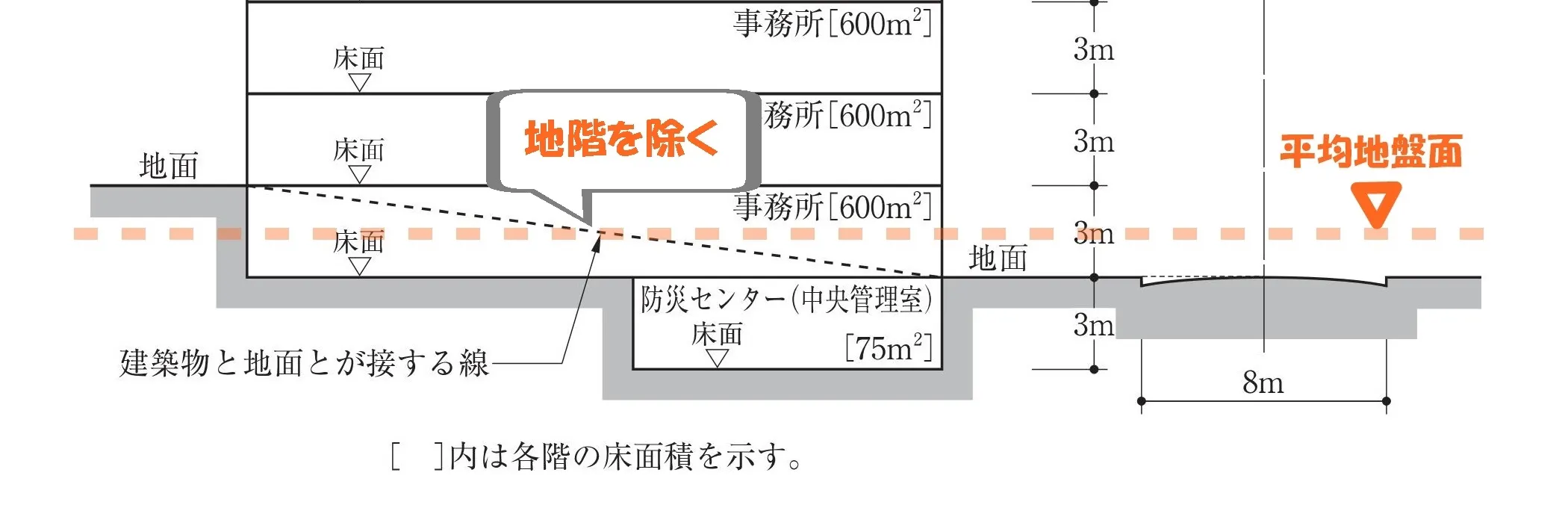



地階とは?
令2条2項:地盤面の位置
地盤面とは、建築物が周囲の地面と接する位置の平均の高さにおける水平面をいう。
建築基準法(一部省略)

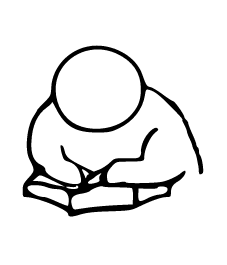
令1条二号:地階
防災センターは、すべてが地盤面下に埋まっているため「地階」になります。



それは地階だよね?
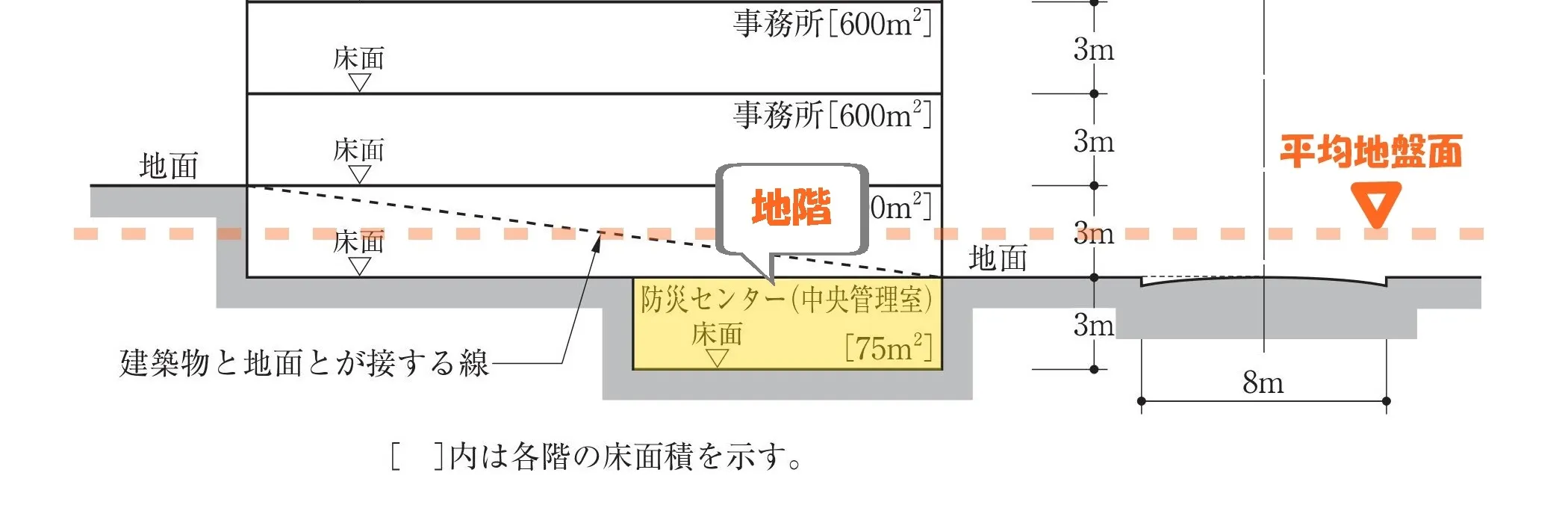
地階の定義
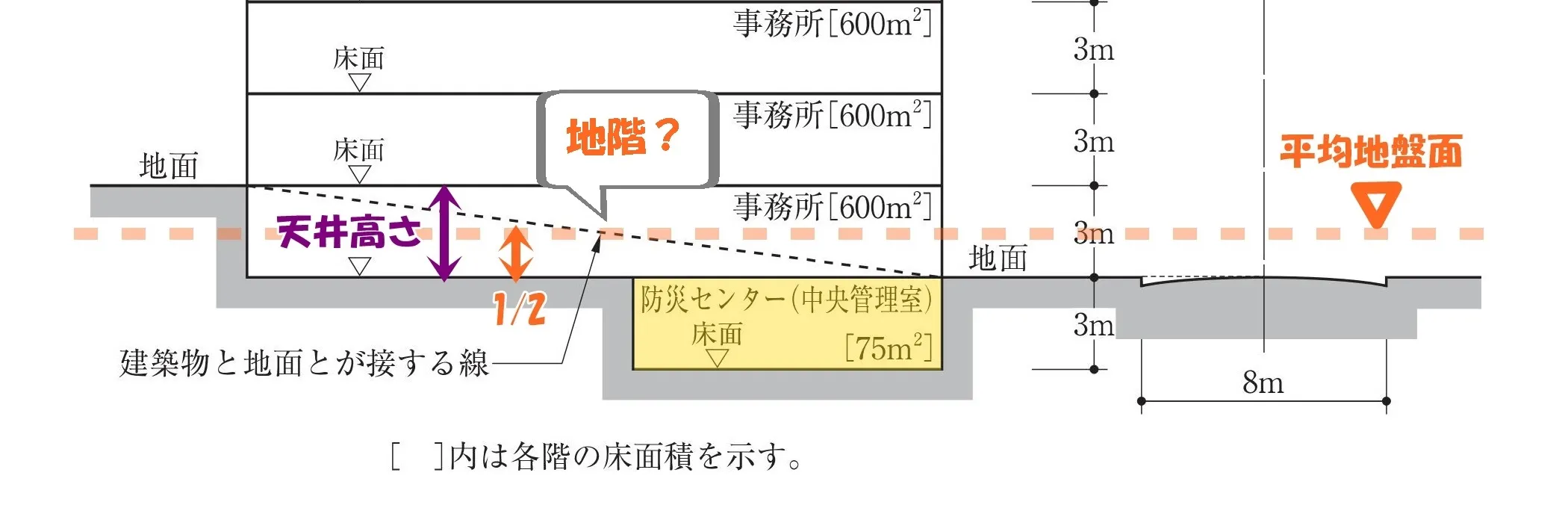

令1条二号:地階
床が地盤面下にある階で、床面から地盤面までの高さがその階の天井の高さの3分の1以上のものをいう。
建築基準法(一部省略)
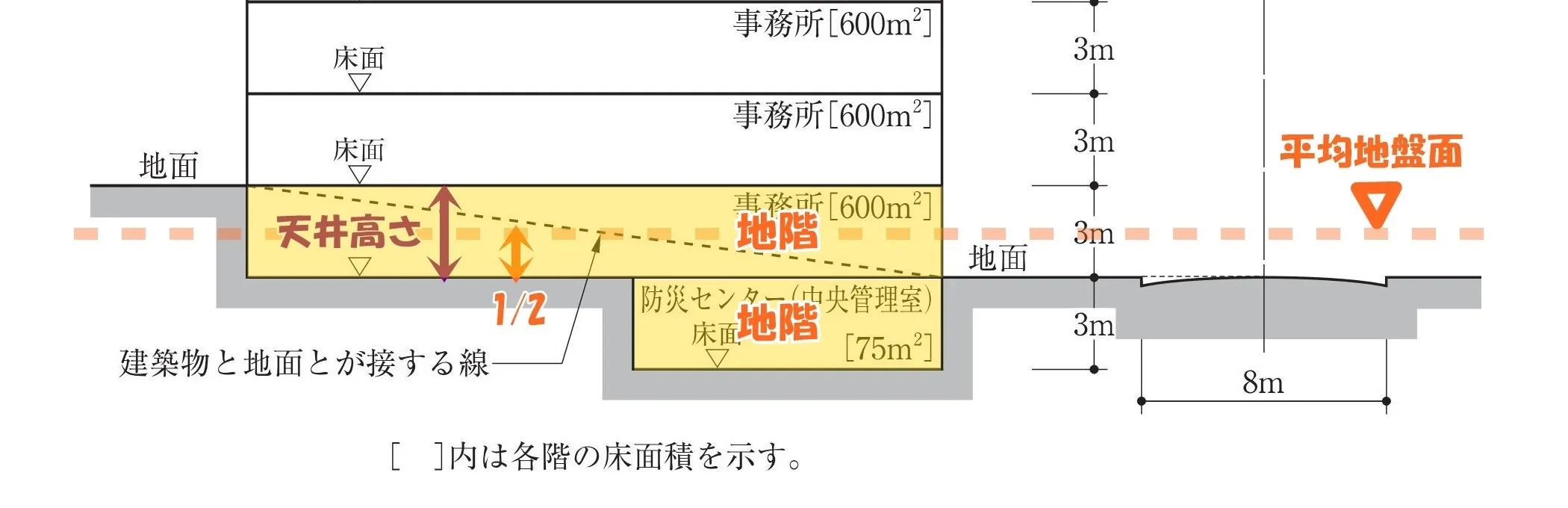

「地盤面=平均地盤面」となり、その高さはFL+1.5m。
1層目の事務所の場合、天井高さがCH=3.0mとすると1.5m/3.0m=1/2
(実際には天井ふところがあるため、1/2より大きくなる。)
よって、防災センターと1層目の事務所はいずれも「地階」の扱いとなります。



1/3が埋まっていれば、
それは「地階」ということ。
昇降機塔は階数に含める?
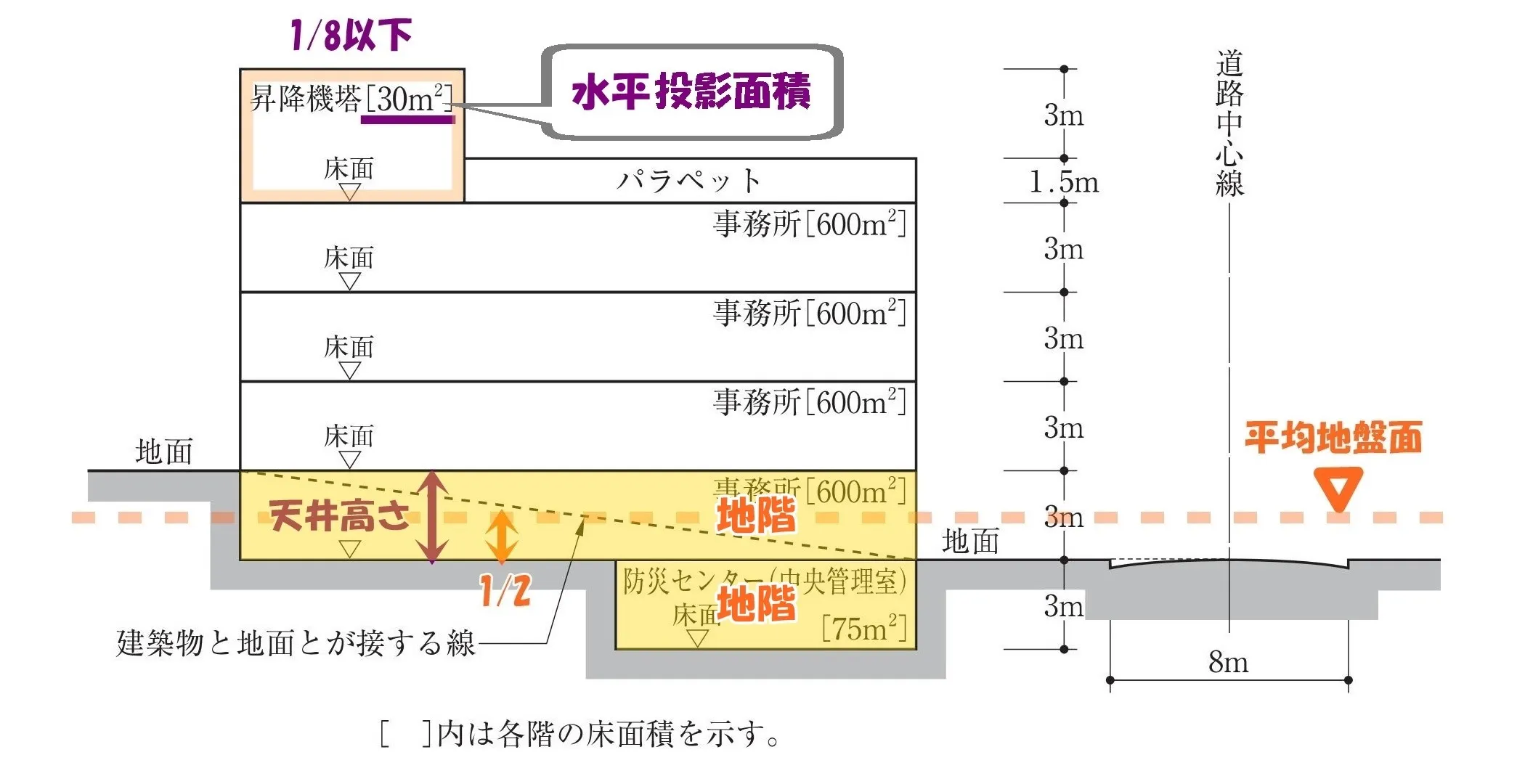

令2条八号:階数
昇降機塔~その他これらに類する建築物の部分で、水平投影面積の合計が~当該建築物の建築面積の8分の1以下のものは、当該建築物の階数に算入しない。
建築基準法(一部省略)



8分の1が来たぞ。
注目!


【建築物の条件】・・昇降機の屋上部分の水平投影面積は30㎡である。
水平投影面積:30㎡/600㎡=1/20(1/8以下)となり、昇降機塔は階数にはカウントしない。



ノーカウント!
階数のカウントは3つ
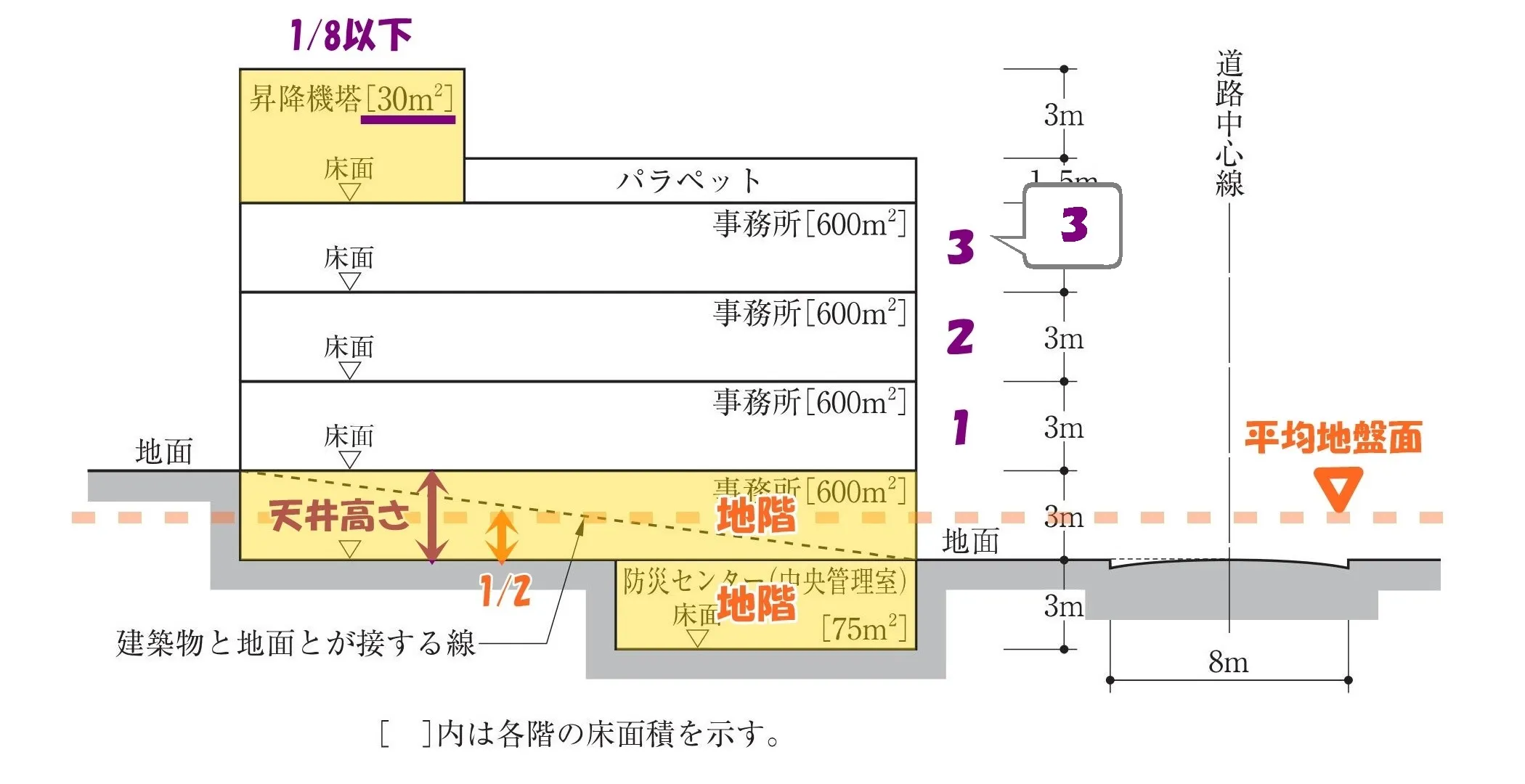

- 令1条二号:地階
- 防災センターと1層目の事務所はいずれも「地階」の扱い。
- 令2条八号:階数
- 昇降機塔の水平投影面積は建築面積の1/8以下のため、階数にはカウントしない。
枝3.の設問は「地階を除く階数は3である」ため、事務所の3フロアだけとなる。(正)



〇
【階数】
枝4.階数


枝4.は地階を含めた、建物全体の階数ということになります。
条文:階数
- 令2条八号:階数
- 令2条八号:昇降機塔の扱い
- 令2条八号:防災センターの扱い
それぞれの扱いについて
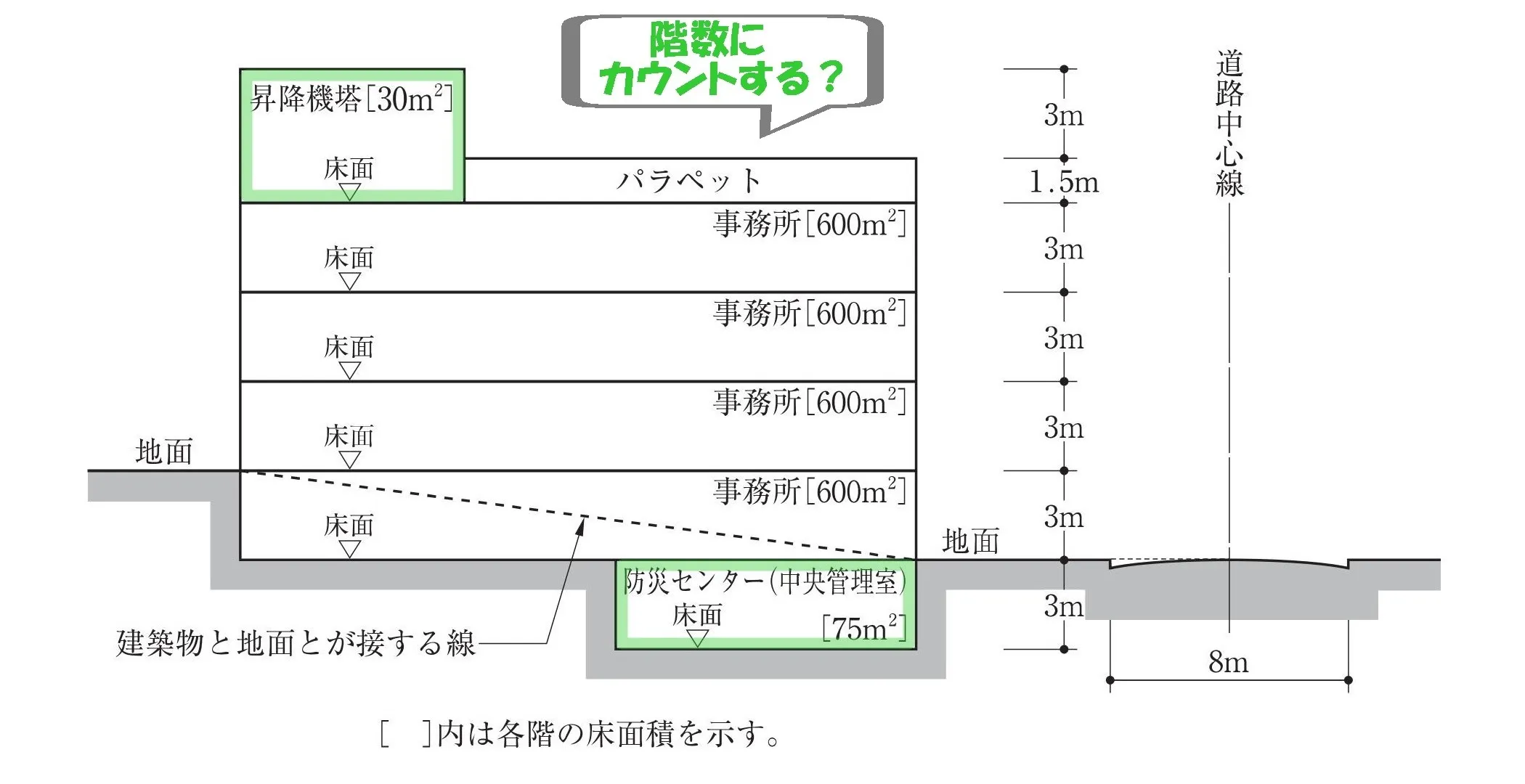

チェックポイント
階数に「昇降機塔」と「防災センター」をカウントするかどうか?



数えるの?どっち?
令2条八号:階数
昇降機塔~その他これらに類する建築物の屋上部分又は地階の倉庫、機械室その他これらに類する建築物の部分で、水平投影面積の合計が~当該建築物の建築面積の8分の1以下のものは、当該建築物の階数に算入しない。
建築基準法(一部省略)



また、8分の1が来たぞ。
注目!





注目!
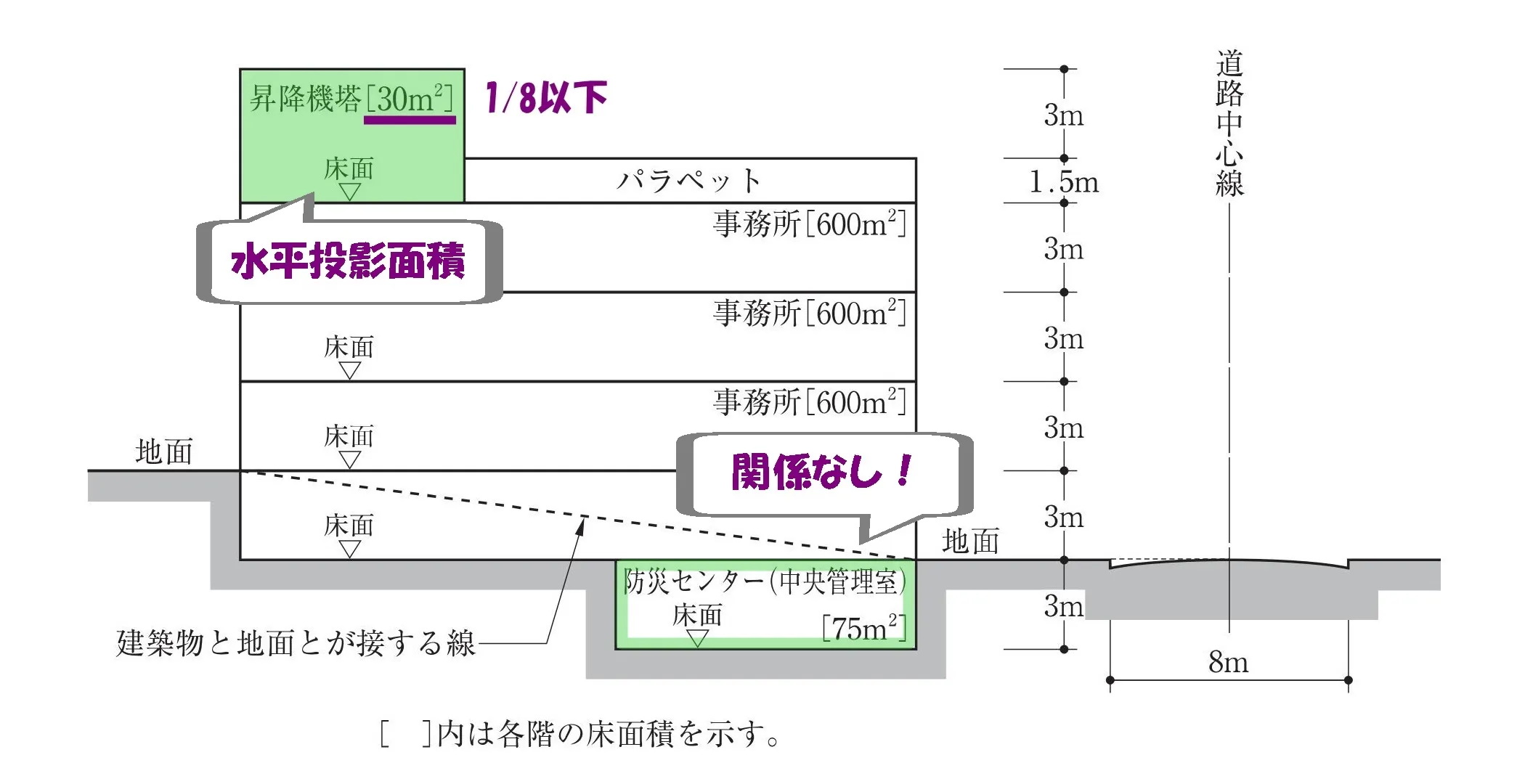

- 令2条八号:昇降機塔の扱い
- 「昇降機塔」の水平投影面積は建築面積の1/8以下のため、階数にはカウントしない。
- 令2条八号:防災センターの扱い
- 「地階の倉庫、機械室その他これらに類する建築物の部分」に該当しないため、階数に含める。



色々とややこしい。
チェックポイント
「それぞれの内容が、条文の”対象物”に含まれるかどうか?」
面積の数値だけに惑わされず、「階数」「地階」「高さ」などを正しく読み取りましょう。



「何が?」を明確にしましょう。
階数のカウントは5つ
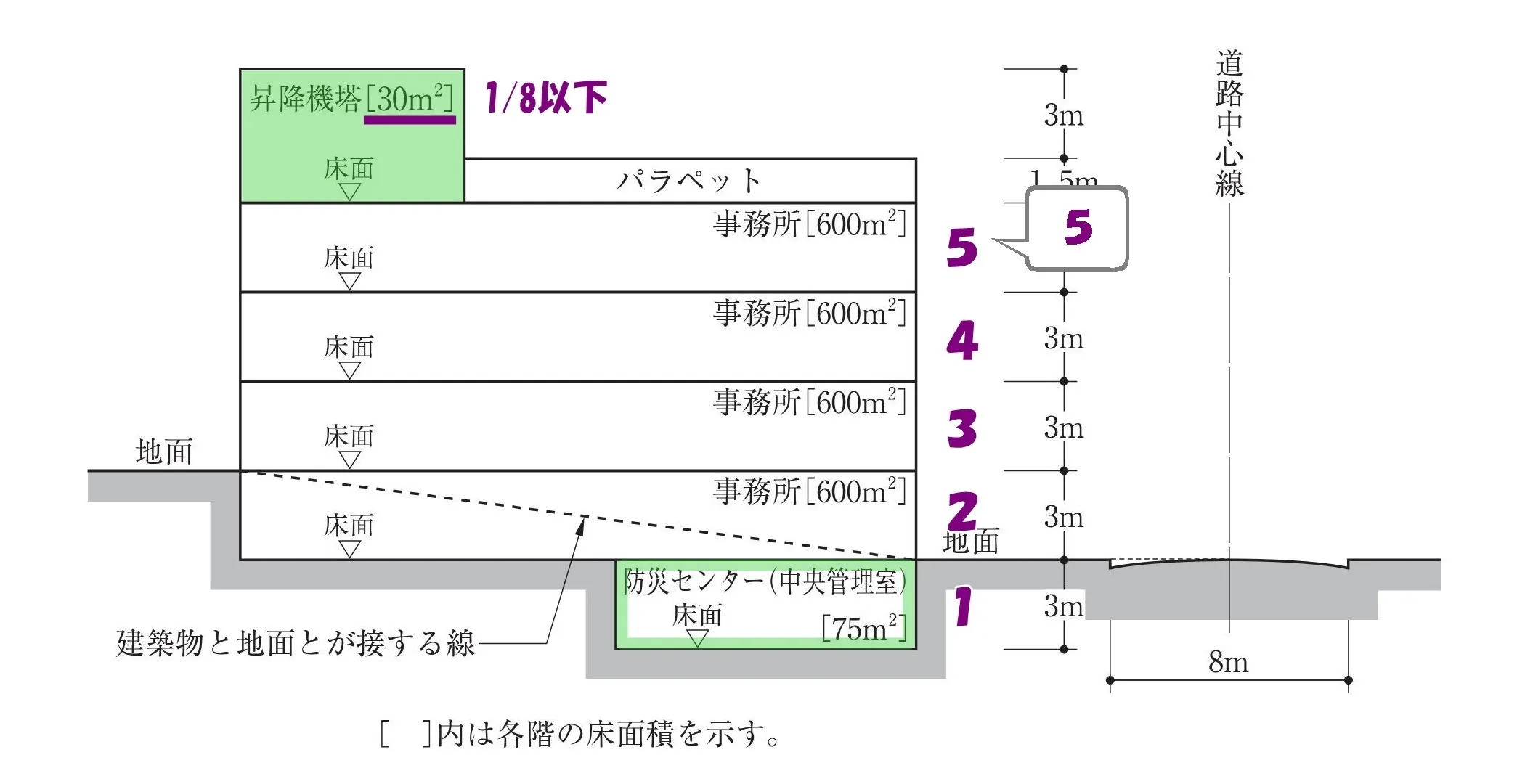

- 昇降機塔は階数に含まれない。
- 防災センターは地階にカウントする。
よって、枝4.建物全体の階数のカウントは5となります。(正)



〇


この動画を YouTube で視聴
【容積率の算定の基礎となる延べ面積】


枝.1
「容積率の算定の基礎となる”延べ面積”は2,435㎡である。」
キーワードは「延べ面積」、ここにアンダーラインを引きましょう。



容積率の算定の
基礎となる延べ面積だね。
インデックス

- 令2条【面積・高さの算定】
- 四号:延べ面積
- 六号:建築物の高さ
- 八号:階数
- 令2条3項:容積率算定における延べ面積の緩和
- 法52条3項:容積率算定におけるエレベーターの昇降路の扱い



延べ面積、準備OK?
容積率の算定の基礎となる延べ面積
- 令2条八号:階数(×延べ面積)
- 令2条3項:容積率算定における延べ面積の緩和
- 法52条3項:容積率算定におけるエレベーターの昇降路の扱い
それぞれが異なる理由で算入する


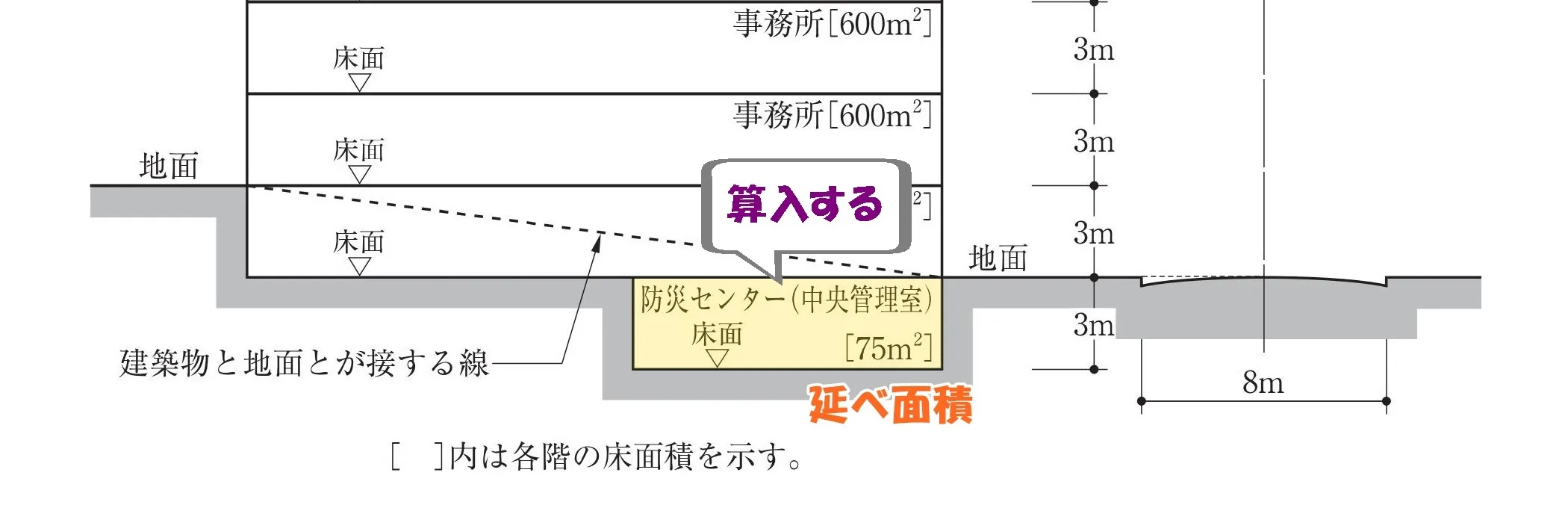

チェックポイント
- 昇降機塔:令2条八号「階数」
- 「昇降機塔の水平投影面積は建築面積の1/8以下」は、延べ面積のことではない。
- 防災センター:令2条3項「容積率算定における延べ面積の緩和」
- 次の各号に掲げる建築物の部分の区分に該当しないため、延べ面積に算入する。
建築基準法(一部省略)
- 一:自動車車庫等 1/5
- 二:備蓄倉庫 1/50
- 三:蓄電池 1/50
- 四:自家発電設備 1/100
- 五:貯水槽 1/100
- 六:宅配ボックス 1/100



見つけた!8分の1。



こら、お待ちなさい!
設問は”延べ面積”ですよ!
そして注目!


エレベーターの昇降路の各階の床面積の合計:40㎡である。



え!?
エレベーターシャフト
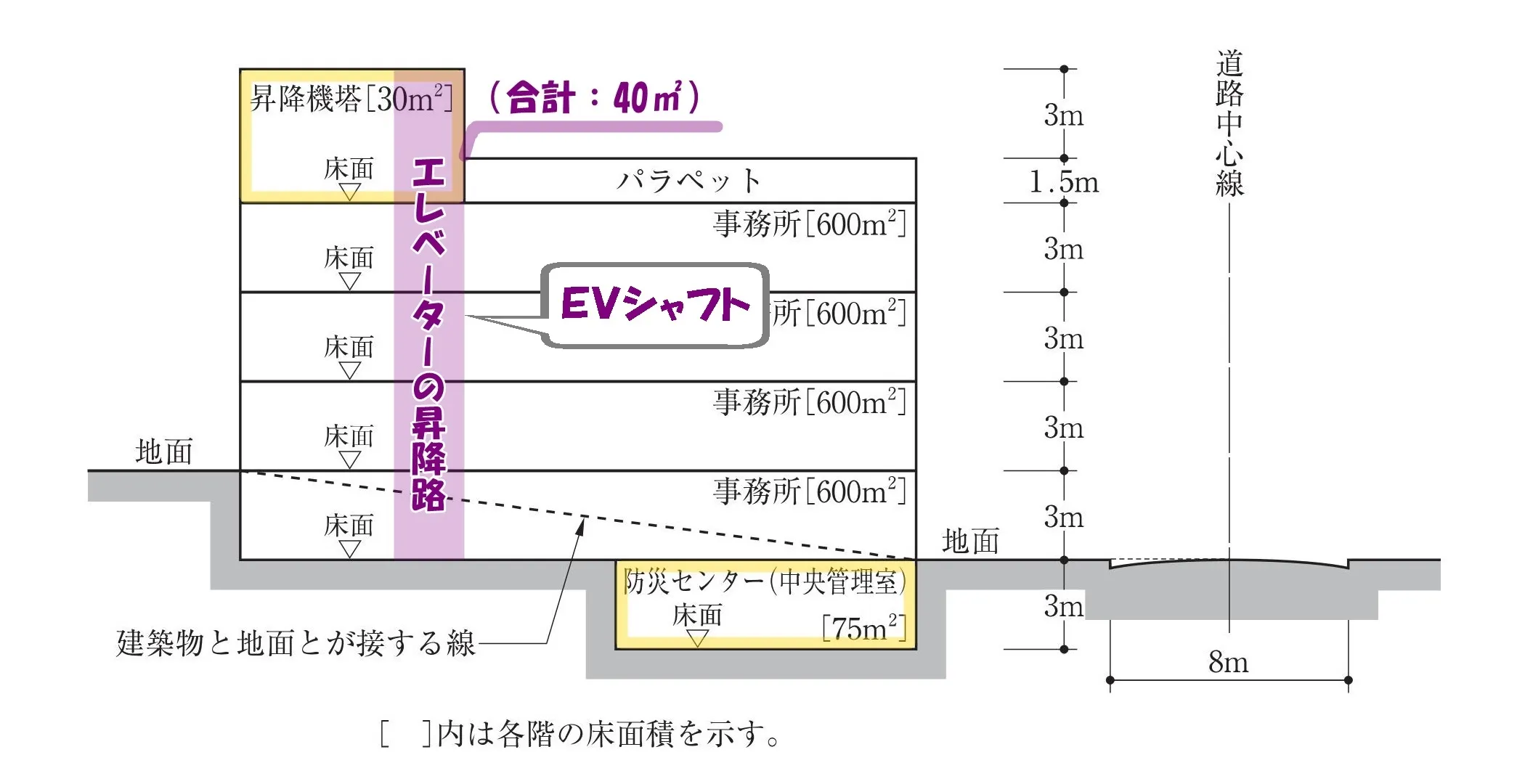

法52条3項:容積率算定におけるエレベーターの昇降路の扱い
第1項~建築物の容積率の算定の基礎となる延べ面積には、~(~昇降機の昇降路の部分~)~は、算入しないものとする。
建築基準法(一部省略)
チェックポイント
エレベーターの昇降路の各階の床面積の合計:40㎡は延べ面積には算入しない。



ここにも落とし穴が・・
延べ面積には算入しない
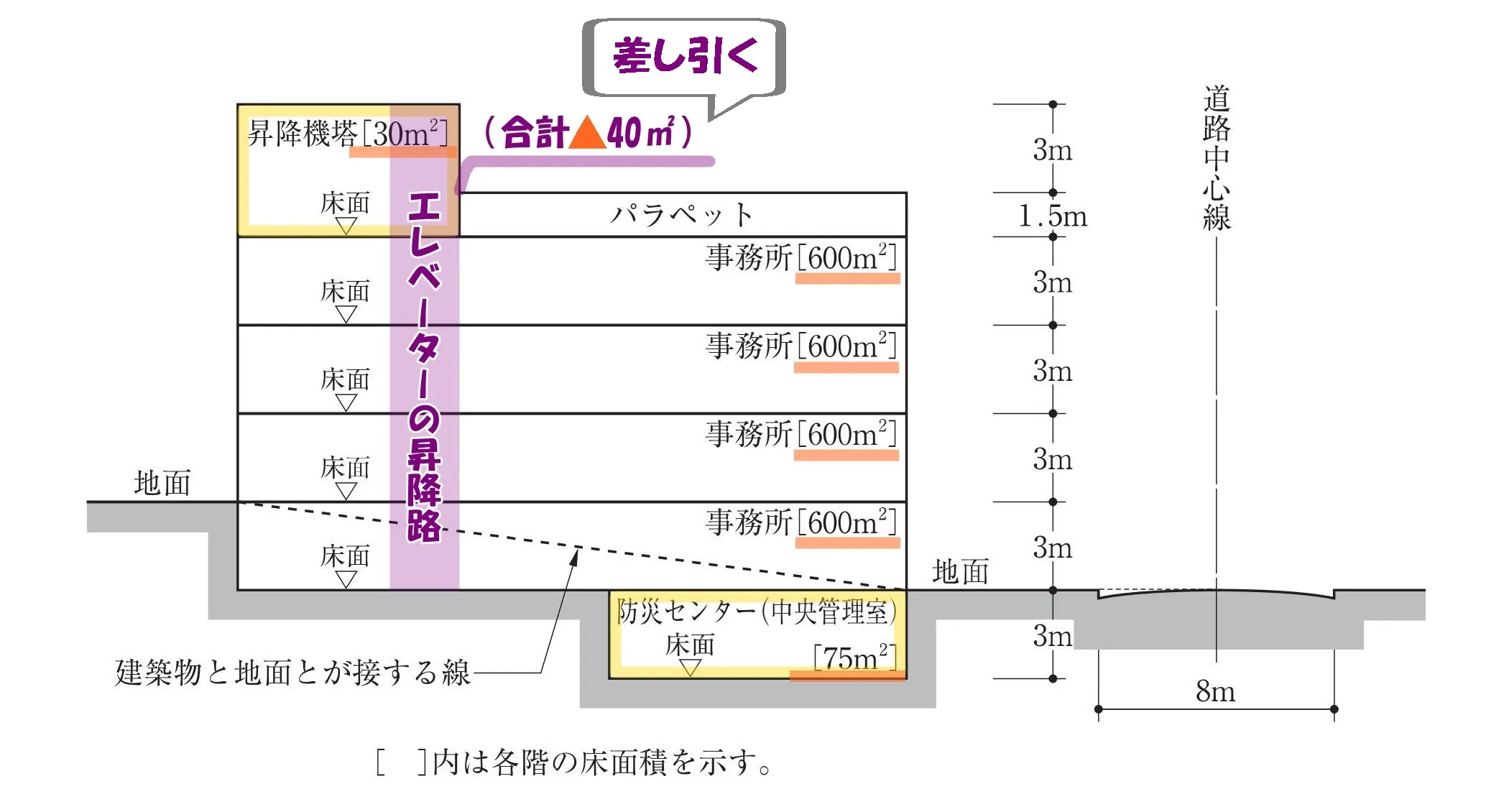

- 法52条3項
- エレベーターの昇降路は「容積率算定における延べ面積の緩和」から差し引く。
30(昇降機塔)+600×4(事務所)+75(防災センター)▲40(ELVの昇降路)=2,465㎡。



はい、誤り!アウト!
答え.1(誤り)





ひとつ検証します。
ちなみにですが、枝.1の設問にある数値「2,435㎡(誤)」の根拠について検証します。
(誤り)の検証
「2,465㎡(正しい数値)▲2,435㎡(誤りの数値)=30㎡」
注目!


昇降機塔の床面積が30㎡なので、誤りの数値は「昇降機塔の床面積を除いた数値」の引っ掛けということが分かりますよね?
設問の”正誤の数値の差”を求めることで、試験元が「何を試そうとしたか?」が読み取れましたね。



そう何度も、
引っかかってたまるか!
補足
「○○○の水平投影面積が建築面積の1/8以下の場合は算入しない」
この条文による算入しない対象とは、「高さ」と「階数」のことを指します。
「延べ面積」は上記の条文とはリンクしていないので、注意して読み取りましょう。
チェックポイント
- 【建築物の高さ】
- 法33条:避雷設備
- 令2条六号:建築物の高さ
- 令2条2項:地盤面の位置
- 【地階を除く階数】
- 令1条二号:地階
- 令2条八号:階数
- 令2条2項:地盤面の位置
- 【階数】
- 令2条八号:階数
- 令2条八号:昇降機塔の扱い
- 令2条八号:防災センターの扱い
- 【容積率の算定の基礎となる延べ面積】
- 令2条八号:階数(×延べ面積)
- 令2条3項:容積率算定における延べ面積の緩和
- 法52条3項:容積率算定におけるエレベーターの昇降路の扱い


この動画を YouTube で視聴
居室の採光
難易度:★★★☆☆



この動画を YouTube で視聴
攻略ポイント
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
インデックス


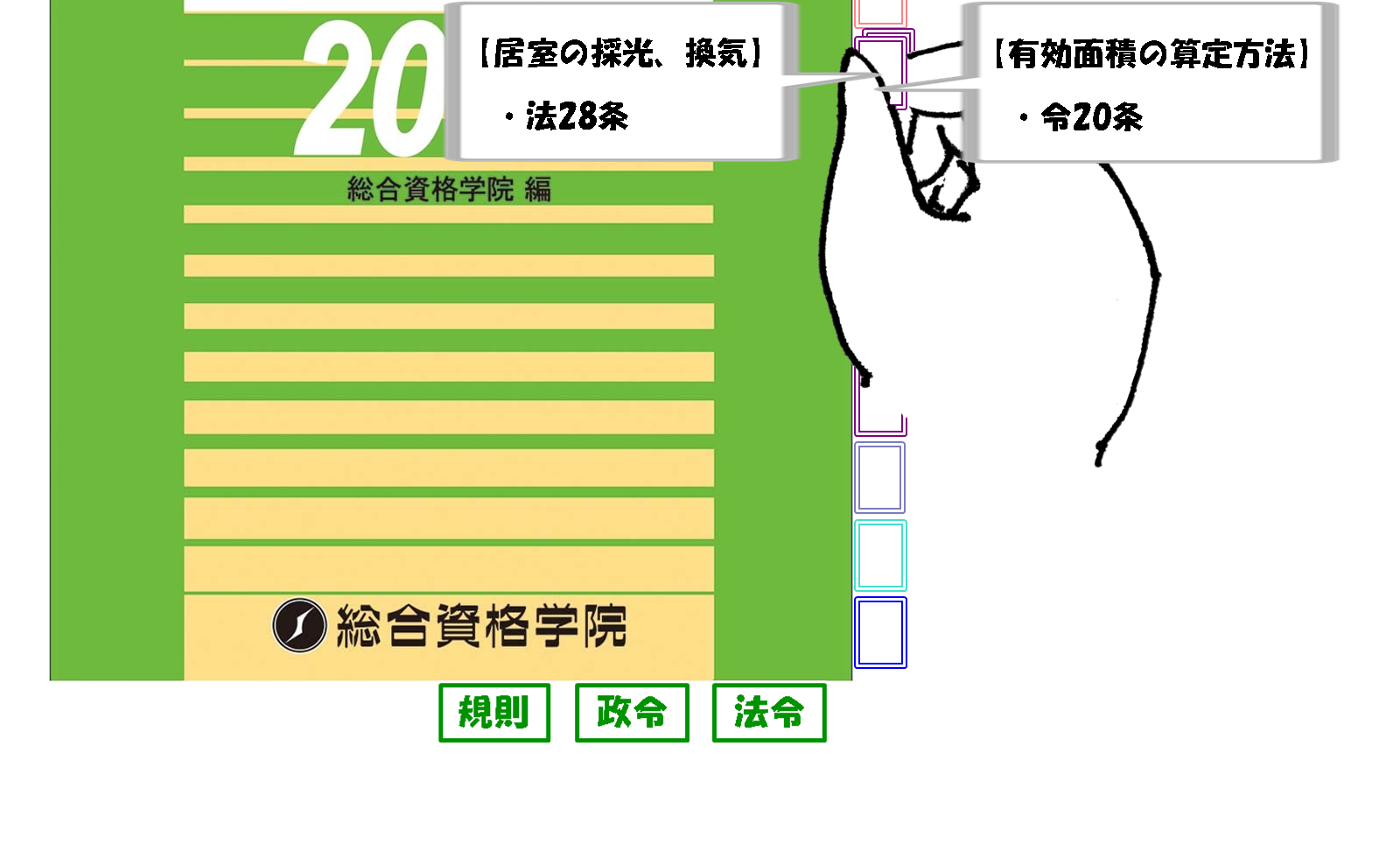
- 法28条【居室の採光・換気】
- 令20条【有効面積の算定方法】
- 2項:採光補正係数
- 一号:採光関係比率(Ⅾ/H)×6 -1.4(補正係数)
- 2項:採光補正係数



さあ、始めますよ。
採光上有効な面積


法28条【居室の採光・換気】
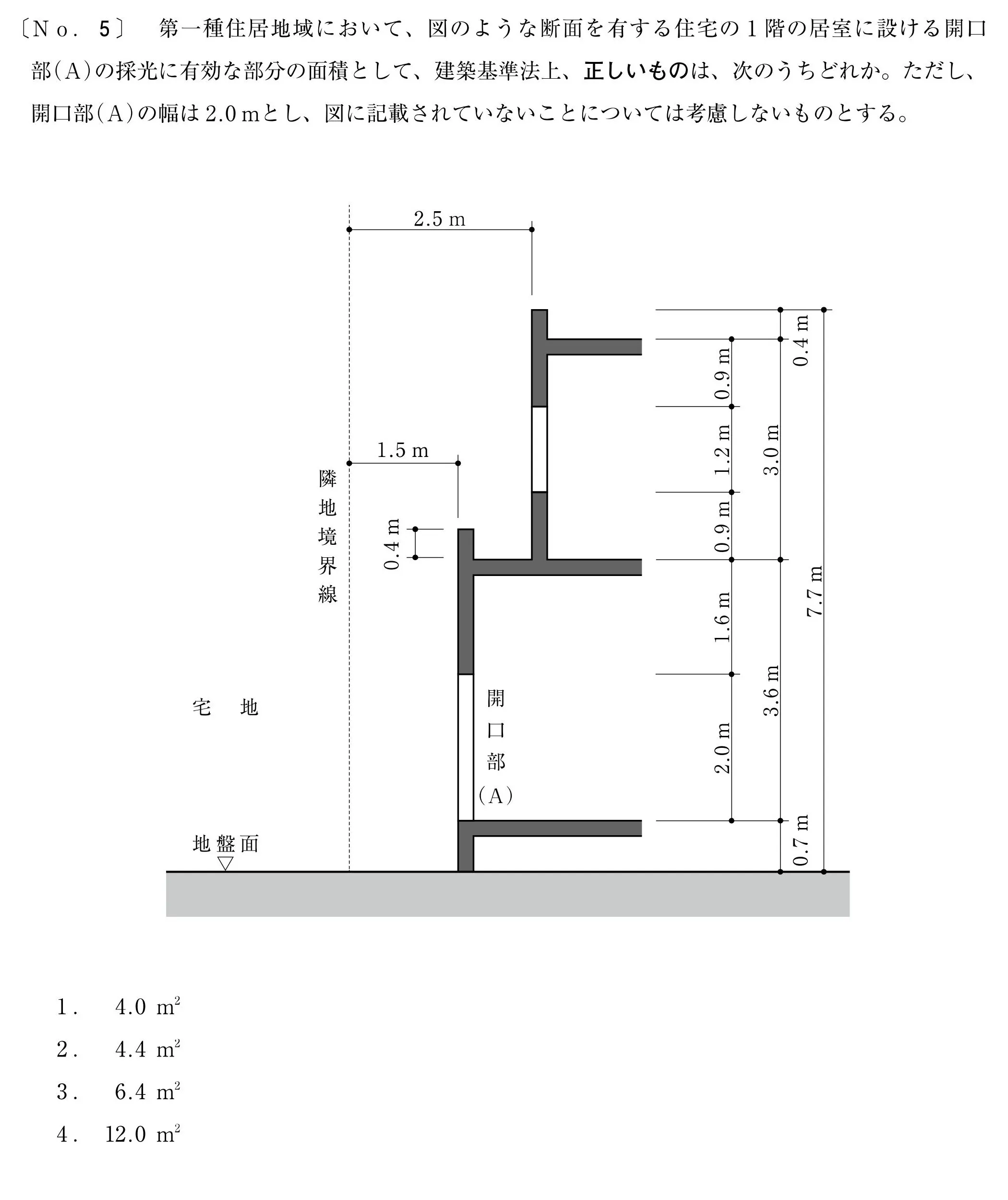
1階の居室に設ける「開口部(A)」の採光上有効な面積を求める。
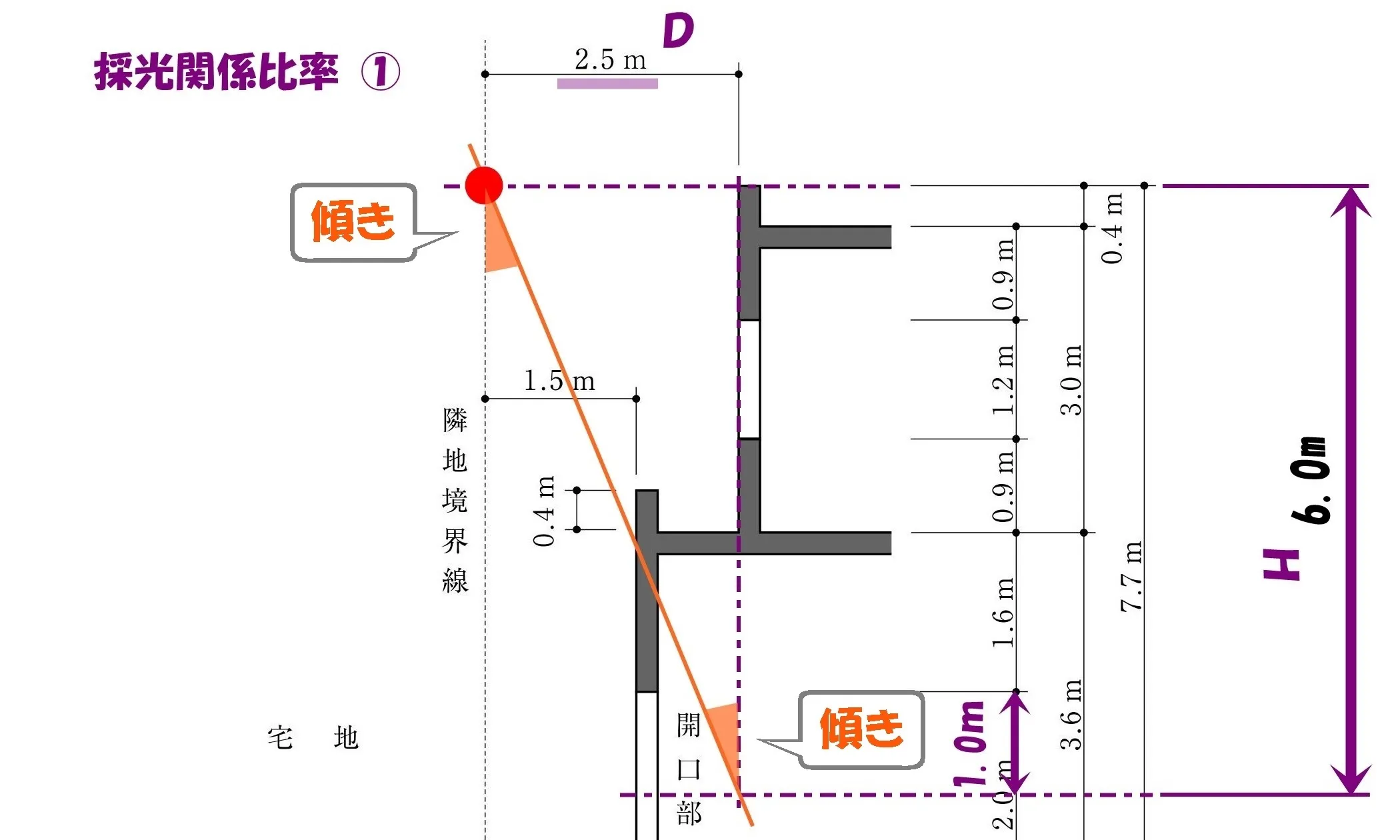
1.DとHの寸法を書き込む
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
先端からの距離を求める
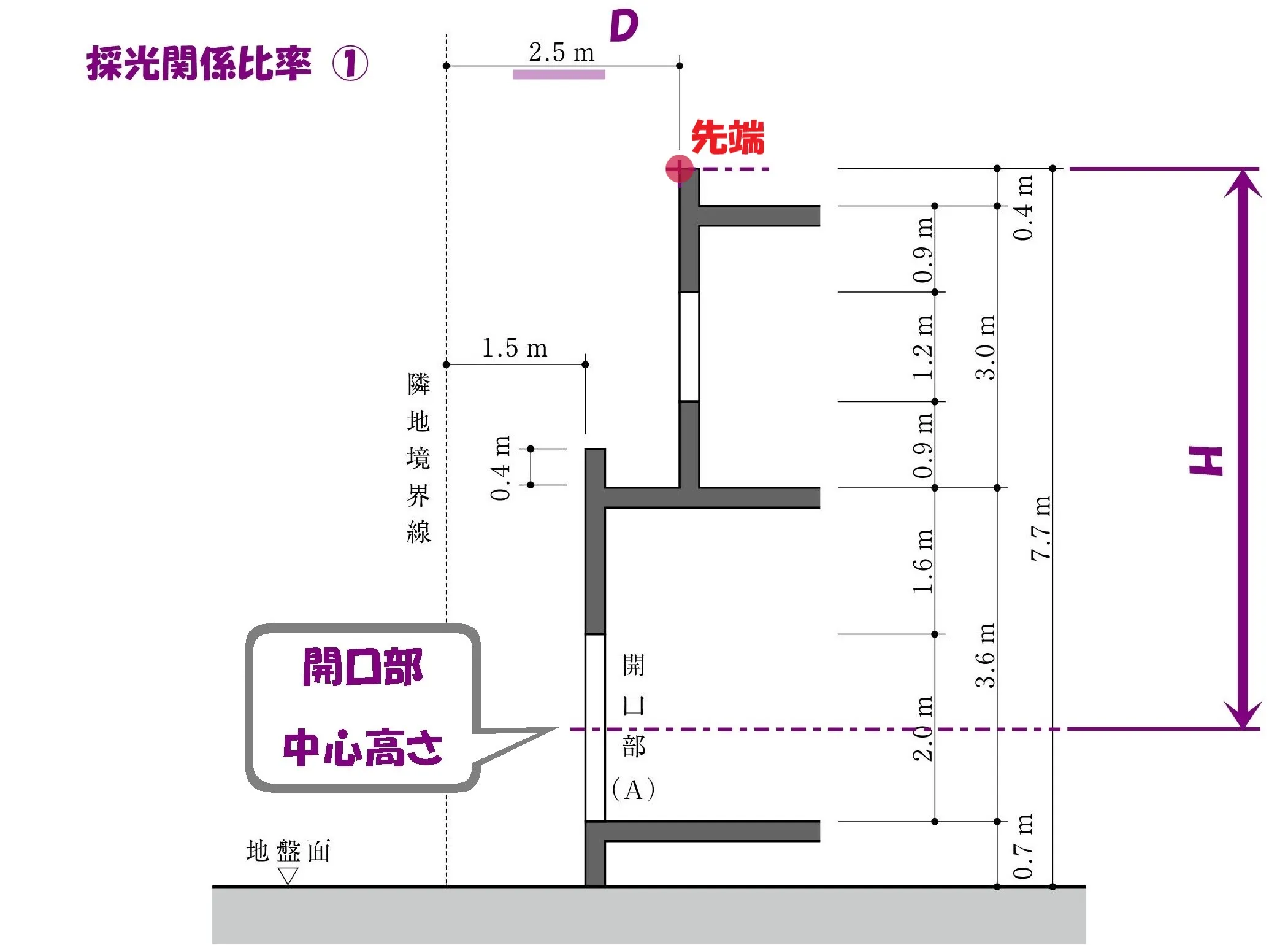

- パラペット先端から隣地境界線までの水平距離:2.5m
- パラペット先端から開口部中心までの垂直距離:0.4+3.0+1.6+1.0=6.0m
寸法をメモする
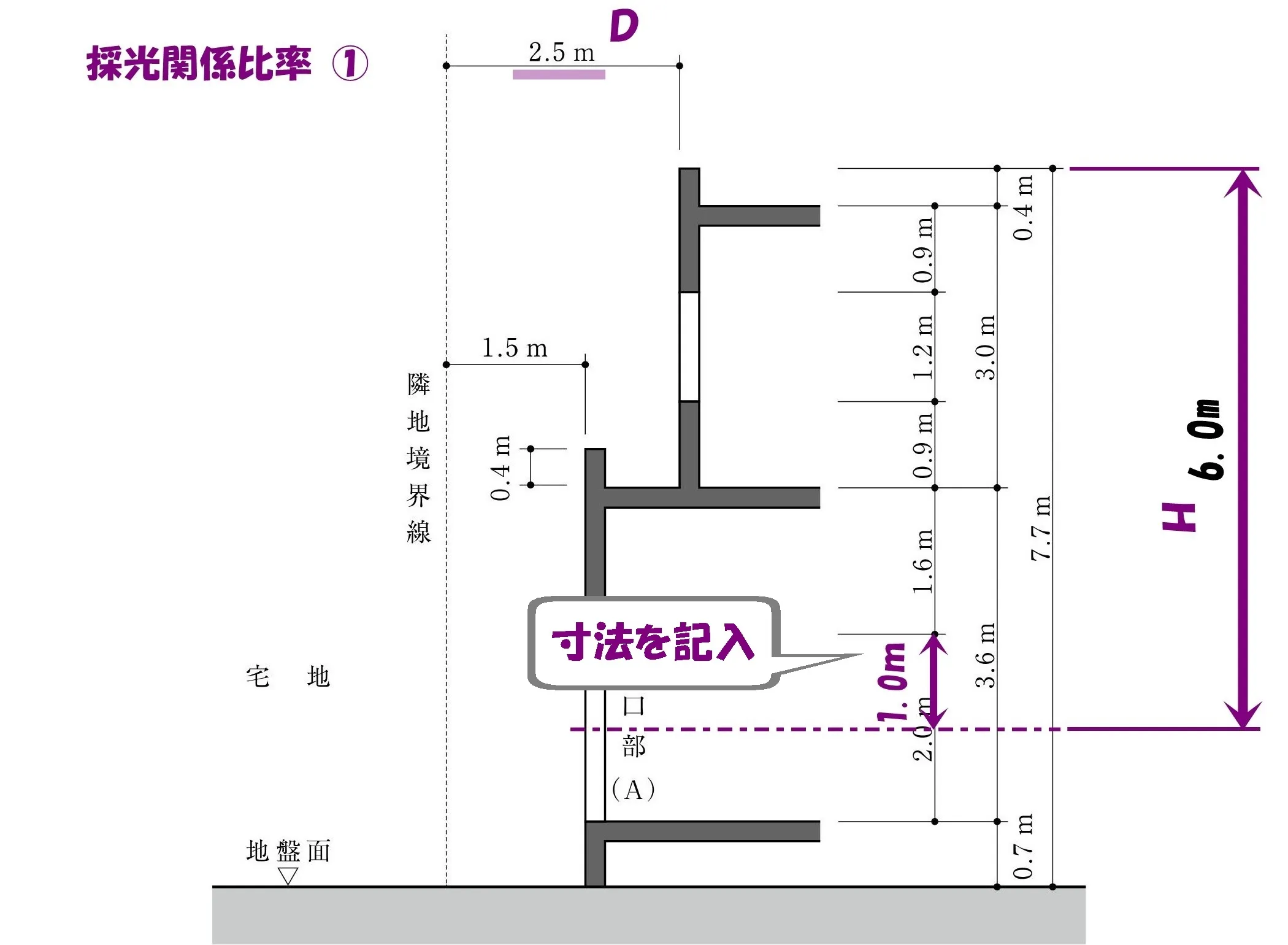

開口部中心までの垂直距離(6.0m)を問題用紙の図にメモしましょう。
水平距離(D)と垂直距離(H)は、採光関係比率(D/H)を求めるのに必要な数値となります。



DとHはどちらも
パラペット先端から図る。
2.採光関係比率:D/Hを求める
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
先端からの交点をとる
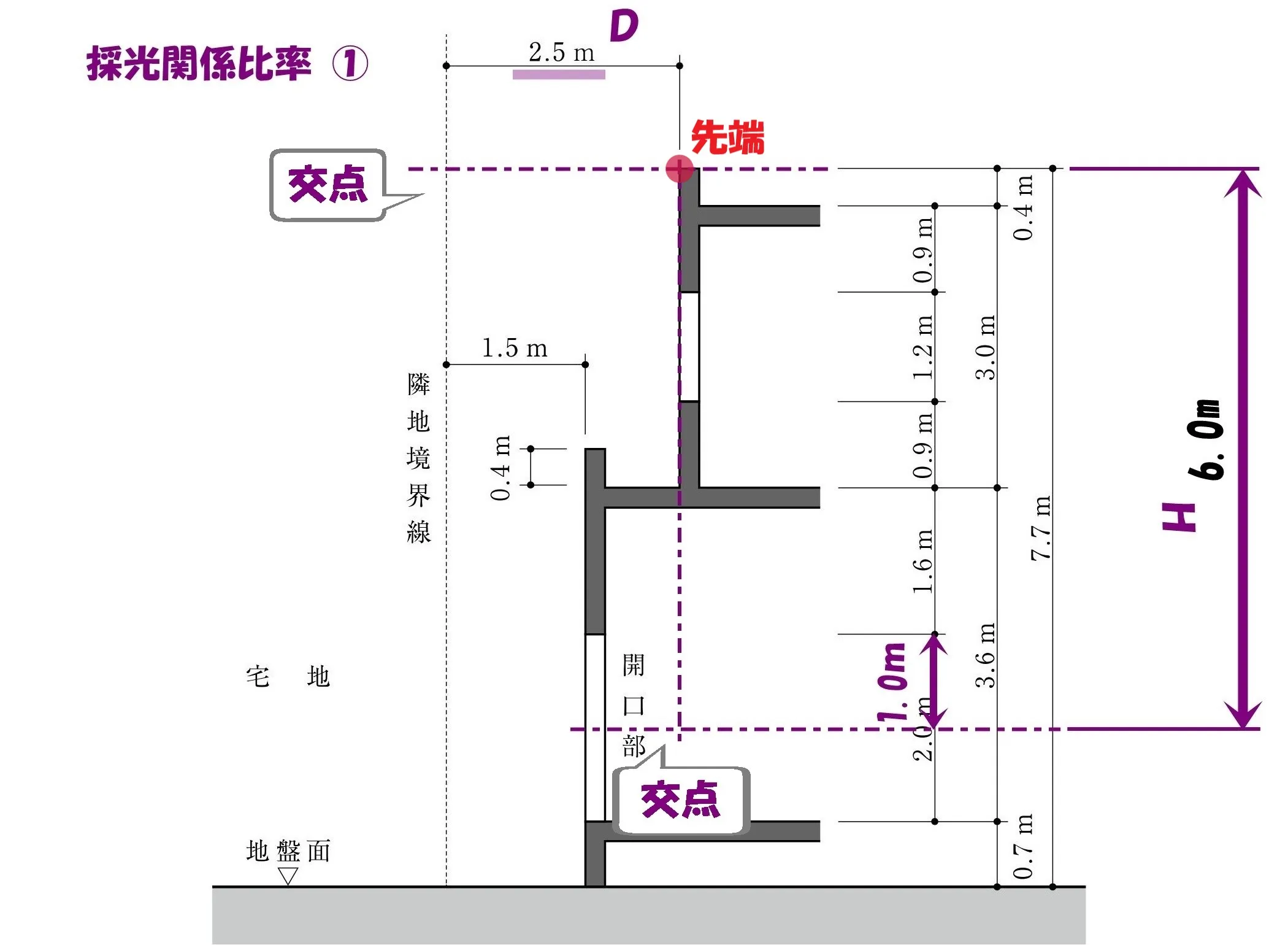

2つの交点
- パラペット先端の水平ラインと、隣地境界線との交点
- パラペット先端の垂直ラインと、開口部中心の水平ラインとの交点
太陽マークからの交点
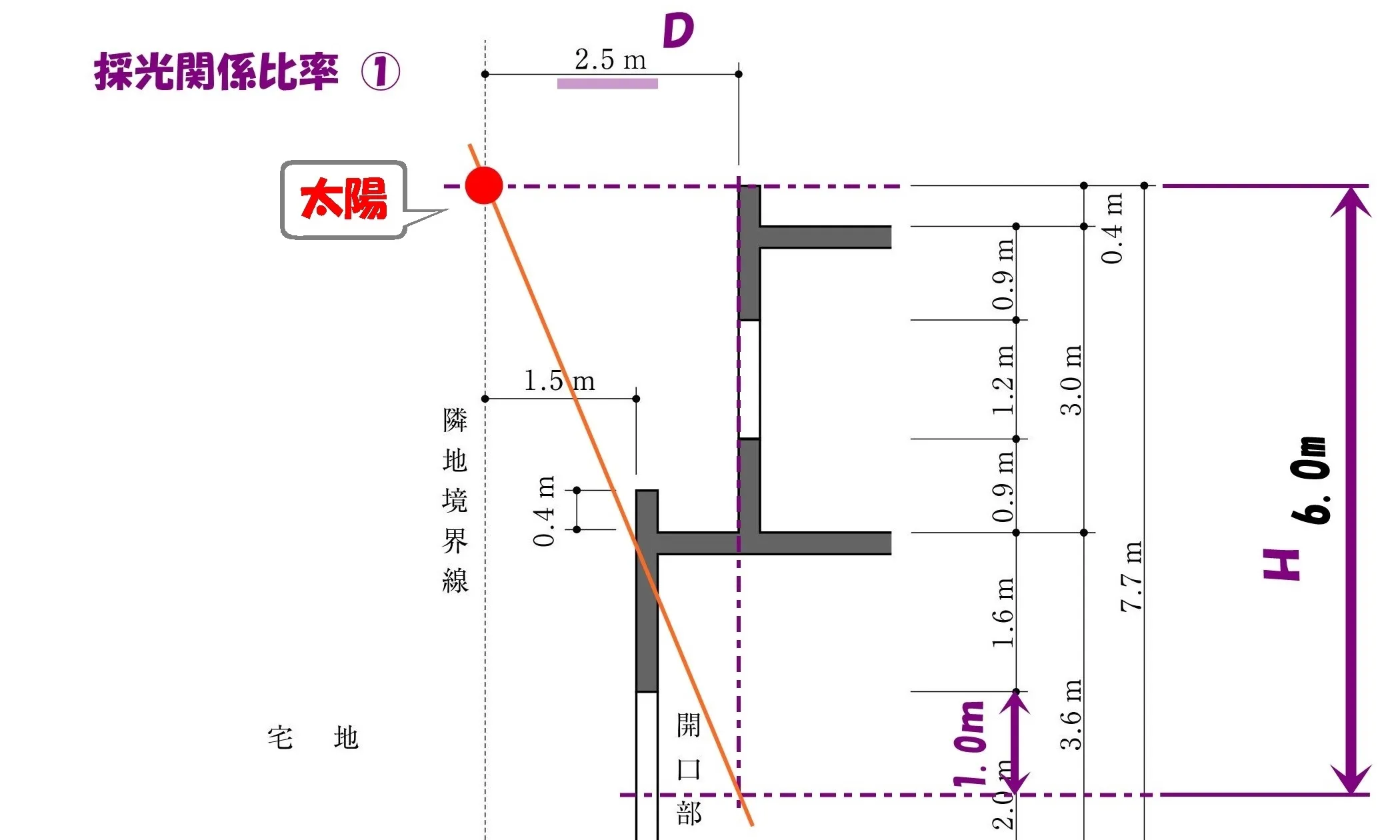

斜線で結ぶ
- パラペット先端の水平ラインと、隣地境界線との交点に「太陽マーク」を描く。
- パラペット先端の垂直ラインと、開口部中心の水平ラインとの交点に向けて斜線で結ぶ。
D/Hとは?


令20条2項一号:採光関係比率(Ⅾ/H)
$$採光関係比率①=\frac{ D }{ H }$$



D/H=「傾き」
開口部の直上にある建築物の各部分~から隣地境界線~までの水平距離(D)~を、その部分から開口部の中心までの垂直距離(H)で除した数値のうちの最も小さい数値(以下「採光関係比率」という。)
建築基準法(一部省略)
用紙を回転





回転!
D/Hの傾き
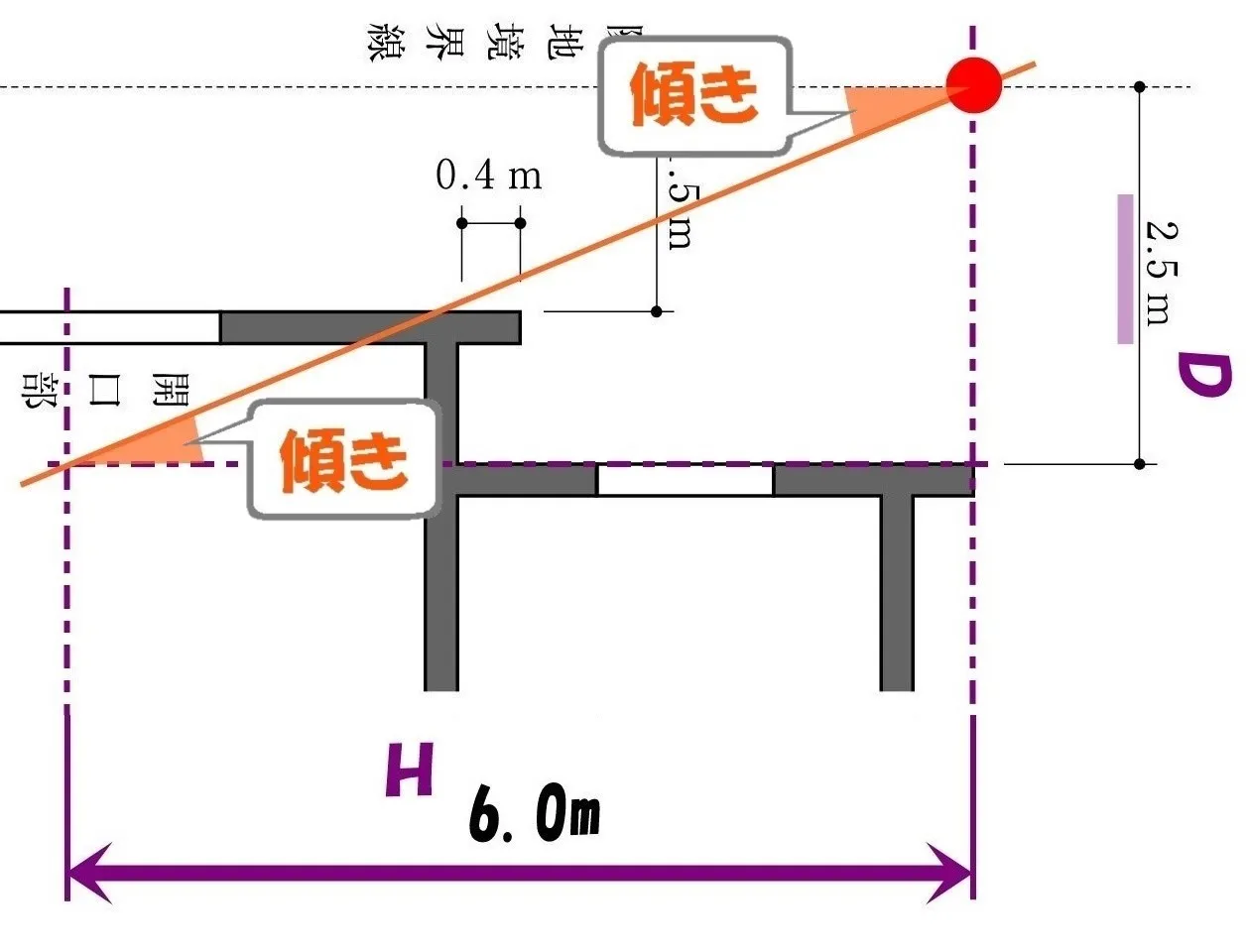

令20条2項一号:採光関係比率(Ⅾ/H)
採光関係比率(D/H)とは、水平距離(D)÷垂直距離(H)のこと。
つまり、太陽マークから、開口部中心位置までの「傾き」を表しているのが分かりますよね?
$$採光関係比率①=\frac{ D }{ H }=\frac{ 2.5 }{ 6.0 }(斜線の傾き)$$



D/Hは採光斜線の傾きです。
1.DとHの寸法を書き込む
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める


あと1セットあります。
先端からの距離を求める
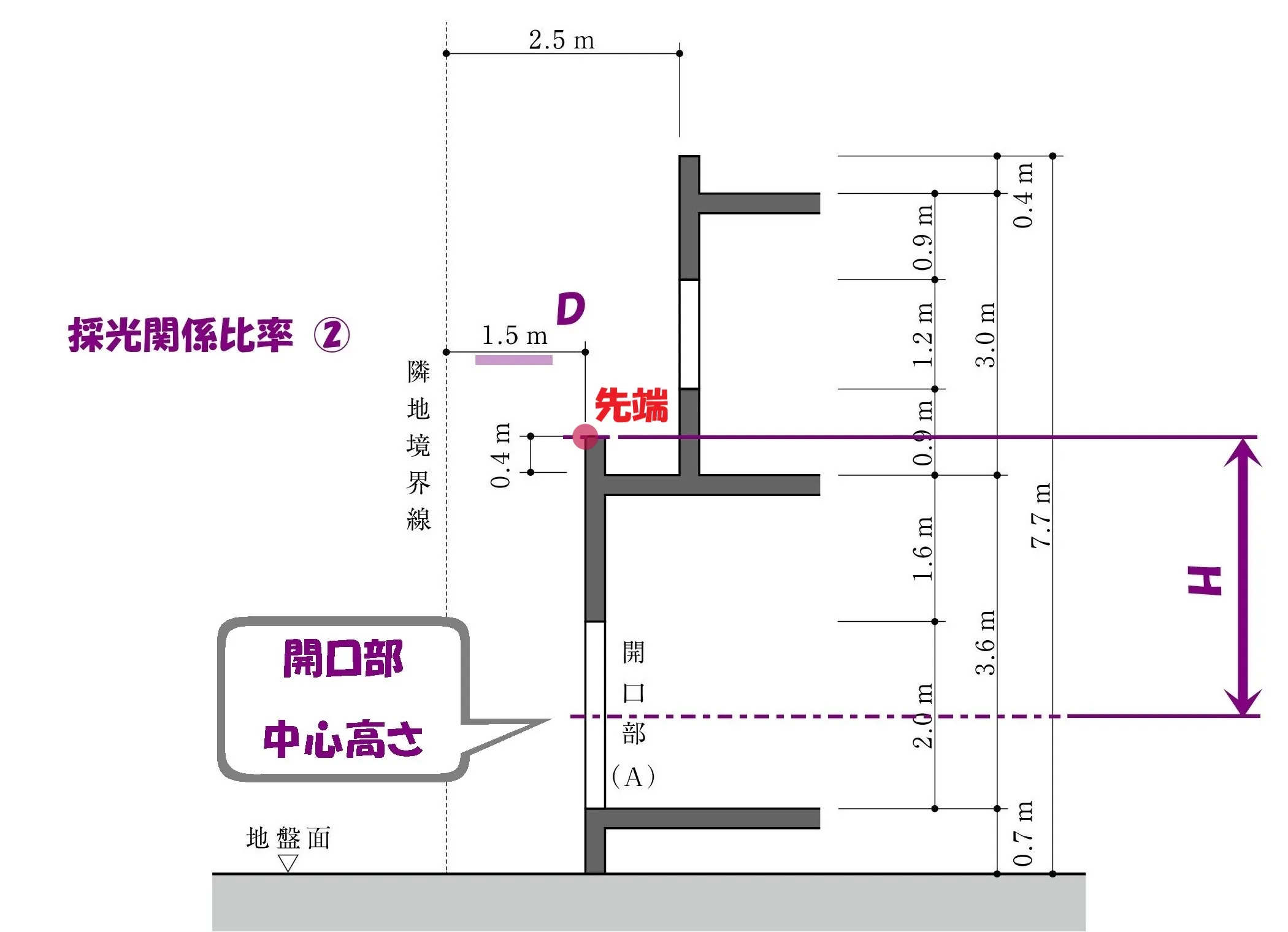

- パラペット先端から隣地境界線までの水平距離:1.5m
- パラペット先端から開口部中心までの垂直距離:0.4+1.6+1.0=3.0m
寸法をメモする
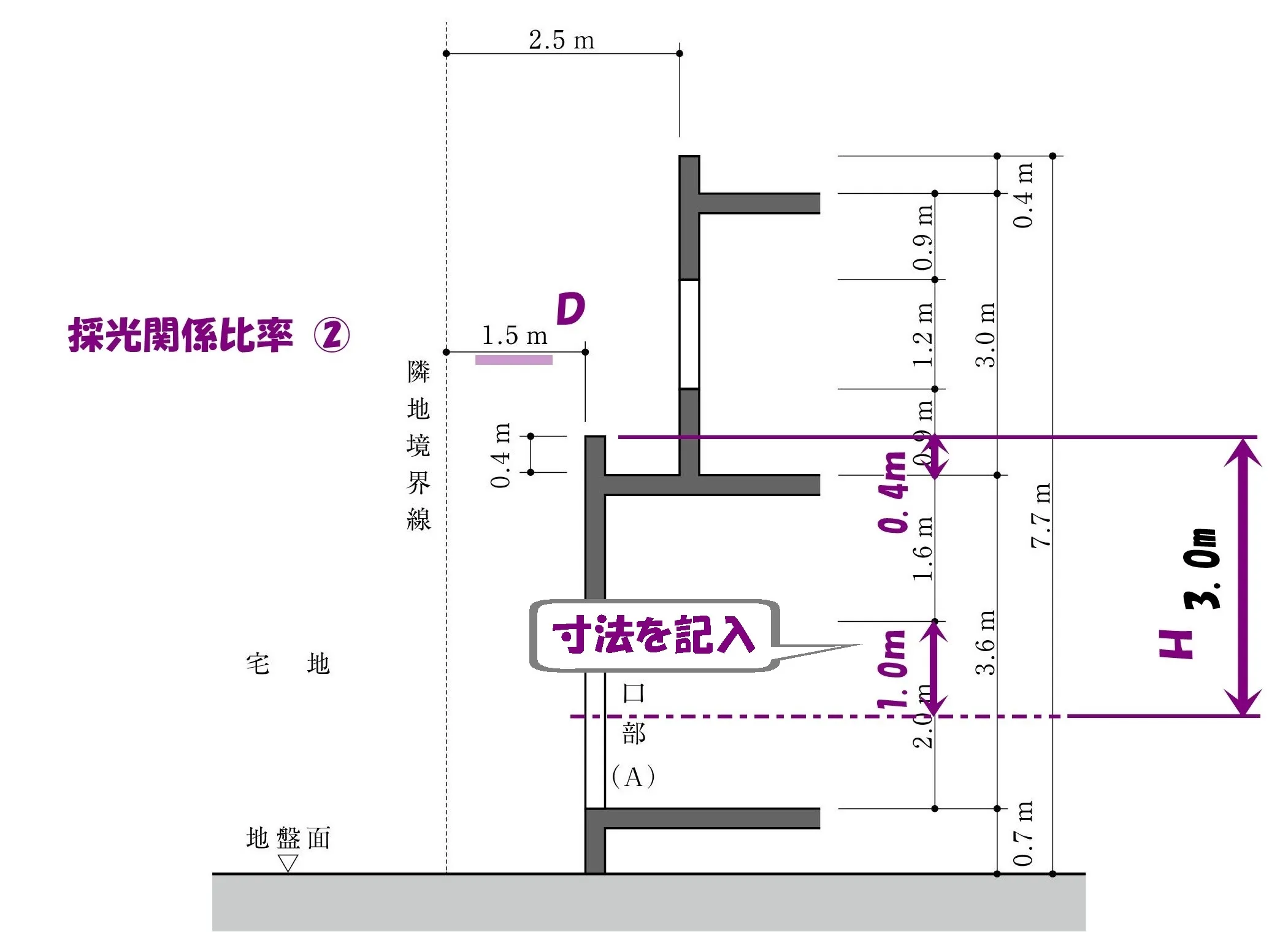

開口部中心までの垂直距離(3.0m)を問題用紙の図にメモしましょう。
水平距離(D)と垂直距離(H)は、採光関係比率(D/H)を求めるのに必要な数値です。



DとHはどちらも
パラペット先端から図る。
2.採光関係比率:D/Hを求める
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
先端からの交点をとる
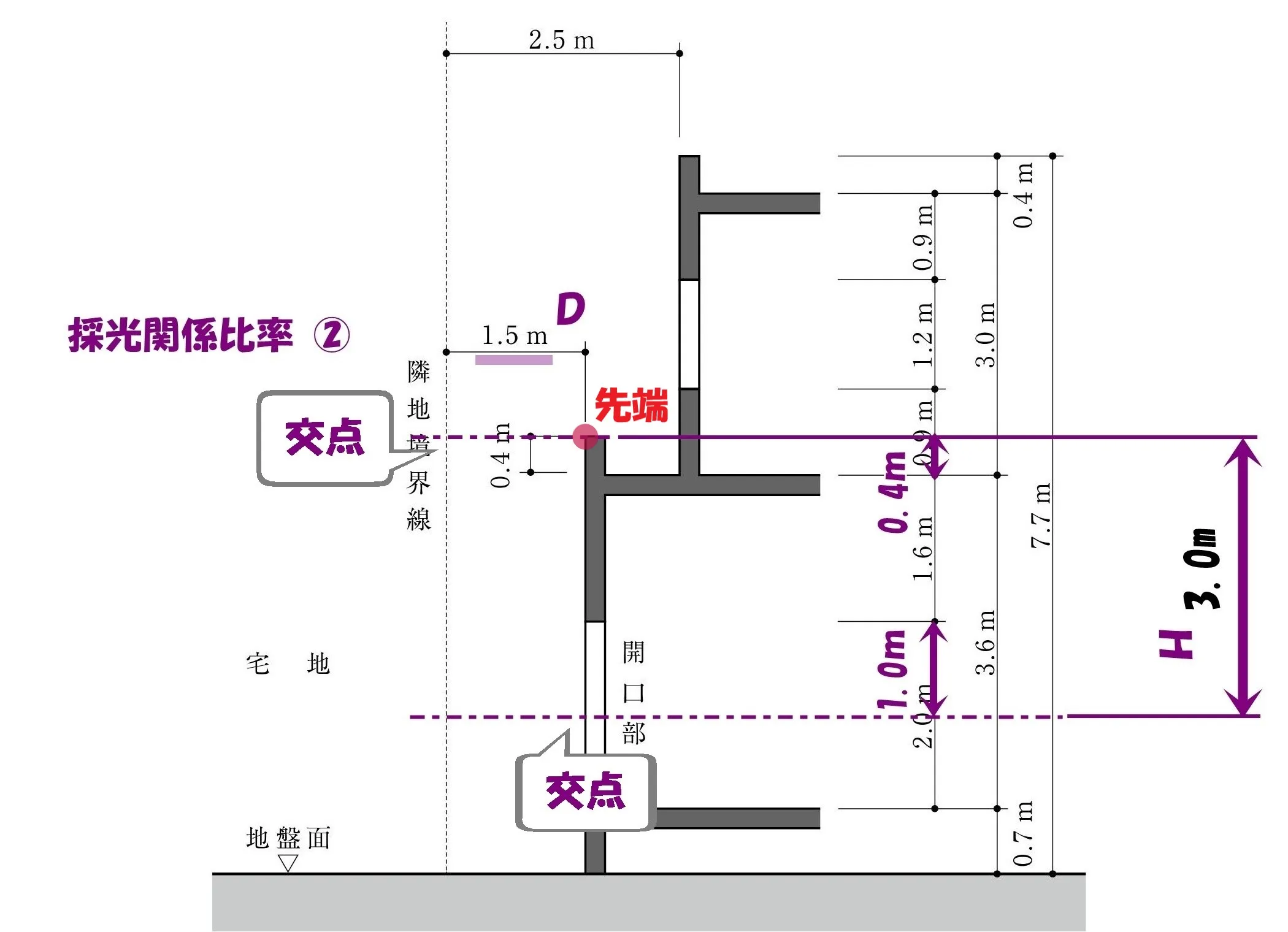

2つの交点
- パラペット先端の水平ラインと、隣地境界線との交点
- パラペット先端の垂直ラインと、開口部中心の水平ラインとの交点
太陽マークからの交点
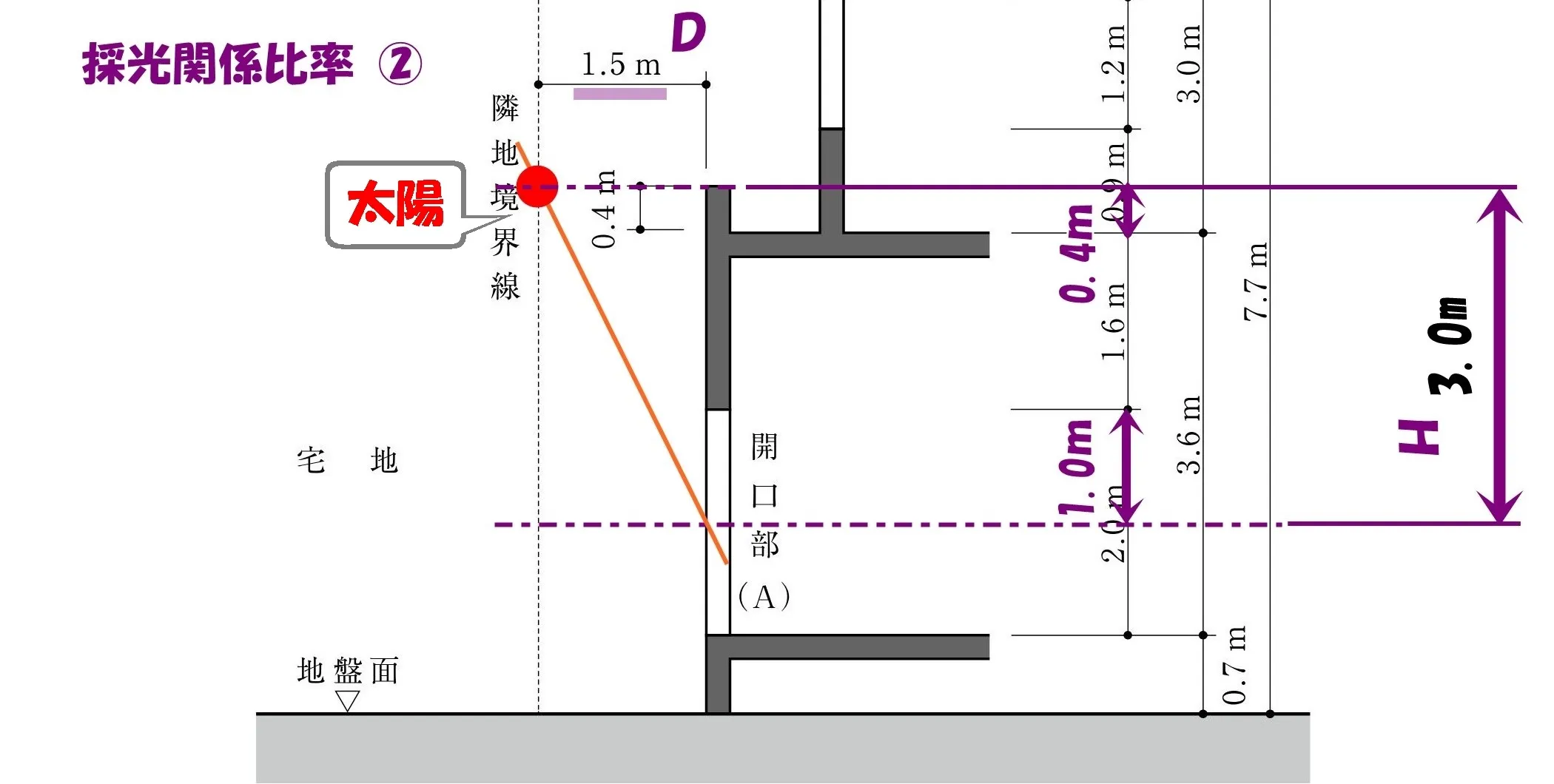

斜線で結ぶ
- パラペット先端の水平ラインと、隣地境界線との交点に「太陽マーク」を描く。
- パラペット先端の垂直ラインと、開口部中心の水平ラインとの交点に向けて斜線で結ぶ。
D/Hとは?
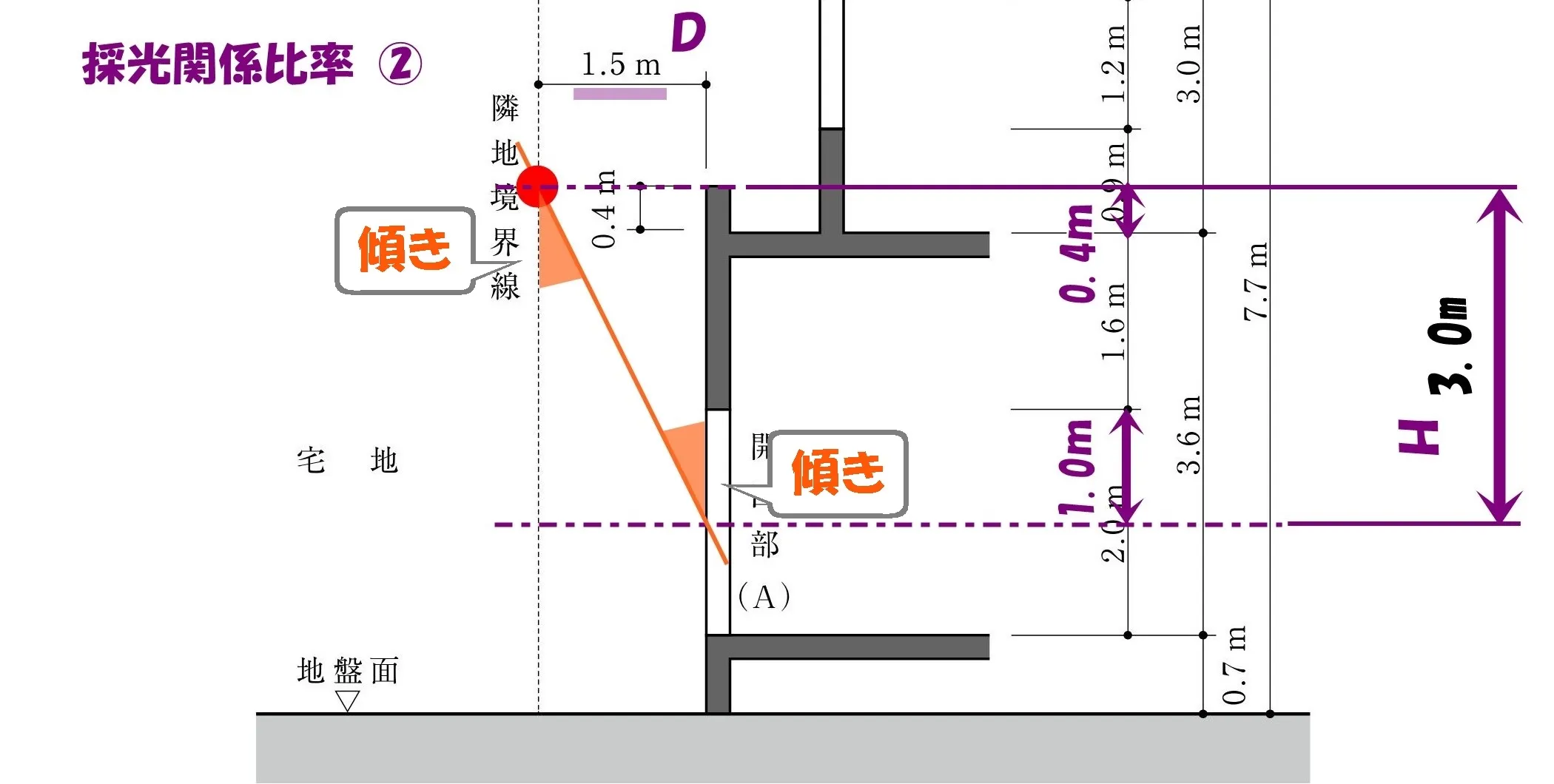

令20条2項一号:採光関係比率(Ⅾ/H)
$$採光関係比率②=\frac{ D }{ H }$$



D/H=「傾き」
開口部の直上にある建築物の各部分~から隣地境界線~までの水平距離(D)~を、その部分から開口部の中心までの垂直距離(H)で除した数値のうちの最も小さい数値(以下「採光関係比率」という。)
建築基準法(一部省略)
用紙を回転





回転!
D/Hの傾き
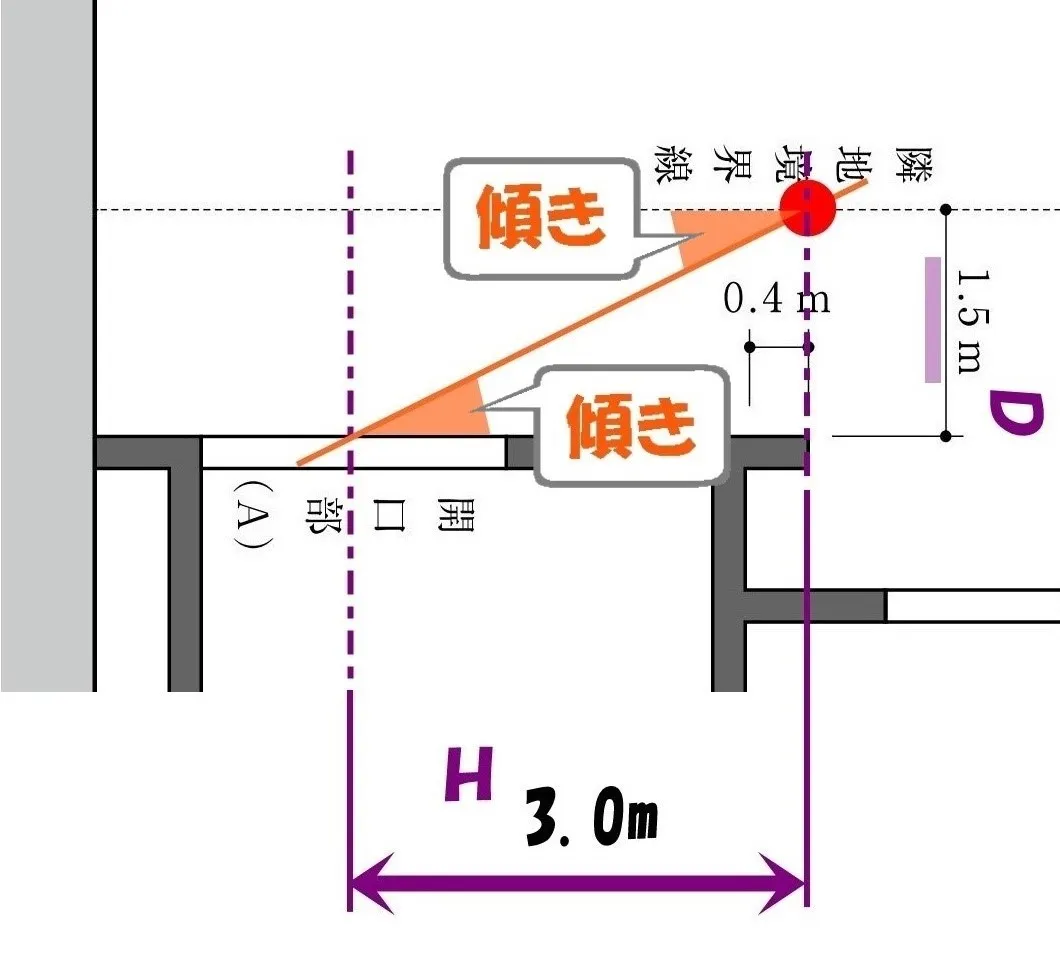

令20条2項一号:採光関係比率(Ⅾ/H)
採光関係比率(D/H)とは、水平距離(D)÷垂直距離(H)のこと。
つまり、太陽マークから、開口部中心位置までの「傾き」を「D/H」で求めます。



D/Hは採光斜線の傾き。
$$採光関係比率②=\frac{ D }{ H }=\frac{ 1.5 }{ 3.0 }(斜線の傾き)$$
$$採光関係比率①=\frac{ 2.5 }{ 6.0 },採光関係比率②=\frac{ 1.5 }{ 3.0 }=\frac{ 3.0 }{ 6.0 }$$
$$\frac{ 2.5 }{ 6.0 }<\frac{ 3.0 }{ 6.0 }より、採光関係比率は”最も小さい値”となる\frac{ 2.5 }{ 6.0 }を採用する。$$



このポーズ、しんどい。
開口部の直上にある建築物の各部分~から隣地境界線~までの水平距離(D)~を、その部分から開口部の中心までの垂直距離(H)で除した数値のうちの最も小さい数値(以下「採光関係比率」という。)
建築基準法(一部省略)
3.採光補正係数:D/H×6-1.4を求める
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
第一種住居地域


令20条2項一号:採光関係比率(Ⅾ/H)×6 -1.4(補正係数)
第一種住居地域
$$採光補正係数=\frac{ D }{ H }*6-1.4$$
$$=\frac{ 2.5 }{ \underline{6.0} }*\underline{6}-1.4=2.5-1.4=1.1(採光補正係数)$$



ここの条文は長い・・
そしてとても読みづらい。
4.開口部(A)の採光に有効な面積を求める
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
開口部Aの幅





ここに記載してある。
- 問題文より、開口部の幅=2.0m
- 断面図より、開口部の高さ=2.0m



何か足りない?
そう、開口部の幅だよね。
×採光補正係数
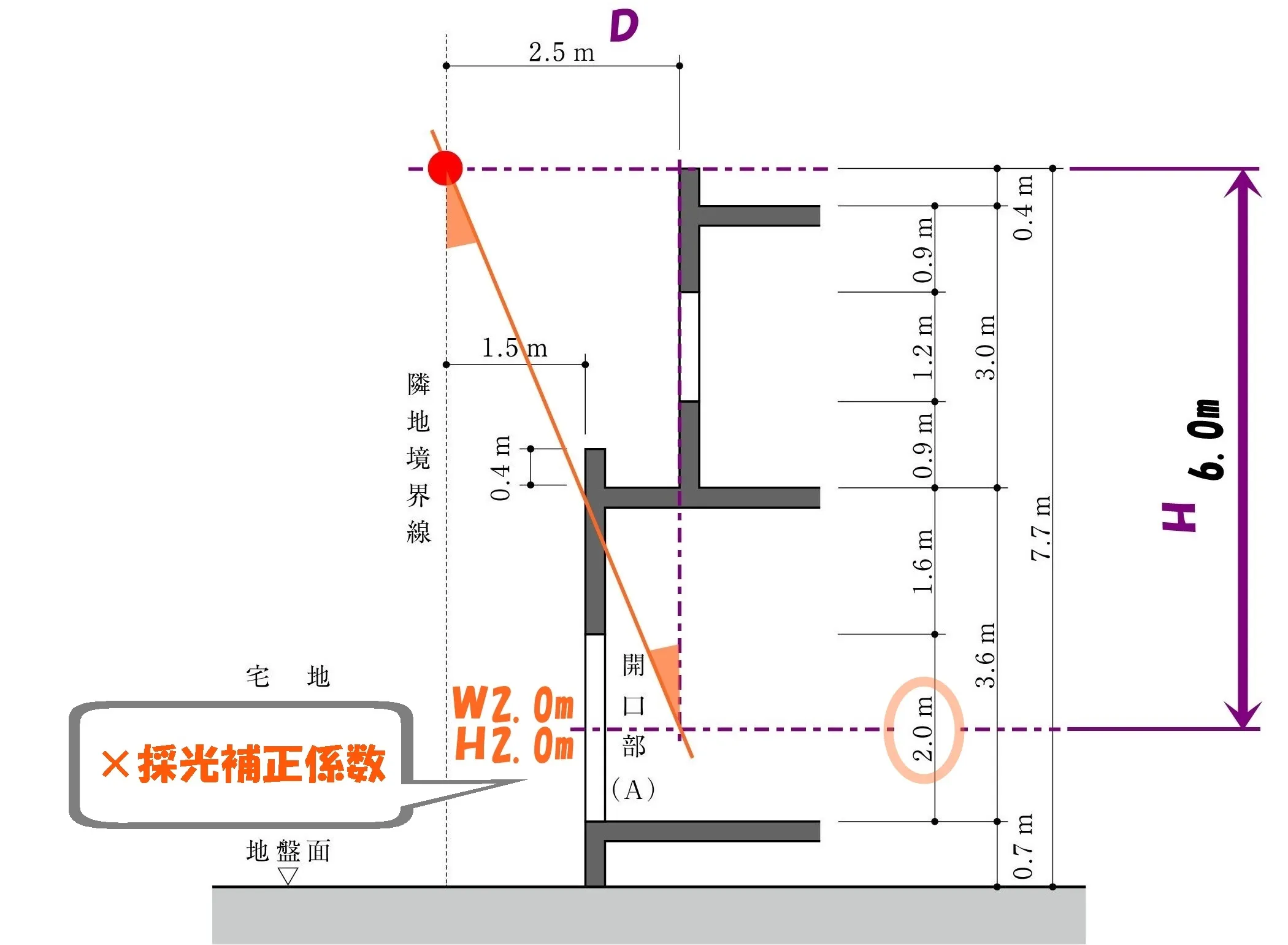

令20条【有効面積の算定方法】
開口部(A)の採光に有効な開口面積は「開口部の面積×採光補正係数」で求める。
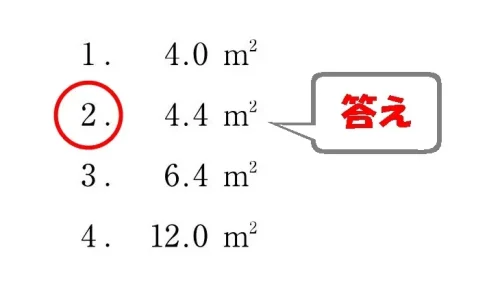
$$2.0m(幅)*2.0m(高さ)*1.1(採光補正係数)=4.4㎡(採光上有効な開口面積)$$



採光を撃破!
答え.2

攻略ポイント
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める
令和5年4月1日施行
住宅の居室に必要な採光上有効な開口面積は、原則として床面積の1/7以上とする。
ただし、「床面において50ルクス以上の照度を確保できる照明設備を設置すること」を条件に、有効な採光方法を確保する措置がなされている場合は、その居室の床面積の1/10以上まで緩和する。


この動画を YouTube で視聴
階段の寸法
難易度:★★★☆☆



この動画を YouTube で視聴
攻略ポイント
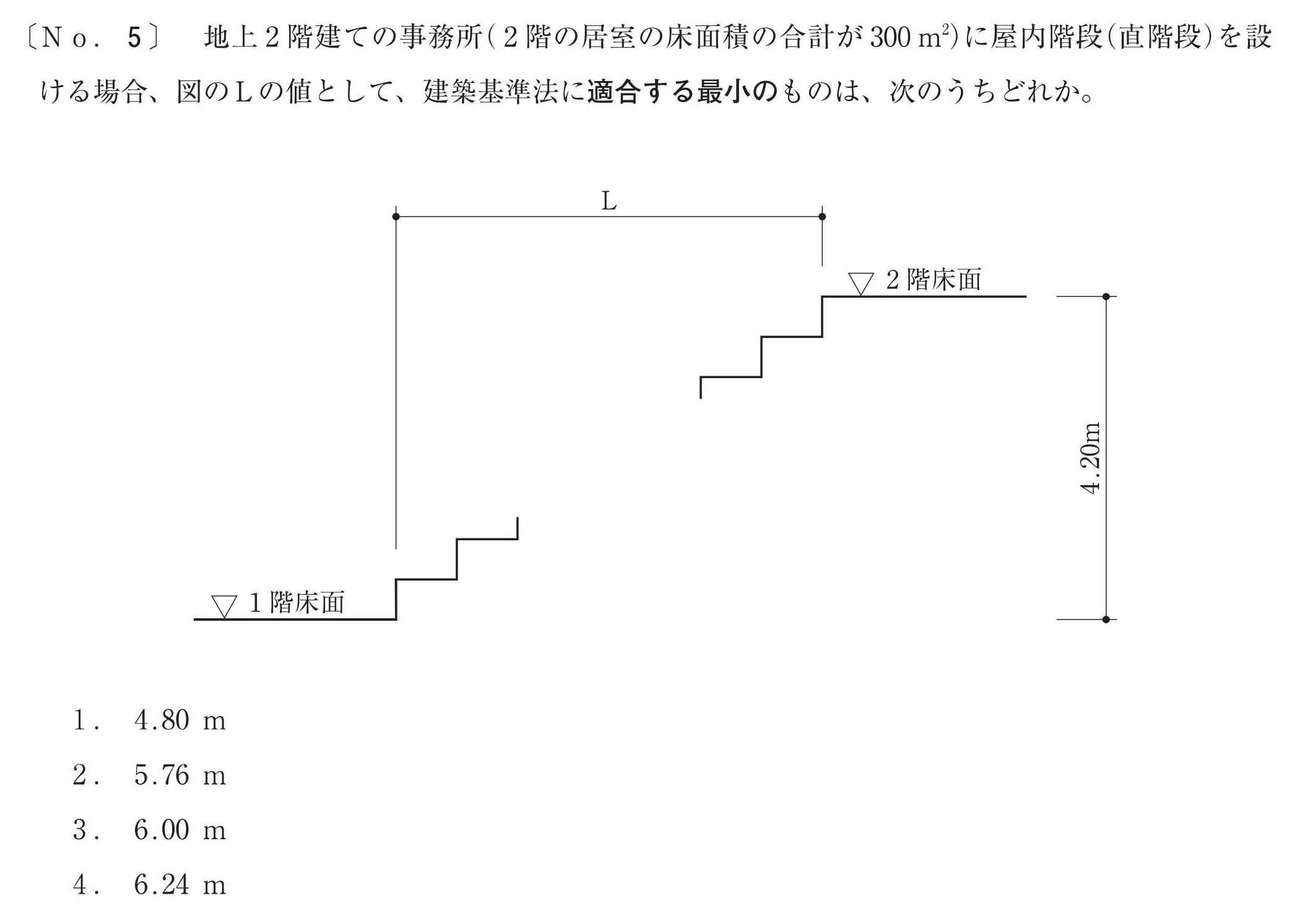
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める
インデックス

- 令23条【階段の蹴上、踏面の寸法】
- 表(3)
- 令24条【踊り場の位置、及び踏幅】
- 1項:踊り場の位置
- 2項:踊り場の踏幅



階段に立ち向かう!
階段の長さLを求める


令23条【階段の蹴上、踏面の寸法】
階段の断面図から情報を読み取り、階段の長さ「L」の値を求める。
1.階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める
令23条(表)
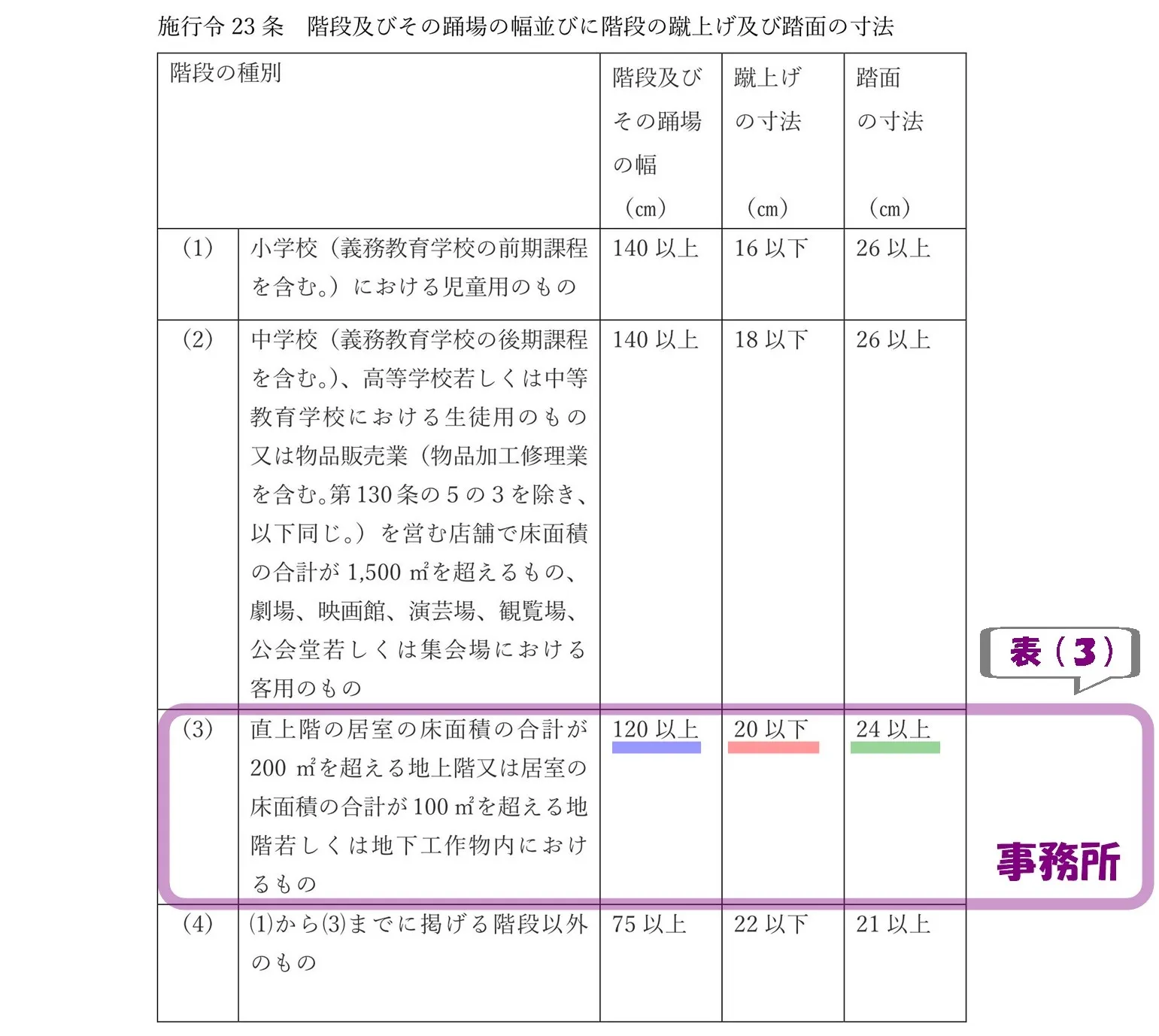

階段と踊り場
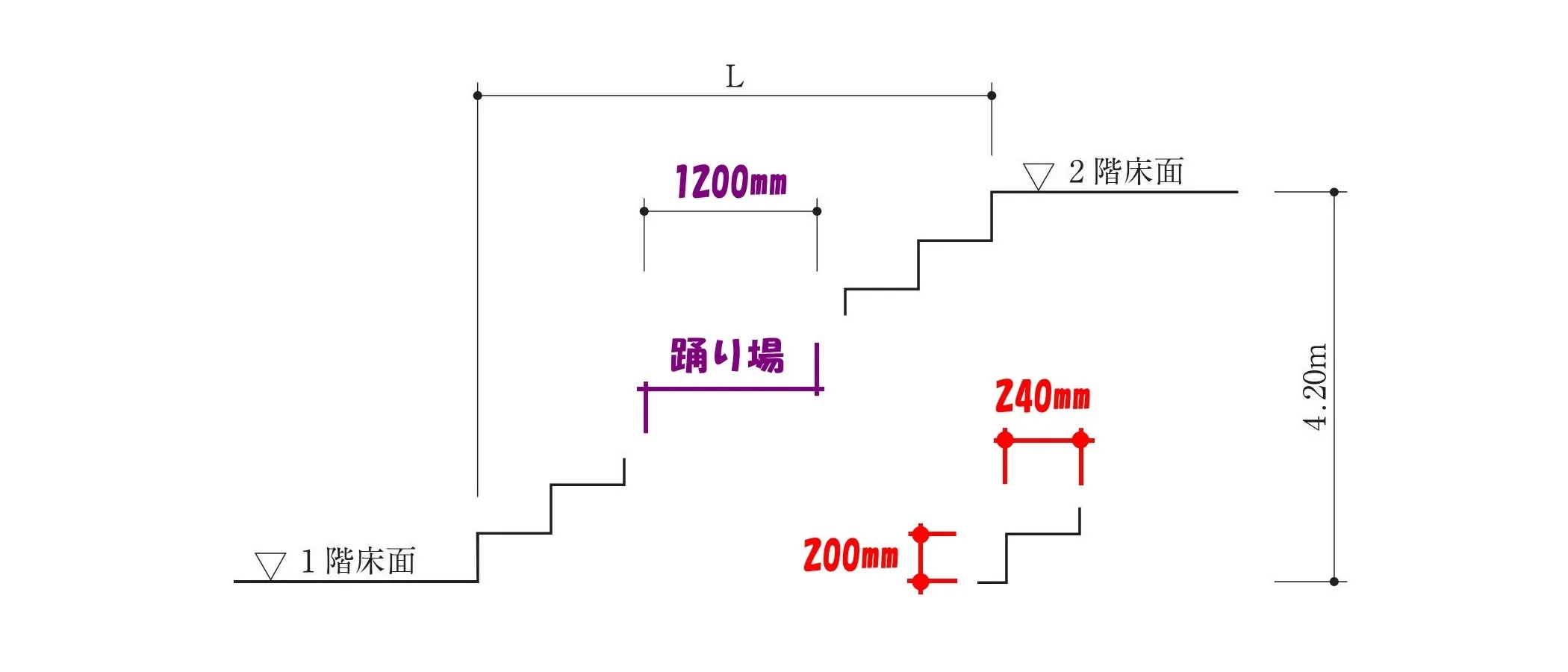

- 令23条 表(3)階段の寸法
- 蹴上げ寸法:20cm以下、踏み面寸法:24cm以上とする。
- 令24条1項:踊り場の位置
- 令23条1項の表(3)にあっては、4m以内ごとに踊り場を設けなければならない。
- 令24条2項:踊り場の踏幅
- 前項の規定によって設ける直階段の踊り場は、1.2m以上としなければならない。



寸法は分かるけど、
単位にバラつきがあるね。
- 階段の寸法:蹴上げ200mm、踏み面240mm
- 踊り場の寸法:奥ゆき1200mm
単位[cm]と[m]は、ごちゃ混ぜにしないように[mm]に統一しましょう。



蹴上げ、踏み面、踊り場、
単位はすべてmmに統一!
チェックポイント
単位は[m]と[cm]を混同させないように、[mm]で統一しておく。
2.階段の「Lの寸法」と「段数」の関係を把握する
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める
階段の寸法と段数
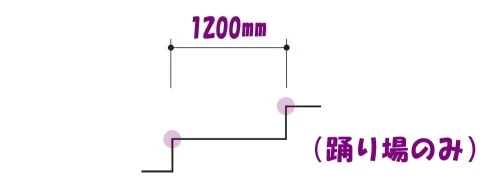

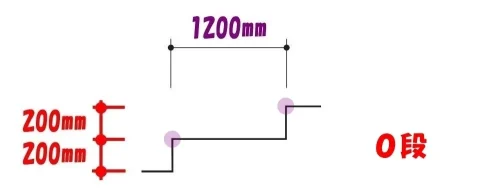

- 階段の段数:0段
- 階段の奥ゆき寸法:1200mm
- 階段の蹴上げ寸法:200*2段



階段を1段ずつ
観察してみましょう。
階段の寸法と段数の関係
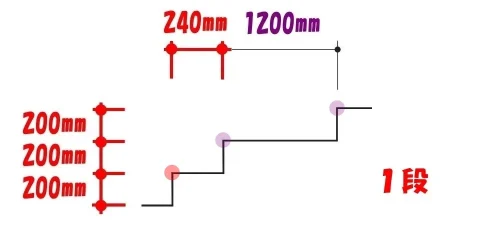

プラス1段
- 階段の段数:1段
- 階段の奥ゆき寸法:1200mm+240*1段
- 階段の蹴上げ寸法:200*3段
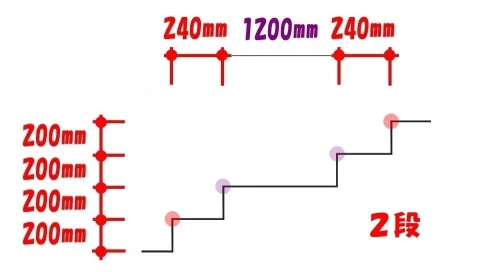

プラス2段
- 階段の段数:2段
- 階段の奥ゆき寸法:1200mm+240*2段
- 階段の蹴上げ寸法:200*4段



1段→3段、ふむふむ
2段→4段、なるほど・・
チェックポイント
階段は1段ずつ増やしながらスケッチを描いてみて、”階段の寸法と段数の関係”を把握する。




プラス〇段
- 階段の段数:〇段
- 階段の奥ゆき寸法:1200mm+240*〇段
- 階段の蹴上げ寸法:200*〇+2段
階段の段数が、蹴上げの数より2段少なくなることが分かるでしょうか?
理由としては「踊り場」と「2階の床面」のそれぞれが、蹴上の数にカウントされるからです。



なるほど!
3.階段を上がるために必要な蹴上げの数を求める
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める
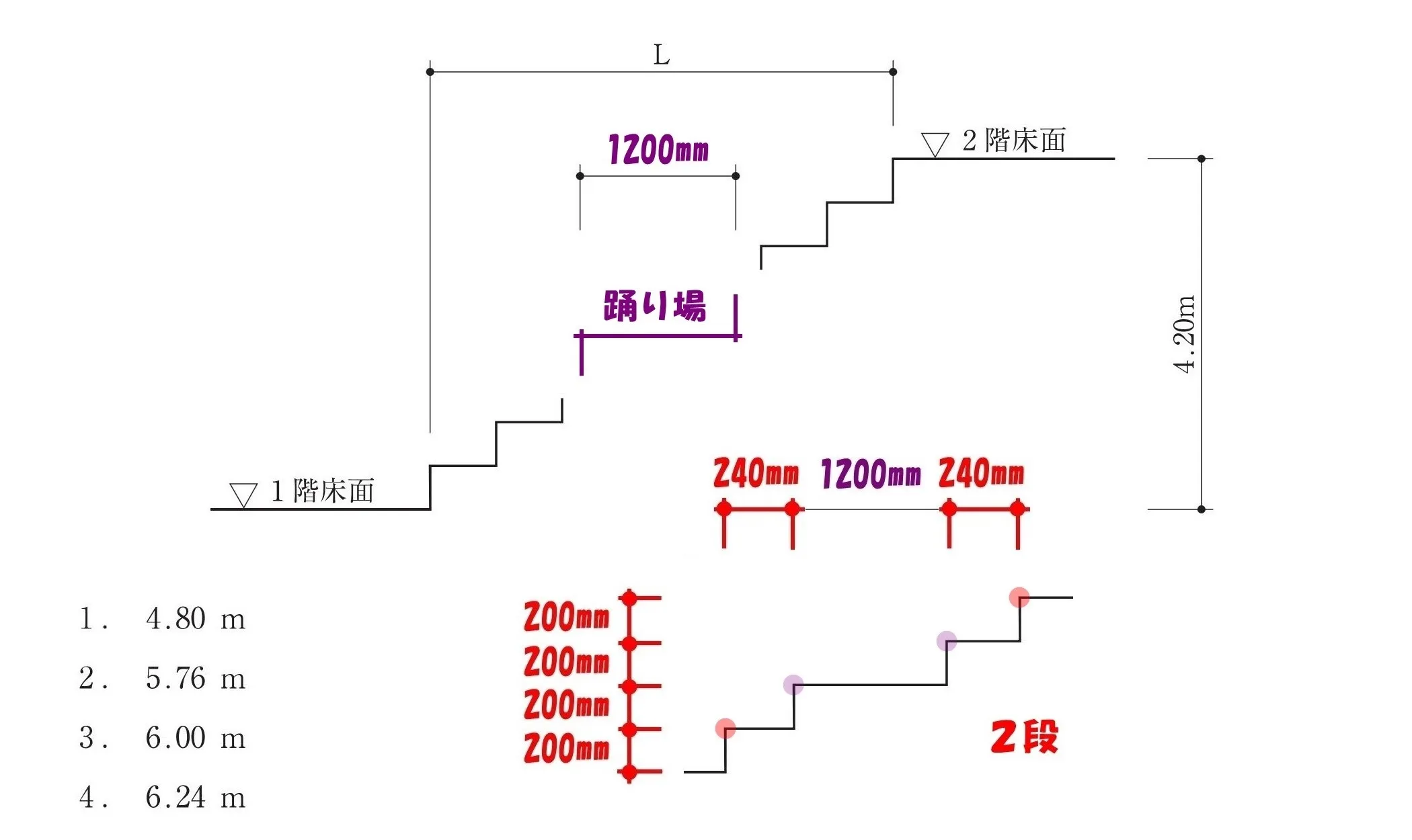

1階と2階の床面の差より、階段を上がるために必要な”蹴上の数”を求める。
$$必要な蹴上の数=4200mm÷200mm=21段$$



蹴上げ数は21段!
ステップ、ステップ!
チェックポイント
階段の踏み面の段数は、蹴上の数より2段(踊り場と2階の床面)少なくなる。
4.階段を上がるために必要なLの長さを求める
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める
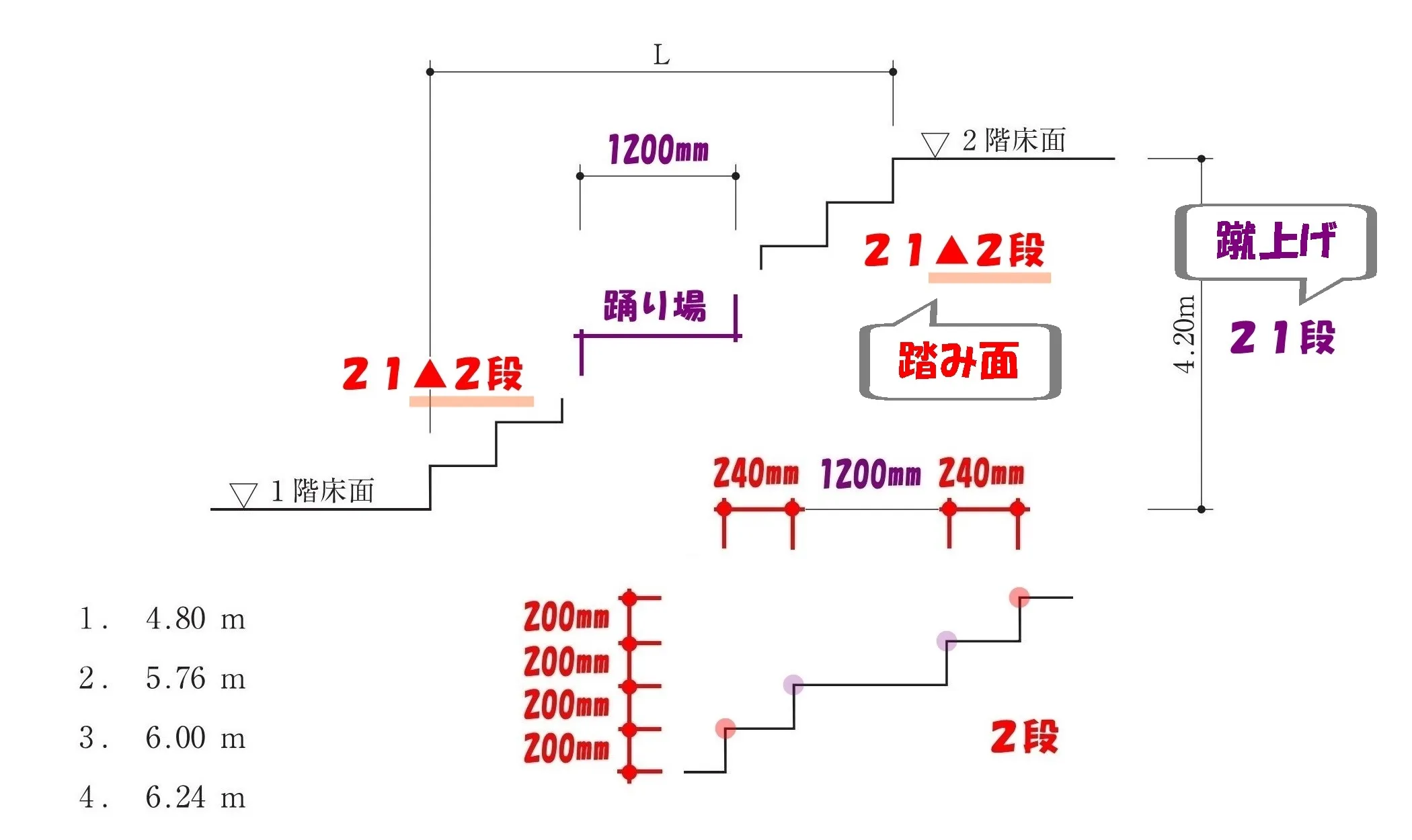

プラス2段
- 階段の段数:21▲2段
- 階段の奥ゆき寸法:1200mm+240*21▲2段
- 階段の蹴上げ寸法:200*21段



蹴上げ数は21段、
踏み面は2段少なくなる。




階段の段数は、蹴上の数より2段少なくなることから、踏み面の数は「21▲2段」
階段の奥ゆき寸法Lは、踊り場寸法+踏み面寸法×(蹴上の数▲2)によって求められる。
$$L=1200mm+240mm*(21▲2)段$$$$1200+240(20-1)=1200+4800-240=6000-240=5760mm$$
よって、蹴上21段の階段に必要な長さ「L」は、5,760mm →「5.76m」となる。



階段をやっつけた!
答え.2

攻略ポイント
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める


この動画を YouTube で視聴
軸組の長さ
難易度:★★★☆☆
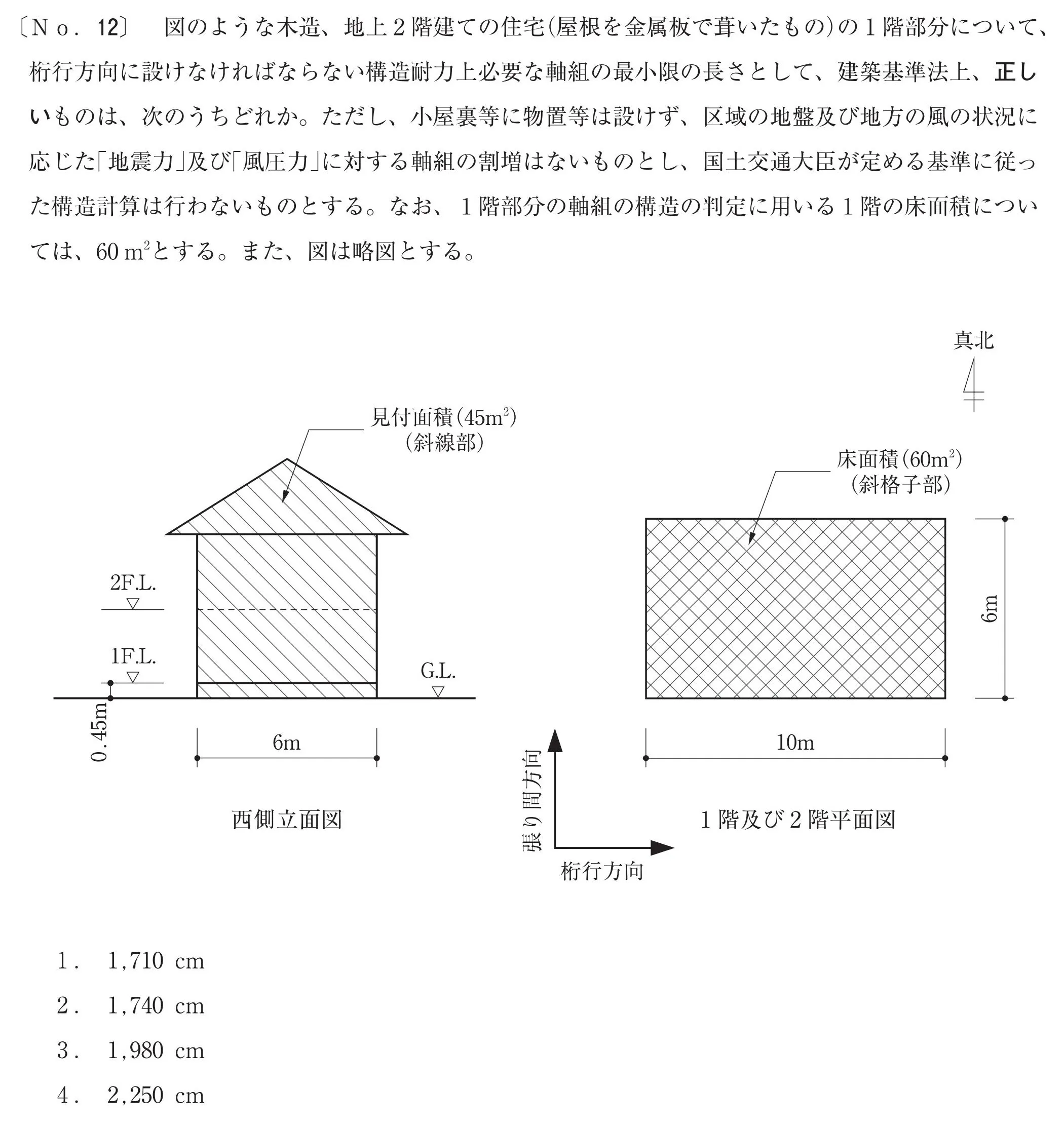

攻略ポイント
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める
インデックス

- 令43条【柱の小径】表(2)
- 令46条【構造耐力上必要な軸組長さ】
- 4項
- ×床面積
- ×見付面積
- 4項:表2
- 4項:表3(2)
- 4項



準備OK?
軸組長さを求めます。
必要な軸組の長さ


チェックポイント
- 2階建ての住宅
- (屋根を金属板で葺いたもの)
- 2階建ての1階部分(桁行方向)の軸組長さ



要チェック!
建築物の条件を読み取り、「構造耐力上必要な軸組長さ」を求める。
令46条【構造耐力上必要な軸組長さ】
軸組長さは、「地震力」と「風圧力」によって異なる数値となる。
いずれの条件も満たすためには、2つの最大値となる軸組長さが必要となります。



戦闘モードOK!
1.建物の床面積に乗ずる数値を確認する
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める
地震力による必要な軸組長さ
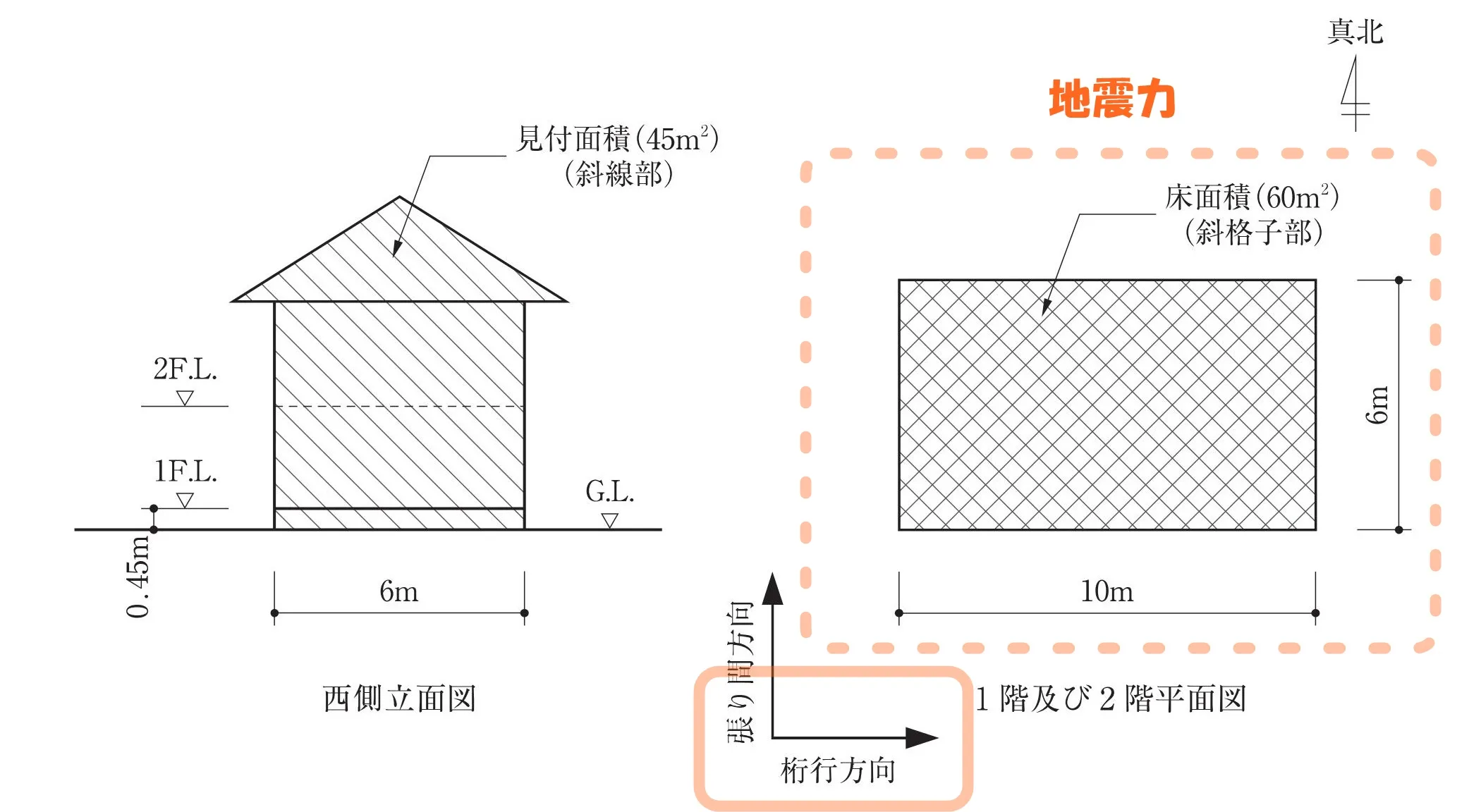

「地震力」における必要な軸組長さは、張り間方向・桁行方向とも同じ数値となる。


地震力に耐える軸組長さは?
2階建ての1階部分


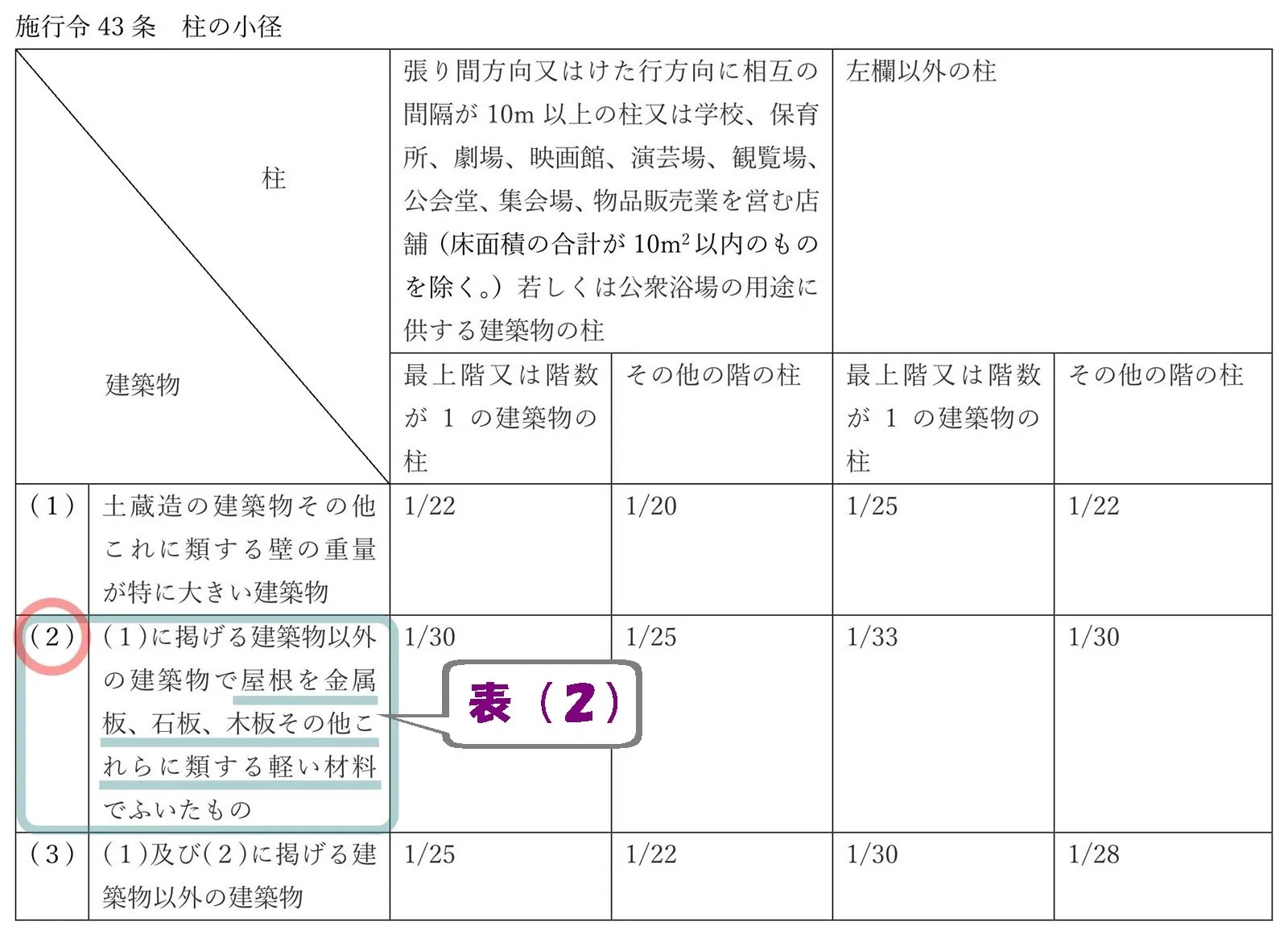

令43条、表(2)
- 2階建ての住宅
- (屋根を金属板で葺いたもの)
- 2階建ての1階部分(桁行方向)の軸組長さ
設問の条件は、令43条(柱の小径)、表(2)に該当します。
(見付けられましたか?)



パラパラパラ・・・
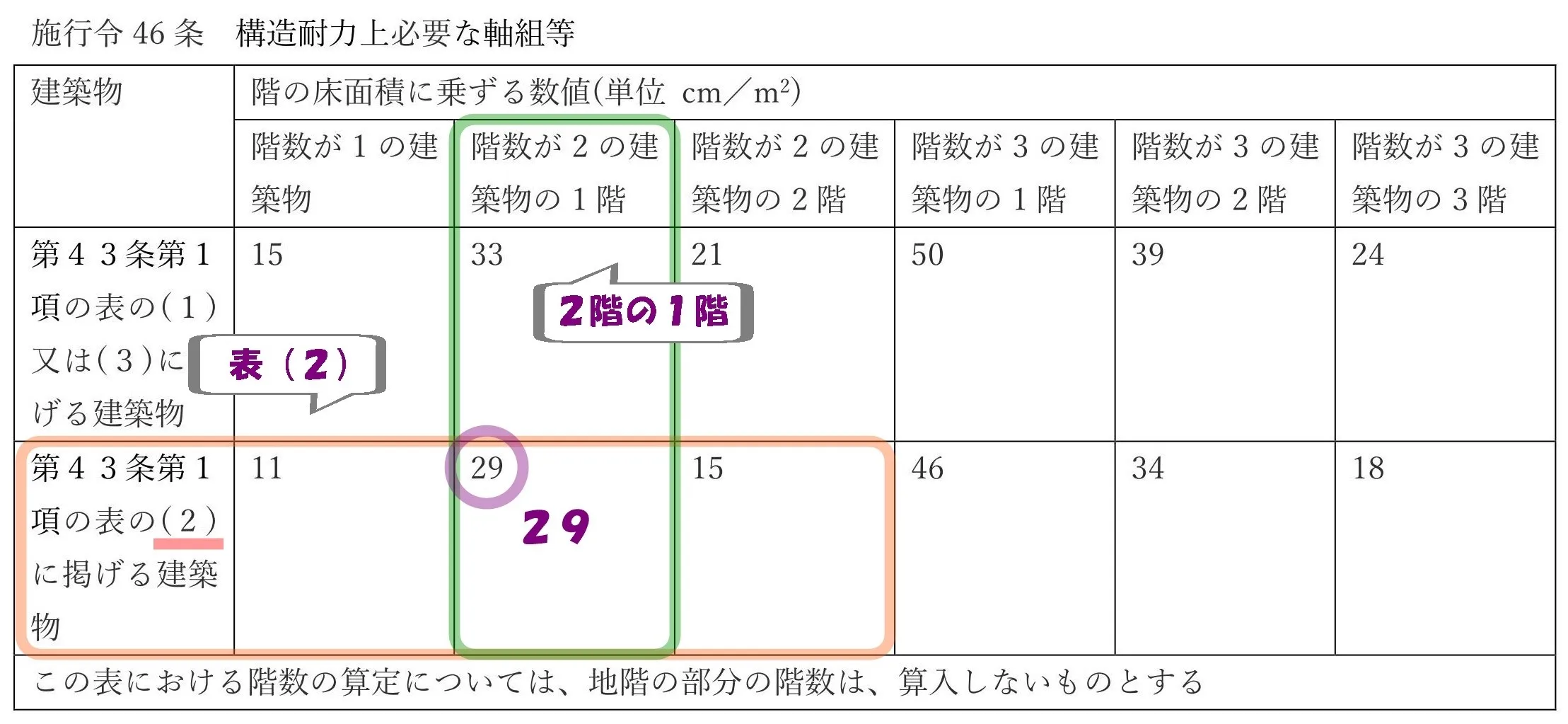




2階建ての1階です。
令46条4項、表2
下段:令43条1項の表の(2)に掲げる建築物
階数が2の建築物の1階の欄に、数値は「29」とありますよね?
表にある数値「29」が、床面積に乗ずる値[単位:cm/㎡]となります。
(がんばって見付けて下さい。)



パラパラパラ・・・



見つけたぞ!
床面積に掛ける数値の単位は[cm/㎡]なので、[m]から[cm]への換算は不要です。
2.地震力における必要な軸組長さを求める
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める
×29
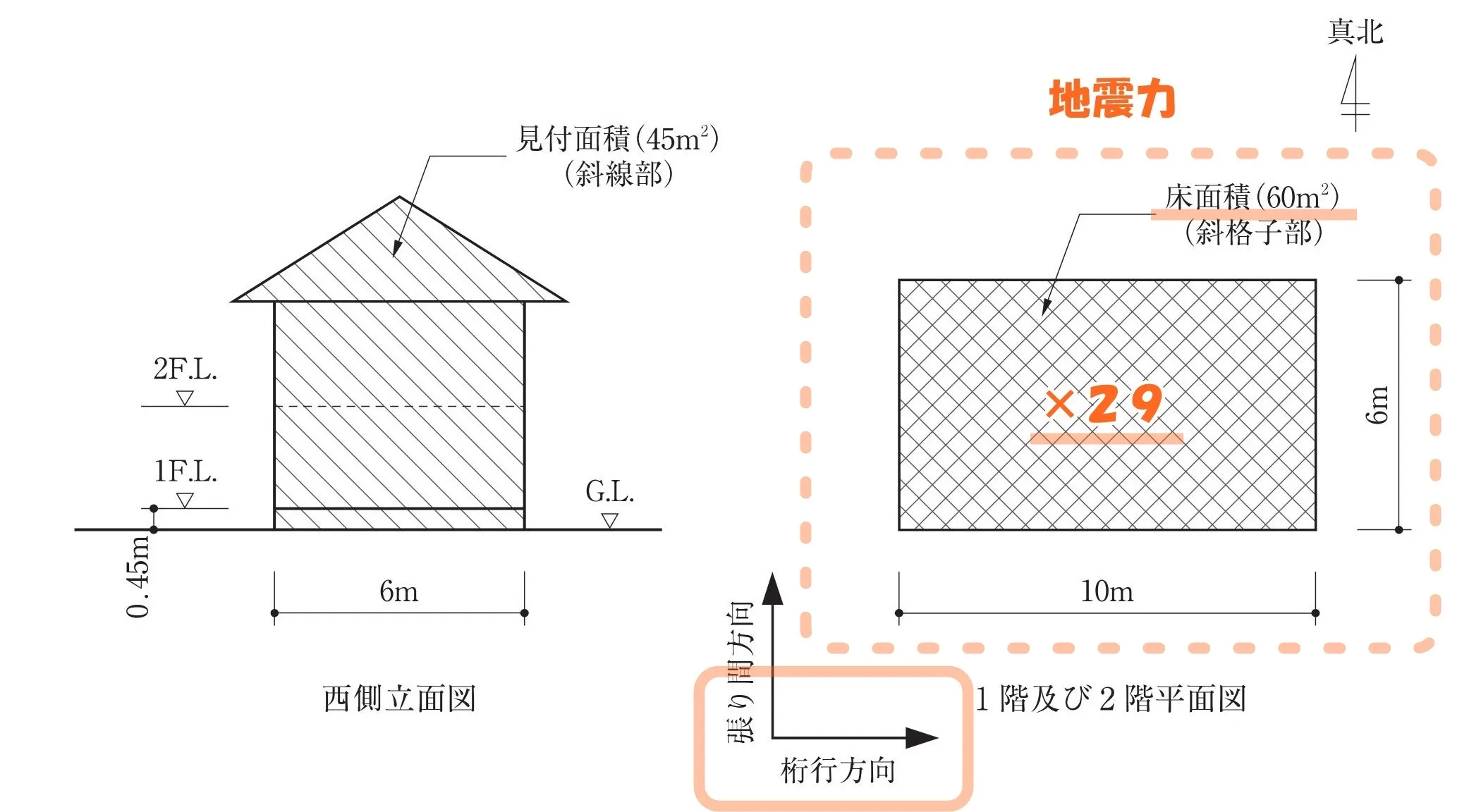

令46条4項:表2
$$必要な軸組長さ[㎝]=床面積[㎡]*29[㎝/㎡]$$
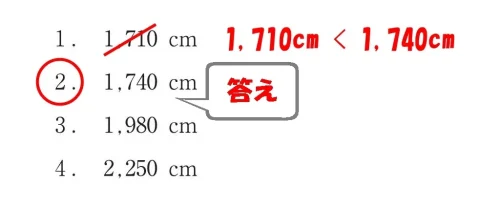
$$L=60*29=60*(30-1)=1,800-60=1,740$$
地震力による必要な軸組長さは、1,740[㎝]となる。



メモしておこう。
令和7年4月1日から施行
施行令43条における早見表の”屋根区分”が変わります。
(軽い屋根・重い屋根の区分を廃止)
屋根・外壁の仕様及び階数ごとに個別に定める早見表(改正)の参照のもとに「床面積に乗ずる値(cm/㎡)」「柱の小径(mm)」を算定して下さい。
3.風圧力における必要な軸組長さを求める
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める
風圧力による必要な軸組長さ







見つけた!
令46条4項:表3、(2)
設問より、見付け面積に乗ずる値は「50」単位は[cm/㎡]となる。
床面積に掛ける数値の単位は[cm/㎡]なので、[m]から[cm]への換算は不要です。



風圧力に耐える軸組長さは?
「風圧力」における必要な軸組長さは、張り間方向・桁行方向の見付け面積によって異なる。
×50
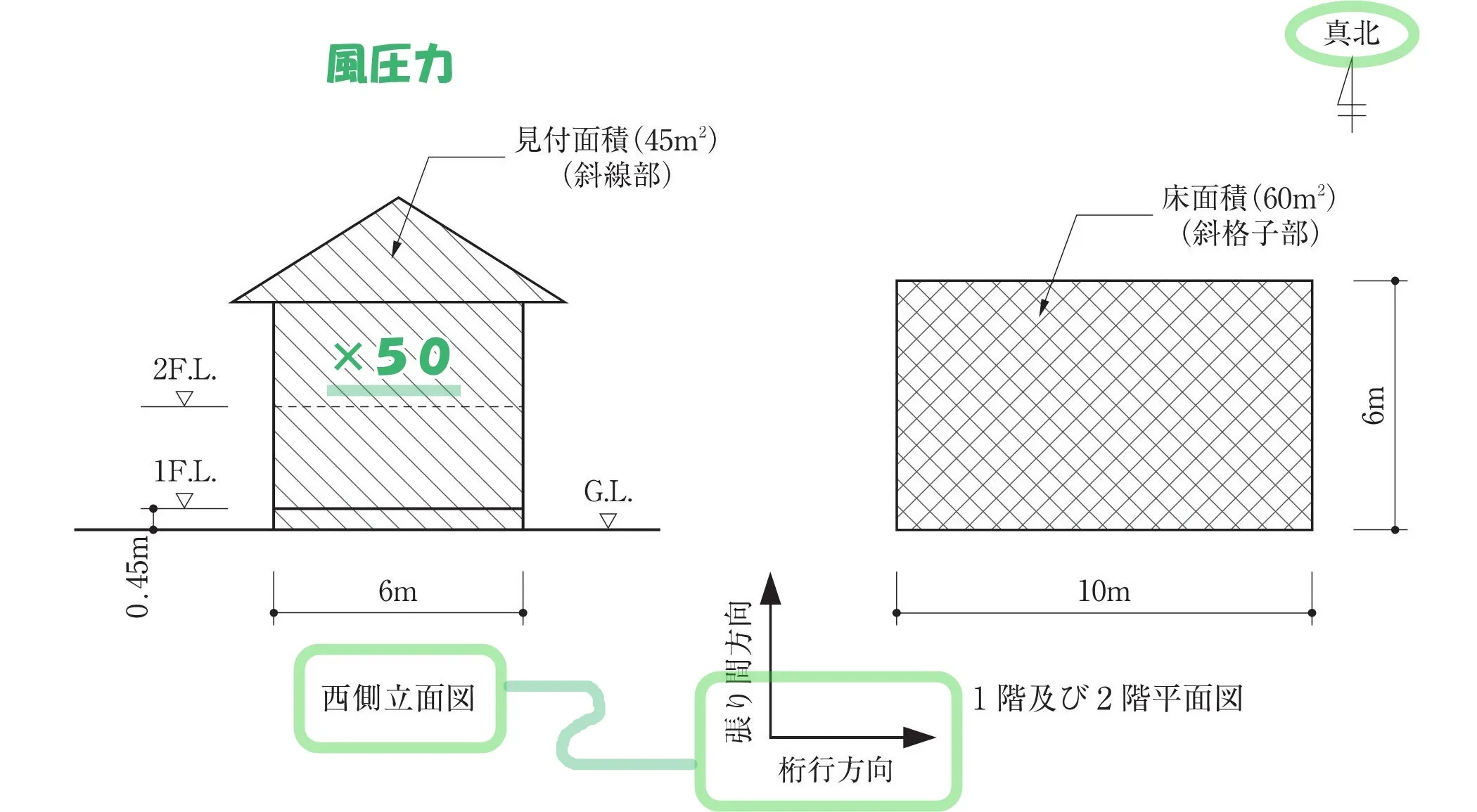

問題用紙に図示してある西側立面図が、平面図における”桁行方向”であることを確認する。



図面をよく確認すること。
算定根拠となる見付け面積
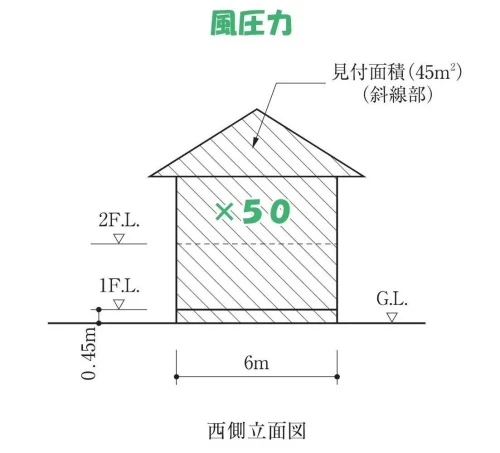


令46条4項
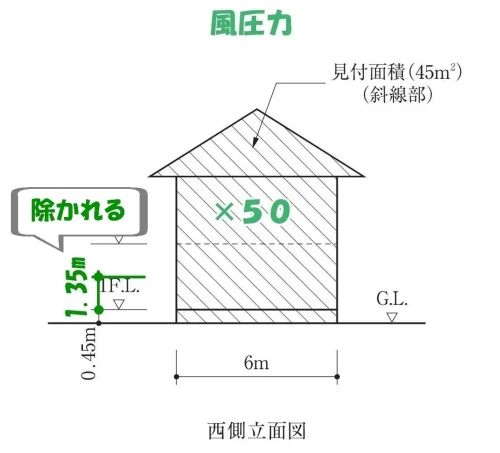
階数が2以上又は延べ面積が50㎡を超える木造の建築物においては~それぞれの方向につき~見付面積から、その階の床面からの高さが1.35m以下の部分の見付面積を減じたものに、次の表3に掲げる数値(×50)を乗じて得た数値以上となるように、国土交通大臣が定める基準に従って設置しなければならない。
建築基準法(一部省略)
風圧力における必要な軸組長さを求める見付面積に、床面から高さ1.35mの範囲は含まない。



基礎の部分も
風圧力に考慮しない。
見付け面積に含まない部分
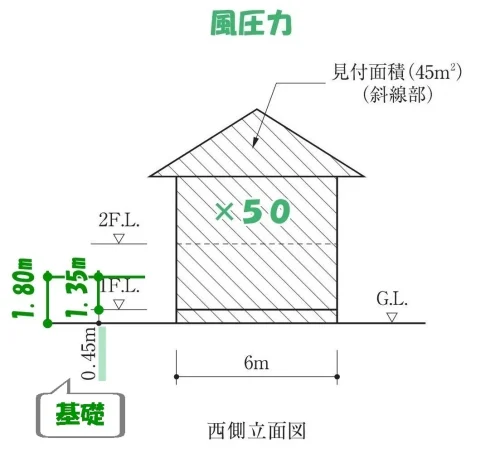

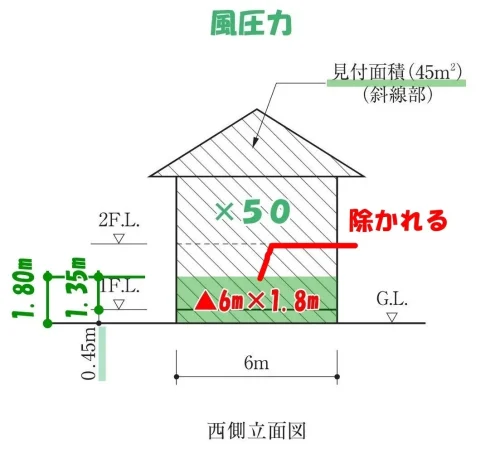

令46条4項
$$必要な軸組長さ[㎝]=(見付面積[㎡]▲床面から1.35mの部分)*50[㎝/㎡]$$
$$L=\{45-6*1.8\}*50=\{45-6*(2.0-0.2)\}*50$$$$=\{45-(12-1.2)\}*50=\{(40+5)-(12-1.2)\}*50$$$$=(2000+250)-(600-60)=2,250-540=1,710$$
風圧力による必要な軸組長さは、1,710[㎝]となる。
地震力による必要な軸組長さは、1,740[㎝]であるため、最大値となる1,740[㎝]が答えとなる。



軸組長さを撃破!
答え.2

攻略ポイント
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める
法令集の紹介
建蔽率
難易度:★★★☆☆



この動画を YouTube で視聴
攻略ポイント
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
インデックス

- 42条【道路の定義】
- 42条2項:みなし道路
- 53条【建蔽率】
- 2項:2以上の区域にわたる場合の建築制限の扱い
- 3項一号:準防火地域内の建築物
- (ロ)準耐火建築物
- 3項二号:街区の角にある敷地
- 8項:敷地が準防火地域とそれ以外の区域にわたる場合



インデックスは、
よく整理しておこう。
1.建築物の耐火仕様と防火地域をチェックする
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
準耐火建築物


53条【建蔽率】
まず始めに、問題文に「建築物の仕様が記載されているか?」をチェックする。
「耐火建築物」「準耐火建築物」は重要なキーワードなので、必ず印しておきましょう。



ここは要チェック!
準防火地域の準耐火建築物
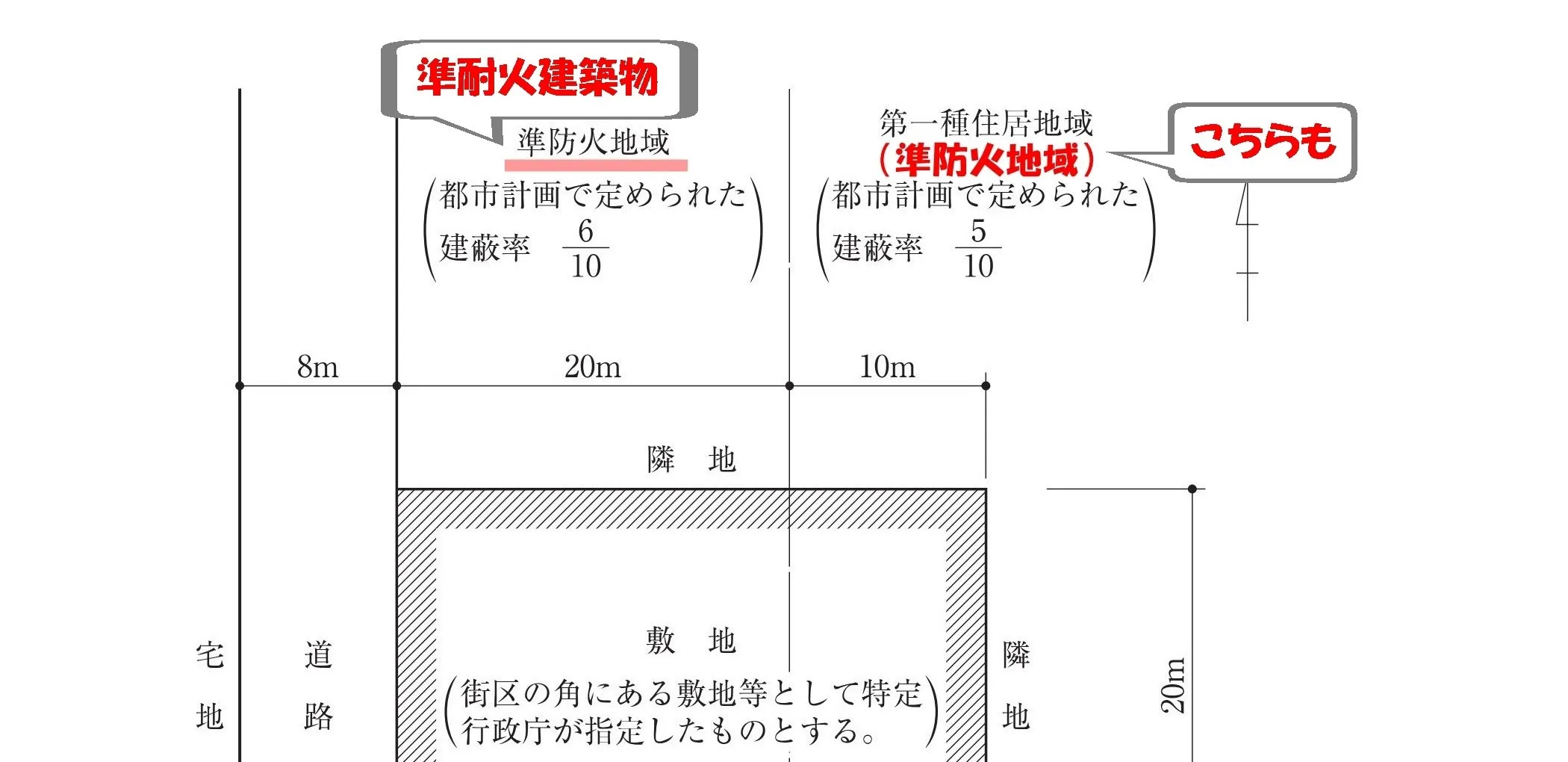

53条3項一号:準防火地域内の建築物
(ロ)準耐火建築物
$$準防火地域内の準耐火建築物は、建ぺい率+\frac{ 1 }{ 10 }$$
53条8項:敷地が準防火地域とそれ以外の区域にわたる場合
その他の区域においても、準防火地域の規定が適用される。



建物が区域をまたがる場合は、
厳しい方が適用されます。
+1/10
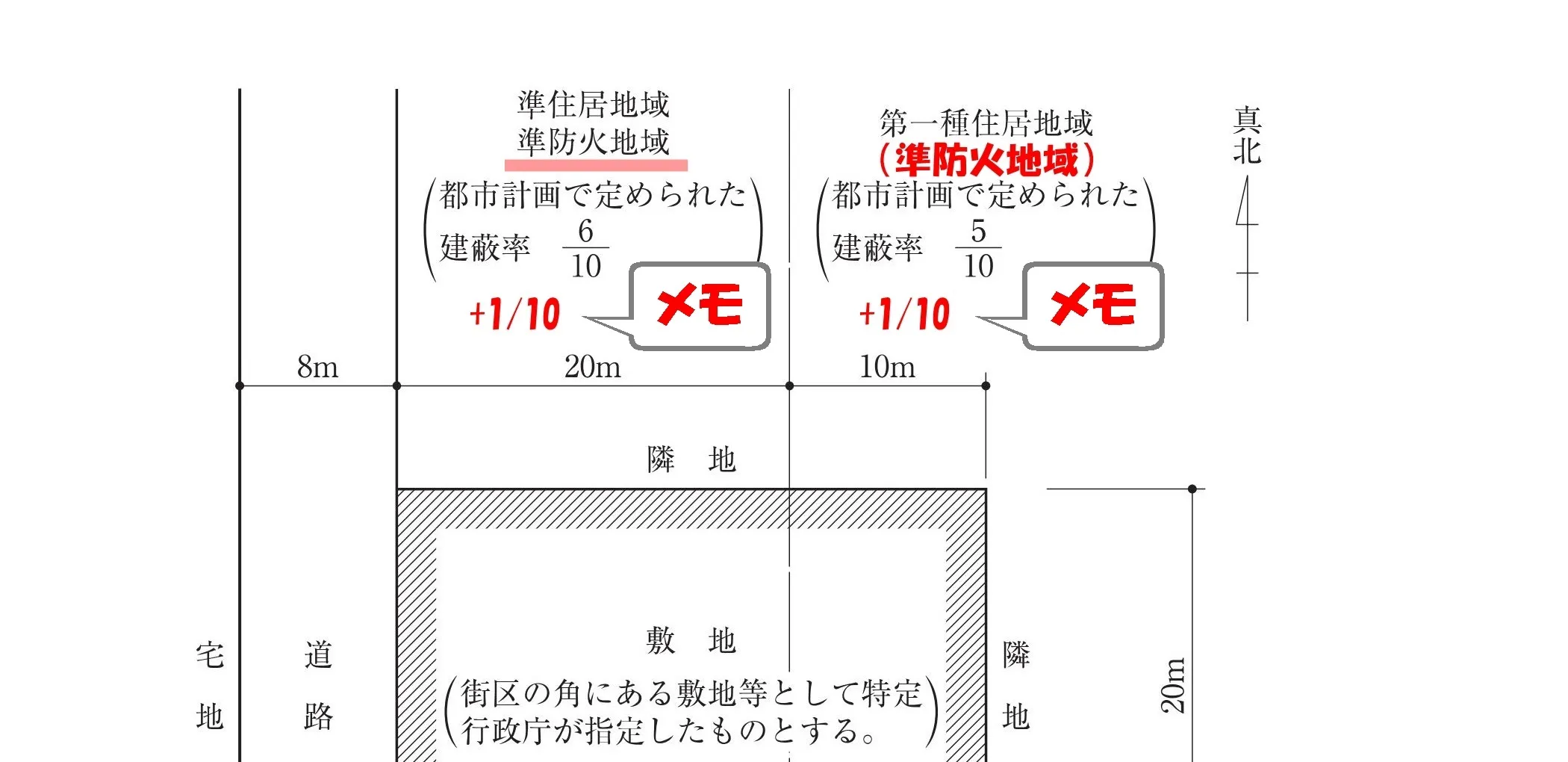

敷地図の建ぺい率の表記にそれぞれ、「+1/10」とメモしておく。



ラッキー!
1/10 をもらえた。
2.敷地の区分と接道条件(角地など)をチェックする
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
敷地に接する”角地”
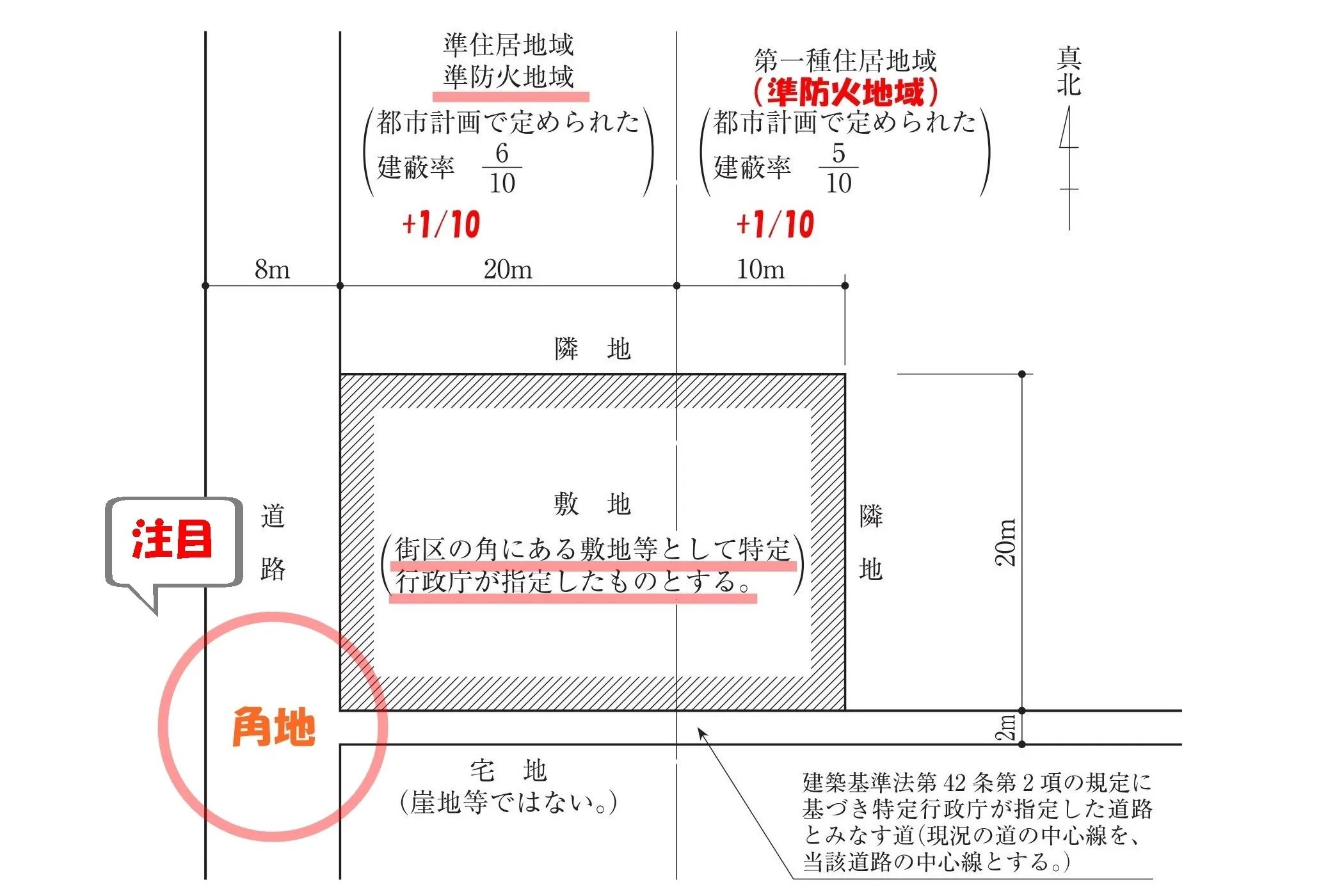

53条3項二号:街区の角にある敷地
$$特定行政庁が指定した角にある敷地は、建ぺい率+\frac{ 1 }{ 10 }$$
+1/10
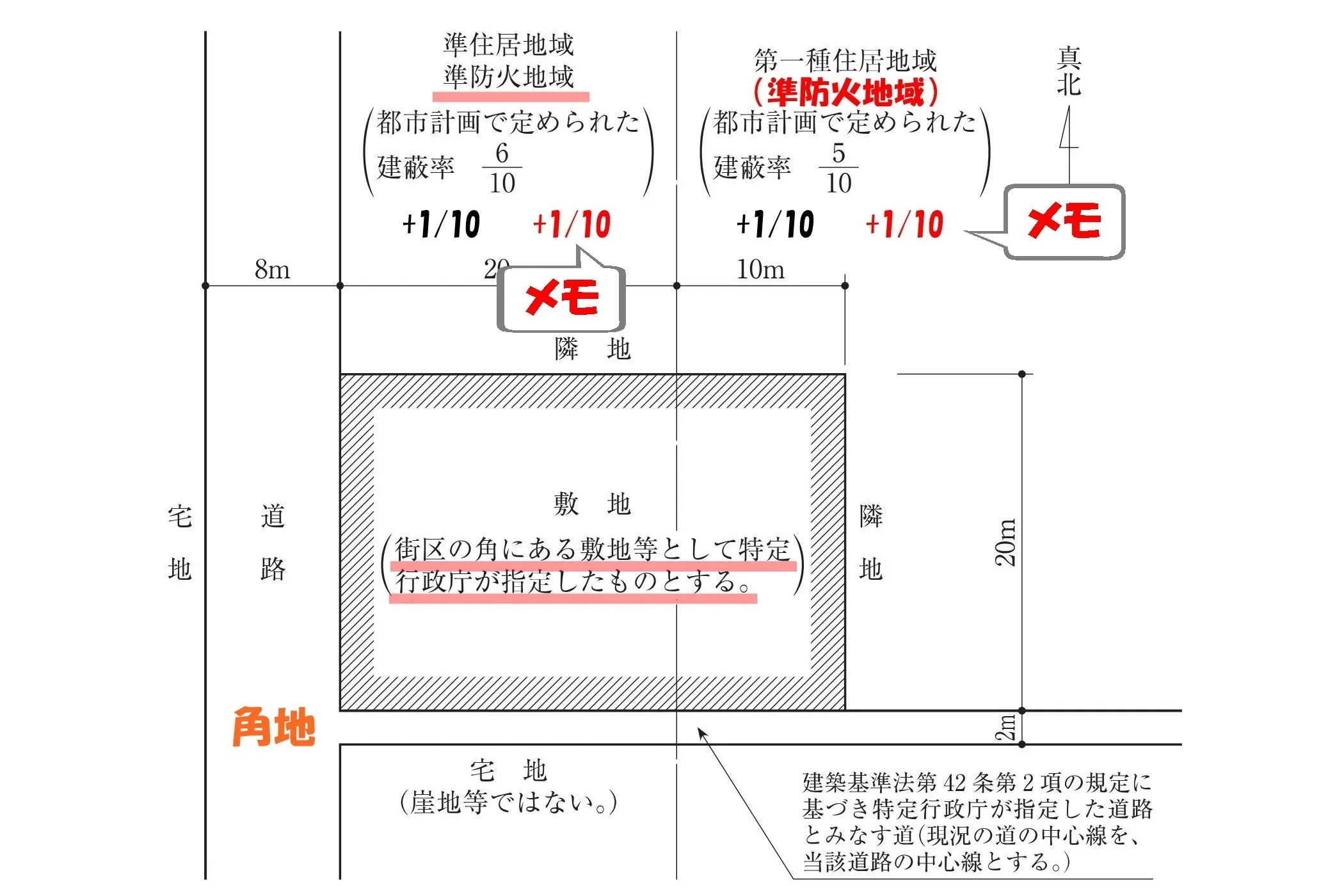

敷地図の建ぺい率の表記にそれぞれ、「+1/10」とメモを足しておく。



ラッキー!×2
また、1/10 がもらえた。



あいつを黙らせろ!
チェックポイント
$$①準防火地域内の準耐火建築物は、建ぺい率+\frac{ 1 }{ 10 }$$
$$②特定行政庁が指定した角にある敷地は、建ぺい率+\frac{ 1 }{ 10 }$$
数値を修正する
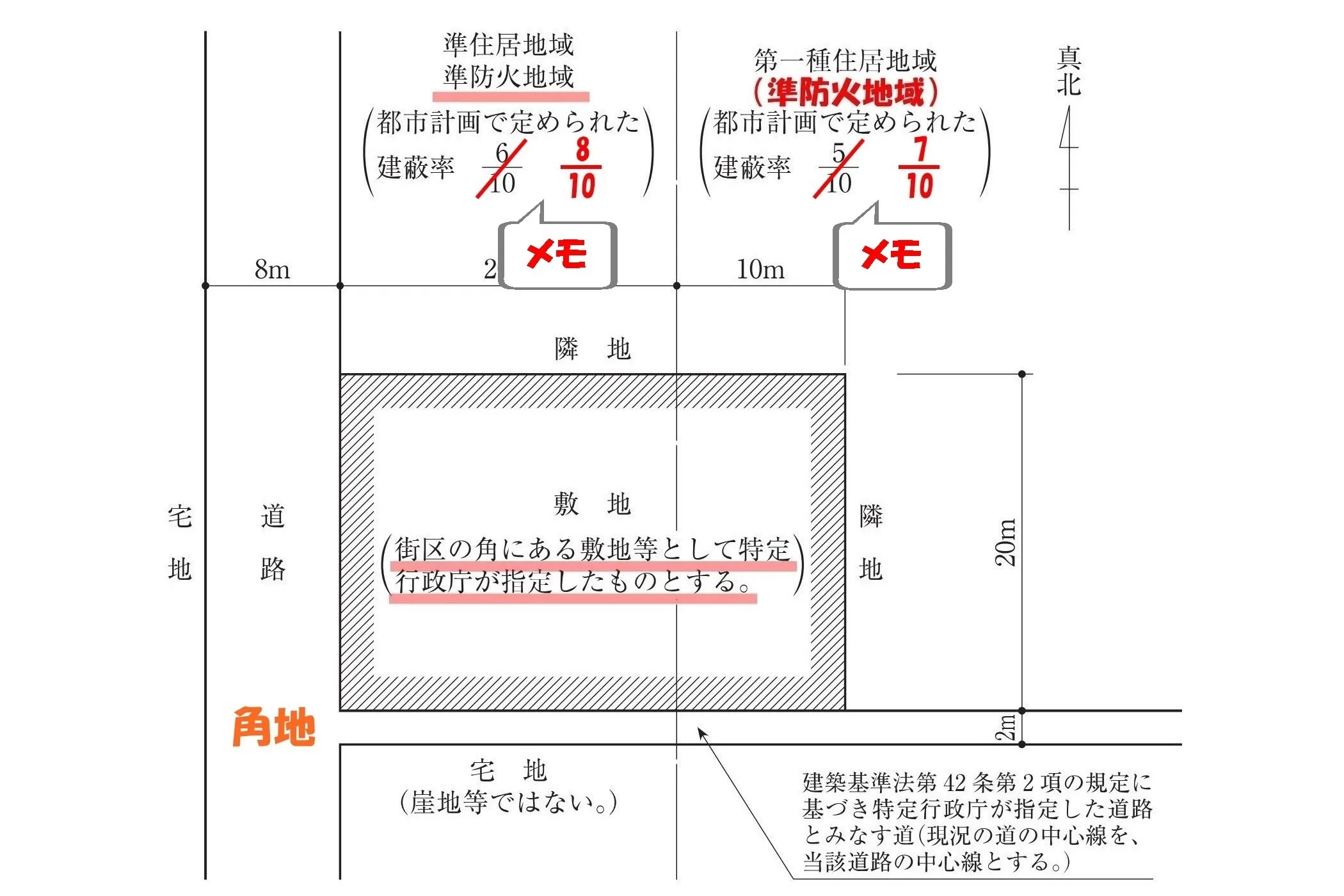

都市計画で定められた建ぺい率の数値を「修正」する。
$$準住居地域:\frac{ 6 }{ 10 }→\frac{ \underline{8} }{ 10 },第一種住居地域:\frac{ 5 }{ 10 }→\frac{ \underline{7} }{ 10 }$$



修正がある箇所は、
必ずメモしましょう。
3.敷地が”みなし道路”により削られる部分は寸法を差し引く
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
幅員4m未満の道
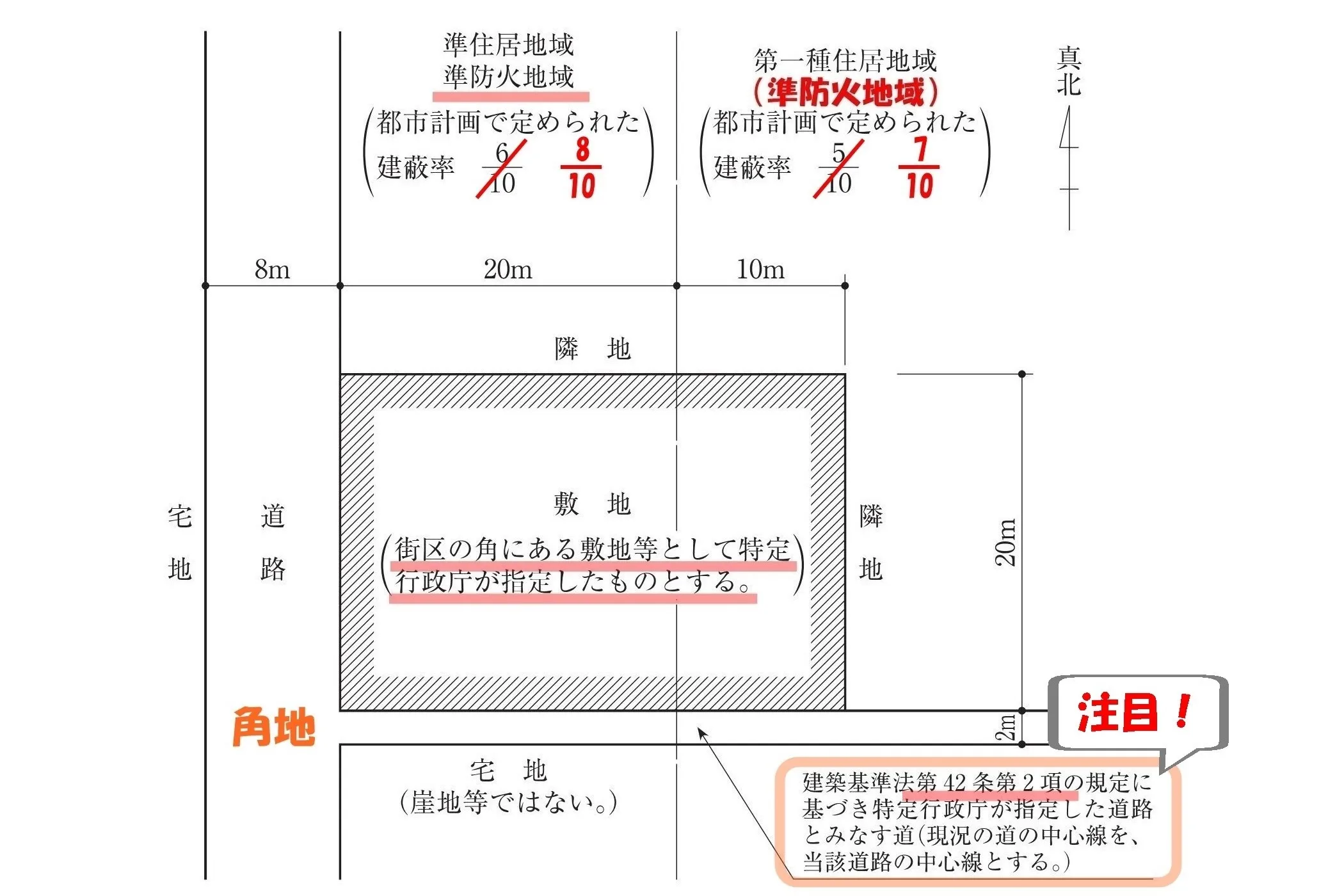

42条【道路の定義】
「道路」とは、次の各号のいずれかに該当する幅員4m以上のものをいう。
建築基準法(一部省略)
みなし道路
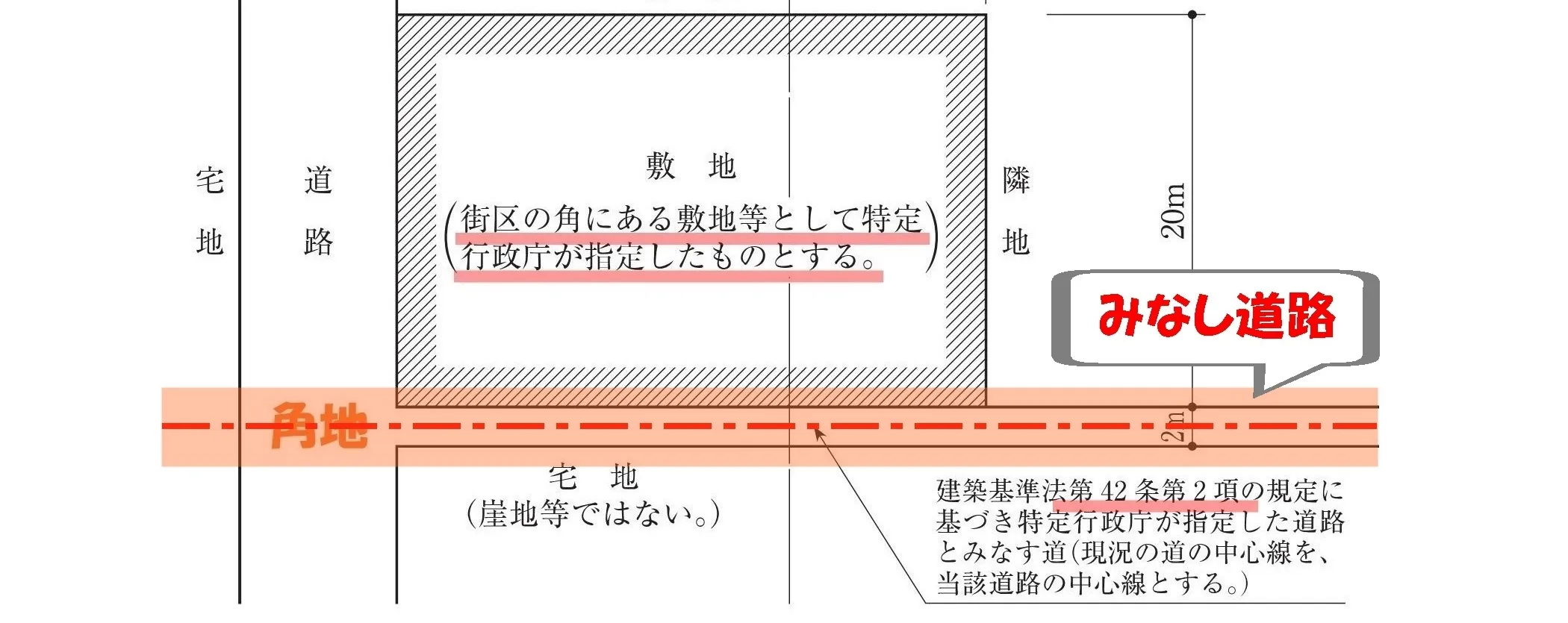




みなし道路の部分は、
敷地の面積が削られます。
建物の敷地の一部に”みなし道路”が含まれる場合は、その部分の面積を差し引くこと。
42条2項:みなし道路
法改正によりこの章の規定が適用されるに至つた際現に建築物が立ち並んでいる幅員4m未満の道で、特定行政庁の指定したものは、~道路とみなし、その中心線からの水平距離2mの線をその道路の境界線とみなす。ただし、当該道がその中心線からの水平距離2m未満で崖地、川、線路敷地その他これらに類するものに沿う場合においては、当該崖地等の道の側の境界線及びその境界線から道の側に水平距離4mの線をその道路の境界線とみなす。
建築基準法(一部省略)
敷地の寸法を修正する
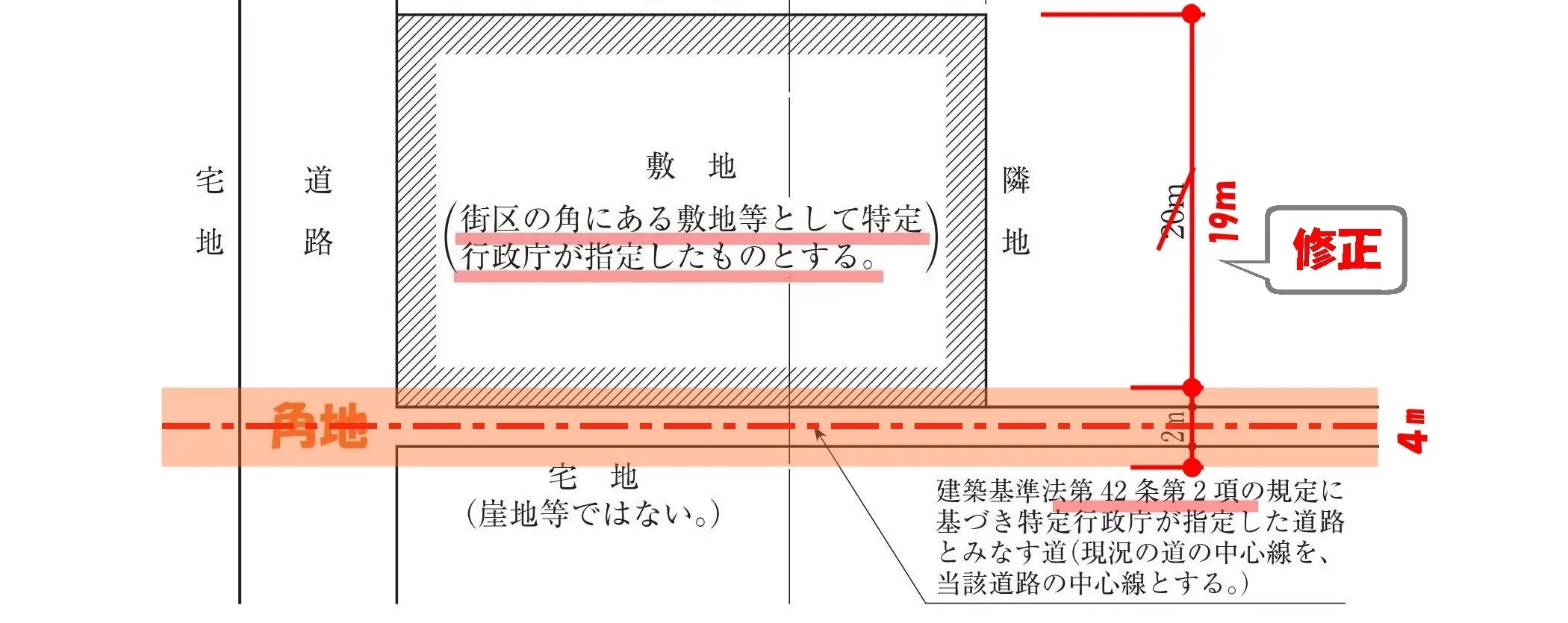

42条2項の”みなし道路”により、敷地境界線が「1m」後退する。
この段階で、敷地図の寸法値も「20m」→「19m」に修正しておきましょう。



修正するところは、
必ずメモしておくこと。
4.それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める
数値を転記する
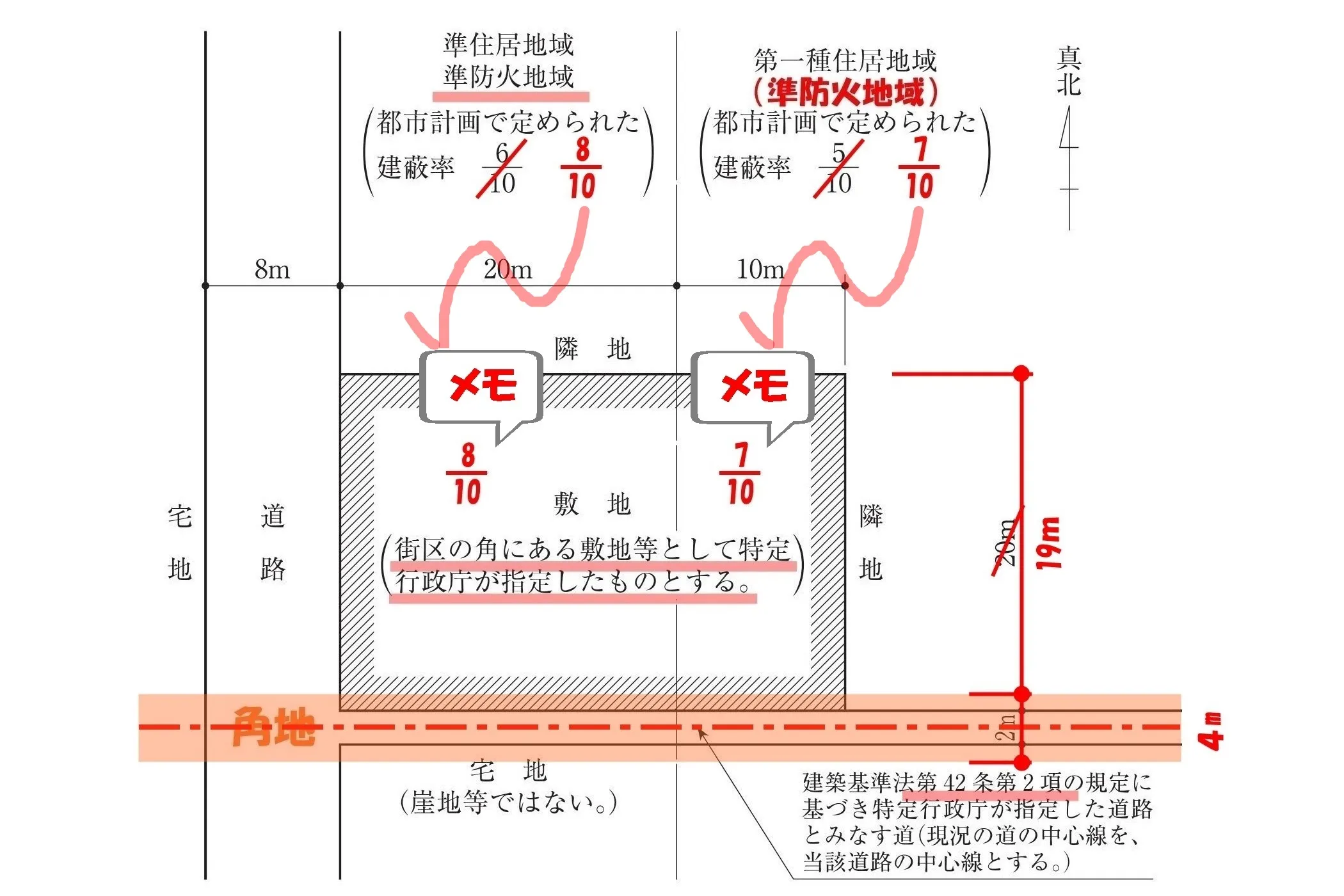

問題用紙にメモした建ぺい率の「数値」を敷地内に、それぞれ転記する。
$$準住居地域の建ぺい率:\frac{ 8 }{ 10 },第一種住居地域の建ぺい率:\frac{ 7 }{ 10 }$$
敷地面積×建ぺい率
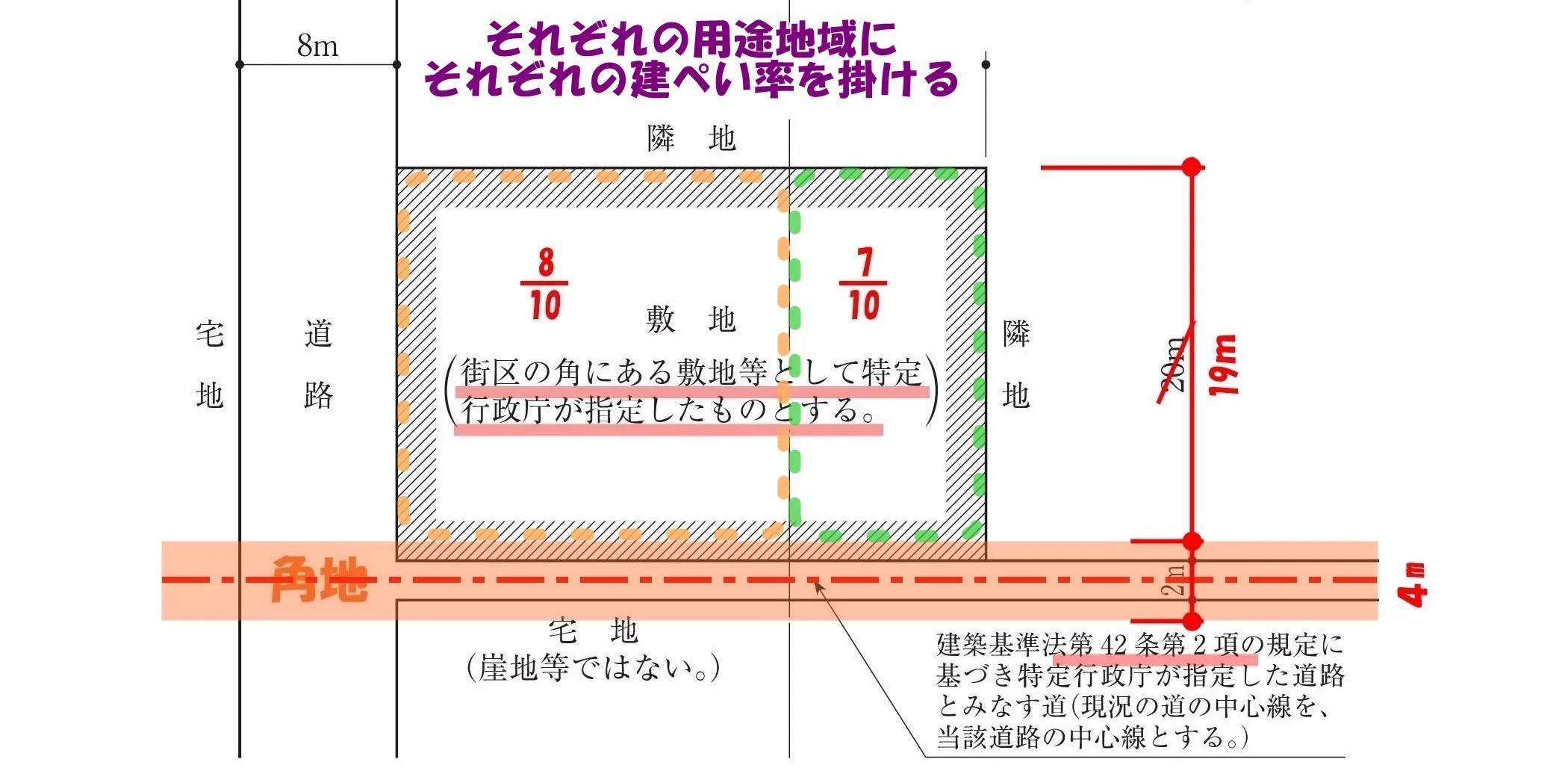

53条【建蔽率】
それぞれの用途地域の面積に、それぞれの建ぺい率の数値を掛ける。
$$建築面積=(敷地面積▲みなし道路部分)*建ぺい率$$
建築面積を求める
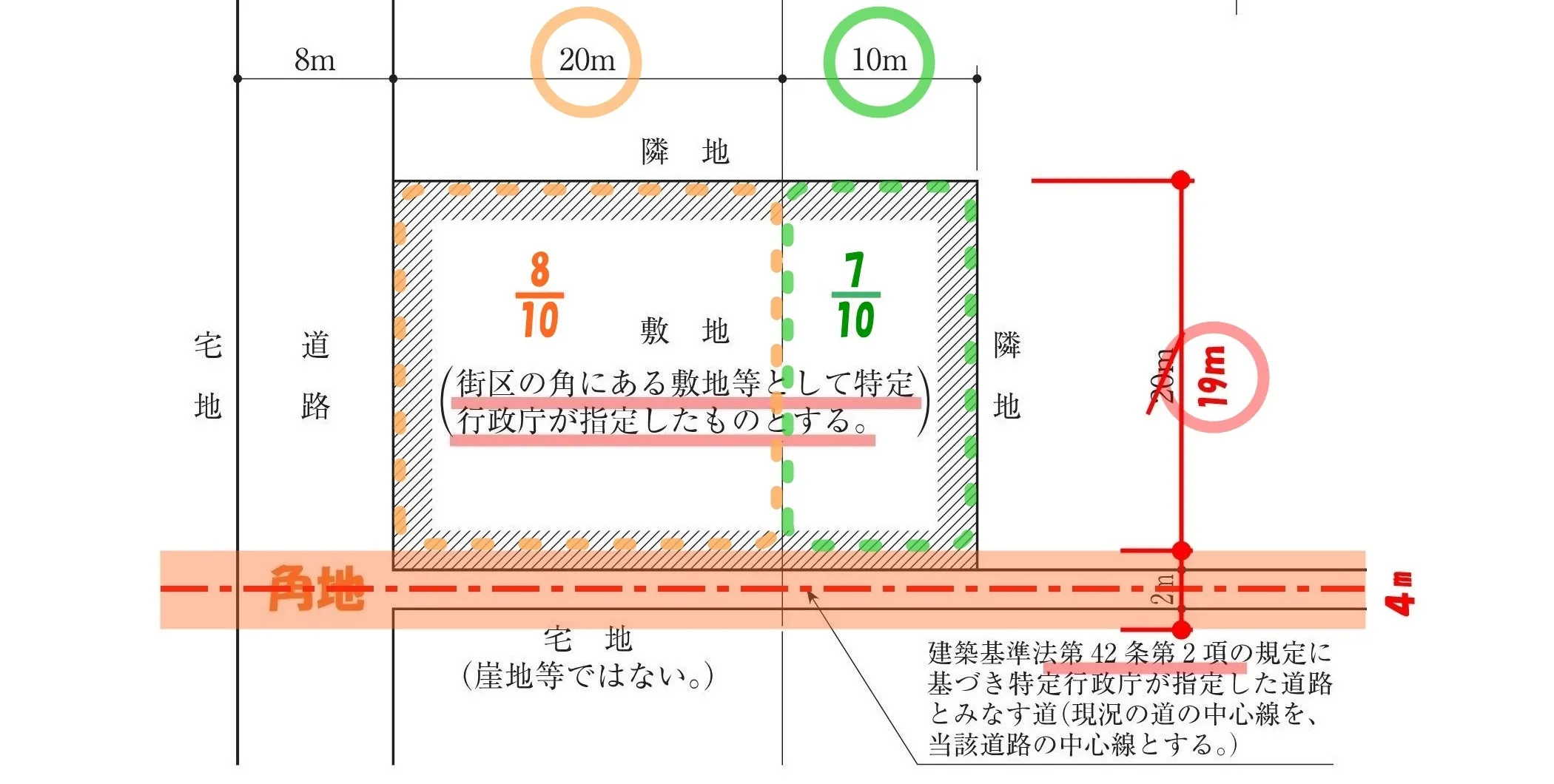

【準住居地域】
$$\underline{20}*(20-1)*\frac{ 8 }{ \underline{10} }=2*(20-1)*8=(20-1)*16=320-16$$
【第一種住居地域】
$$\underline{10}*(20-1)*\frac{ 7 }{ \underline{10} }=(20-1)*7=140-7$$
【建築面積の合計】
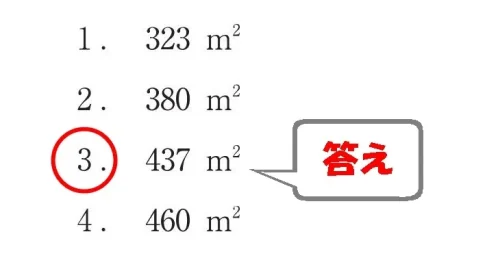
$$(320-16)+(140-7)=320+140-16-7=460-23=\underline{437㎡}$$



建ぺい率、撃破!
答え.3

攻略ポイント
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める


この動画を YouTube で視聴
容積率
難易度:★★★★☆



この動画を YouTube で視聴
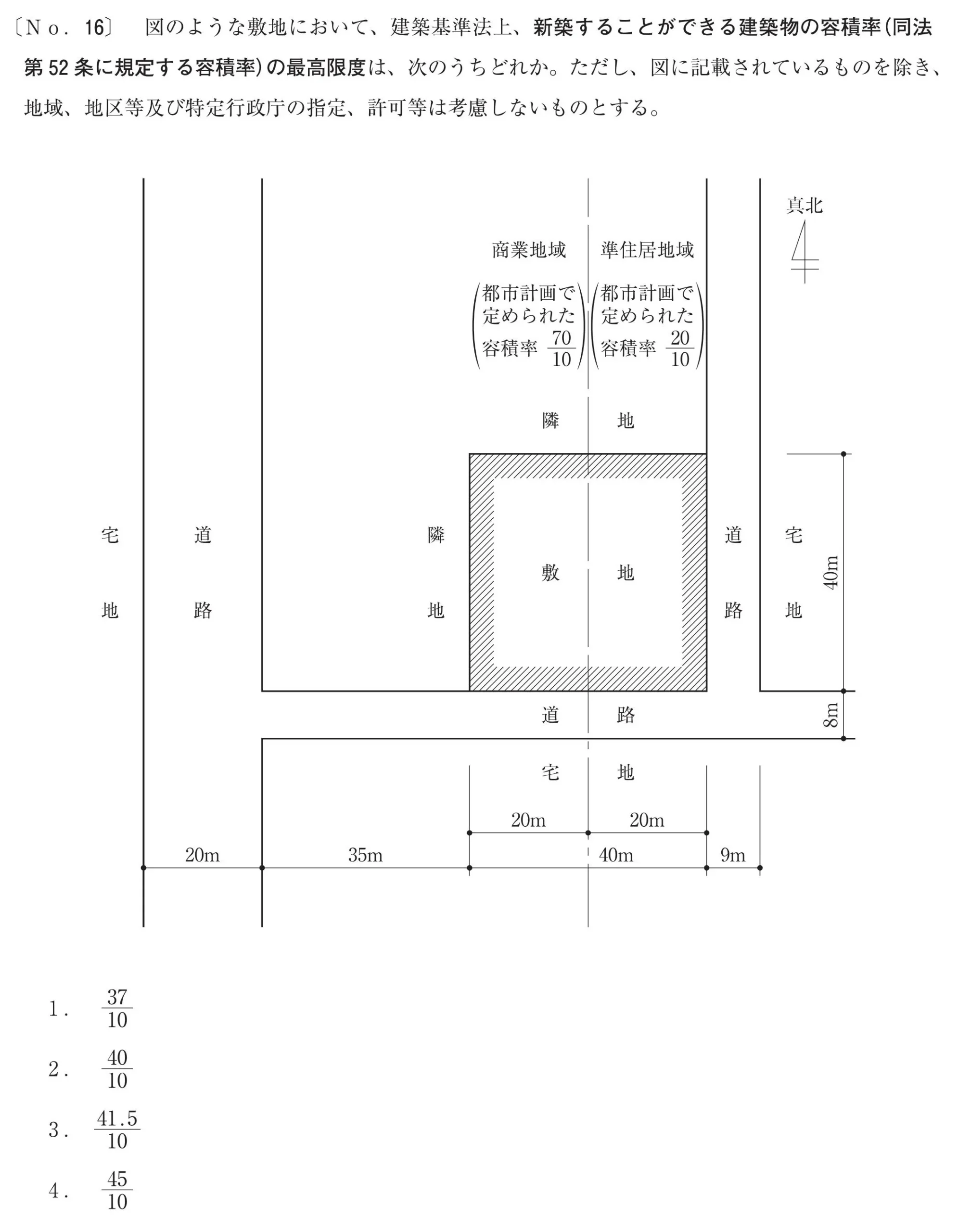
攻略ポイント
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
インデックス


- 法52条【容積率】
- 1項:法定容積率
- 2項:道路容積率
- 7項:建築物の区域が2以上にわたる場合の算定
- 9項:特定道路に接続する幅員6m以上12m未満の道路
- 令135条の18:Wa=(12-Wr)×(70-L)/ 70



インデックスは、
関連条文をグルーピングする。
容積率を求める


法52条【容積率】
チェックポイント
- 都市計画で定める容積率(法定容積率)
- 前面道路の幅員に数値を掛けて、算出される容積率
- どちらの容積率も満たす必要があるため、厳しい方の数値を選択する。



戦闘モードOK!
1.都市計画で定められる法定容積率を確認する
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
法定容積率
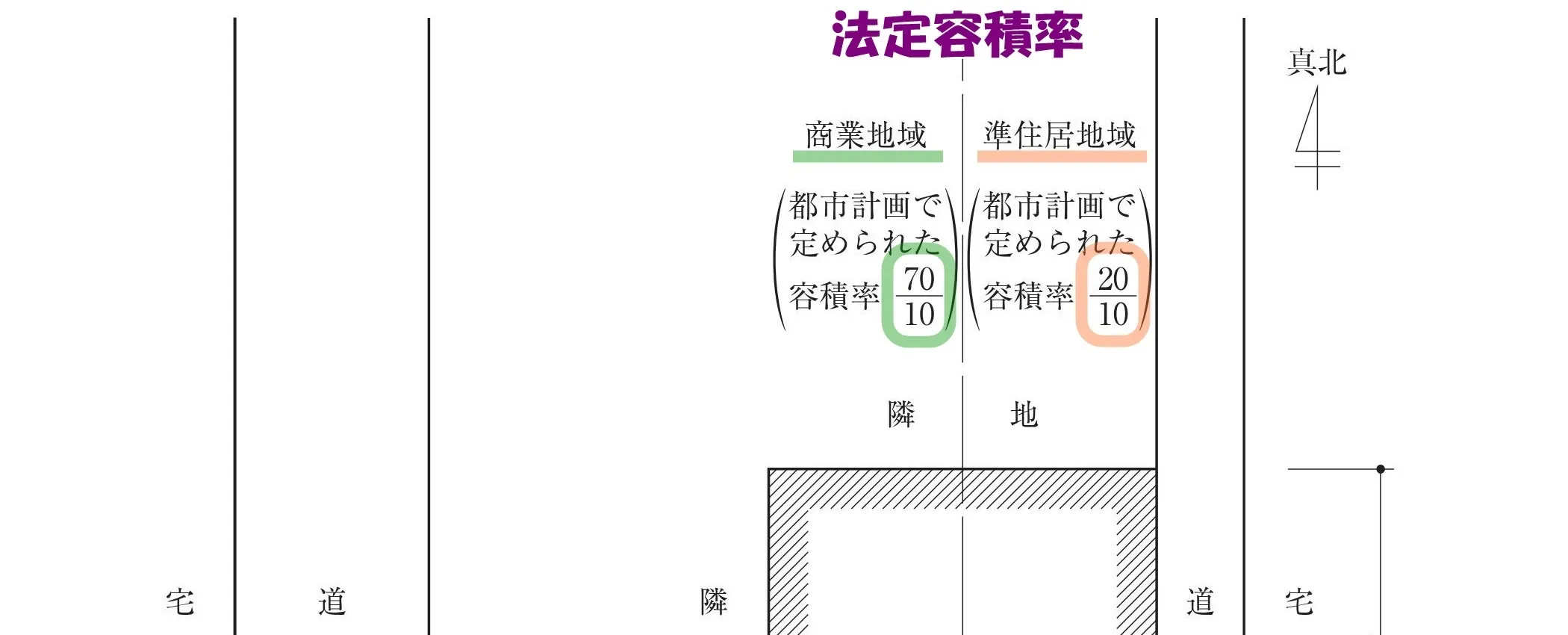

法52条1項:法定容積率
$$商業地域:\frac{ 70 }{ 10 },準住居地域:\frac{ 20 }{ 10 }$$



見るだけ?
2.道路条件と道路の幅から、道路容積率を算出する
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
道路容積率
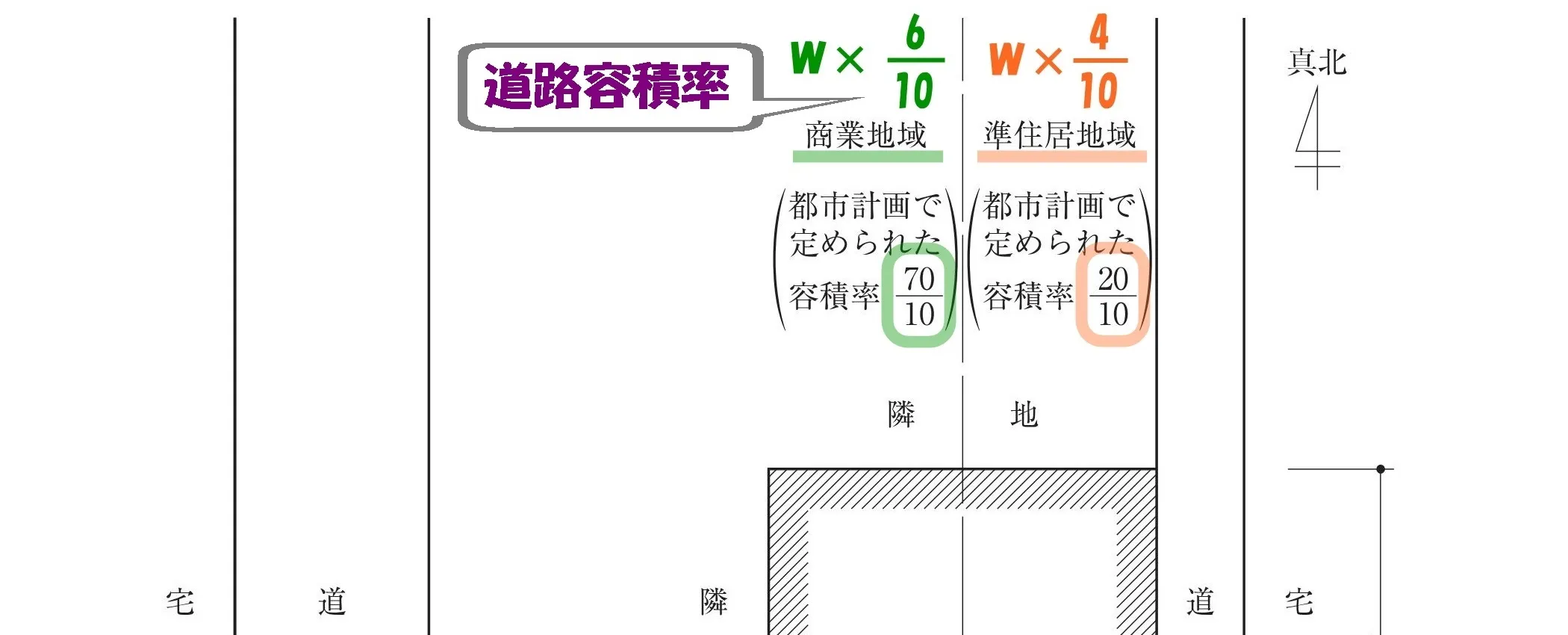

法52条2項:道路容積率
$$商業地域:W*\frac{ 6 }{ 10 },準住居地域:W*\frac{ 4 }{ 10 }$$
$$(W:前面道路の幅員)$$



「×6/10」「×4/10」
それだけ先に書いておこう。
幅員15m以上の道路
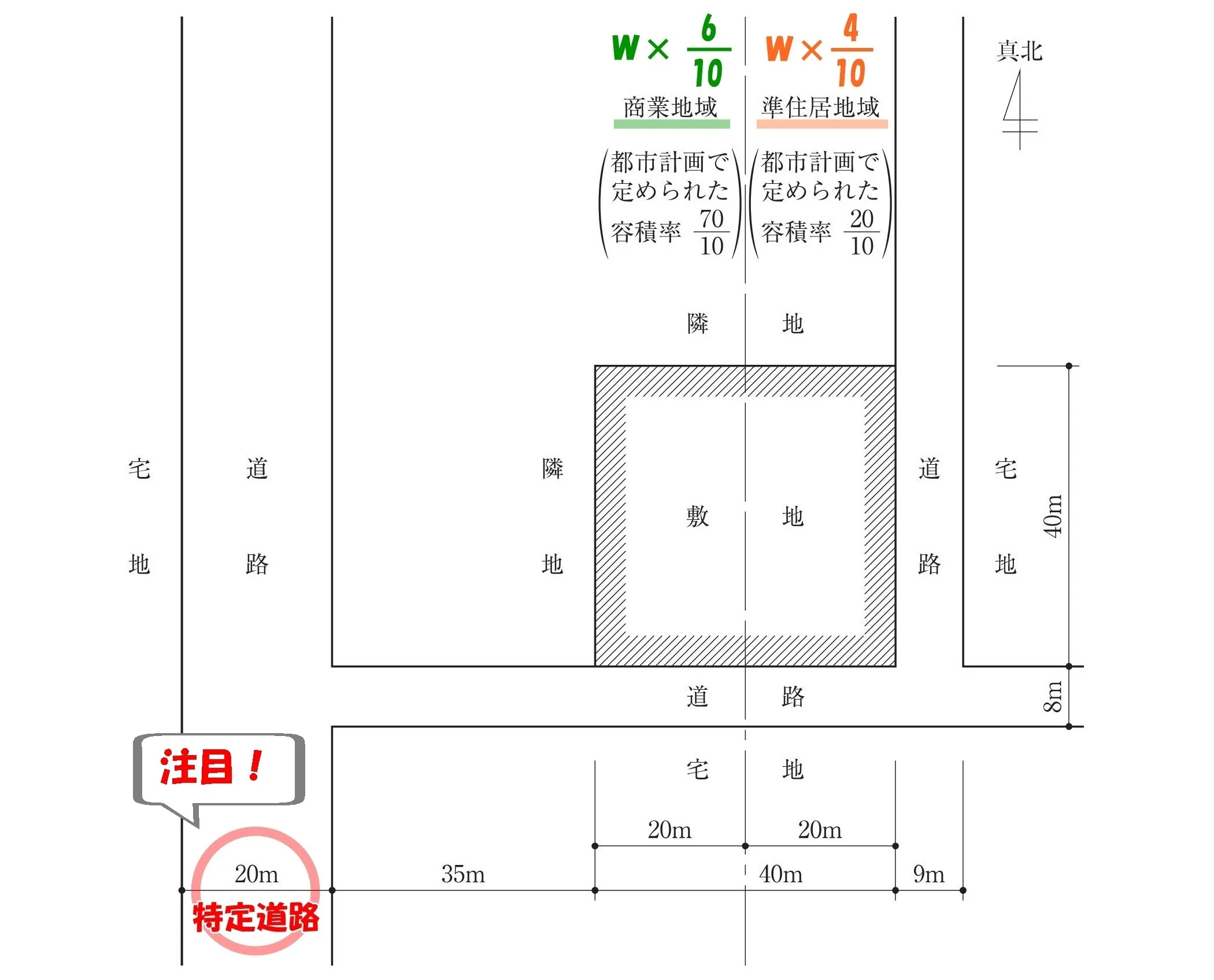




特定道路が登場する。
ということは・・!?
法52条9項:特定道路に接続する幅員6m以上12m未満の道路
建築物の敷地が、幅員15m以上の道路~「特定道路」~に接続する、幅員6m以上12m未満の前面道路のうち、特定道路からの延長が70m以内の部分において接する場合における~「幅員」とあるのは、特定道路からの延長が70m以内の部分にあつては、その幅員に”特定道路から建築物の敷地が接する前面道路の部分までの延長に応じて政令で定める数値を加えたもの”とする。
建築基準法(一部省略)



あの式がまたやって来る。
3.Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
インデックス


- 法52条【容積率】
- 9項:特定道路に接続する幅員6m以上12m未満の道路
- 令135条の18:Wa=(12-Wr)×(70-L)/ 70
$$Wa=\frac{ (12-Wr)×(70-L) }{ 70 }$$



計算式が気持ち悪い・・
何となく、ややこしそう。



大丈夫!
図解で話を進めていくよ。
攻略ポイント
ここでは「Wa」を求めるために、その位置を敷地図に「図示」していく方法をとります。
起点を取る
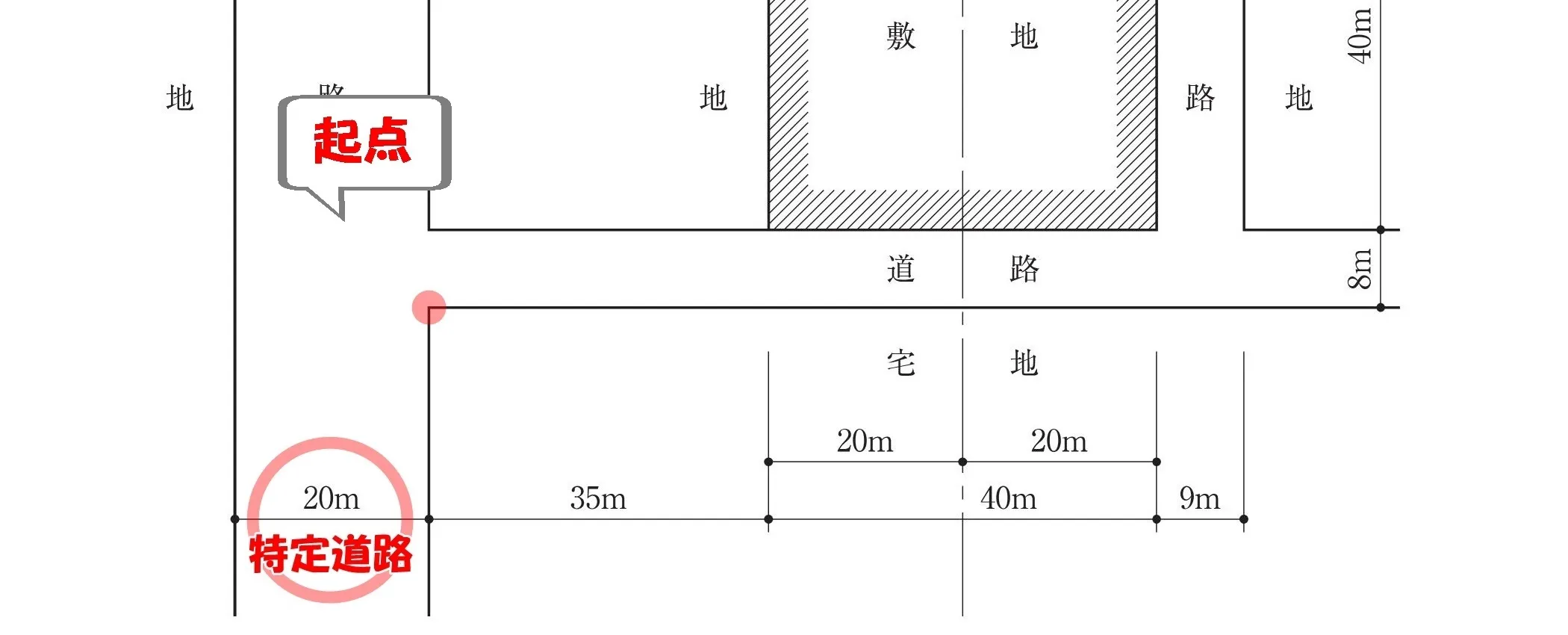

Wa=(12-Wr)×(70-L)/ 70
特定道路と前面道路の交差点の角に、〇印(起点)をつける。
起点から70mの位置
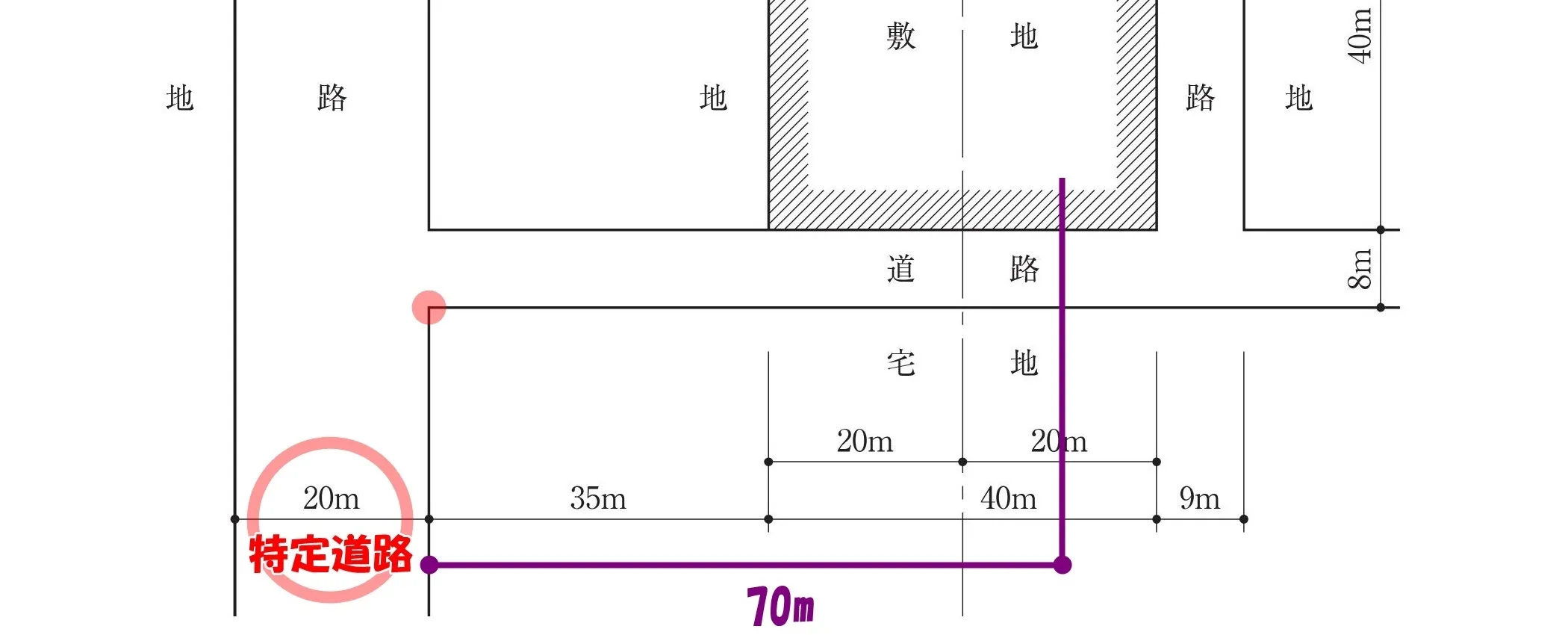

Wa=(12-Wr)×(70-L)/ 70
「起点」となる位置から敷地に向かって、「70m」の位置をとる。



交差点の角から、
敷地に向かって「70m」
起点から12mの位置
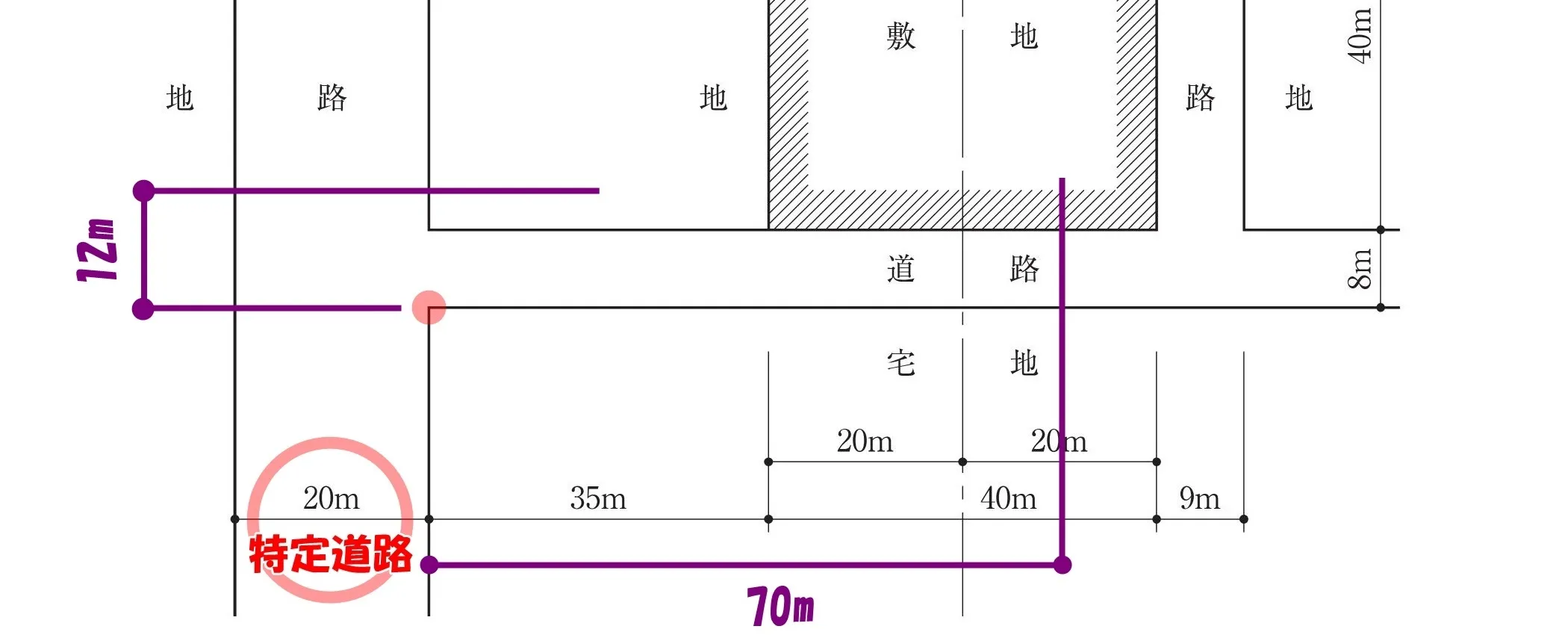

Wa=(12-Wr)×(70-L)/ 70
「起点」となる位置から敷地に向かって、「12m」の”道路の幅”をとる。



交差点の角から「12m」
道路を確保するイメージ。
道路境界線との交点をとる
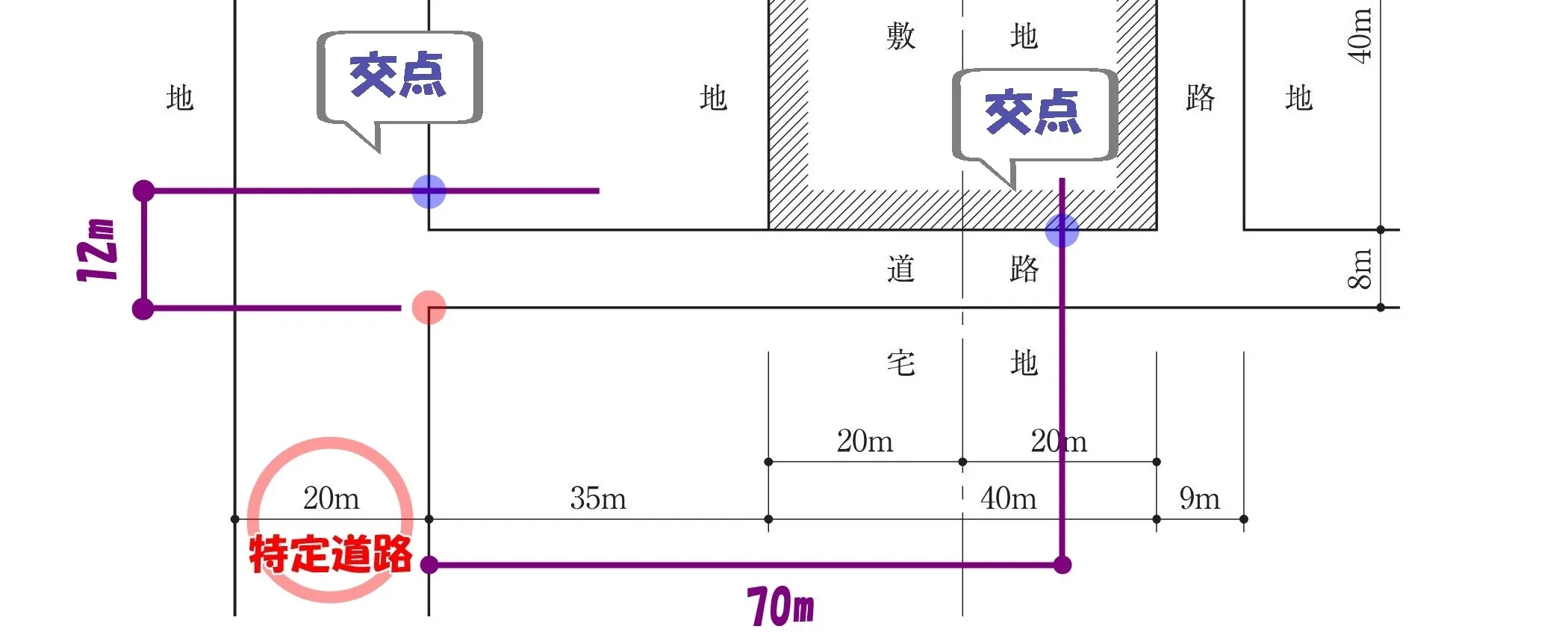

Wa=(12-Wr)×(70-L)/ 70
「起点」から敷地に向かって「12m」の道路の幅と、道路境界線との交点をとる。
交点を結ぶ
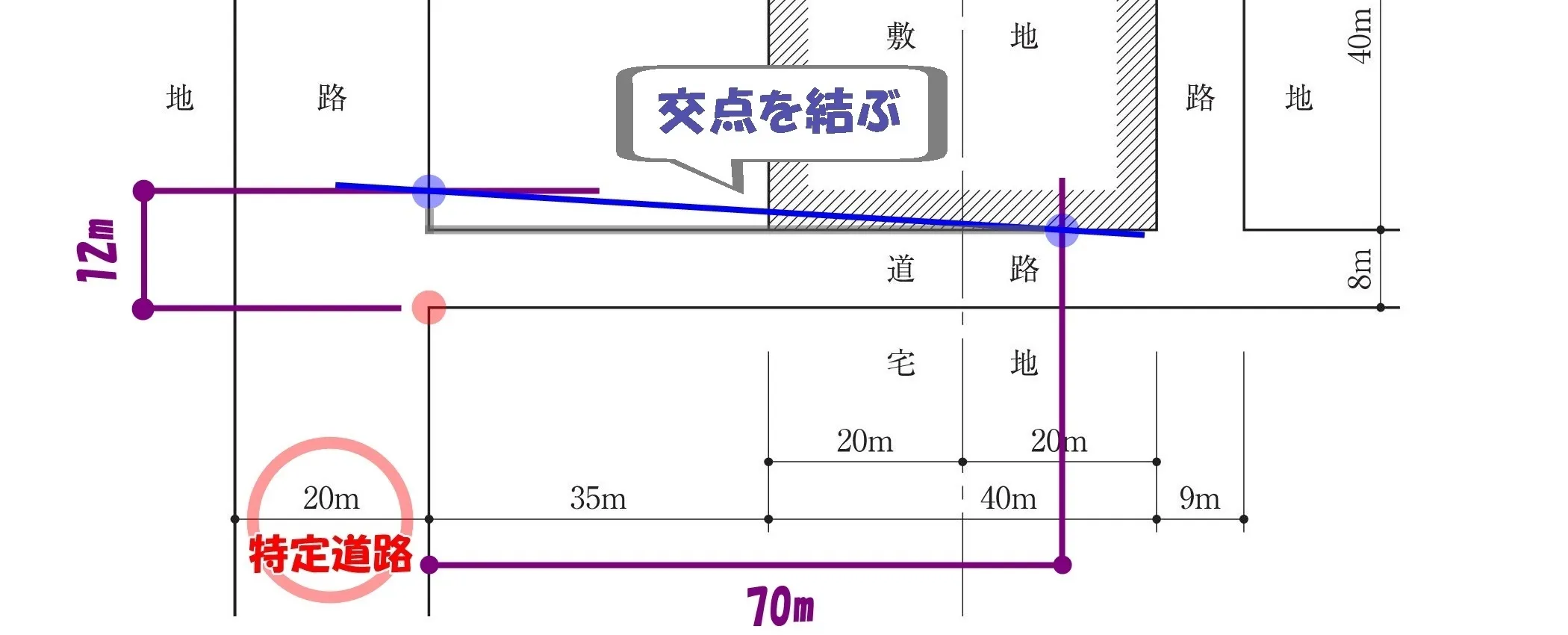

Wa=(12-Wr)×(70-L)/ 70
- 「起点」から敷地に向かって「70m」の位置
- 「起点」から敷地に向かって「12m」の道路の幅
この2つの交点を斜線で結び、道路境界線に囲まれた”直角三角形”をつくる。



交点を結んで、
小さな三角形をつくる。
Waの位置づけ
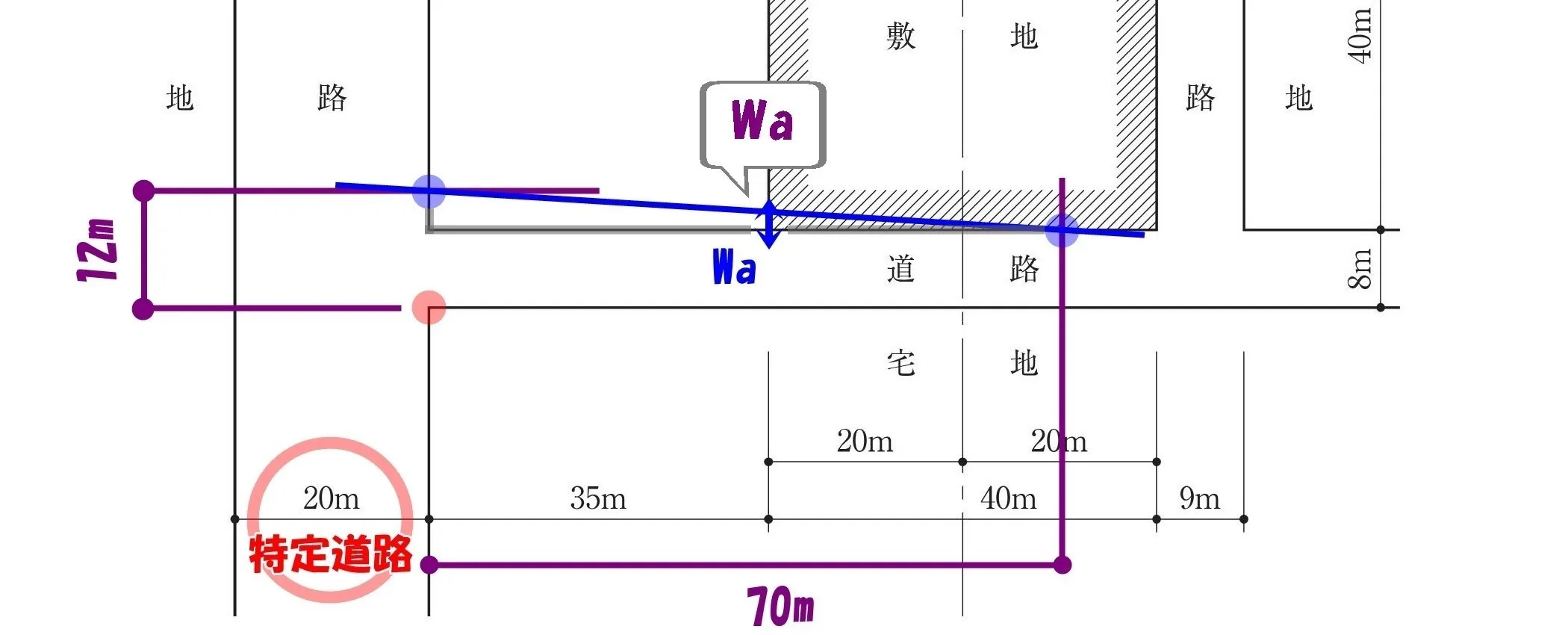

法52条9項:特定道路に接続する幅員6m以上12m未満の道路
$$Wa=\frac{ (12-Wr)×(70-L) }{ 70 }$$



出たな!Waの式よ。
各部分の寸法を書き込む
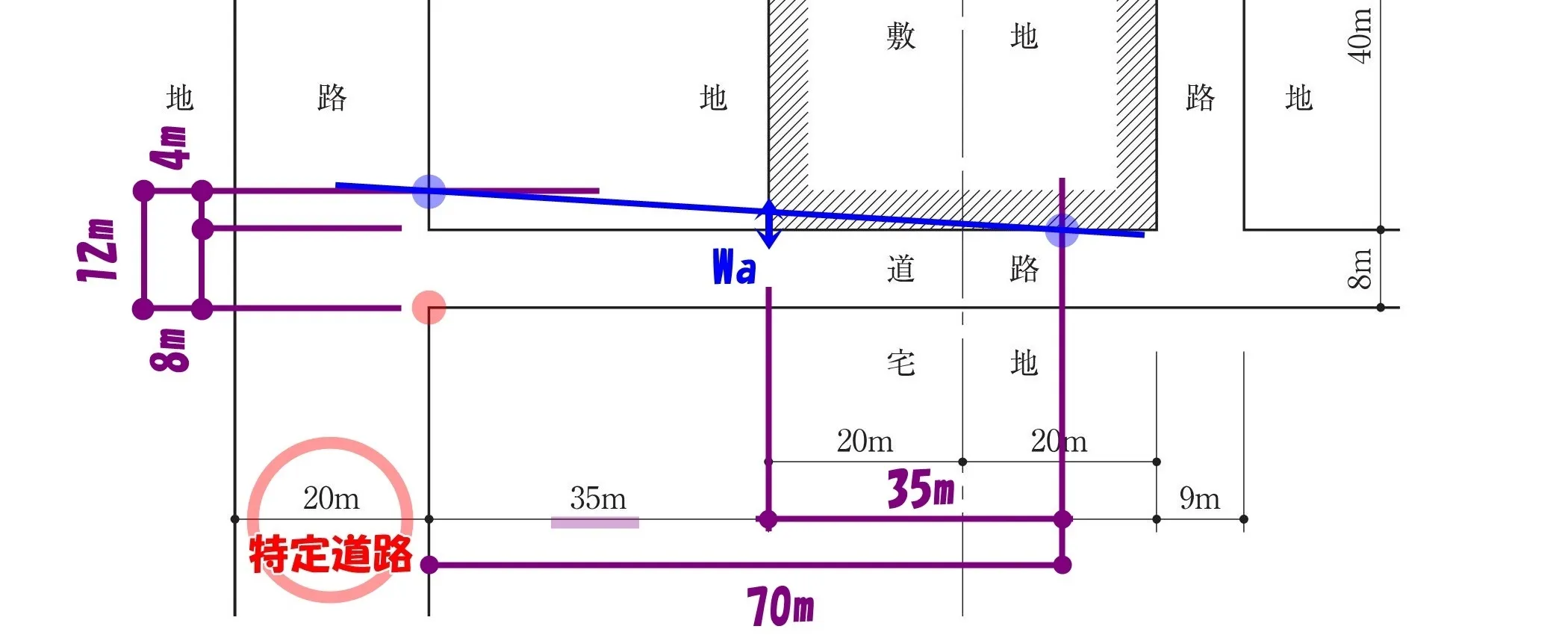

Wa=(12-Wr)×(70-L)/ 70
斜線と道路境界線とWaに囲まれた”小さな三角形”の寸法を書き込む。



Waはどこだ?
三角形の辺の比でWaの値を求める
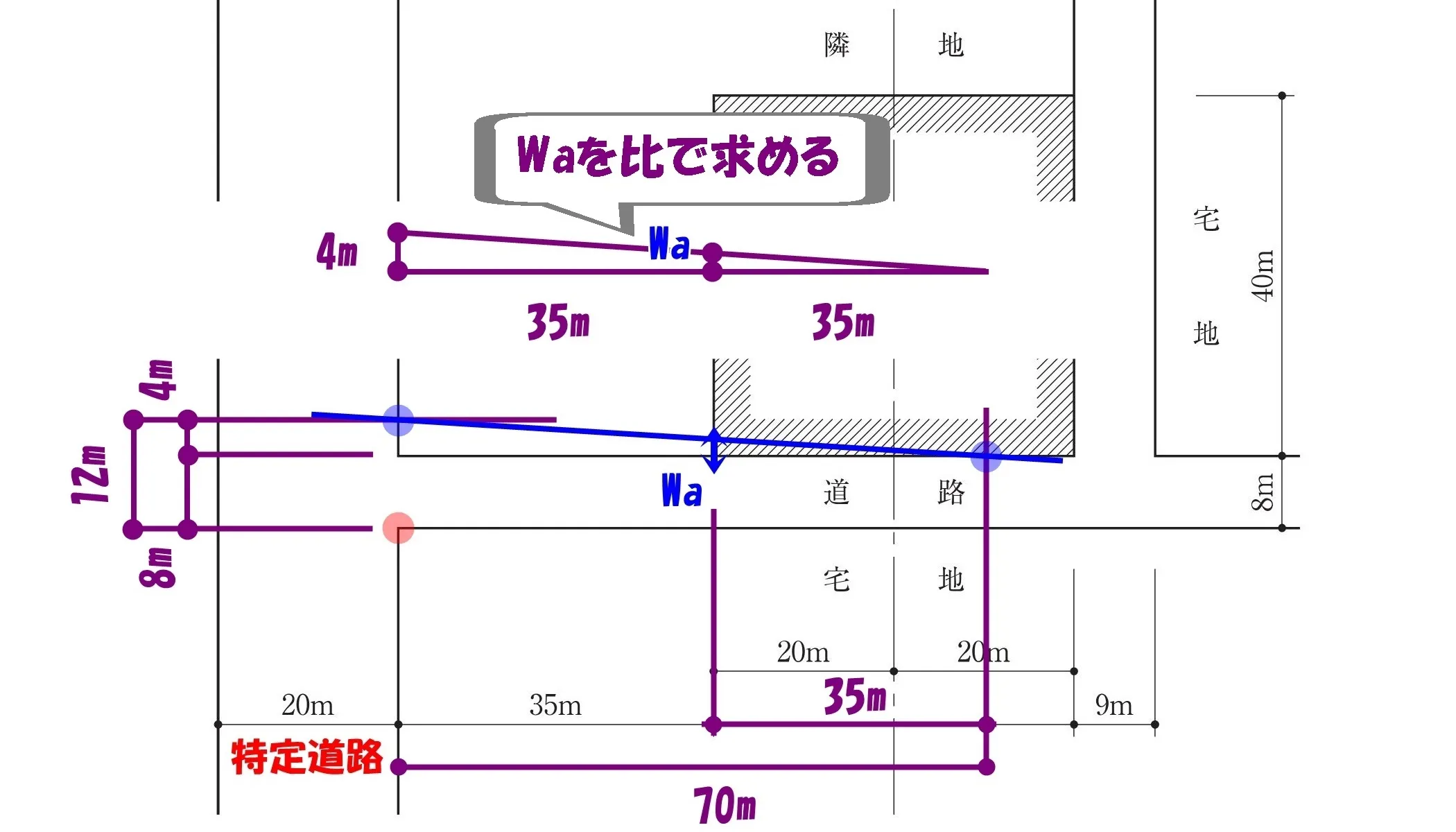

Wa=(12-Wr)×(70-L)/ 70
ここからは計算式ではなく、「三角形の辺の比」でWaの値を求めていきます。



Waを求めます。
三角形の辺に数値をメモする
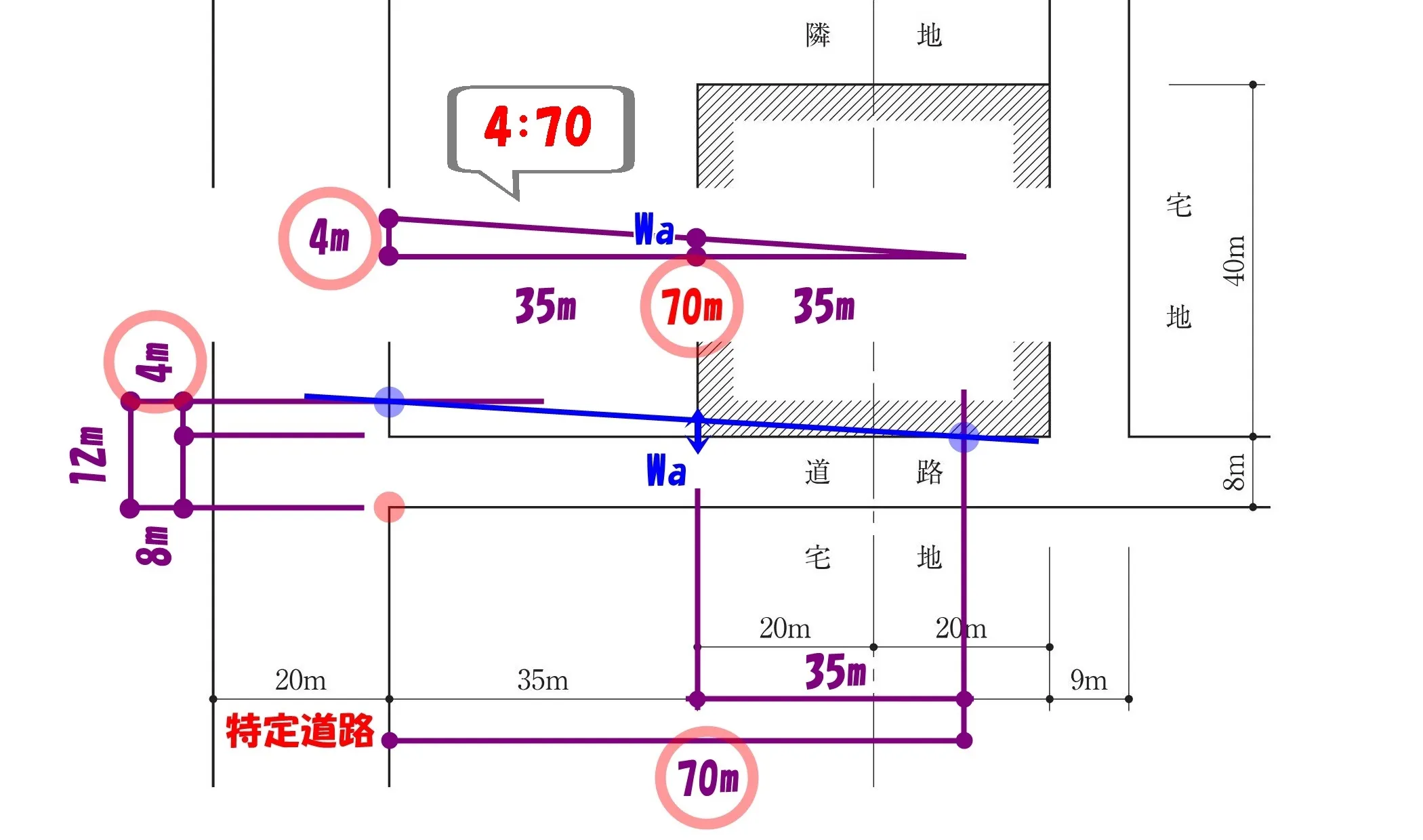

メモする
- 三角形の底辺:70m
- 三角形のタテ辺:4m
- 小さな三角形の底辺:35m
- 小さな三角形のタテ辺:Wa



Waが見えてきたぞ!
三角形の辺の比でWaの値を求める
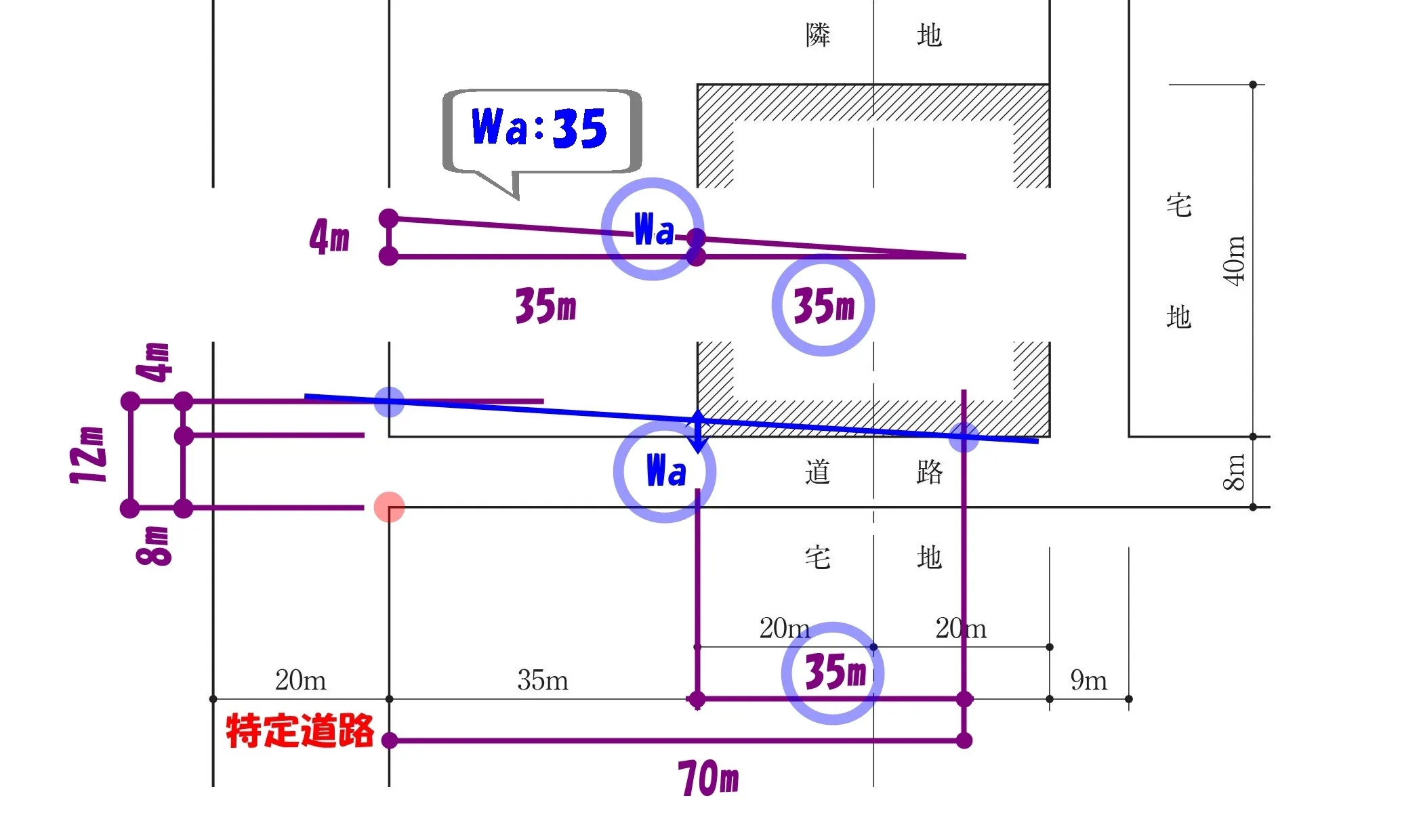

$$4:70=Wa:35→(内*内=外*外)の法則より,$$$$70*Wa=4*35→Wa=\frac{ 4*\underline{35} }{ \underline{70} }=4*\frac{ 1 }{ 2 }=2m$$
Wa=2m
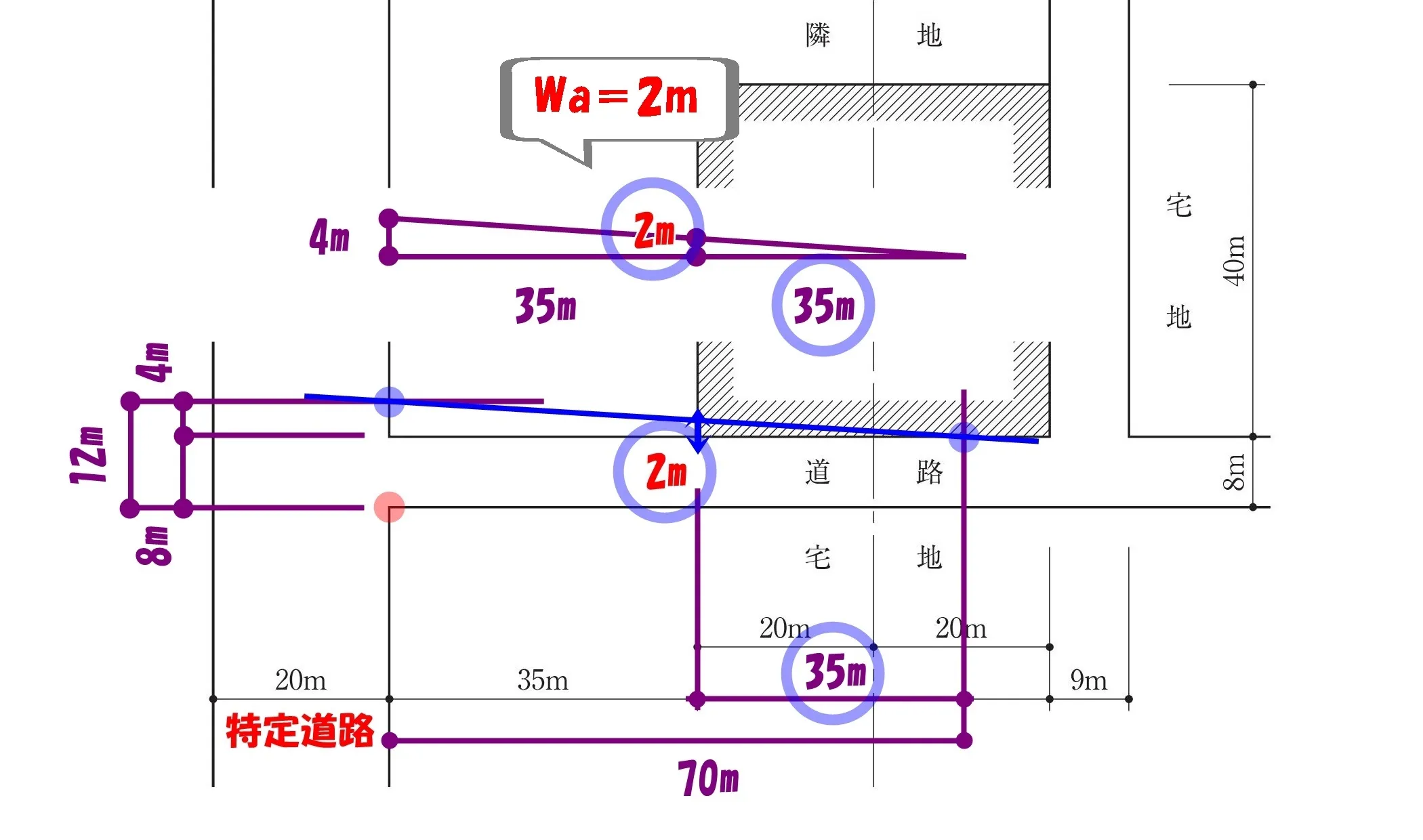

$$Wa=\frac{ (12-Wr)×(70-L) }{ 70 }$$
$$Wr=8m,L=35mを代入しても、答えは”2m”となる。$$



イメージで見ると、
理屈は単純ですよね?
敷地図の道路に書き込む
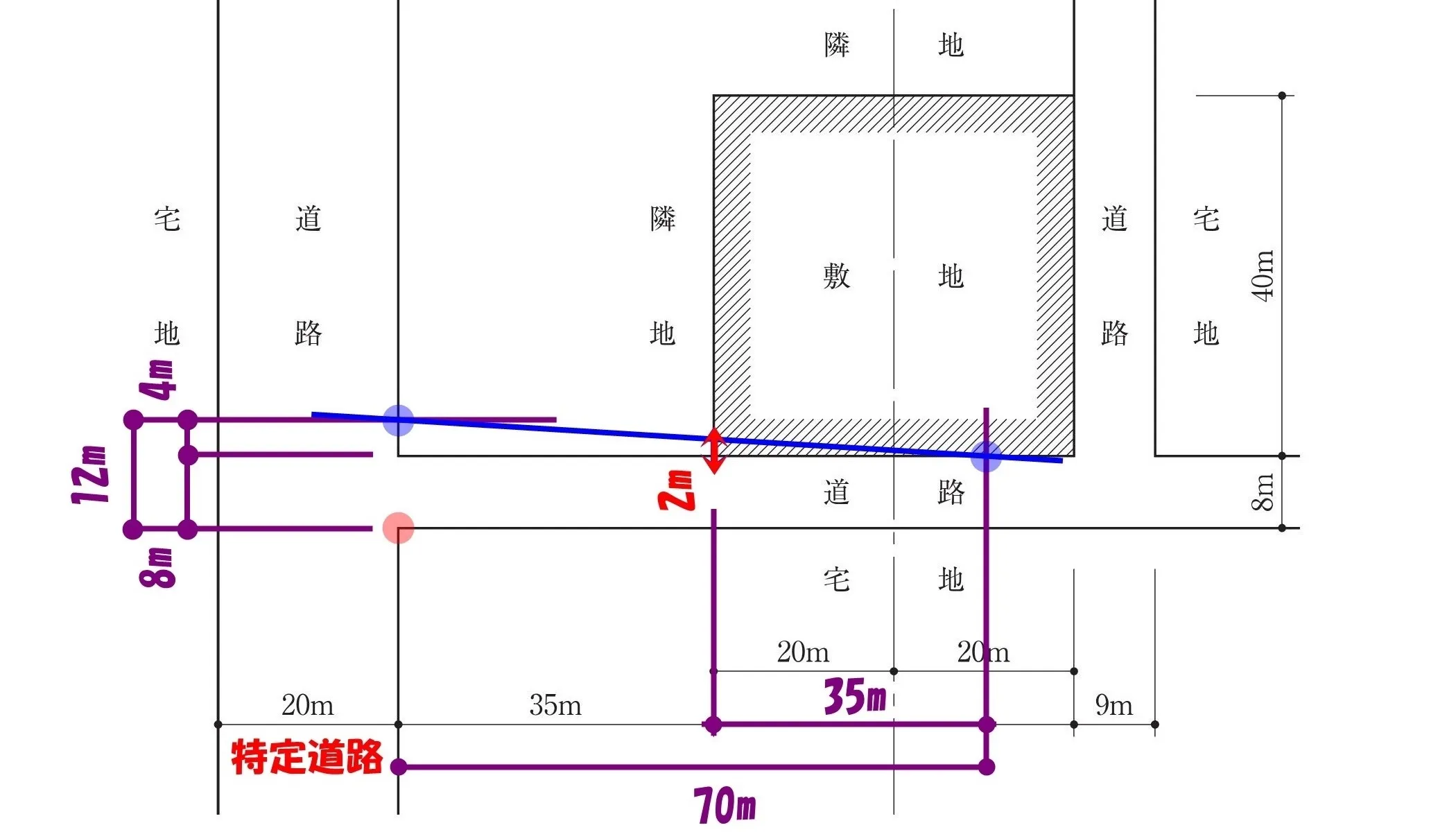

三角形の辺の比で求めたWaの数値「2m」を敷地図に書き込む。
前面道路の幅は+2m
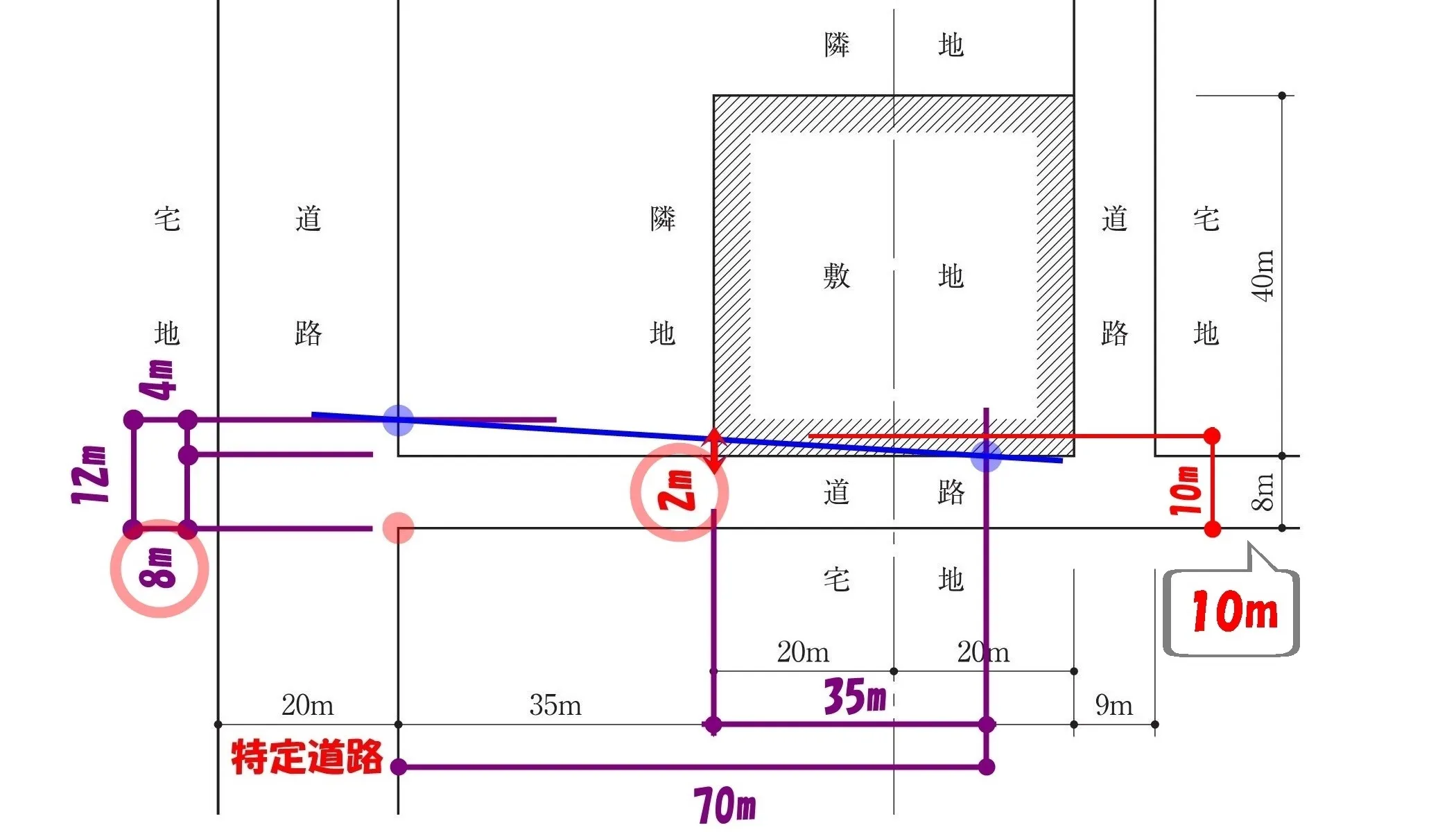

法52条9項:特定道路に接続する幅員6m以上12m未満の道路
前面道路の幅に「2m」をプラスして、「8m」→「10m」に修正しておく。



修正部分は忘れずに、
メモしておきましょう。
建築物の敷地が、幅員15m以上の道路~「特定道路」~に接続する、幅員6m以上12m未満の前面道路のうち、特定道路からの延長が70m以内の部分において接する場合における~「幅員」とあるのは、特定道路からの延長が70m以内の部分にあつては、その幅員に”特定道路から建築物の敷地が接する前面道路の部分までの延長に応じて政令で定める数値を加えたもの”とする。
建築基準法(一部省略)
2面道路の幅を修正する
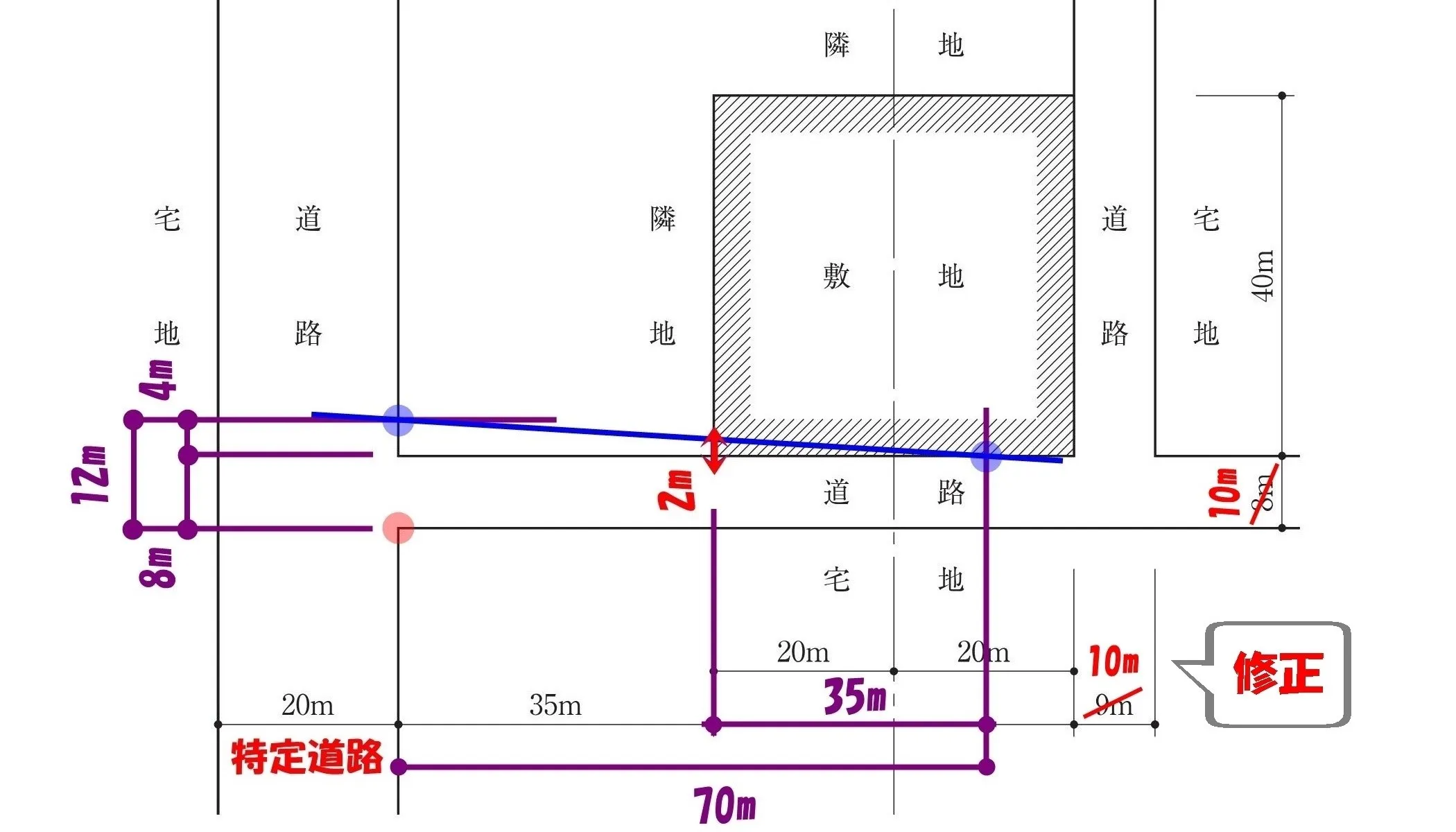

この時点で、もう一方の「9m」道路の幅も「9m」→「10m」に修正しておきましょう。



道路の幅は最大値を適用する。
~(前面道路が2以上あるときは、その幅員の最大のもの。~)
建築基準法(一部省略)
4.法定容積率と道路容積率から、厳しい数値を選択する
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
法52条2項:道路容積率
前面道路(前面道路が2以上あるときは、その幅員の最大のもの。以下この項及び第12項において同じ。)の幅員が12m未満である建築物の容積率は、当該前面道路の幅員のmの数値に、次の各号に掲げる区分に従い、当該各号に定める数値を乗じたもの以下でなければならない。
建築基準法(一部省略)
道路幅「10m」をメモする
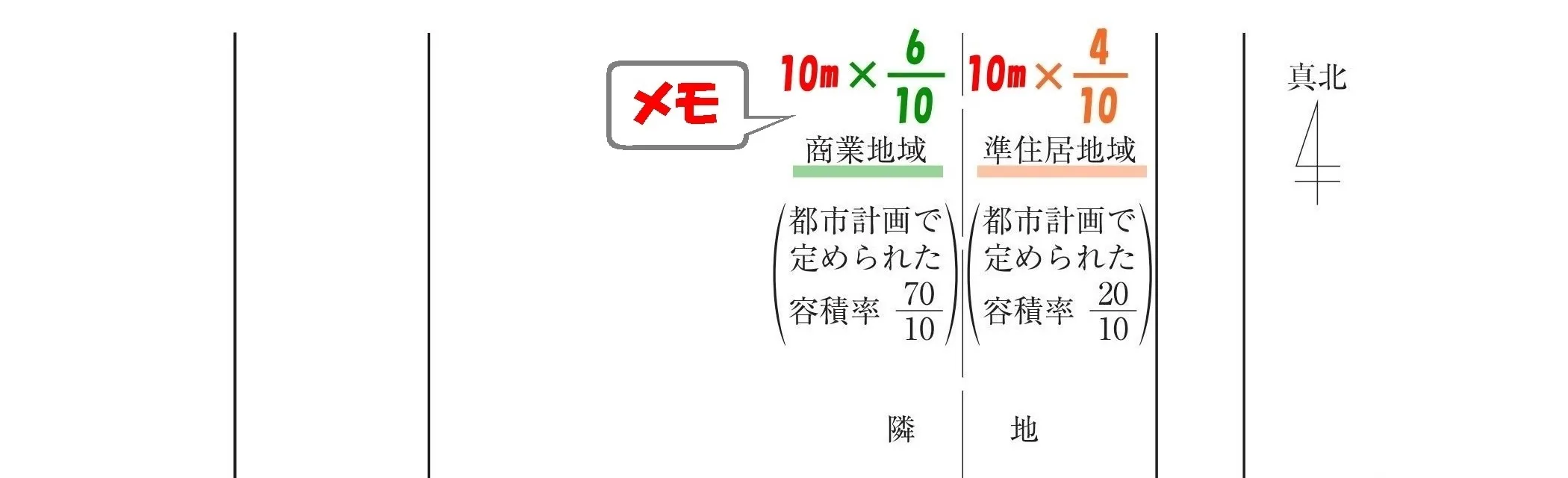

$$商業地域:W*\frac{ 6 }{ 10 },準住居地域:W*\frac{ 4 }{ 10 }$$
$$商業地域:10*\frac{ 6 }{ 10 }=\frac{ 60 }{ 10 },準住居地域:10*\frac{ 4 }{ 10 }=\frac{ 40 }{ 10 }$$
数値を転記して比べる
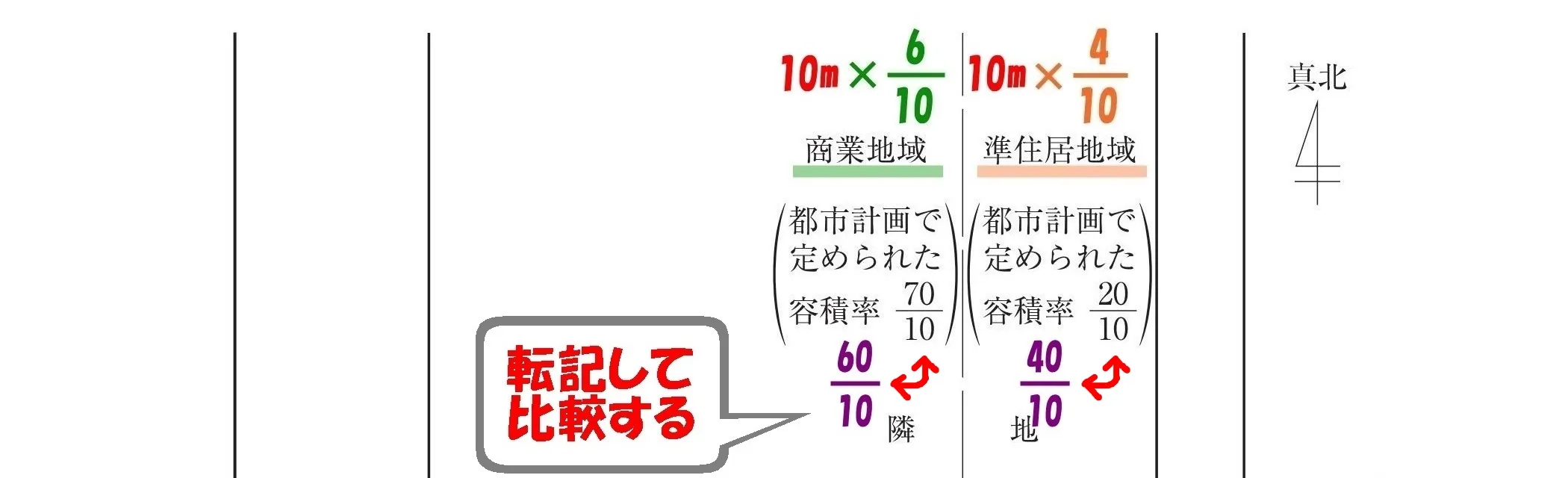

$$商業地域の容積率の比較:\underline{\frac{ 60 }{ 10 }}<\frac{ 70 }{ 10 }$$
$$準住居地域の容積率の比較:\frac{ 40 }{ 10 }>\underline{\frac{ 20 }{ 10 }}$$
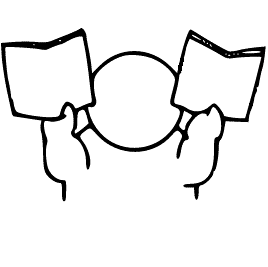


法定容積率と道路容積率
2つ比べて厳しいほうを選ぶ。
数値を修正する
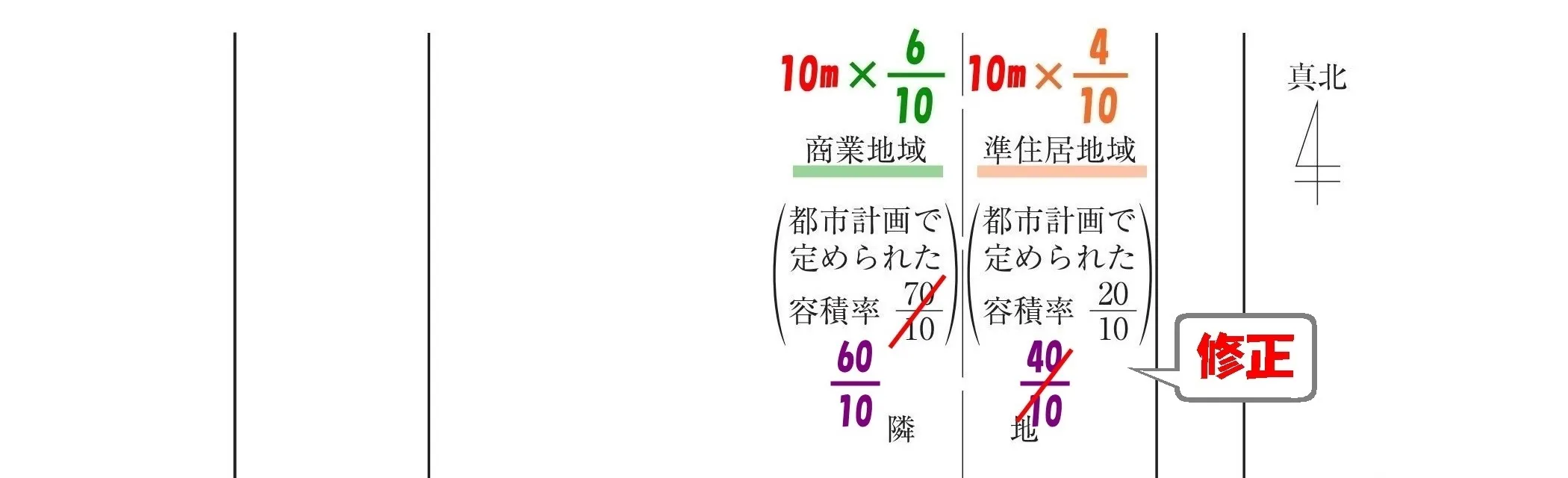

採用する容積率を間違えないために、大きい数値は斜線で消しておく。
厳しい容積率を選択する
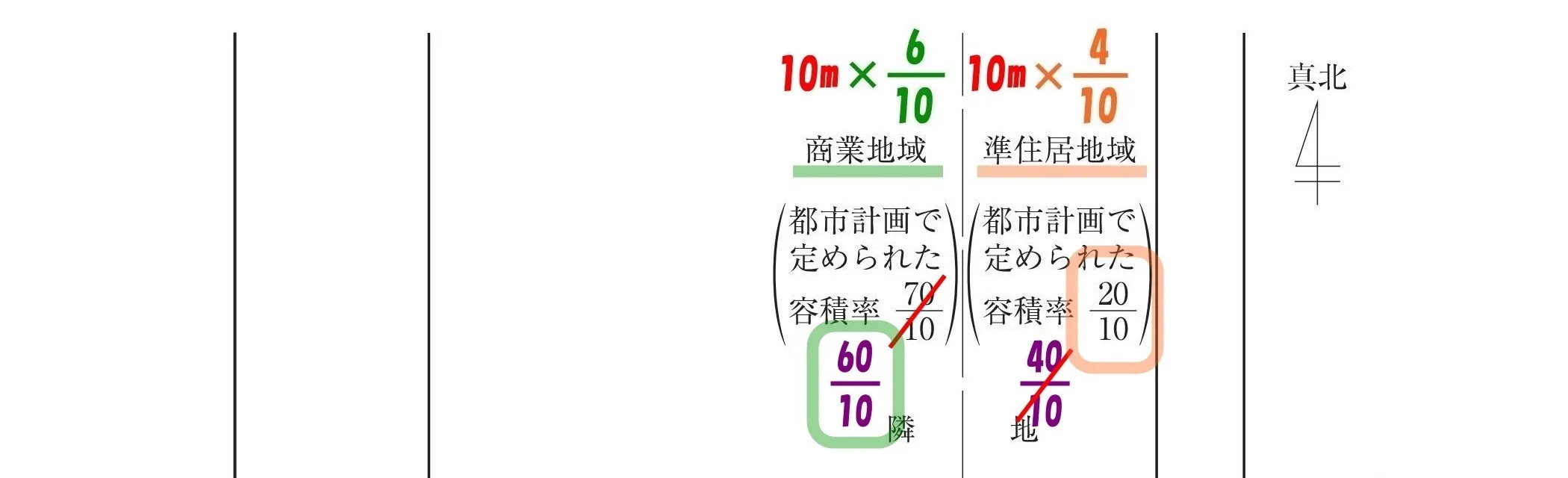

$$商業地域の容積率:\frac{ 60 }{ 10 },準住居地域の容積率:\frac{ 20 }{ 10 }$$



採用しない数値は、
バツ印を入れて間違いを防ぎます。
5.それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く
敷地面積×容積率
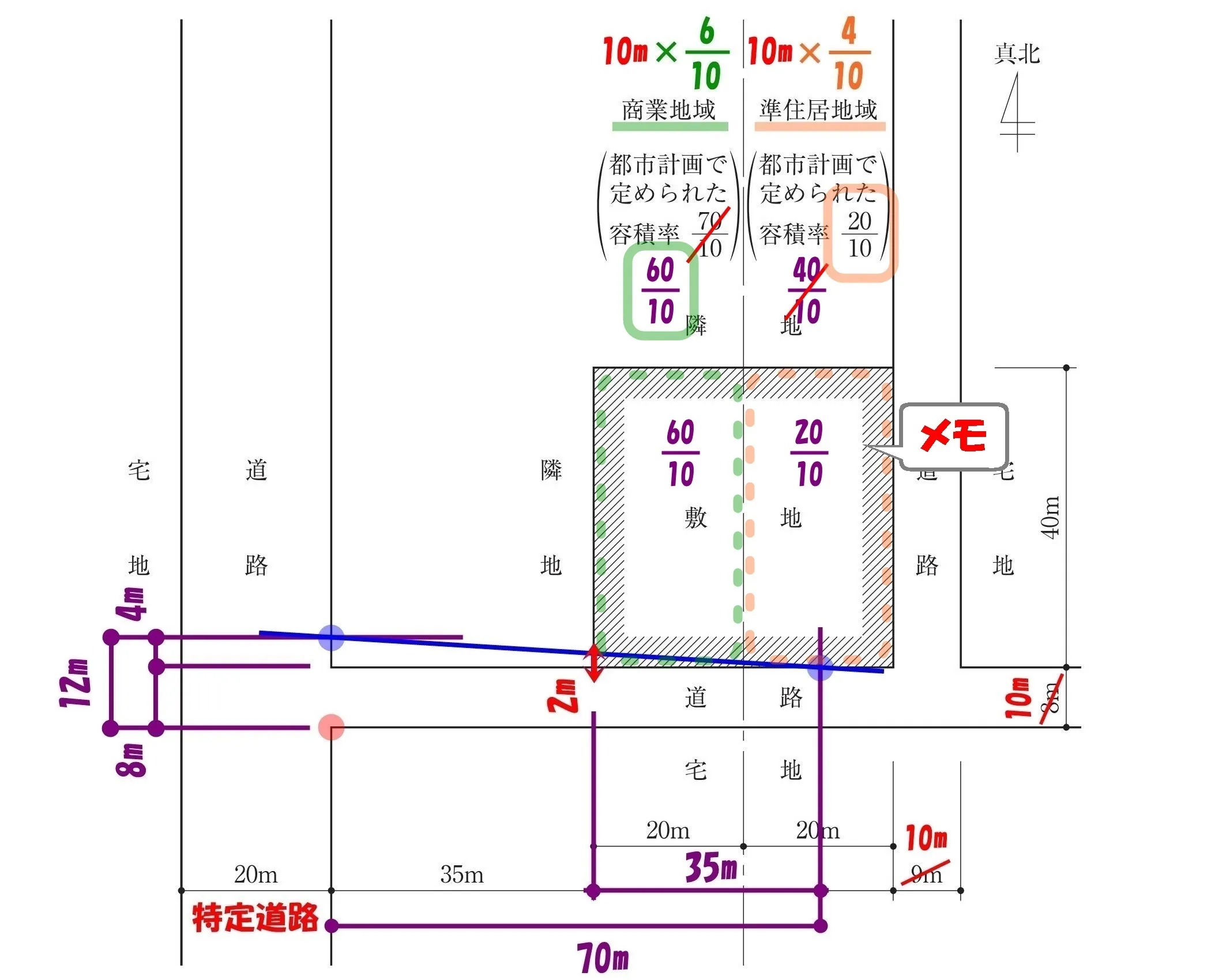

法52条7項【容積率】の加重平均
$$\frac{ (A*\frac{ a }{ 10 })+(B*\frac{ b }{ 10 }) }{ (A+B) }$$$$AとB:それぞれの敷地面積、a/10とb/10:それぞれの容積率$$


加重平均、やめて~
その式を見せないでくれ。
【加重平均が計算できない場合の対象法】
- Aの敷地×aの容積率=Aの延べ面積を求める。
- Bの敷地×bの容積率=Bの延べ面積を求める。
- AとBの延べ面積の合計÷AとBの敷地の合計(建物の敷地全体)=容積率を求める。



私はこっちでいく!
容積率を求める
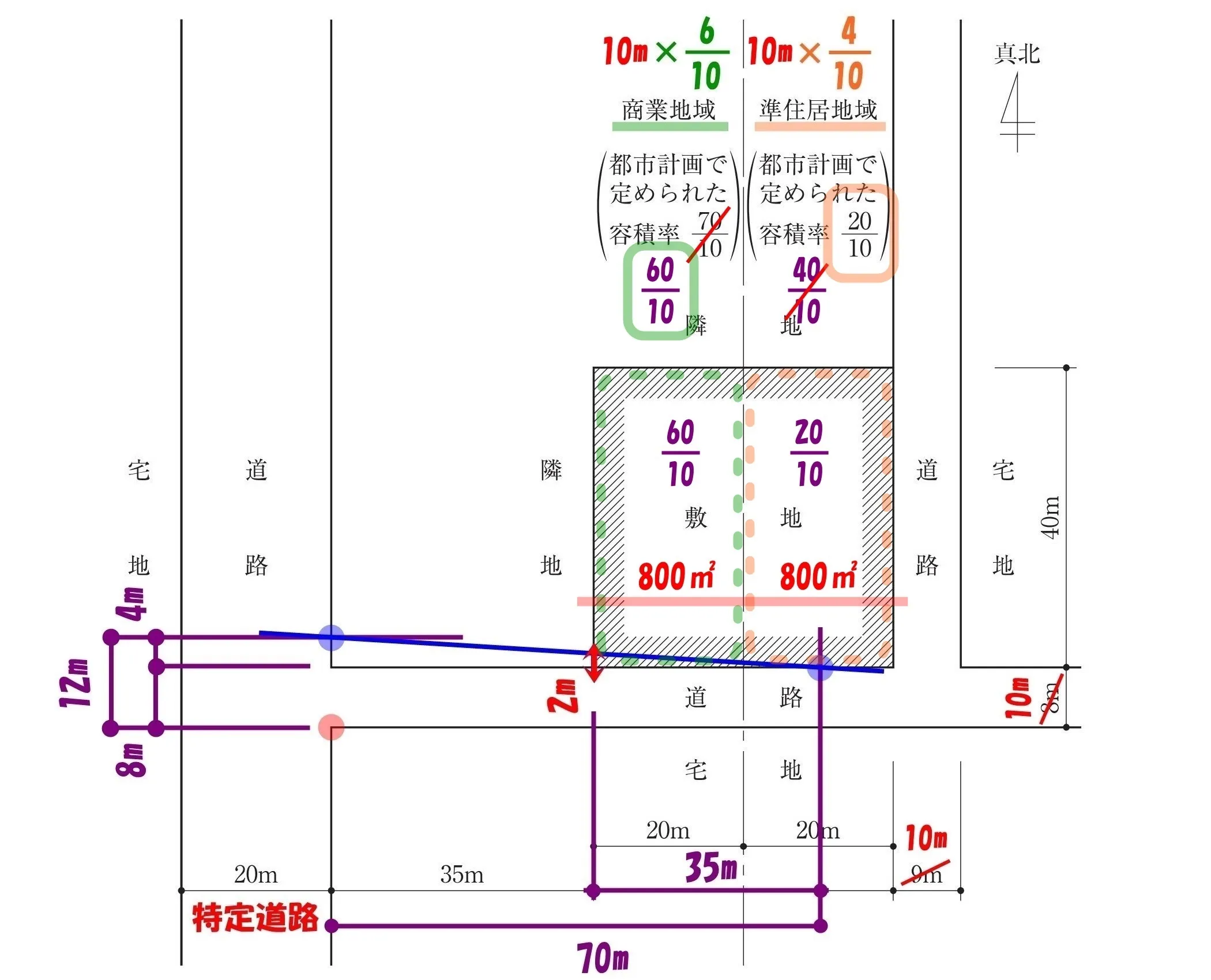

$$容積率:\frac{ (A*\frac{ a }{ 10 })+(B*\frac{ b }{ 10 }) }{ (A+B) }より$$
$$\frac{ (800*\frac{ 60 }{ 10 })+(800*\frac{ 20 }{ 10 }) }{ (800+800) }=\frac{ (\underline{800}*\frac{ 60 }{ 10 })+(\underline{800}*\frac{ 20 }{ 10 }) }{ (\underline{800}*2) }$$
$$=\frac{ (\frac{ 60 }{ 10 })+(\frac{ 20 }{ 10 }) }{ 2 }=\frac{ 1 }{ 2 }*\{(\frac{ 60 }{ 10 })+(\frac{ 20 }{ 10 }) \}=\frac{ 30 }{ 10 }+\frac{ 10 }{ 10 }=”\frac{ 40 }{ 10 }”$$



ふう・・ふう・・
容積率を何とか撃破!
答え.2

攻略ポイント
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く


この動画を YouTube で視聴
高さ制限
難易度:★★★★★





高さ制限に挑戦!



この動画を YouTube で視聴
攻略ポイント
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
インデックス


- 法56条【高さ制限】
- 一号:道路斜線
- 二号:隣地斜線
- 三号:北側斜線
- 法別表第3
- (い)前面道路との関係
- (ろ)用途地域との関係
- (は)道路斜線の適用距離
- (に)×数値
- 令132条:2以上の前面道路の緩和
- 令135条の2【敷地の高低差】
- 道路斜線の起点の高さ
- 令135条の4【敷地の高低差】
- 二号:北側斜線の起点の高さ



インデックスの奥義!
関連条文をグルーピングする。
問題文の要点をマーキング


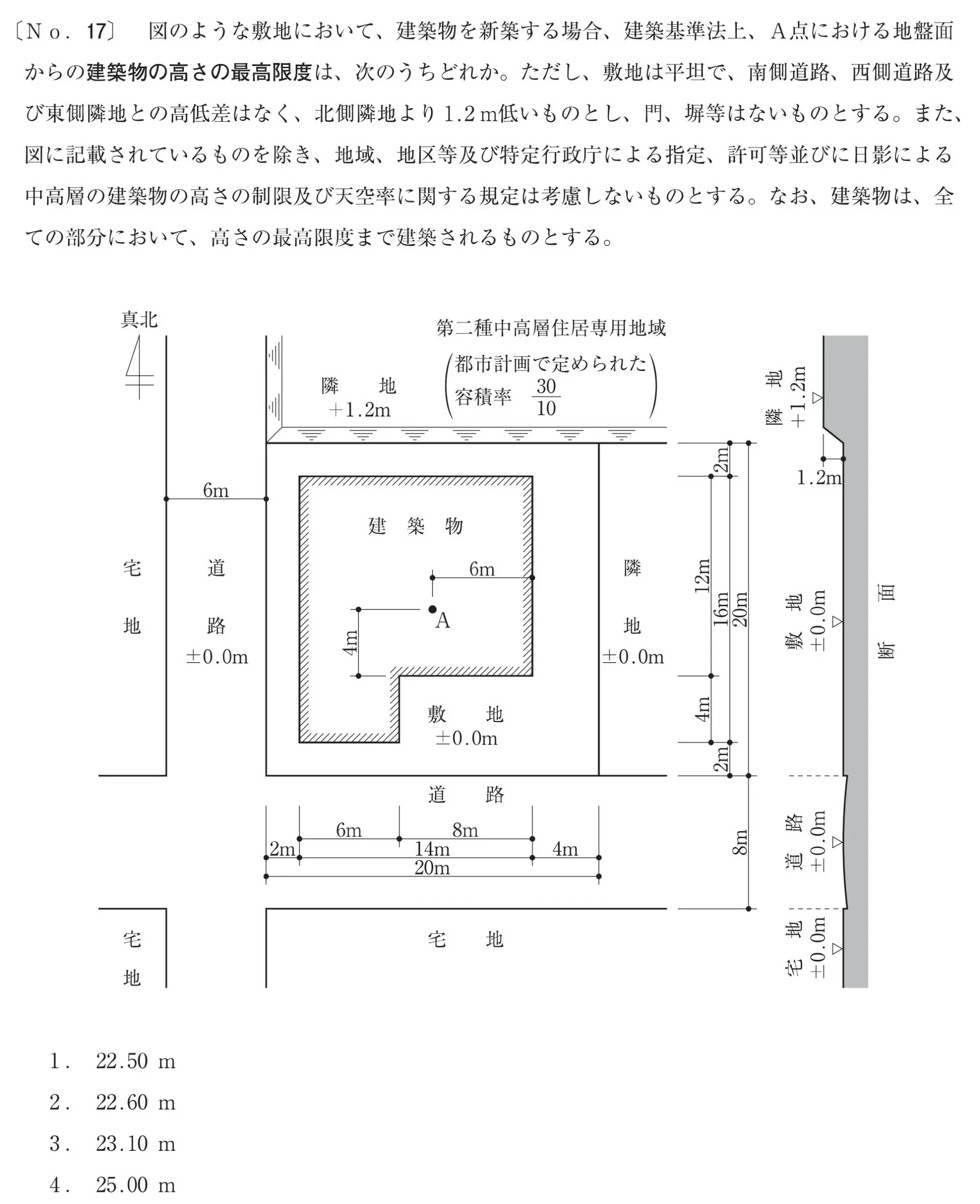
チェックポイント
- 1.建築物の高さの最高限度を求める。
- 2.建築物の敷地は平坦で、北側隣地より1.2m低い。
- 3.建築物は、全ての部分において高さの最高限度まで建築される。



エネルギーを注入!
1.用途地域から、検討する高さ制限をメモする
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
用途地域をチェック!
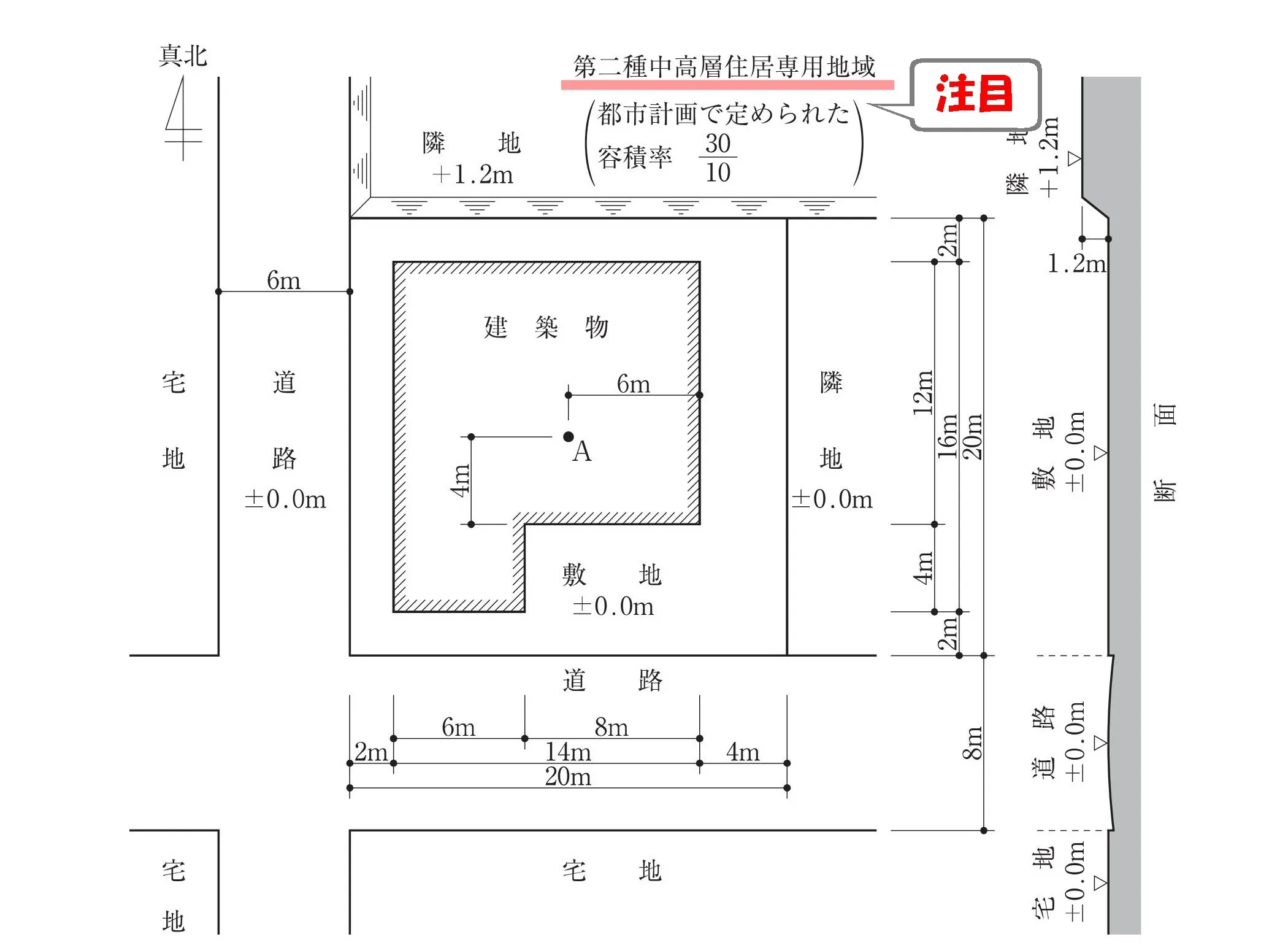



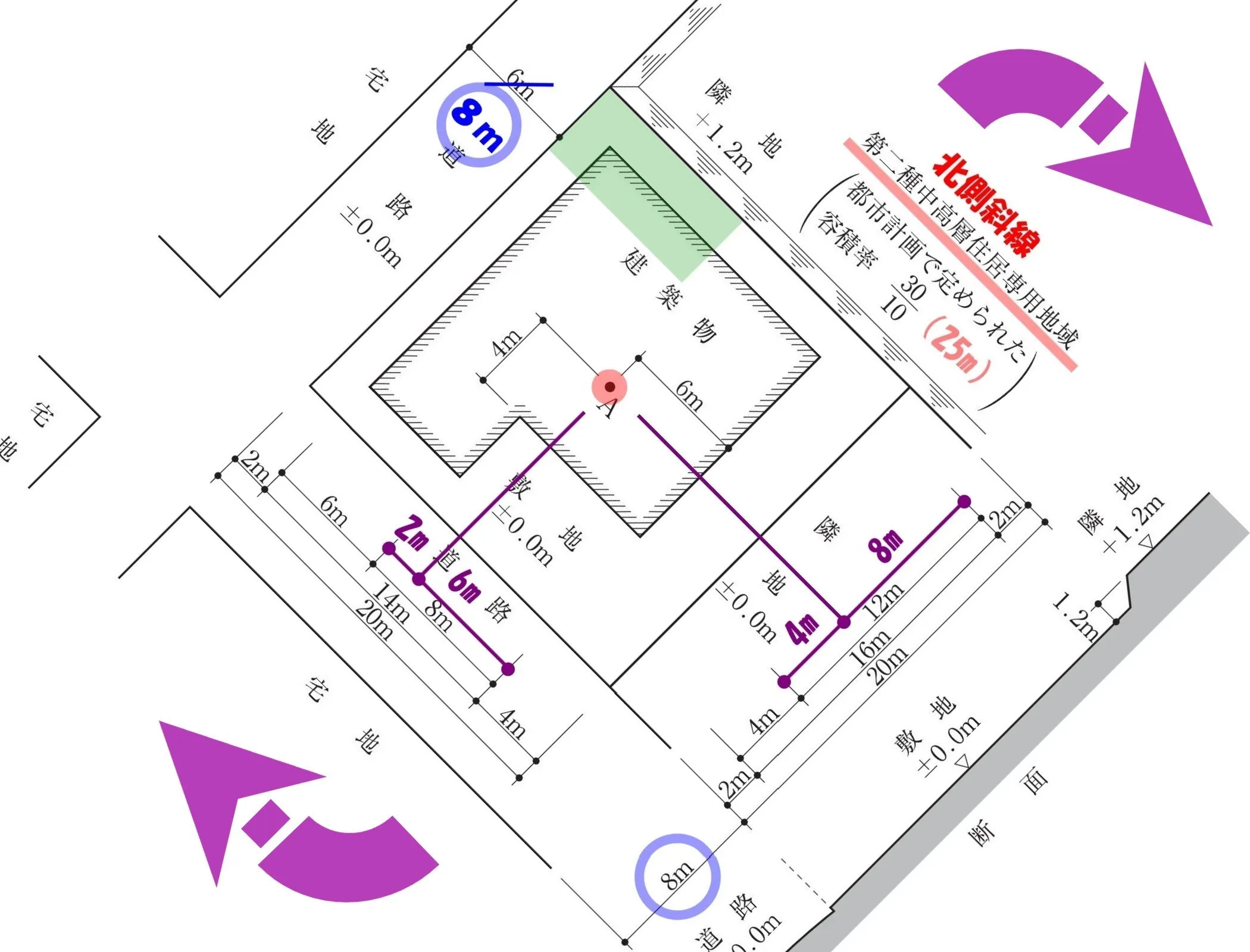
法別表第3(に)×数値
道路斜線における水平距離に掛ける「1.25」「1.5」は、法別表第3で確認する。
用途地域が「第二種中高層住居専用地域」なので、道路斜線の倍率は「×1.25」になります。



×1.25


法別表第3(は)適用距離
容積率は「30/10」、法別表第3により道路斜線の適用距離「25m」を確認する。



道路斜線は25mまで。
道路斜線の適用距離
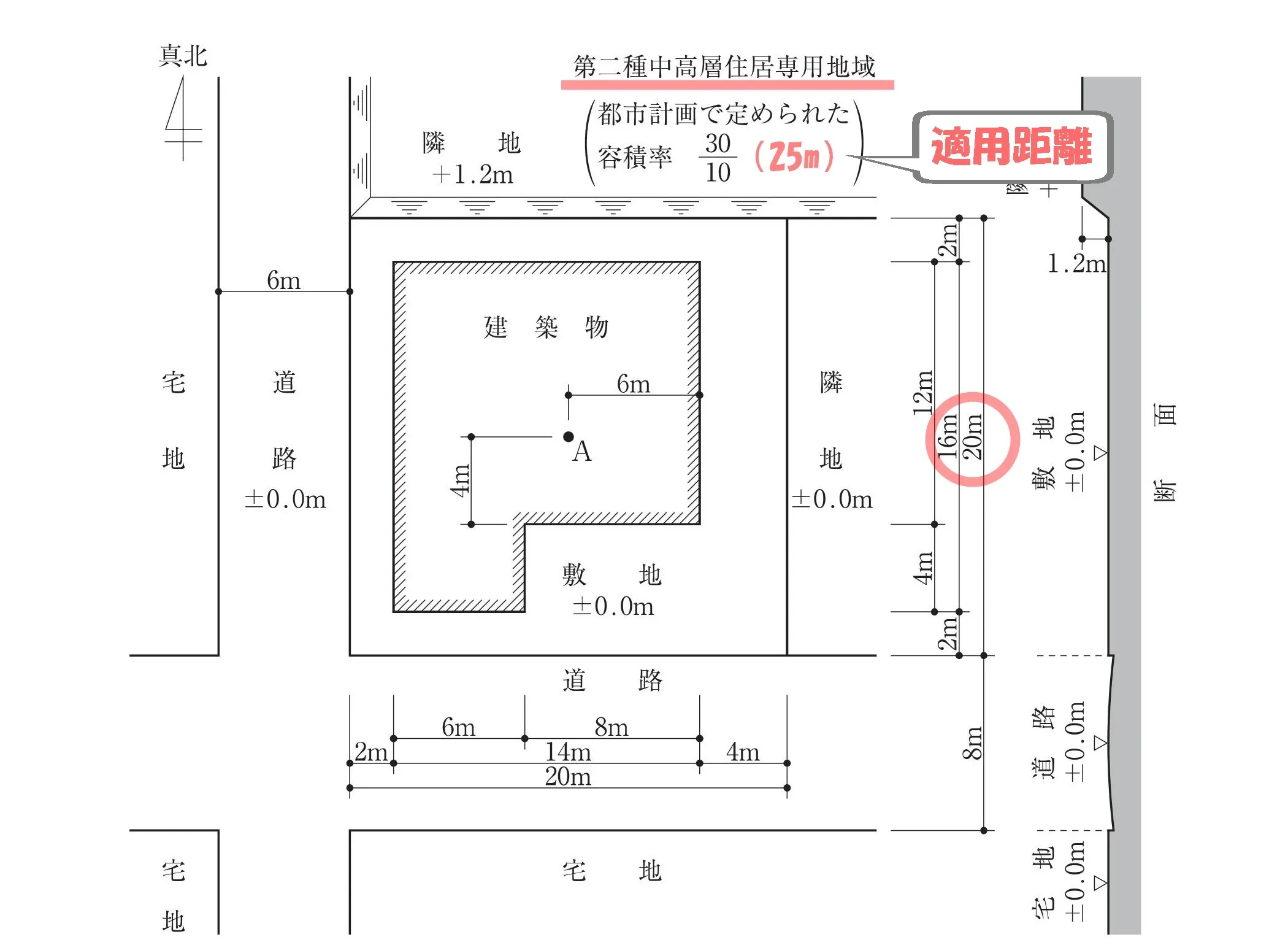

敷地のサイズは「20m×20m」なので、敷地内はすべて道路斜線の適用範囲内となります。



高さ制限の問題なので、
道路斜線は外せないよね。
北側斜線が適用される
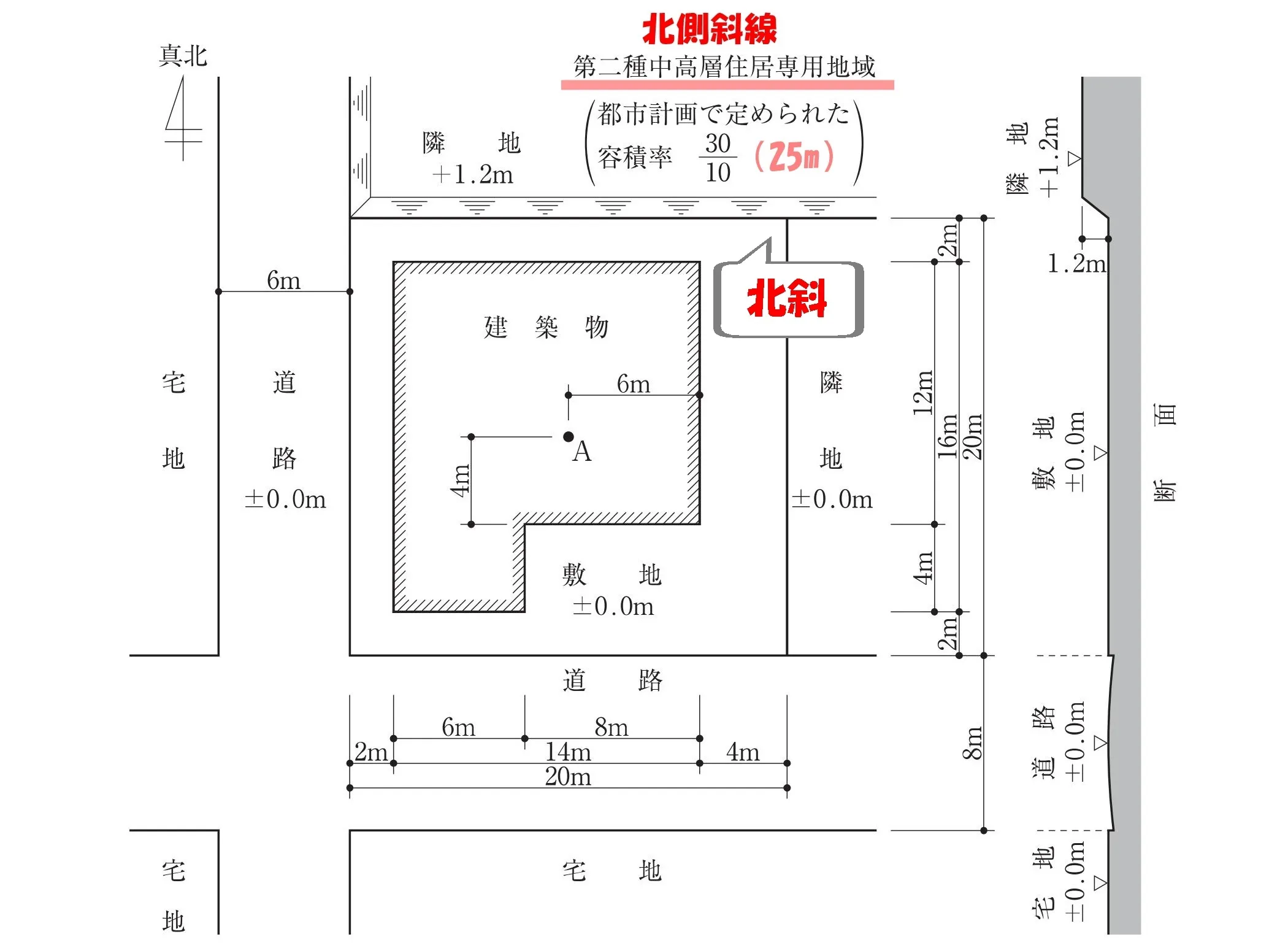




やだ、北側斜線いらない。
法56条【高さ制限】三号:北側斜線
チェックポイント!
「第二種中高層住居専用地域」より、高さ制限は「北側斜線」のチェックも必要となる。



たった1問の中に、
詰め込み過ぎなんだよな。
問題用紙の余白にメモする
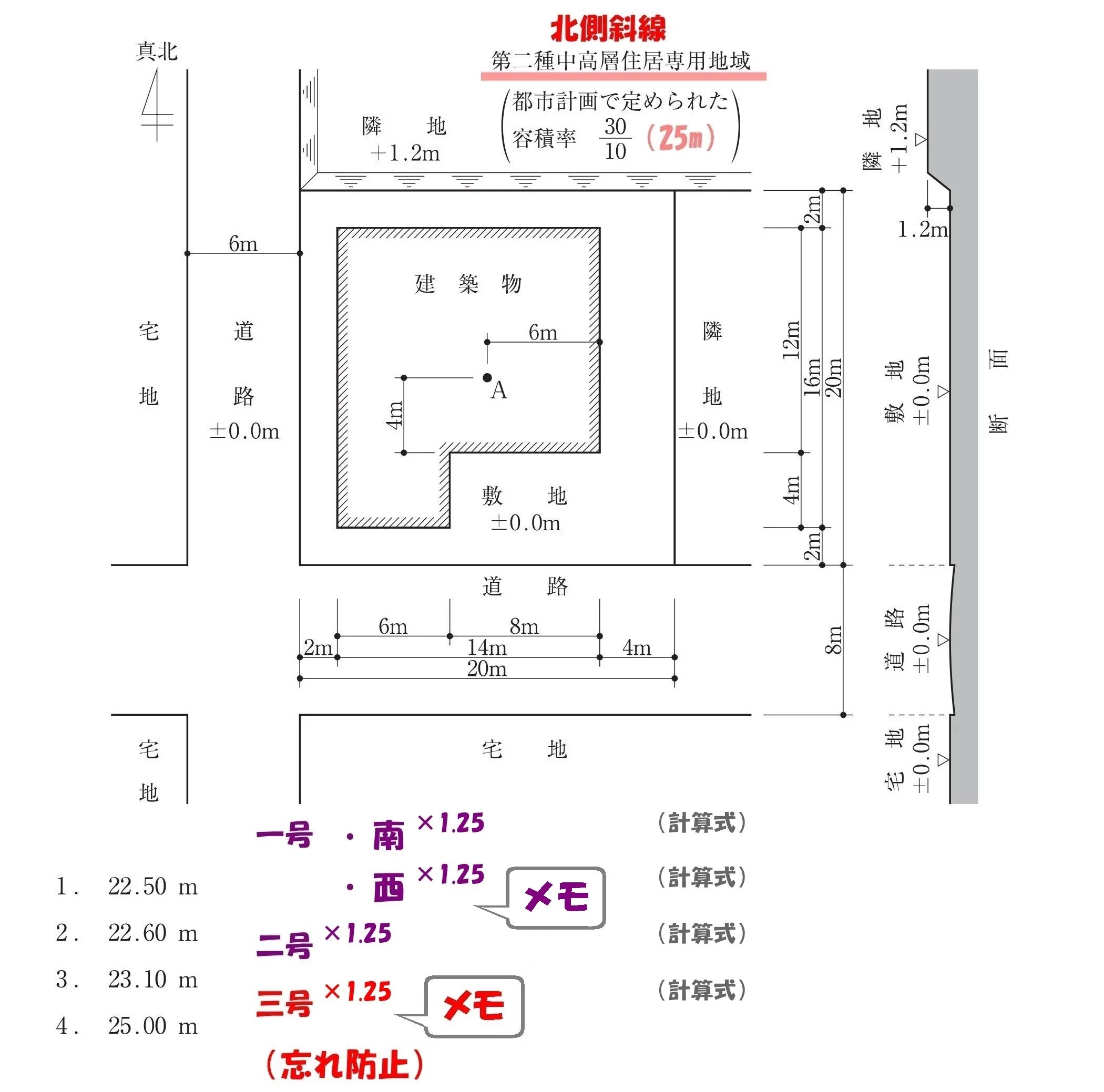

- 一号(道路斜線):×1.25
- 二号(隣地斜線):×1.25+20m
- 三号(北側斜線):×1.25+10m



一号、二号、三号、
余白に全てメモしておこう。



やることリストは先に作る。
そうすれば、後は解くだけ。
チェックポイント!
問題用紙の余白に、検討するべき斜線制限の項目を先にメモしておく。(忘れ防止)
2.道路斜線における高さ制限の最高高さを求める
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
A点の最高限度を求める
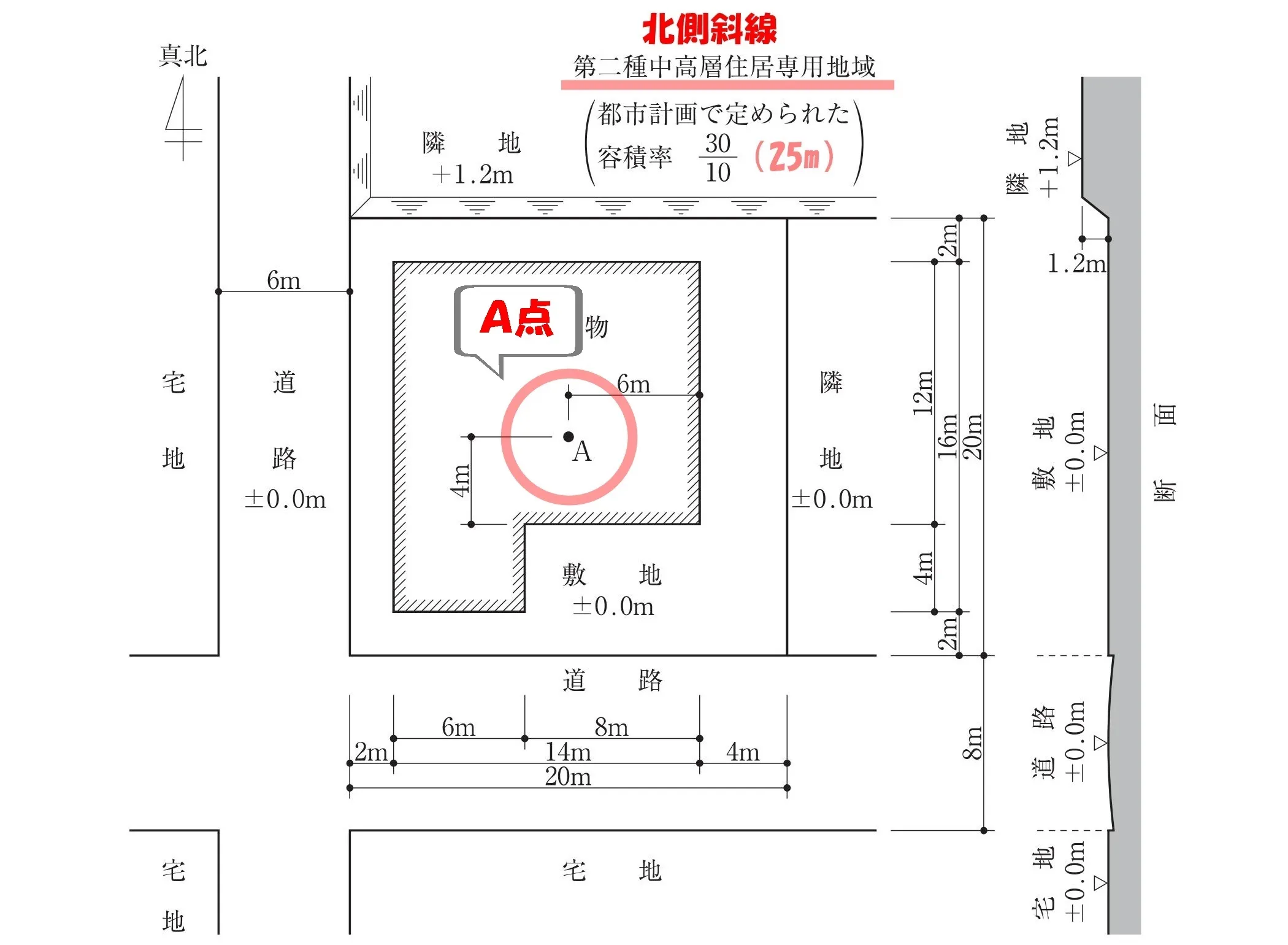

法56条【高さ制限】一号:道路斜線
設問は「A点」の高さの最高限度を求めること。



かかって来なさい!
A点までの寸法を書き込む
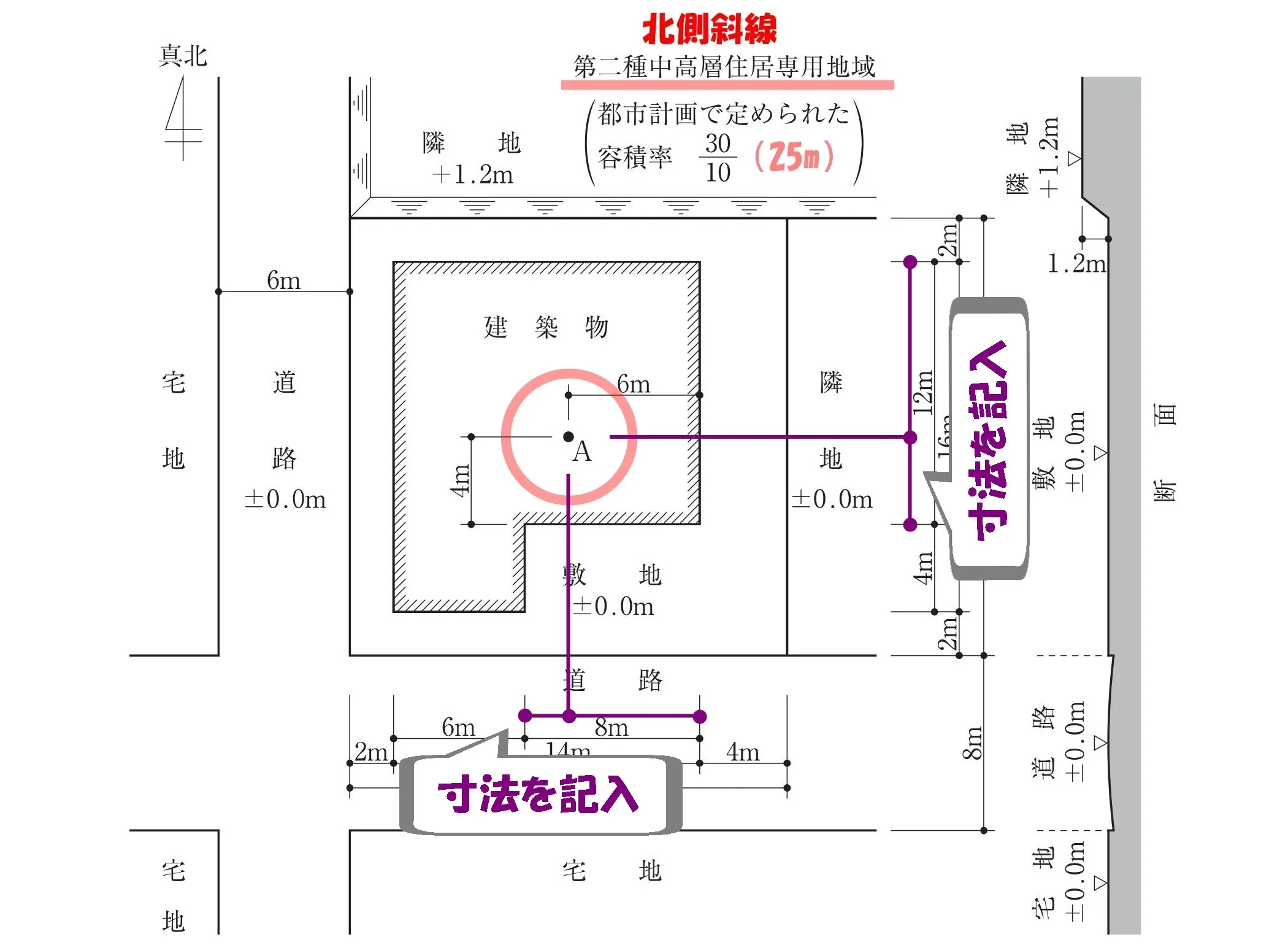

「A点」の位置を明確にするために必要な”寸法線”を書き込む。
準備OK!
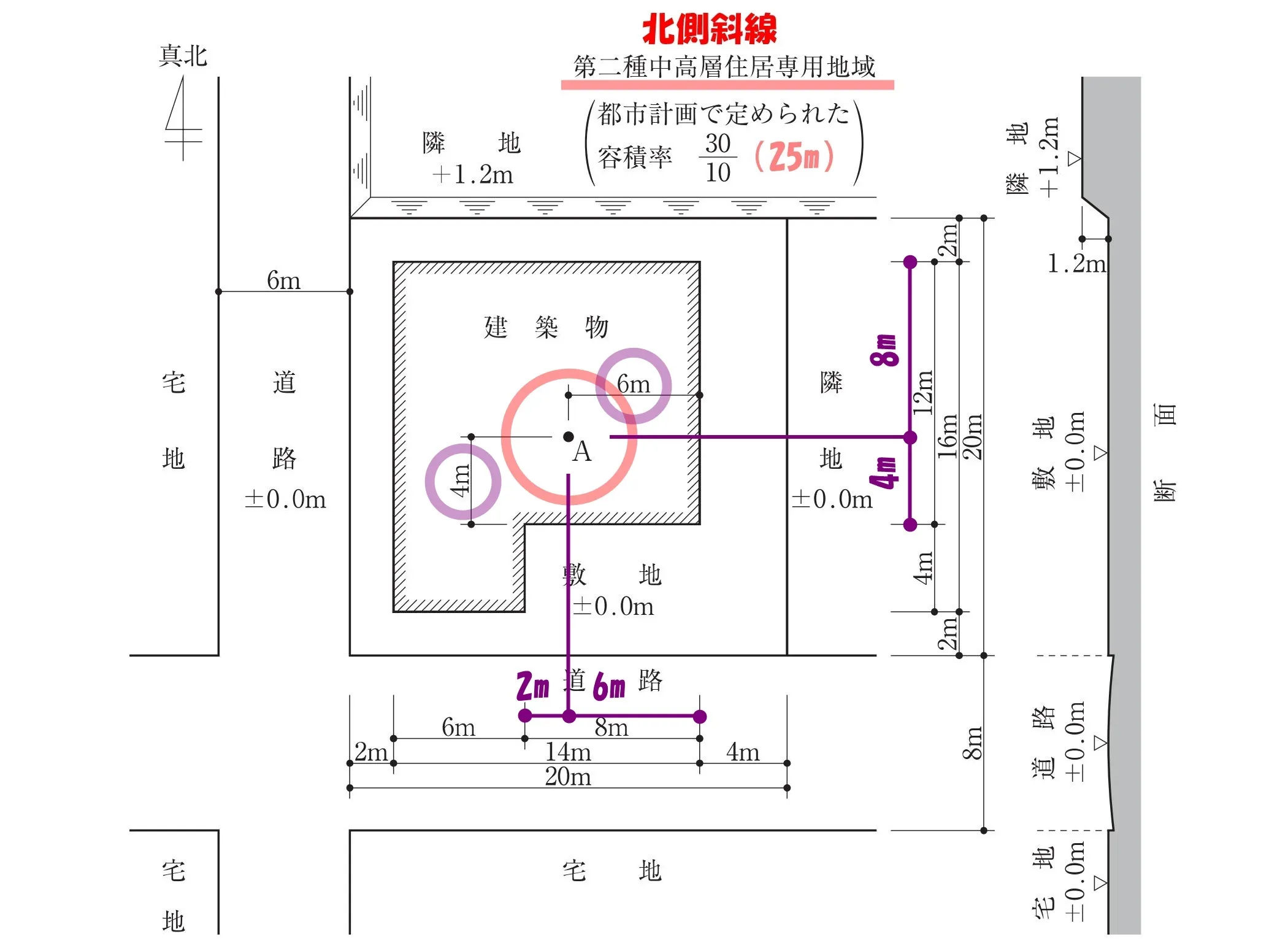

「A点」の位置までの”寸法の数値”を書き込めば、準備完了です。



準備OK!
2面道路の幅が異なる
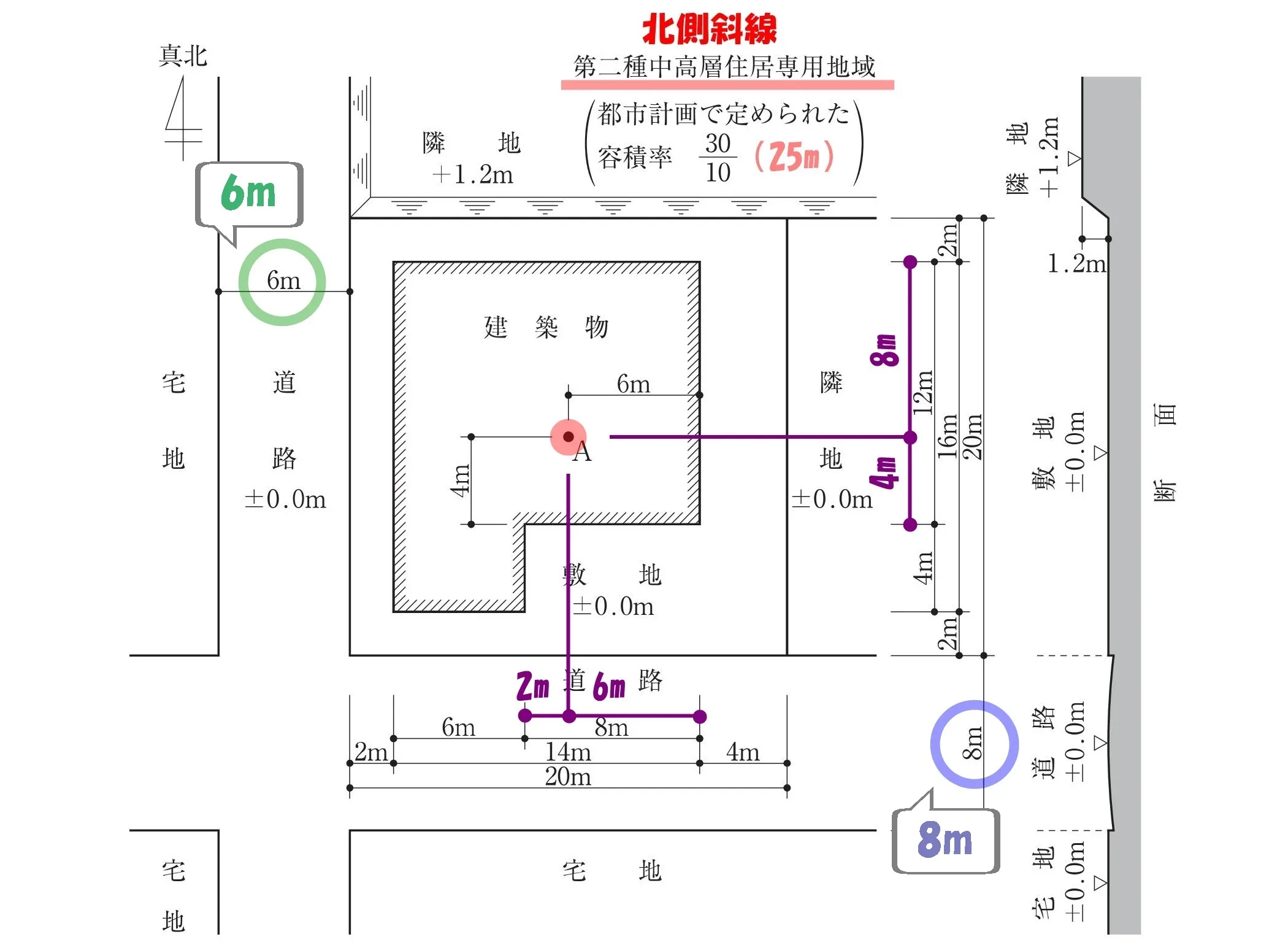

令132条:2以上の前面道路の緩和
建築物の前面道路が2以上ある場合においては、幅員の最大な前面道路の境界線からの水平距離がその前面道路の幅員の2倍以内で、かつ、35m以内の区域及びその他の前面道路の中心線からの水平距離が10mをこえる区域については、すべての前面道路が幅員の最大な前面道路と同じ幅員を有するものとみなす。
建築基準法(一部省略)



覚えたほうが速いです。
2aかつ 35m以内
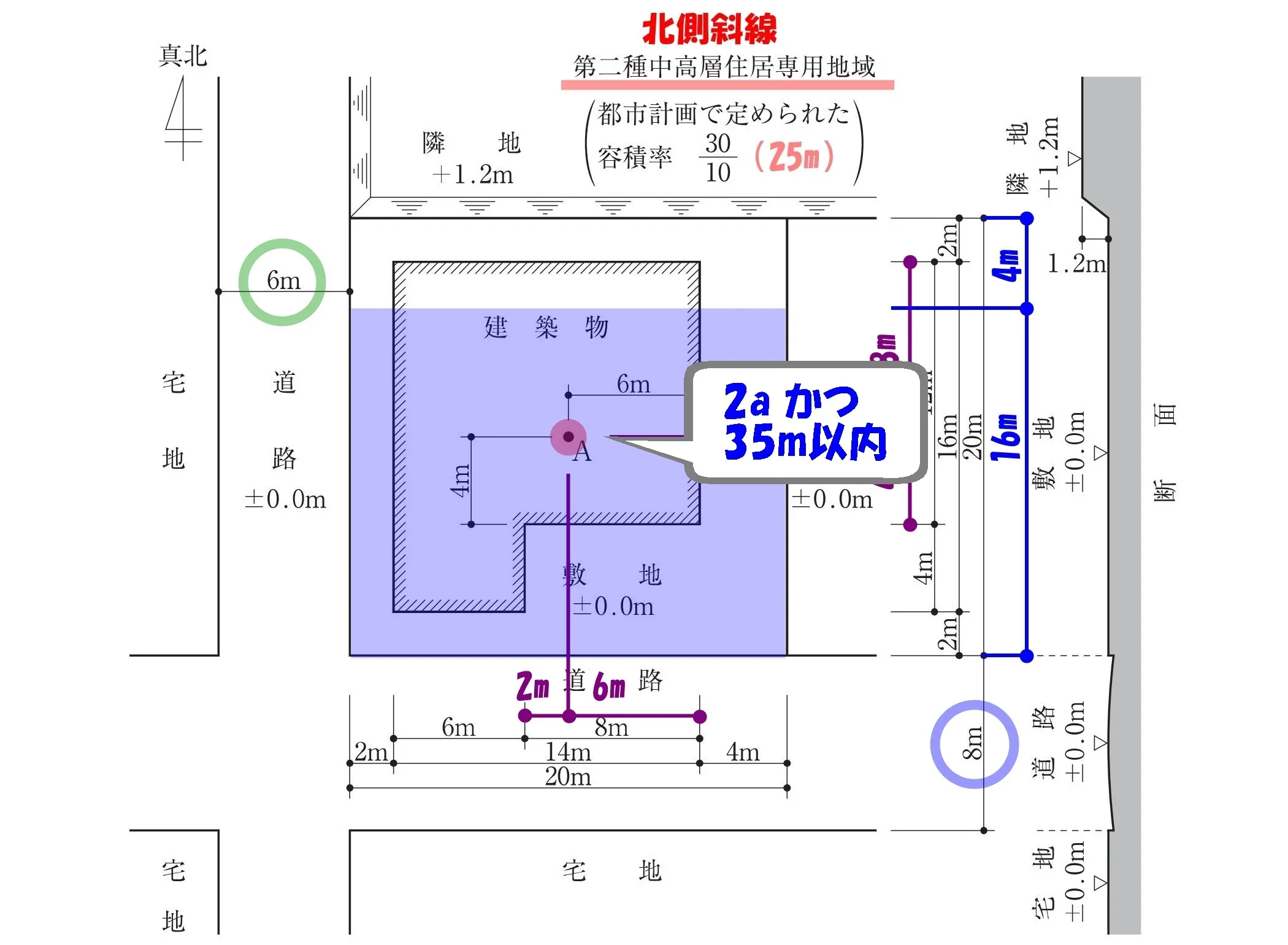

令132条:2以上の前面道路の緩和
最大幅員(8m)の道路から、2aかつ35m以内:8m×2=16m<35m。
その範囲を敷地図に”薄い線”で書き込んでおきましょう。



2aかつ35m以内・・・
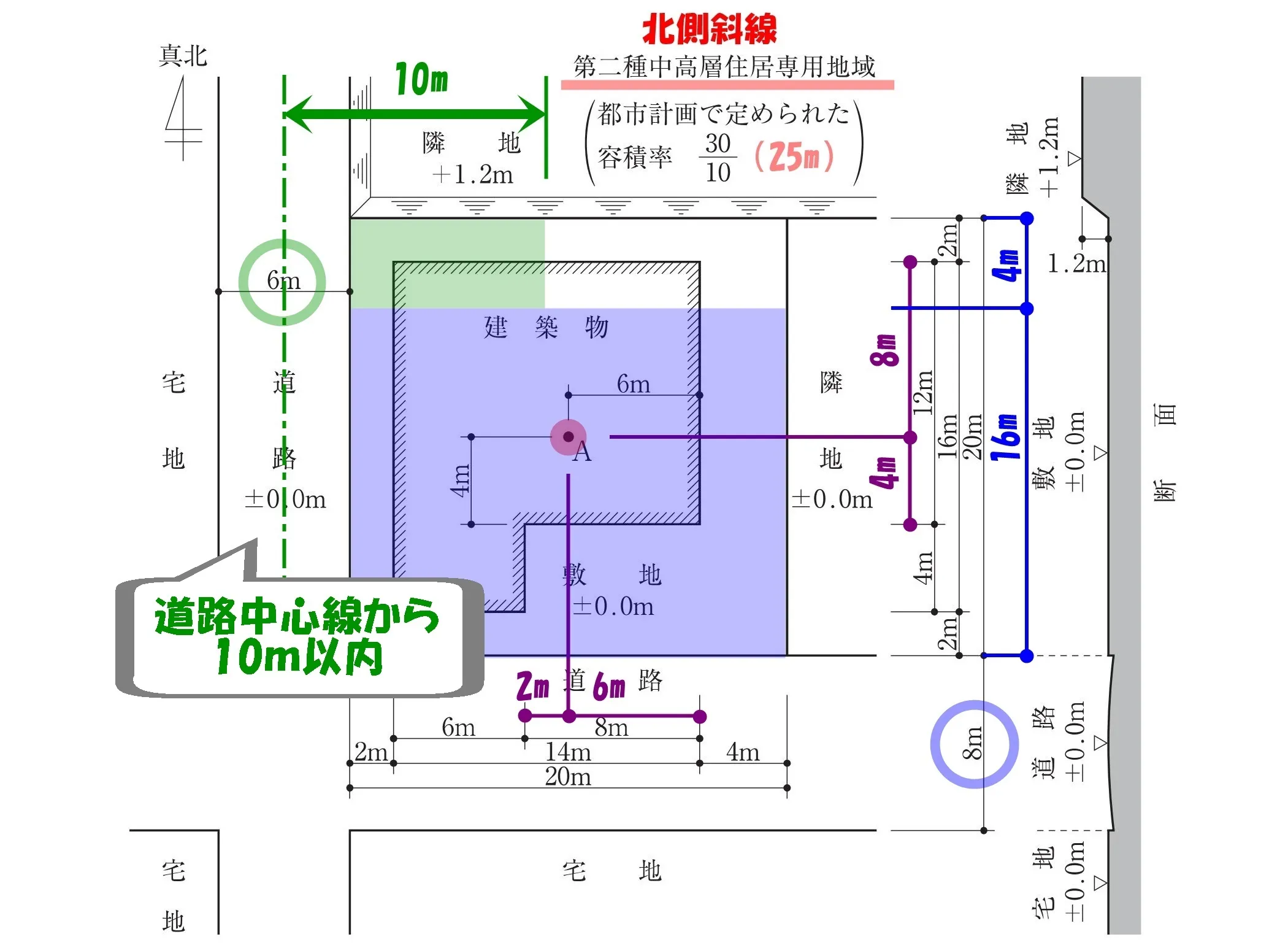
道路の中心から10m以内




中心から10m以内?
令132条:2以上の前面道路の緩和
その他(6m)の道路の中心線から10m以内、ここには6m道路の斜線制限が適用される。
建築物の前面道路が2以上ある場合においては、幅員の最大な前面道路の境界線からの水平距離がその前面道路の幅員の2倍以内で、かつ、35m以内の区域及びその他の前面道路の中心線からの水平距離が10mをこえる区域については、すべての前面道路が幅員の最大な前面道路と同じ幅員を有するものとみなす。
建築基準法(一部省略)
A点の道路斜線の適用は?
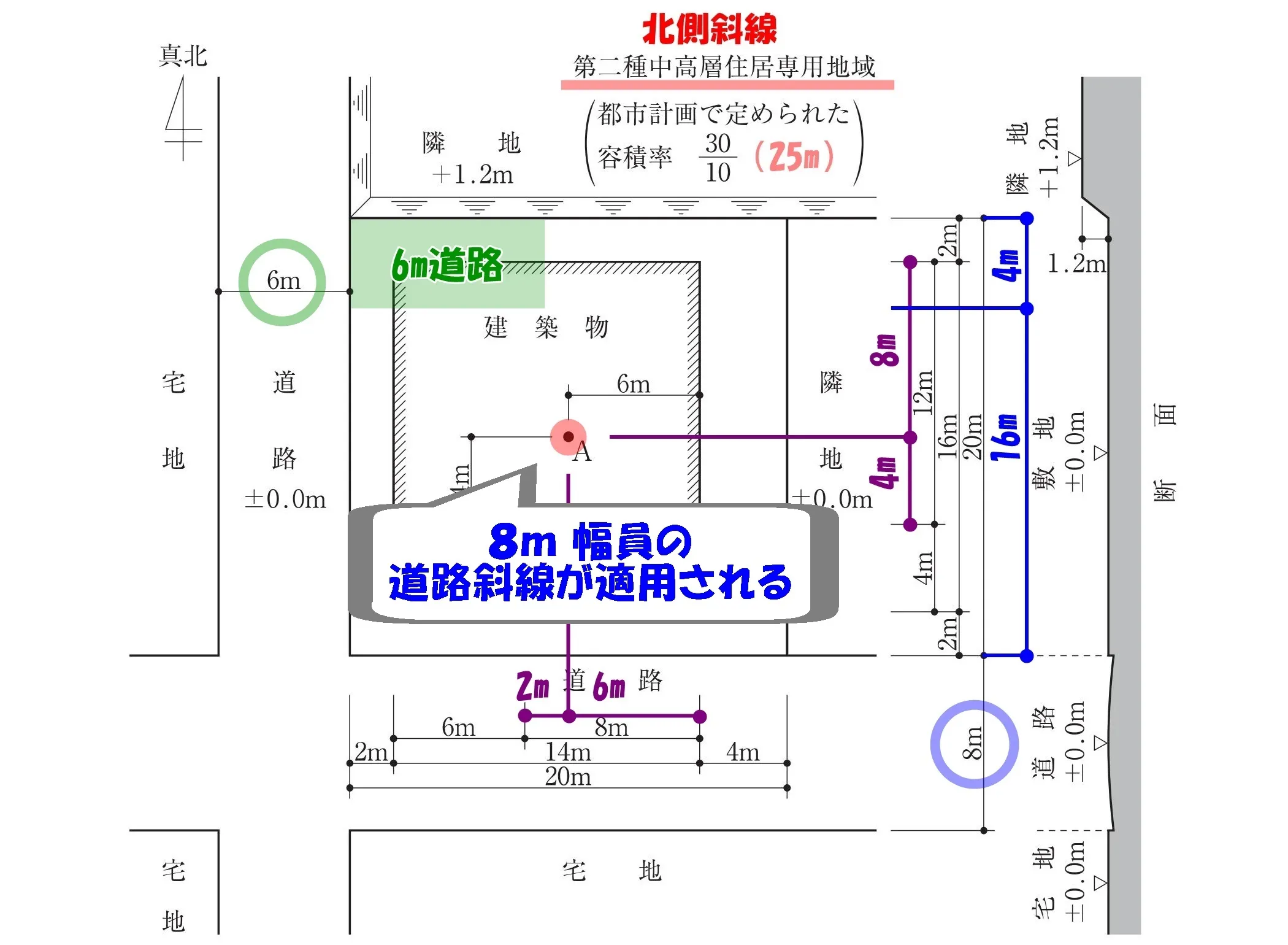

それぞれの道路斜線の範囲
- 【6m道路の斜線制限の適用範囲】
- その他(6m)の道路の中心線から、10m以内。
- 最大幅員(8m)の道路から、2aかつ35mを超える範囲。
- 【8m道路の斜線制限の適用範囲】
- その他(6m)の道路の中心線から、10mを超える部分。
- 最大幅員(8m)の道路から、2aかつ35m以内の範囲→(A点)。



う~ん、う~ん。
もう、ついて行けない。
よって、「A点」には最大幅員となる8m道路の斜線制限が適用されることになります。
6m道路の幅を修正する
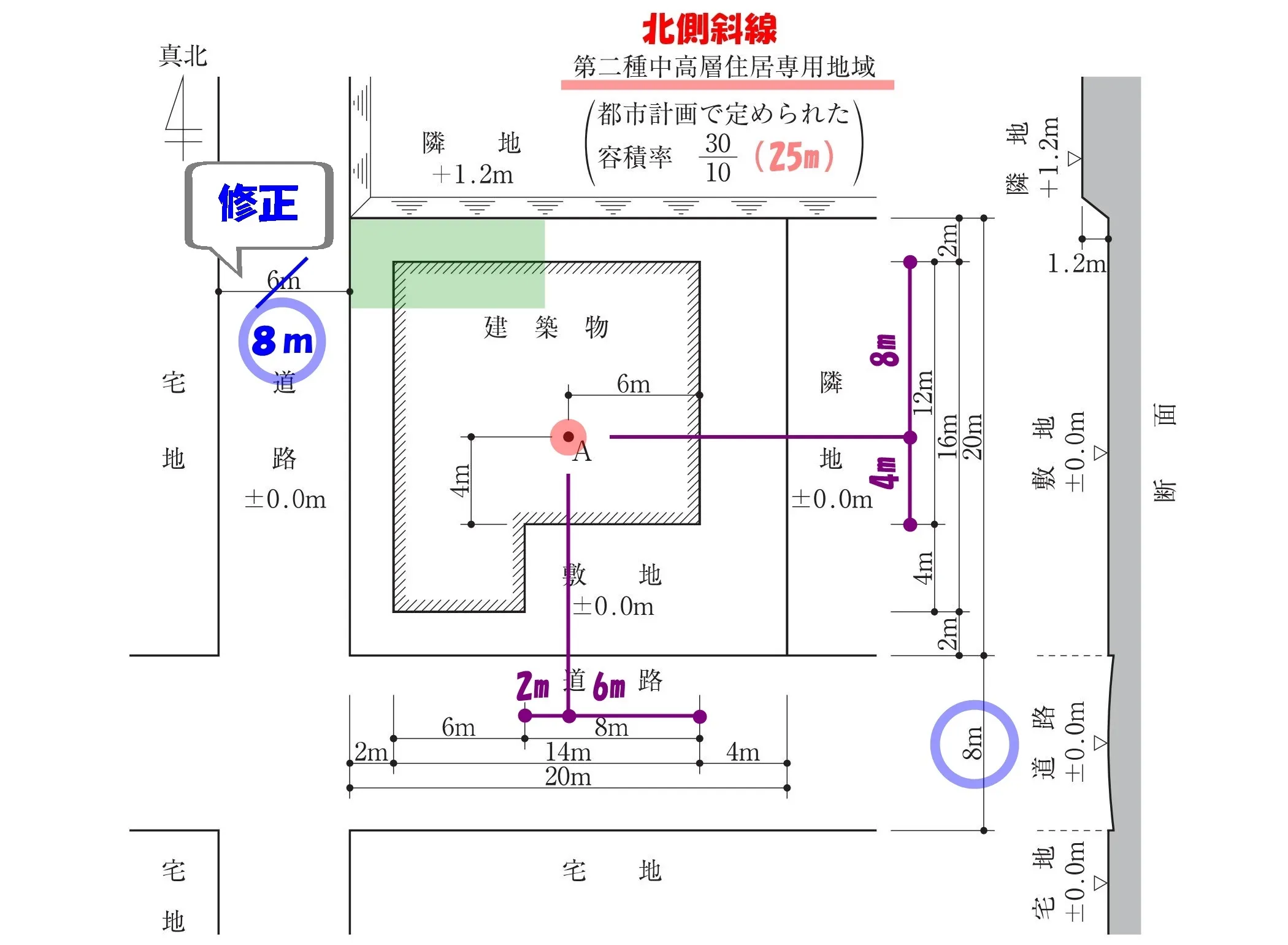

令132条:2以上の前面道路の緩和
2面道路の緩和を踏まえて、その他(6m)の道路の幅を「6m→8m」に修正しておきましょう。



忘れないうちに、
道路幅を修正しておこう。
後退距離を確認する
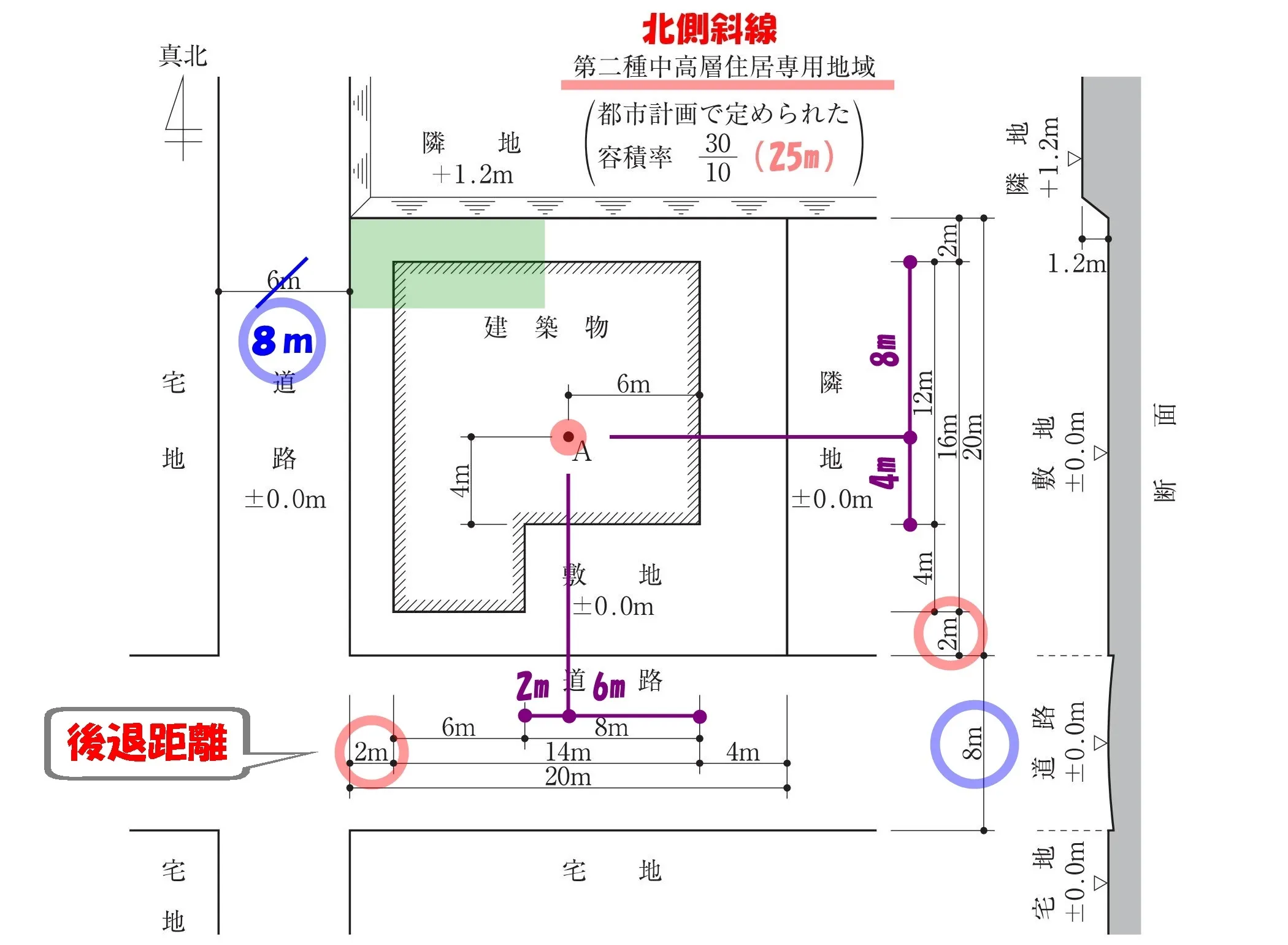

法56条【高さ制限】一号:道路斜線
道路境界線からの建物の後退距離は「2m」
後退距離の寸法値は、〇印で囲んでおきましょう。



後退距離は2m!
セットバックの寸法を入れる
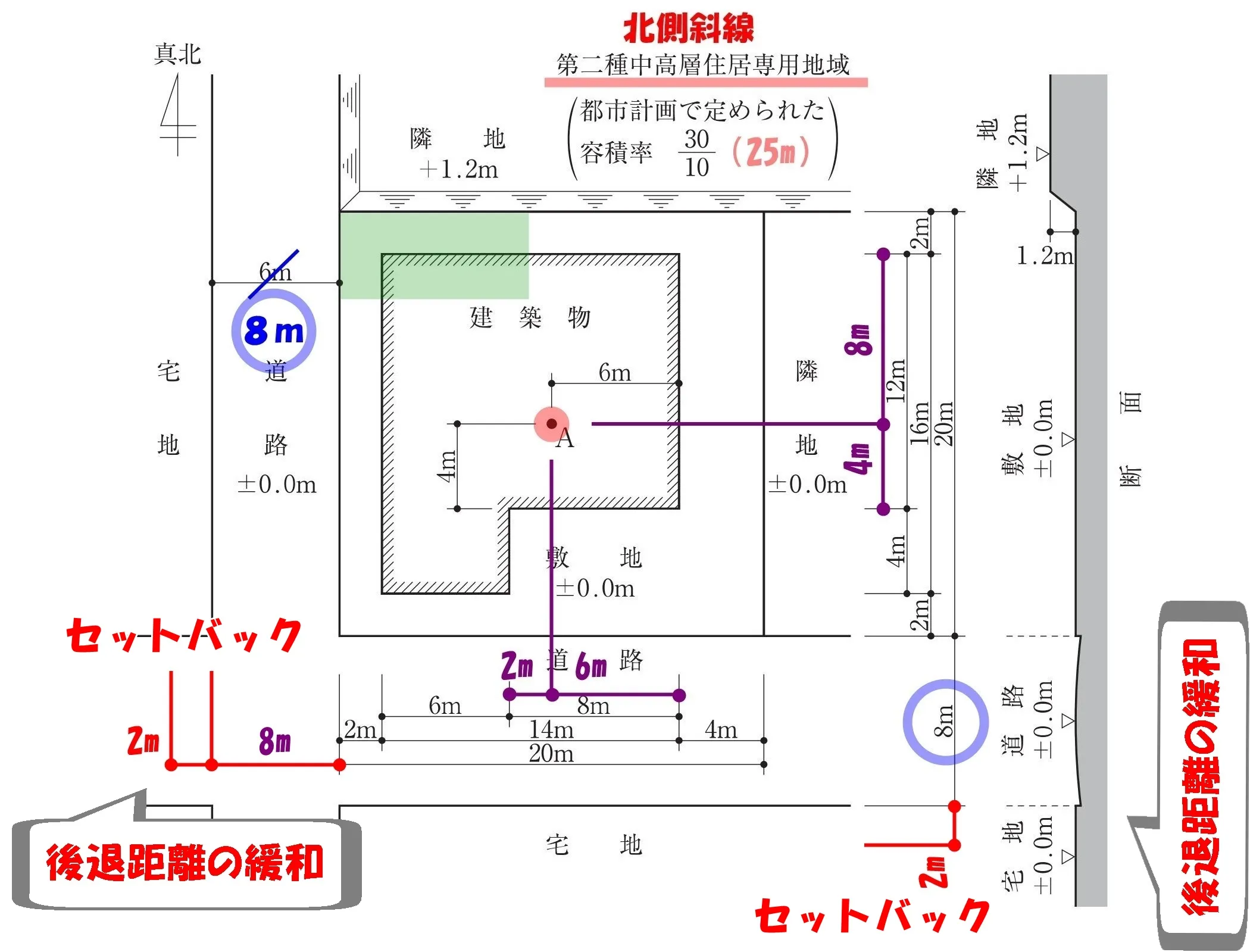

道路境界線からの建物の後退距離は「2m」
道路を挟んだ反対側にも同じ後退距離が適用されます。
セットバックの寸法値、「2m」を書き込んでおきましょう。



セットバック!
水平距離×1.25
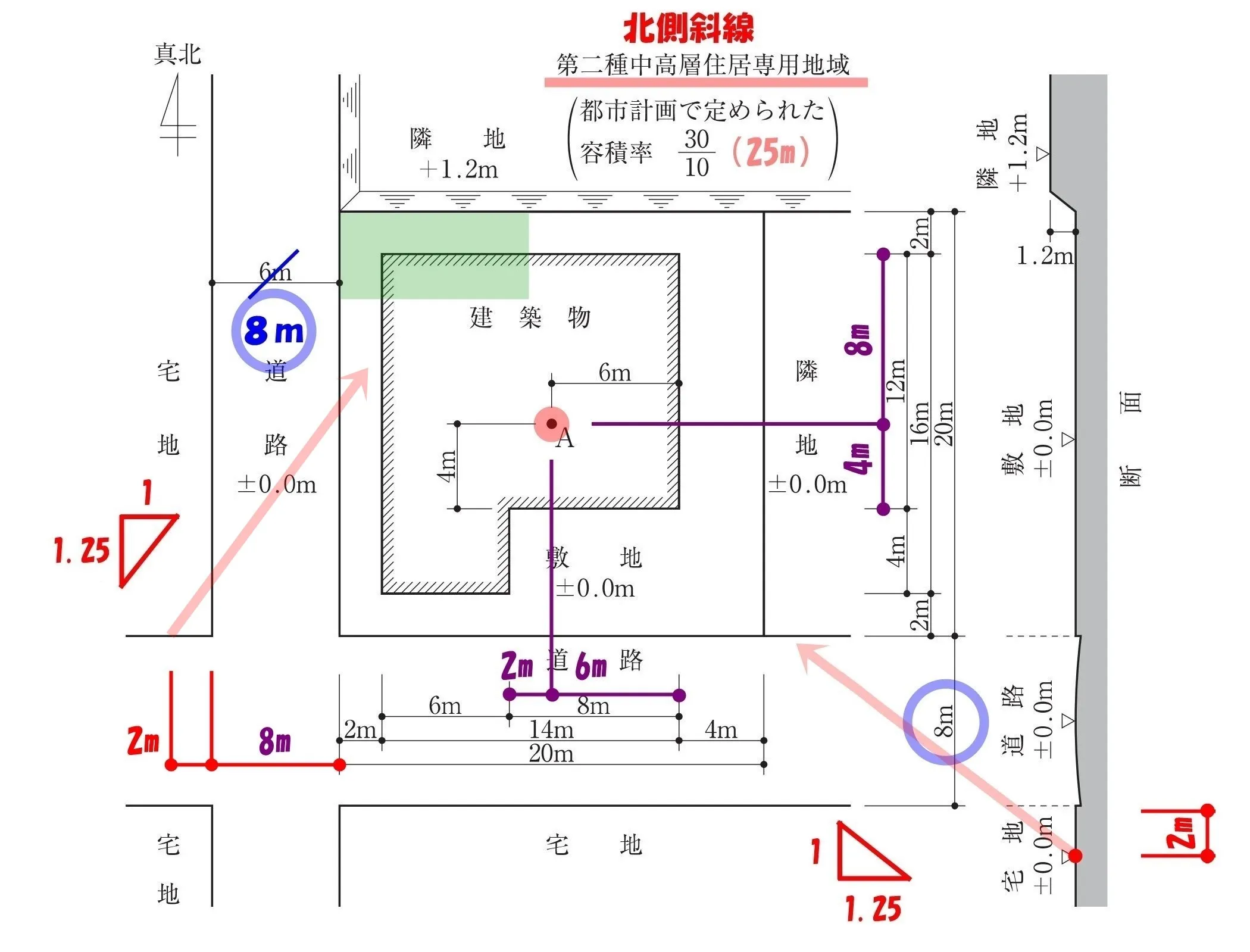

法56条一号:道路斜線
$$道路斜線の最高高さ=水平距離*\frac{ 5 }{ 4 }$$
$$(1.25=\frac{ 5 }{ 4 }に置き換えると計算処理がし易い)$$
【西側の道路斜線】
$$(2+8+2+6+2)*\frac{ 5 }{ 4 }=20*\frac{ 5 }{ 4 }=5*\underline{4}*\frac{ 5 }{ \underline{4} }=5*5=25m$$
【南側の道路斜線】
$$(2+8+2+4+4)*\frac{ 5 }{ 4 }=20*\frac{ 5 }{ 4 }=5*\underline{4}*\frac{ 5 }{ \underline{4} }=5*5=25m$$
法56条一号:道路斜線による高さの最高限度はいずれも「25m」となる。



とりあえず、
道路斜線に一撃(バシ!)


この動画を YouTube で視聴
3.隣地斜線における高さ制限の最高高さを求める
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
隣地斜線の高さを求める
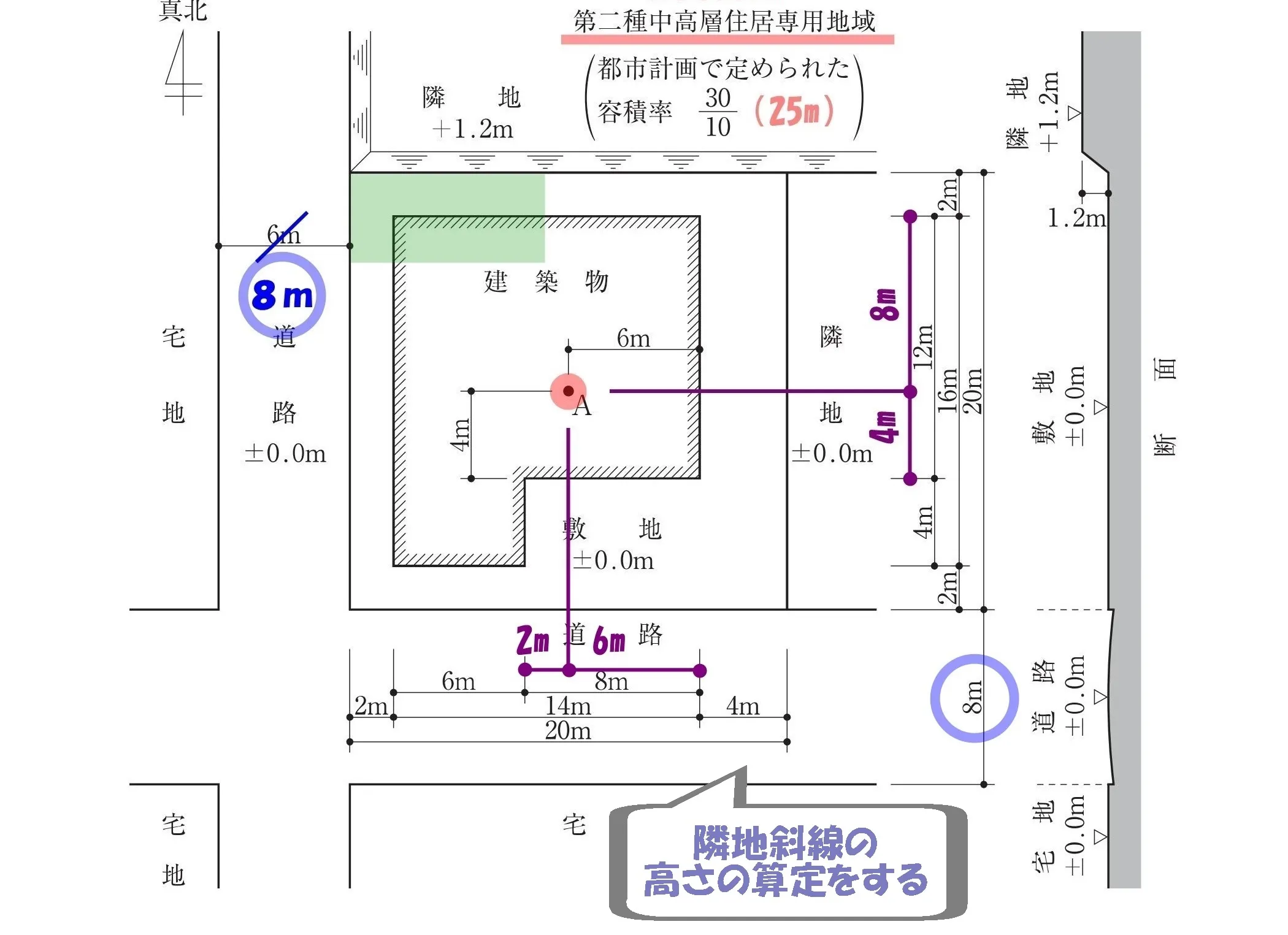




かかって来い!
法56条【高さ制限】二号:隣地斜線
ワンポイント
道路斜線の適用範囲外でない限り、「隣地斜線の高さの最高限度」が答えになることはない。



検討する必要はなさそう。
参考として?ということで。
3.に注目する


チェックポイント
隣地斜線の勾配は、法56条二号(イ)より「×1.25」



×1.25!
令135条の7、二号(隣地との関係について)
問題文:建築物はすべての部分において、高さの最高限度(20m超え)まで建築される。
この条件によって、「セットバックの緩和」も適用されます。



ここの当たりは、
条文からは分かりにくい。
セットバックの寸法を入れる
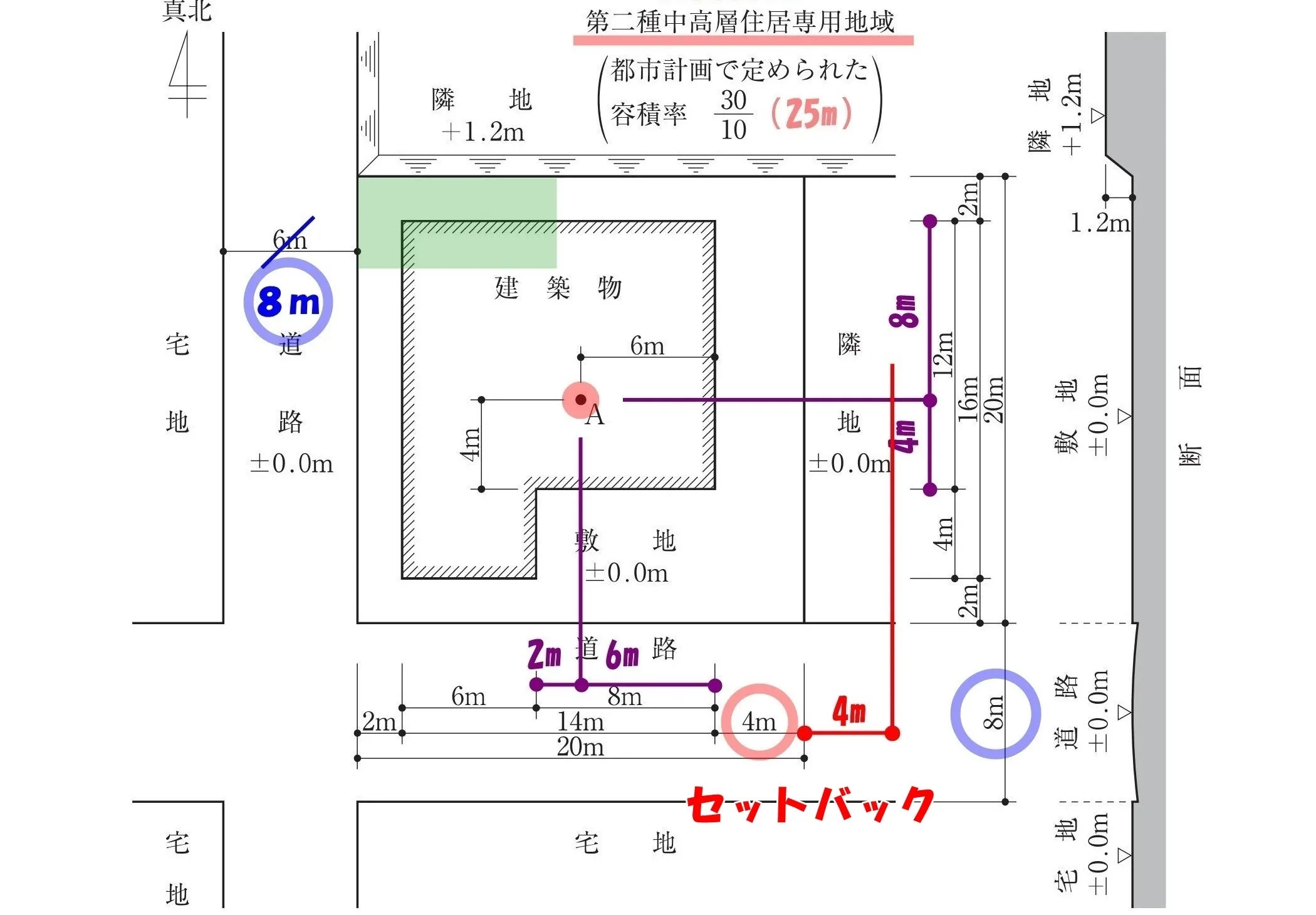

隣地境界線からの建物の後退距離は「4m」
隣地を挟んだ反対側にも同じ後退距離が適用されます。
セットバックの寸法値、「4m」を書き込んでおきましょう。



セットバック!
隣地斜線の起点は?
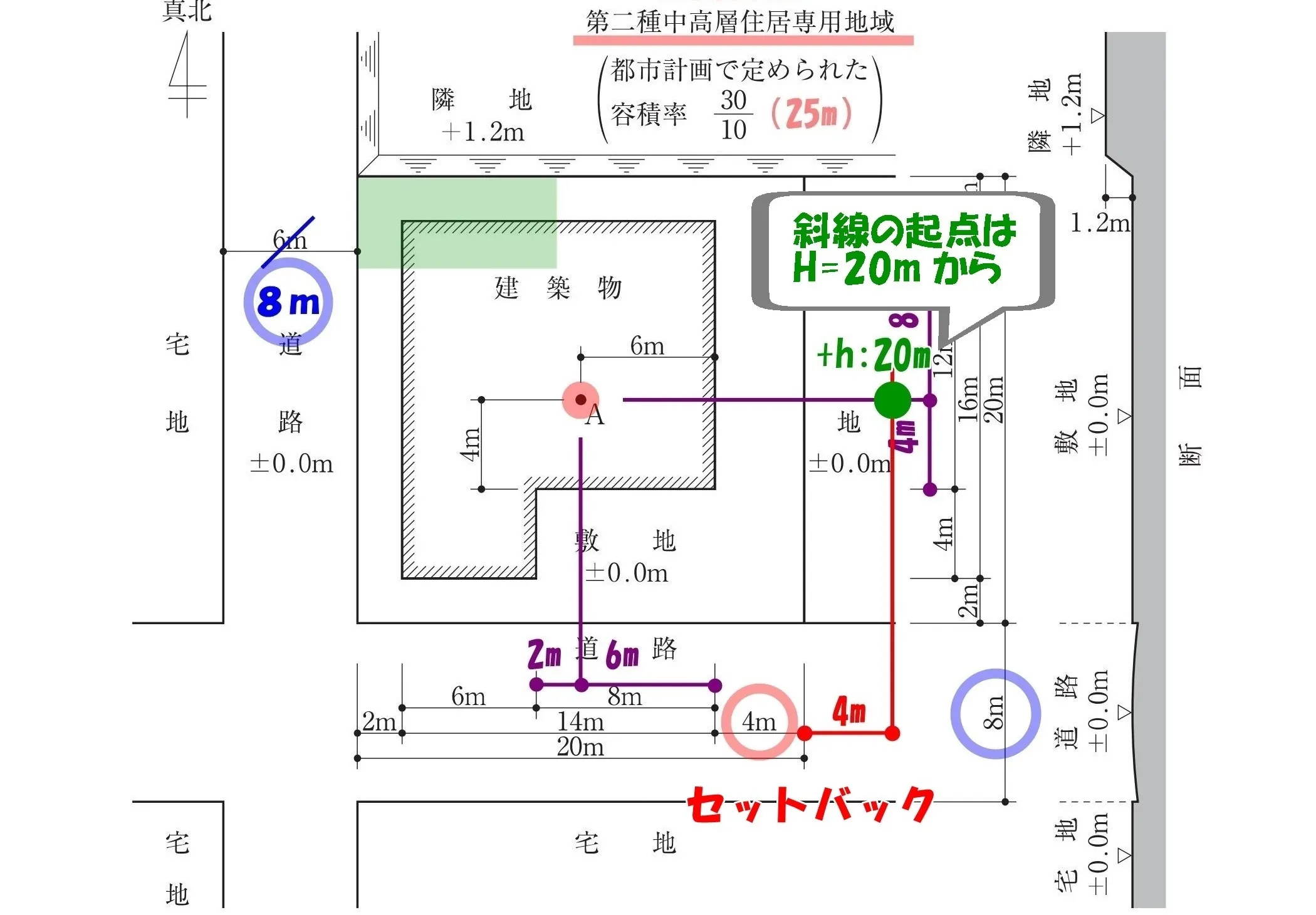




20mジャンプ!
そこから斜線×1.25!
法56条二号:隣地斜線
$$隣地斜線の最高高さ=水平距離*\frac{ 5 }{ 4 }+\underline{20m}$$
$$(1.25=\frac{ 5 }{ 4 }に置き換えると計算処理がし易い)$$
$$(6+4+4)*\frac{ 5 }{ 4 }+20=(12+2)*\frac{ 5 }{ 4 }+20=(3*\underline{4}+2)*\frac{ 5 }{ \underline{4} }+20$$
$$=3*5+\frac{ 5 }{ 2 }+20=15+2.5+20=37.5m$$
法56条二号:隣地斜線による高さの最高限度は「37.5m」となる。



隣地斜線を撃破!
(バシバシ!)
5.北側斜線における高さ制限の最高高さを求める
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
北側斜線の高さを求める
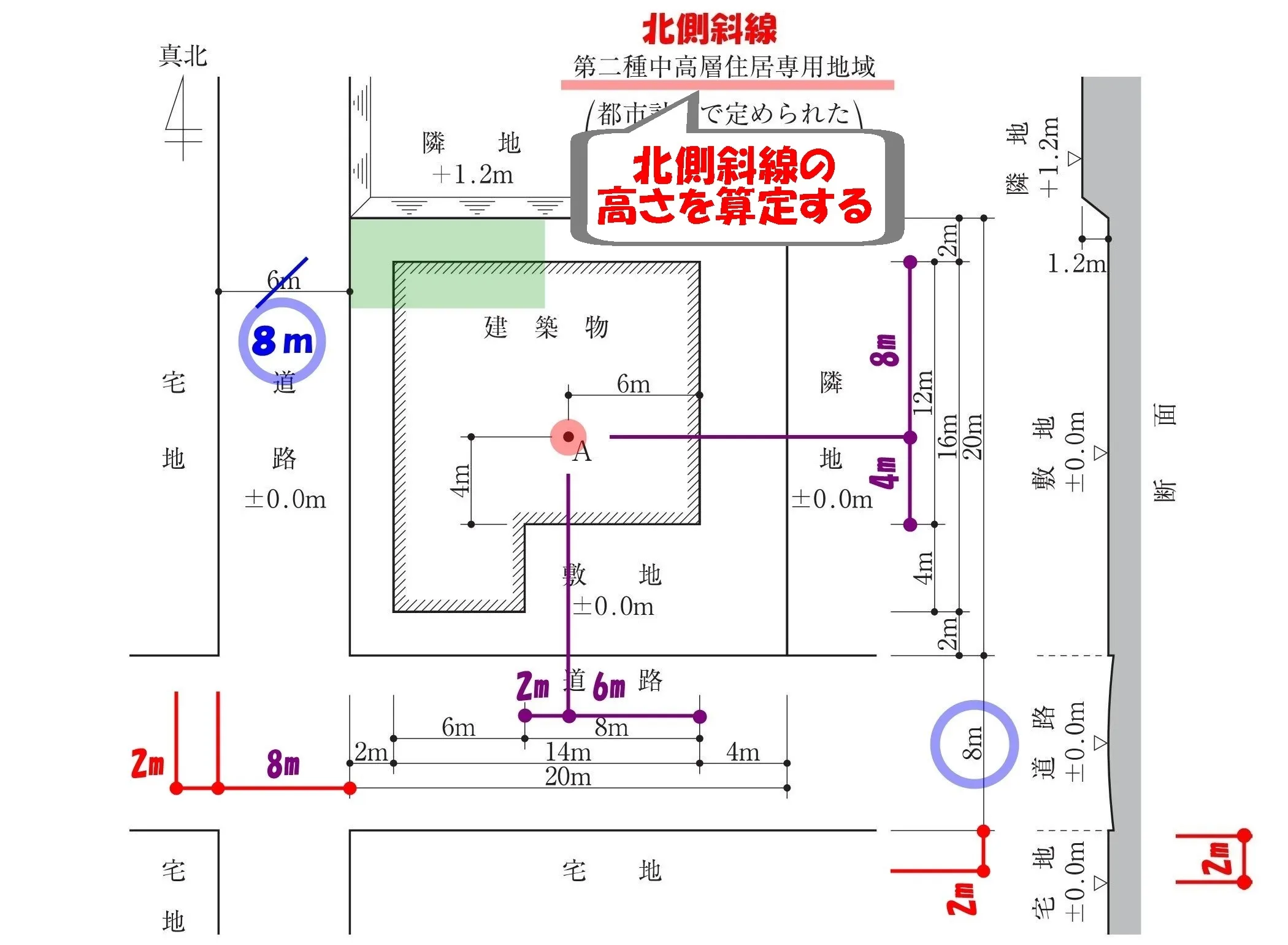




やっつけるぞ!
法56条【高さ制限】三号:北側斜線
高さ制限のラストとなる「北側斜線の高さの最高限度」を求める。
問題に図示してある”地盤の断面図”を活用するため、用紙を回転させましょう。



また回るか・・
用紙を回転させる





回転!
A点までの寸法を書き込む
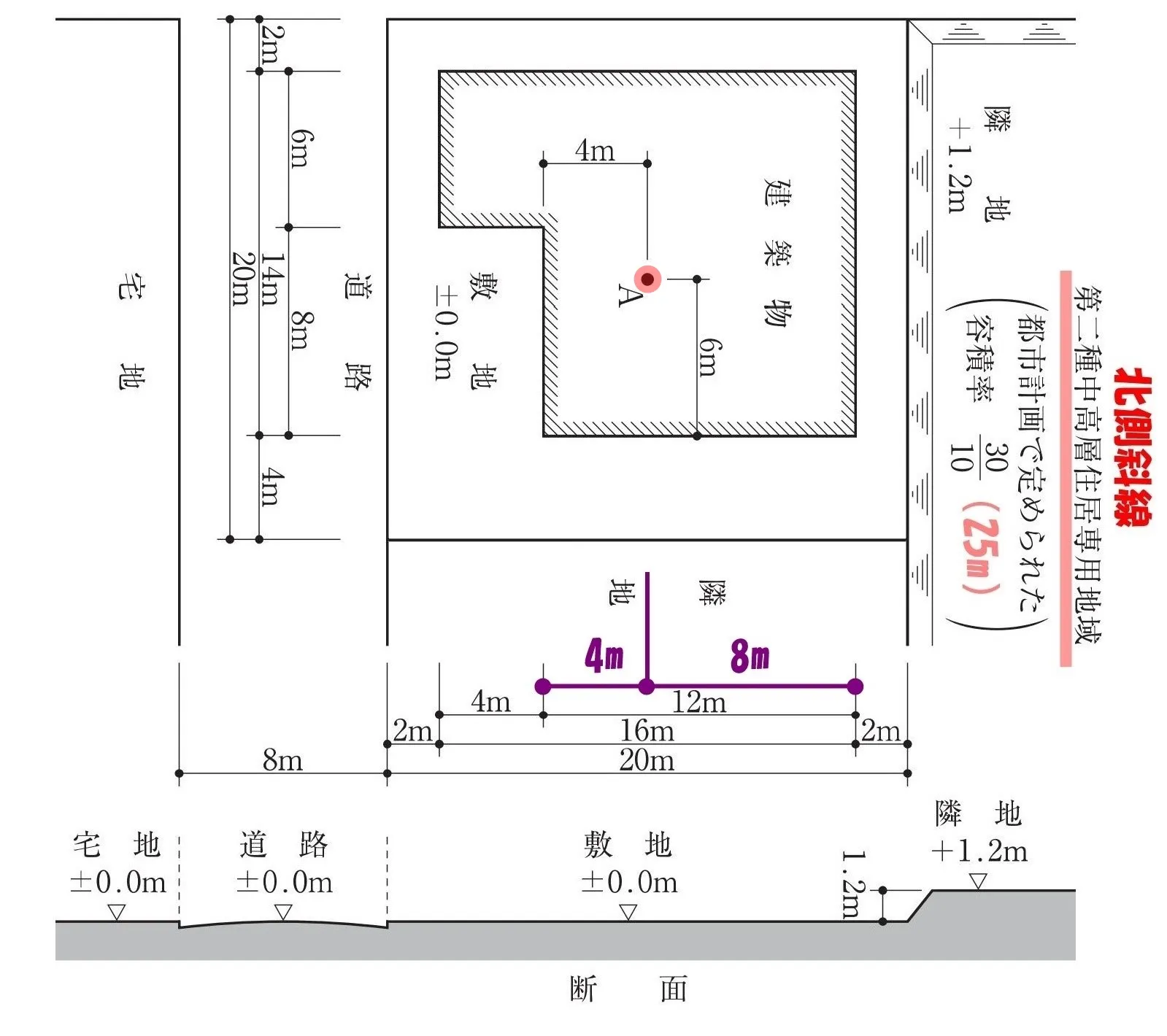

「A点」の位置までの”寸法の数値”を書き込めば、準備完了です。



準備OK!
4.敷地の高低差より、起点となるレベルを求める
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
問題文の要点をチェック





やめてくれ~。
高低差とか考えたくない。
令135条の4、二号【敷地の高低差】
チェックポイント
「建築物の敷地は平坦で、北側隣地より1.2m低い」ことから、敷地には高低差がある。
敷地の高低差▲1m
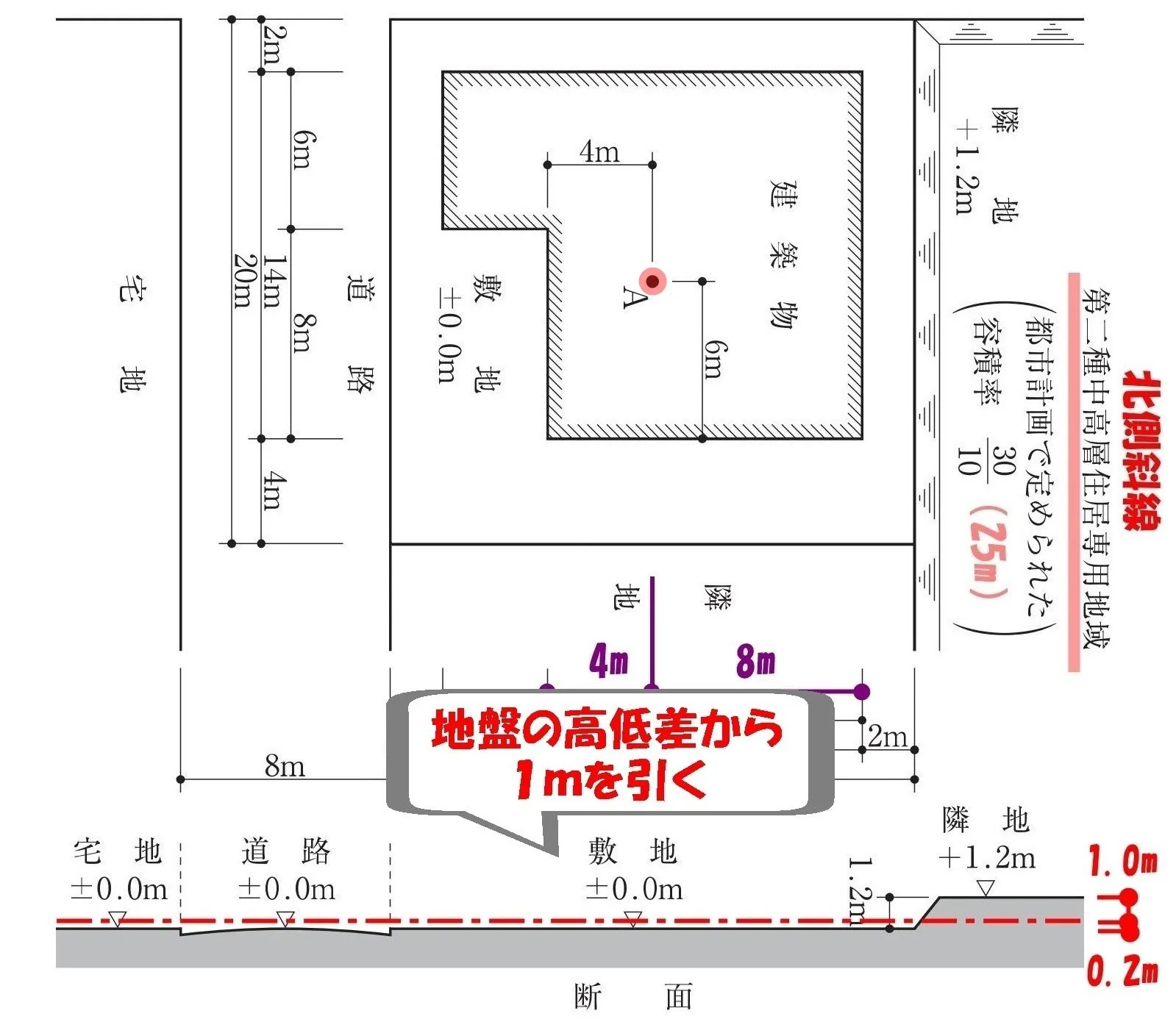

令135条の4、二号【敷地の高低差】
建築物の敷地の地盤面が北側の隣地の地盤面より1メートル以上低い場合においては、その建築物の敷地の地盤面は、当該高低差から1メートルを減じたものの 1/2 だけ高い位置にあるものとみなす。
建築基準法(一部省略)



高低差を乗り越えよう。
×1/2
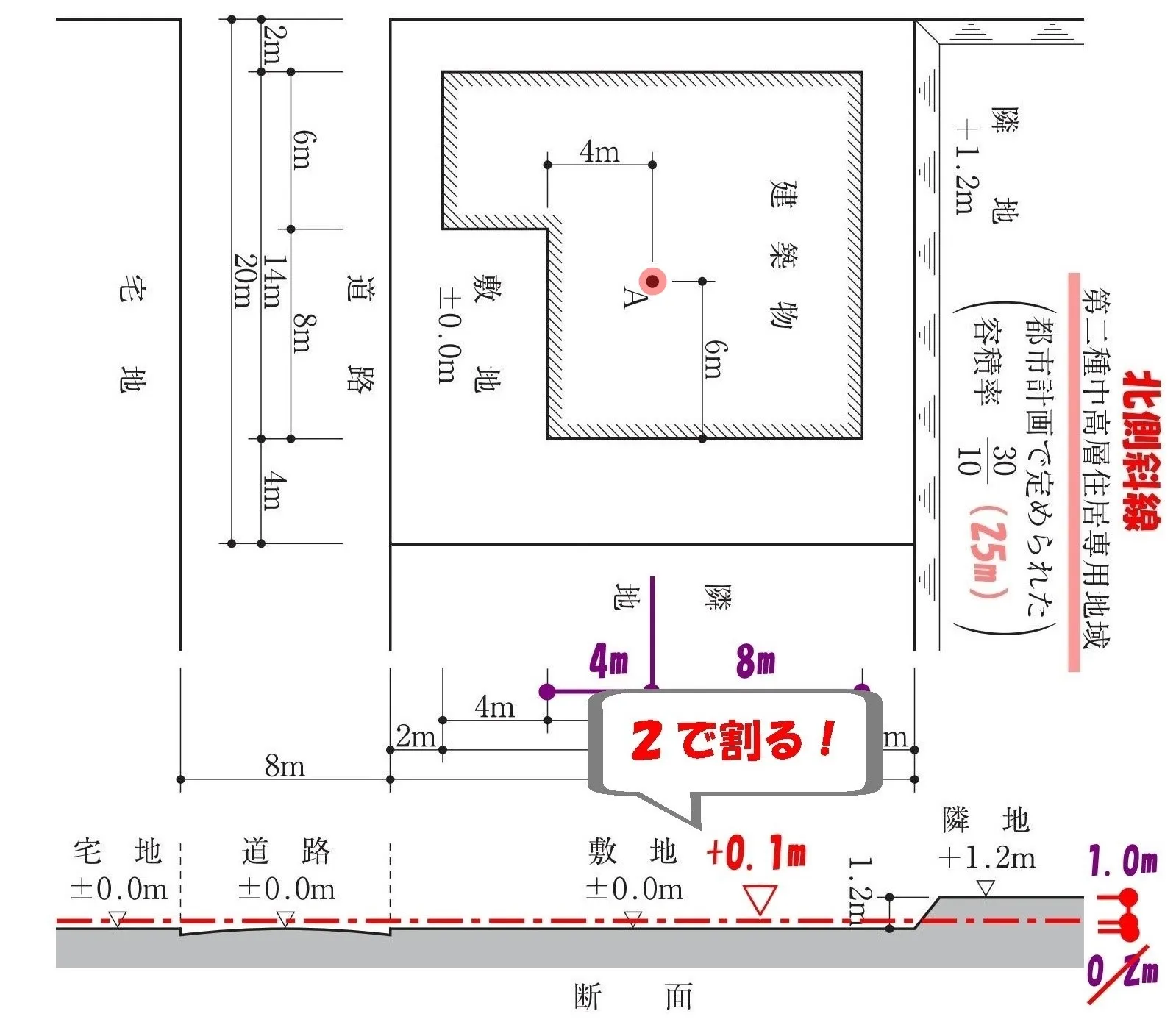

攻略ポイント!
令135条の4、二号【敷地の高低差】
$$敷地の地盤面=\frac{ (1.2-1.0) }{ 2 }=\frac{ 0.2 }{ 2 }=0.1→GL\underline{+0.1}$$



GL+0.1m
建築物の敷地の地盤面が北側の隣地の地盤面より1メートル以上低い場合においては、その建築物の敷地の地盤面は、当該高低差から1メートルを減じたものの 1/2 だけ高い位置にあるものとみなす。
建築基準法(一部省略)
5.北側斜線における高さ制限の最高高さを求める
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める
北側斜線の高さを求める
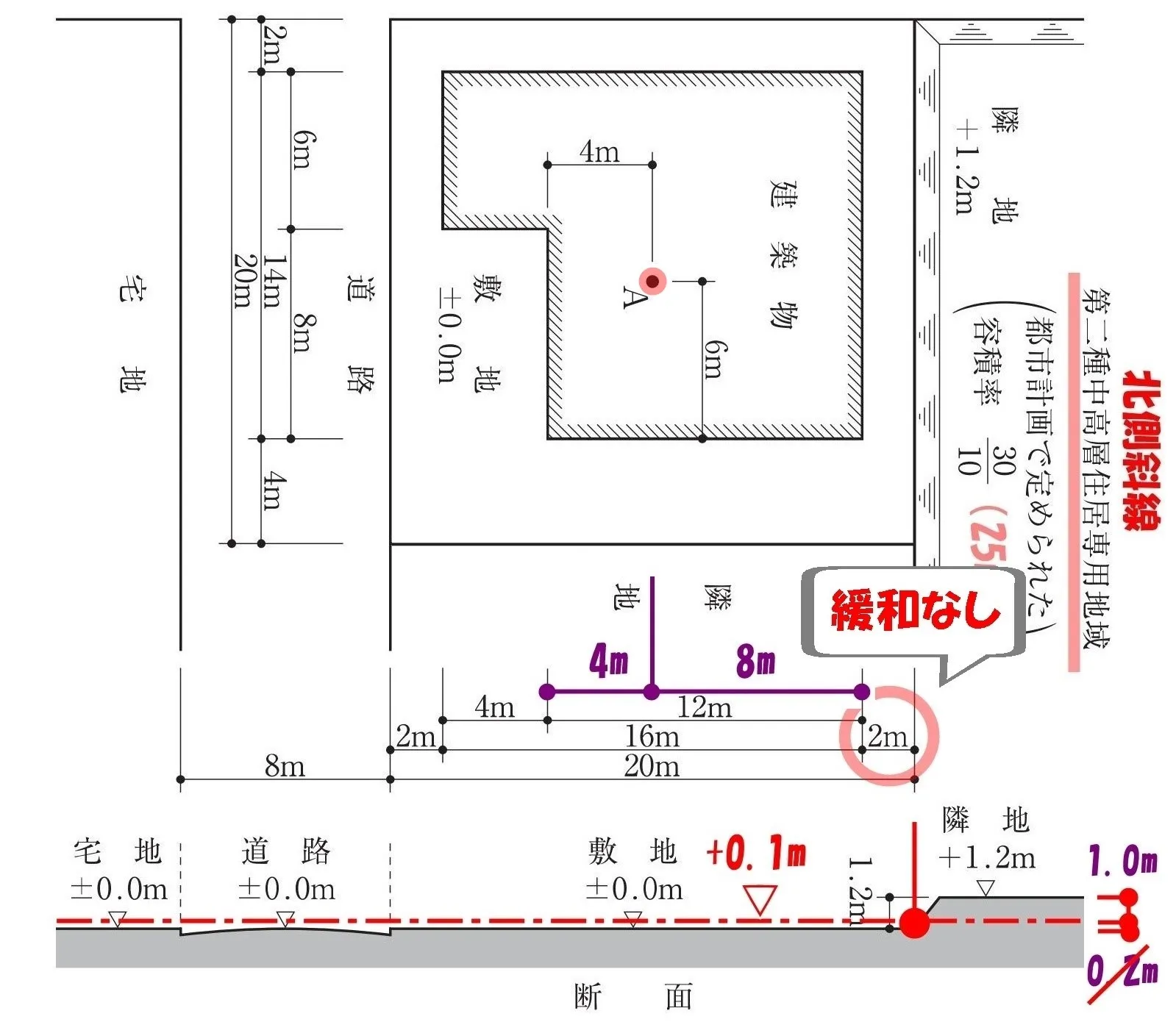




高低差を乗り越えて
北側斜線をやっつける!
法56条【高さ制限】三号:北側斜線
要注意!
北側斜線に後退距離(セットバック)の緩和はない。



セットバック無いの?
北側斜線の起点は?
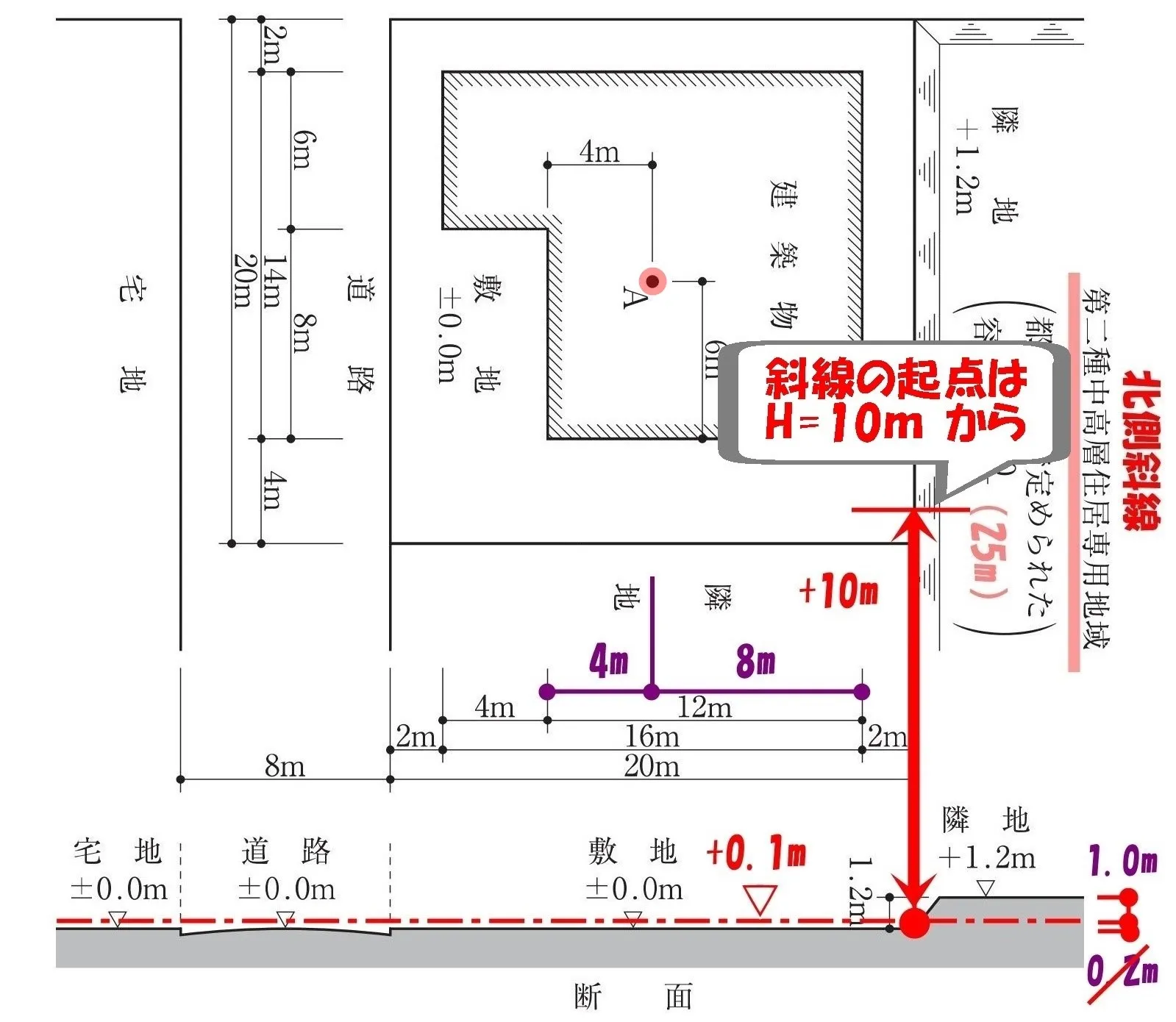




10mジャンプ!
そこから斜線×1.25!
法56条三号:北側斜線
$$北側斜線の最高高さ=水平距離*\frac{ 5 }{ 4 }+\underline{10m+0.1m}$$



「GL+0.1m」
その苦労を無駄にしないで。
チェックポイント
北側斜線の計算式に、地盤の高低差による「GL+0.1」を足し忘れないこと。
水平距離×1.25
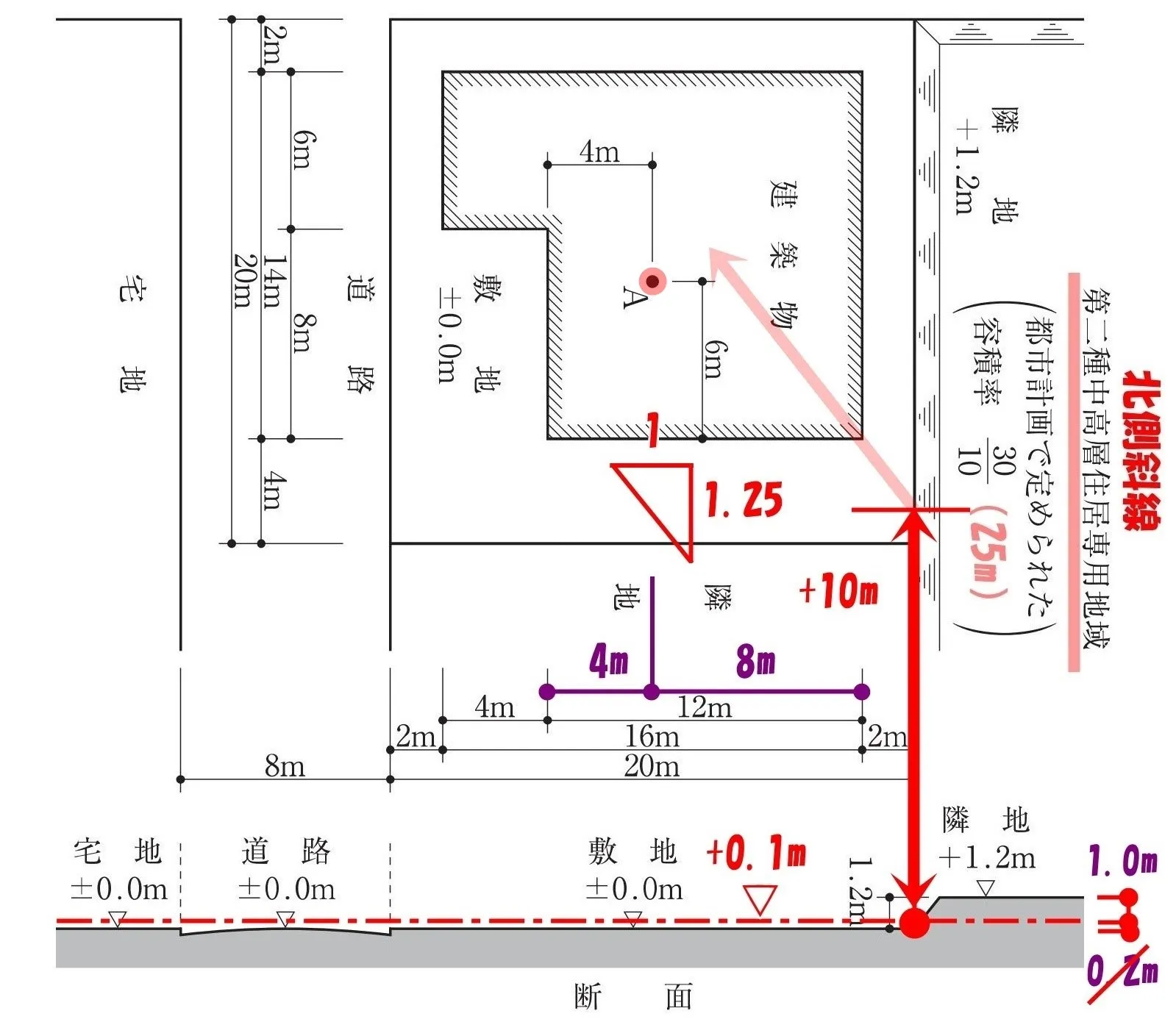

$$北側斜線の最高高さ=水平距離*\frac{ 5 }{ 4 }+\underline{10m+”0.1m”}$$
$$(1.25=\frac{ 5 }{ 4 }に置き換えると計算処理がし易い)$$
$$(\underline{8}+2)*\frac{ 5 }{ \underline{4} }+10+0.1=(2*\underline{4}+2)*\frac{ 5 }{ \underline{4} }+10+0.1$$
$$=2*5+\frac{ 5 }{ 2 }+10+0.1=10+2.5+10+0.1=22.5+0.1=22.6m$$



北側斜線を撃破!
計算結果
- 一号(道路斜線):×1.25
- 計算結果=25.0m
- 二号(隣地斜線):×1.25+20m
- 計算結果=37.5m
- 三号(北側斜線):×1.25+10m+0.1
- 計算結果=22.6m
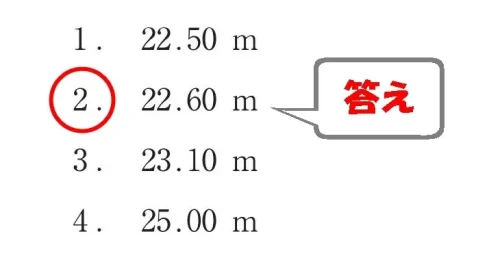
以上の計算結果を踏まえて、斜線制限における高さの最高限度は北側斜線の「22.6m」となる。



もう終わり?
答え.2



高さ制限を撃破!
攻略ポイント
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める


この動画を YouTube で視聴
法令集の紹介
お疲れ様でした、まとめに入ります。

一級建築士|法規の計算問題に挑戦して攻略ポイントを解説
(まとめ)
計算問題の対策
- 答えを導くための手順や工程を確立しておく
- 数値や公式は覚えておき、自分の知識で対応する
- ケアレスミスを避けるために、残り時間を明確にする



最後のまとめ!


(令和4年度出題:No.1)
チェックポイント
- 【建築物の高さ】
- 法33条:避雷設備
- 令2条六号:建築物の高さ
- 令2条2項:地盤面の位置
- 【地階を除く階数】
- 令1条二号:地階
- 令2条八号:階数
- 令2条2項:地盤面の位置
- 【階数】
- 令2条八号:階数
- 令2条八号:昇降機塔の扱い
- 令2条八号:防災センターの扱い
- 【容積率の算定の基礎となる延べ面積】
- 令2条八号:階数(×延べ面積)
- 令2条3項:容積率算定における延べ面積の緩和
- 法52条3項:容積率算定におけるエレベーターの昇降路の扱い


(令和5年度出題:No.5)
攻略ポイント
- DとHの寸法を書き込む
- 採光関係比率:D/Hを求める
- 採光補正係数:D/H×6-1.4を求める
- 開口部(A)の採光に有効な面積を求める


(令和2年度出題:No.5)
攻略ポイント
- 階段(蹴上げ、踏み面)と踊り場の寸法をメモする
- 階段の「Lの寸法」と「段数」の関係を把握する
- 階段を上がるために必要な蹴上げの数を求める
- 階段を上がるために必要なLの長さを求める


(令和3年度出題:No.12)
攻略ポイント
- 建物の床面積に乗ずる数値を確認する
- 地震力における必要な軸組長さを求める
- 風圧力における必要な軸組長さを求める


(令和2年度出題:No.16)
攻略ポイント
- 建築物の耐火仕様と防火地域をチェックする
- 敷地の区分と接道条件(角地など)をチェックする
- 敷地が”みなし道路”により削られる部分は寸法を差し引く
- それぞれの用途地域に応じて、建ぺい率を掛けて面積を求める


(令和元年度出題:No.16)
攻略ポイント
- 都市計画で定められる法定容積率を確認する
- 道路条件と道路の幅から、道路容積率を算出する
- Wa=(12-Wr)×(70-L)/ 70のWaの数値は図示で求める
- 法定容積率と道路容積率から、厳しい数値を選択する
- それぞれの用途地域の容積率から、延べ面積を求めて答えを導く


(平成30年度出題:No.17)
攻略ポイント
- 用途地域から、検討する高さ制限をメモする
- 道路斜線における高さ制限の最高高さを求める
- 隣地斜線における高さ制限の最高高さを求める
- 敷地の高低差より、起点となるレベルを求める
- 北側斜線における高さ制限の最高高さを求める

法規の計算問題(7問)を立て続けに斬ってきました。
画像を挿入したイラスト解説で、メモを入れながらお伝えしてきました。
計算問題を確実にモノにするポイントは、数値や公式よりも「解く手順」を覚えること。
(数値や公式は法令集に掲載されてますからね。)



計算問題は出来るだけ
法令集を使わずに解きたい。
苦手意識を克服するには、法令集から必要な情報を取り出し、ひとつずつ問題用紙にメモをする習慣を付けましょう。
この記事では、法規の難問である計算問題の攻略ポイントをギュッと絞って解説しました。
最後まで記事を読んでいただき、本当にありがとうございます!



注意点があります。
当記事は「令和6年度に施行されている法規」を取り扱っています。
法改正により、出来る限りの更新をしていきますが、最新の情報はご自身で確認して下さい。
また、引用させていただいた条文は、円滑な情報伝達の視点から一部を省略しています。
詳細を含めた正確な情報は、法令集を活用するなどして、ご自身で確認して下さい。






力学の攻略ポイントを集結!
.webp)
.webp)


-300x197.webp)








