一級建築士の構造力学は好きですか?
「構造なんて大嫌い!30問も要らないよ」
「数字や公式、計算式を見るだけでアレルギーが出る」
そういった計算問題を苦手とする方のために、私が攻略ポイントをまとめました。
解説のポイント
- 難しい理論や専門用語を省く。
- 理論よりも「イメージを優先」して伝える。
- 数値や公式よりも「解く手順」にフォーカスを当てる。
この記事では、一級建築士試験の構造に苦戦している受験生に向けて、魅力的なイラスト解説により攻略ポイントを分かりやすくお伝えします。

「構造を極める」

「計算問題に挑戦」

「イラスト解説」


この動画を YouTube で視聴
こんな人におすすめ!
- 苦手な構造を克服したい
- 理論や計算と向き合いたくない
- 分かりやすいイメージで理解したい



構造力学は実に奥が深い。
一級建築士の構造力学が苦手な人に向けて
構造力学の勉強をするうえで、計算問題に明け暮れる日々を過ごしてはいませんか?
公式が分かったとしても方程式が組み立てられず、桁数の多い計算に時間を浪費させられます。
構造あるある
- 解き方が分からずに堂々巡り
- 解説文と向き合うたびに身体はへとへと
- 何度もつまずき、構造アレルギーが増えるばかり
構造力学を苦手とする人は、その解き方について”理論と向き合い過ぎる”ところがあります。



構造力学はお手上げです。
攻略のポイント
理論よりもイメージで読み解く



これを待ってました!
計算問題に取り組むときのポイントは、数値や公式よりも「解く手順」を覚えること。
苦手意識を克服するためには、理論ではなく「イメージ」から考え方を知る必要があります。
イラスト解説により視覚的な要素を取り入れることで「構造問題のトラウマ」から解放しましょう。
トラスの攻略はこちら!


一級建築士(構造)計算問題に挑戦して、攻略ポイントを解説!
解説のコンセプトについて
- 計算問題を攻略するうえで、理論や専門用語をできるだけ排除する。
- 私が手作りしたオリジナルのイラストを使って視覚的に分かりやすく解説する。
- 過去問題に挑戦した実践的なプロセスを踏まえ、解く手順やポイントを伝える。



気合を入れるぞ!



準備は良いか?
モーメント図
難易度:★☆☆☆☆
$$モーメント=力×距離$$
「モーメントは力×距離」が基本。
この「力」というのは問題によって様々な言葉に置き換わります。
力の名称
- 反力
- 水平力
- せん断力
問題の種別により「力の名称」は変わります。
しかし、モーメントの基本はあくまでも「力×距離」ということを覚えておきましょう。



これが基本の公式!
$$モーメント=力×距離$$
攻略ポイント
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
問題
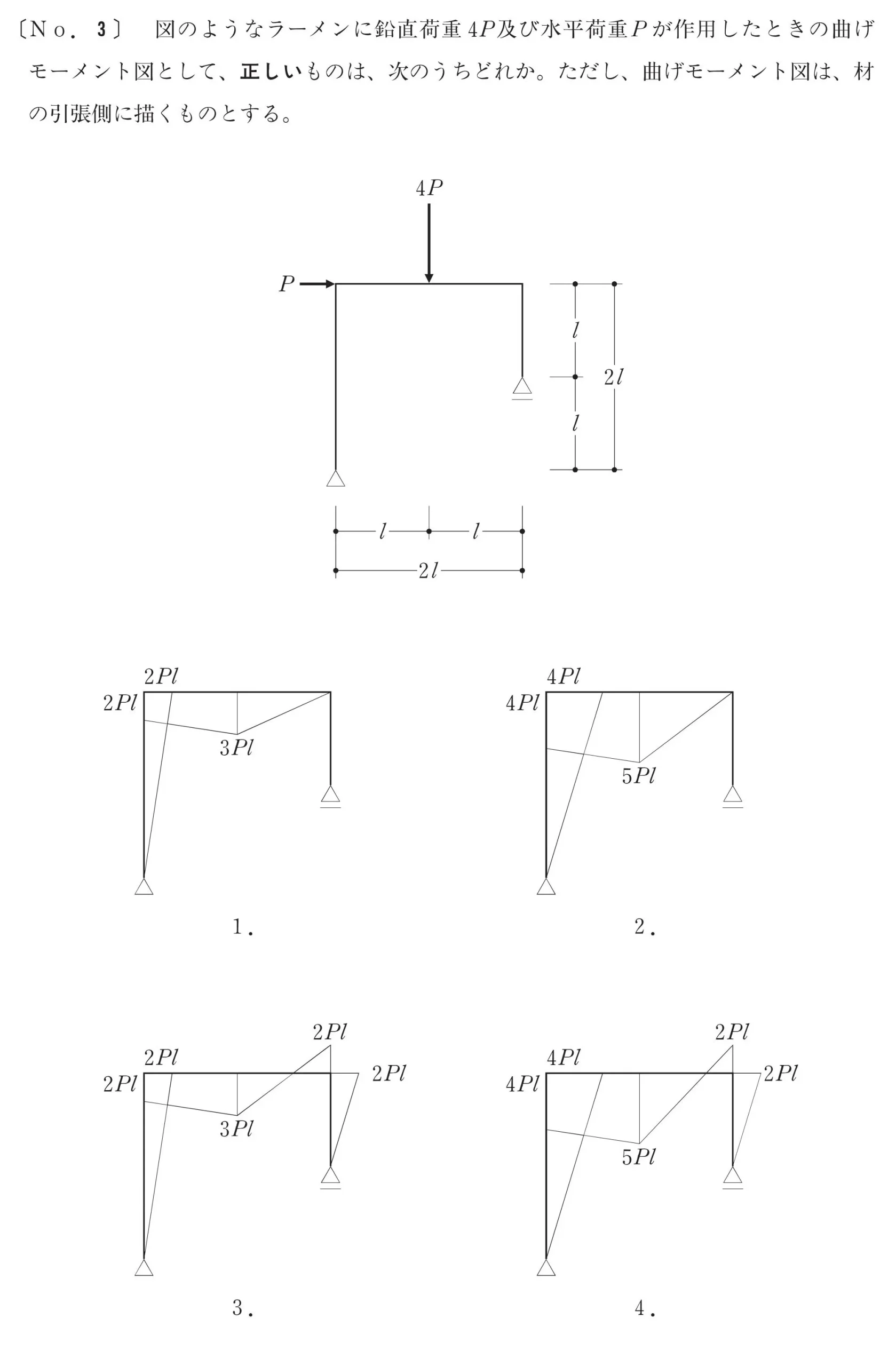

モーメント図を正確に描く力を試される問題です。
どの問題においてもモーメント図の基本形は「集中荷重の片持ち梁」と捉えましょう。



モーメント図は
片持ち梁に置き換える。
モーメント図の基本形


モーメント図の基本形は「集中荷重の片持ち梁」に置き換える。
モーメント図(参考)






この動画を YouTube で視聴
1.支点反力を求める
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
反力を求める
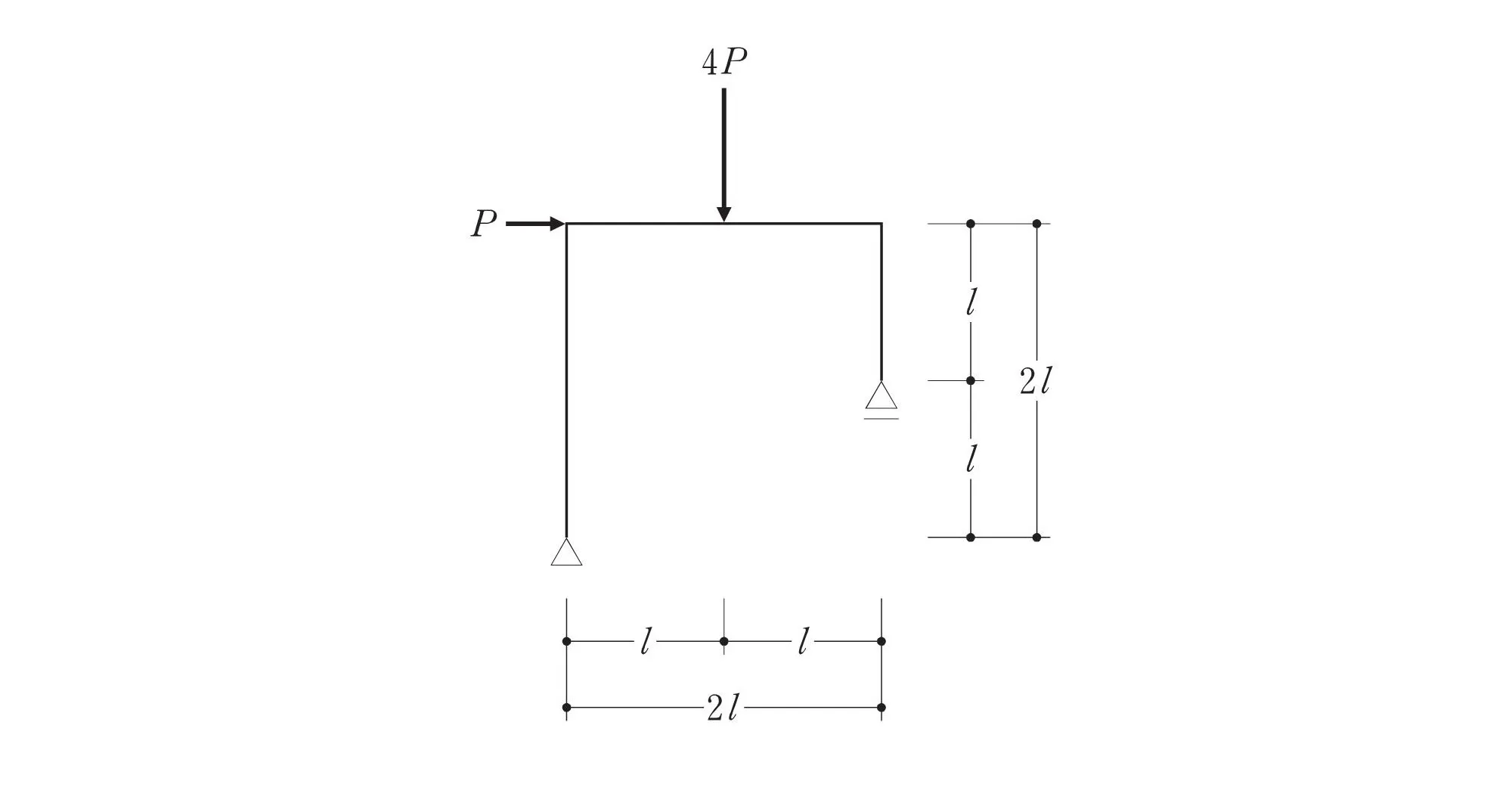

ラーメンの柱脚に注目
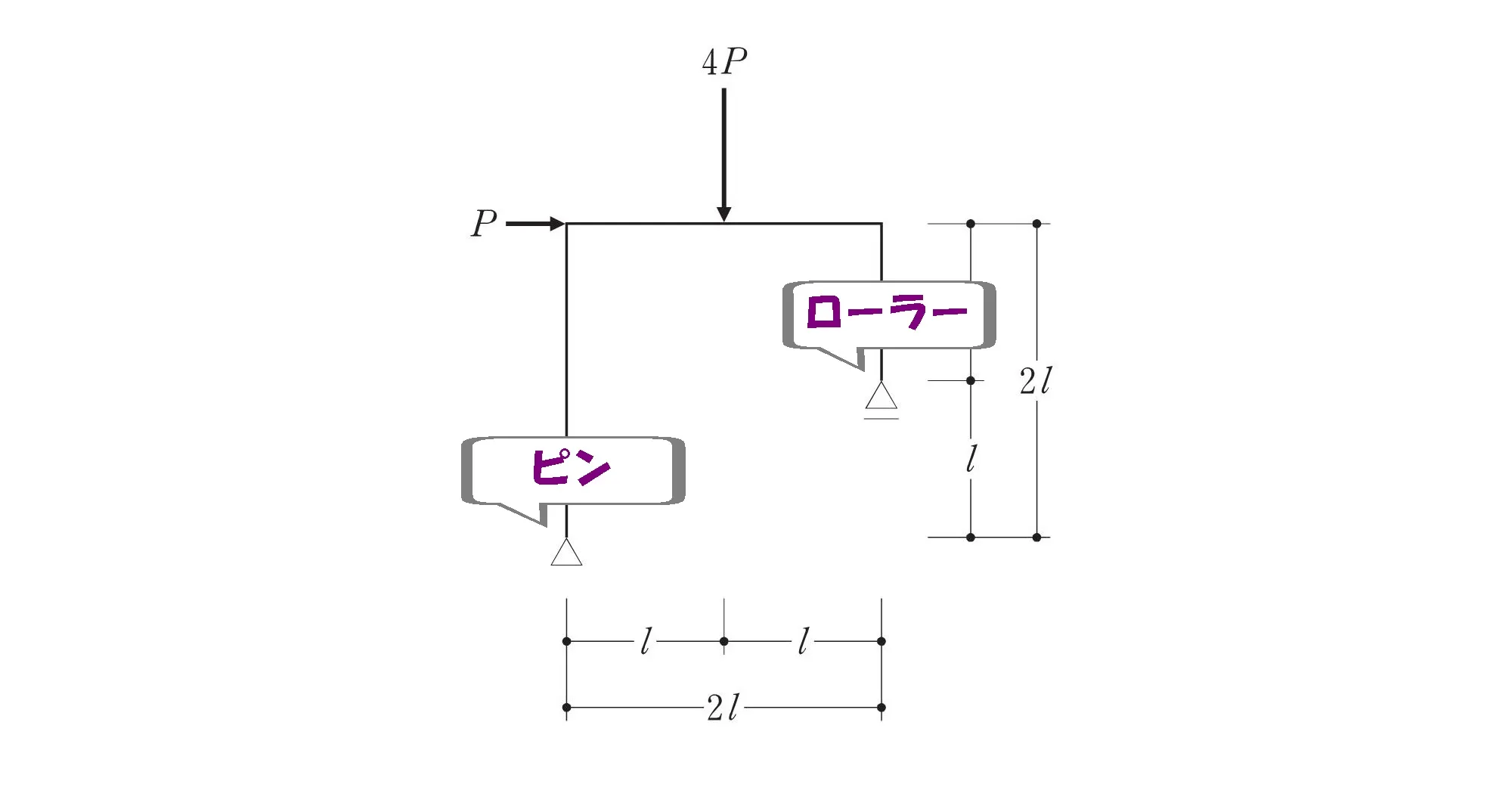

左:ピン支点
右:ローラー支点
柱脚はピンとローラー支点なので、支持部分での回転力は発生しません。
ここがポイント!
ピンとローラーの支持部分におけるモーメントはゼロになる。
鉛直反力を書く
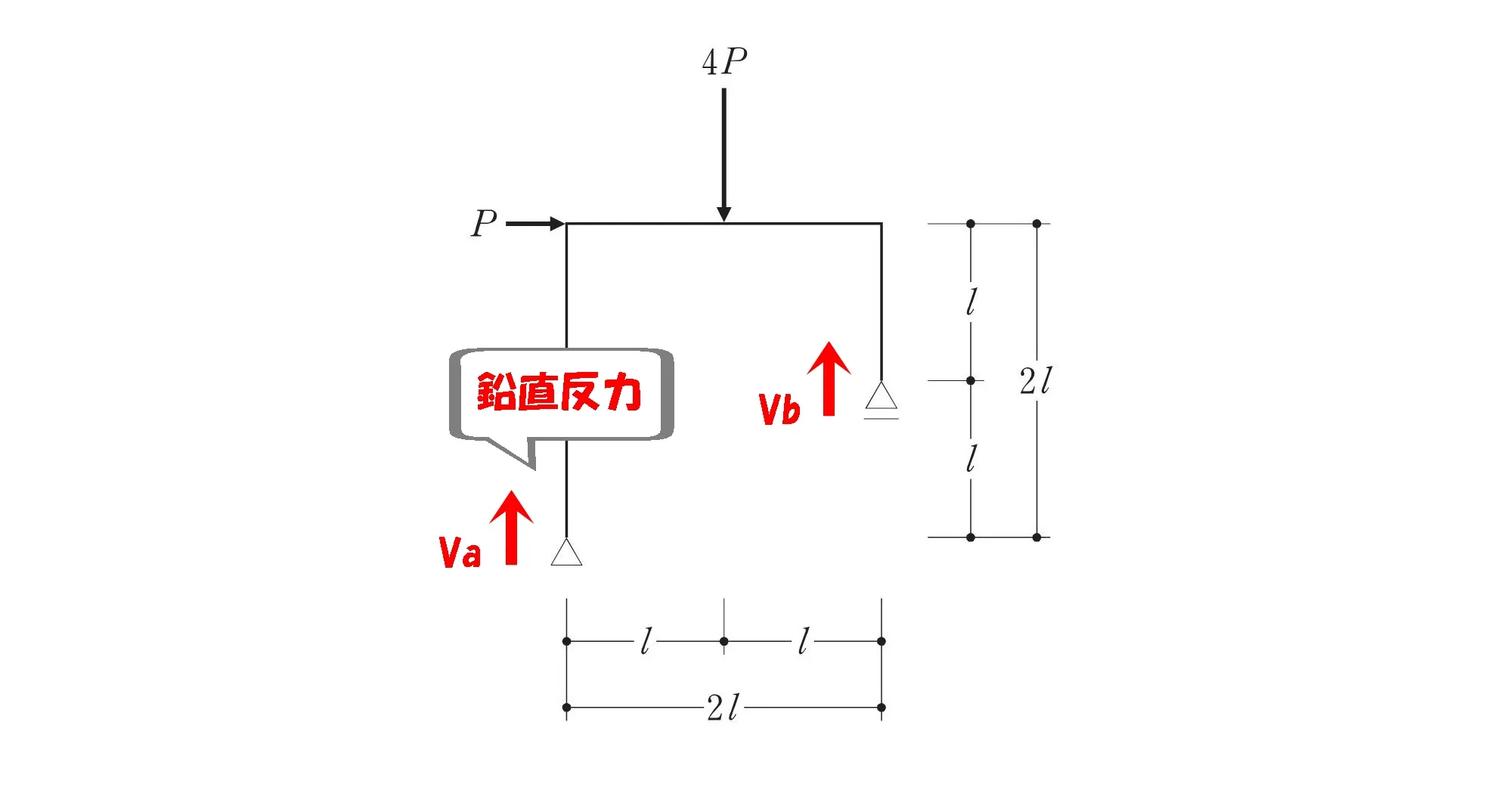

モーメント図を描くうえで始めにすることは「反力」を書き出すこと。
水平反力を書く
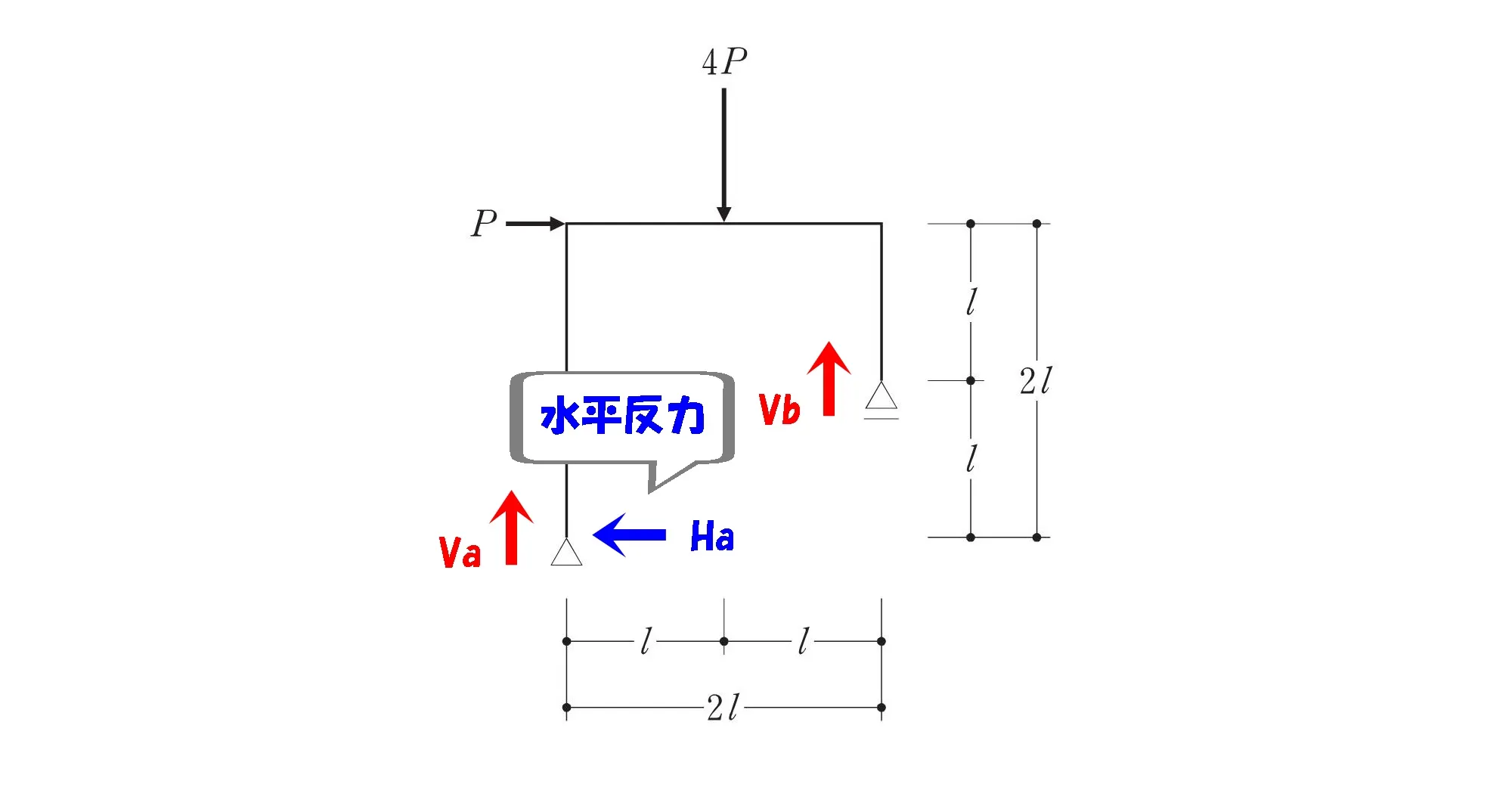

モーメント図を描くうえで始めにすることは「反力」を書き出すこと。(繰り返し)



そう!
支点反力を求める。
ローラー支点は?
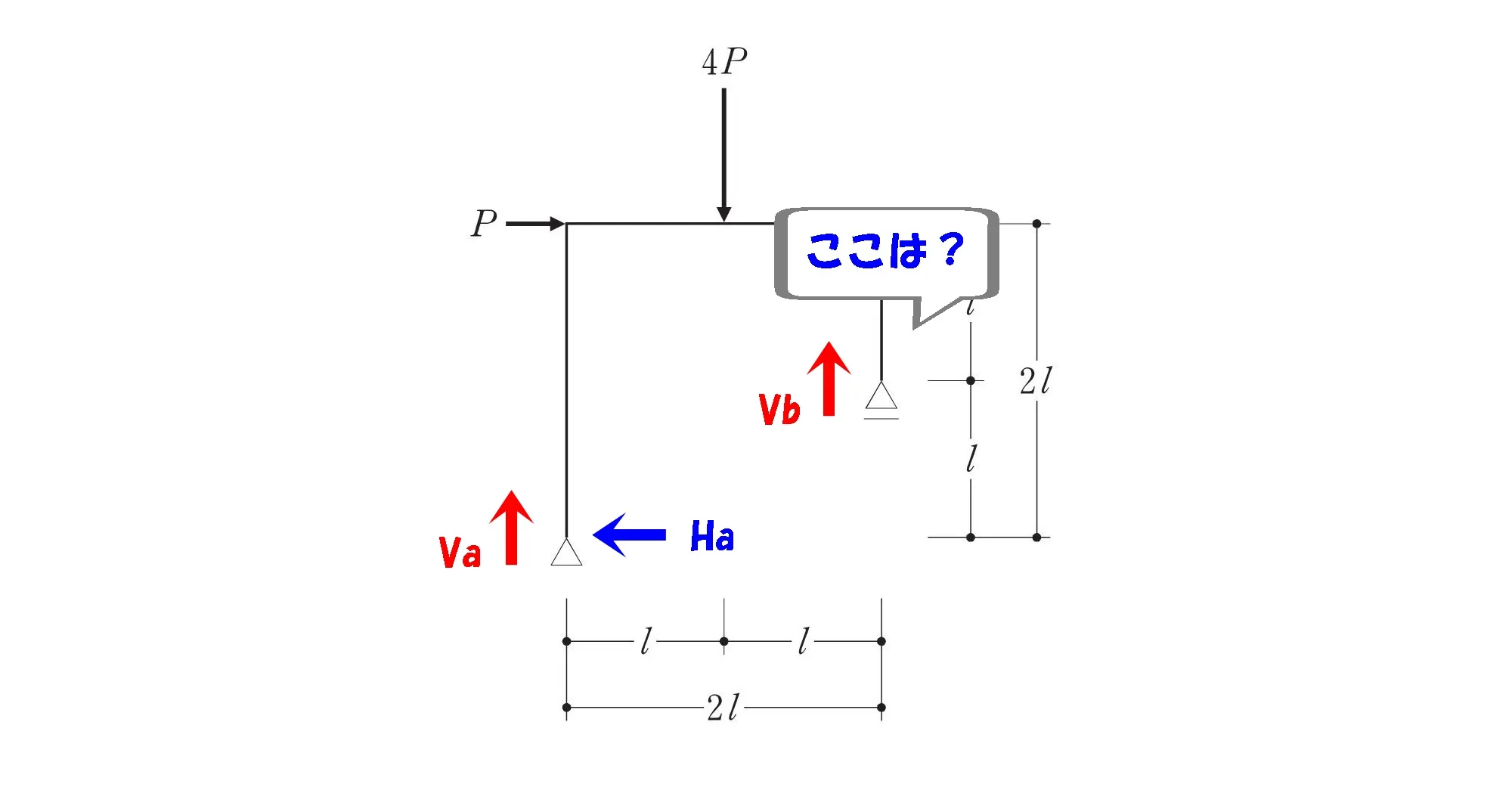

水平反力なし
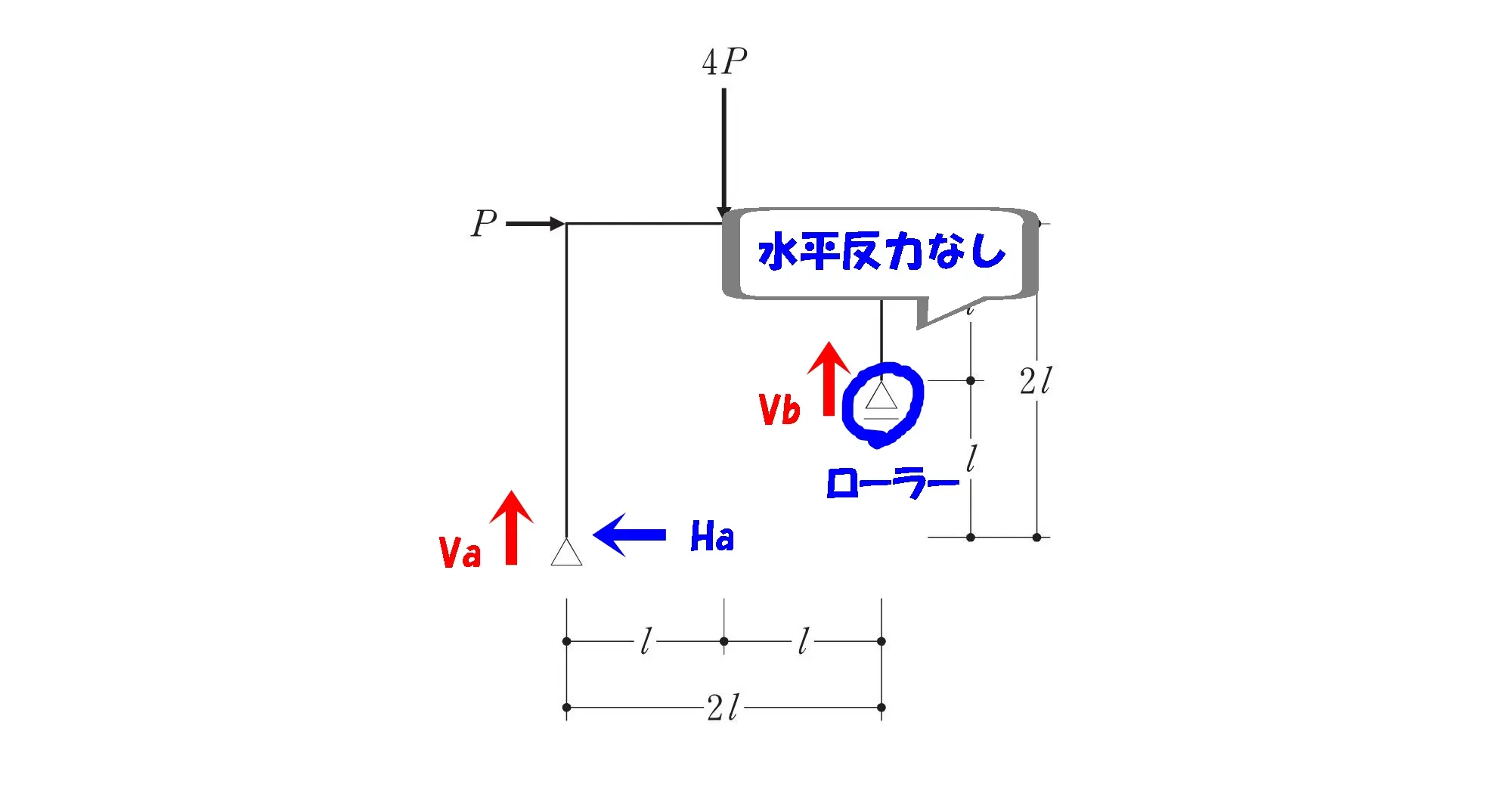

ローラー支点は水平方向の力に対して自由にスライドするため、「水平反力はゼロ」になります。



そう!
ローラーだからね。
1.支点反力を求める
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
水平力の吊り合い
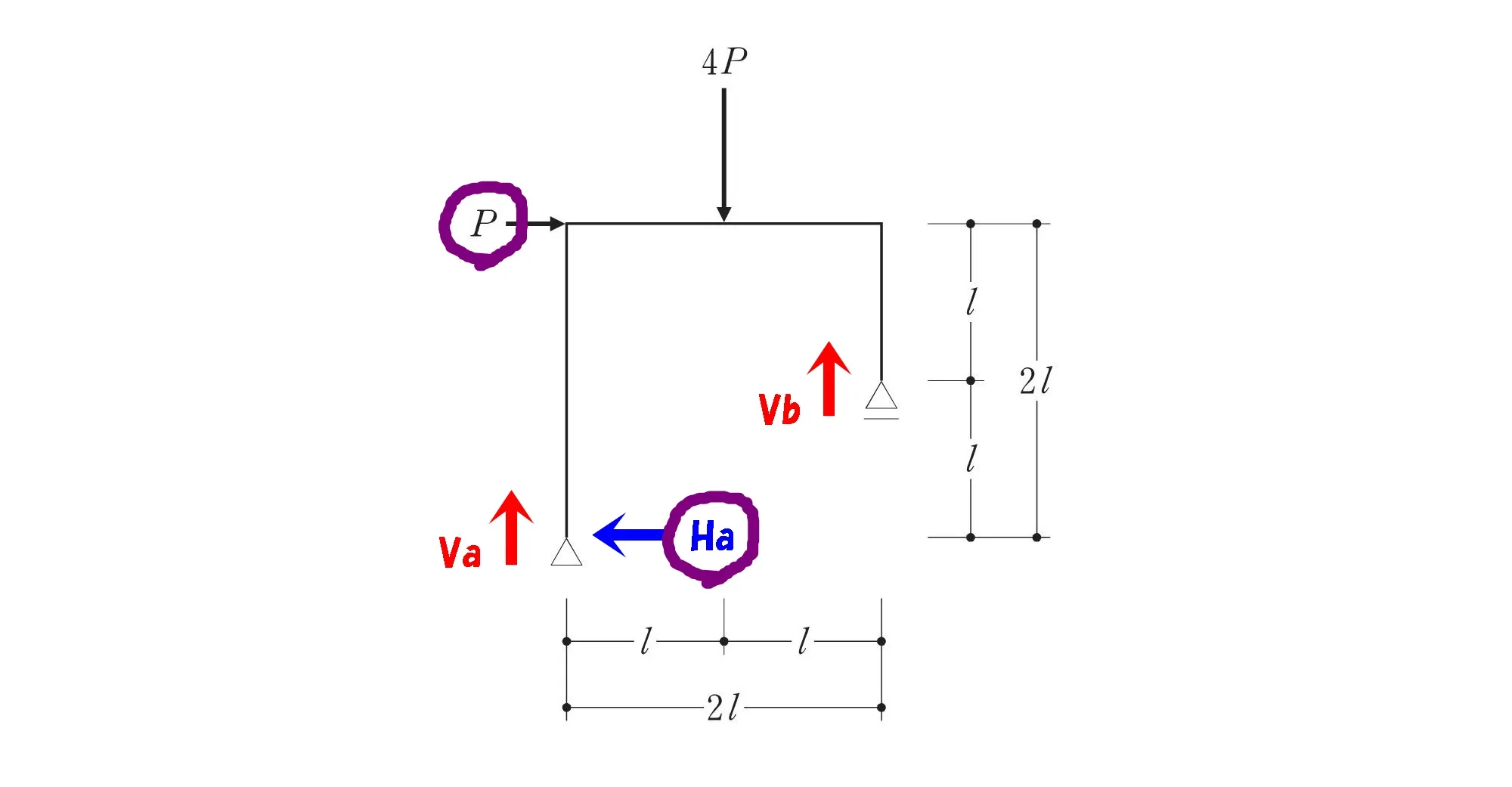

水平力の吊り合いを使って反力を求める。
公式
$$\Sigma X=0$$



Σエックス!
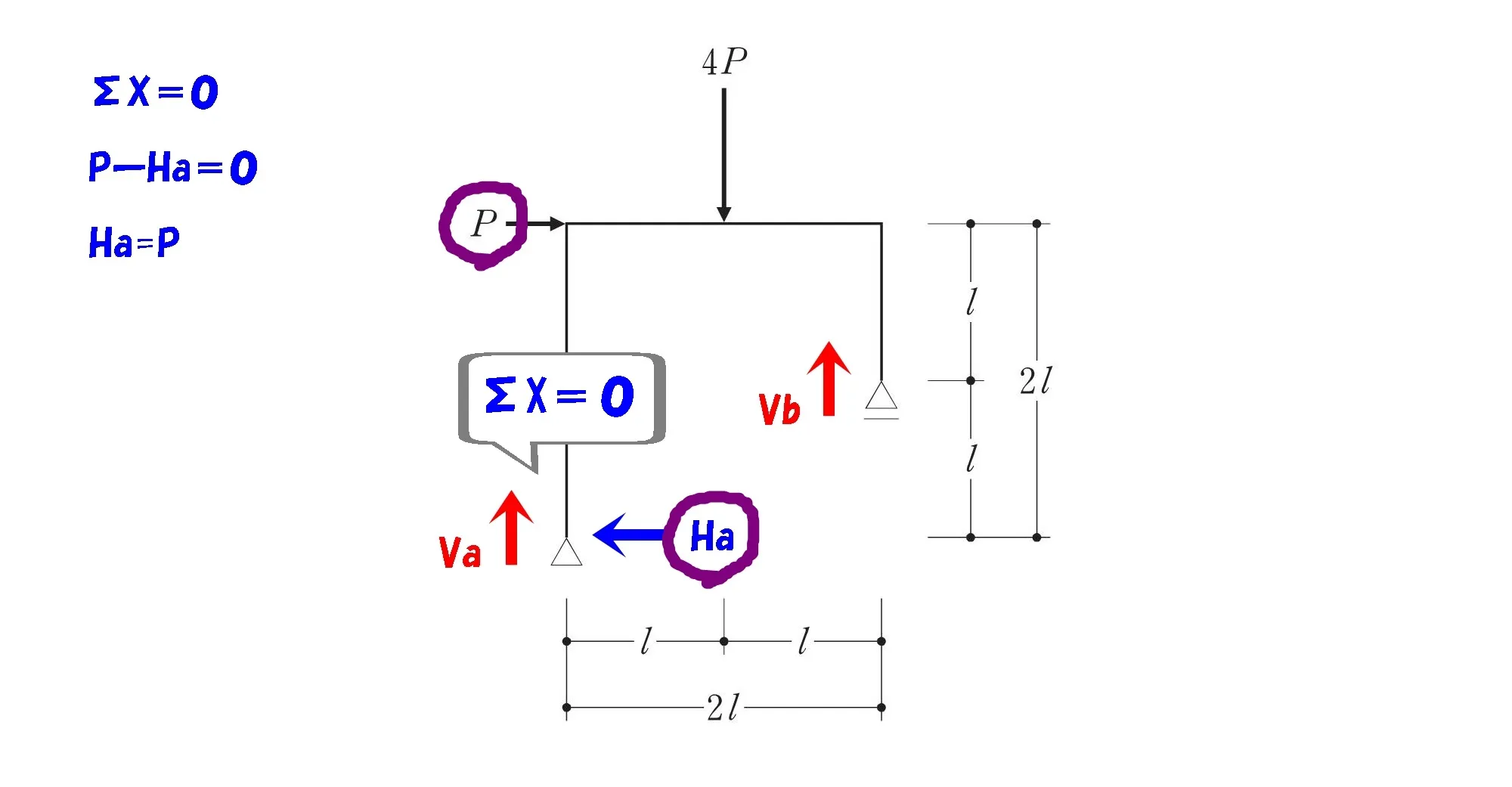

$$\Sigma X=0より$$$$P-Ha=0$$$$Ha=P$$
水平力の吊り合いを使って「P」を求めまります。
Ha=P

3つの公式
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!
1.支点反力を求める
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
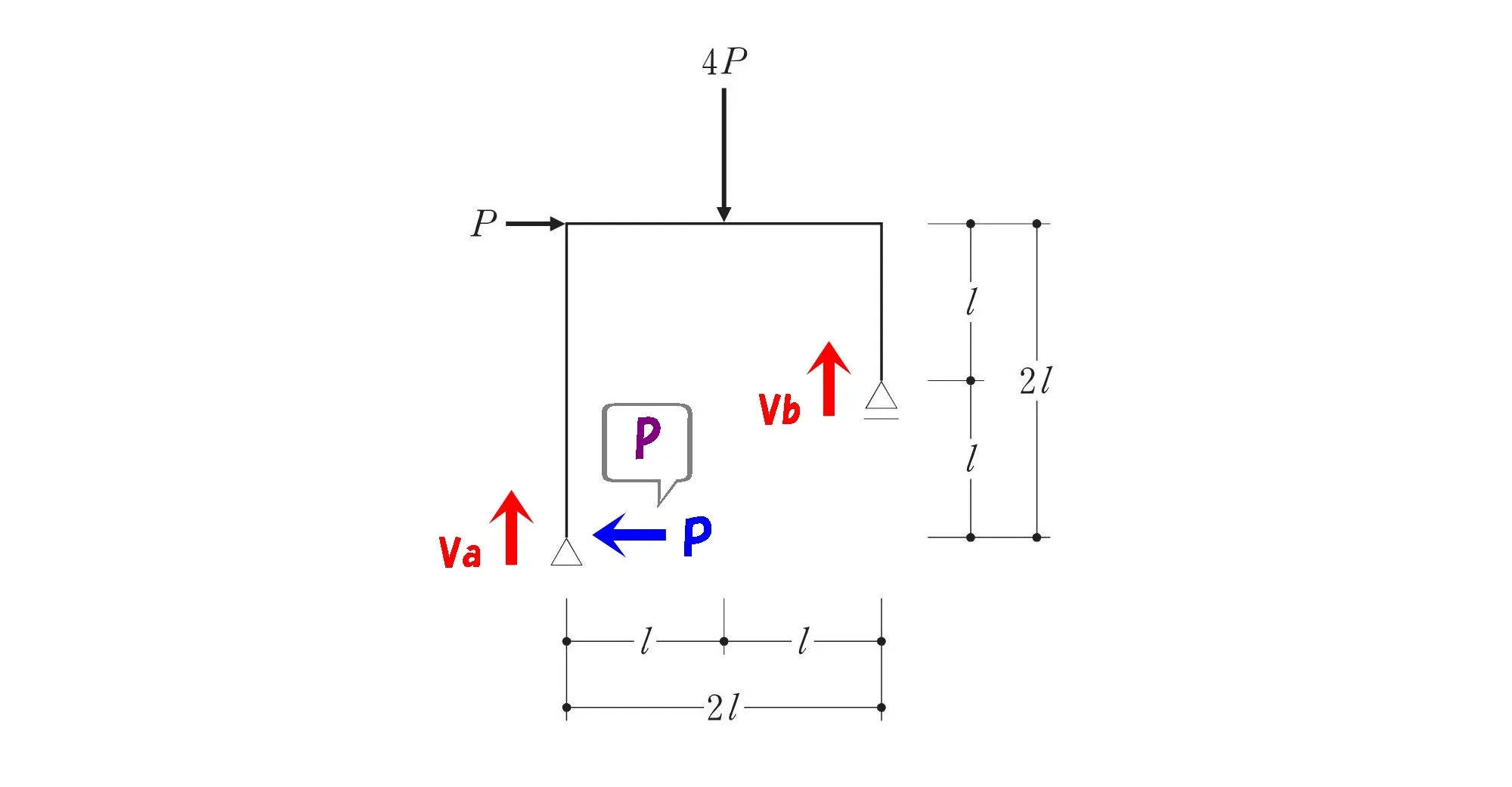
鉛直反力を求める

ラーメンに発生する反力はすべて求める。
公式
$$\Sigma M=0$$



Σエム!
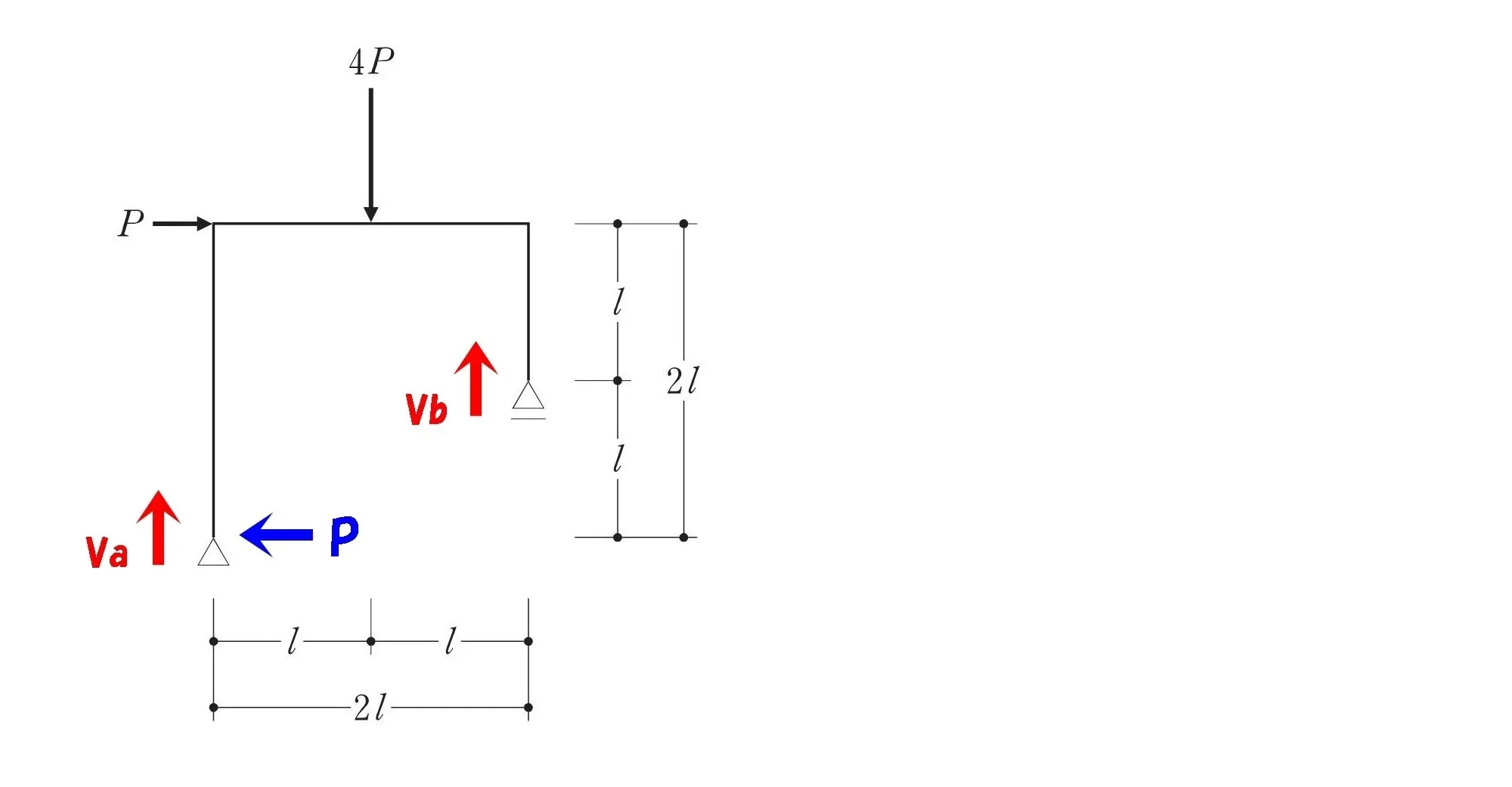
モーメントの吊り合い

ここがポイント!
ピンとローラーの支持部分におけるモーメントはゼロになる。
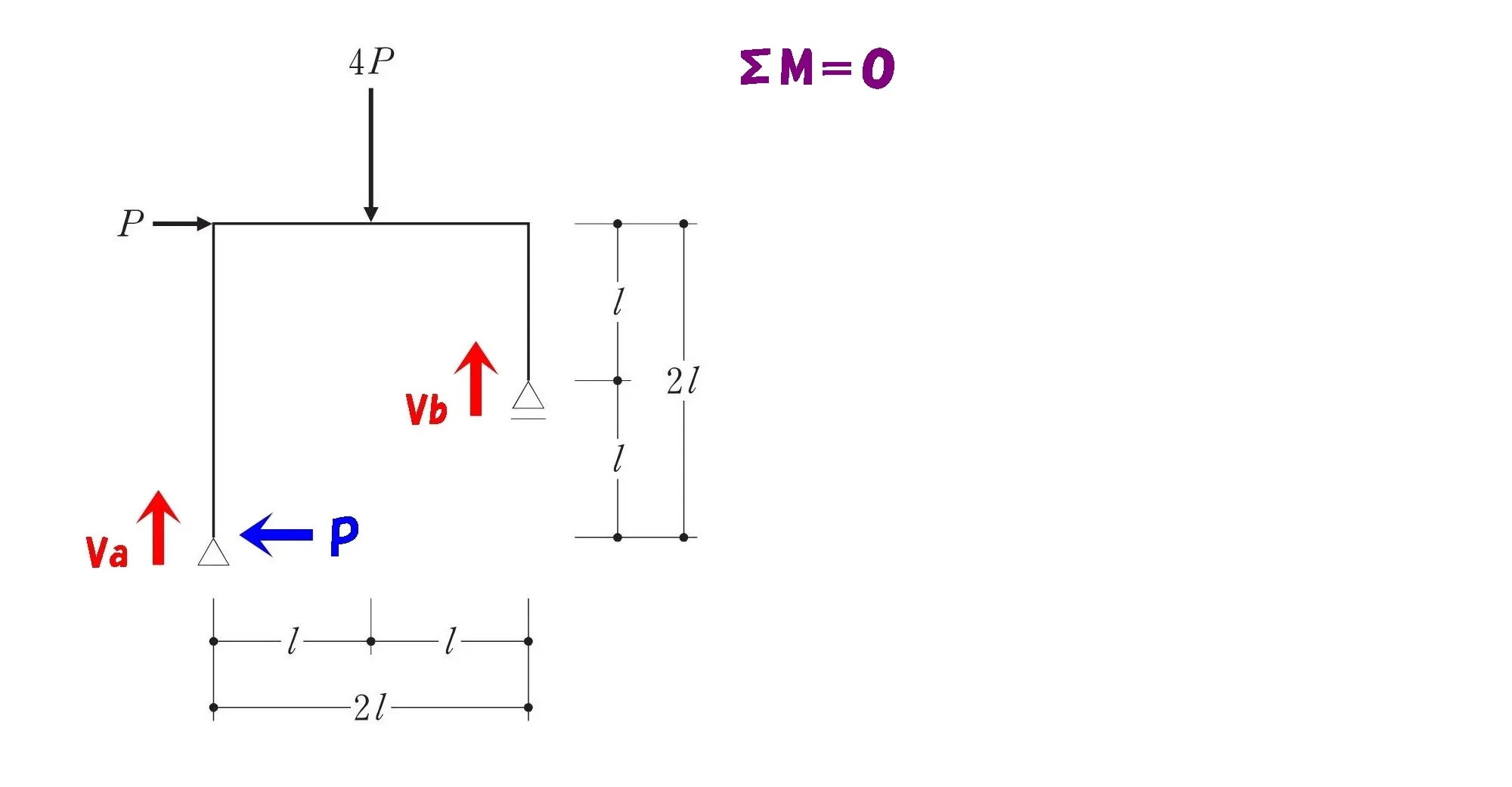
柱脚のピンとローラー支点の「モーメントはゼロになる」ことから、吊り合い式を作ります。
支点に発生する反力の数
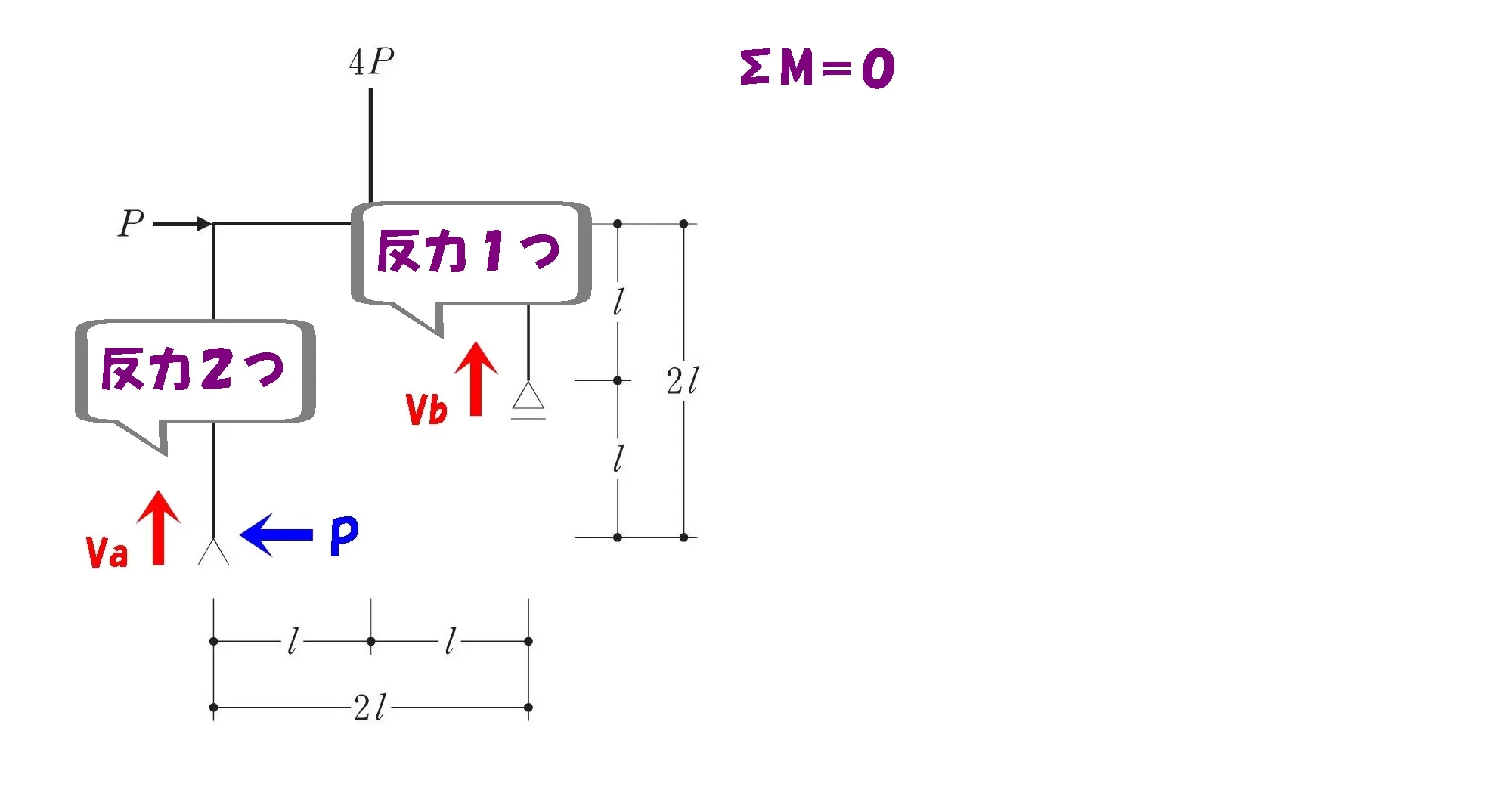

支点に発生する反力の数
- 左の柱脚:ピン支点に発生する反力はVaとPの2つ
- 右の柱脚:ローラー支点に発生する反力はVbの1つ
反力の多いピン支点を起点にする
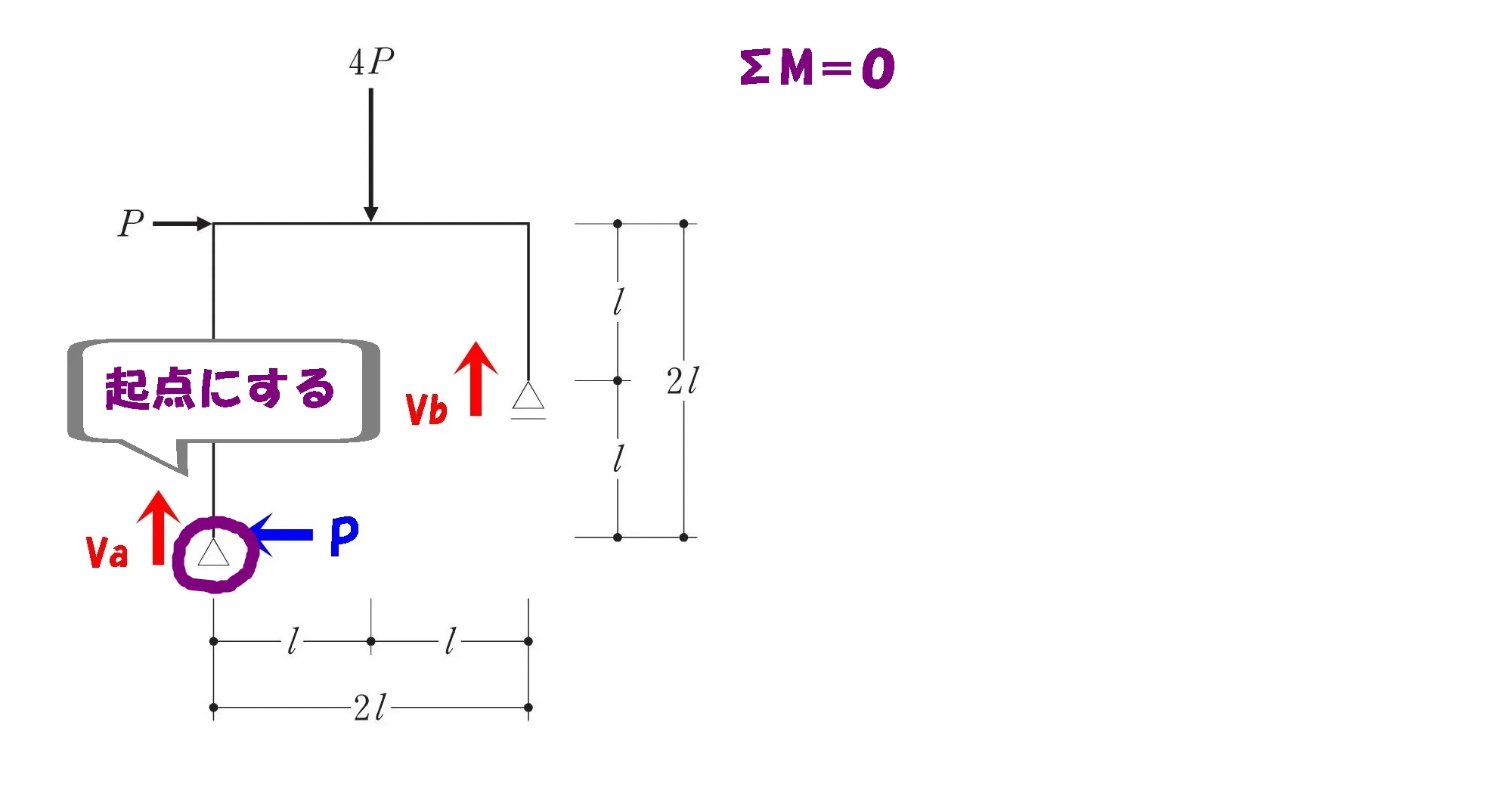

ここがポイント!
反力の多いピン支点を起点にΣM=0
起点に向かう反力のモーメントはゼロになります。
(距離がゼロになるため、力×距離=0)
そのため、モーメントの吊り合い式から2つの反力を消すことが出来るのです。



モーメントの式に
ジャマものは要らない。
2.片持ち梁の絵を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
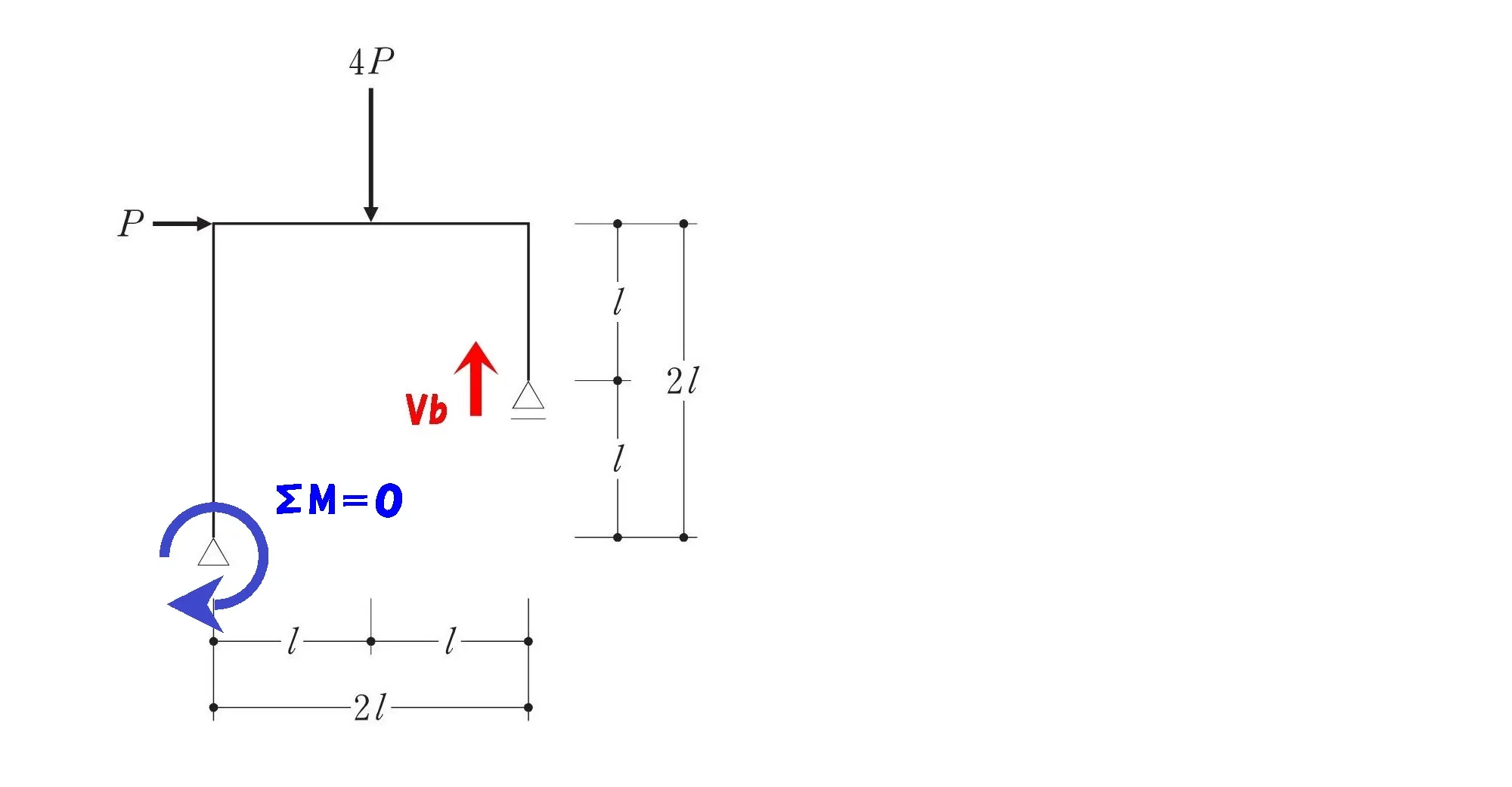

シンプルな片持ち梁の絵を描く
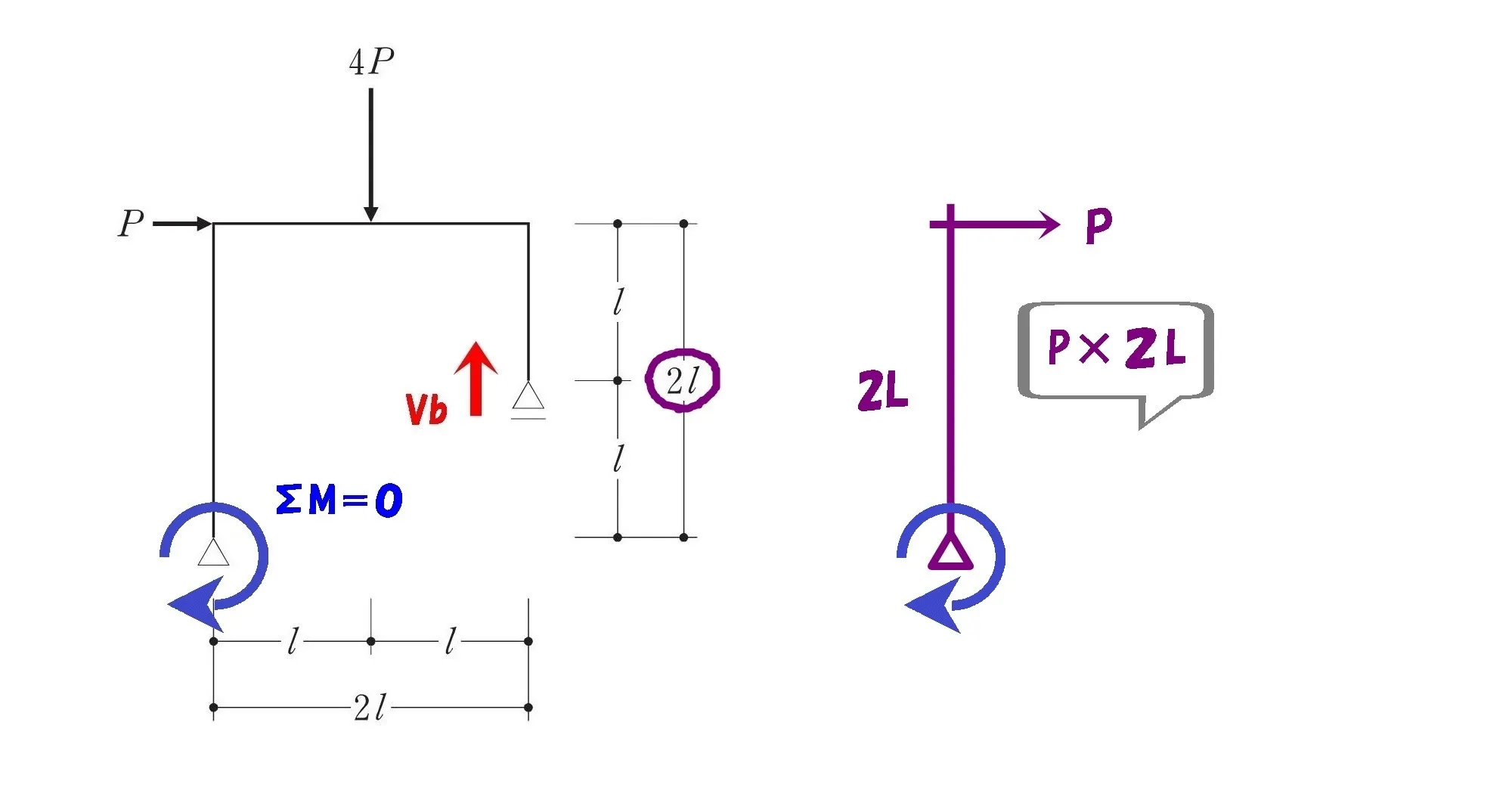

$$P*2L$$
シンプルな片持ち梁の絵を描く
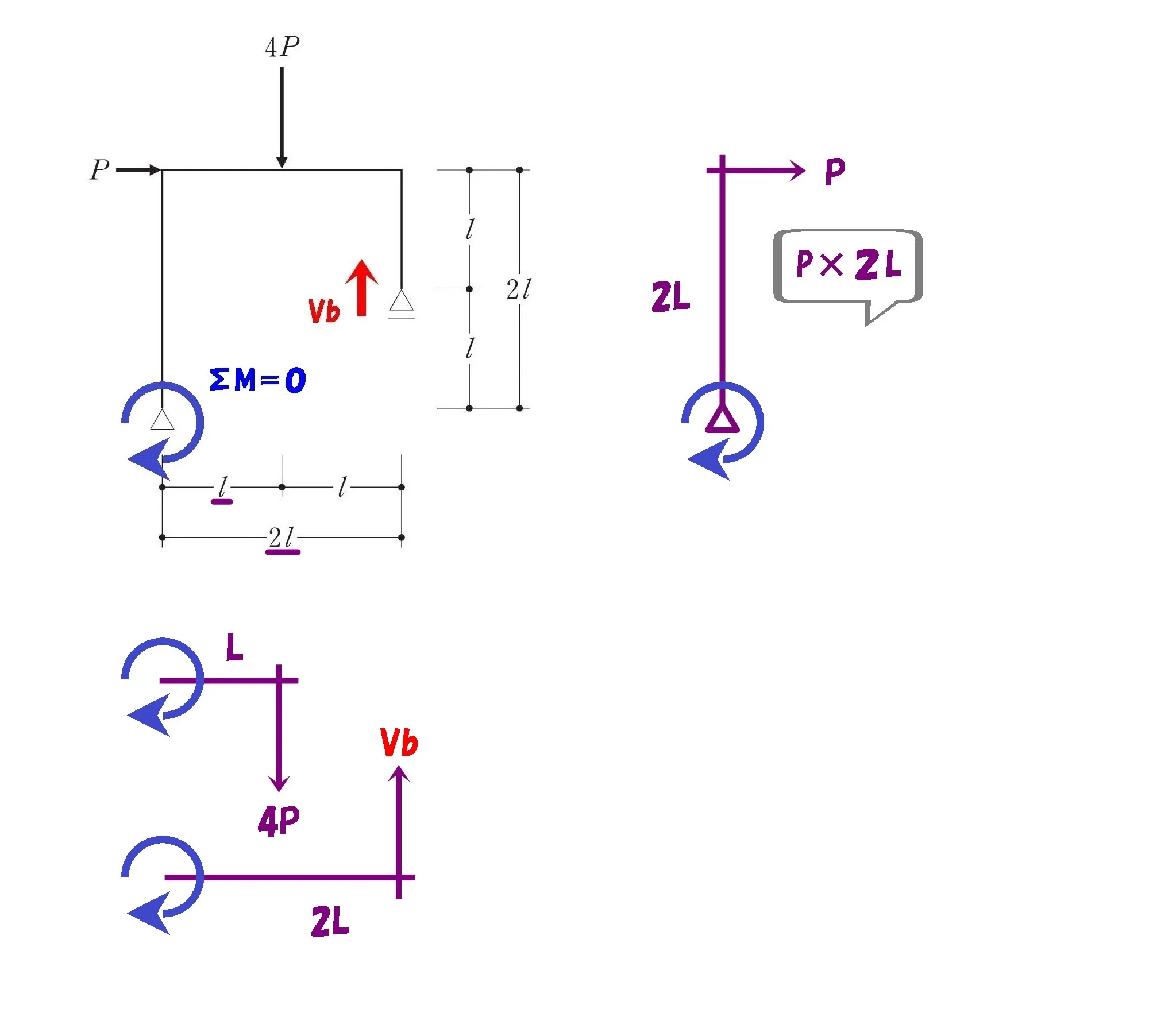

公式
$$\Sigma M=0$$



Σエム!
モーメント=力×距離
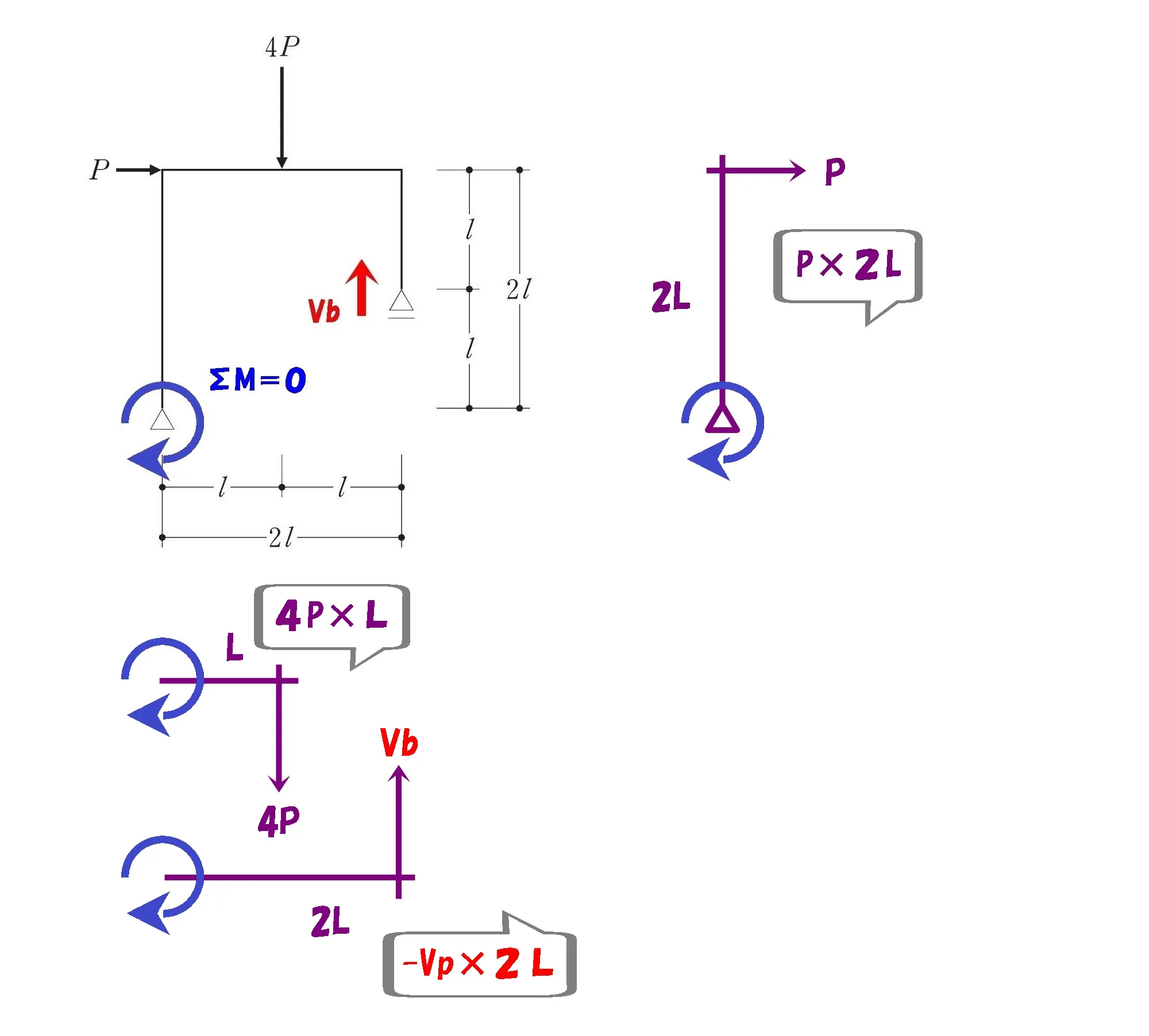

$$+P*2L+4P*L-Vb*2L=0$$
ΣM=0
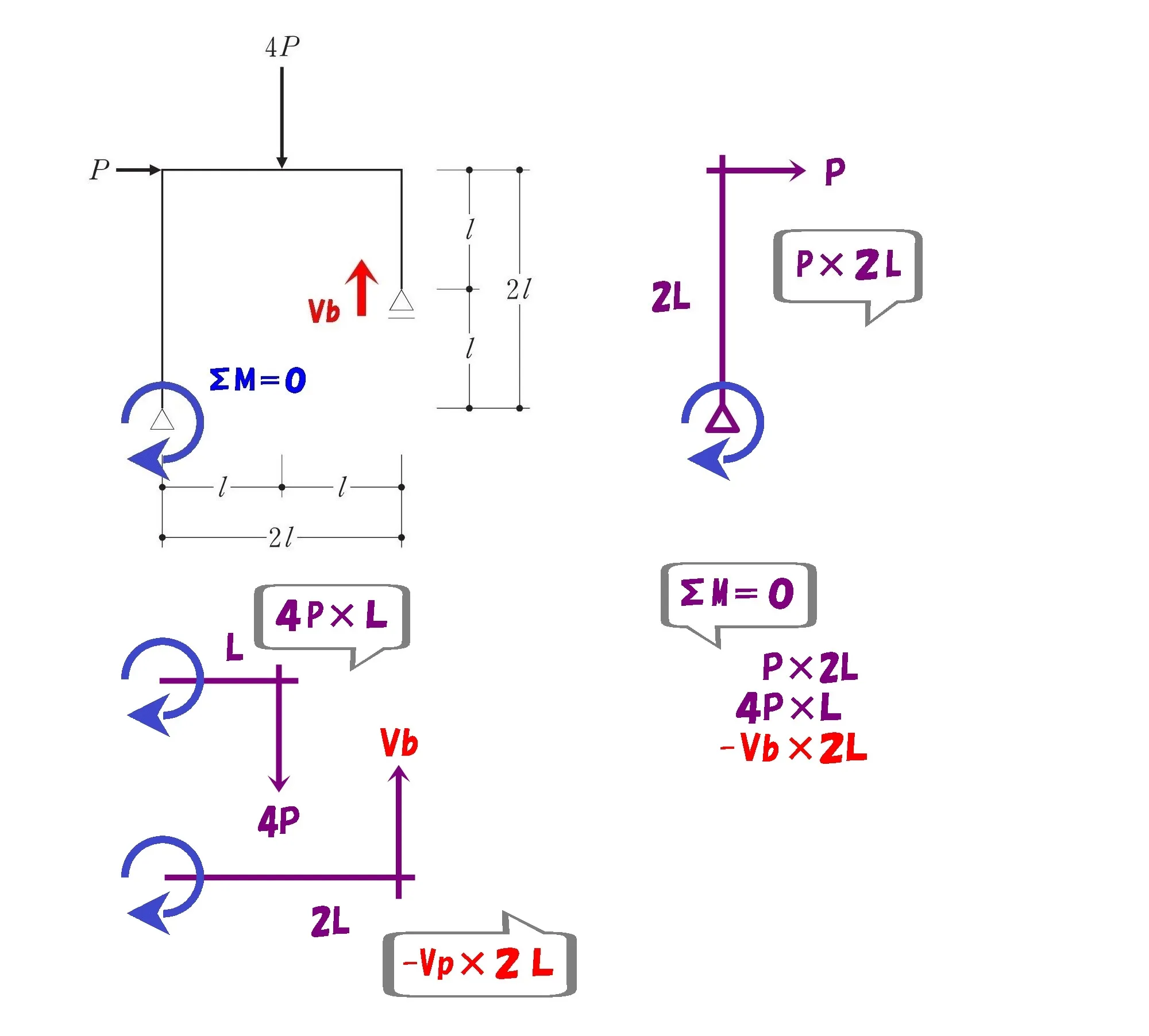

$$\Sigma M=0より$$
$$+P*2L+4P*L-Vb*2L=0$$$$2VbL=6PLより,Vb=3PL$$
3つの公式
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!
1.支点反力を求める
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
ΣY=0
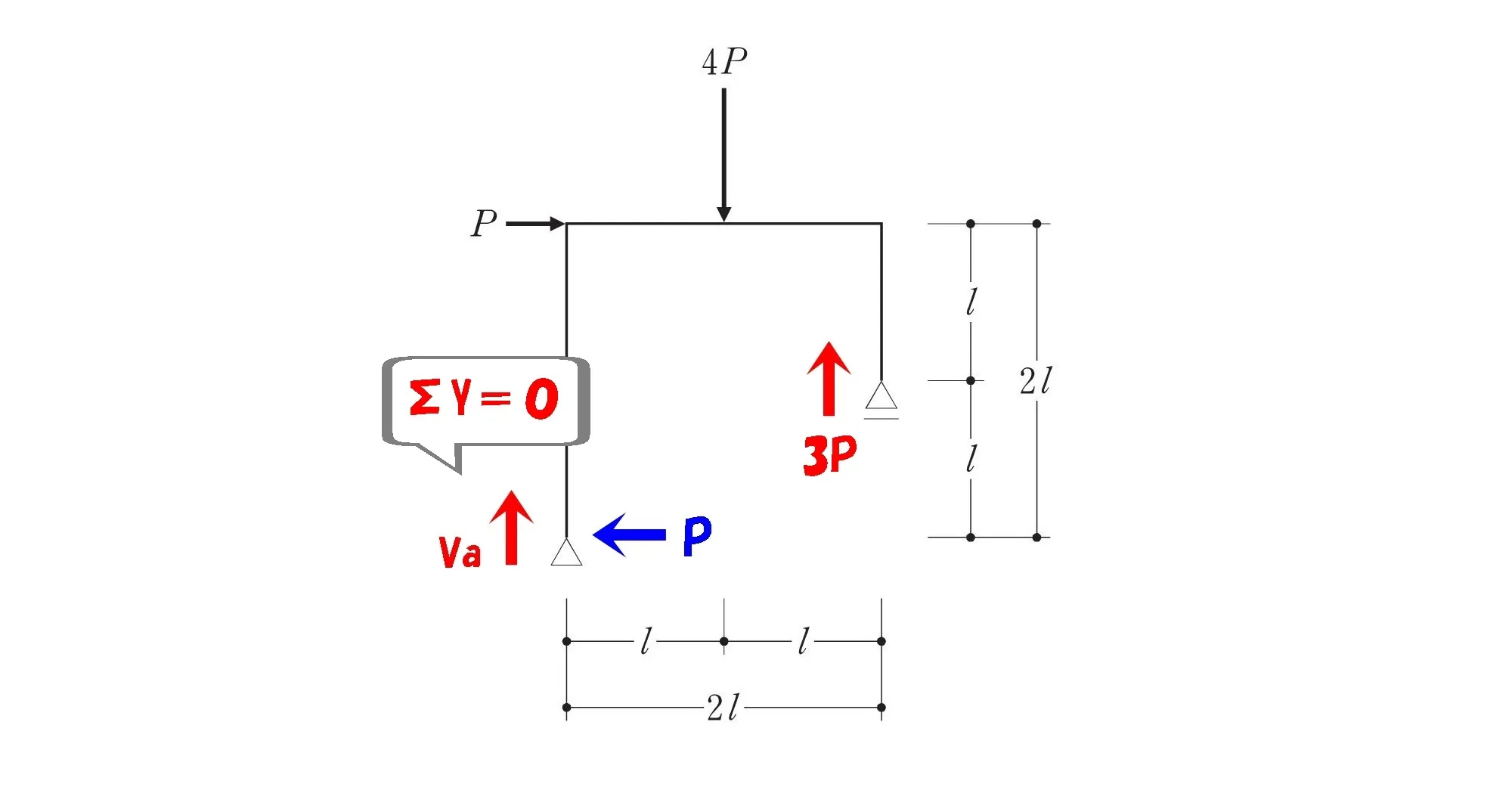

ΣY=0の吊り合いより、Vaを求めます。
公式
$$\Sigma Y=0$$



Σワイ!
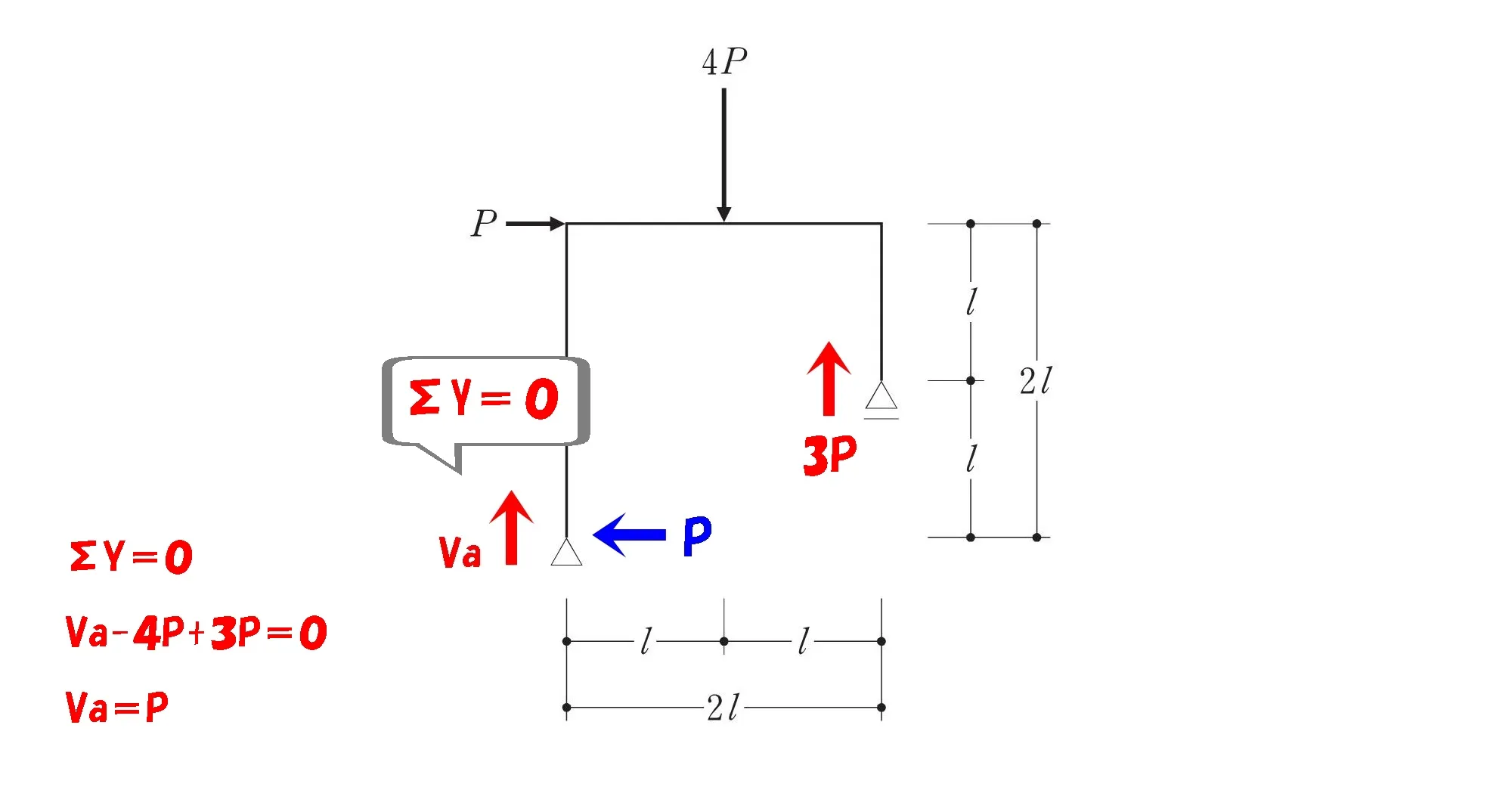

$$\Sigma Y=0より$$$$Va-4P+3P=0となるので,Va=P$$
3つの公式
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!
2.片持ち梁の絵を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
3つの反力
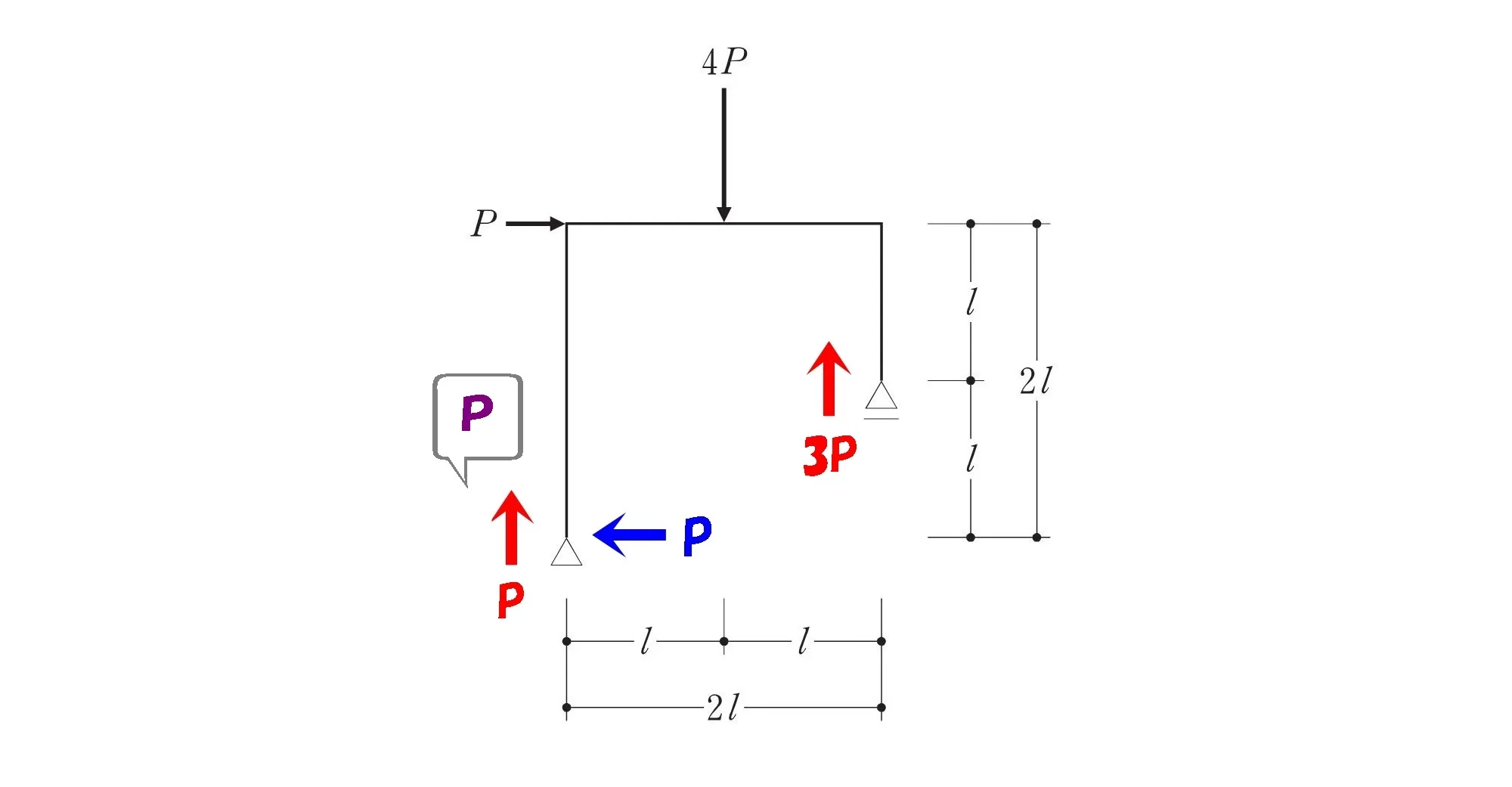

反力はそれぞれ、↑P・←P・↑3Pが求まりました。
この反力によってモーメント図が描けるようになります。
シンプルな片持ち梁の絵を描く
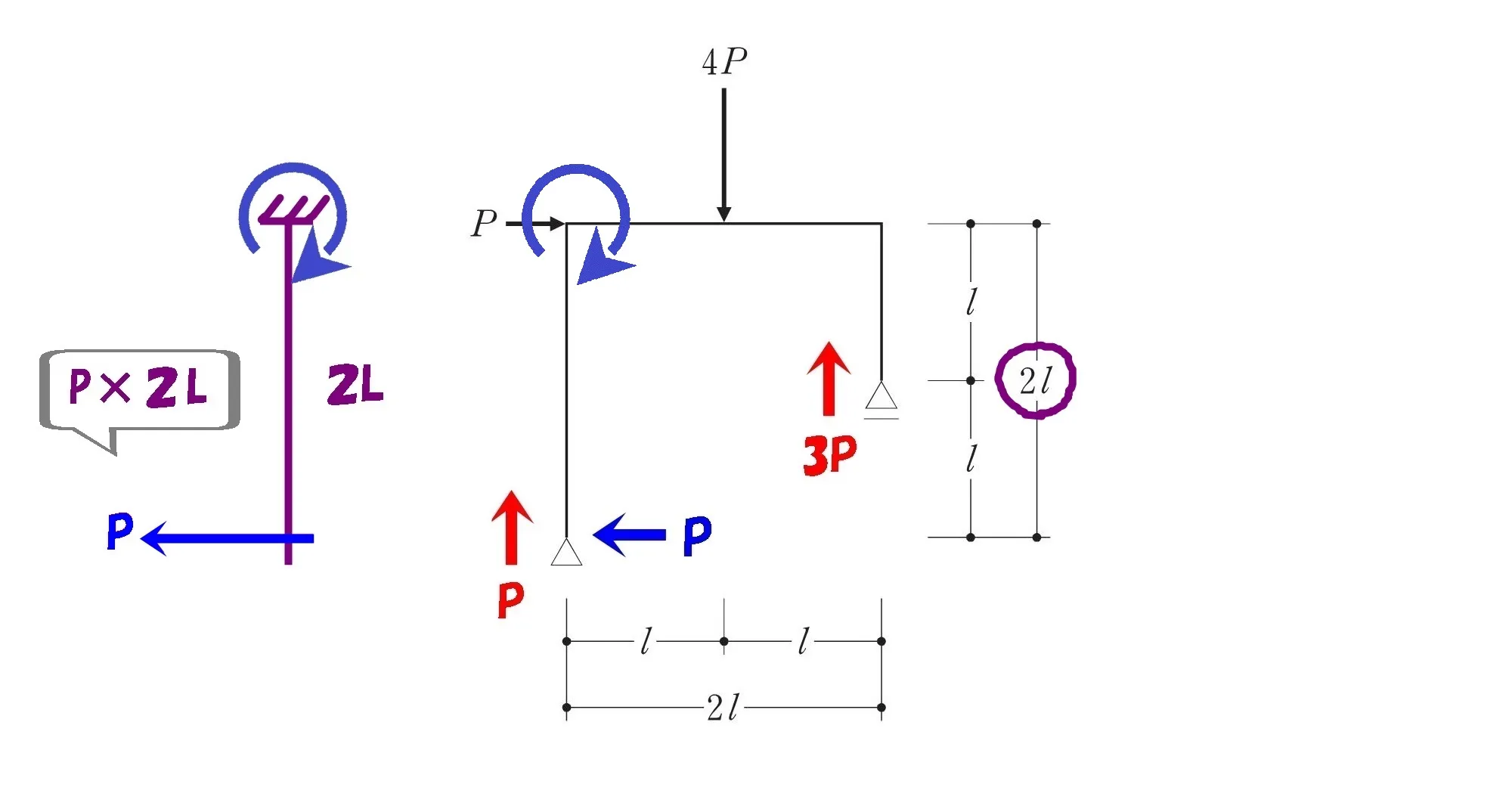

3.モーメント図を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
モーメント=力×距離
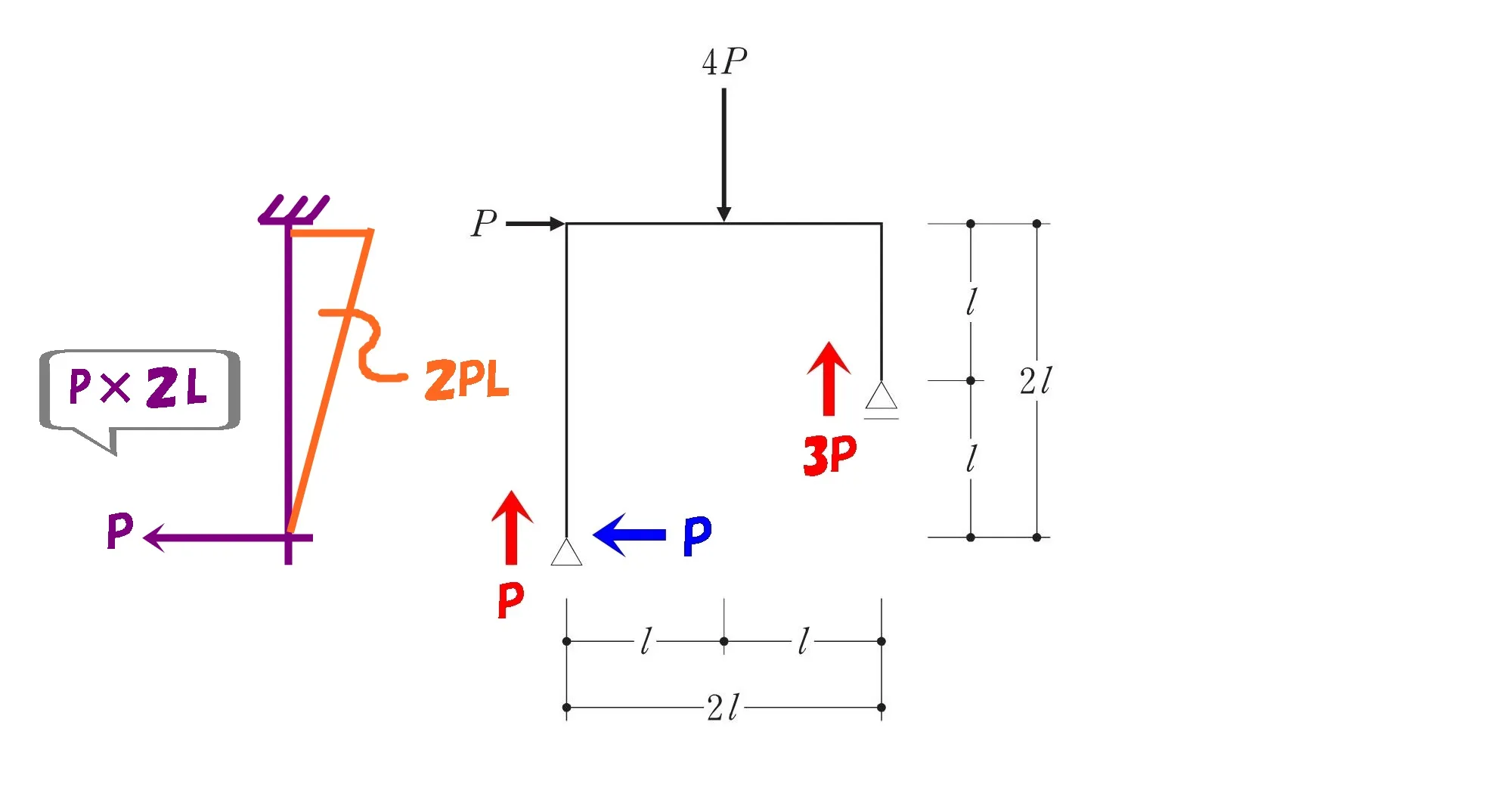

$$M=P*2L$$
モーメント=2PL
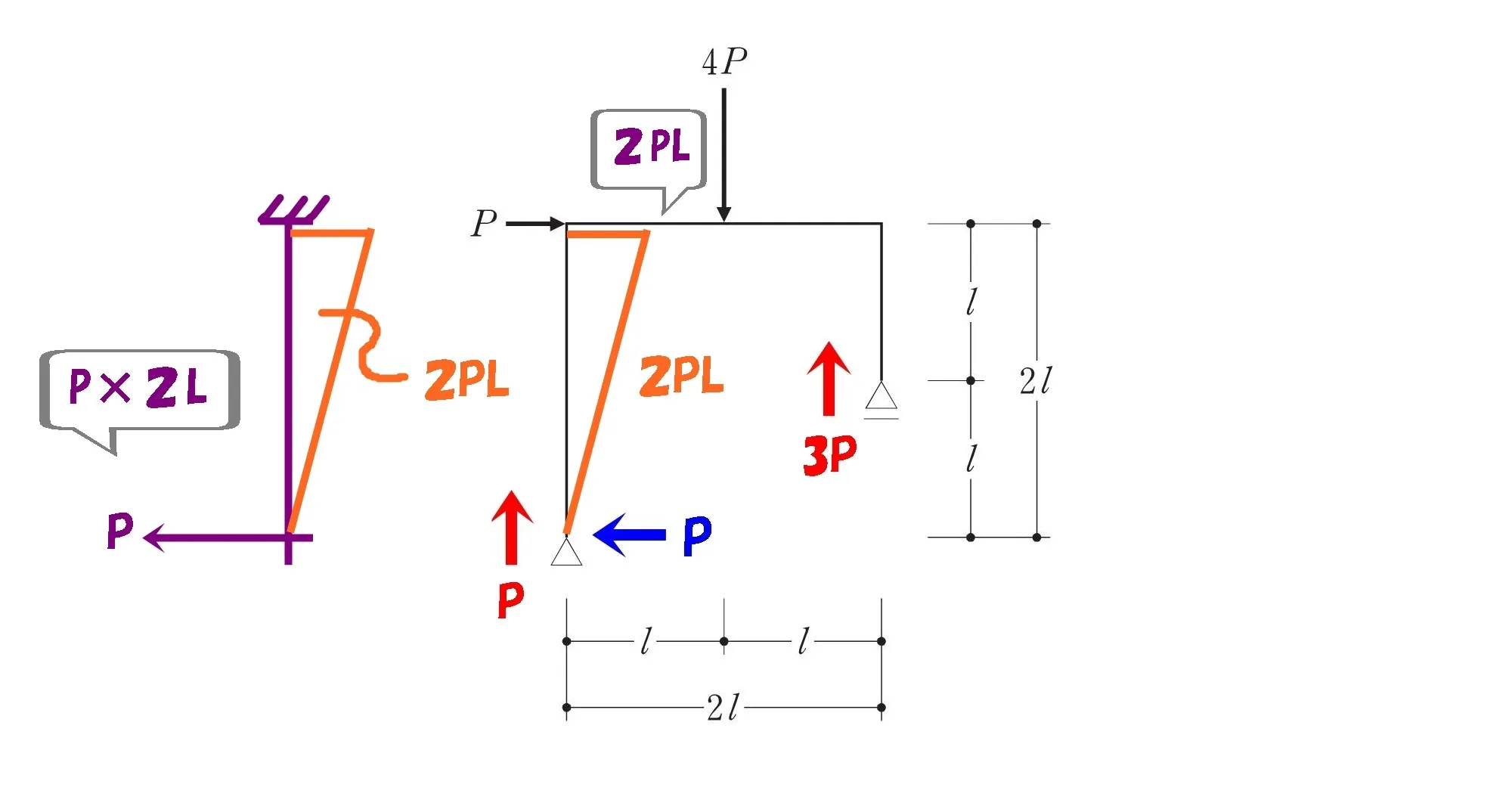

$$M=P*2L=2PL$$
2.片持ち梁の絵を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
部材を取り出す
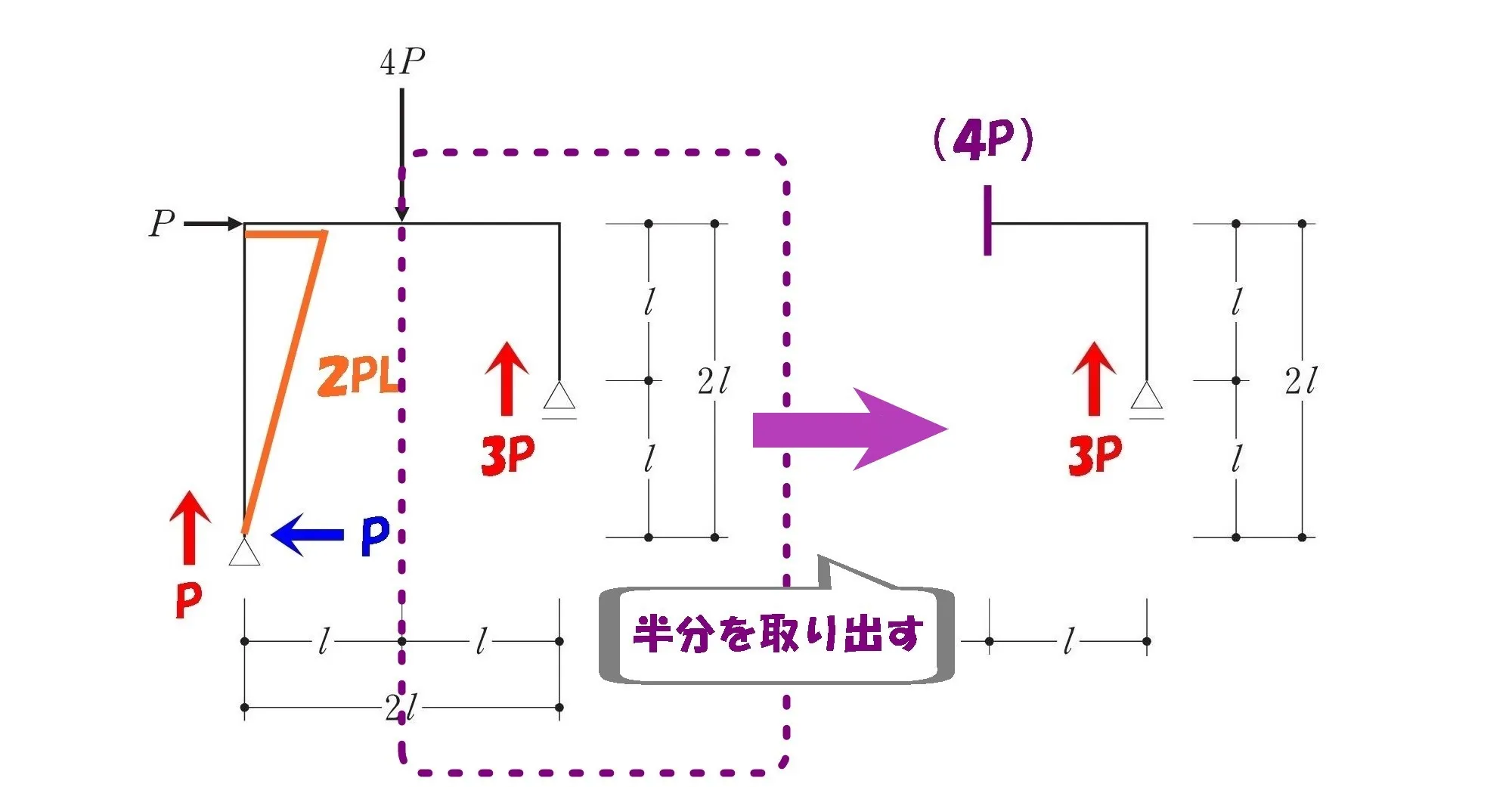

ラーメン梁の中央(4P↓の位置)のモーメントを求めるため、部材を切断して半分を取り出します。



ラーメン斬り!
シンプルな片持ち梁の絵を描く
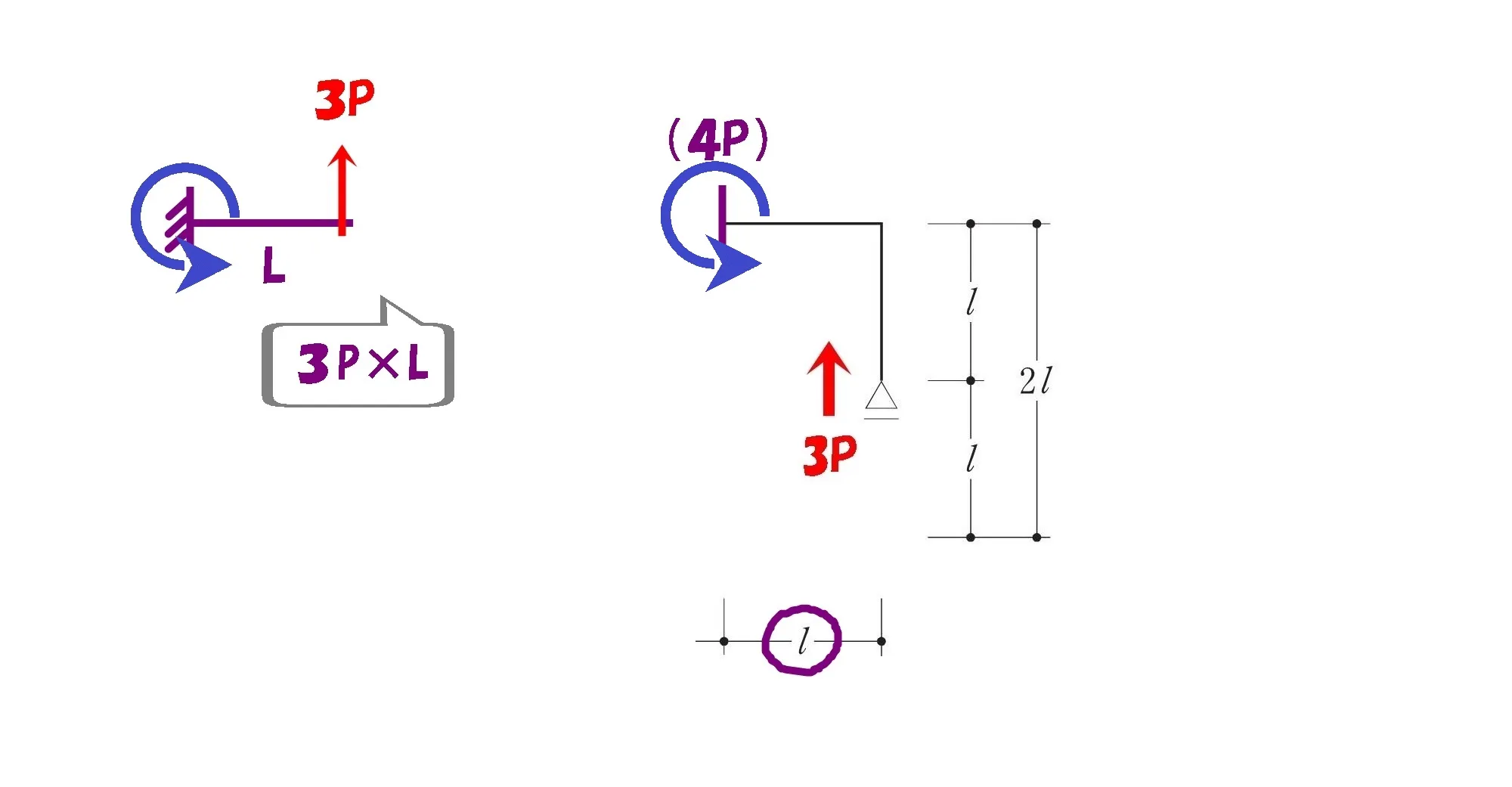

3.モーメント図を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
モーメント=力×距離

$$M=3P*L$$
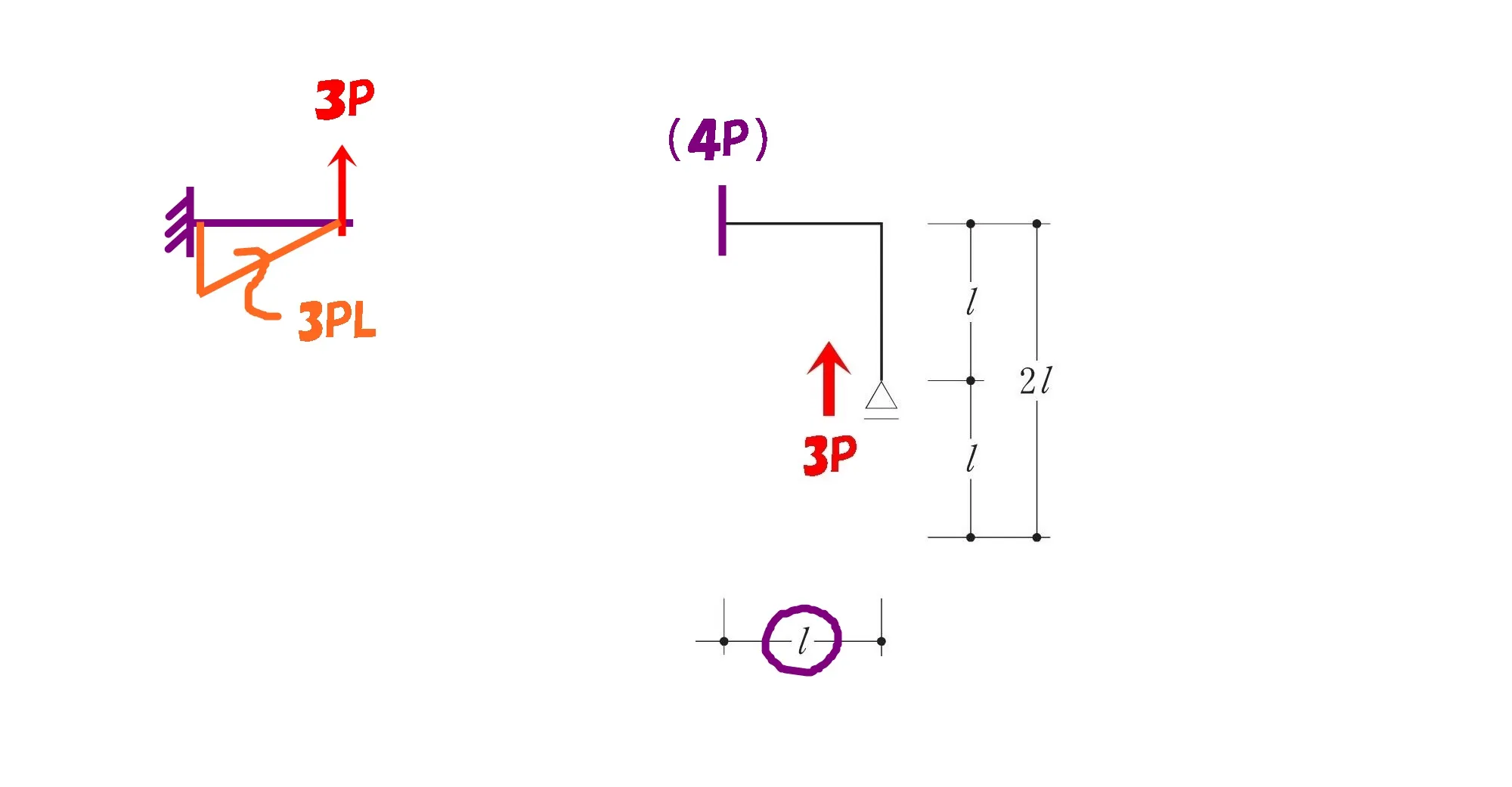
M=3PL
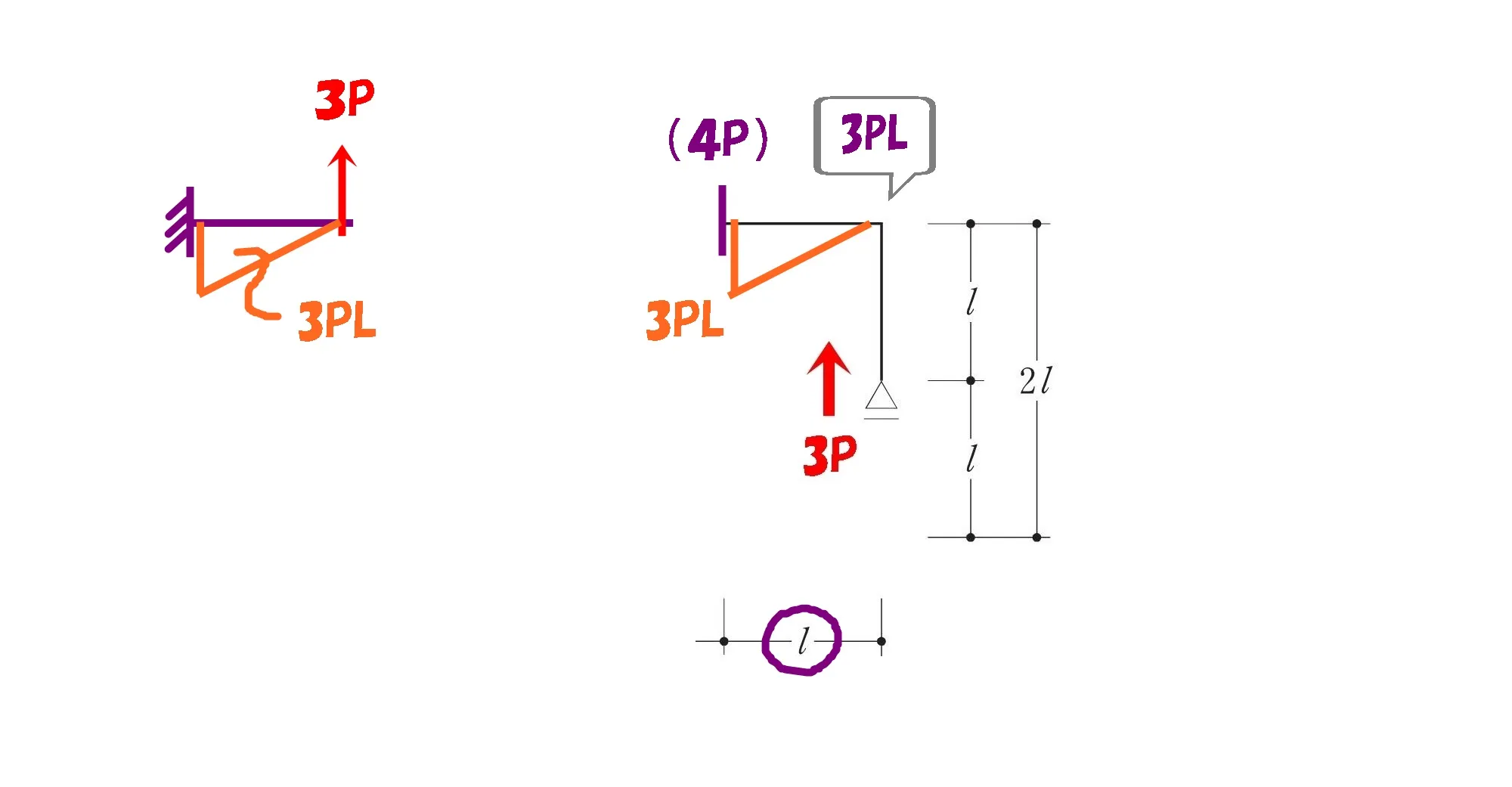

$$M=3P*L=3PL$$
右L字部分のモーメントは?
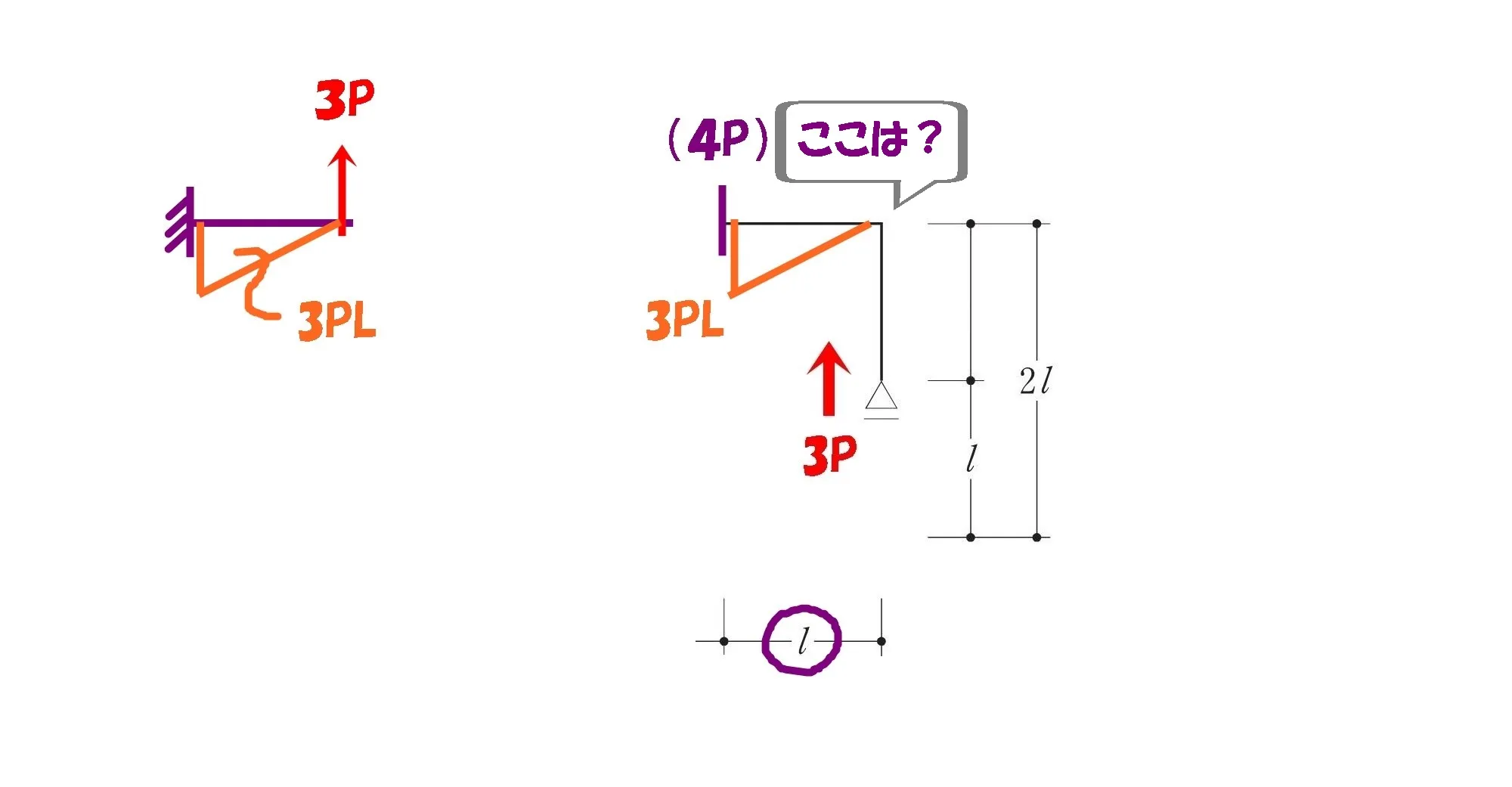

ローラーは水平力を伝えない
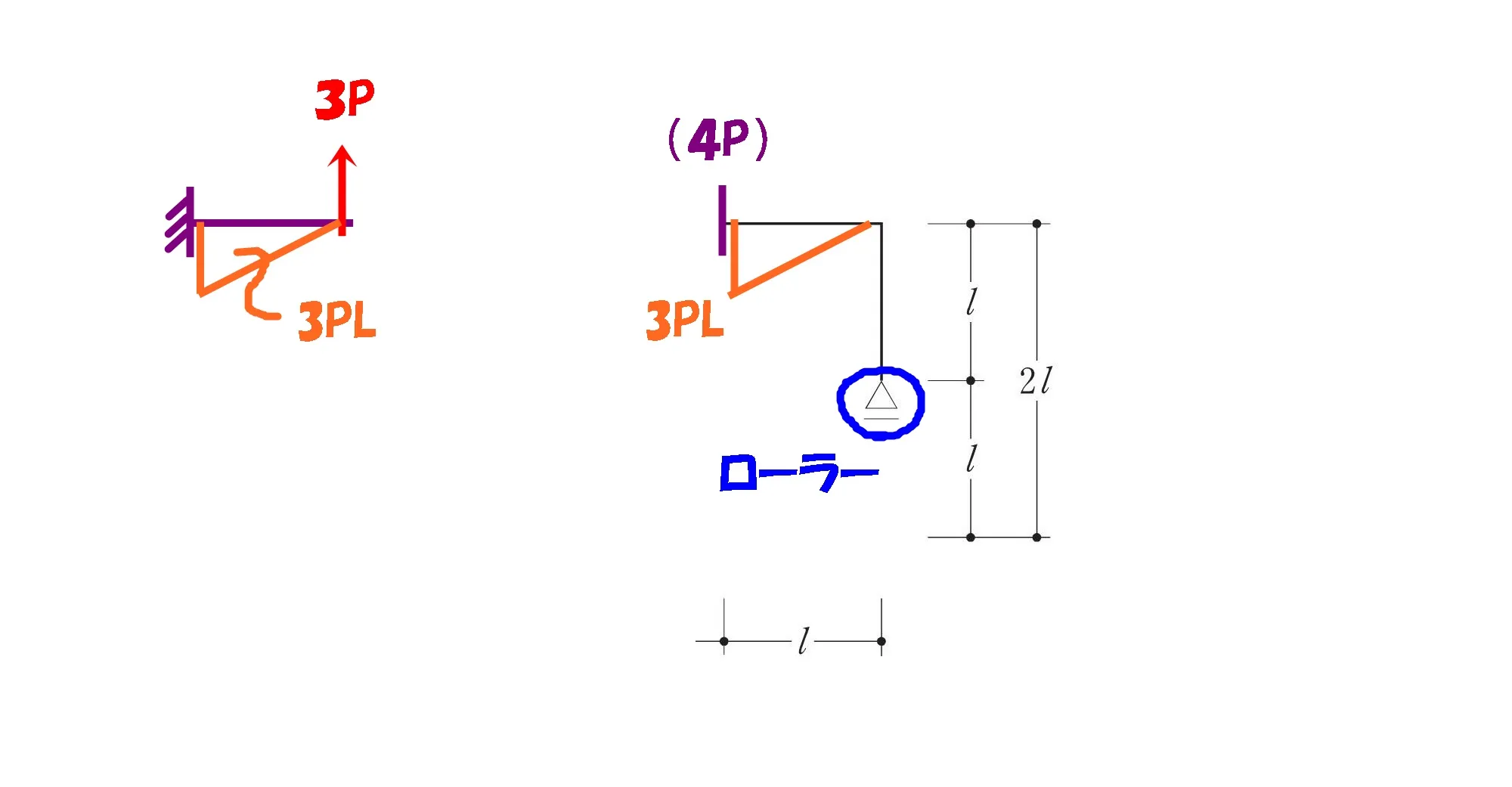

モーメントはゼロ
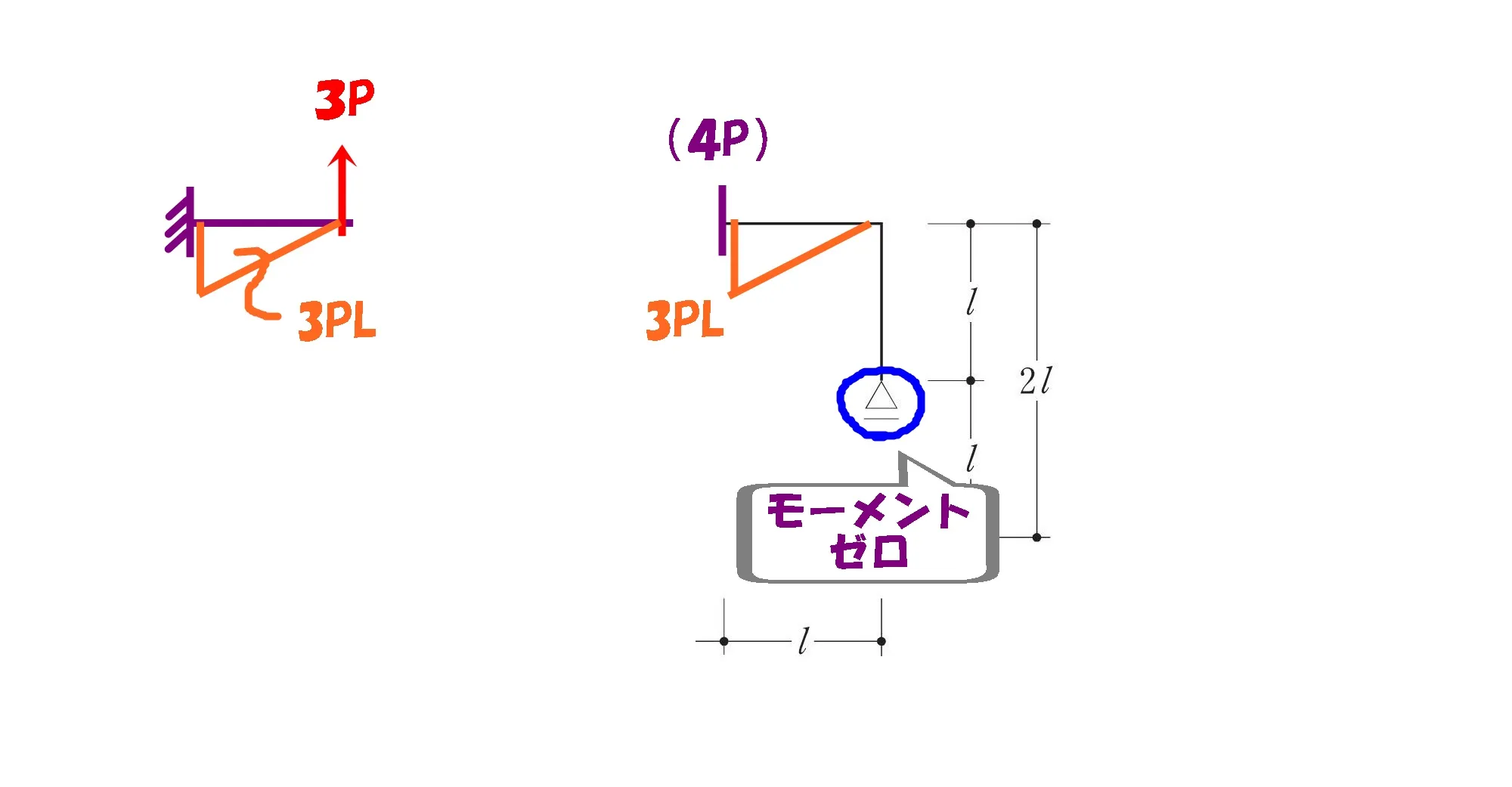

$$M=0*L,反力がゼロなので,M=0となる。$$



ローラー支点に
水平反力は生じない。
3.モーメント図を描く
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く
モーメント図を描く
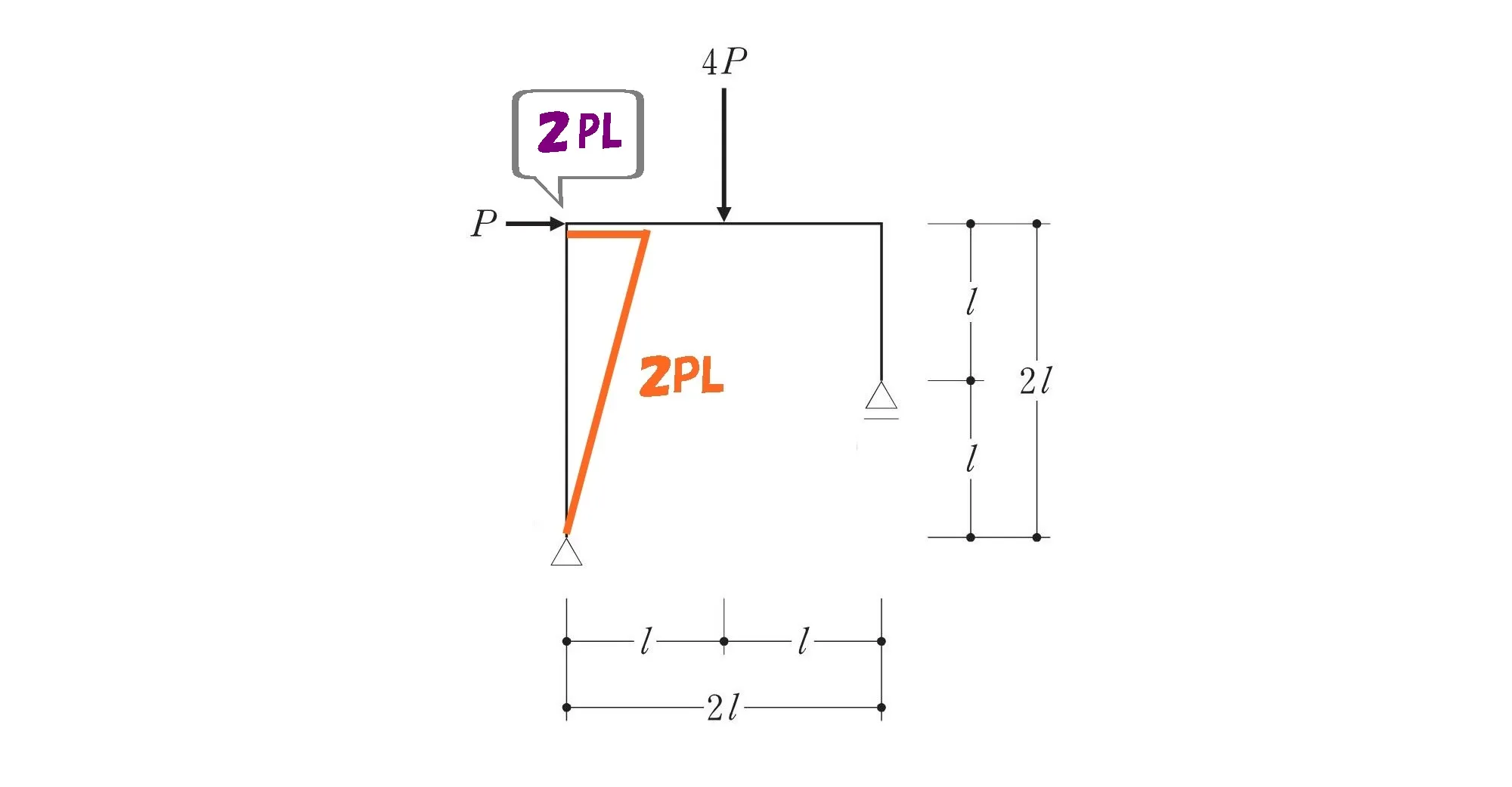

モーメント図を描く
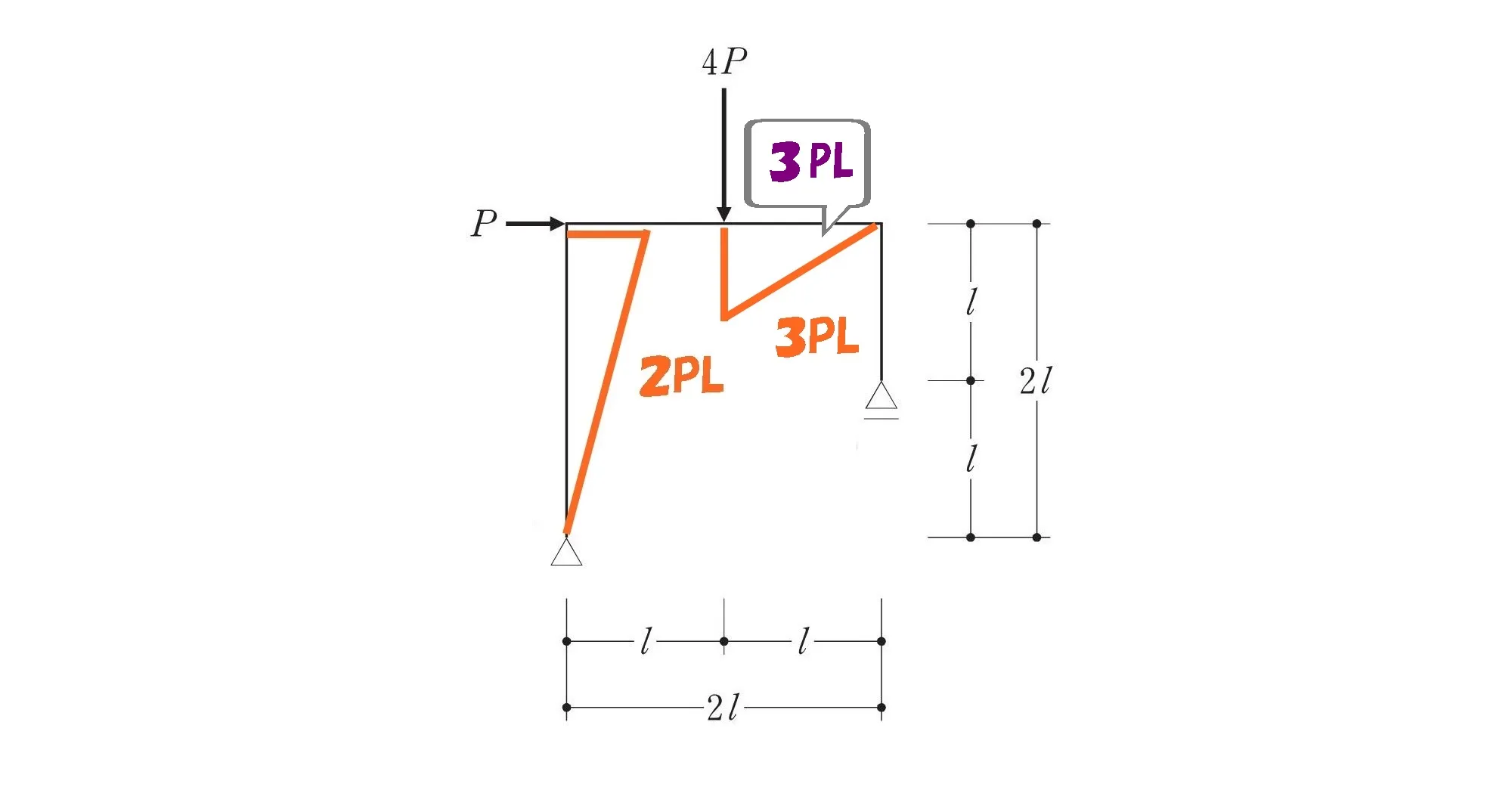

左L字部分のモーメントは?
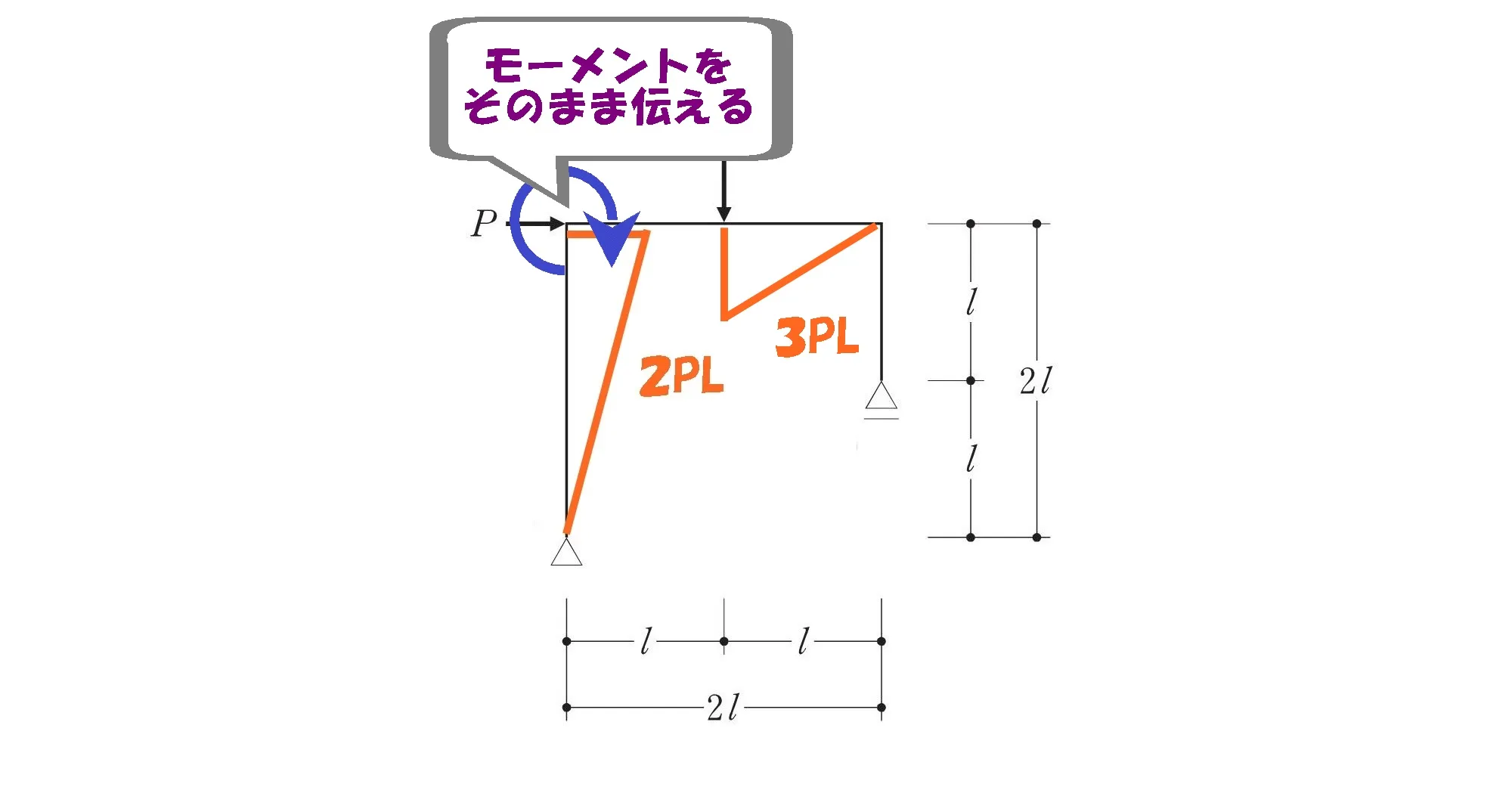

左L字部分は「剛接合」、柱頭2PLのモーメントをそのまま梁にも2PL伝達することになります。



剛接合は回転力を
そのまま伝える。
左L字部分のモーメント2PL
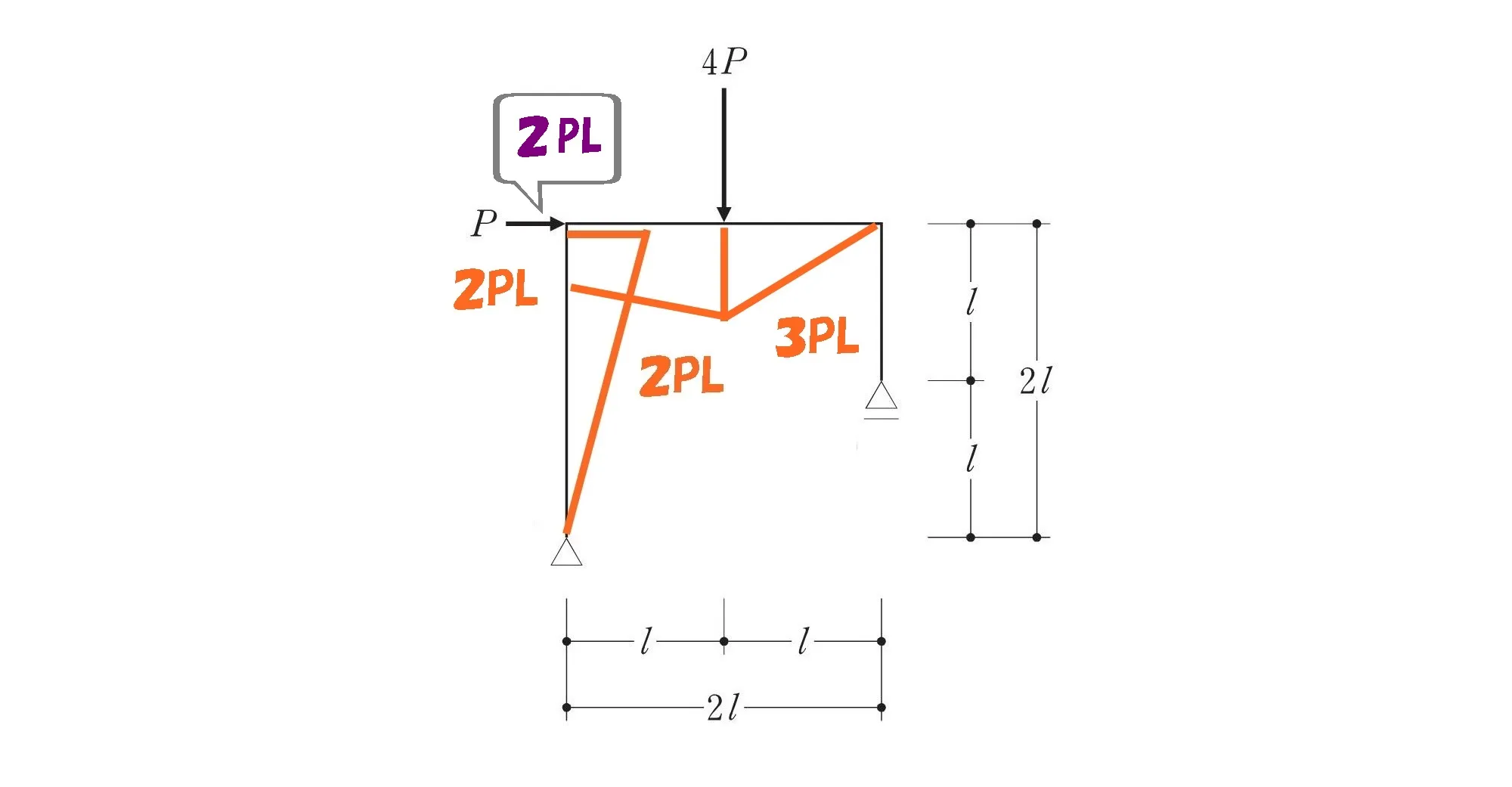

ここがポイント!
剛接合は回転モーメントを柱から梁へそのまま伝える。
答え.1
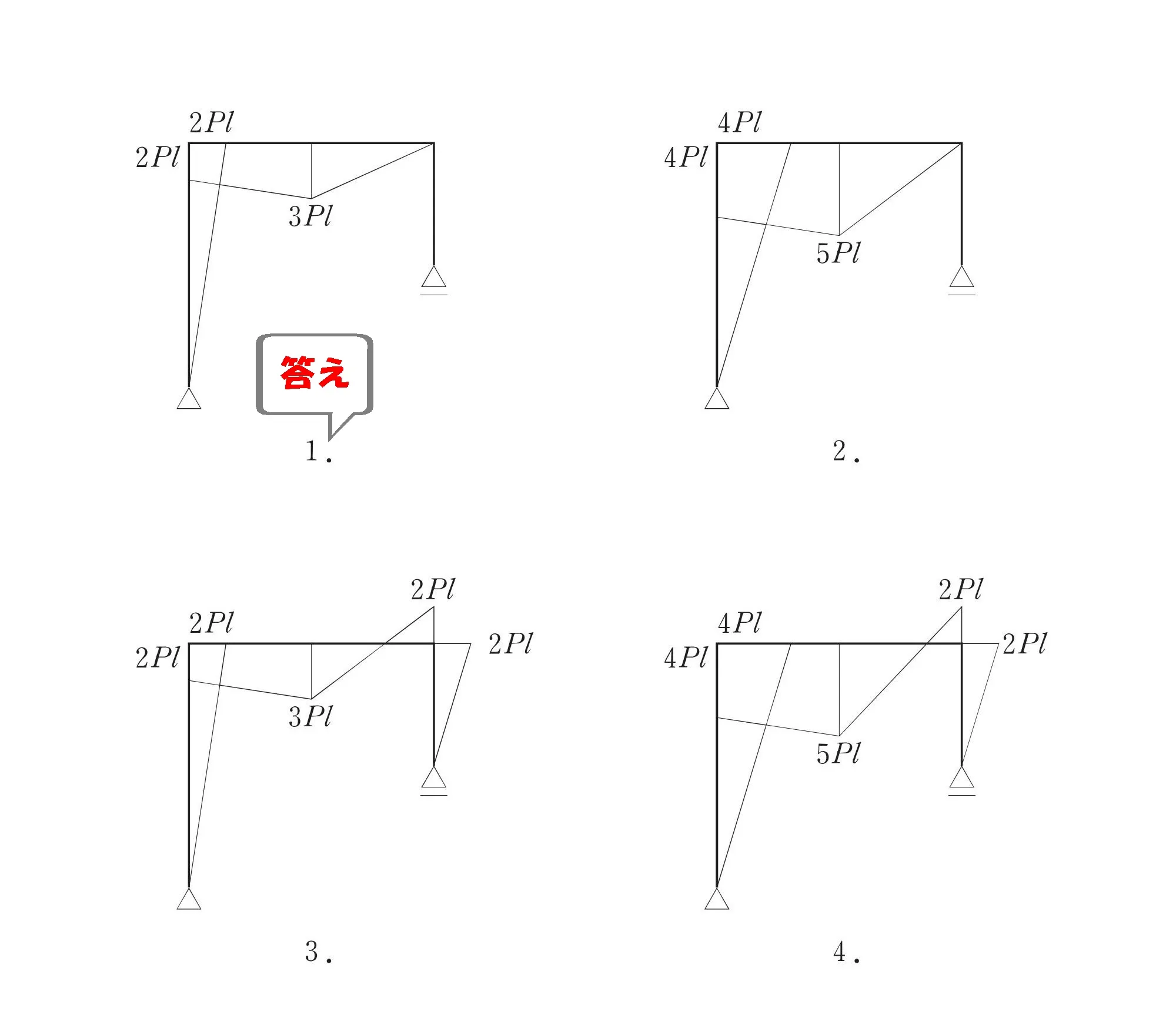

攻略ポイント
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く


この動画を YouTube で視聴
分割モーメント
難易度:★☆☆☆☆
$$モーメント=力×距離$$
攻略ポイント
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される
問題
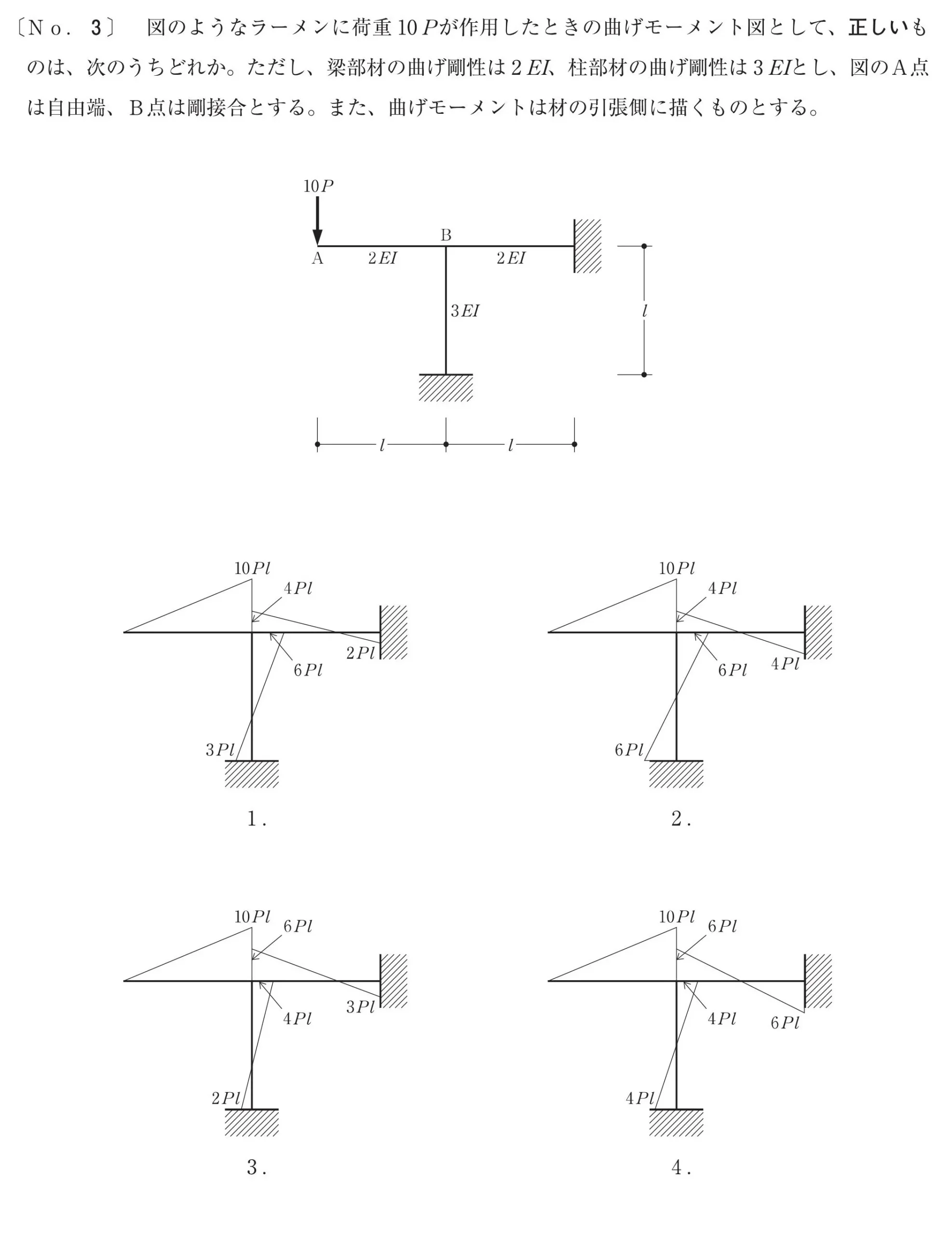

剛接合により構成されたラーメンに、モーメント図を正確に書き出せるか?という問題です。
ラーメン図
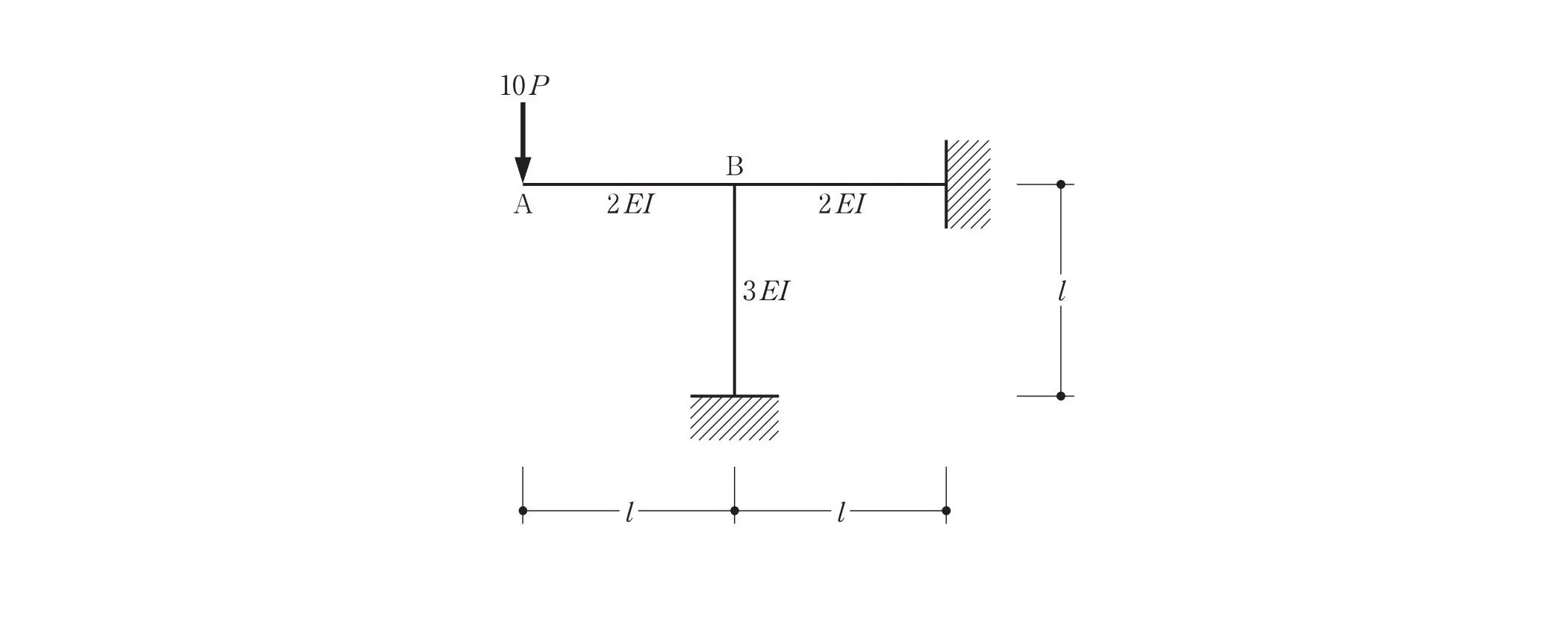

ラーメン図から読み解く
10Pが加わる位置A点のみ自由端、残りの接合部はすべて剛接合。



剛接合になると
モーメント図も変わる。
1.力×距離よりモーメント図を描く
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される
モーメント図を描く
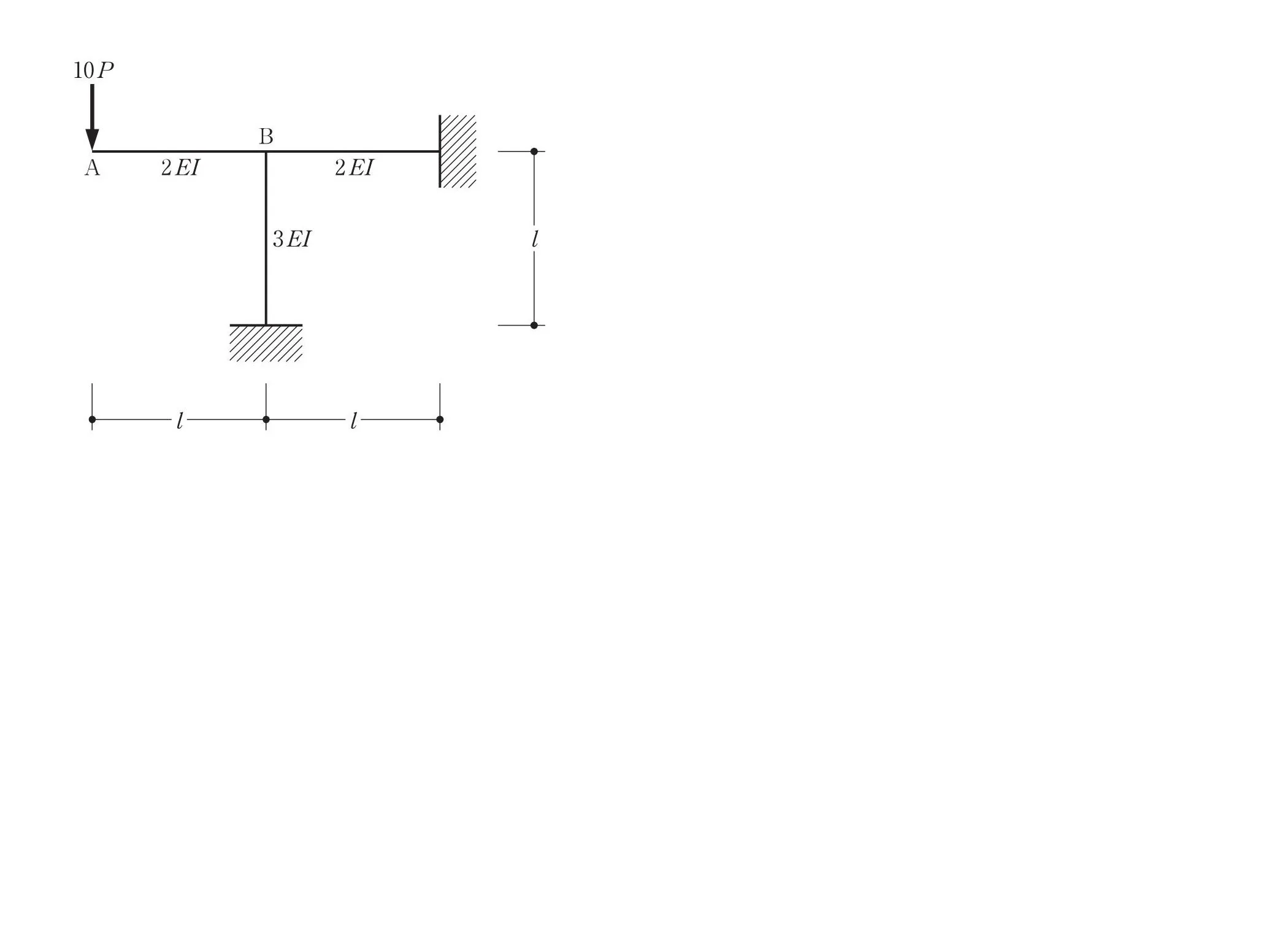

A点に加わる10Pを頼りに、モーメント図を描きます。
片持ち梁の絵を描く
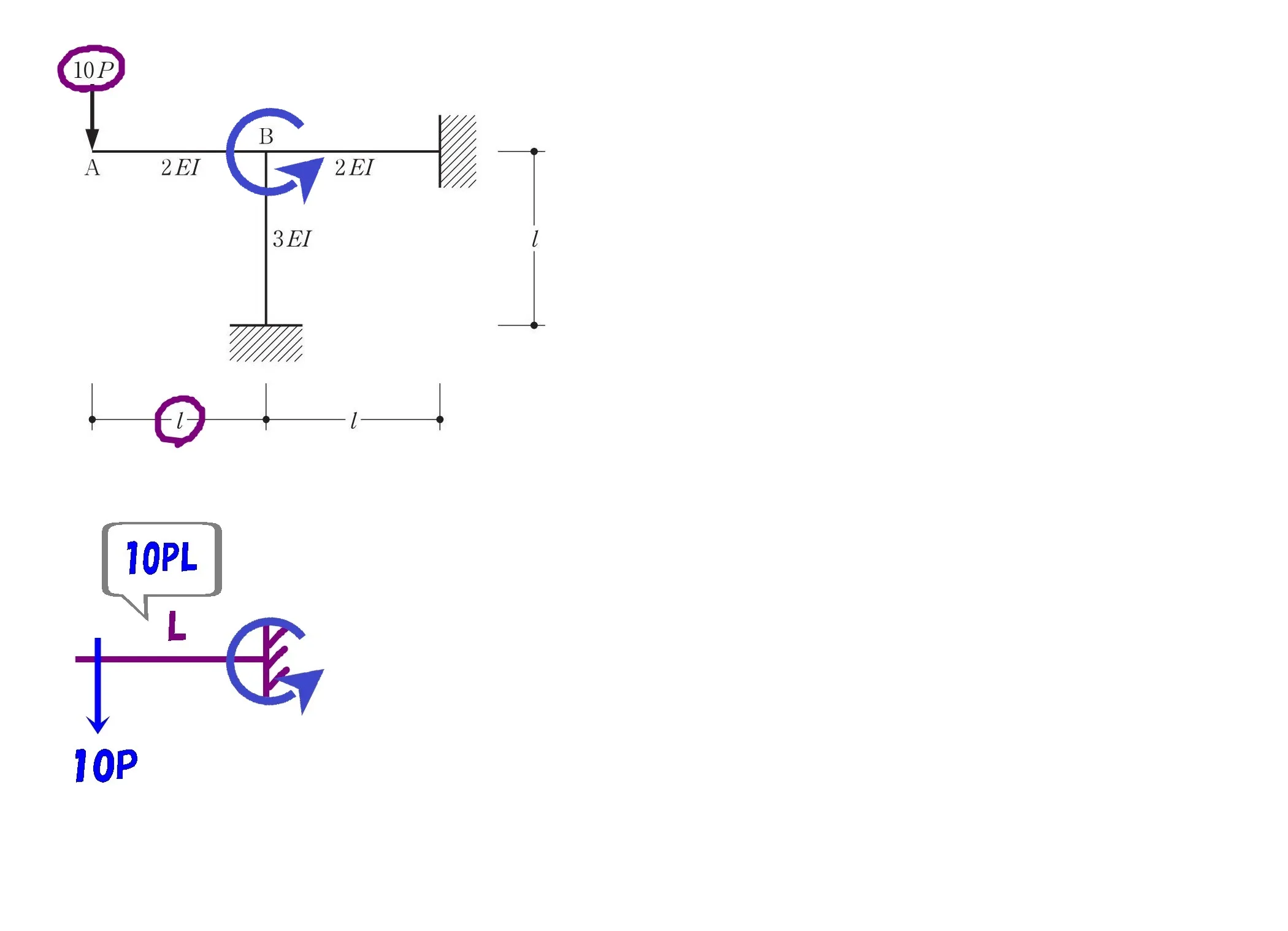

モーメント=力×距離
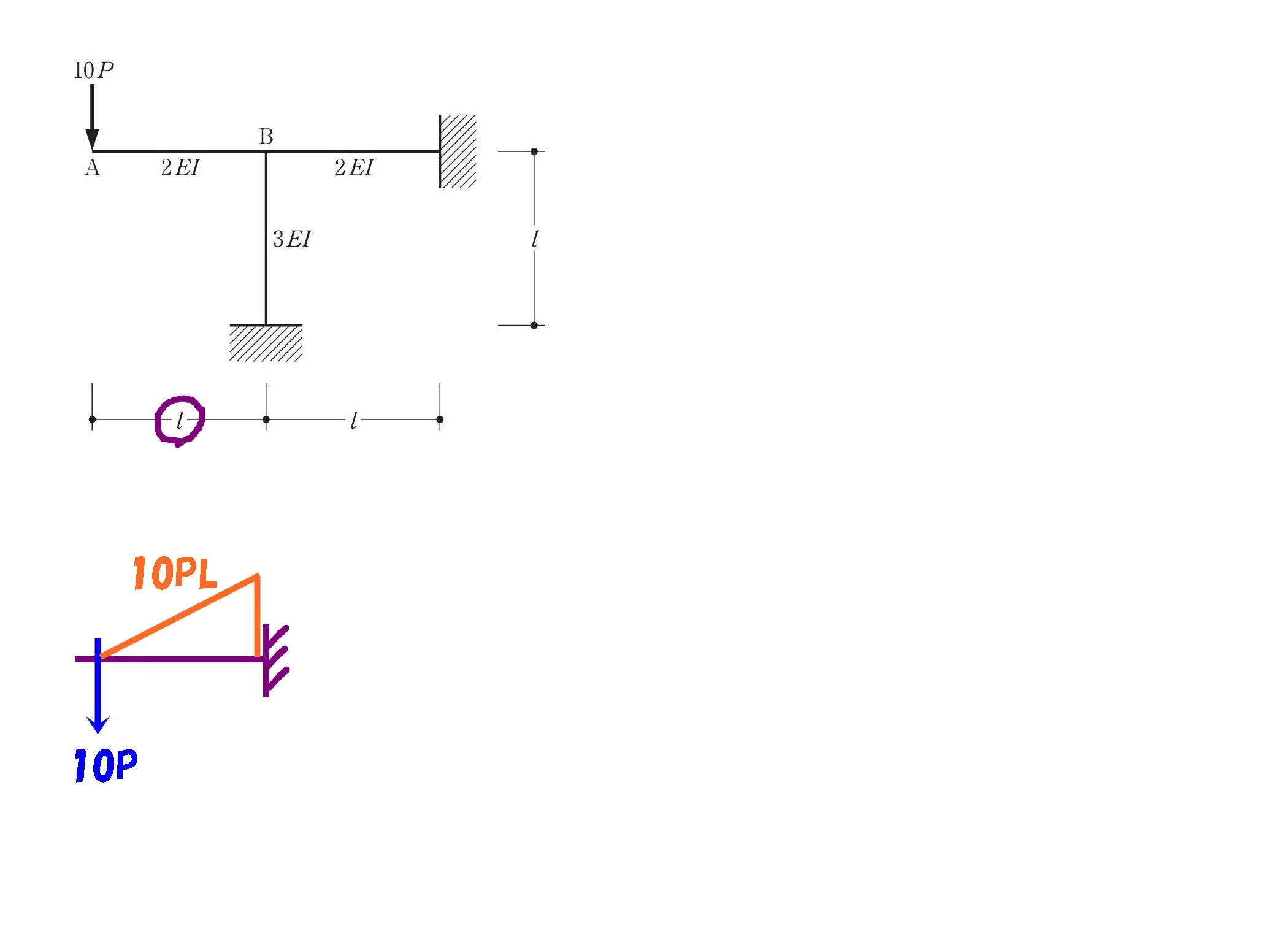

$$M=10P*L$$
モーメント=10PL
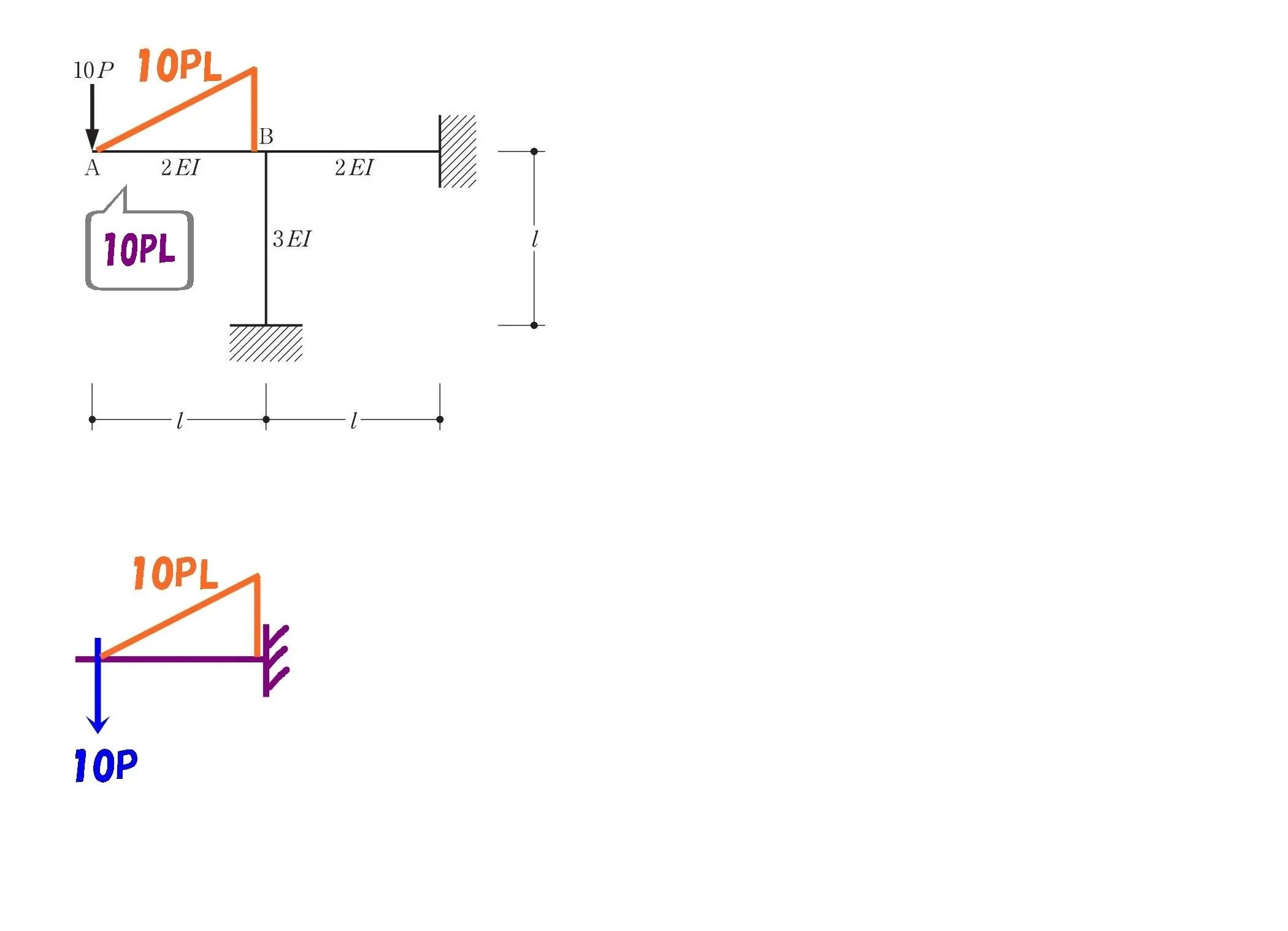

$$M=10P*Lより,M=10PL$$
2.モーメントの大きさを「部材の剛比」で振り分ける
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される
剛接合のモーメントは?
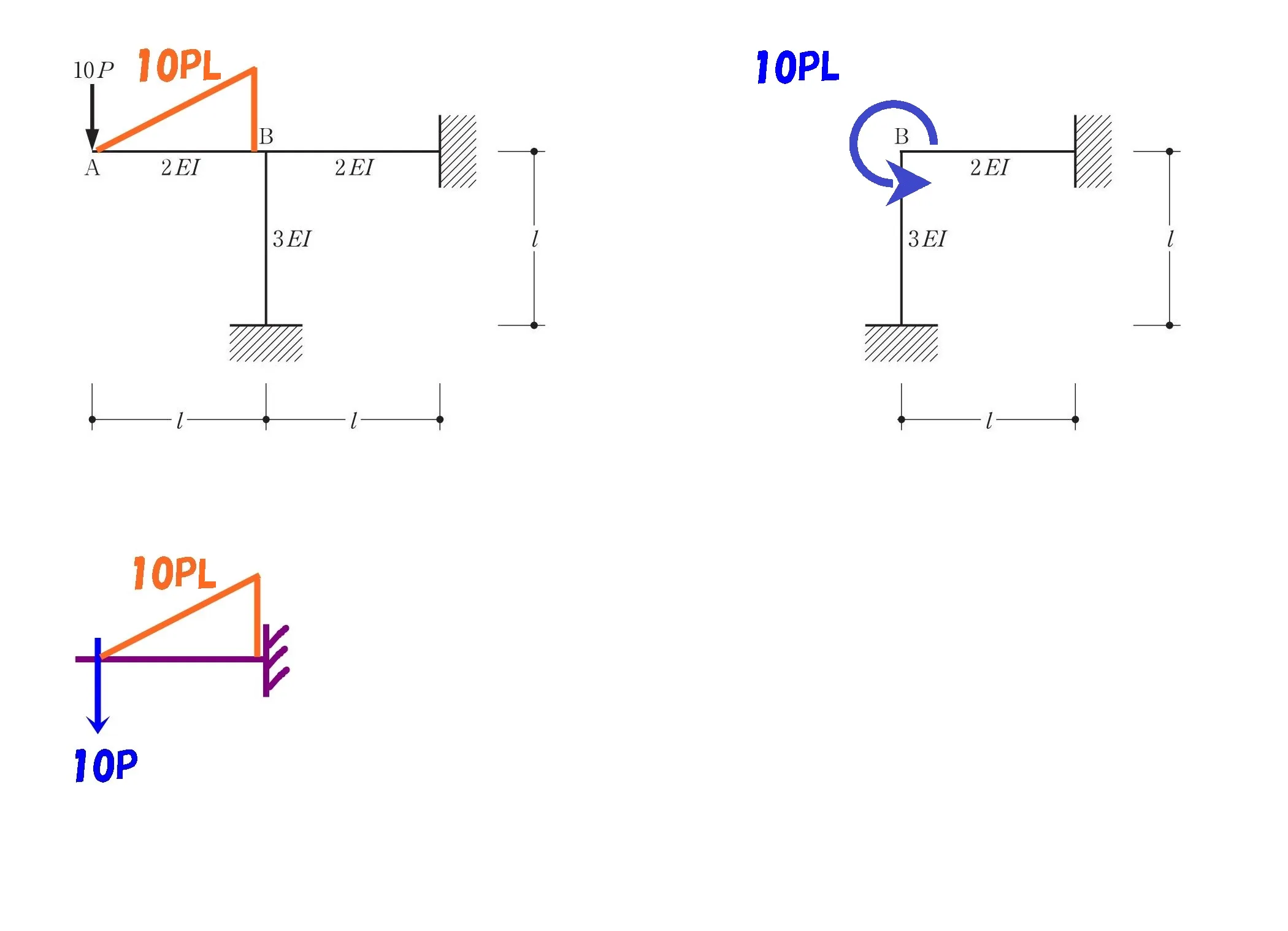

中央の柱梁は剛接合なので、B点に加わる10PLのモーメントはそのまま柱・梁に伝達される。



剛接合は回転力を
そのまま伝える。
モーメント10PLの振り分け
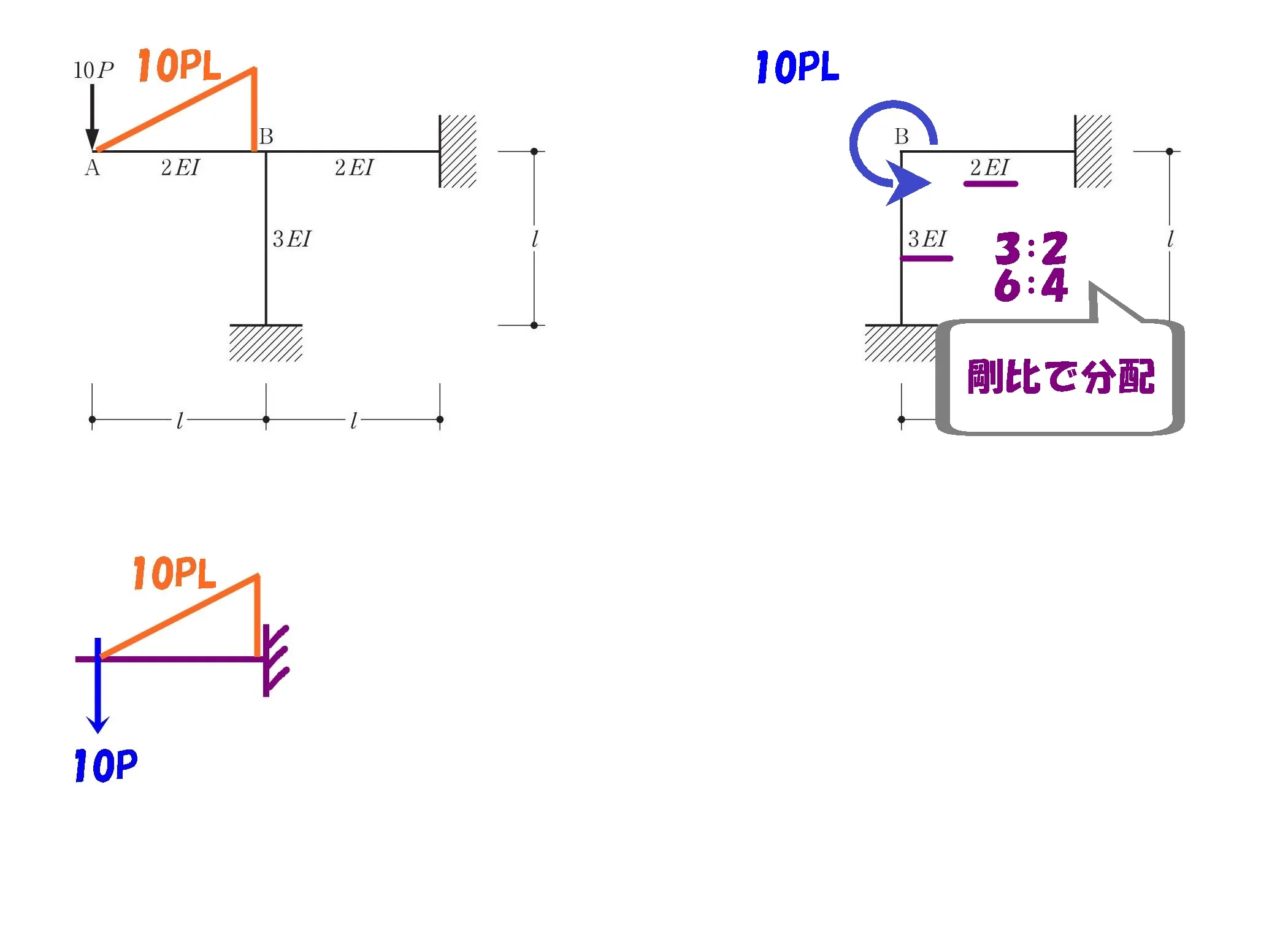

モーメントを剛比で振り分ける
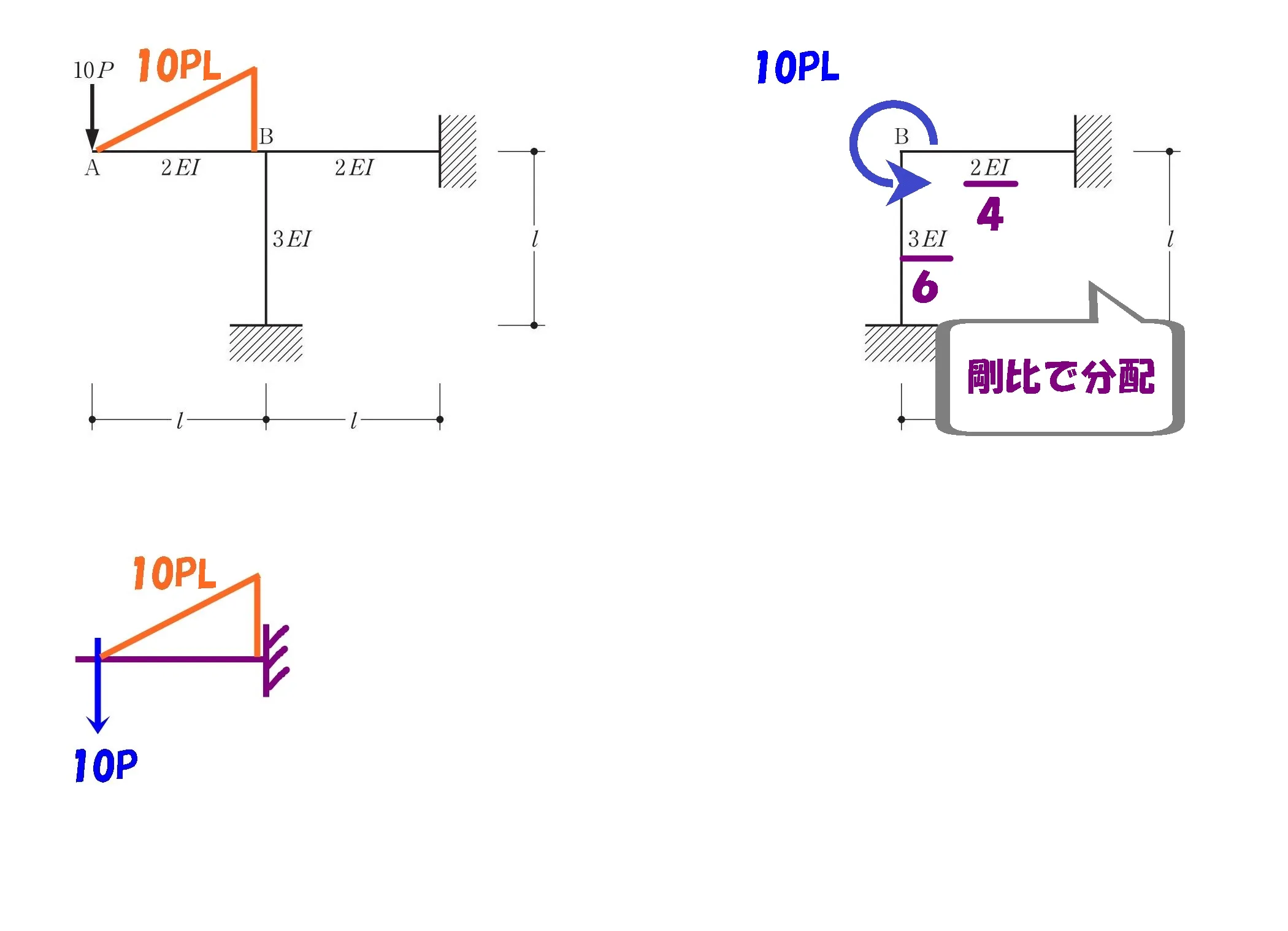

$$柱:梁の剛比=3EI:2EI(6EI:4EI)より$$
$$M柱=10PL*\frac{ 3 }{ 3+2 }=6PL$$
$$M梁=10PL*\frac{ 2 }{ 3+2 }=4PL$$
10PL=6PL+4PL
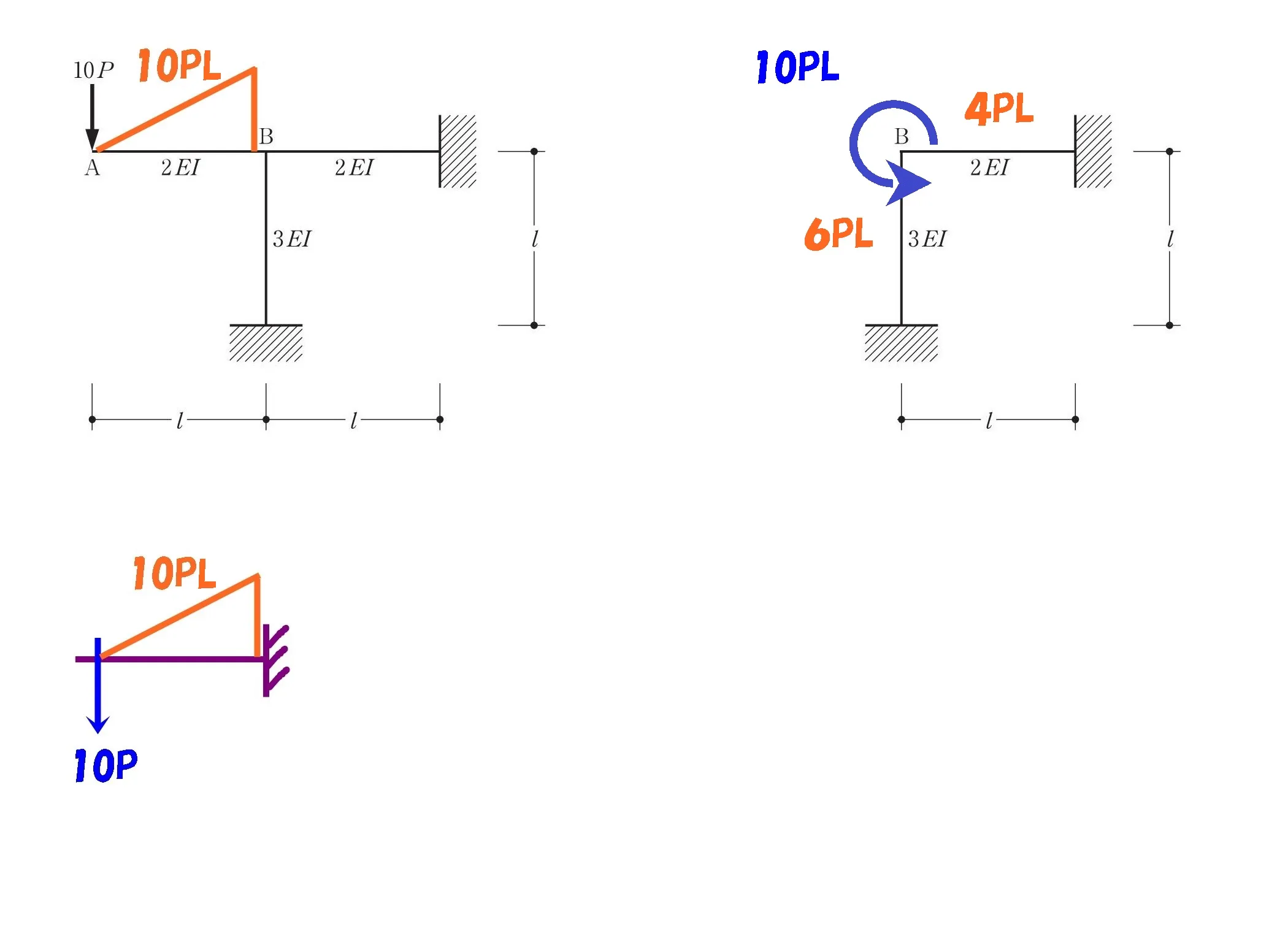

$$M柱=6PL,M梁=4PL$$
3.柱と梁それぞれのモーメントは2:1で分布される
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される
柱と梁を分解する
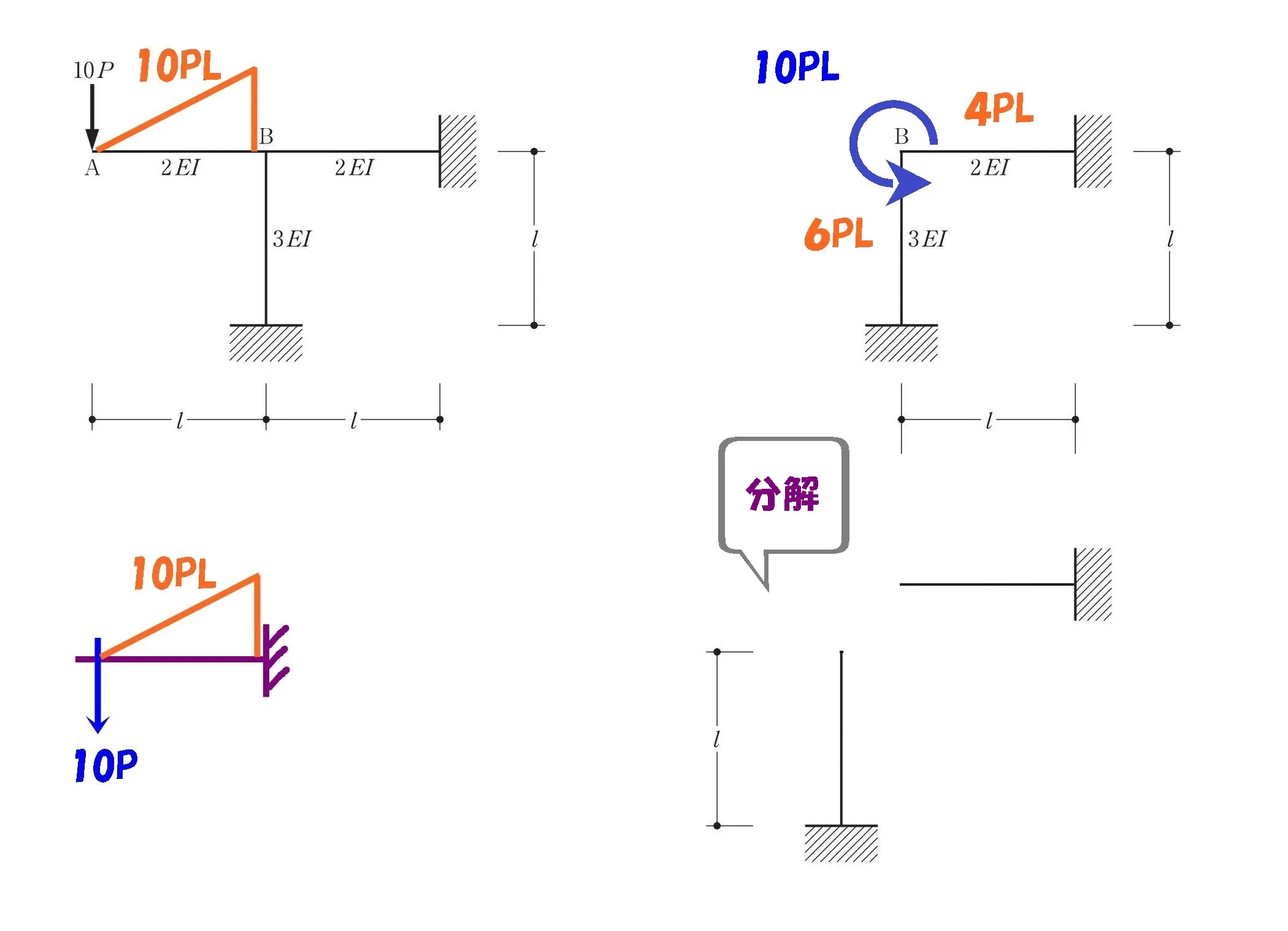

この問題はあと、”ひとひねり”あります。
それぞれの部材のモーメント図を正確に書き出すために、柱と梁を分解します。
ラーメンを分解することで、それぞれが片持ち梁になりますよね?


ラーメンを分解?
それぞれのモーメント図は?
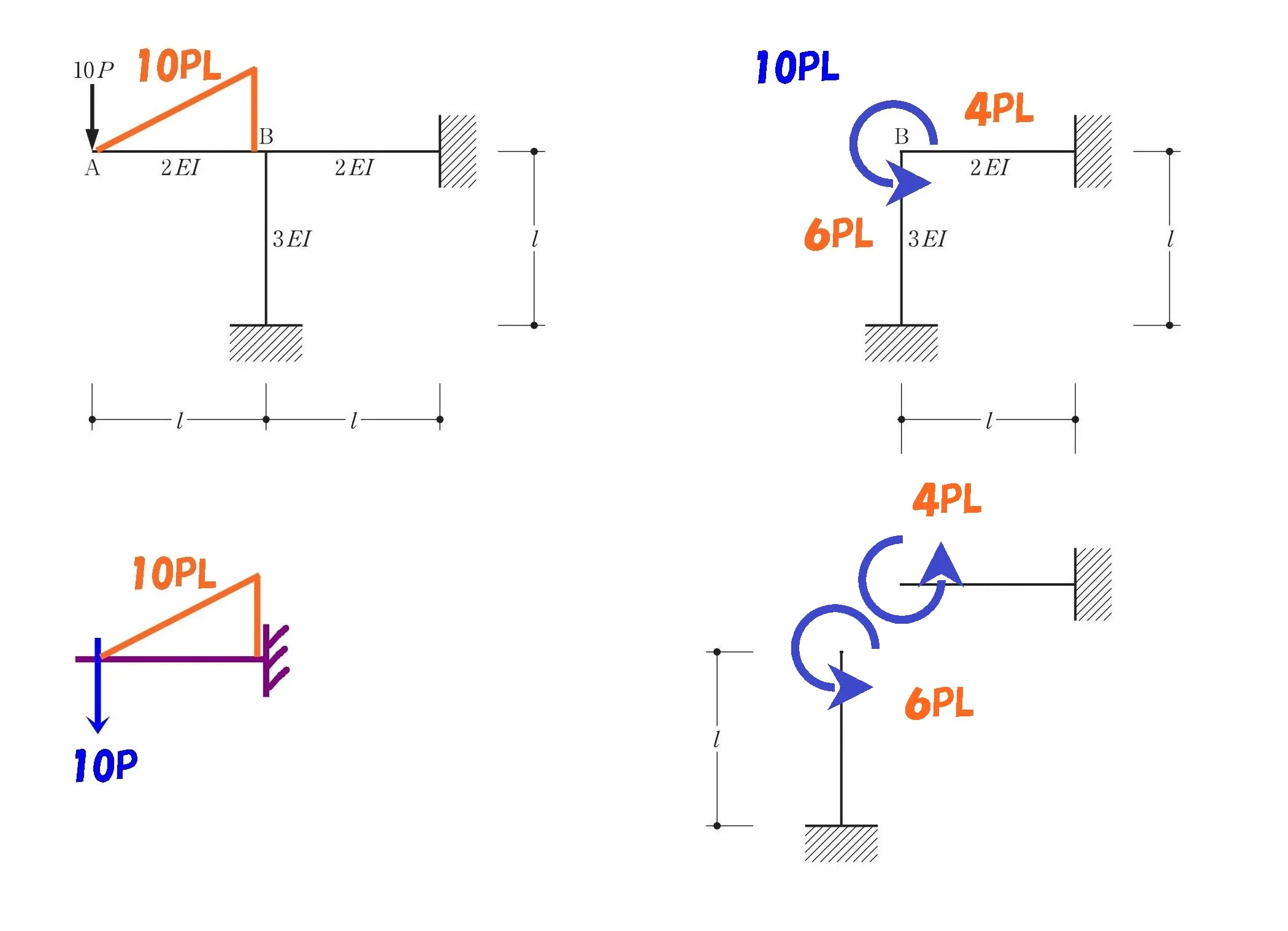

固定端にもモーメントが発生する
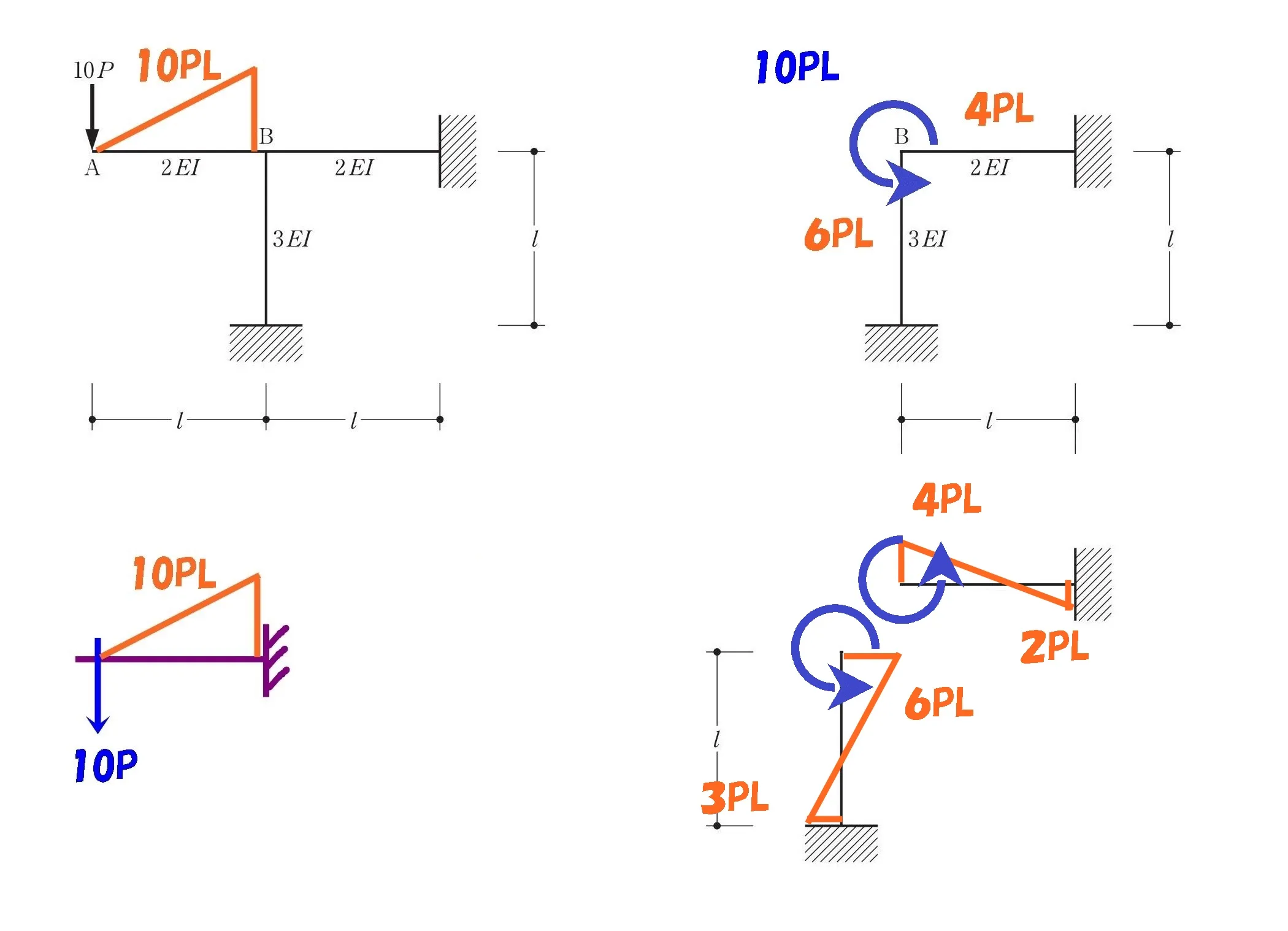

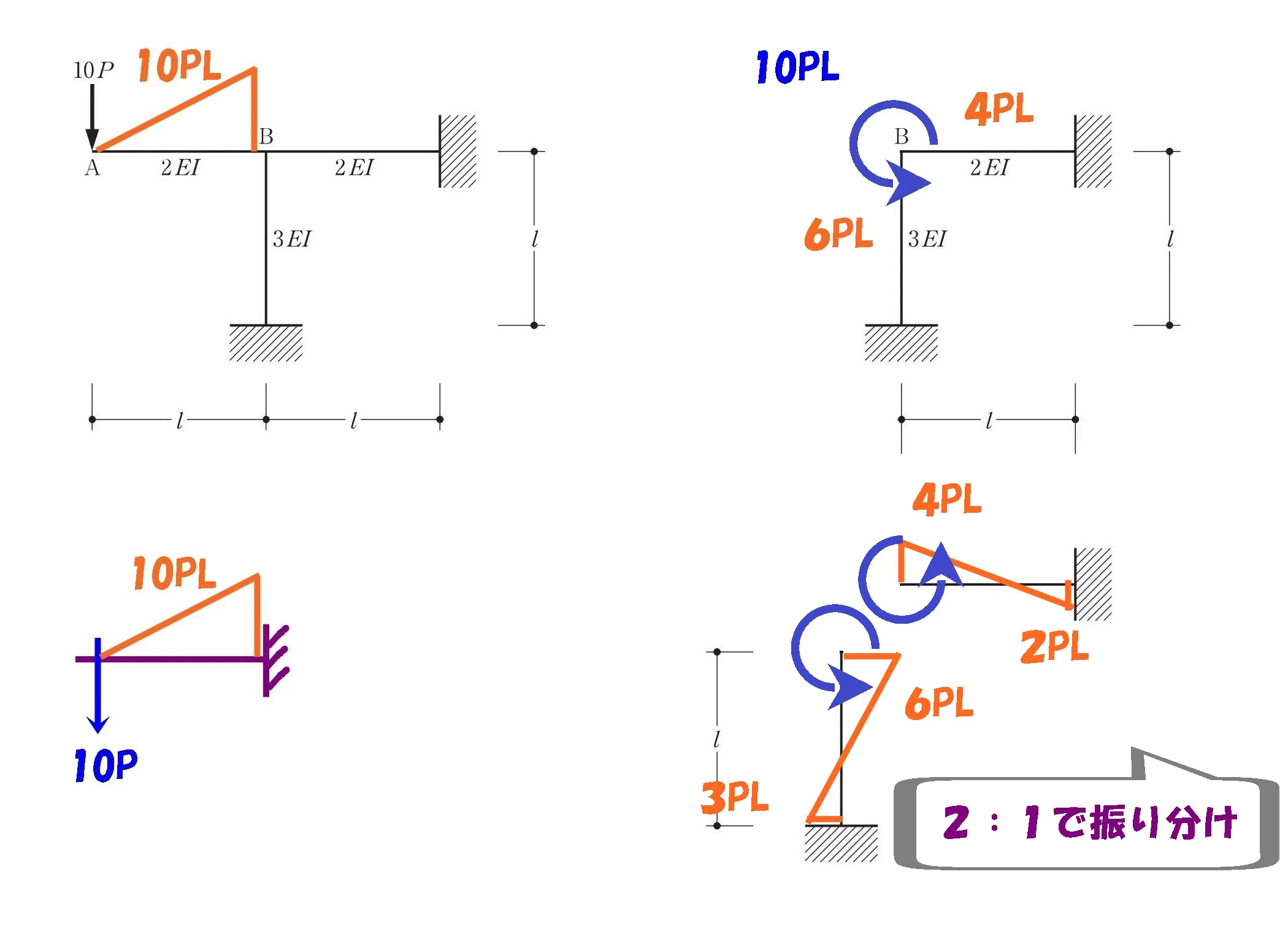
モーメント図は2:1に分布される

モーメント図の完成!
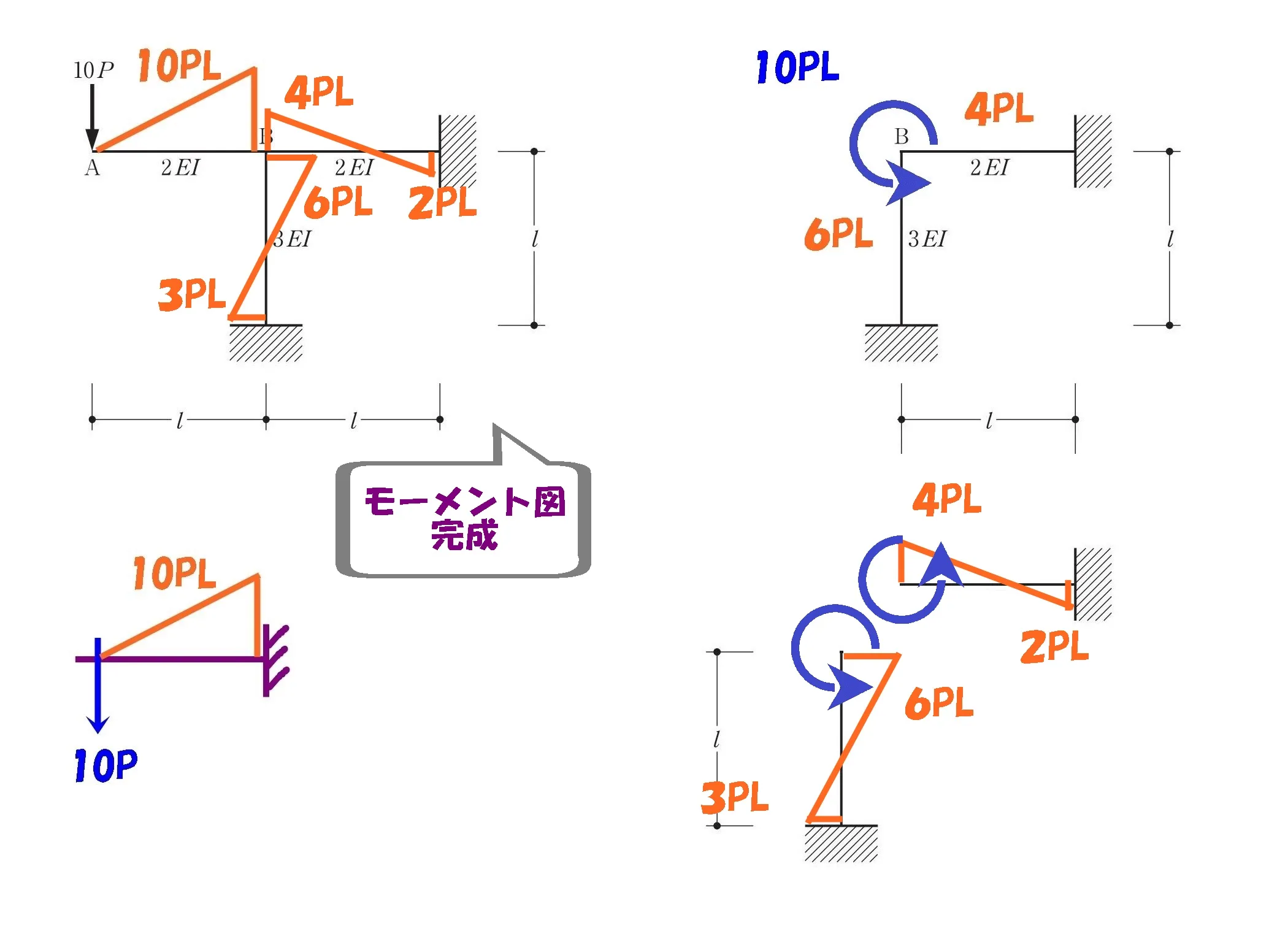

答え.1
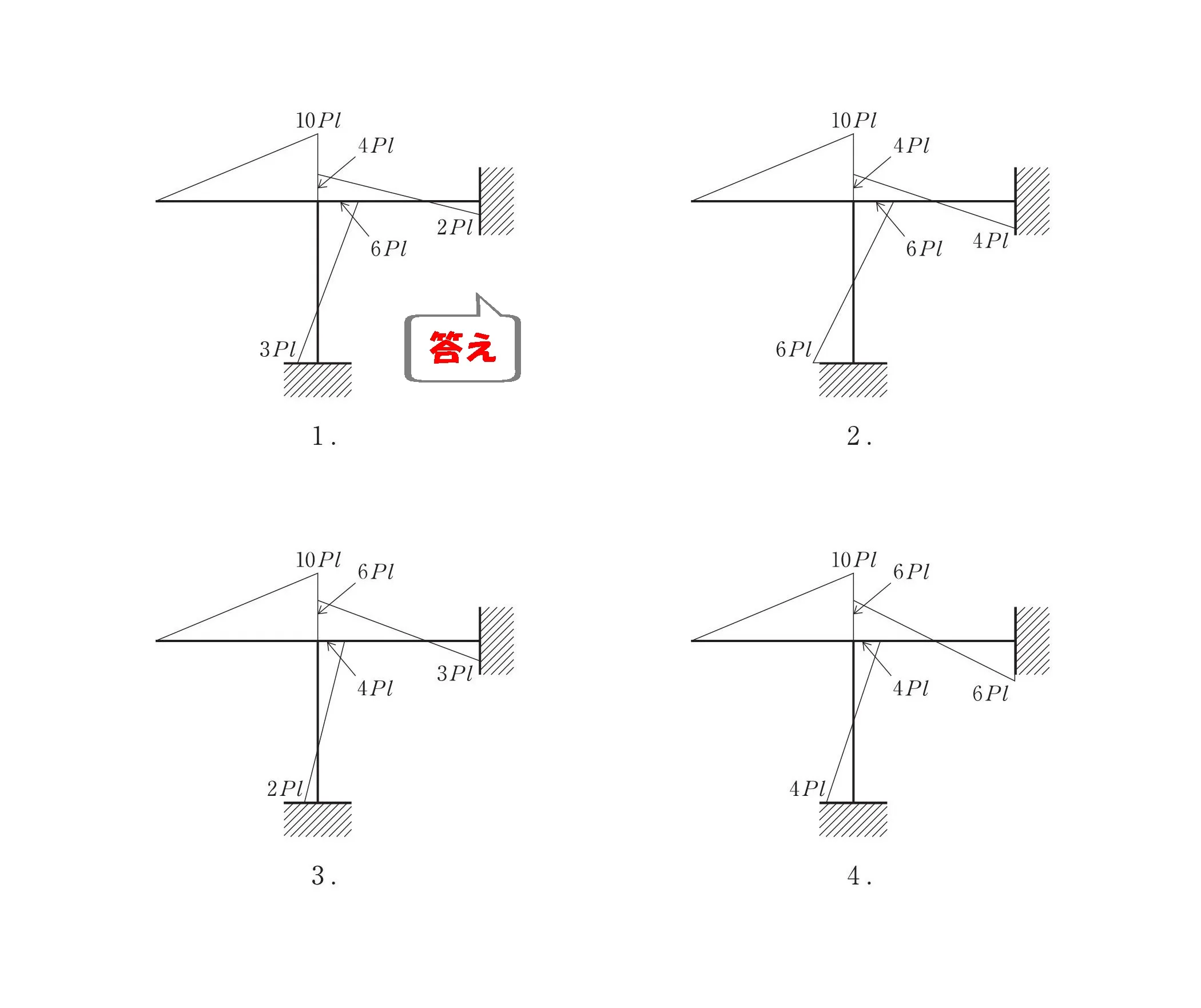

攻略ポイント
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される


この動画を YouTube で視聴
3ヒンジラーメン
難易度:★★★☆☆
連立方程式の組み立てから、モーメントを求める問題です。
この計算を想像するだけで「気が滅入る」という方も多いですよね?
そういう方のために「欲しい答えを導く」方程式の組み方もお伝えしましょう。



連立方程式!?
いやな予感がする。
攻略ポイント
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
問題
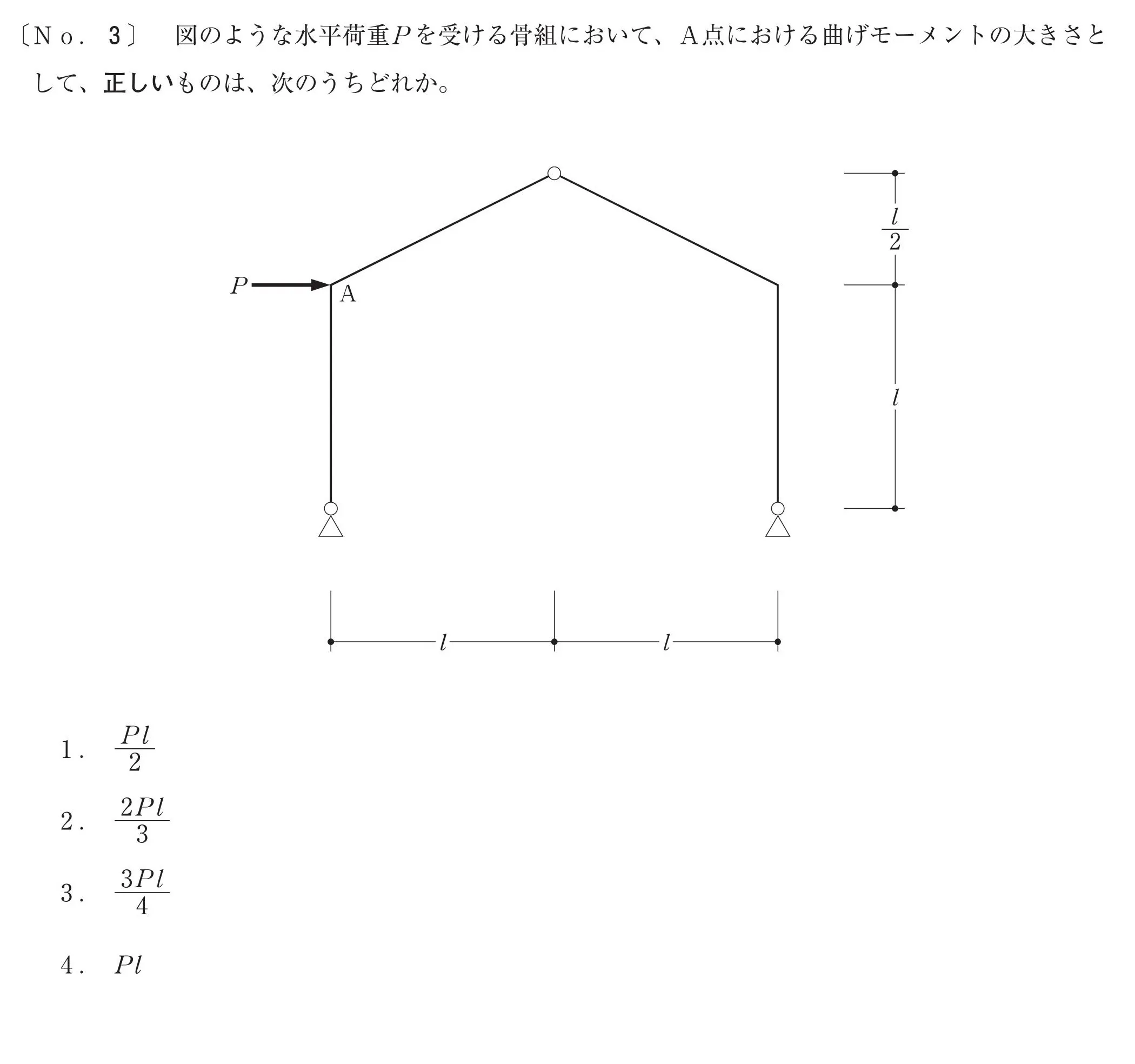

柱脚の支持条件
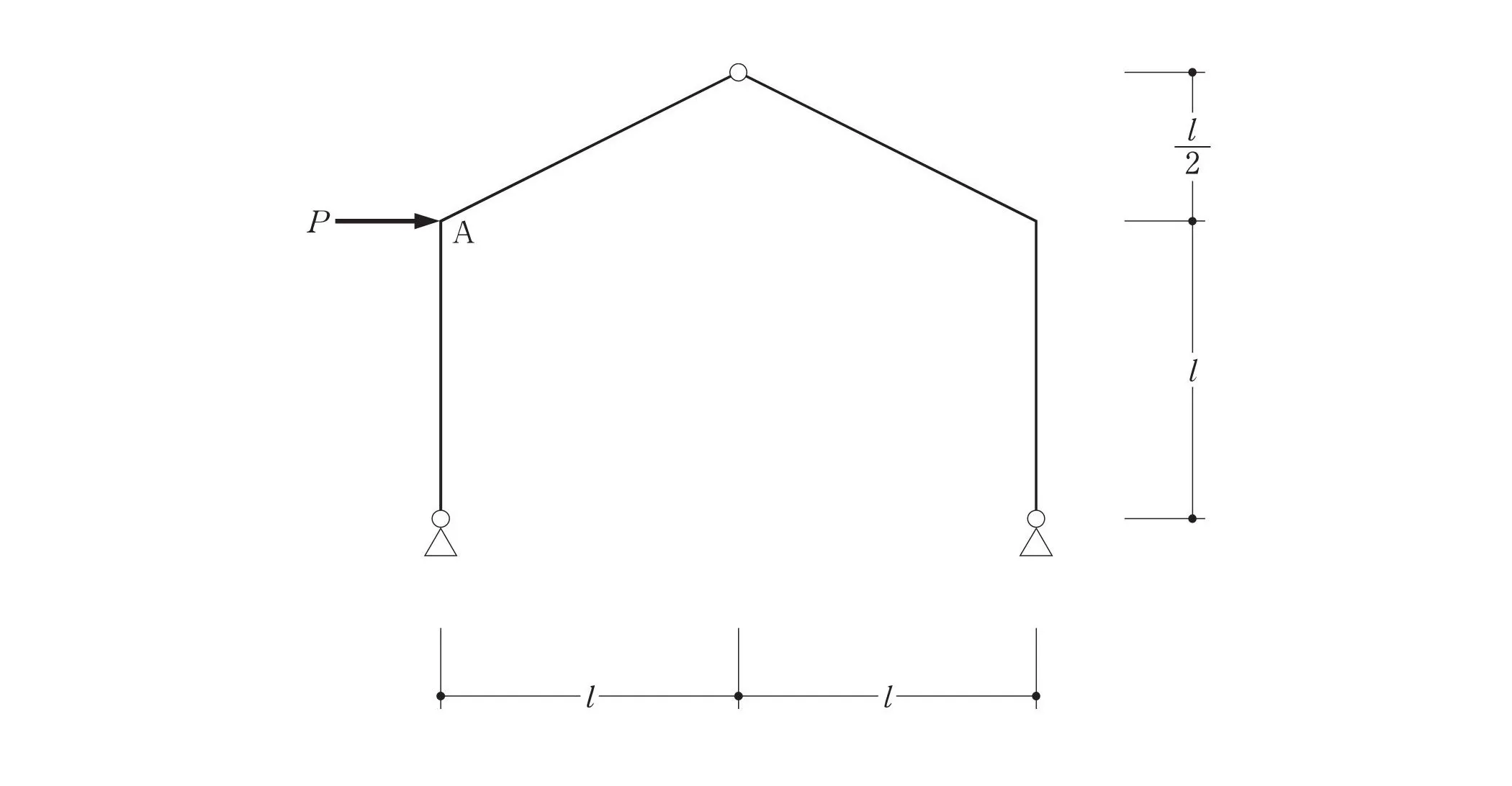

左:ピン支点
右:ピン支点
3ヒンジラーメン
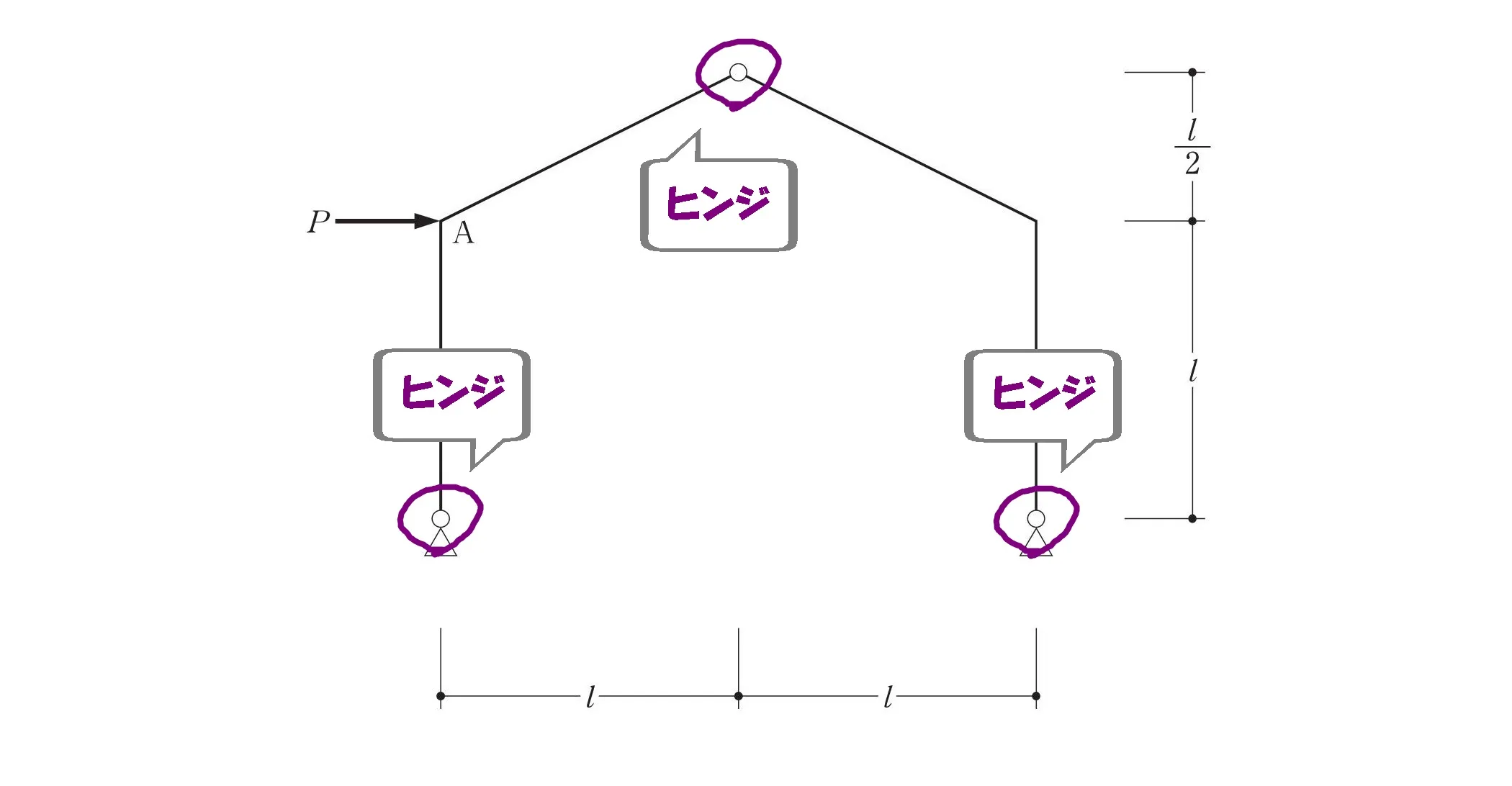

- ピン支点の柱脚のヒンジ(左)
- ピン支点の柱脚のヒンジ(右)
- 登り梁の中央にあるヒンジ(上)
1.答えに繋がる反力を見定める
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
アンダーラインに注目する
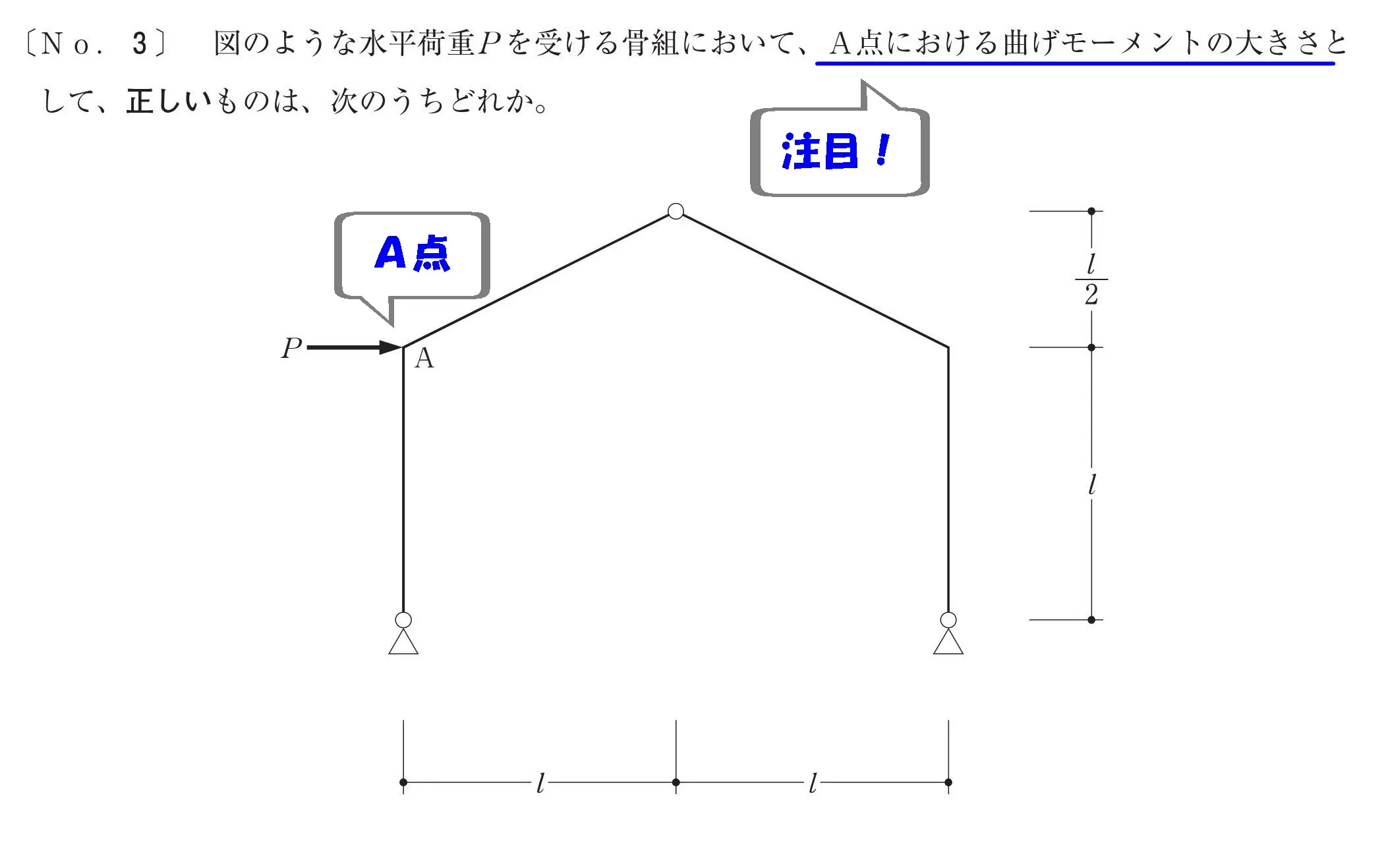

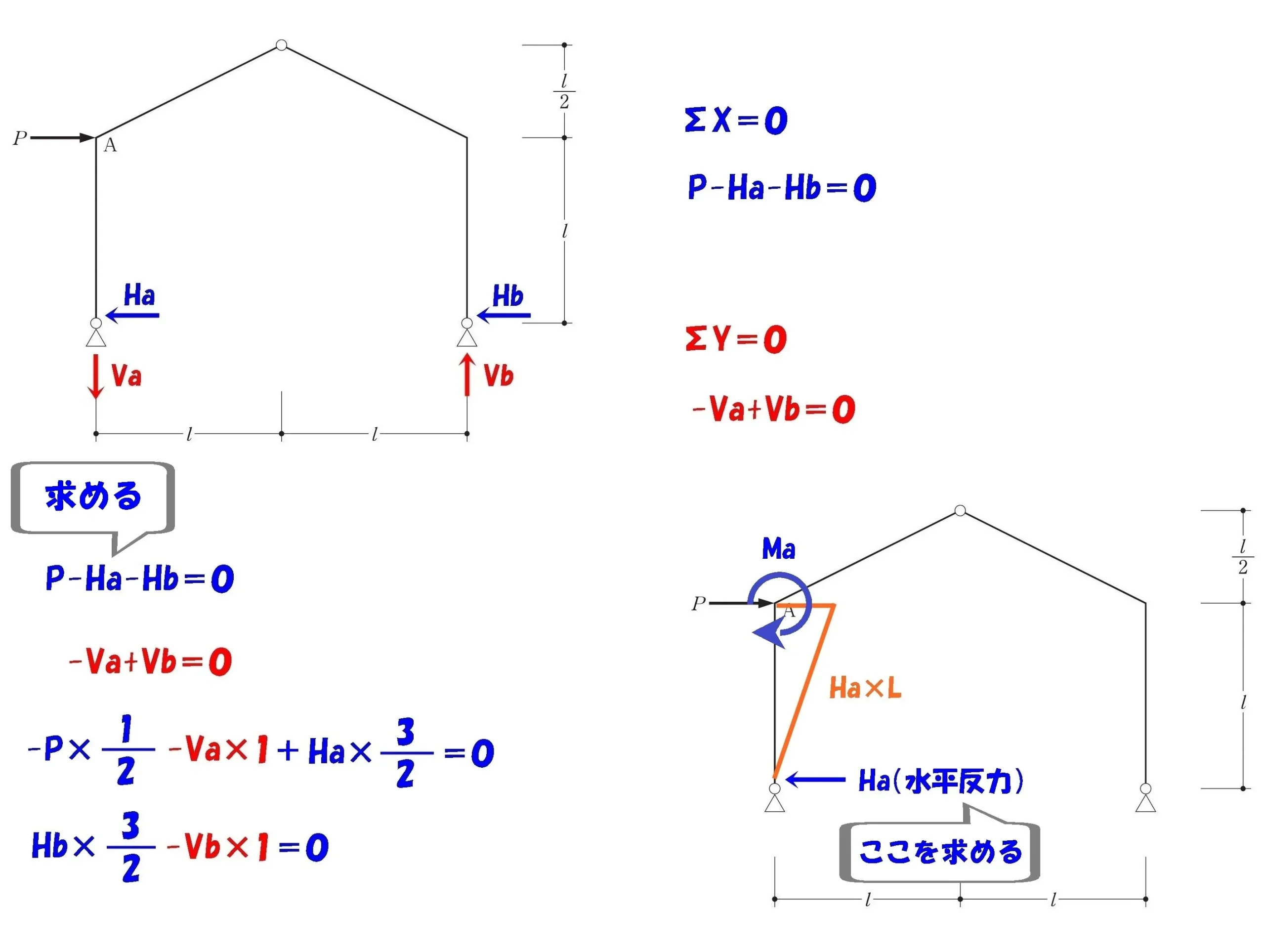
ここを求める
A点の曲げモーメントの大きさを求める。



求めるターゲットを
しっかりと見定めよう!
A点のモーメント図を描く
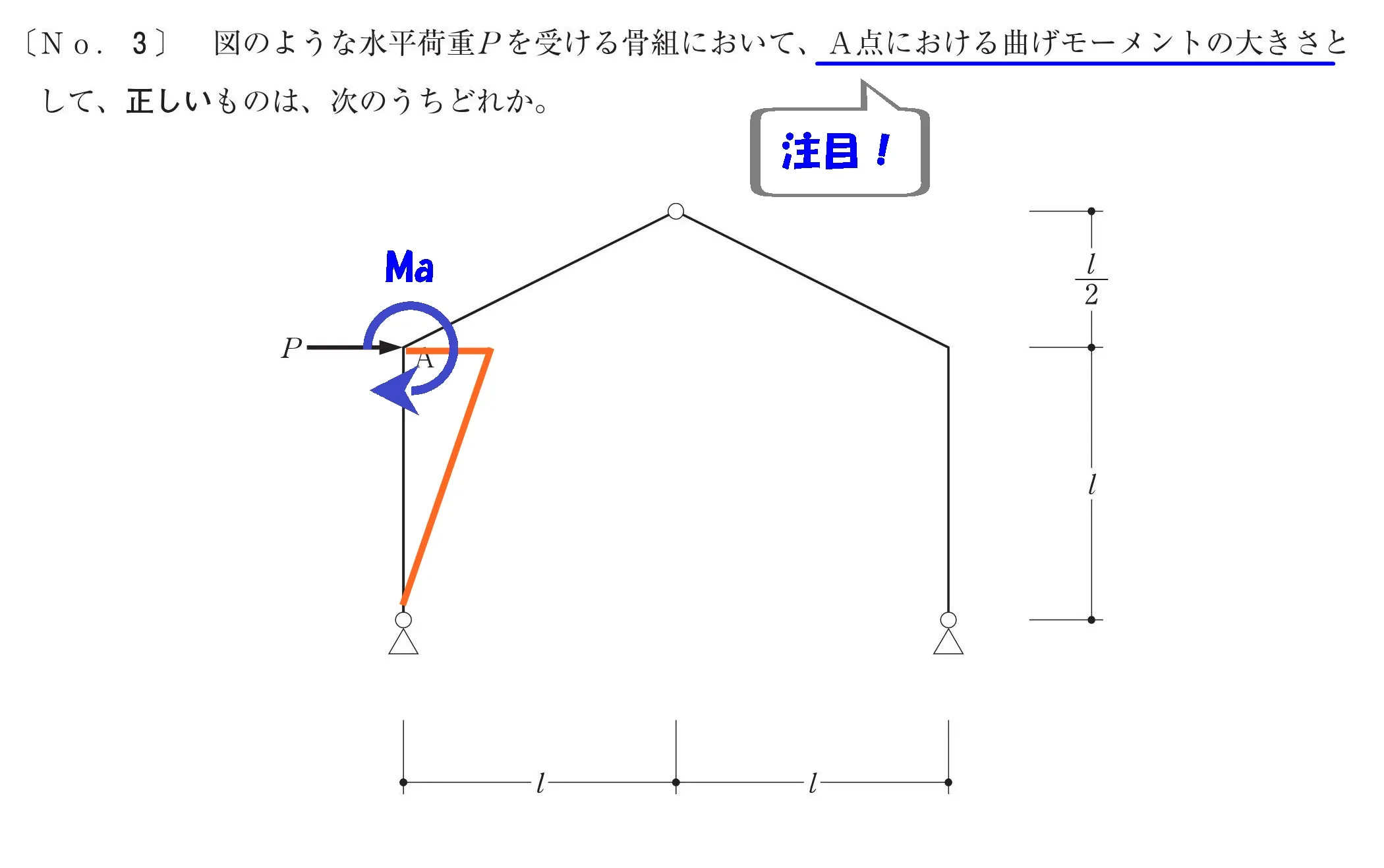

A点のモーメント図を描いてみましょう。
$$モーメント=力×距離$$
モーメント=力×距離
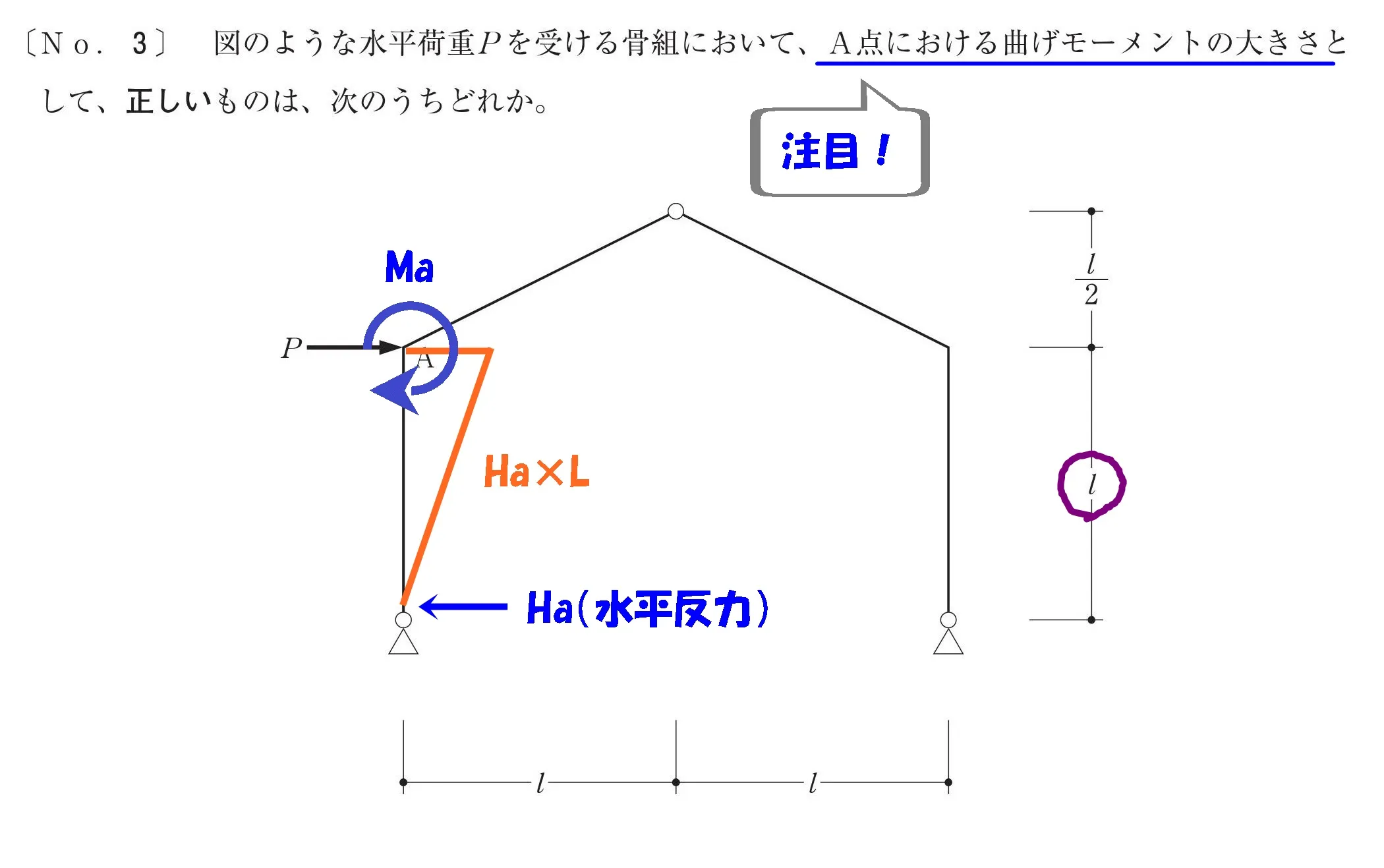

$$モーメント=力×距離より$$$$Ma=Ha(水平反力)*L$$
求めるものは水平反力
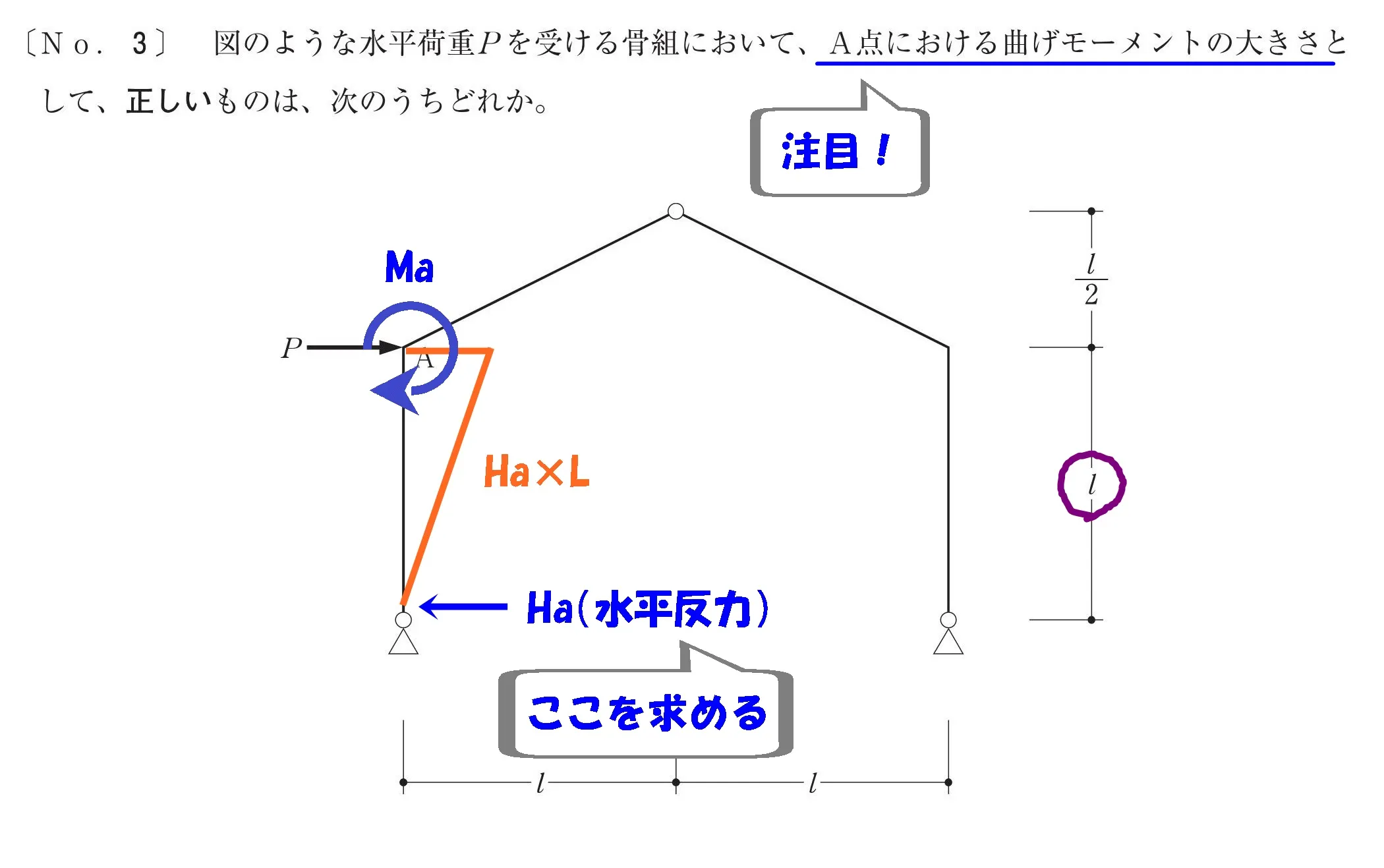

この問題における「答えに繋がる反力」とは水平反力「Ha」になることが分かりました。
ここを求める
モーメントを導くためには水平反力:Haを求める。



水平反力Ha、これが
問題を解くカギとなる。
2.支点に作用する反力を書き込む
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
反力を図示する
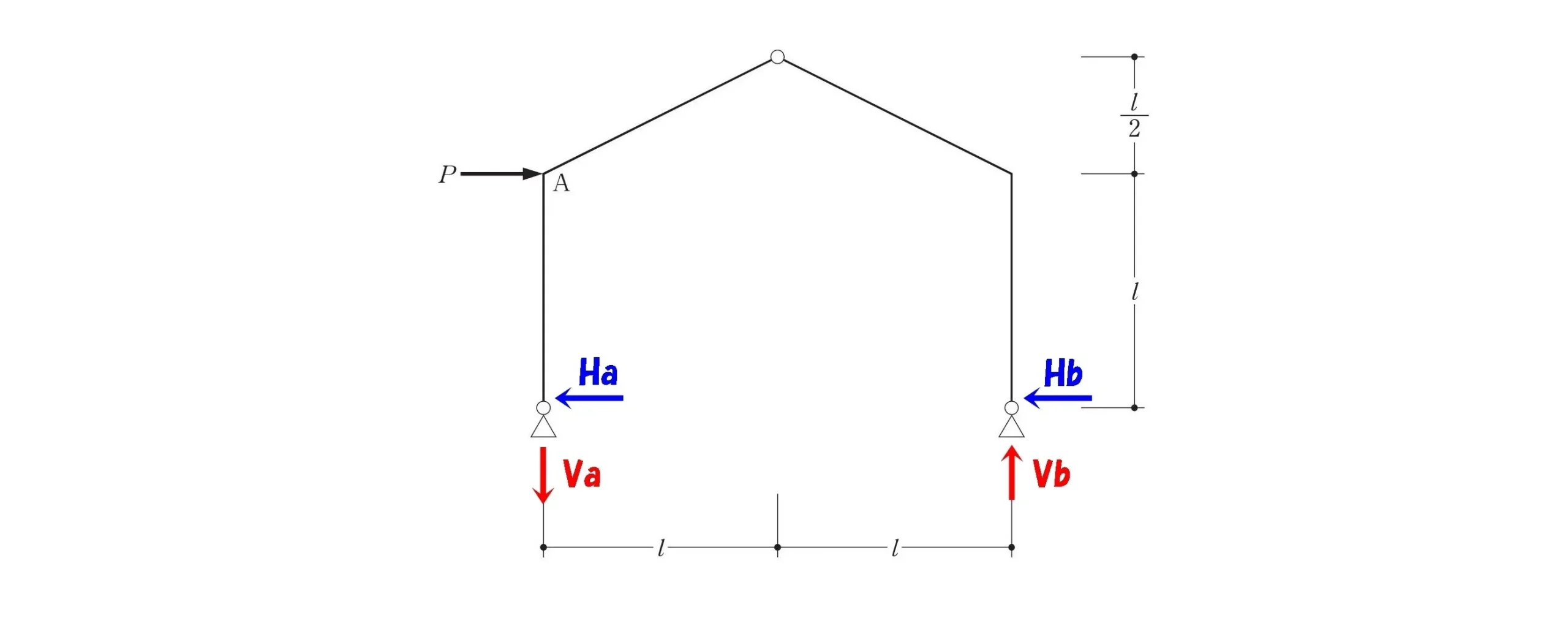

反力は4つ
$$水平反力:Ha,Hb$$$$鉛直反力:Va,Vb$$
必要な方程式の数
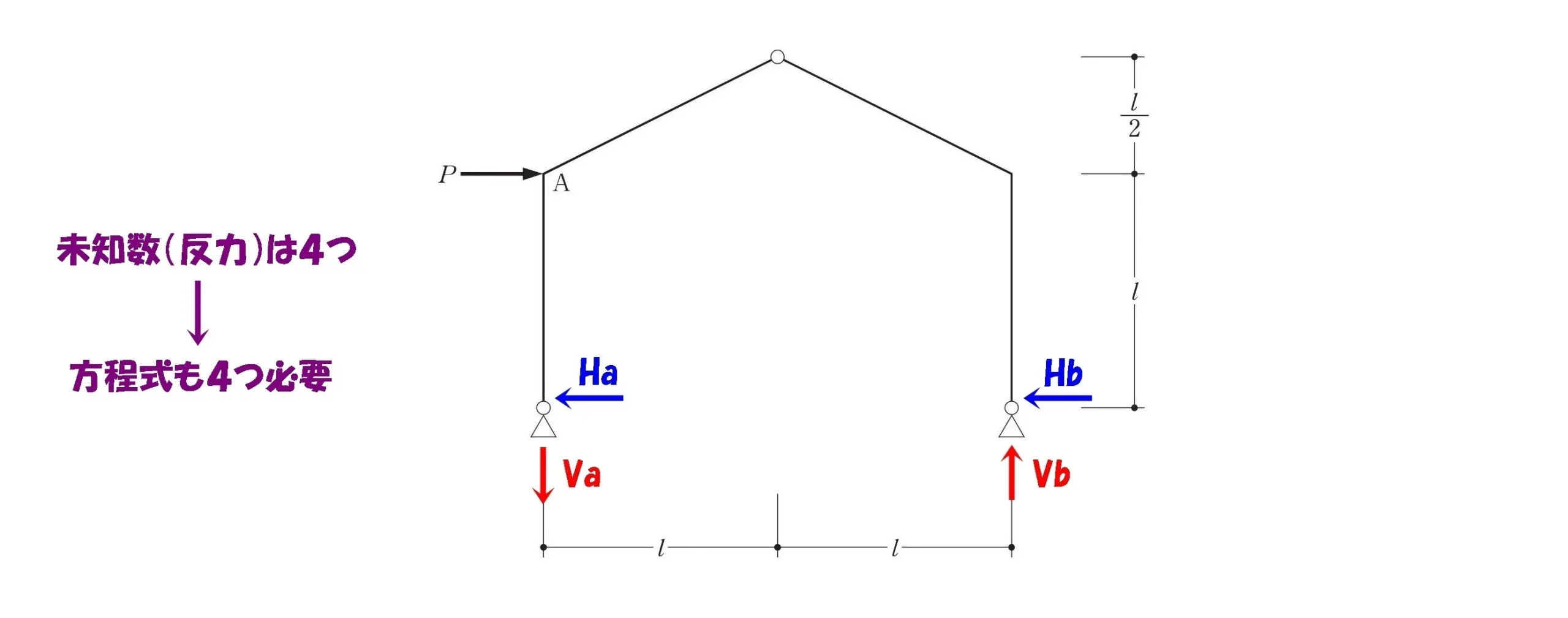

未知数となる反力は4つなので、連立させる方程式も4つ以上必要となる。



未知数4つ?多いね。
中央のヒンジに注目!
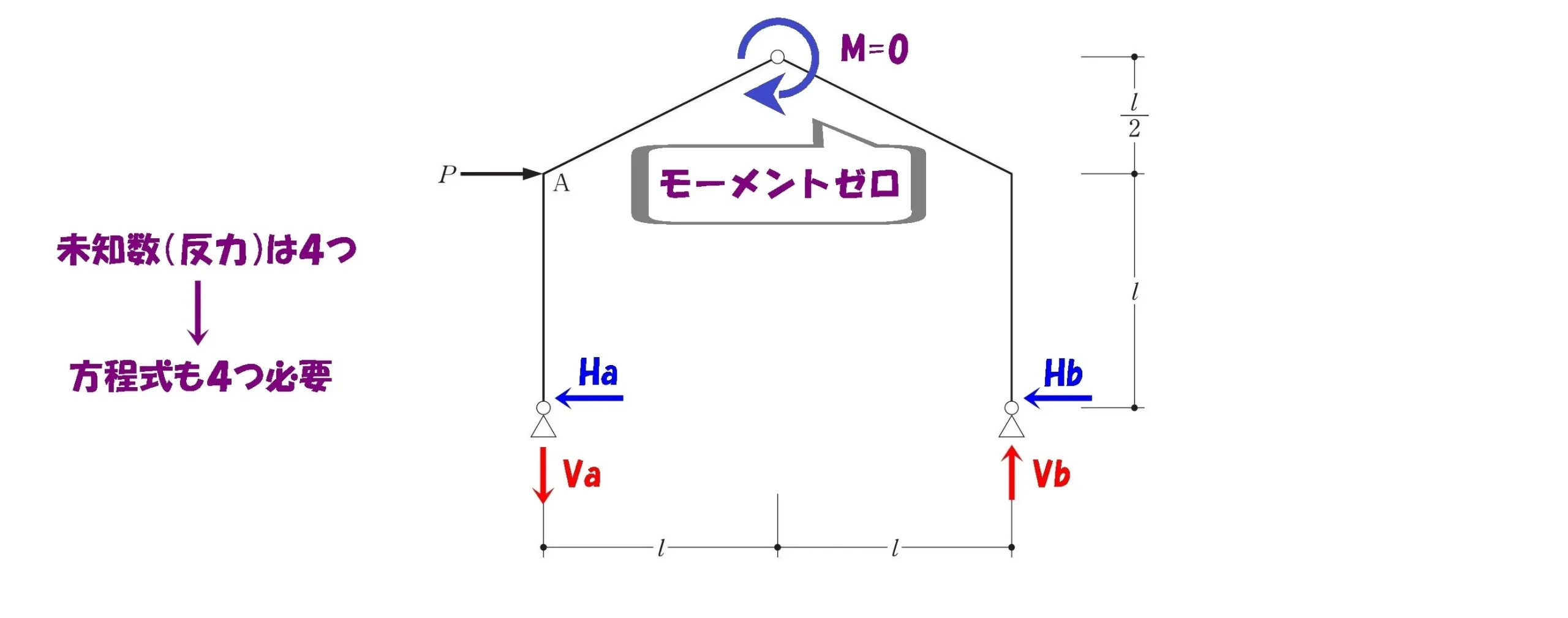

ヒンジ部分におけるモーメントはゼロになる。
ヒンジを中心にM=0が成立する
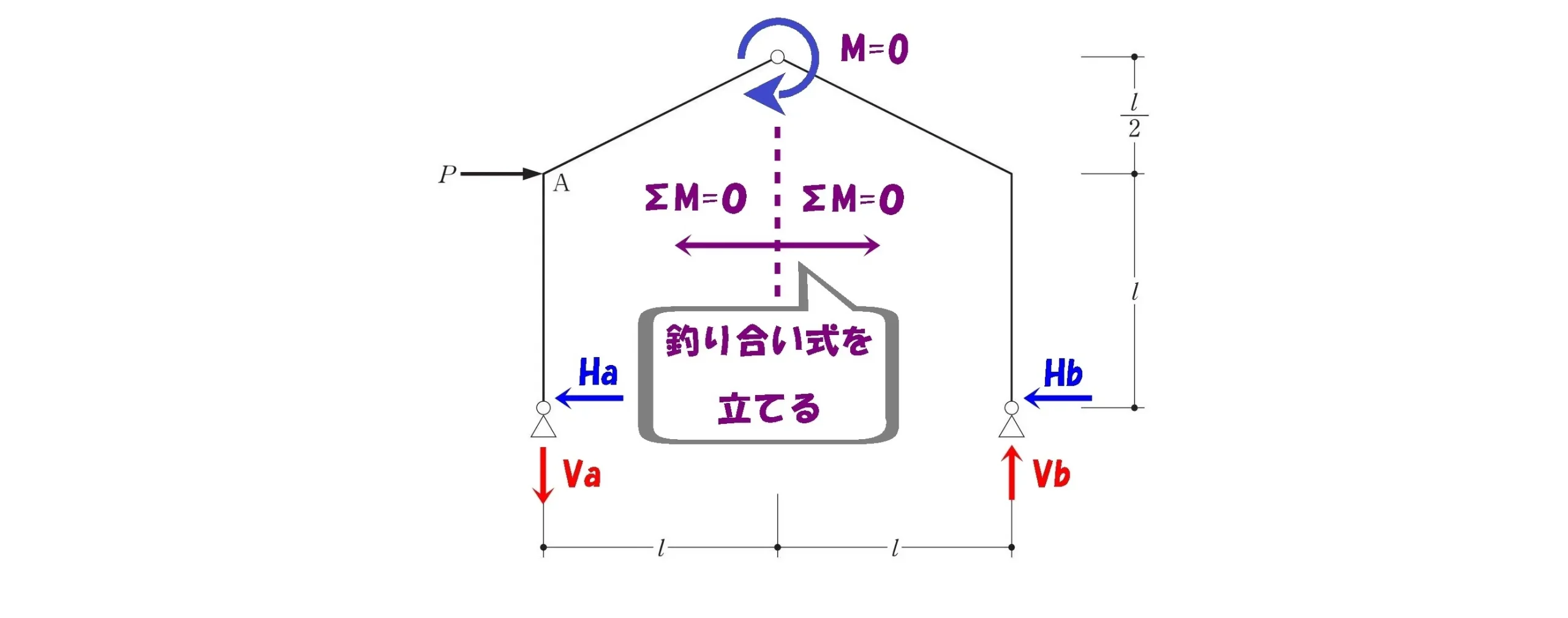

「ヒンジ部分におけるモーメントはゼロになる」ことからモーメントの吊り合い式を立てます。
4つの吊り合い式
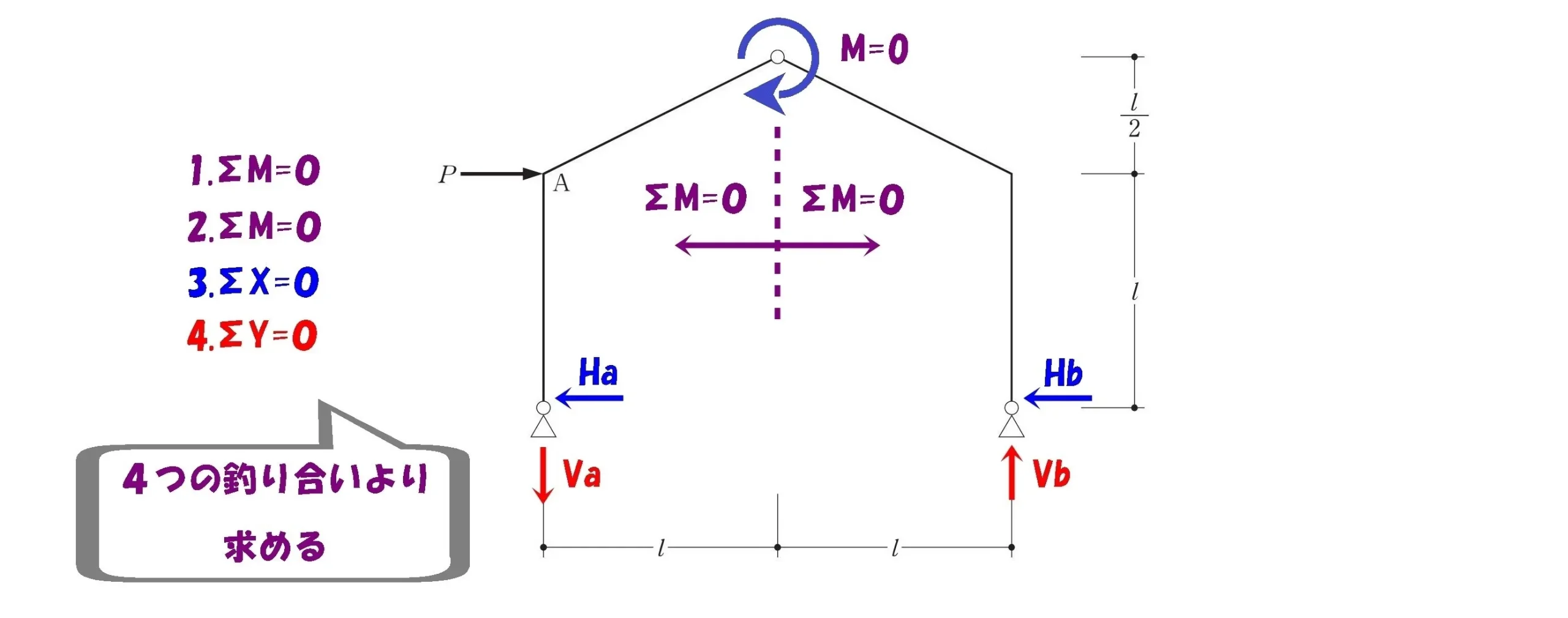

4つの連立方程式
$$モーメントの吊り合い$$
$$\Sigma M=0(左)$$
$$\Sigma M=0(右)$$
$$反力の吊り合い$$
$$\Sigma X=0$$
$$\Sigma Y=0$$
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!
3.ヒンジを起点にΣM=0
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
ヒンジを中心にM=0が成立する


中央のヒンジを起点にモーメントの吊り合い式を作りましょう。
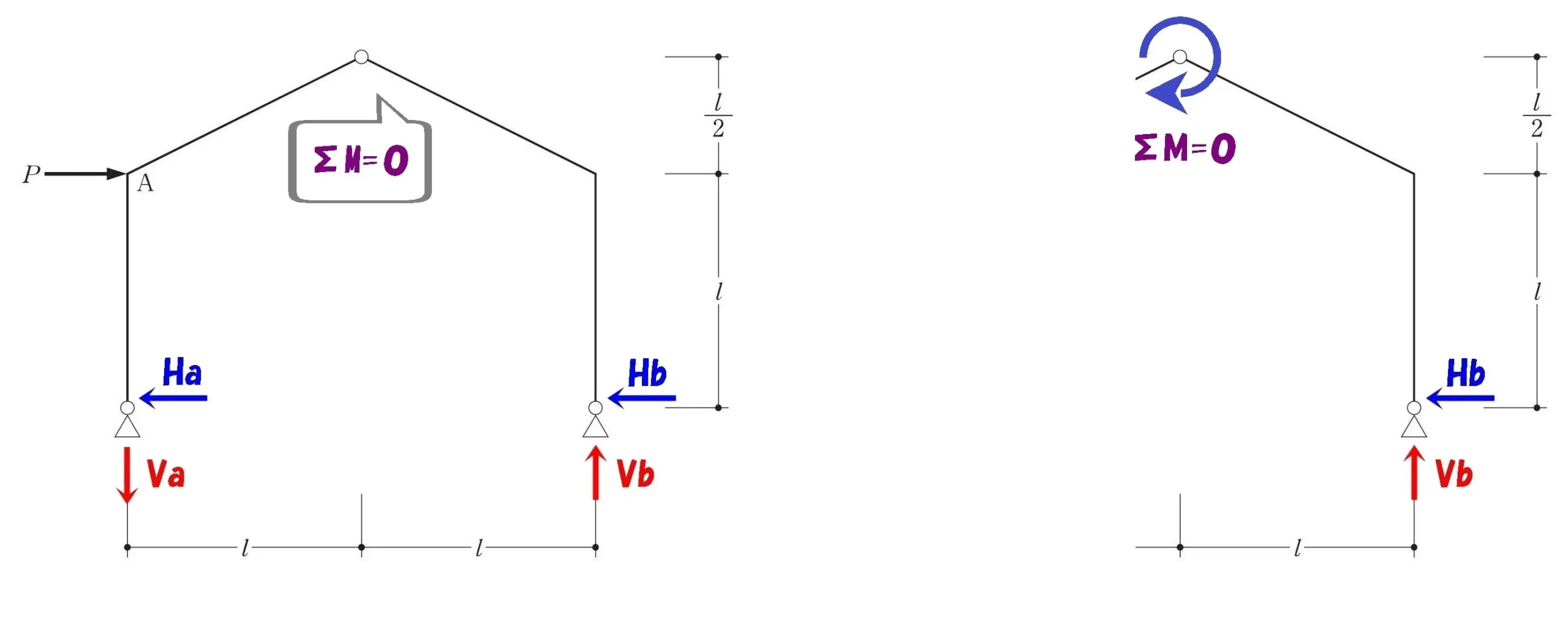
ヒンジを起点に左側でΣM=0
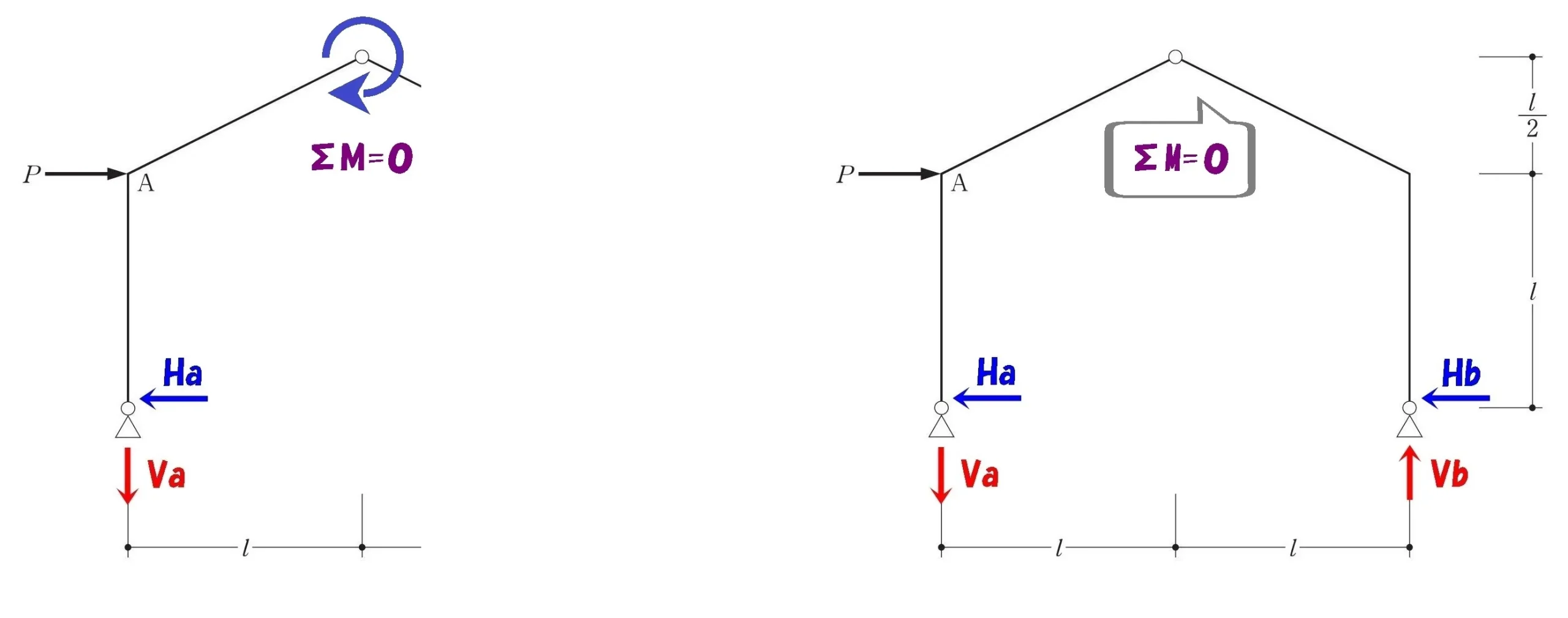

ヒンジを起点に右側でΣM=0

それぞれのΣM=0から式を立てる
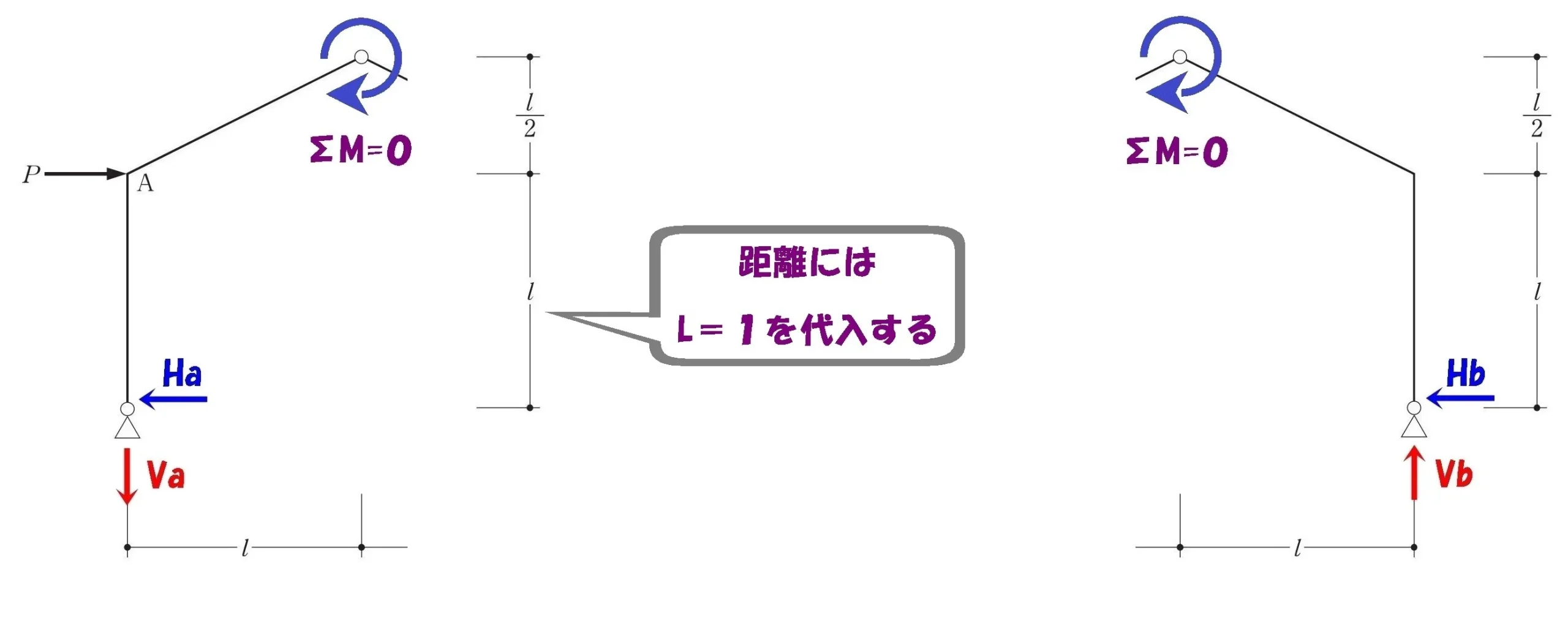

ワンポイント
計算を楽にするには、アルファベットLを入れないようにすること。
長さLには0以外の数値であれば、何を代入しても答えに差し支えはありません。
「L=1」を代入することで、計算式が簡略化されて数値の読み間違いリスクを減らせます。



いいね!
ヒンジを起点に左側でΣM=0
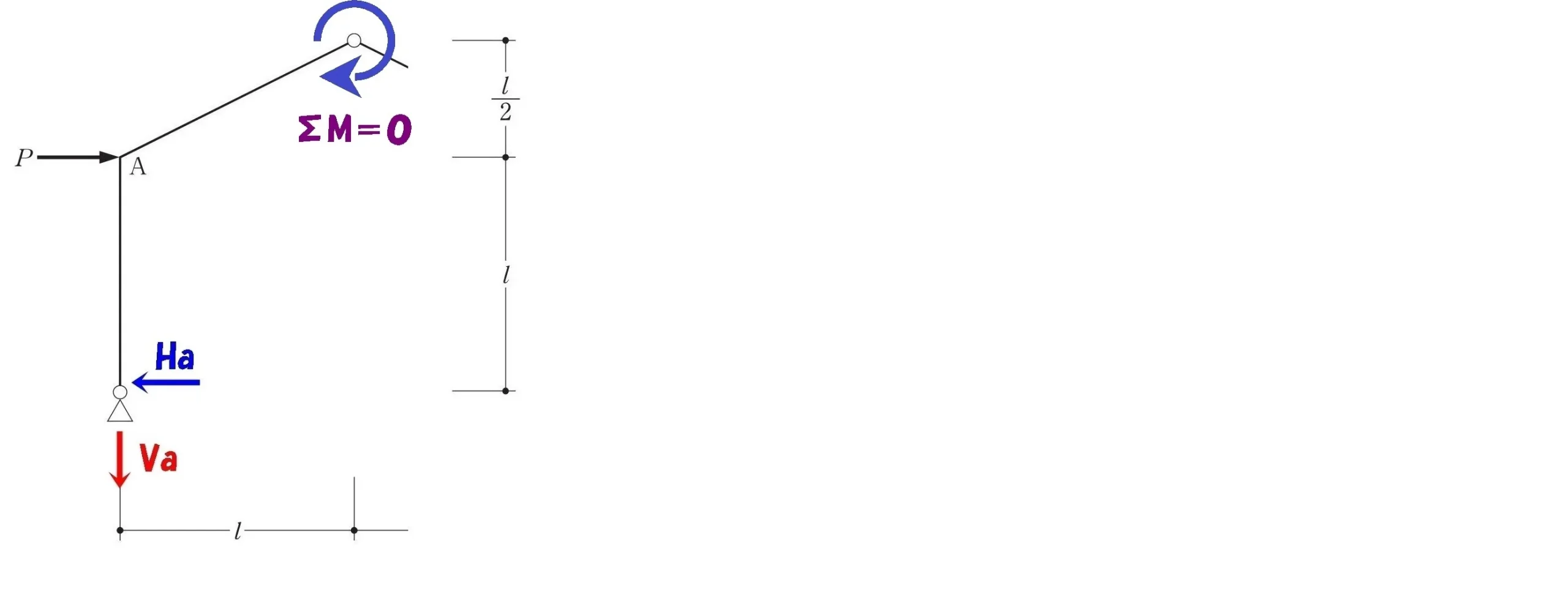

シンプルな片持ち梁の絵を描く
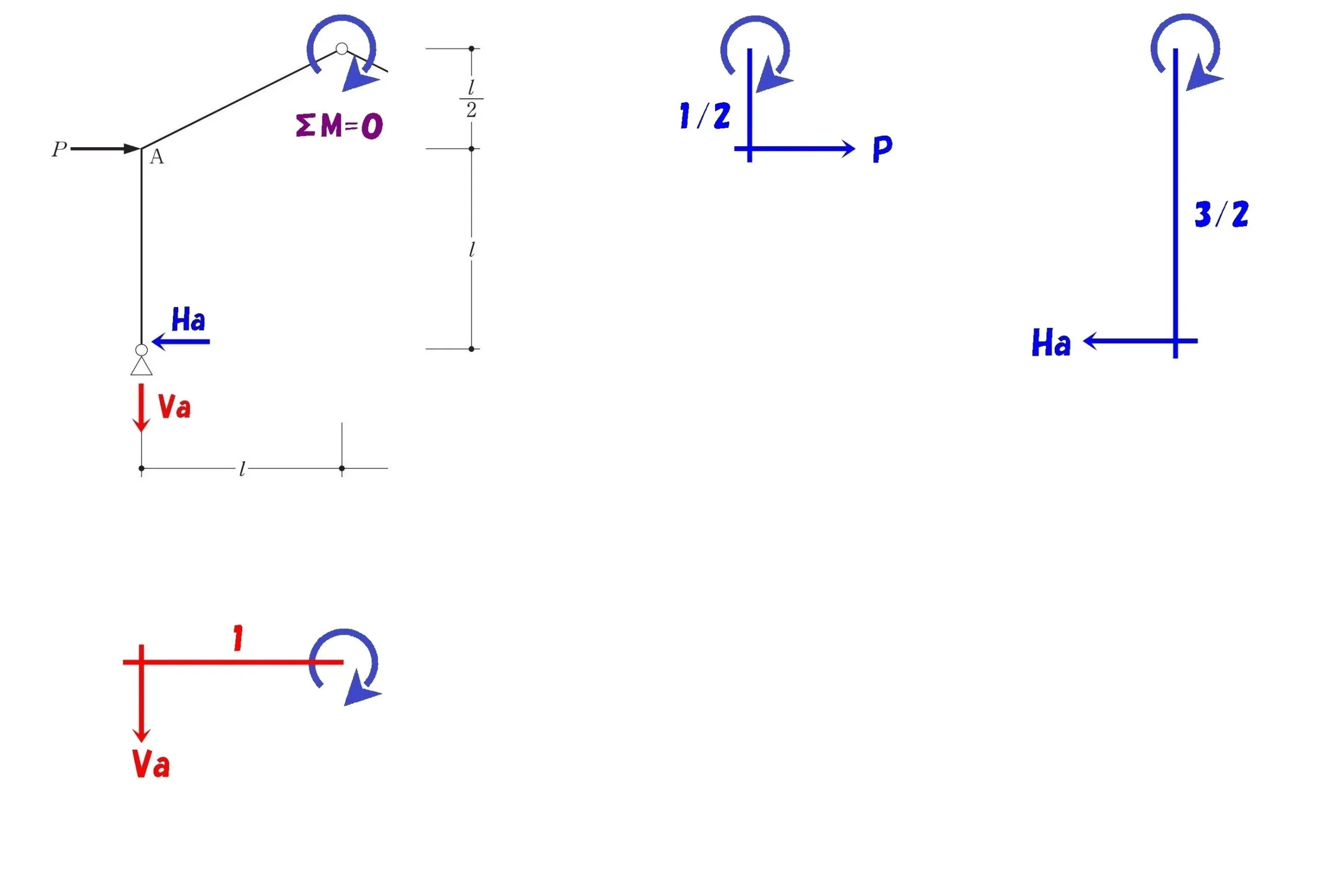

モーメント=力×距離
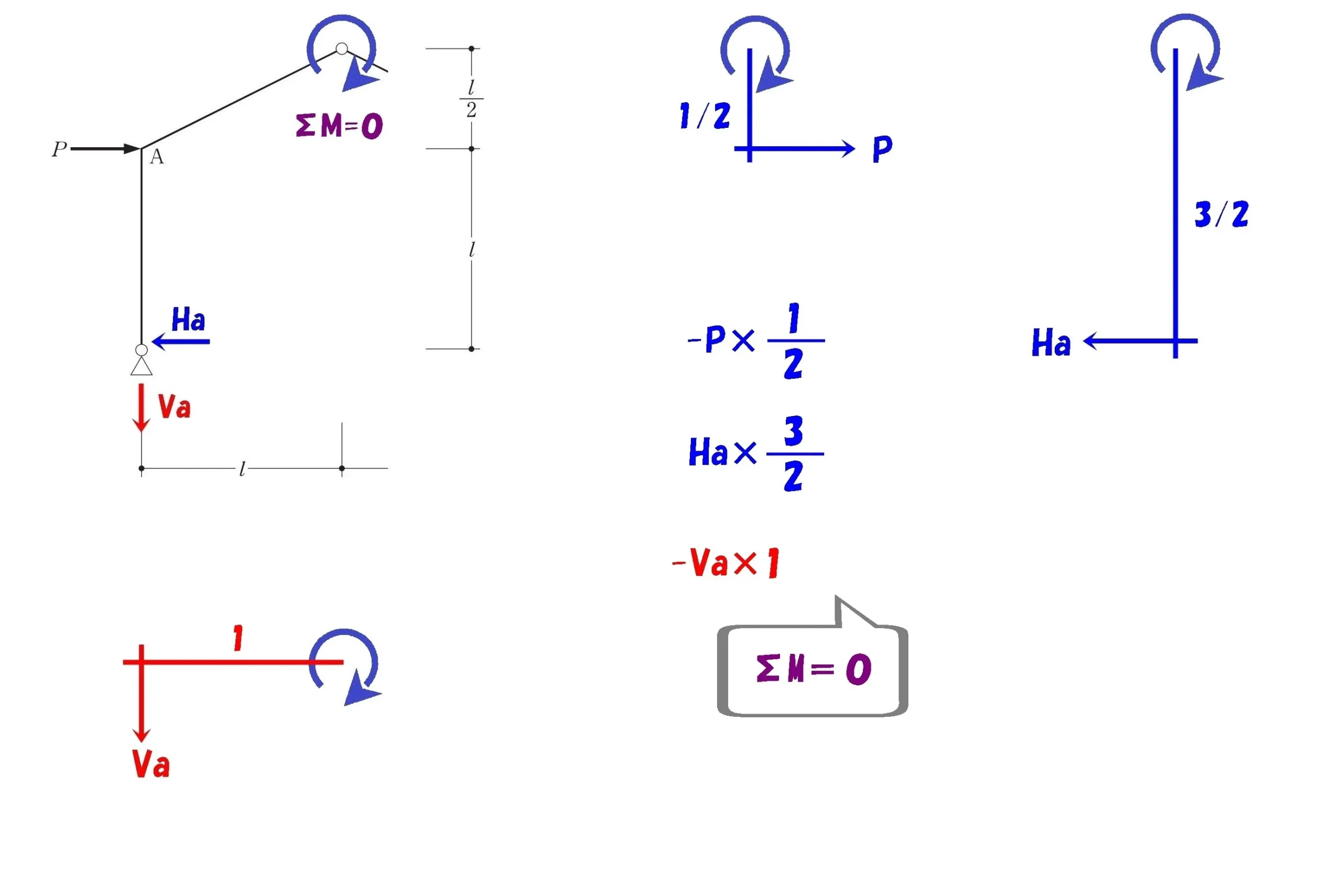

$$-P*\frac{ 1 }{ 2 }-Va*1+Ha*\frac{ 3 }{ 2 }=0$$
ヒンジを起点に右側でΣM=0
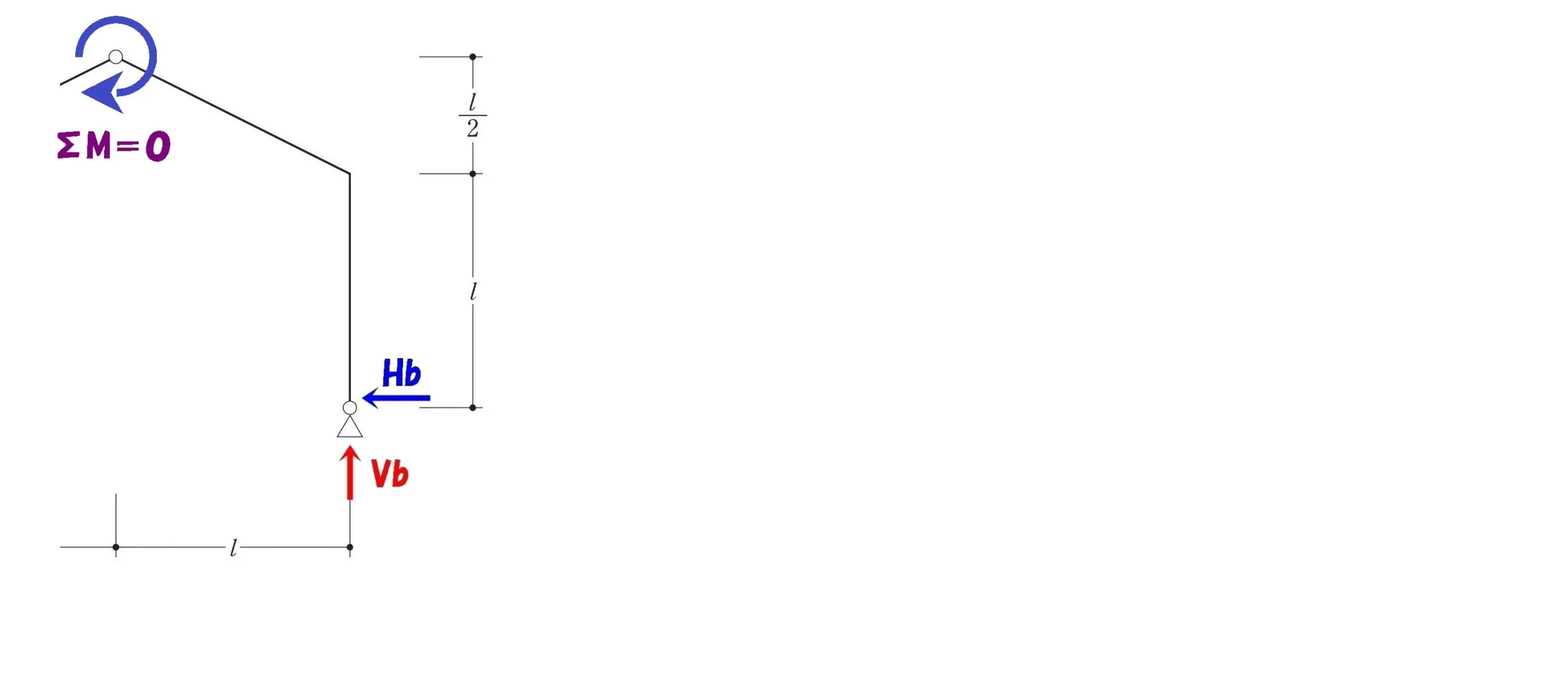

シンプルな片持ち梁の絵を描く
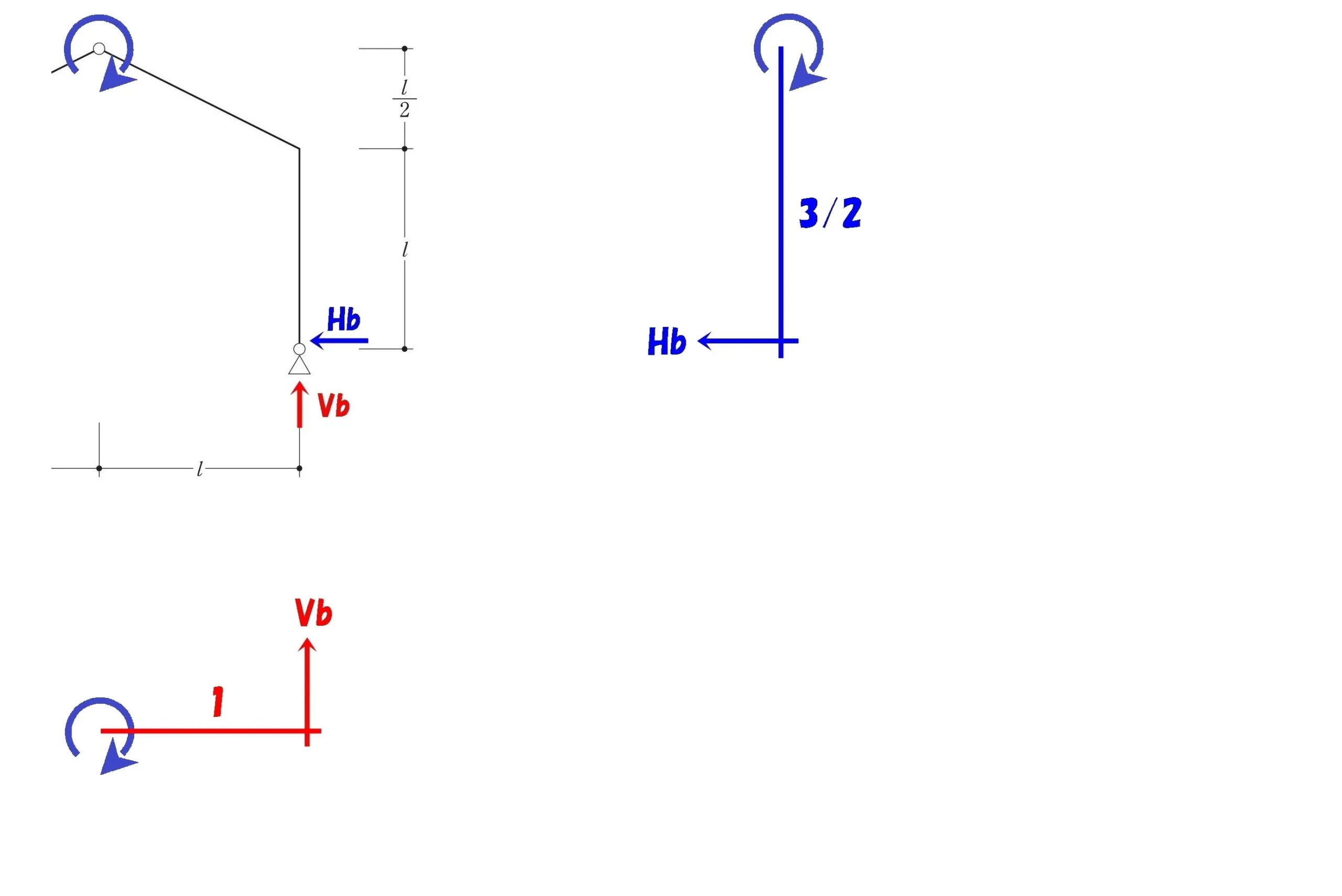

モーメント=力×距離
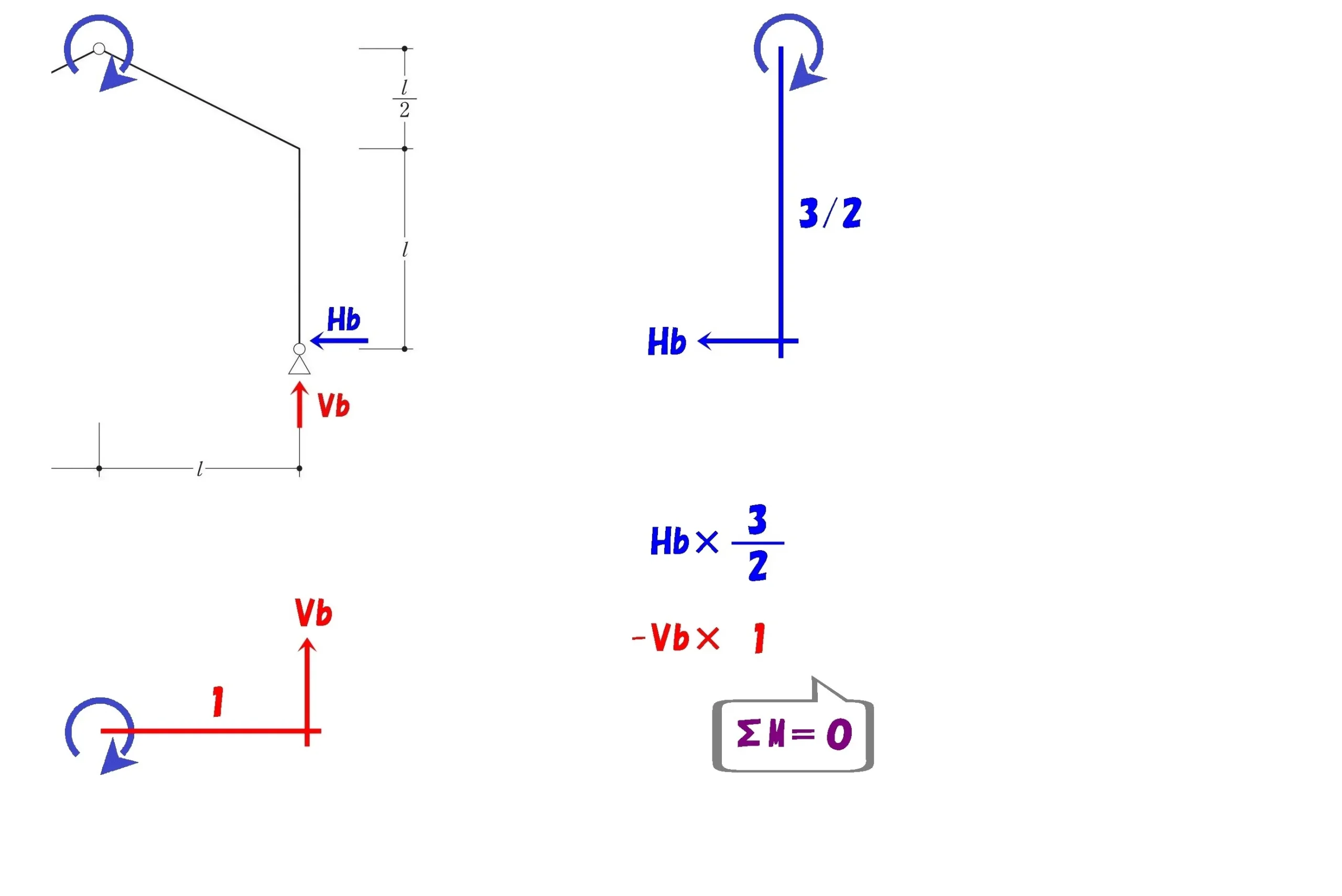

$$+Hb*\frac{ 3 }{ 2 }-Vb*1=0$$
公式
$$\Sigma M=0$$



Σエム!
4.力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
反力の吊り合い式
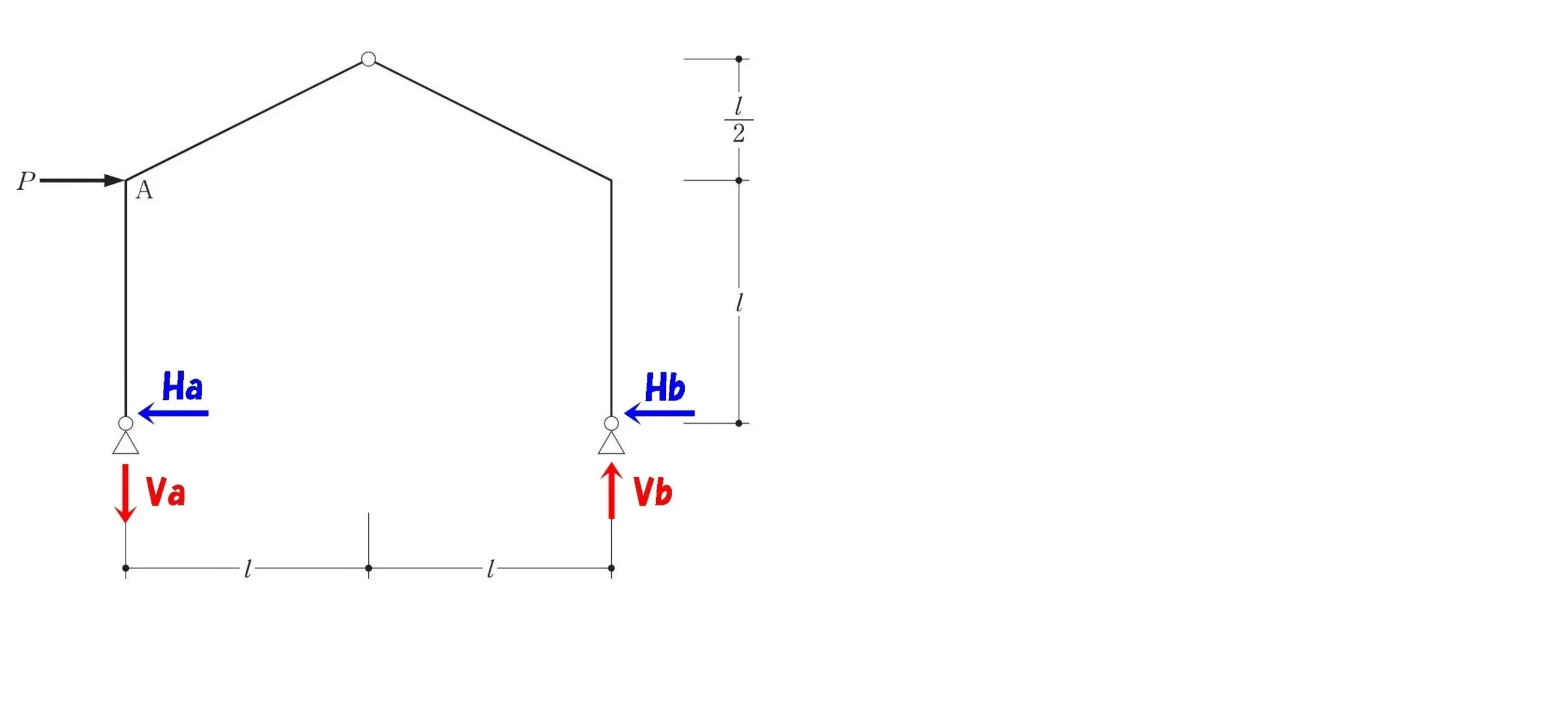

ΣX=0、ΣY=0
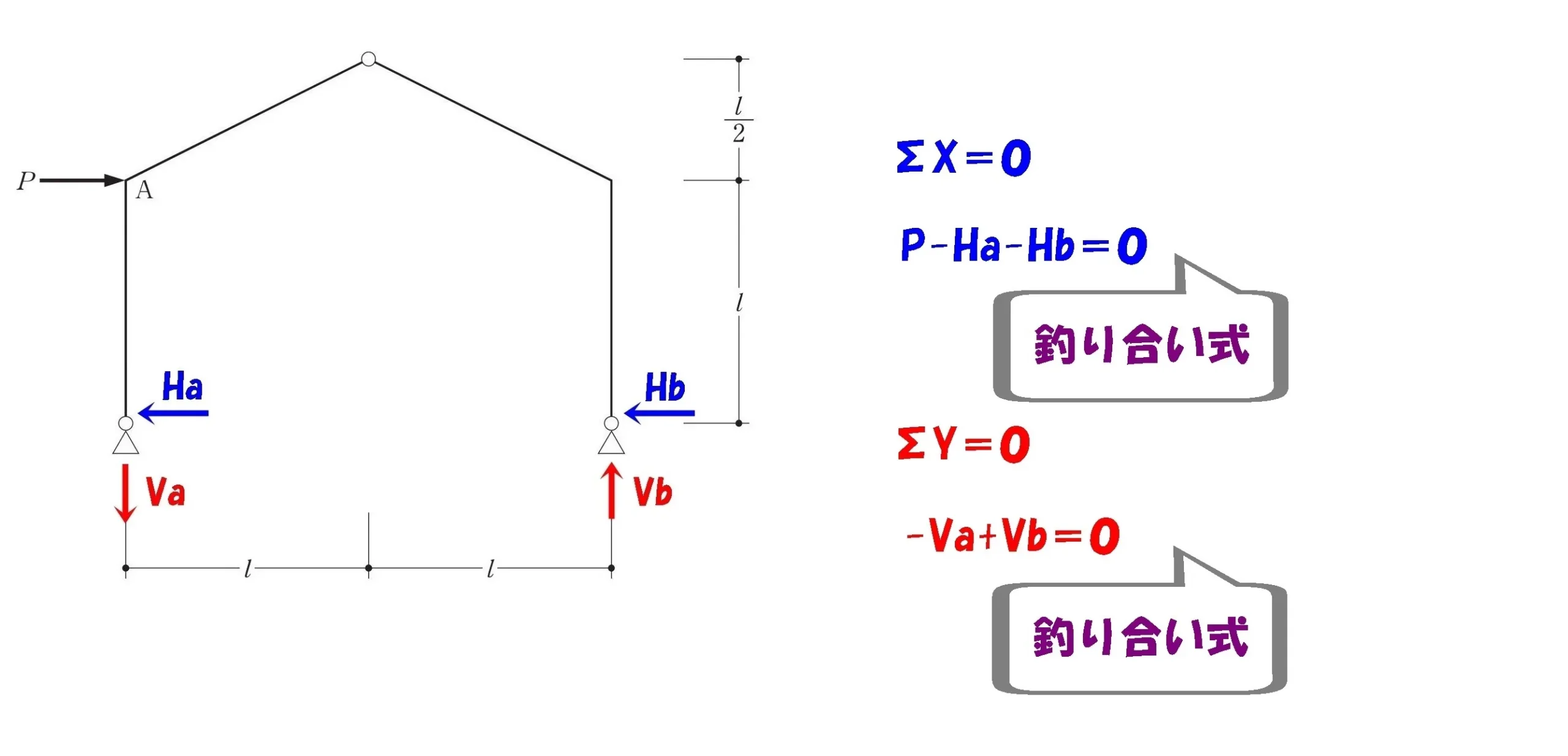

$$\Sigma X=0より,P-Ha-Hb=0$$
$$\Sigma Y=0より,-Va+Vb=0$$
公式
$$\Sigma X=0$$$$\Sigma Y=0$$



Σエックス!Σワイ!
4つの方程式を並べる
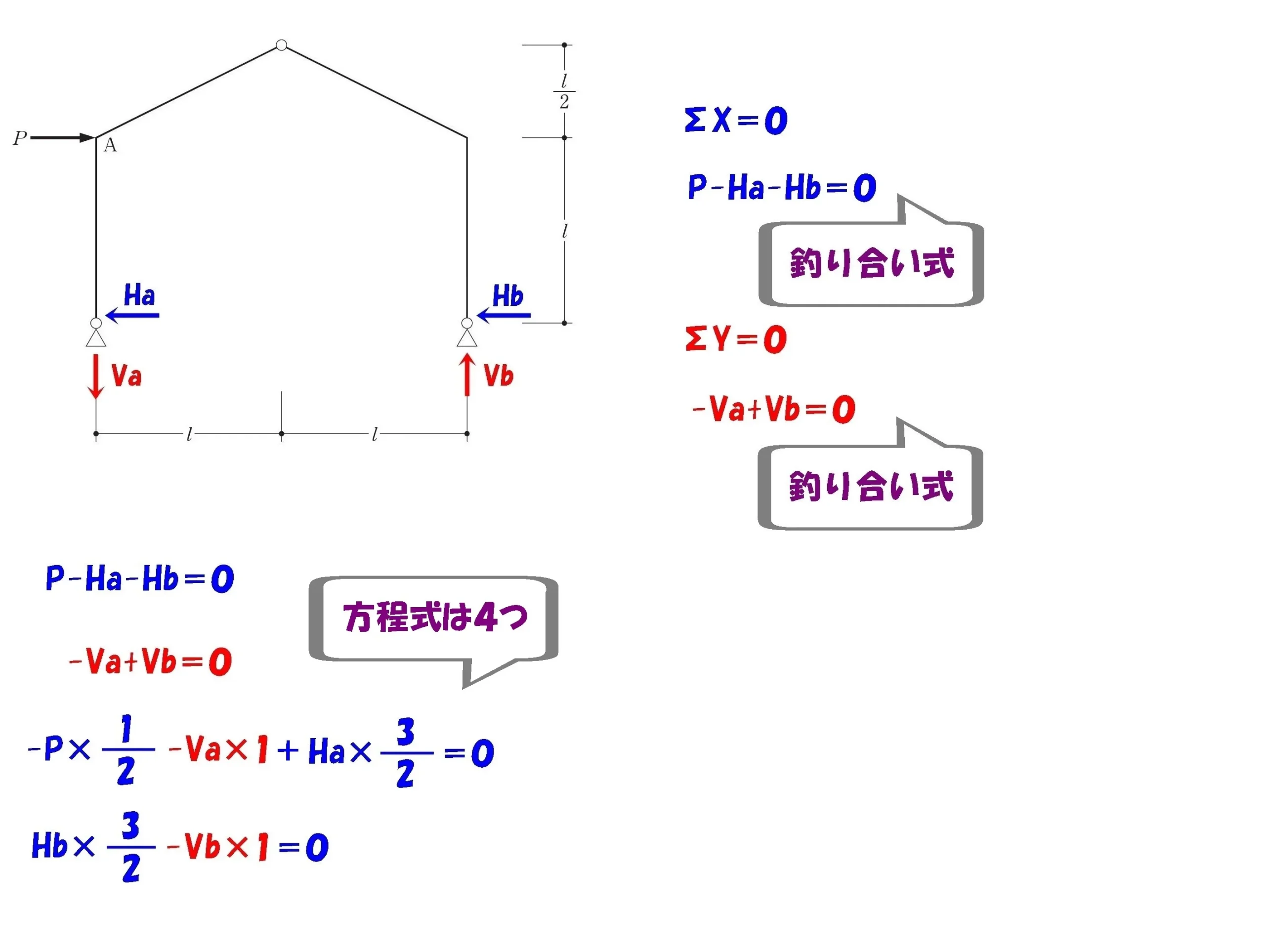

$$①式:P-Ha-Hb=0$$
$$②式:-Va+Vb=0$$
$$③式:-P*\frac{ 1 }{ 2 }-Va*1+Ha*\frac{ 3 }{ 2 }=0$$
$$④式:+Hb*\frac{ 3 }{ 2 }-Vb*1=0$$
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!


この動画を YouTube で視聴
5.答えに繋がる反力を定めて連立方程式を組む
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
求める未知数はHa

A点のモーメントを求めるために必要な未知数は「Ha」
連立方程式を組むにあたって、「答えに繋がる反力」はHaであることを再確認しましょう。



水平反力Haを求める。
これを見失わないこと。
連立方程式の組み方
- 「答えに繋がる反力」を含む2つの式で連立方程式をつくる。
- 「答えに繋がる反力」以外の未知数に他の式を代入して、置き換える。
- 「答えに繋がる反力」以外の未知数により構成される式を連立方程式に代入する。
連立方程式の組み方
1.「答えに繋がる反力」を含む2つの式で連立方程式をつくる。
$$①式:P-Ha-Hb=0$$
$$②式:-Va+Vb=0$$
$$③式:-\frac{ 1 }{ 2 }P-Va+\frac{ 3 }{ 2 }Ha=0$$
$$④式:+\frac{ 3 }{ 2 }Hb-Vb=0$$
「答えに繋がる反力」は「Ha」になります。
式①~式④の中で、「Ha」を含む式①と式③の2つで連立方程式を組みましょう。
連立方程式
\(\left\{\begin{array}{l}①式:P-Ha-Hb=0\\③式:-\frac{ 1 }{ 2 }P-Va+\frac{ 3 }{ 2 }Ha=0\end{array}\right.\)
この2つの式が連立方程式の軸になります。
しかし、このままの式ではHaは求まらないですよね?
連立方程式をPとHaの2つだけにより構成される式に置き換える必要があります。
連立方程式の組み方
2.「答えに繋がる反力」以外の未知数に他の式を代入して、置き換える。
連立方程式
\(\left\{\begin{array}{l}①式:P-Ha-Hb=0\\③式:-\frac{ 1 }{ 2 }P-Va+\frac{ 3 }{ 2 }Ha=0\end{array}\right.\)
「答えに繋がる反力(Ha)」以外の未知数とは式①の「Hb」と式③「Va」になります。
この2つの未知数に式②と式④をそれぞれ代入して、置き換えましょう。
$$式①の「Hb」には式④を代入する。$$
$$④式:+\frac{ 3 }{ 2 }Hb-Vb=0より,④-2式:Hb=\frac{ 2 }{ 3 }Vb$$
$$式③の「Va」には式②を代入する。$$
$$②式:-Va+Vb=0より,②-2式:Va=Vb$$



ちょっと休憩させて。
連立方程式の組み方
3.「答えに繋がる反力」以外の未知数により構成される式を連立方程式に代入する。
$$④-2式:\underline{Hb}=\frac{ 2 }{ 3 }Vb⤵$$
$$①式:P-Ha-\underline{Hb}=0の\underline{Hb}へ代入する。$$
$$②-2式:\underline{Va}=Vb⤵$$
$$③式:-\frac{ 1 }{ 2 }P-\underline{Va}+\frac{ 3 }{ 2 }Ha=0の\underline{Va}へ代入する。$$
代入する
\(\left\{\begin{array}{l}①式:P-Ha-\underline{\frac{ 2 }{ 3 }Vb}=0\\③式:-\frac{ 1 }{ 2 }P-\underline{Vb}+\frac{ 3 }{ 2 }Ha=0\end{array}\right.\)



未知数に式を代入!
並べ替え
\(\left\{\begin{array}{l}①式:P-Ha-\underline{\frac{ 2 }{ 3 }Vb}=0\\③式:-\frac{ 1 }{ 2 }P+\frac{ 3 }{ 2 }Ha-\underline{Vb}=0\end{array}\right.\)
$$連立方程式から\underline{Vb}を消去する。$$
式①に×3/2
\(\left\{\begin{array}{l}①式:\frac{ 3 }{ 2 }P-\frac{ 3 }{ 2 }Ha-\underline{Vb}=0\\③式:-\frac{ 1 }{ 2 }P+\frac{ 3 }{ 2 }Ha-\underline{Vb}=0\end{array}\right.\)
式①-式③
$$\frac{ 4 }{ 2 }P-\frac{ 6 }{ 2 }Ha=0$$
$$\frac{ 6 }{ 2 }Ha=\frac{ 4 }{ 2 }Pより,Ha=\frac{ 4 }{ 2 }P*\frac{ 2 }{ 6 }$$
$$Ha=\frac{ 2 }{ 3 }P$$



やっと答えに
たどり着いたぞ!
連立方程式の組み方
- 「答えに繋がる反力」を含む2つの式で連立方程式をつくる。
- 「答えに繋がる反力」以外の未知数に他の式を代入して、置き換える。
- 「答えに繋がる反力」以外の未知数により構成される式を連立方程式に代入する。
モーメントAを求める
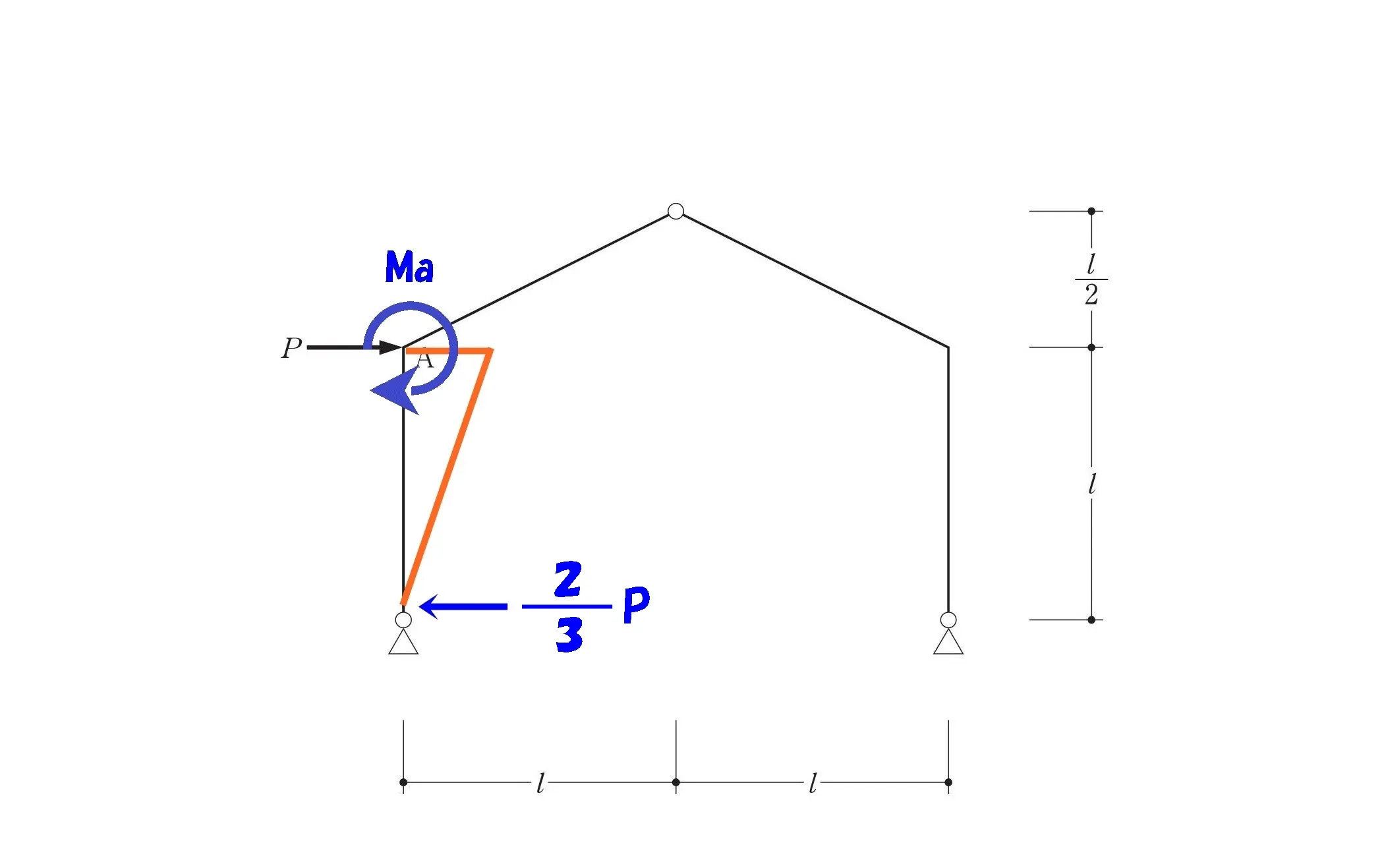

$$水平反力HaにHa=\frac{ 2 }{ 3 }Pを代入する。$$
モーメント=力×距離
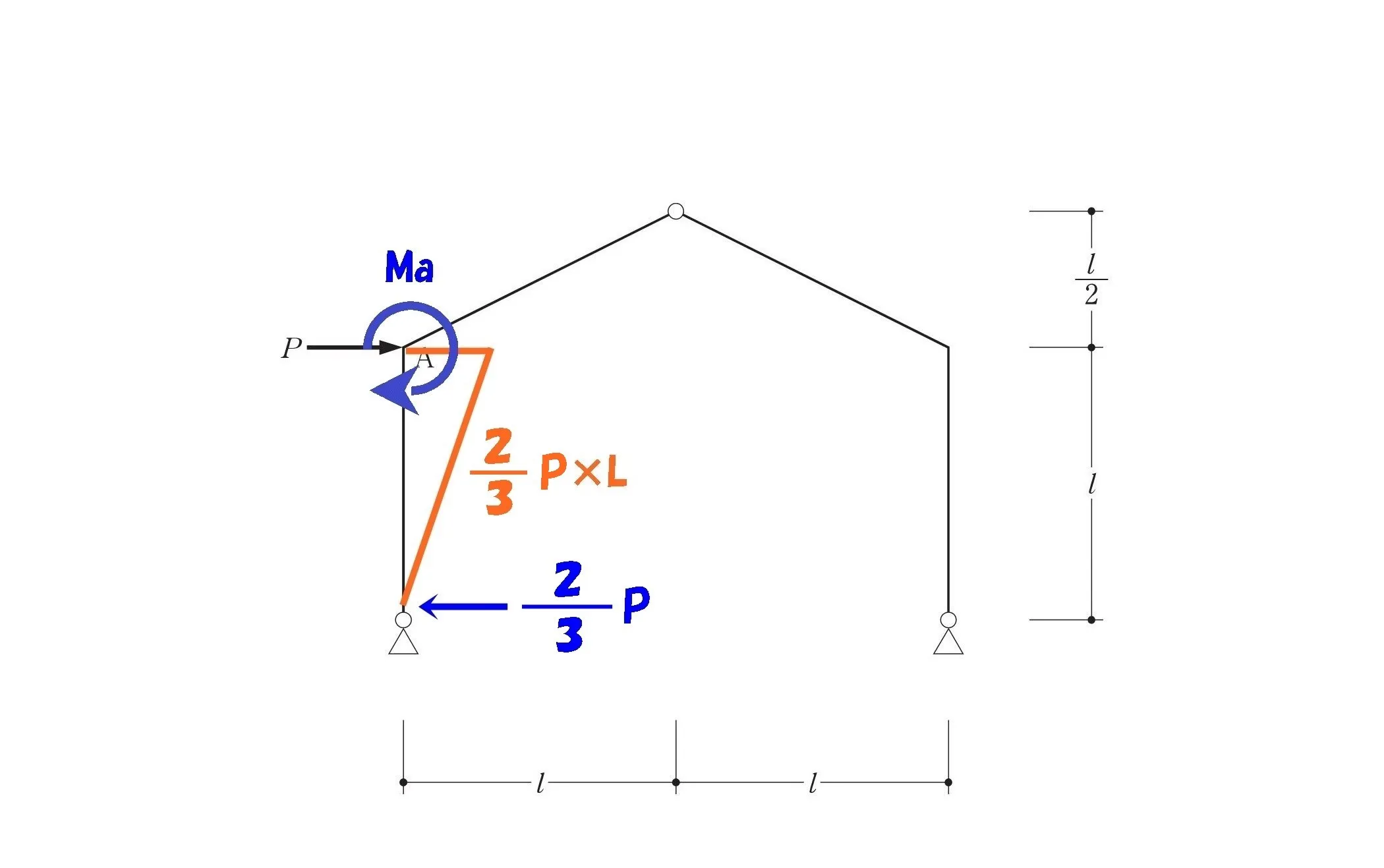

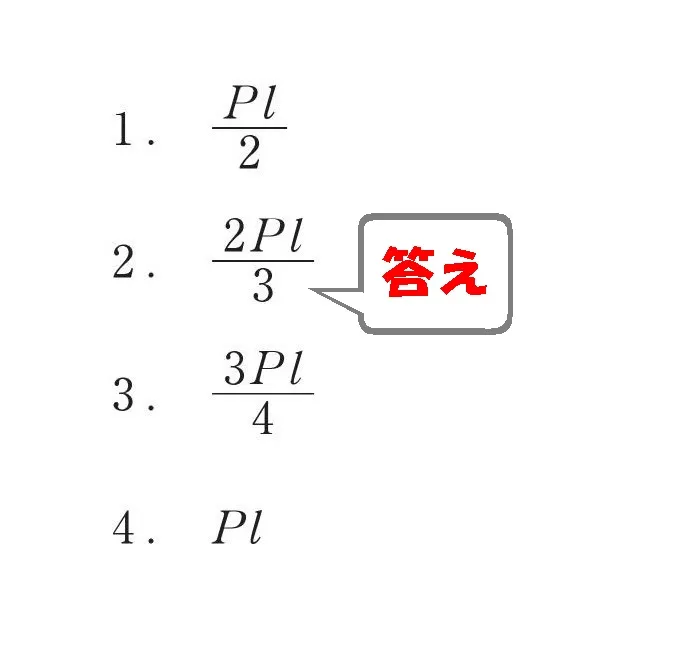
$$モーメント=力×距離より,$$$$Ma=\frac{ 2 }{ 3 }P*L=\frac{ 2PL }{ 3 }$$
答え.2




ふう~。
なかなか手強いでござる。
攻略ポイント
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む
応力と応力度
難易度:★★☆☆☆
- 応力とは軸力・曲げ力に抵抗する力、単位は[N]
- 応力度とは単位面積当たりの応力、単位は[N/m㎡]



言葉と単位は
セットで覚えよう。

公式
$$軸力による応力度:\sigma=\frac{ N }{ A }[N/mm^2]$$
$$曲げによる応力度:\sigma=\frac{ M }{ Z }[N/mm^2]$$
$$合成による応力度:\sigma=-\frac{ A }{ N }±\frac{ M }{ Z }[N/mm^2]$$
応力度の符号は引張り(+)・圧縮(-)このルールは、どの問題においても共通です。
このルールは必ず覚えておきましょう。


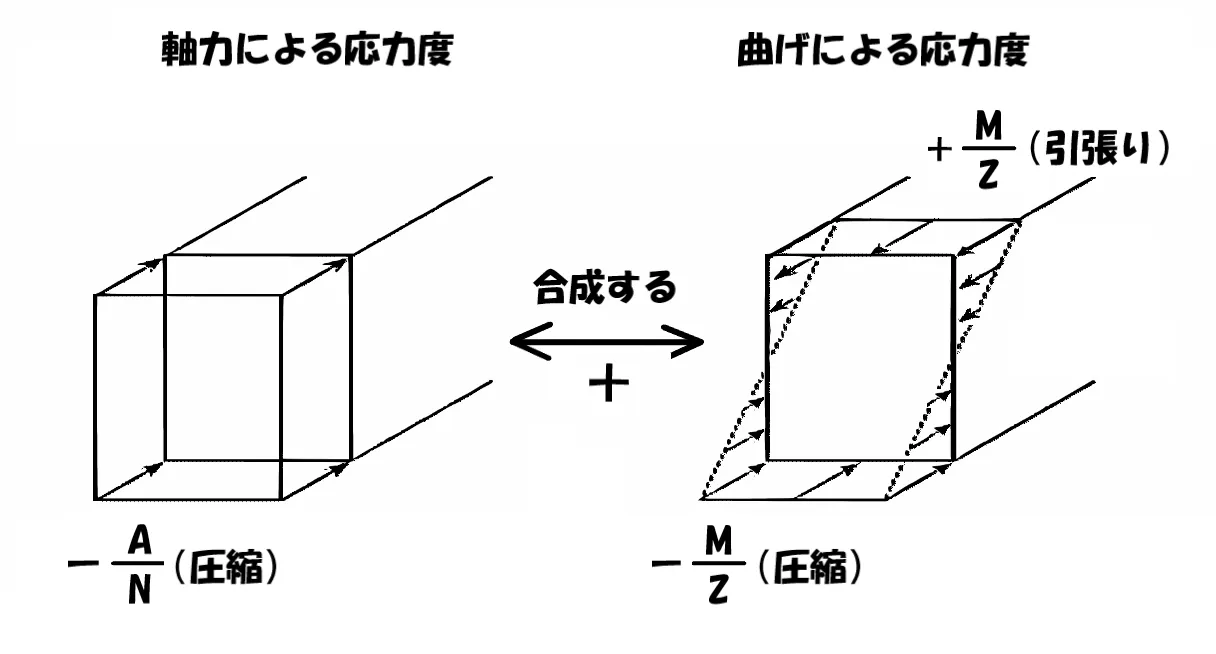
応力度の合成
$$圧縮:\sigma=-\frac{ N }{ A }-\frac{ M }{ Z }$$$$引張り:\sigma=-\frac{ N }{ A }+\frac{ M }{ Z }$$
M/Zの補足
応力度の公式について「M/Zにピンと来ない」という方もいるかもしれません。
ここでひとつ、公式の”単位”に注目して下さい。
単位に注目!
- 応力度(単位面積あたりの応力)の単位は[N/mm²]
- モーメントの単位は[N.mm]、断面係数の単位は[mm³]
$$曲げ応力度:\sigma=\frac{ M }{ Z }$$
$$単位=\frac{ P*L[N.mm] }{ bh^2/6[mm³] }=\frac{ [N]\underline{[mm]} }{ [mm²]\underline{[mm]} }=\frac{ [N] }{ [mm²] }$$
$$分子分母で[mm]が約分されて応力度と同じ単位[N/mm²]になる。$$


この動画を YouTube で視聴
攻略ポイント
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
問題
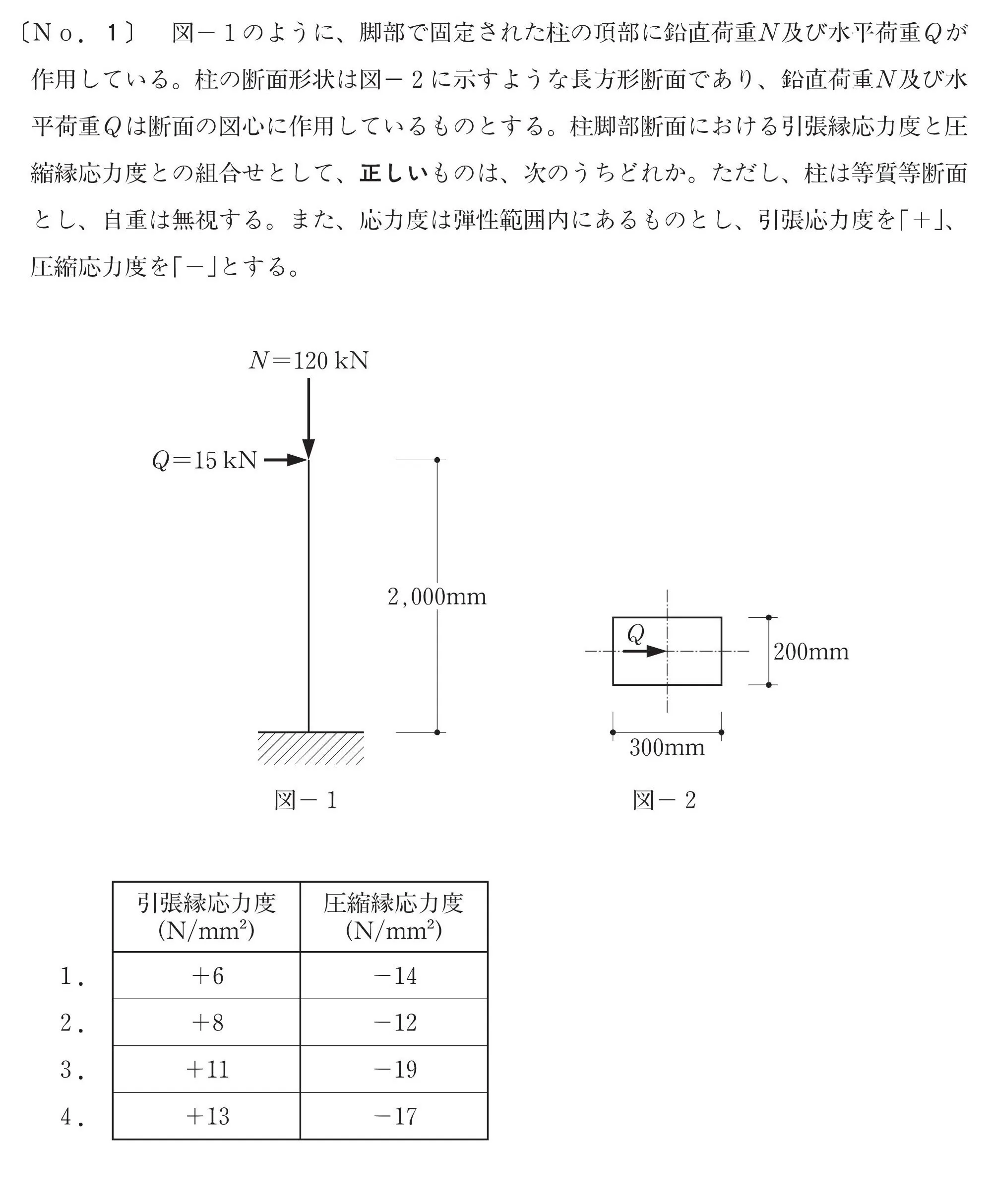

問題文をチェックする


求めるもの
- 引張縁応力度「+」
- 圧縮縁応力度「-」

1.軸力と曲げ力を求める
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
必要な3つの公式
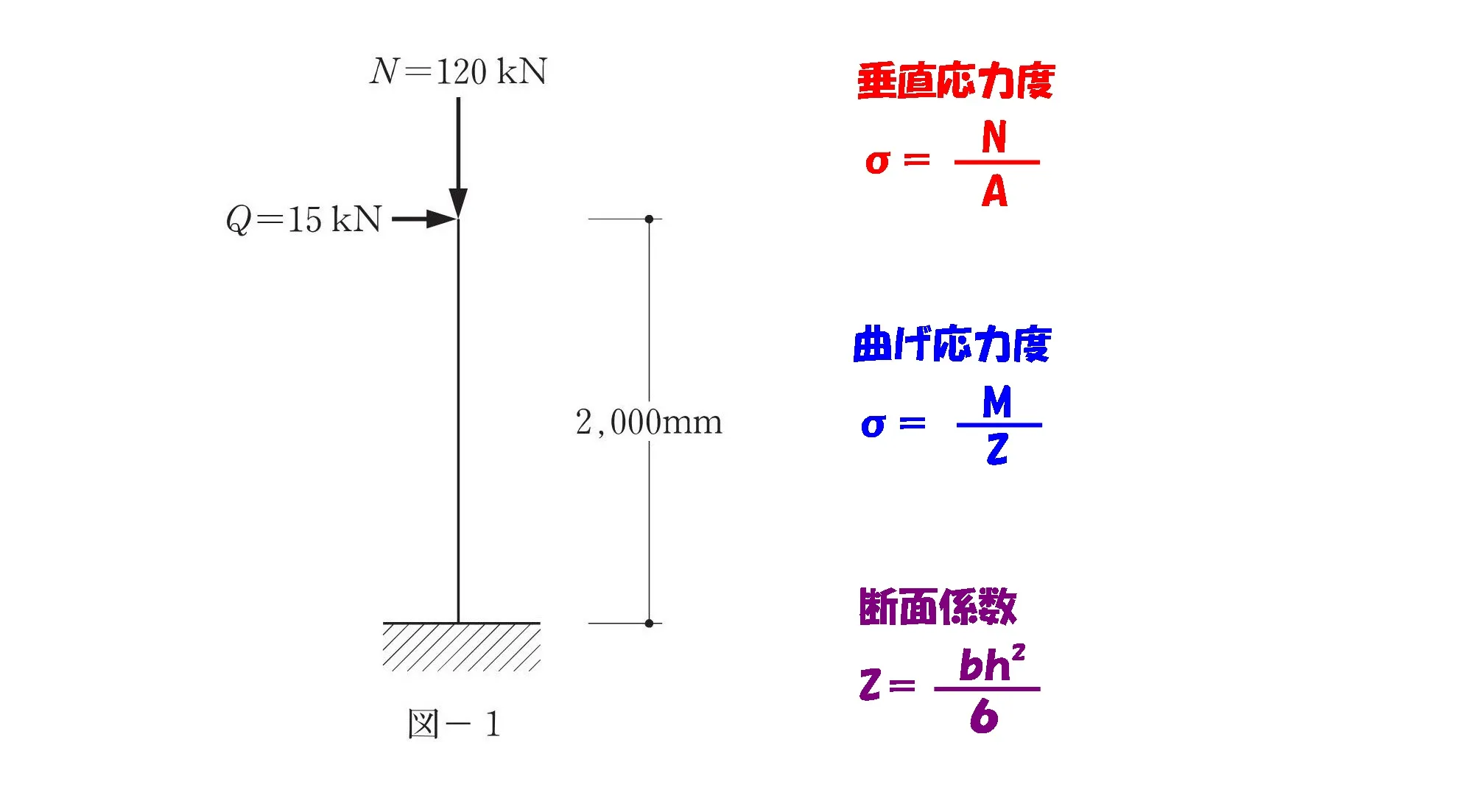

3つの公式
$$垂直応力度:\sigma=\frac{ N }{ A}[N/mm^2]$$
$$曲げ応力度:\sigma=\frac{ M }{ Z }[N/mm^2]$$
$$断面係数:Z=\frac{ bh^2 }{ 6 }[mm^3]$$



3つの公式で
テンポよく解き進める。
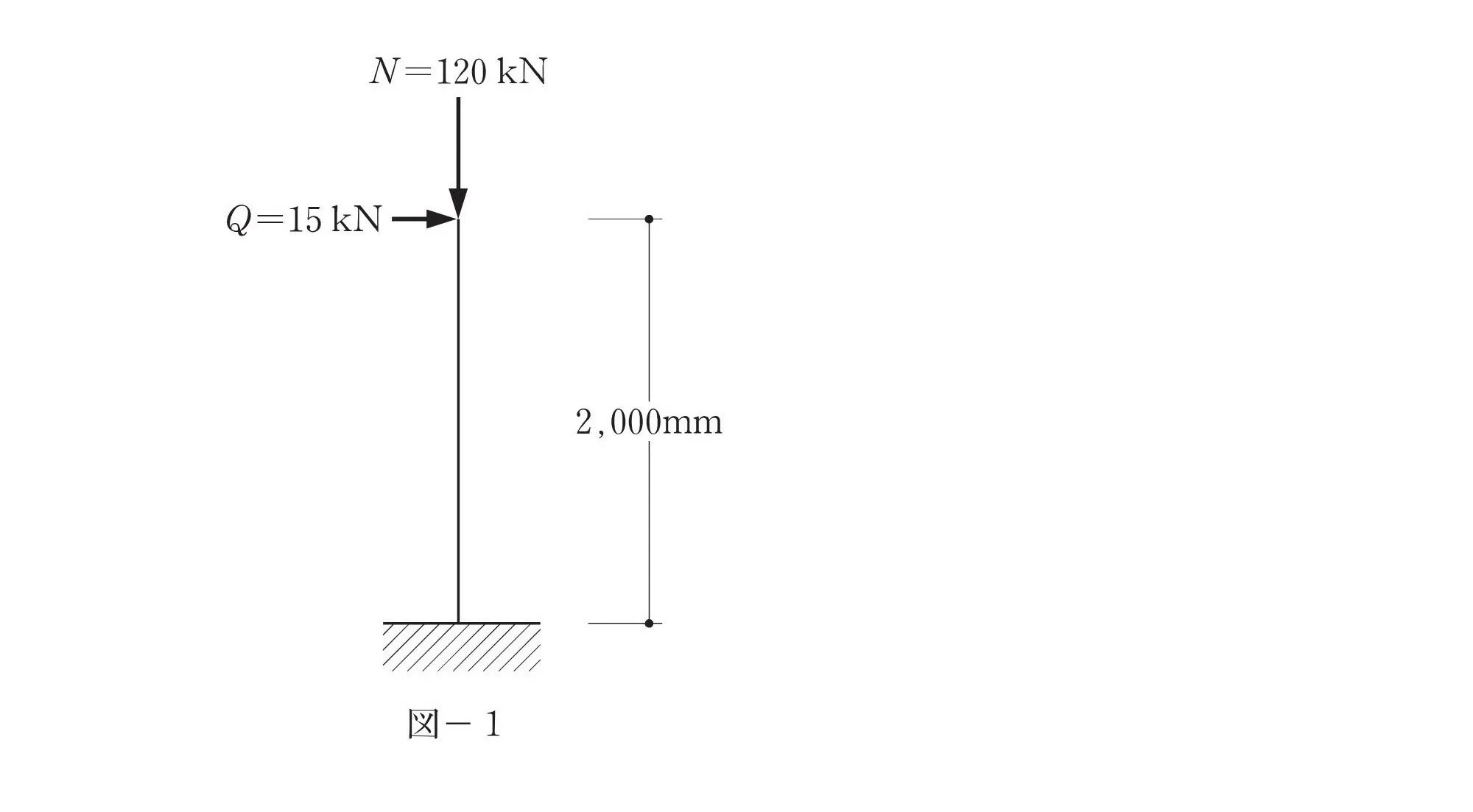
数値を代入する
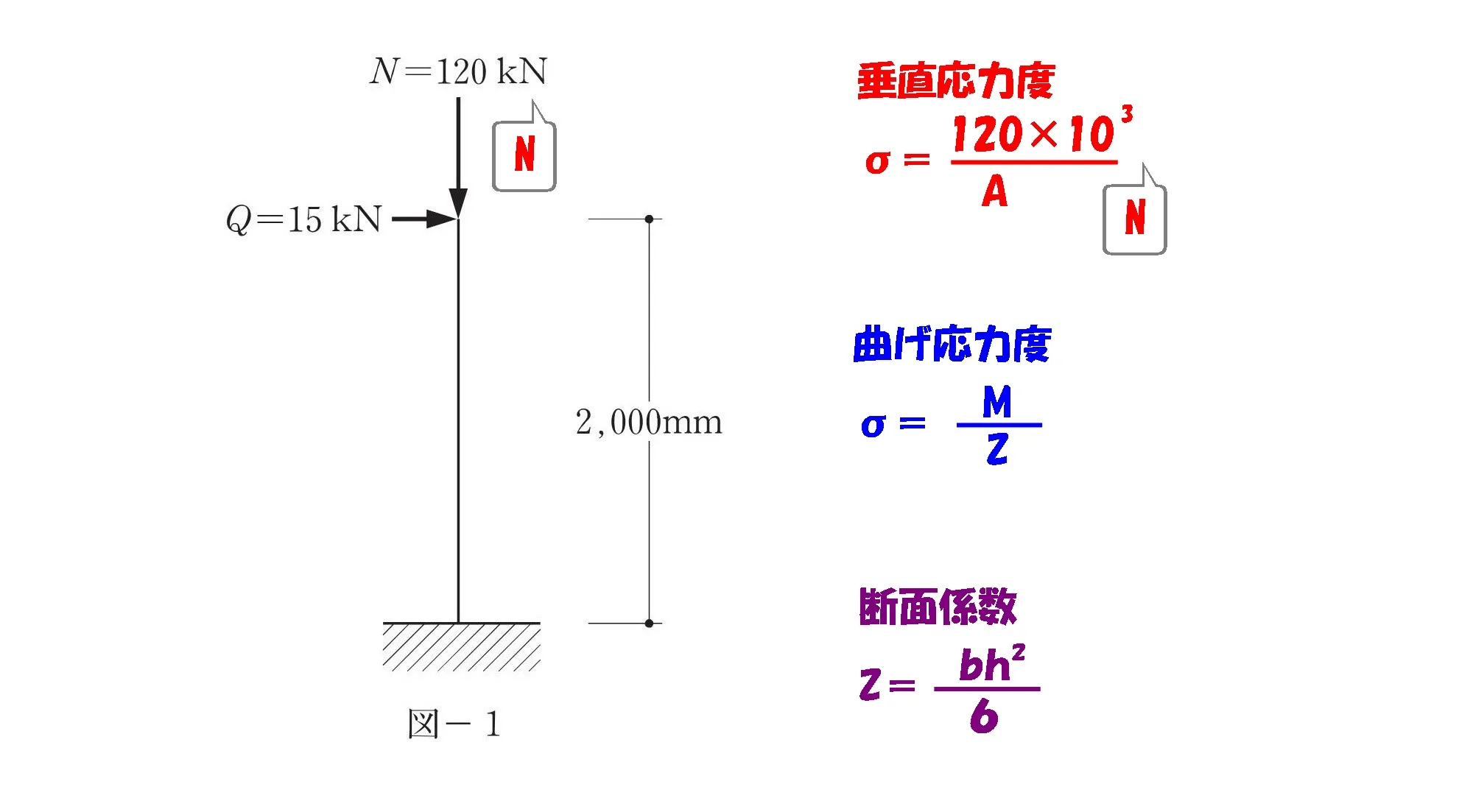

$$鉛直荷重:N=120[kN](120*10^3[N])より$$$$垂直応力度:\sigma=\frac{ 120*10^3 }{ A}[N/mm^2]$$
モーメントを求める
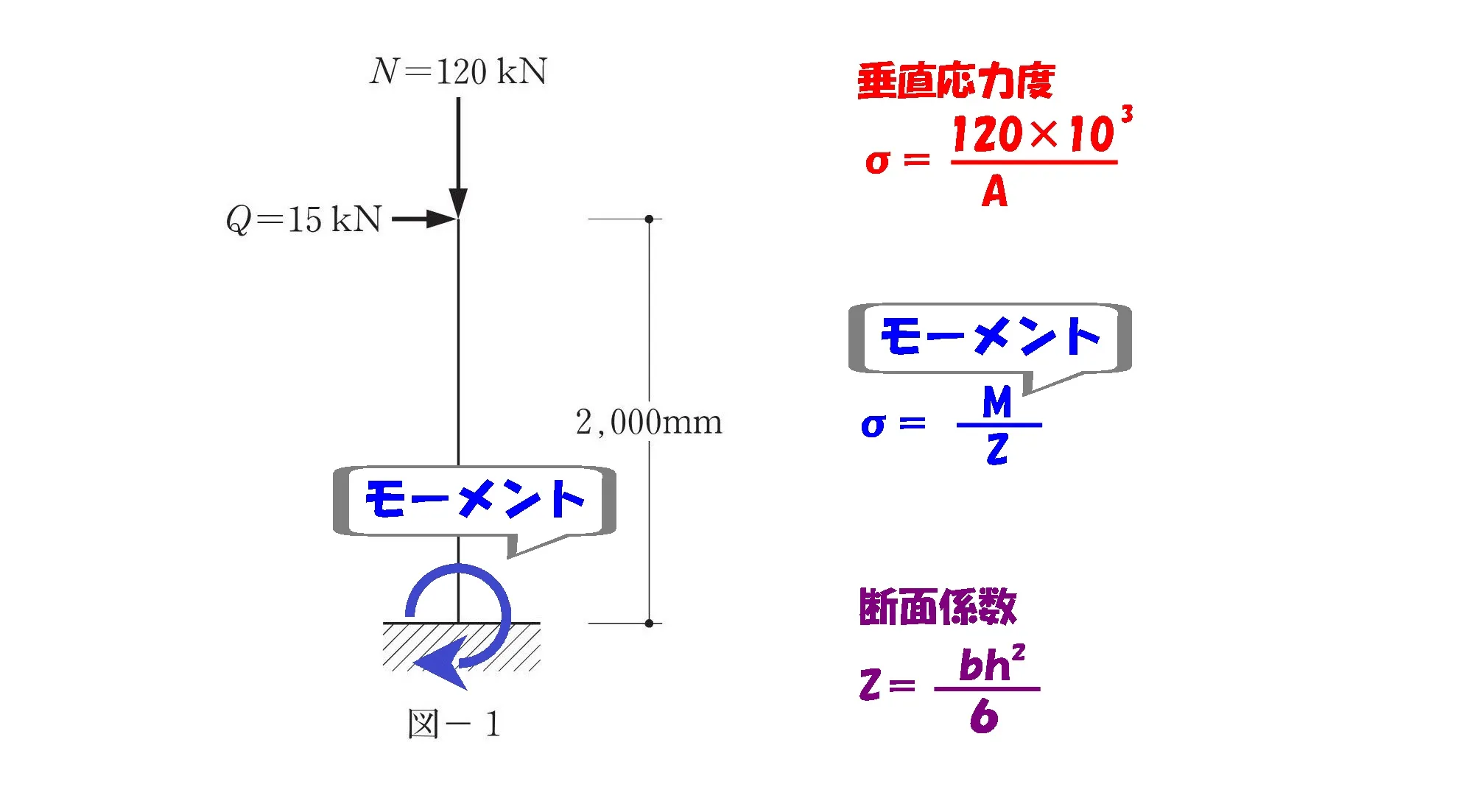

モーメント=力×距離
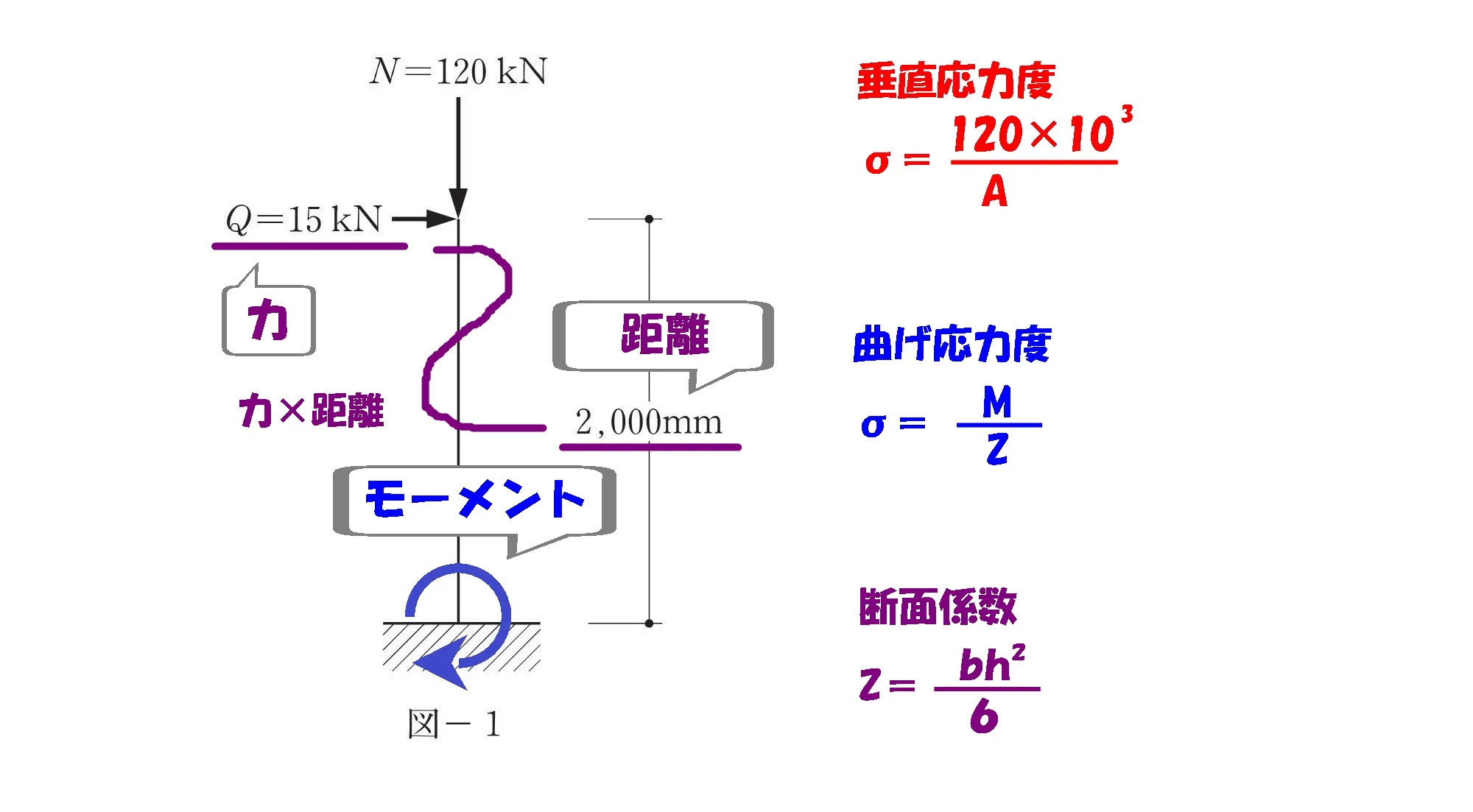

$$水平荷重(力):Q=15[kN](15*10^3N)$$$$柱の長さ(距離):L=2000[mm](2*10^3[mm])$$
モーメント=力×距離
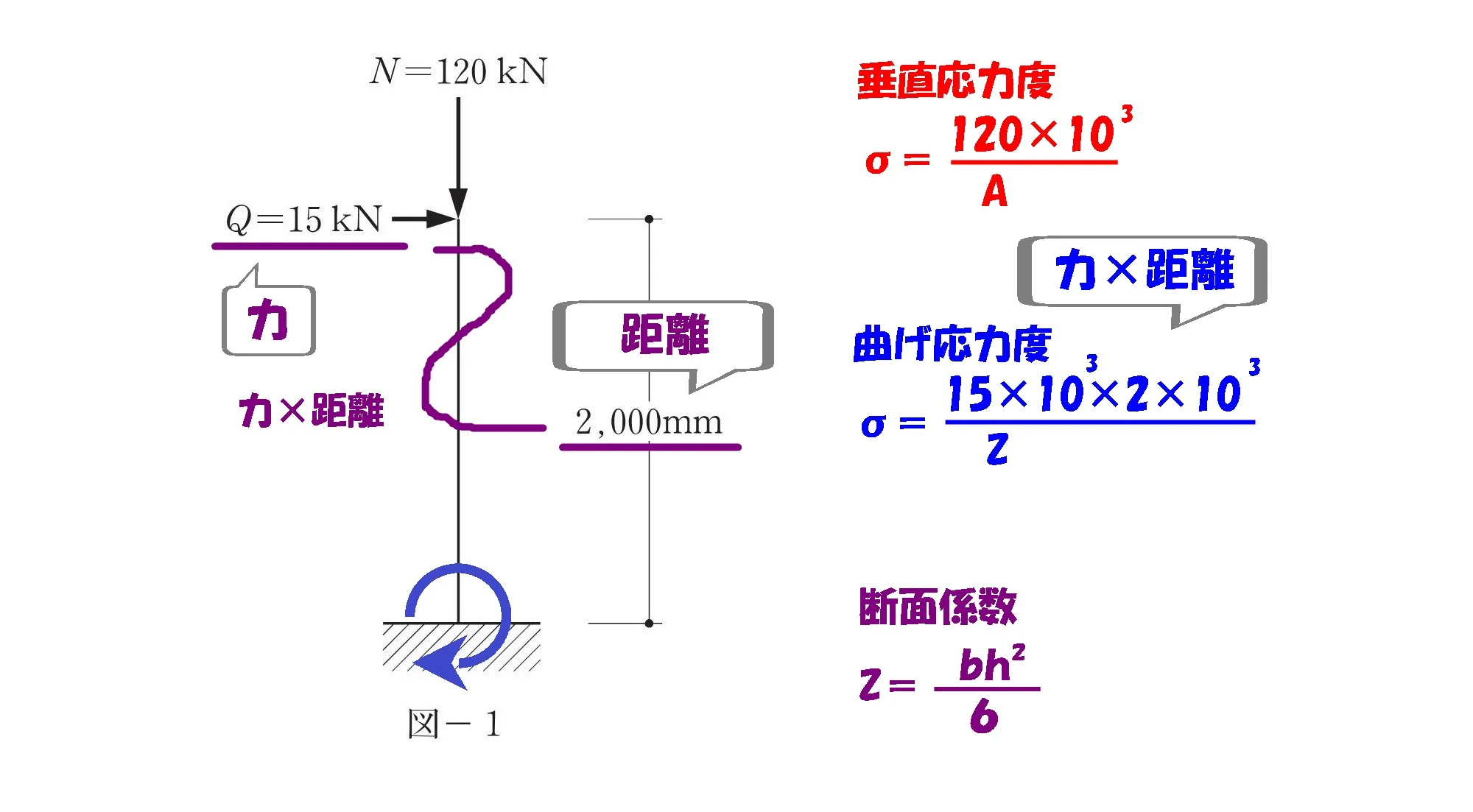

$$曲げ応力度:\sigma=\frac{ 15*10^3*2*10^3 }{ Z }[N/mm^2]$$
2.軸力による応力度:N/Aを求める
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
柱の断面A(面積)を求める
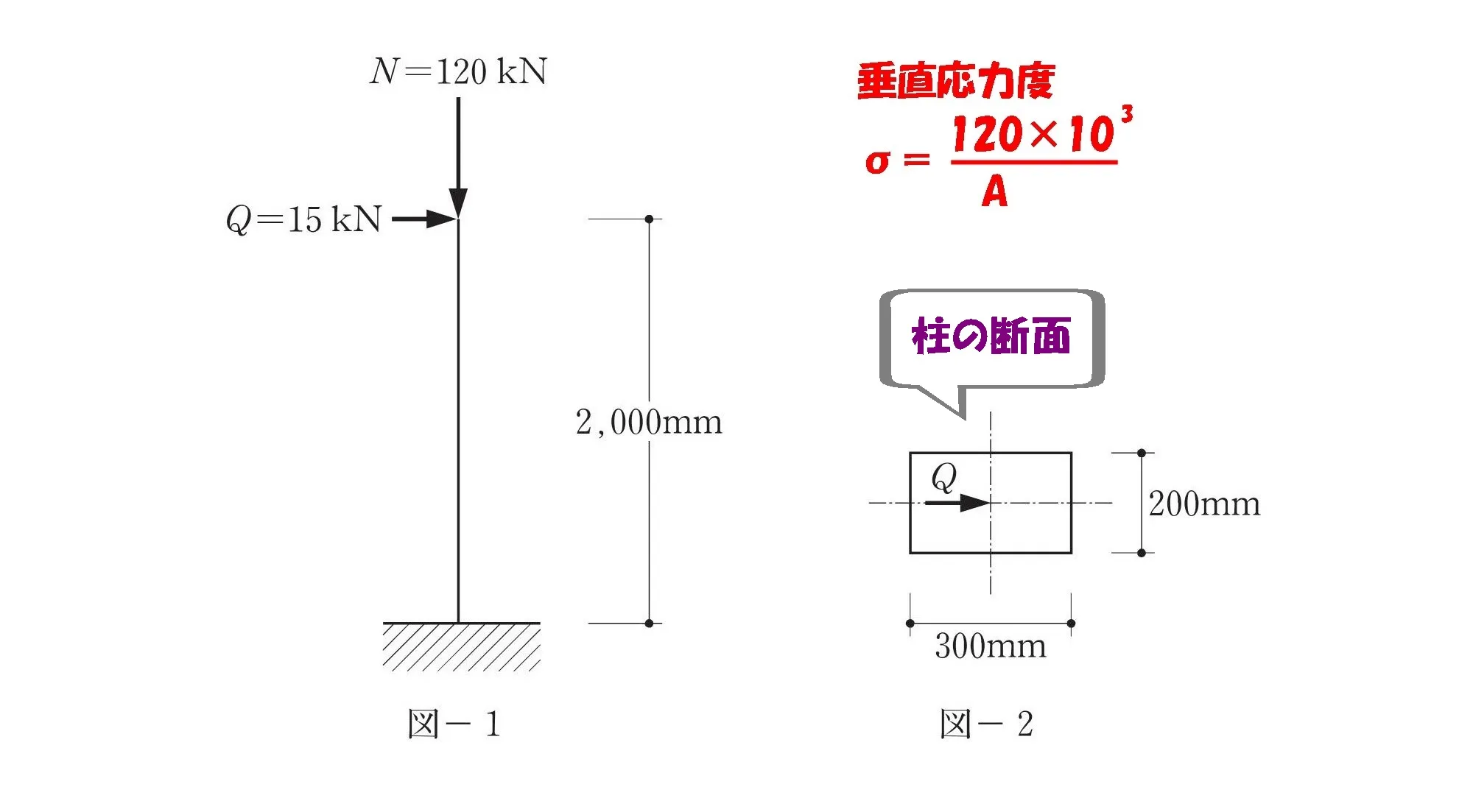

$$柱の断面(図-2)より、面積:A=300*200[mm^2]$$
垂直応力度を求める
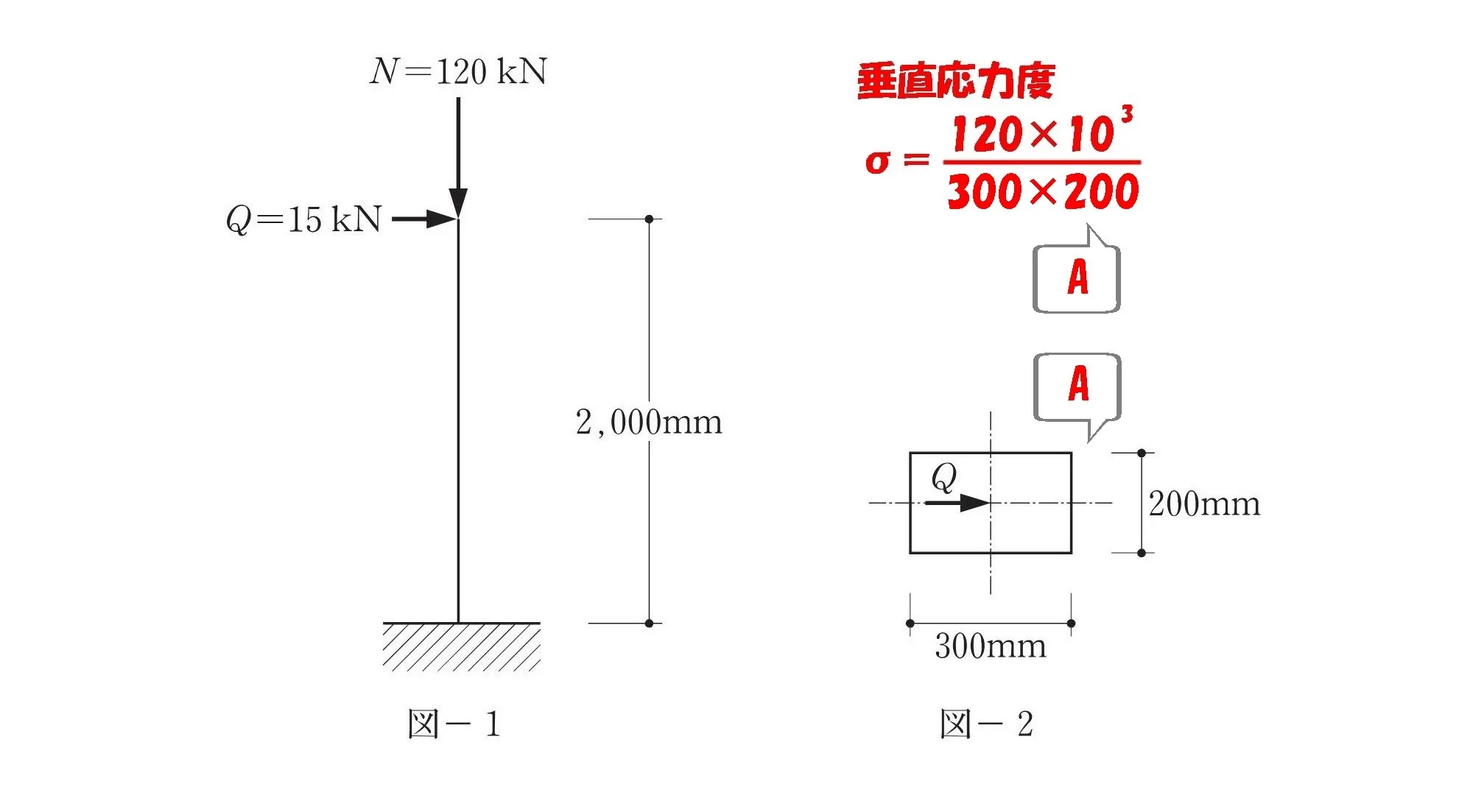

公式
$$軸力による応力度:\sigma=\frac{ N }{ A }[N/mm^2]$$
$$垂直応力度:\sigma=\frac{ 120*10^3 }{ 300*200}$$$$=\frac{ 12*10^4 }{ 3*2*10^4}=\frac{ 12 }{ 3*2}=2$$$$垂直応力度(圧縮):\sigma=-2[N/mm^2]$$


圧縮力はマイナス。
3.断面係数:bh²/6の式をつくる
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
断面係数を求める
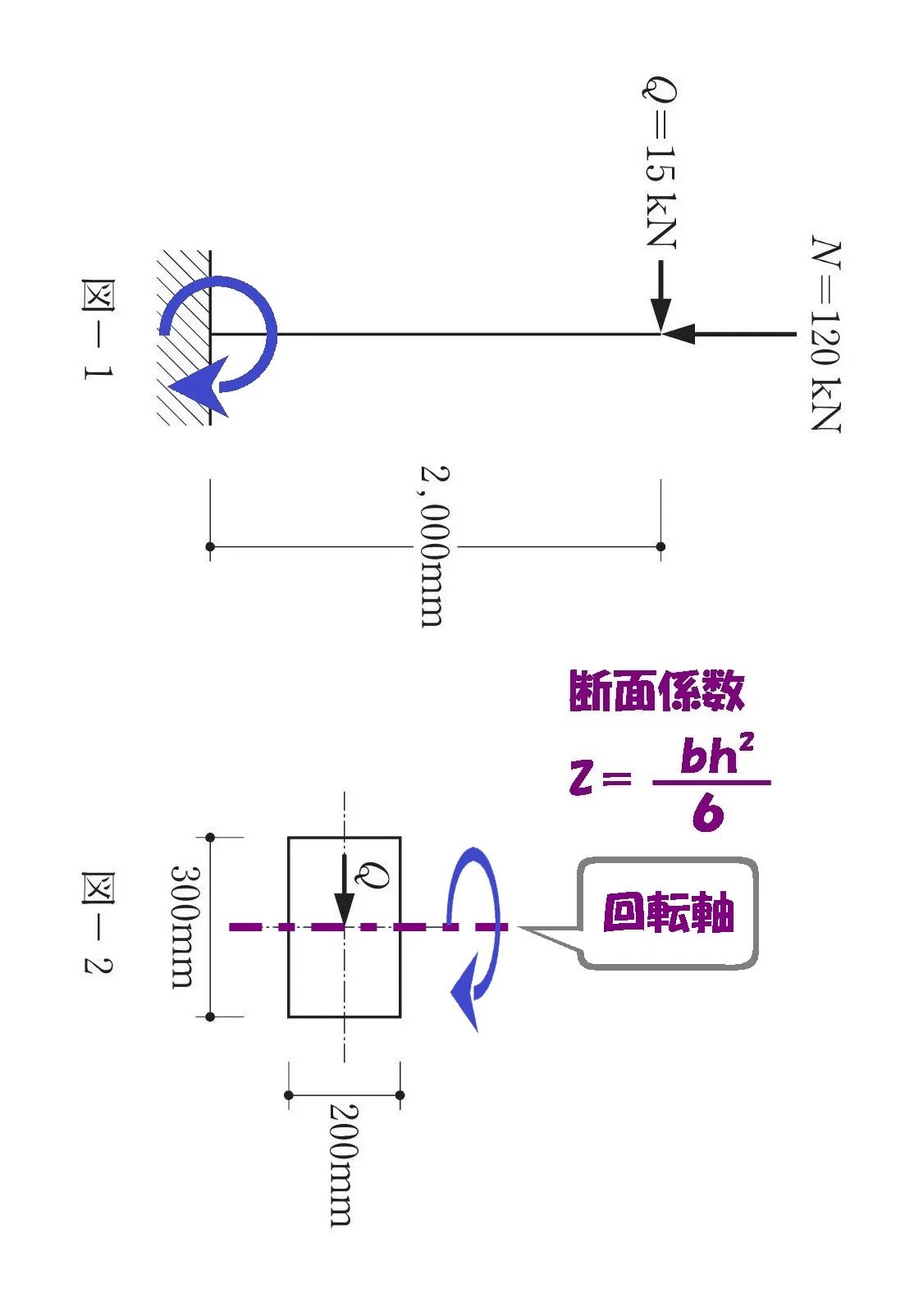

注意点
水平荷重Qの向きによって、柱断面(図-2)のbとhの位置づけが異なります。
柱に掛かるモーメントの回転軸はQに対して直交方向に取りましょう。



問題用紙を
90度回転させる。
b=200mm・h=300mm
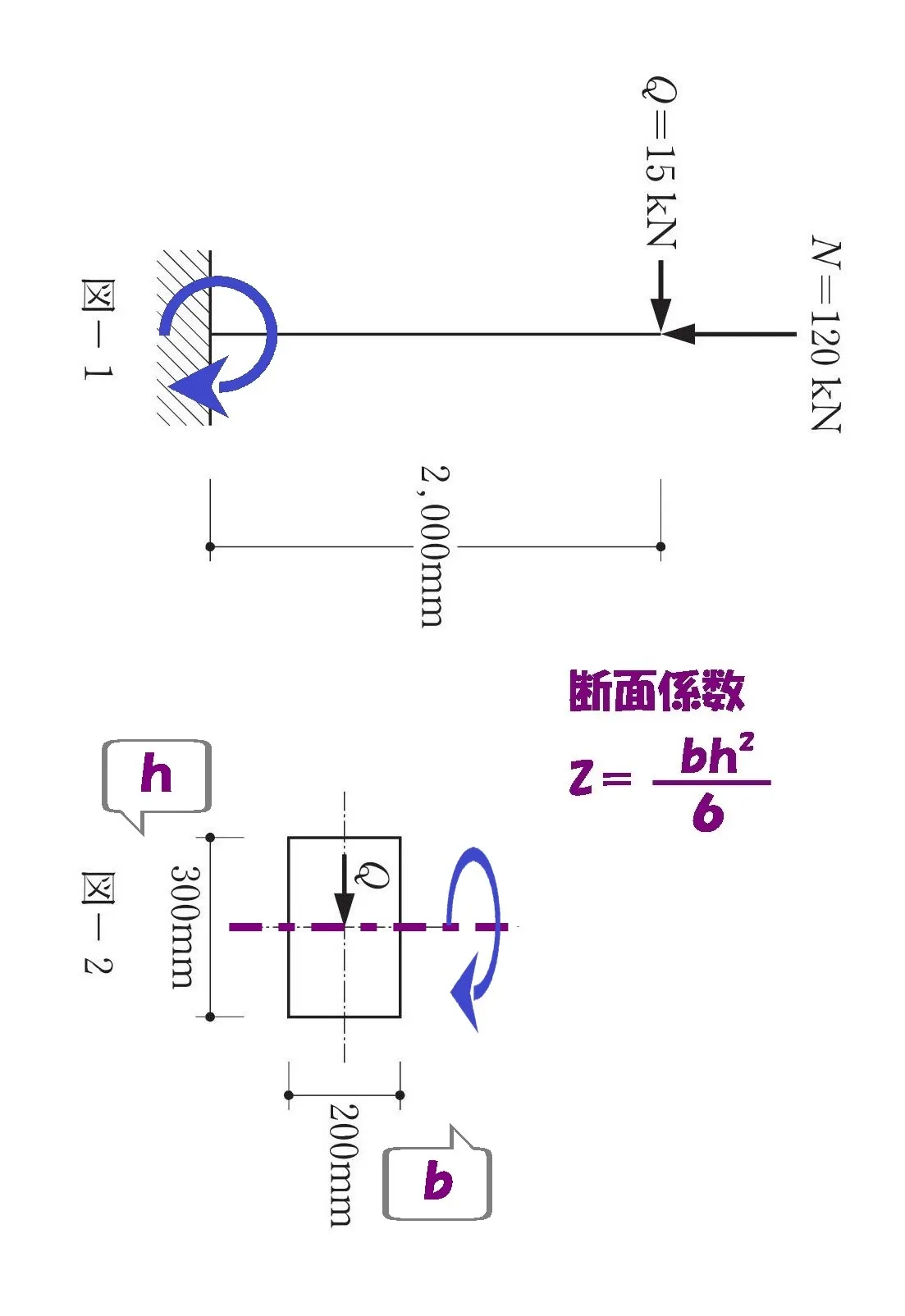

公式
$$断面係数:Z=\frac{ bh^2 }{ 6 }[mm^3]$$
$$柱に掛かるモーメントの回転軸はQに対して直交方向$$$$b=200mm,h=300mm$$
$$断面係数:Z=\frac{ bh^2 }{ 6 }より,Z=\frac{ 200*(300)^2 }{ 6 }$$
4.曲げ力による応力度:M/Zを求める
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
モーメントを求める。
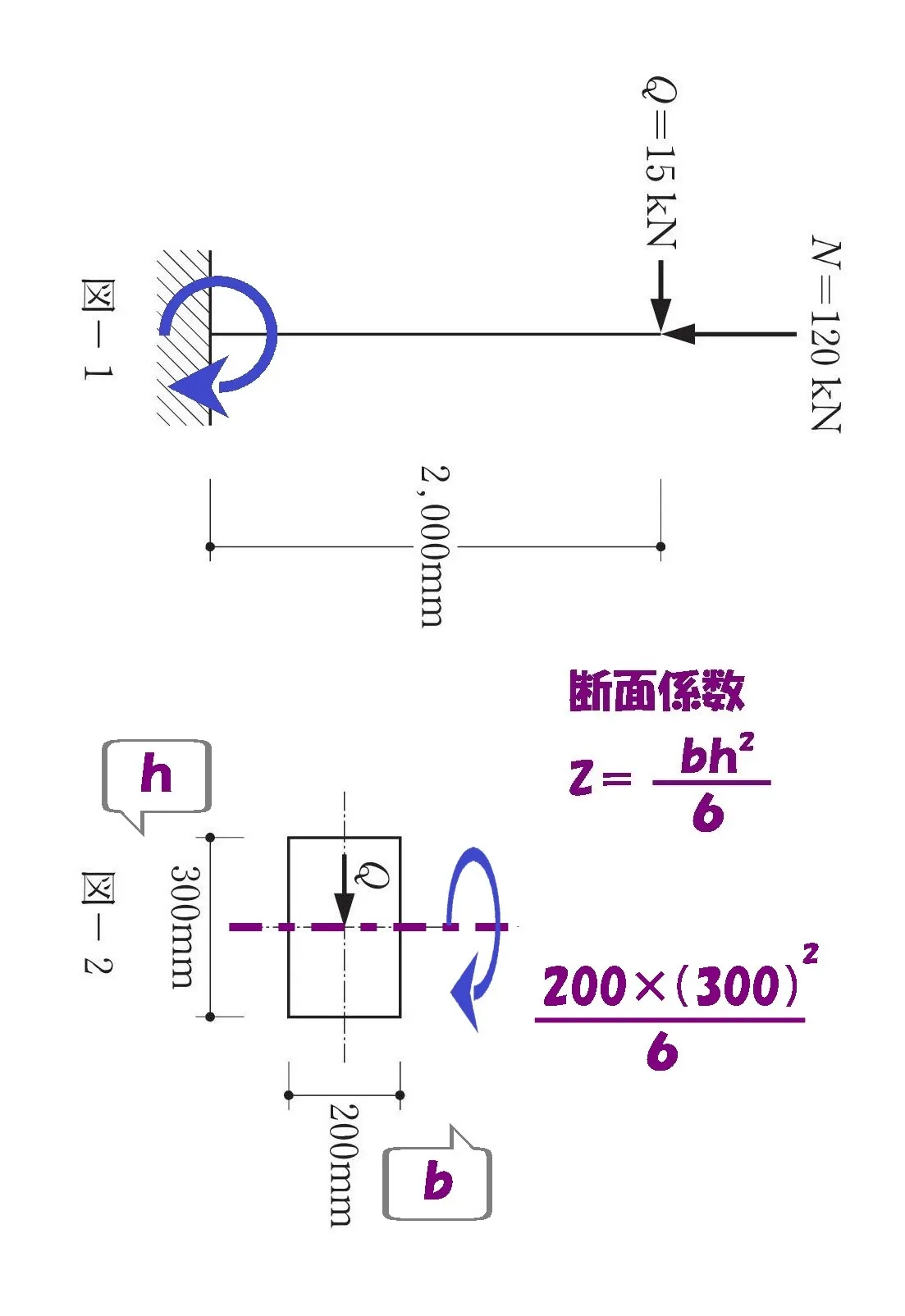

公式
$$曲げ応力度:\sigma=\frac{ M }{ Z }[N/mm^2]$$
$$断面係数:Z=\frac{ bh^2 }{ 6 }より$$$$Z=\frac{ 200*(300)^2 }{ 6 }$$
$$曲げ応力度:\sigma=\frac{ M }{ Z }より$$$$\frac{ 15000*2000 }{ 200*(300)^2/6 }=\frac{ 15*10^3*2*10^3 }{ 200*(300)^2/\underline{6} }=\frac{ 15*10^3*2*10^3*\underline{6} }{ 200*(300)^2 }$$$$=\frac{ \underline{(15)}*10^3*2*10^3*\underline{(6)} }{ \underline{200*(300)^2} }=\frac{ \underline{(3*5)}*10^3*2*10^3*\underline{(2*3)} }{ \underline{200*300*300} }$$$$=\frac{ \underline{(3*5)}*2*\underline{(2*3)}*10^6 }{ \underline{(2*3*3)}*10^6 }=\frac{ \underline{(2*3*3)}*2*5*\underline{10^6} }{ \underline{(2*3*3)}*\underline{10^6} }=2*5=10[N/mm^2]$$
5.応力度を合成する(ーN/A±M/Z)
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)
応力度を合成する


応力度の公式
$$垂直応力度:\sigma=\frac{ N }{ A}[N/mm^2]$$
$$曲げ応力度:\sigma=\frac{ M }{ Z }[N/mm^2]$$
圧縮(-)、引張り(+)
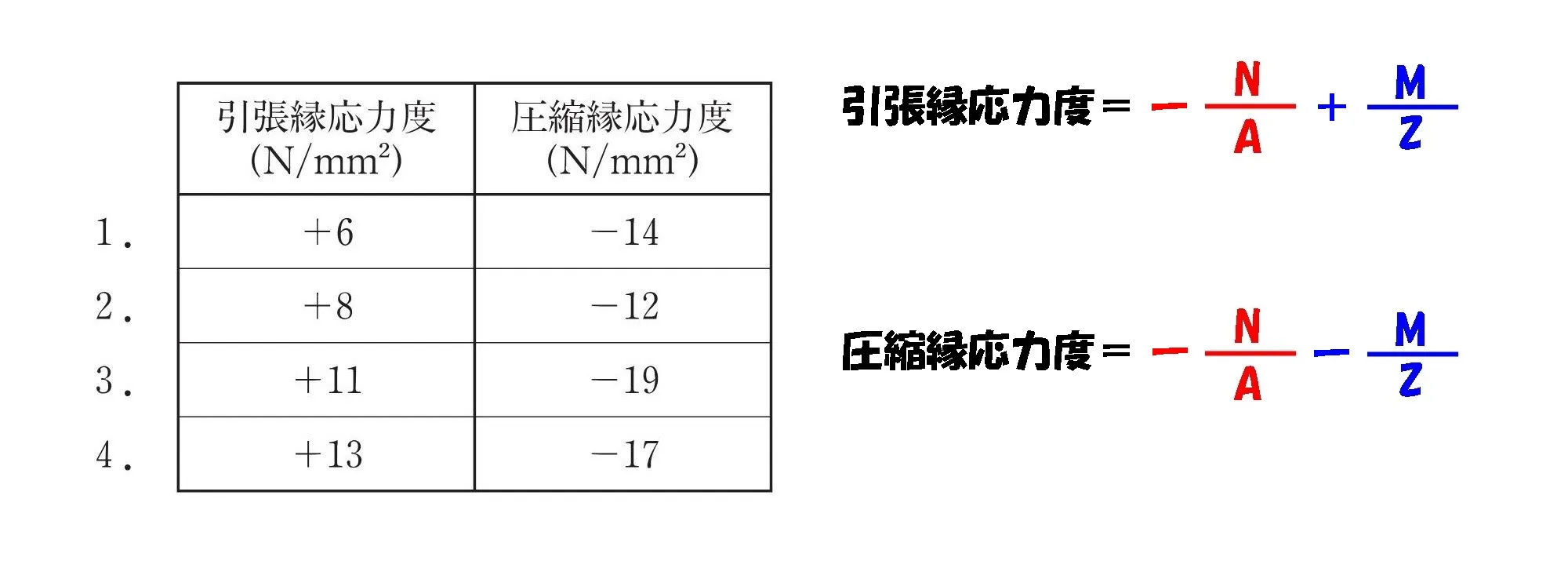

応力度の合成
$$引張縁応力度:\sigma=-\frac{ N }{ A }+\frac{ M }{ Z }$$$$圧縮縁応力度:\sigma=-\frac{ N }{ A }-\frac{ M }{ Z }$$



応力度を合成させる。
N/A、M/Zを代入する


$$引張縁応力度:\sigma=-\frac{ N }{ A }+\frac{ M }{ Z }=-2+10=+8[N/mm^2]$$$$圧縮縁応力度:\sigma=-\frac{ N }{ A }-\frac{ M }{ Z }=-2-10=-12[N/mm^2]$$
答え.2


攻略ポイント
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)


この動画を YouTube で視聴
全塑性モーメント
難易度:★★★☆☆
この問題では、軸力と曲げ力が同時に作用する部材の応力度を読み解きます。
断面形状や応力度分布から「軸力」と「曲げ力」の2つに分ける作業が、肝となるポイントです。



軸力



曲げ力



2つの力を合成する。
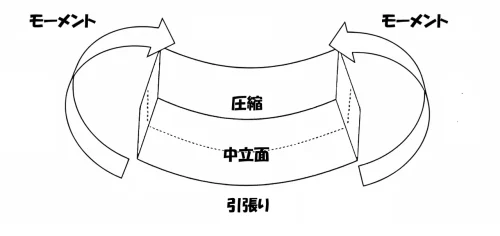
全塑性とは?

塑性イメージ
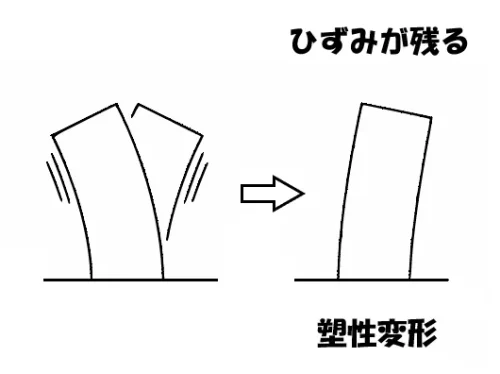

- 建物+外力→建物が変形する。
- 建物-外力(外力を取り除く)→建物にひずみが残る状態。
建物に及ぼす外力を取り除いたときに、建物に変形した状態が残る性質を「塑性」といいます。
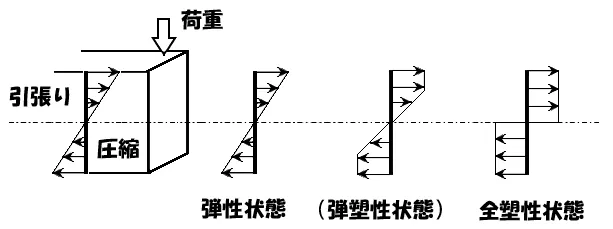

部材に加わる荷重を大きくする
- 弾性状態
- 変形が進む
- 全塑性状態
部材に荷重を加えると、応力度分布は中立軸を起点に縁に向かって大きく伸びていきます。
圧縮と引張の応力度分布が中立軸まで到達したときに、部材は完全に塑性化した(全塑性状態)ということになるのです。



う~ん。呼吸を整えて・・・
後でじっくり解釈しよう。
全塑性モーメントの分布

攻略ポイント
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
問題
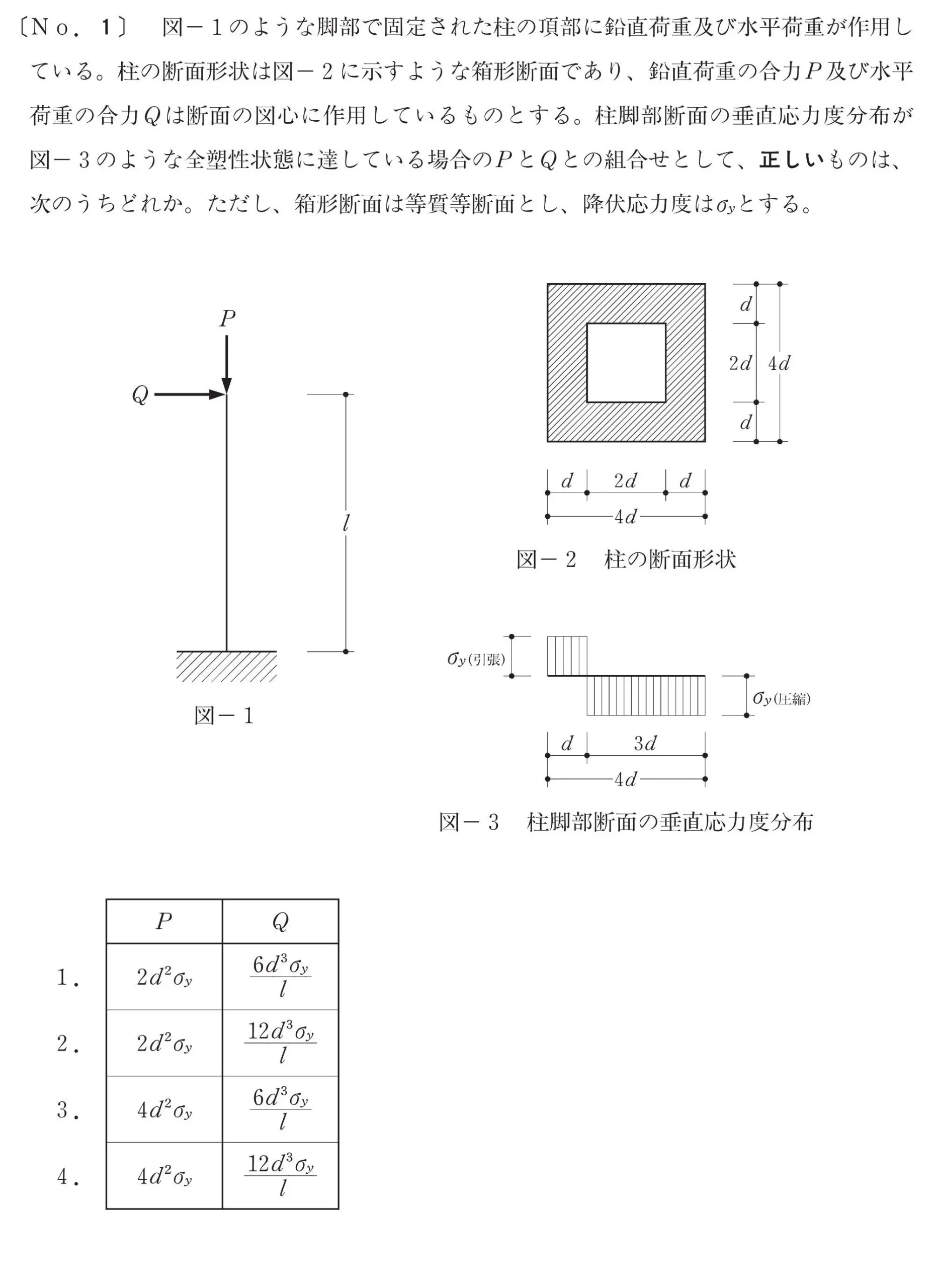

1.モーメント=力×距離
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
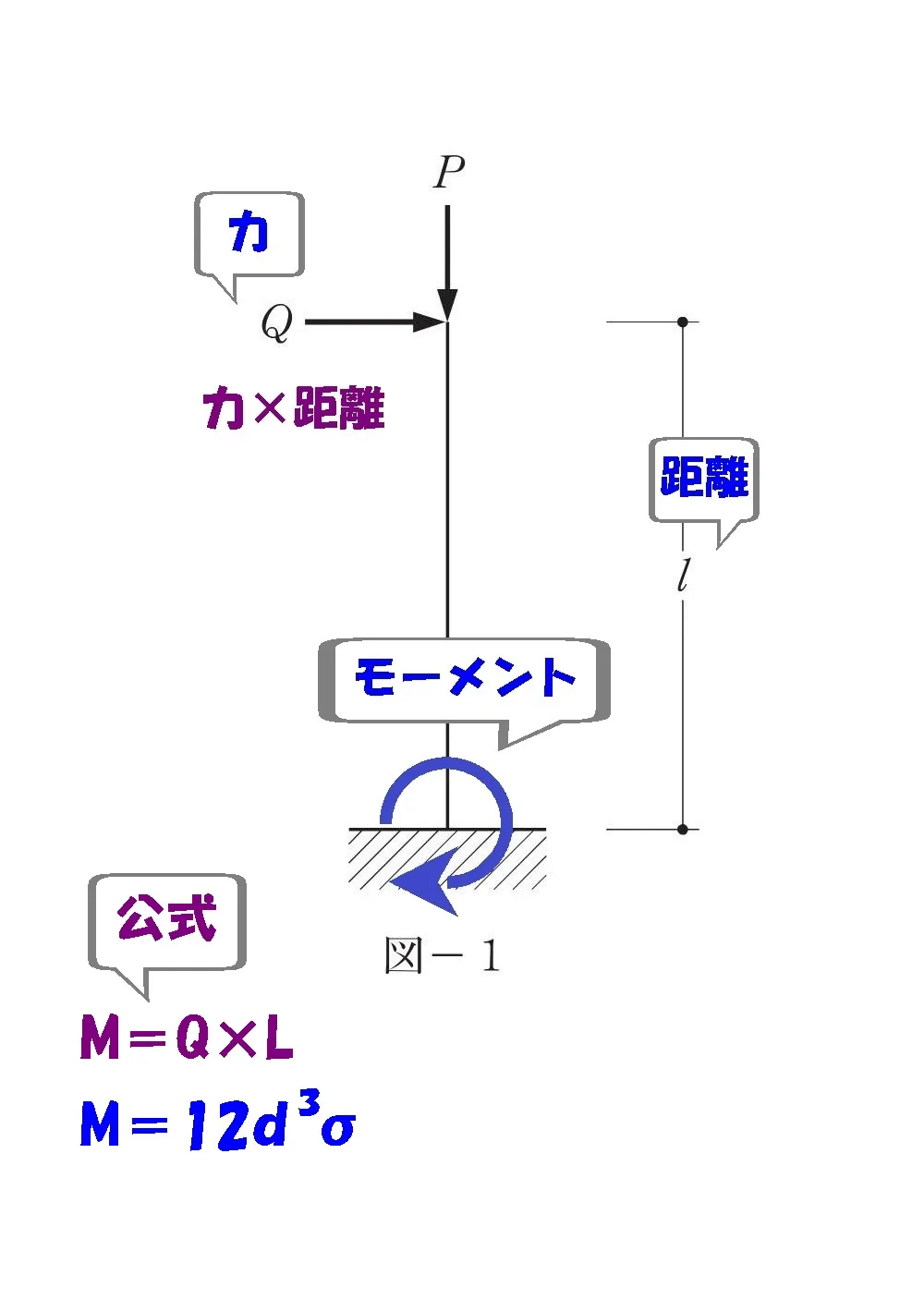
モーメントを求める
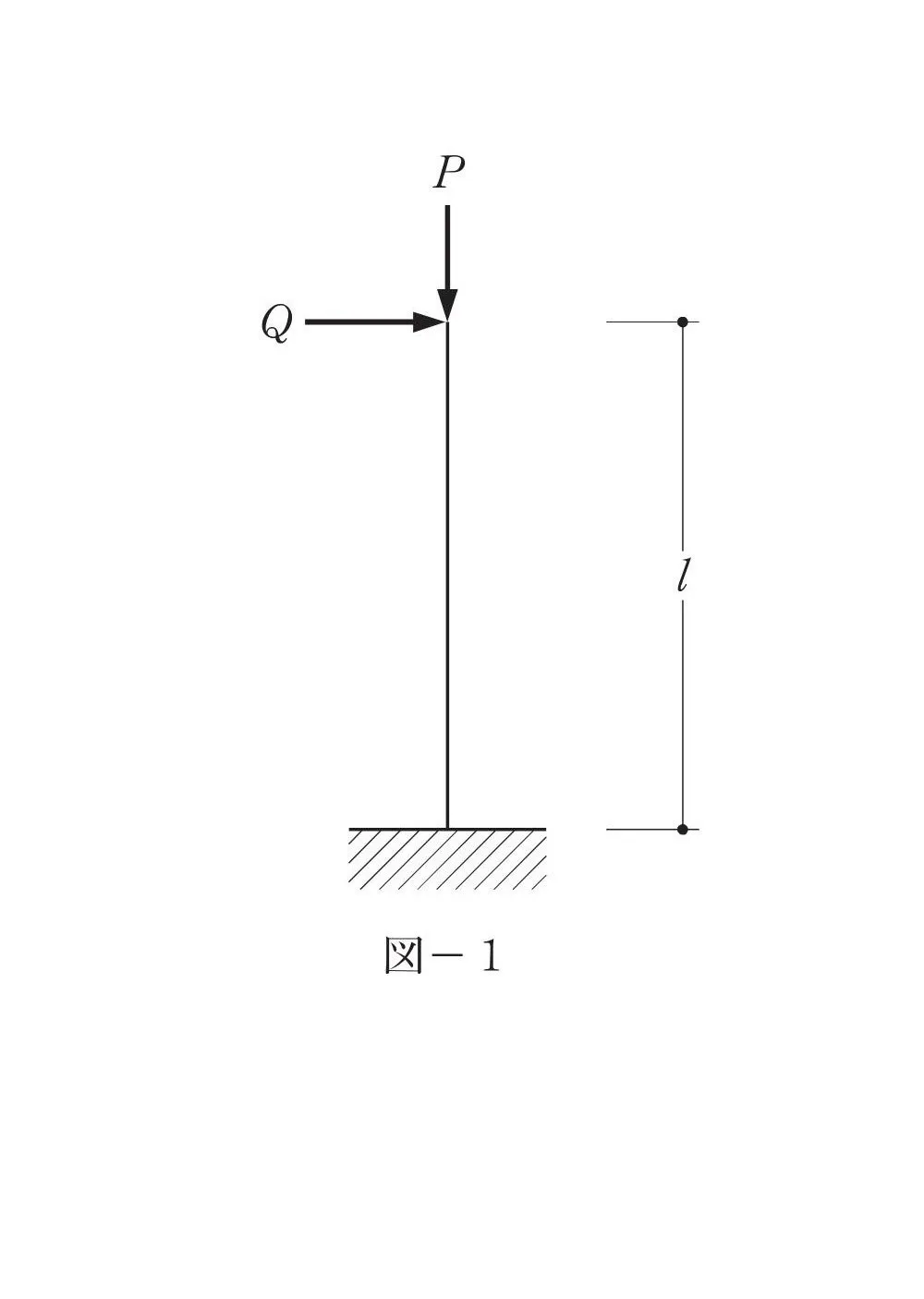

水平荷重Q(力)向きは左 ⇨ 右
モーメント=力×距離
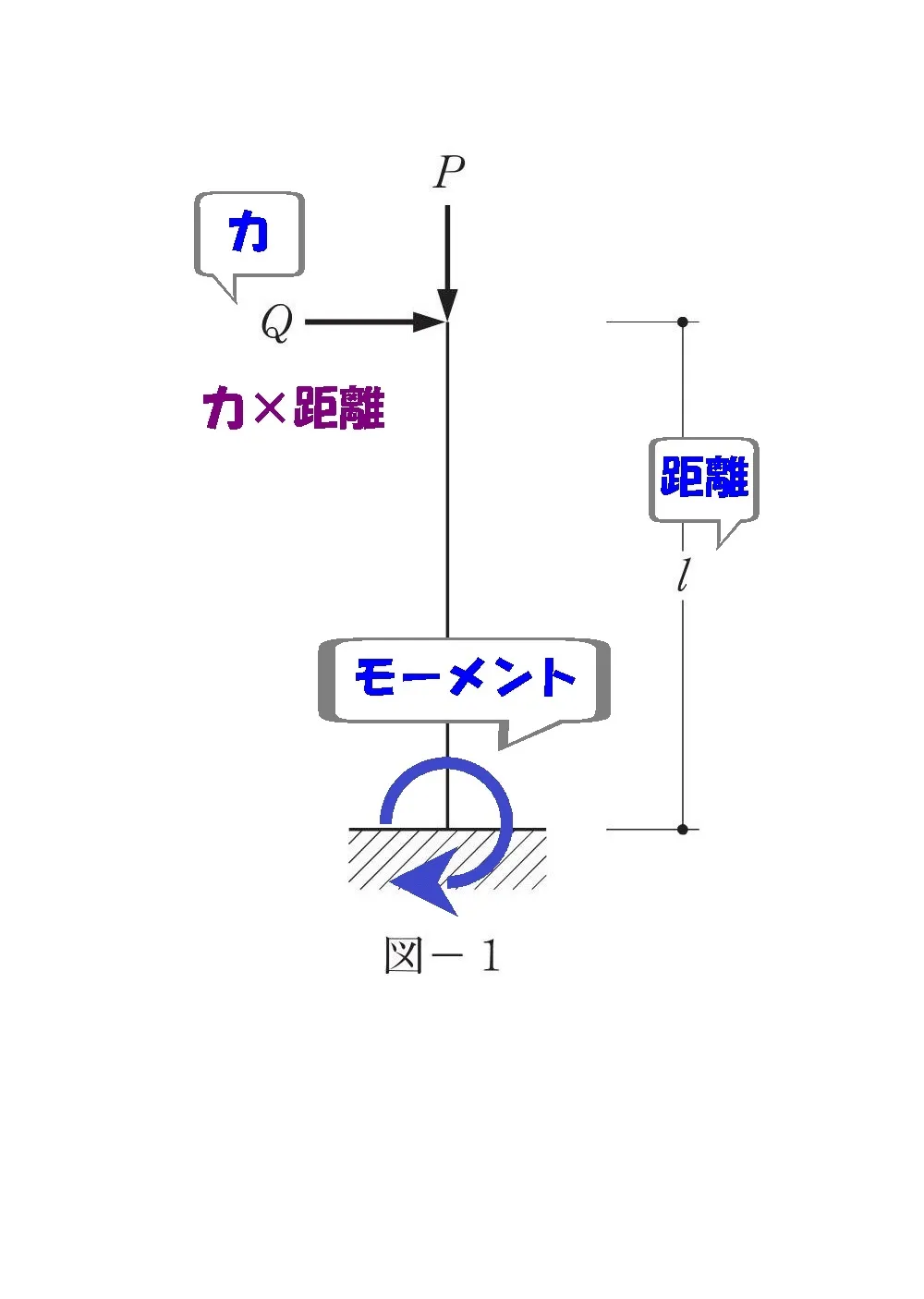

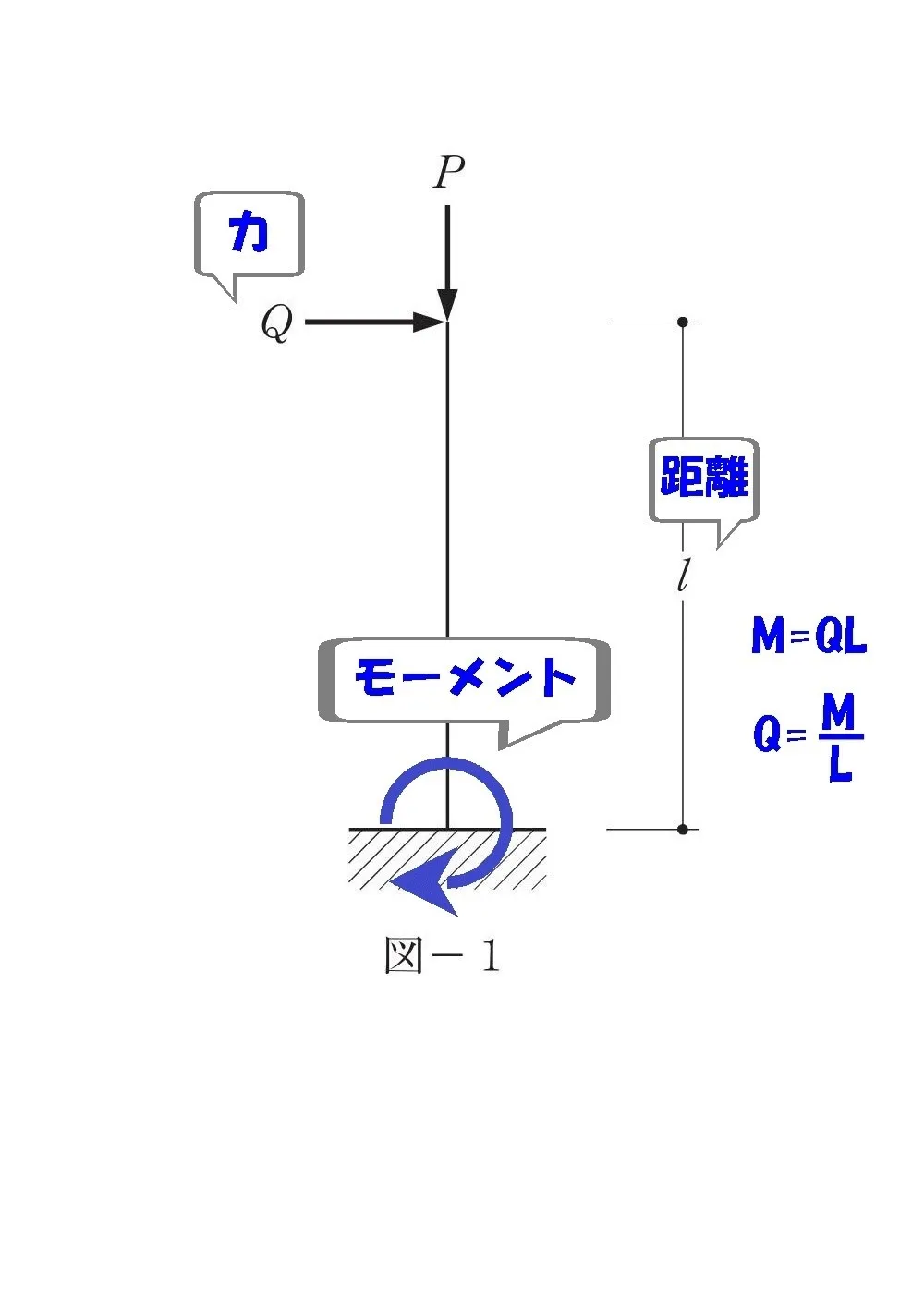

$$M=Q*Lより,Q=\frac{ M }{ L }$$
$$M:モーメント,Q:水平荷重(力),L:部材の長さ(距離)$$
公式
$$モーメント=力×距離$$
2.断面形状を軸力と曲げ力に分ける
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
断面形状の読み方
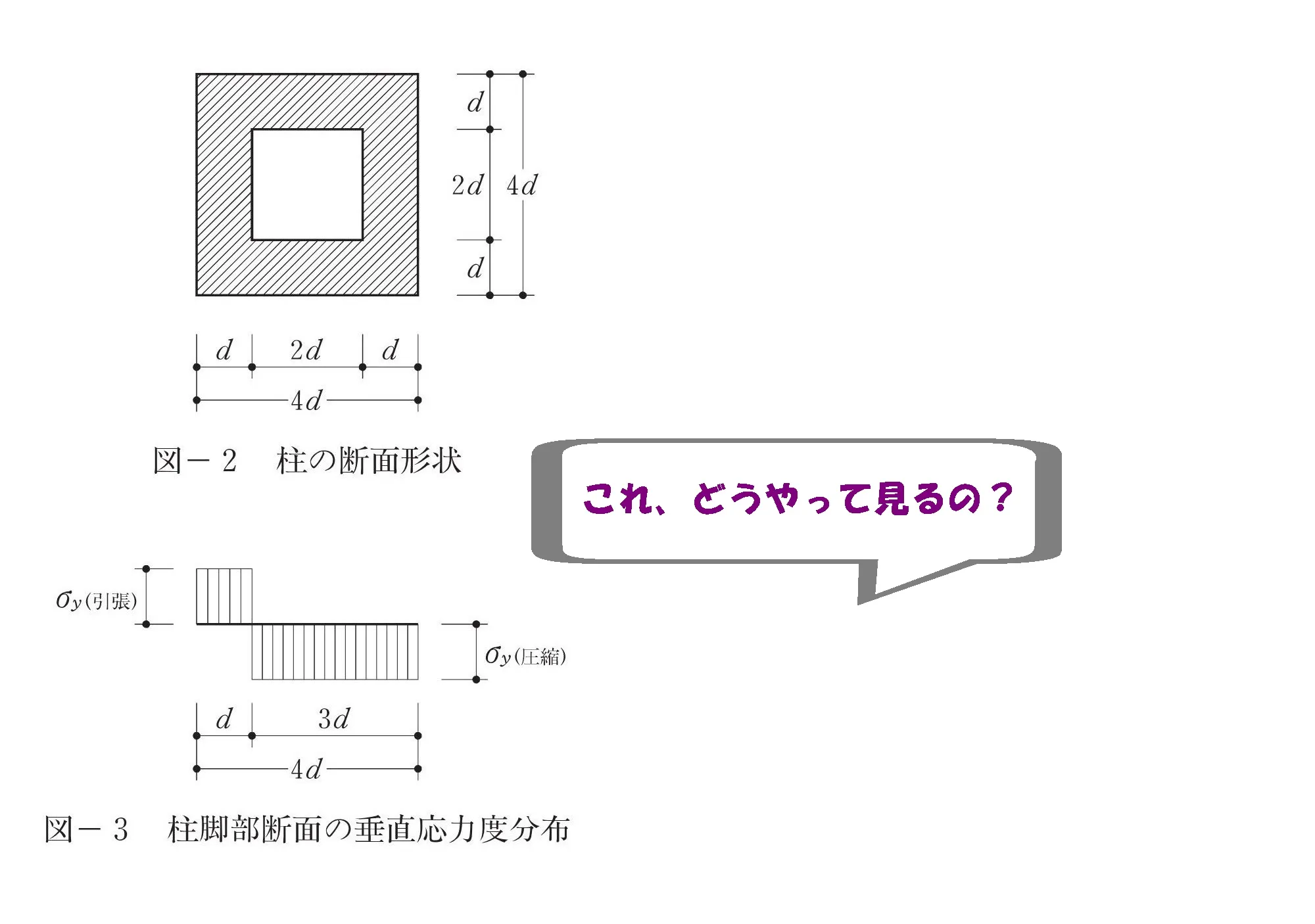




これ、
どうやって見るの?
「これ、どうやって見るの?」図-2の見方について解説していきましょう。


水平荷重Q(力)向きは左 ⇨ 右
柱の断面形状を分割する
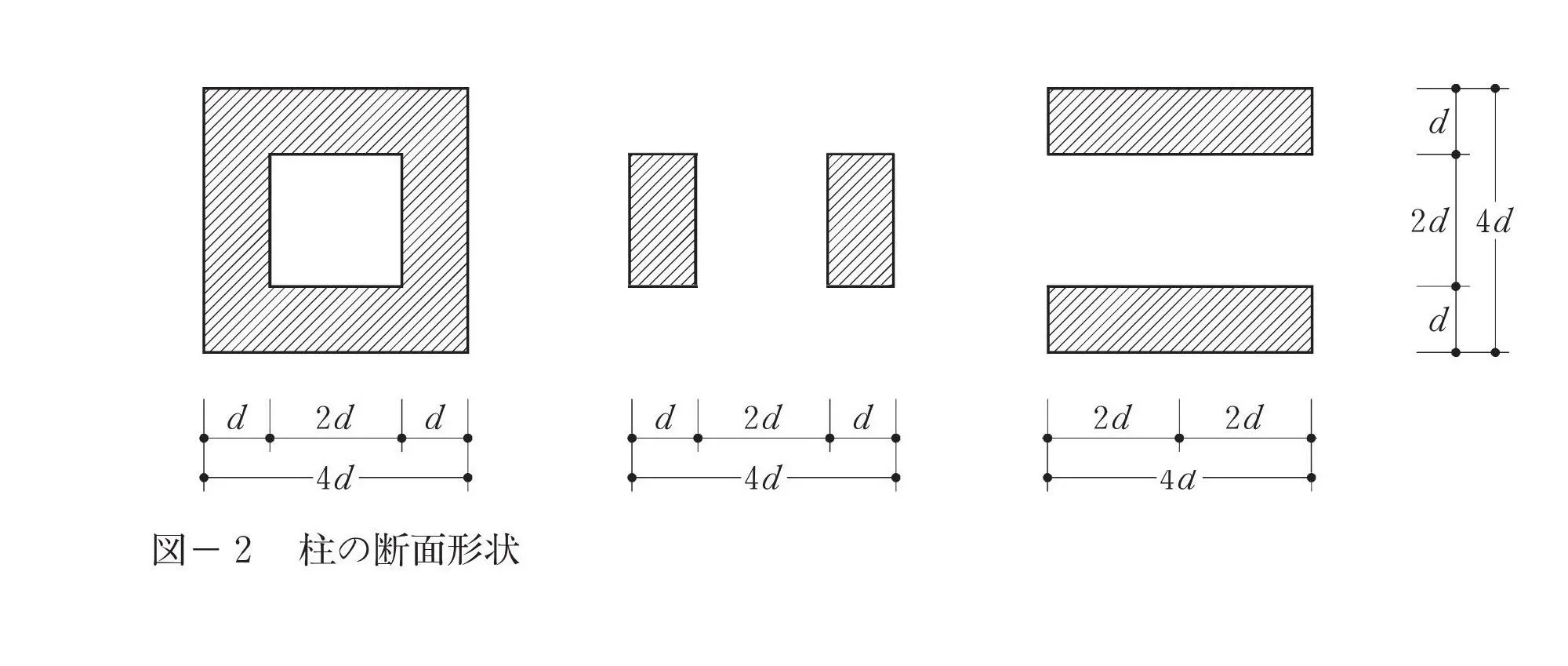

「水平荷重Q(力)向きは左 ⇨ 右」を踏まえて柱の断面形状を2つに分割します。
3.応力度に作用する断面積を求める
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める


水平荷重Q(力)向きは左 ⇨ 右



力の向きは左 ⇨ 右
モーメントの曲がり軸
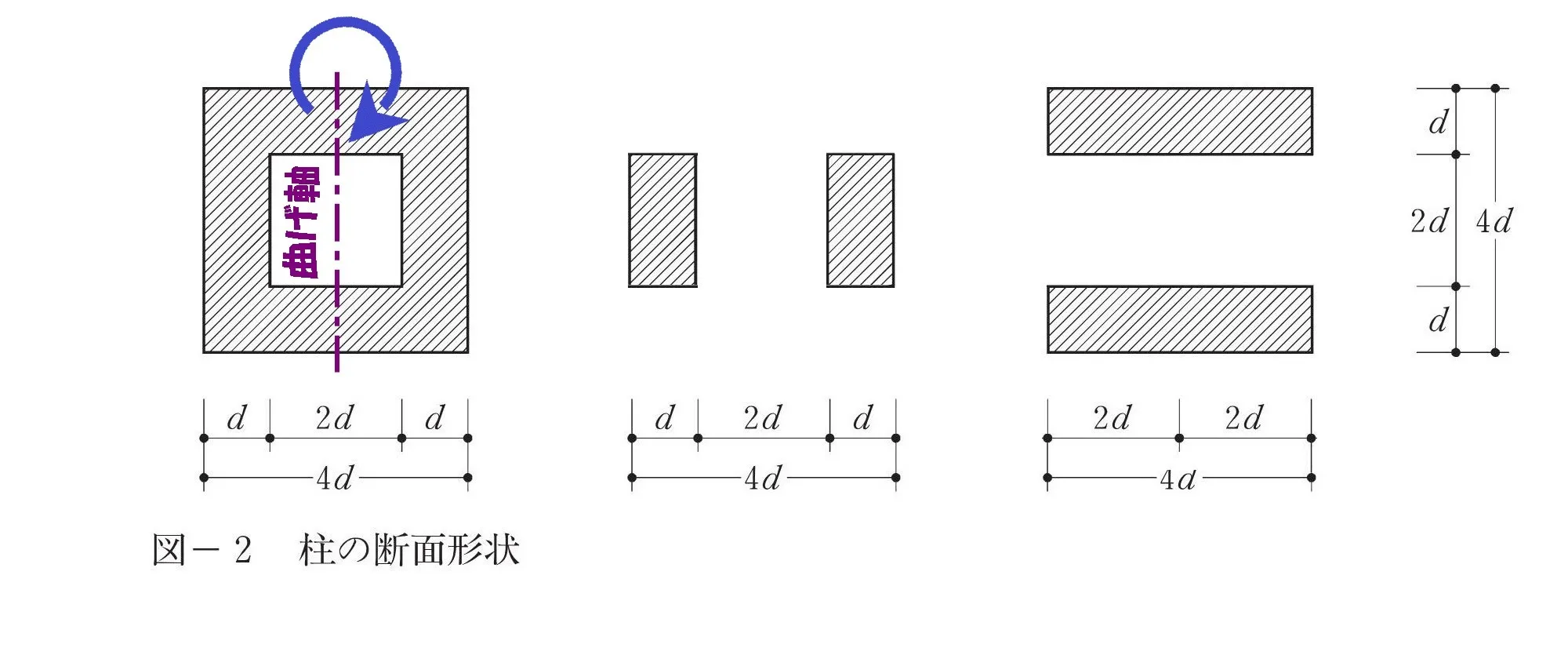

部材は「左 ⇨ 右に曲がる」ことから、モーメントの曲がり軸はQに対して直交方向に取ります。
垂直応力度の断面
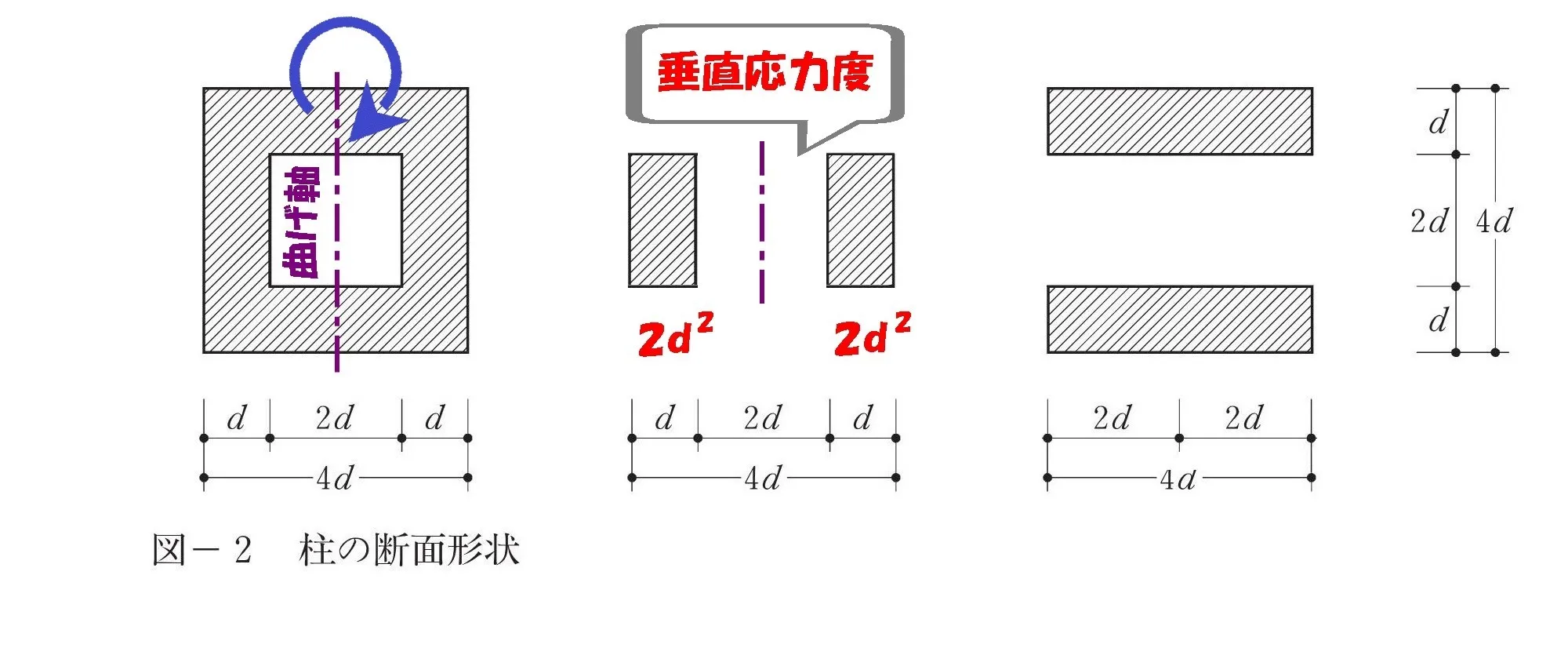

垂直応力度の断面は「曲がり軸と交わらない」断面形状となります。
$$(垂直応力度の断面積=d*2d+d*2d)$$
曲げ応力度の断面
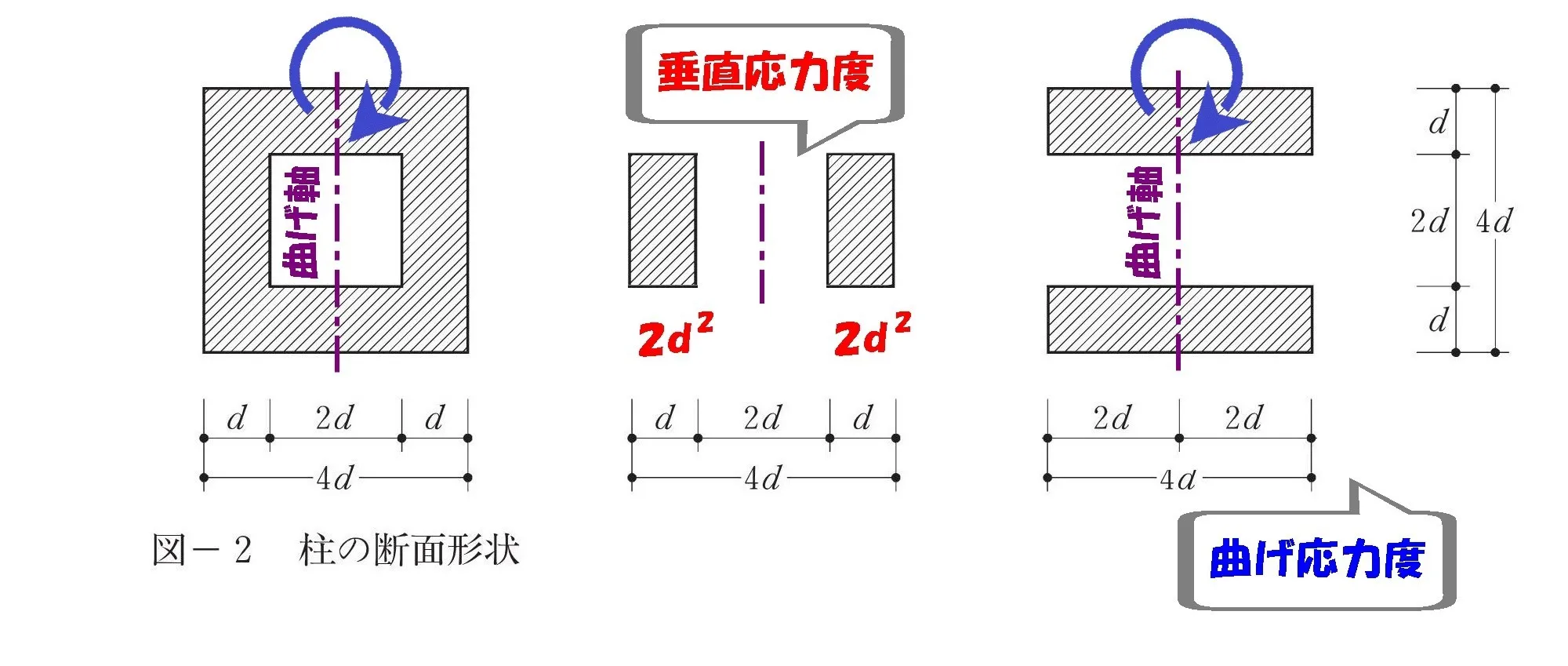

曲げ応力度の断面は「曲がり軸と交わる」断面形状となります。
曲げ応力度の断面積
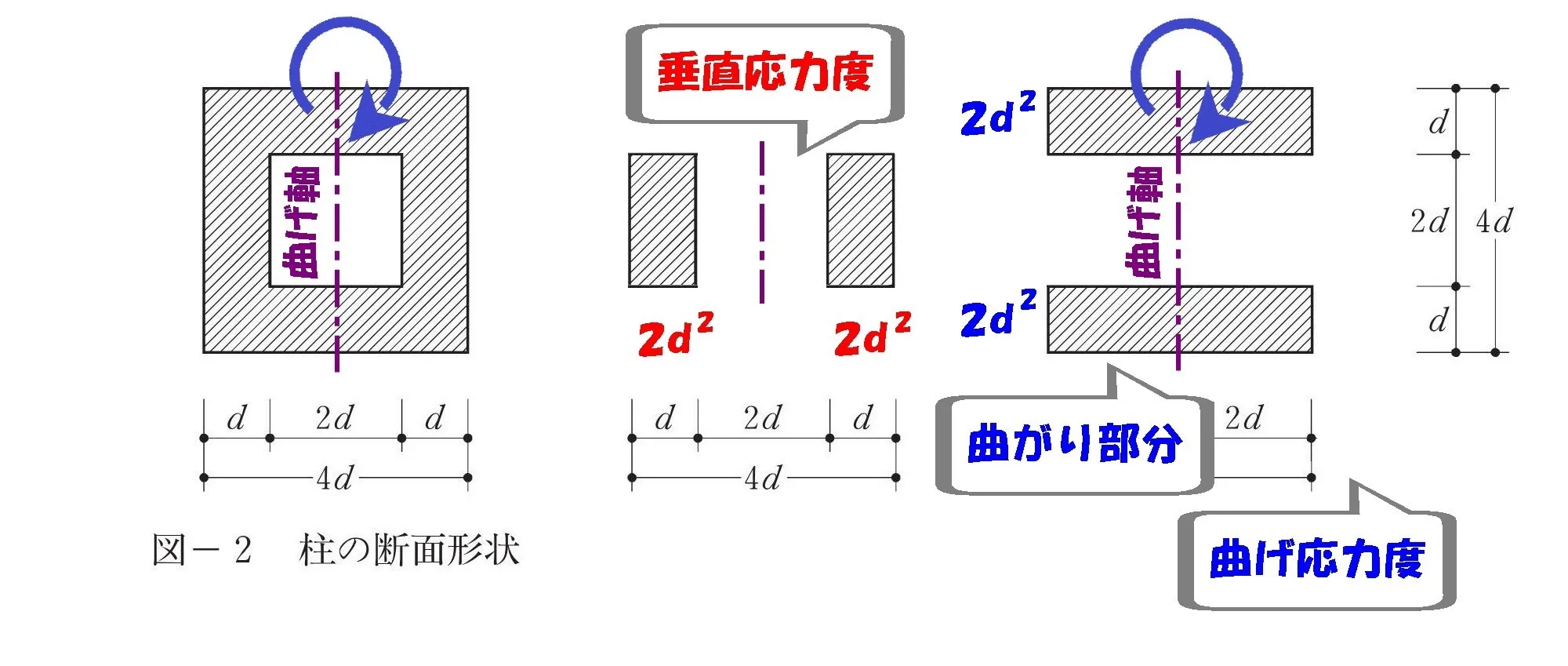

$$(曲げ応力度の断面積=2d*d+2d*d)$$
注意!
※「4d*d+4d*d」ではありません。
モーメントは”偶力”により、部材の断面に働きかけるものだからです。
(詳しくは後ほど解説しましょう。)
4.応力度分布を軸力と曲げ力に分ける
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
応力度分布の読み方
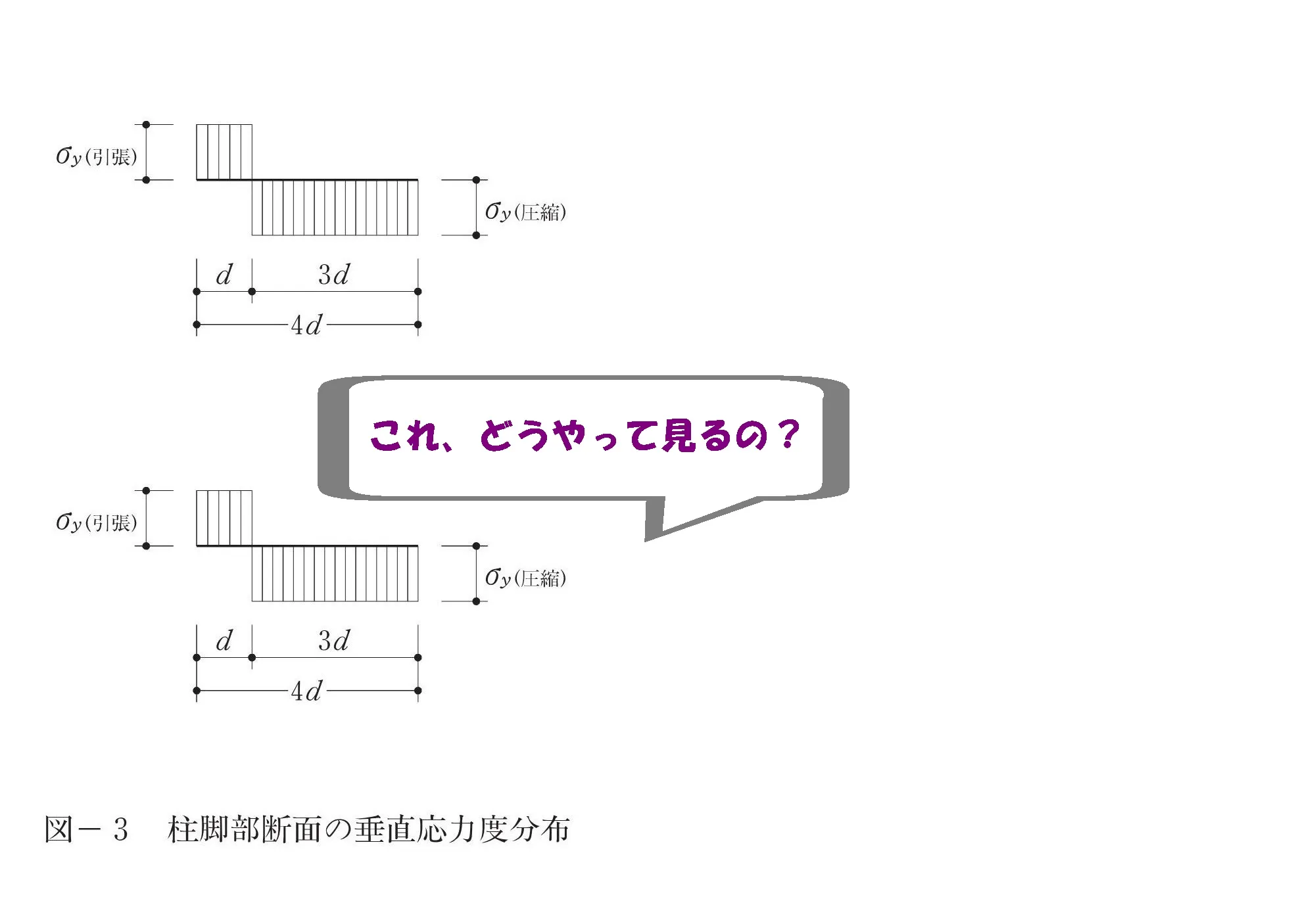




これ、
どうやって見るの?
「これ、どうやって見るの?」図-3の見方について解説していきましょう。
「水平荷重Q(力)向きは左 ⇨ 右」
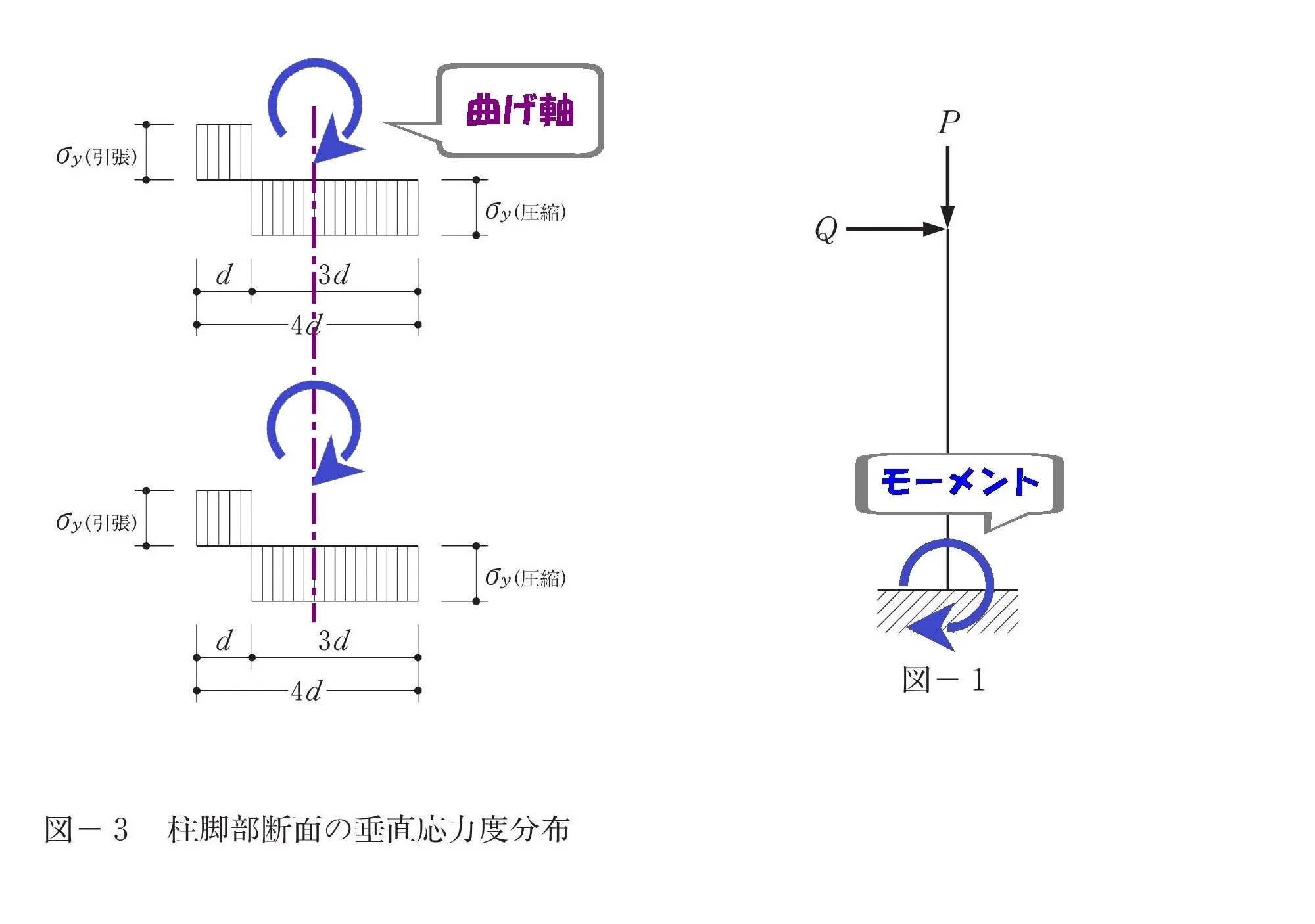

部材は「左 ⇨ 右に曲がる」ことから、モーメントの曲がり軸はQに対して直交方向に取ります。
応力度分布を分解
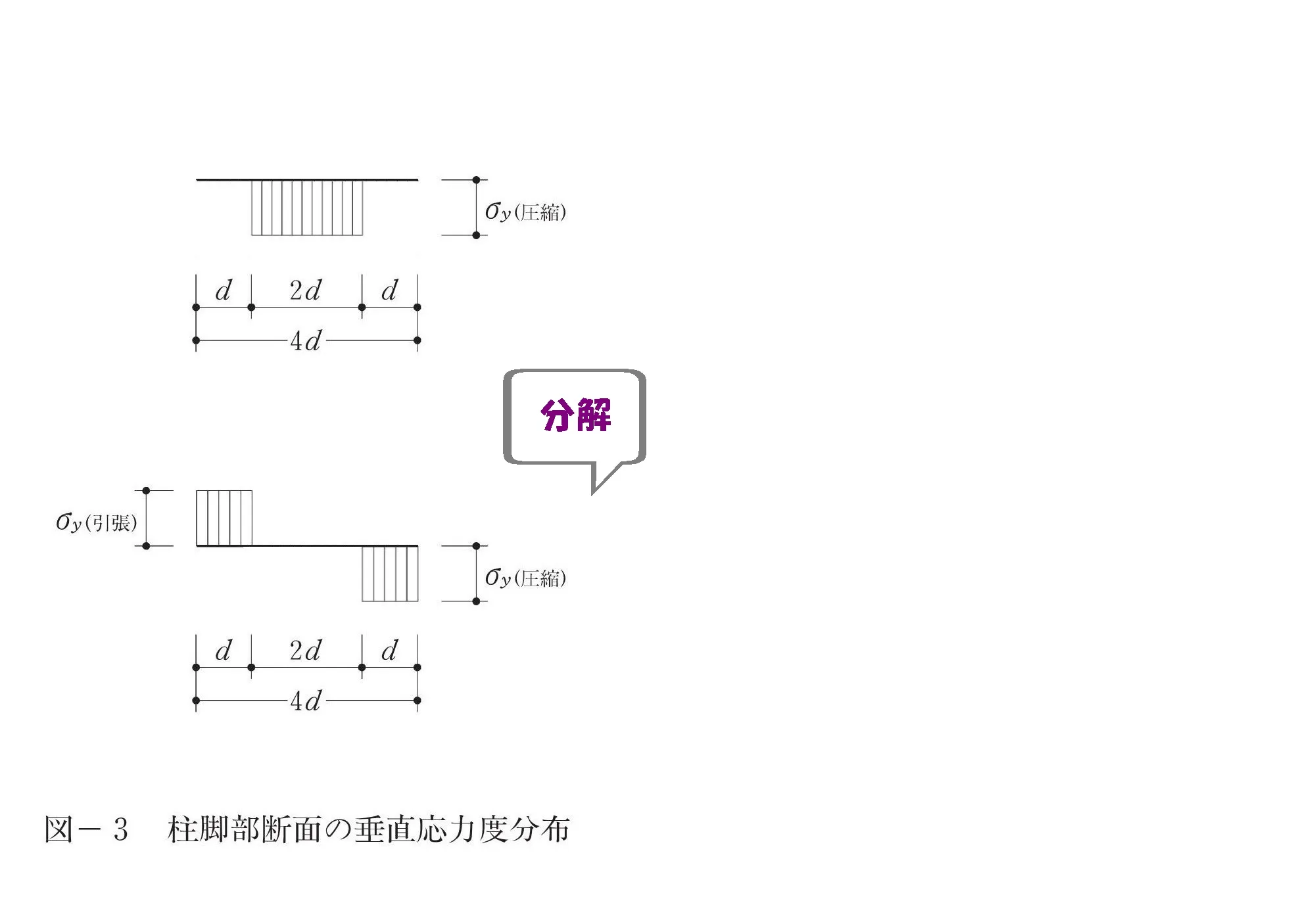

垂直と曲げに分解する
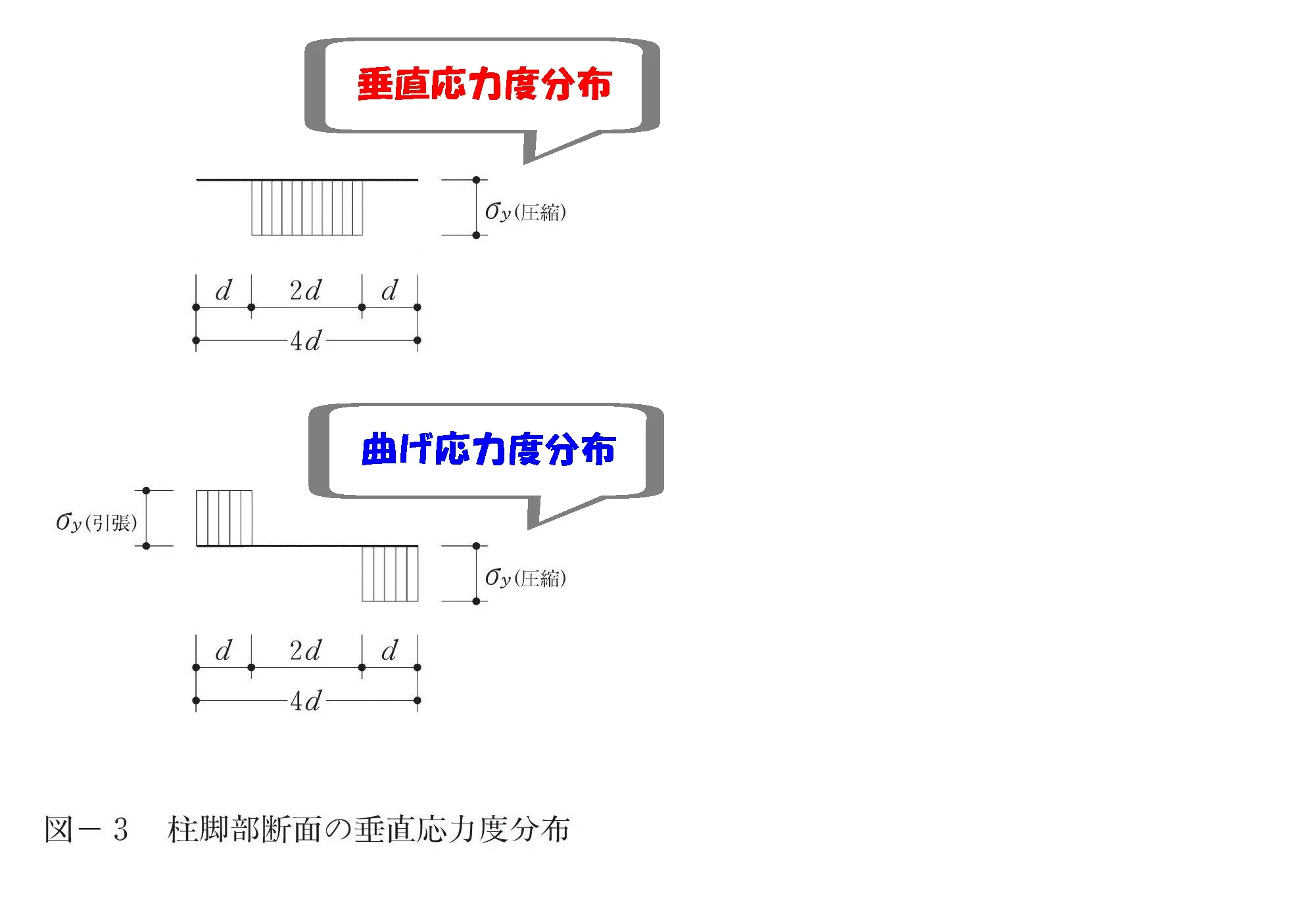

- 垂直応力度:圧縮力のみ負担することから、中央の圧縮部分。
- 曲げ応力度:圧縮力と引張り力を対に負担することから、引張り部分を含む両端の部分。
垂直と曲げを合成してみる
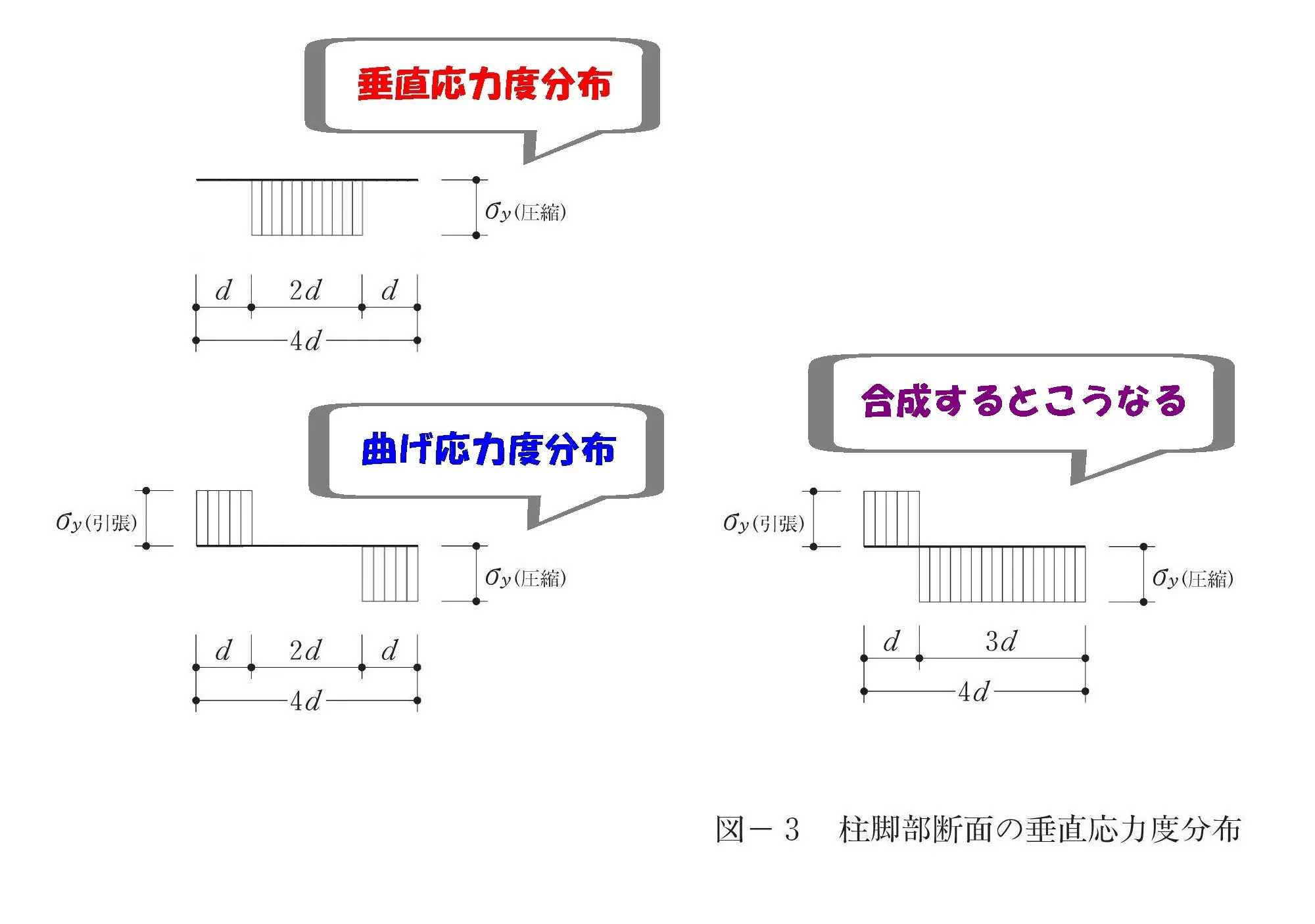




2つ合わせると
もと通りになる。



そりゃそうだろ。
5.軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
垂直応力度
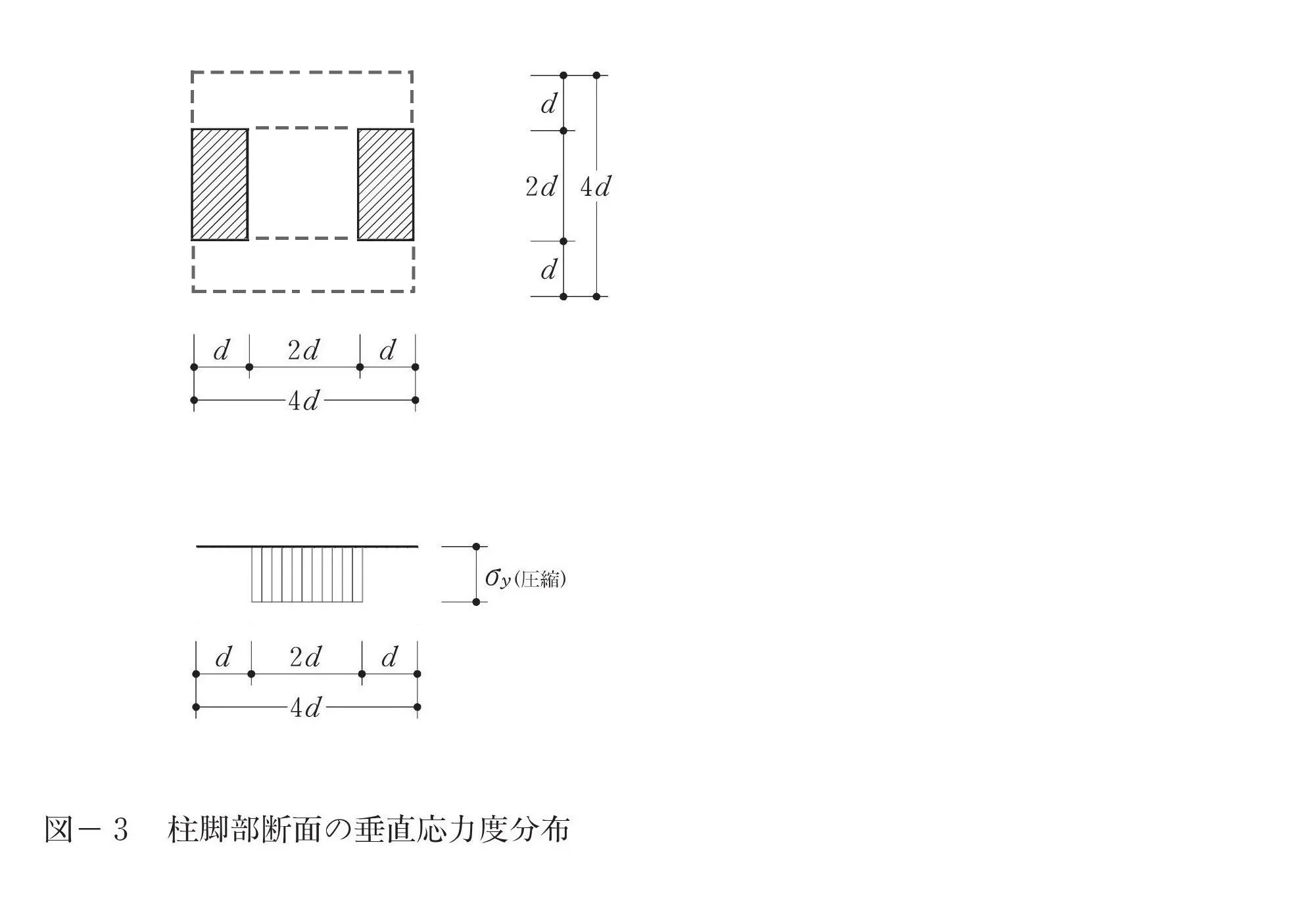

公式
$$軸力=面積×σ$$
断面積を求める
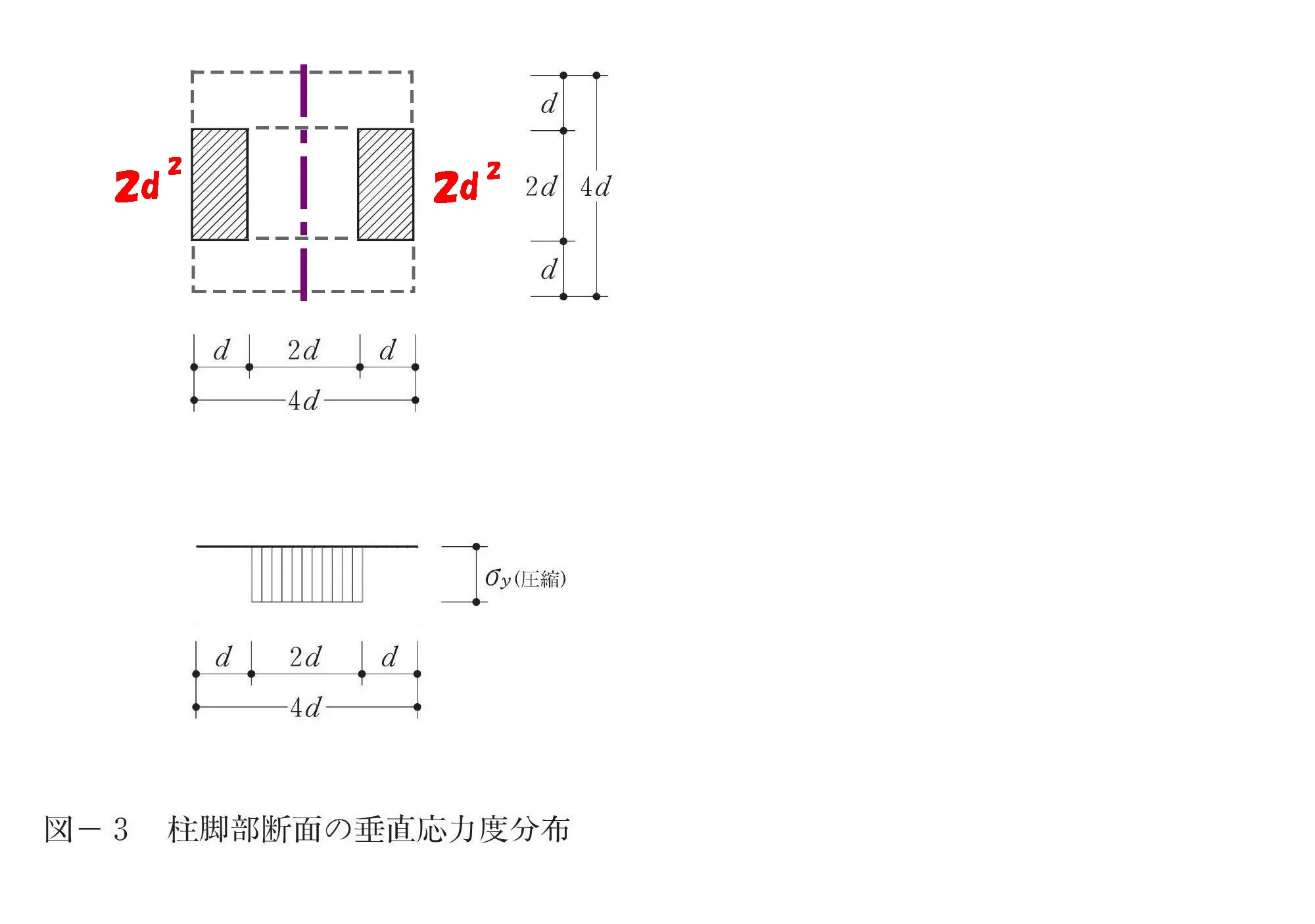

$$垂直応力度の断面積=d*2d+d*2d=4d^2$$
圧縮応力度はσ
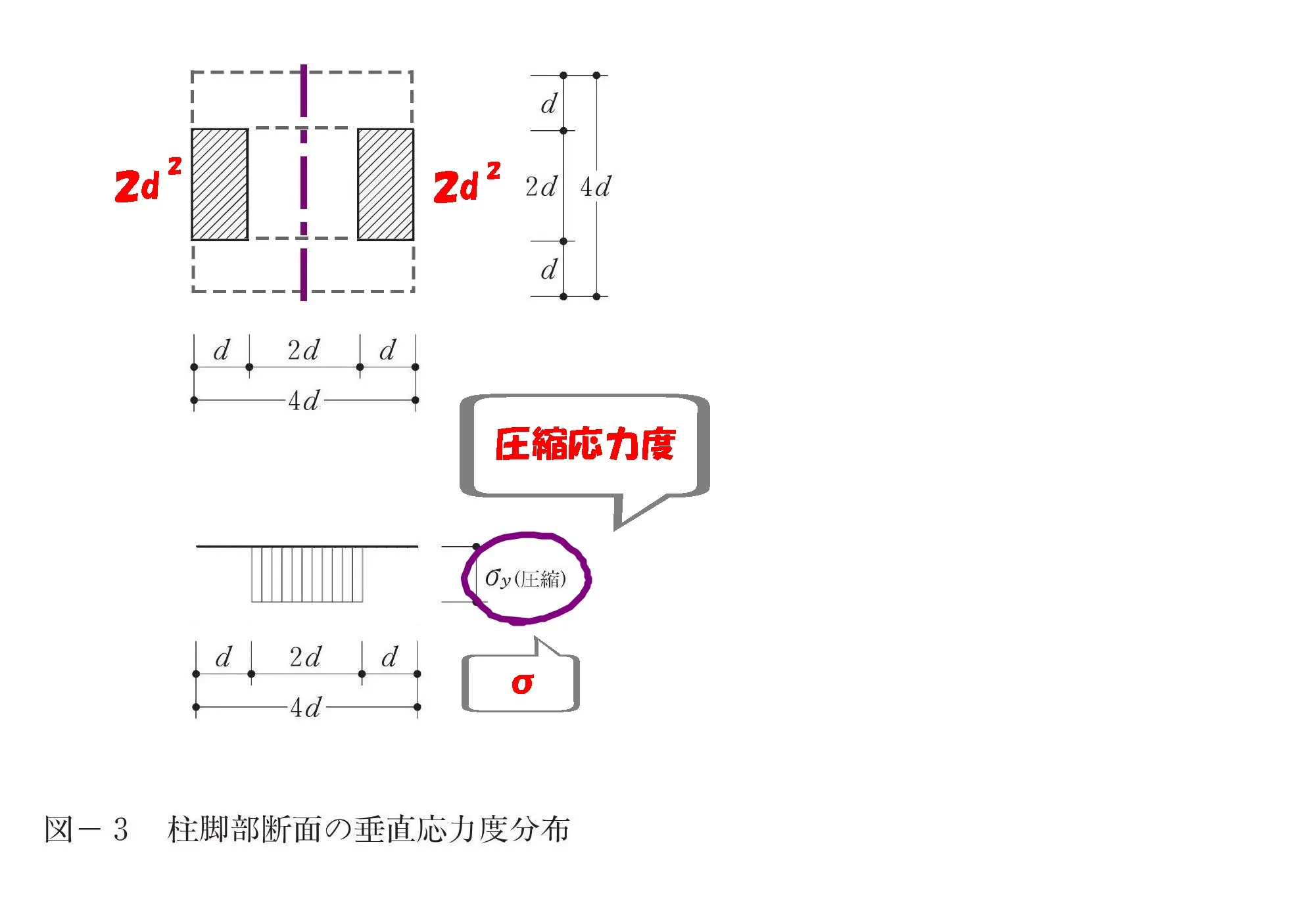

P=σ×A
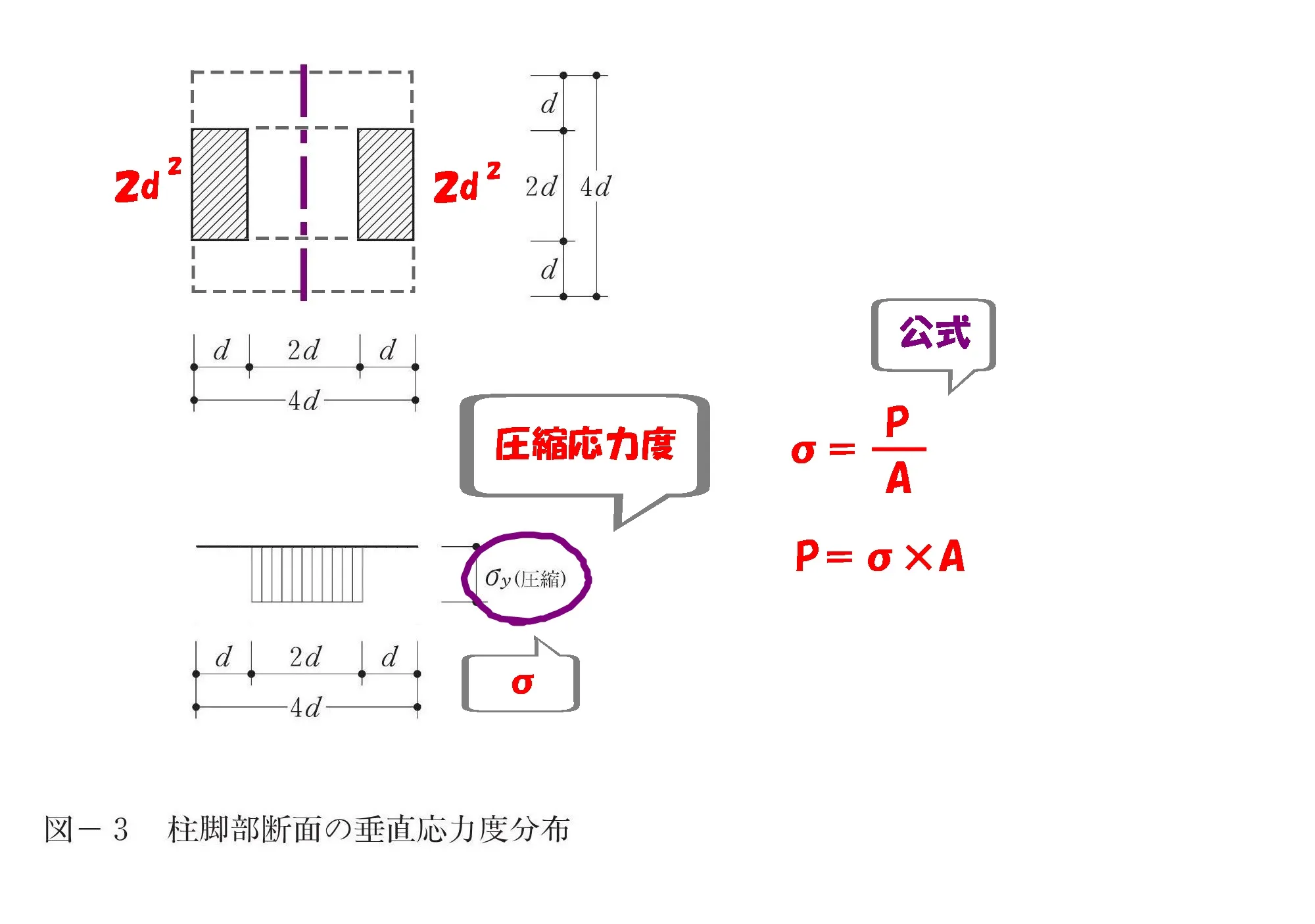

$$応力度\sigma=\frac{ P }{ A }より、P=\sigma*A$$
軸力Pを求める
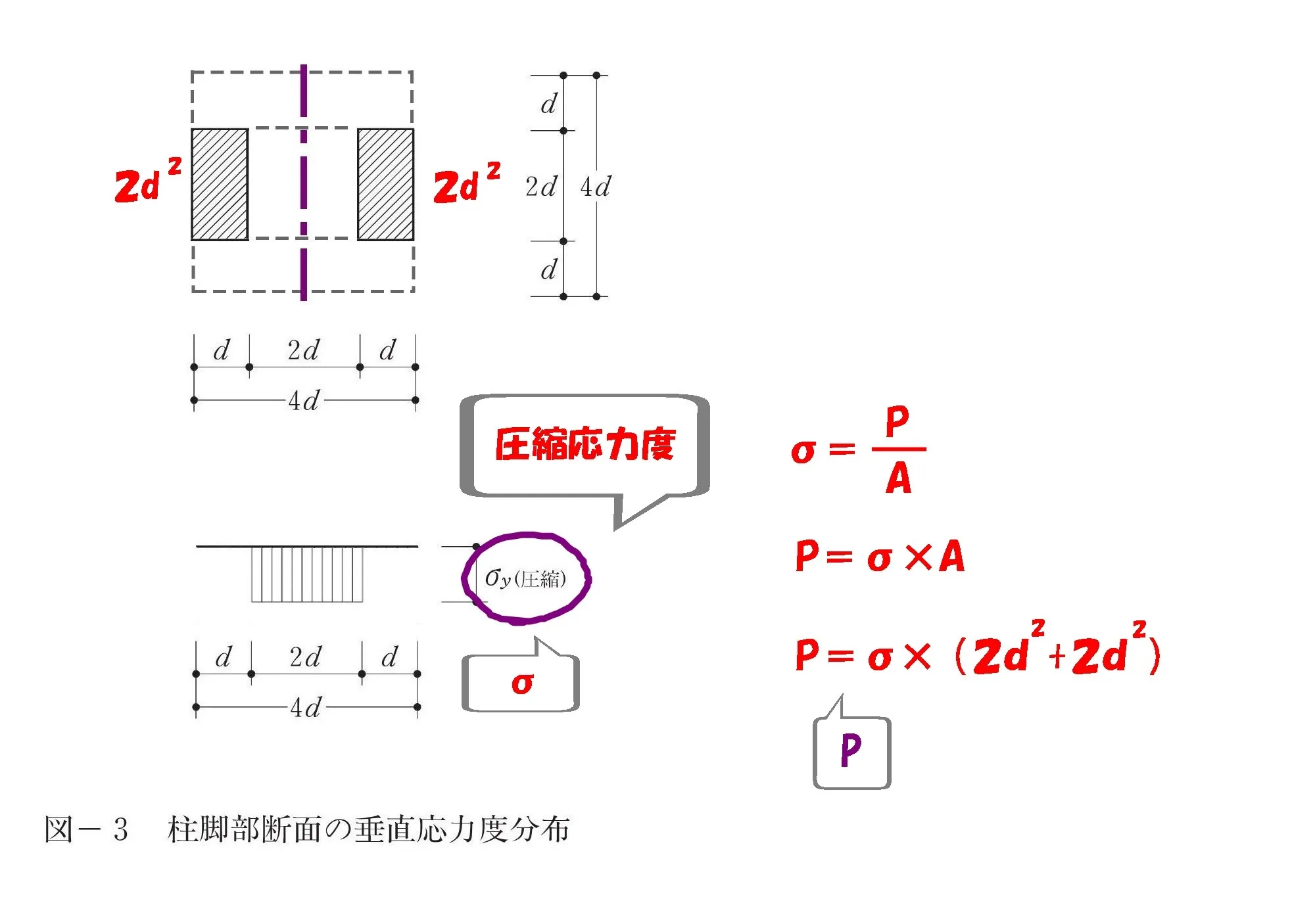

$$P=\sigma*A=\sigma*(2d^2+2d^2)=4d^2\sigma$$



圧縮力の求め方は
とてもシンプル。
公式
$$軸力=面積×σ$$
6.モーメント=力(面積)×距離×σより、水平荷重Qを求める
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める
垂直応力度
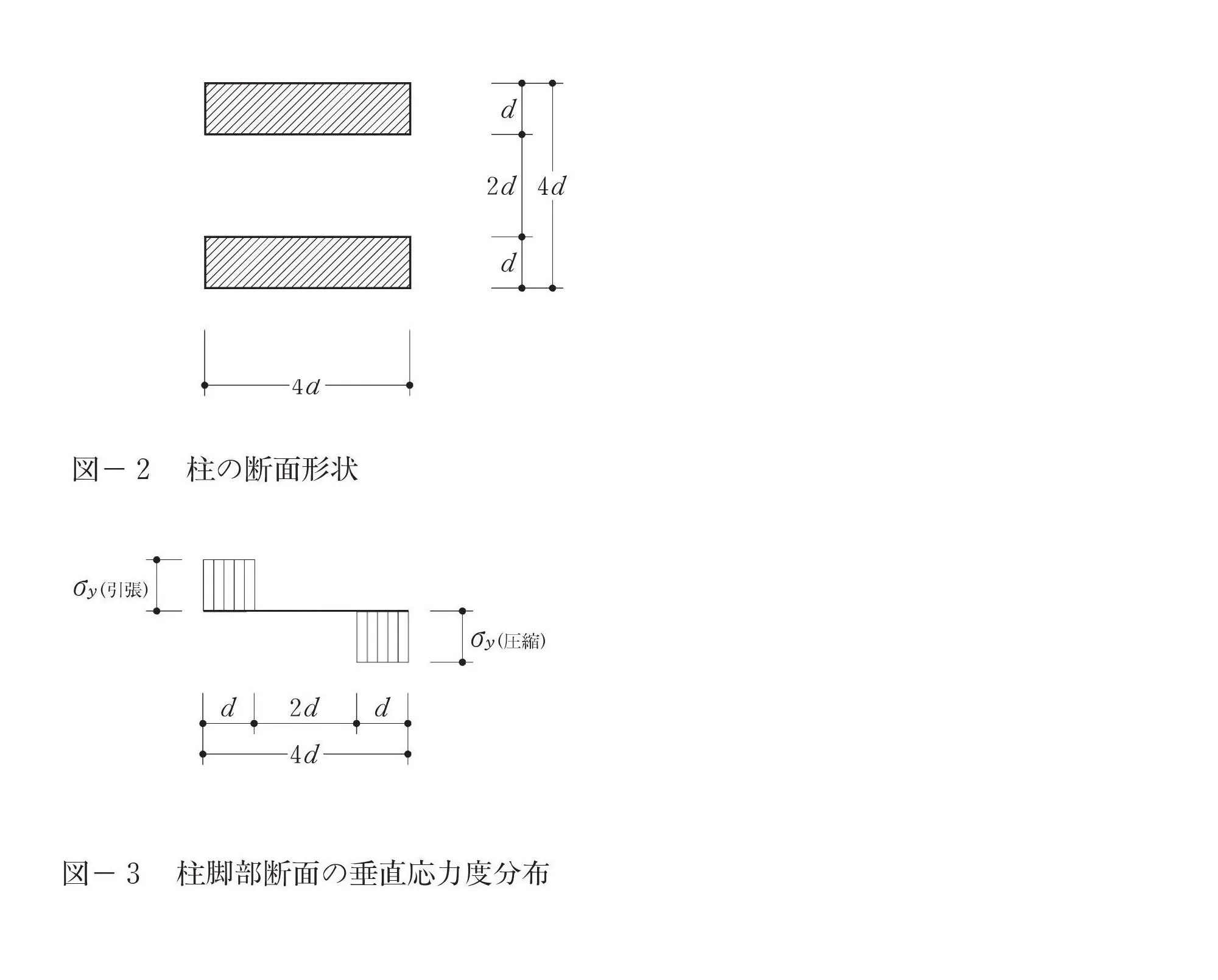

公式
$$モーメント=力(面積)×距離×σ$$
曲がり軸
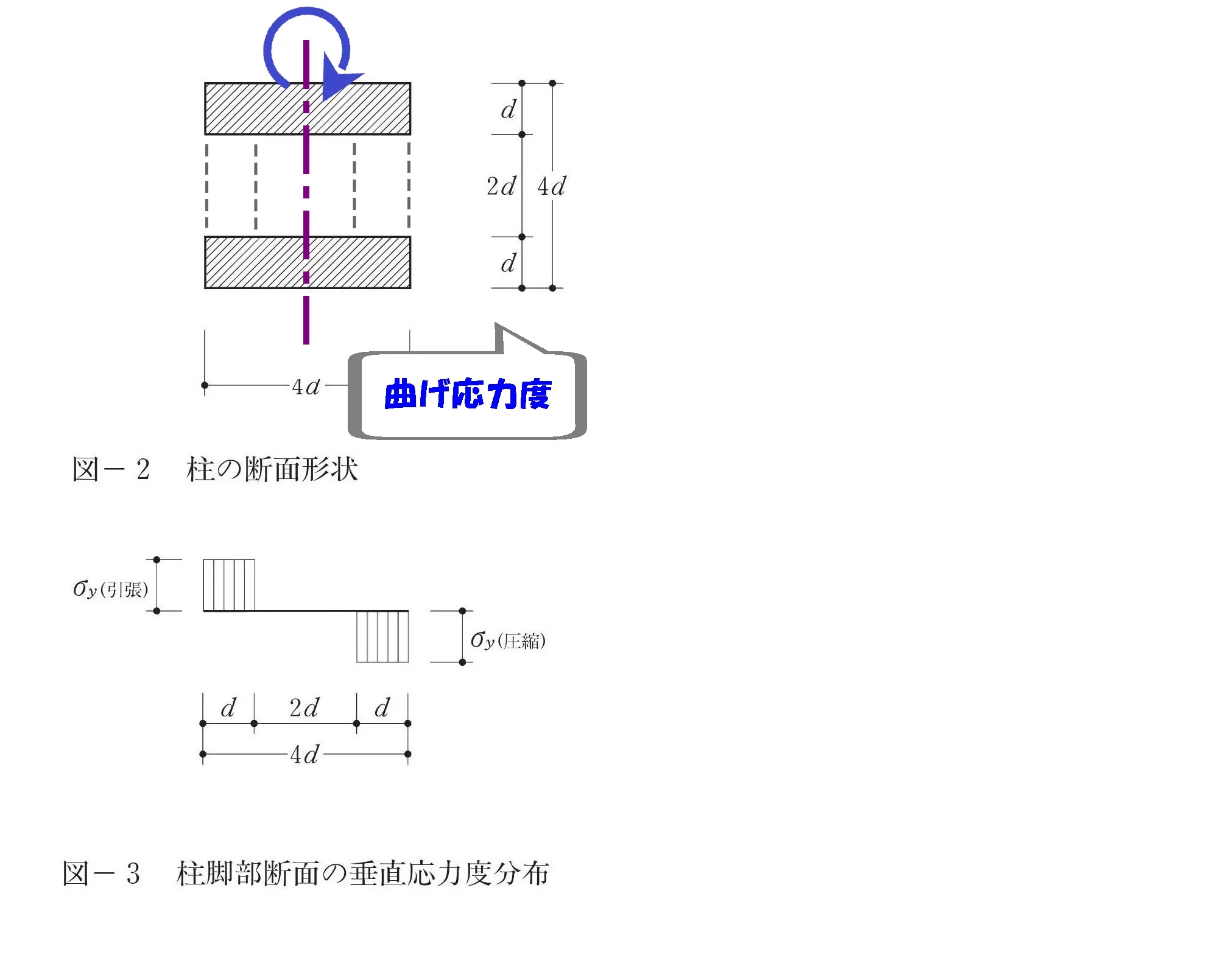




力の向きは左 ⇨ 右
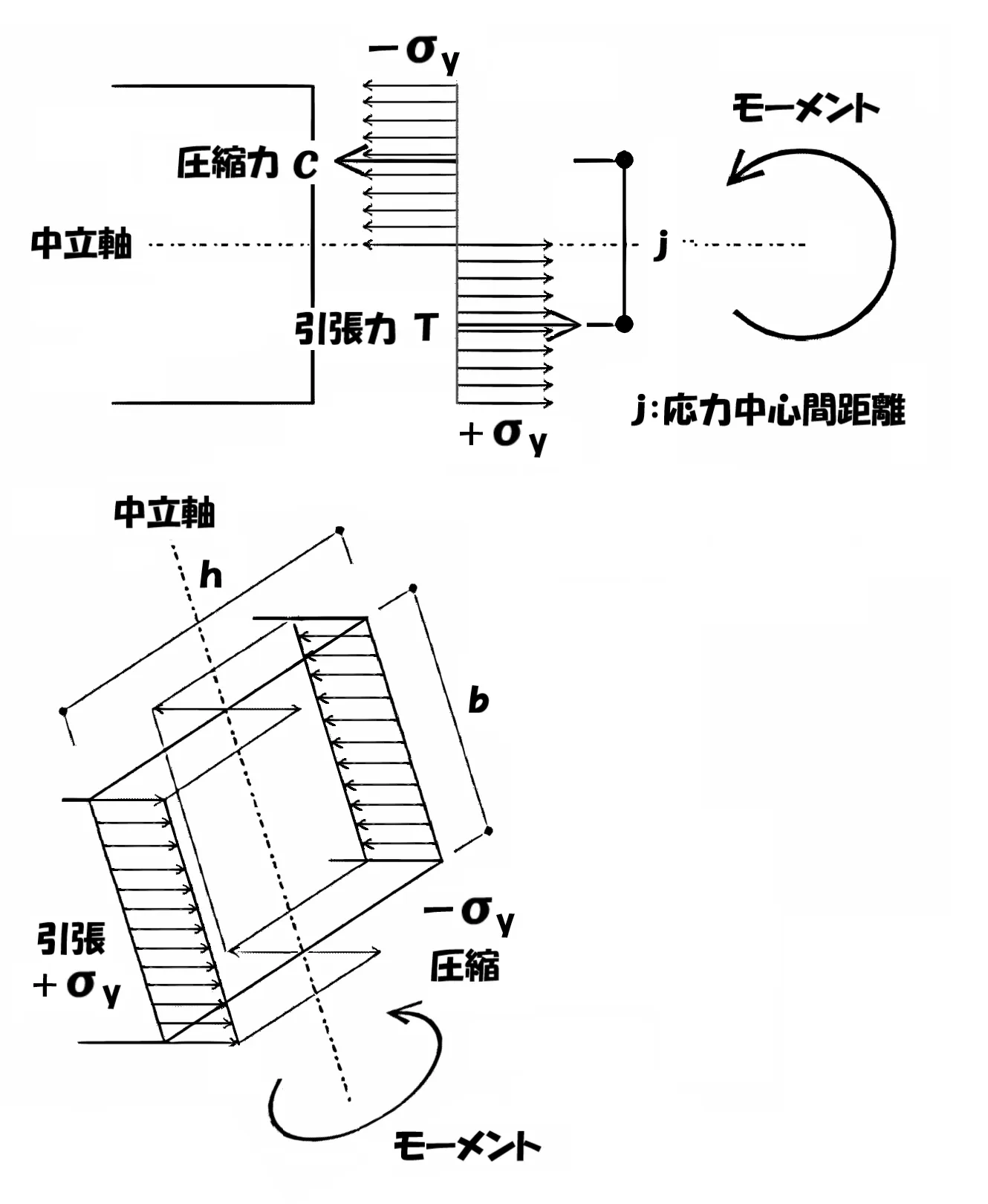
回転力は偶力
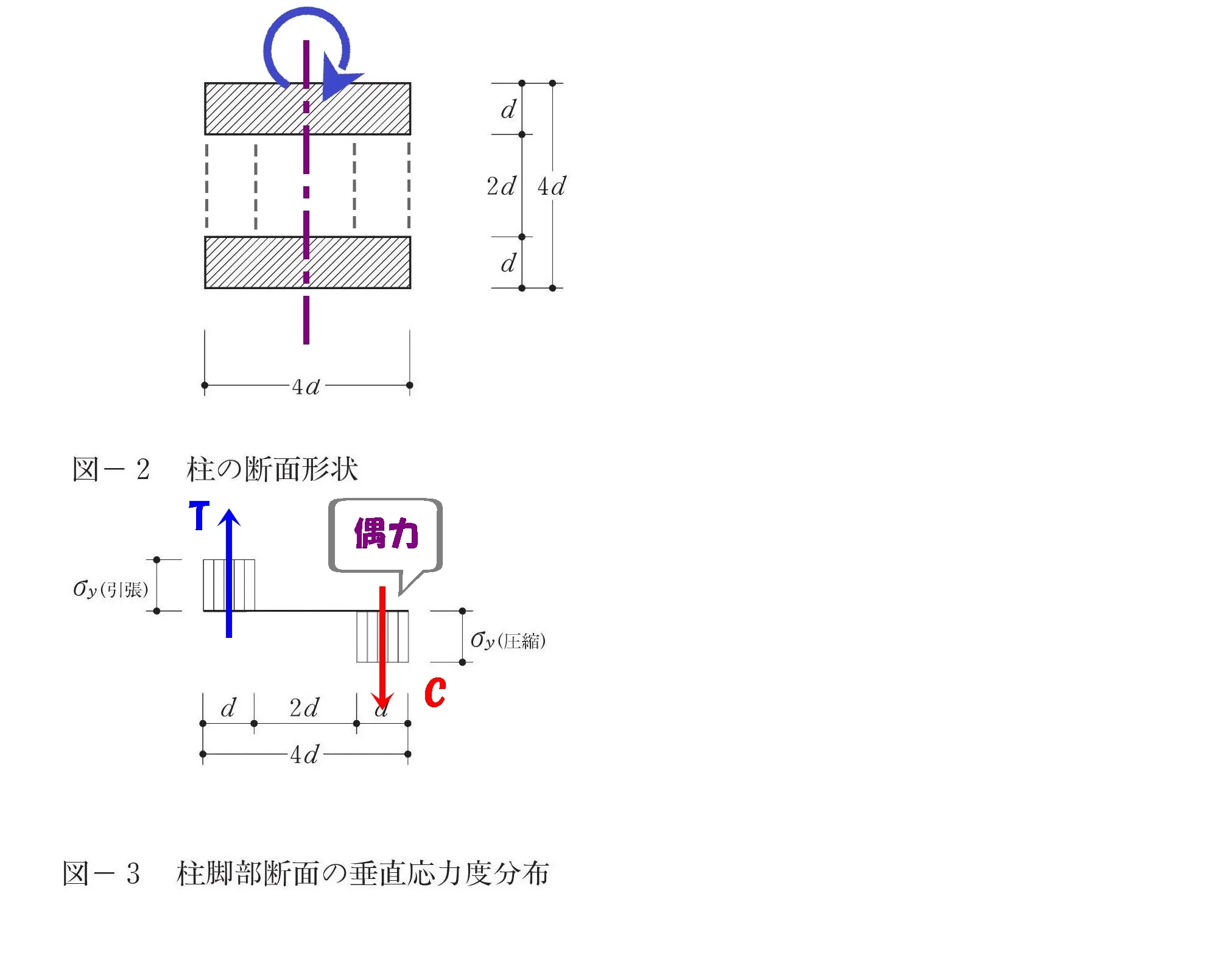

$$モーメントは引張り力:Tと圧縮力:Cからなるもの。$$
TとCは同じ大きさの力で、互いに反対方向に作用する「偶力」の関係です。



モーメントは偶力。
モーメントの距離=偶力の距離
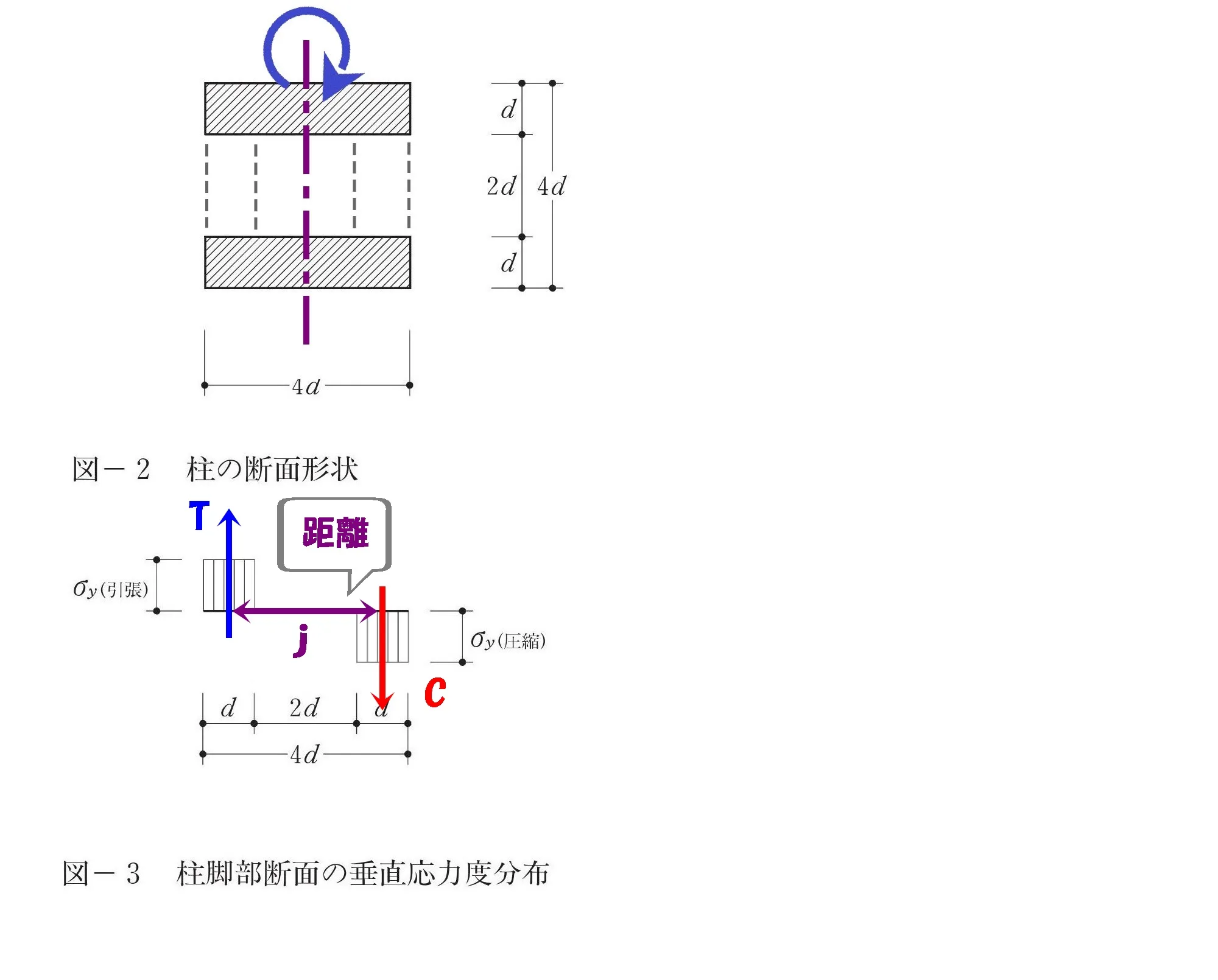

$$モーメントは引張り力:Tと圧縮力:Cからなるもの。$$
j:応力中心距離



TとCに続いて
いきなり「j」って何だ?
TとCの間隔を「j」と位置づけ、この「j」が「モーメント=力×距離」の「距離」になります。
TとCは偶力の関係
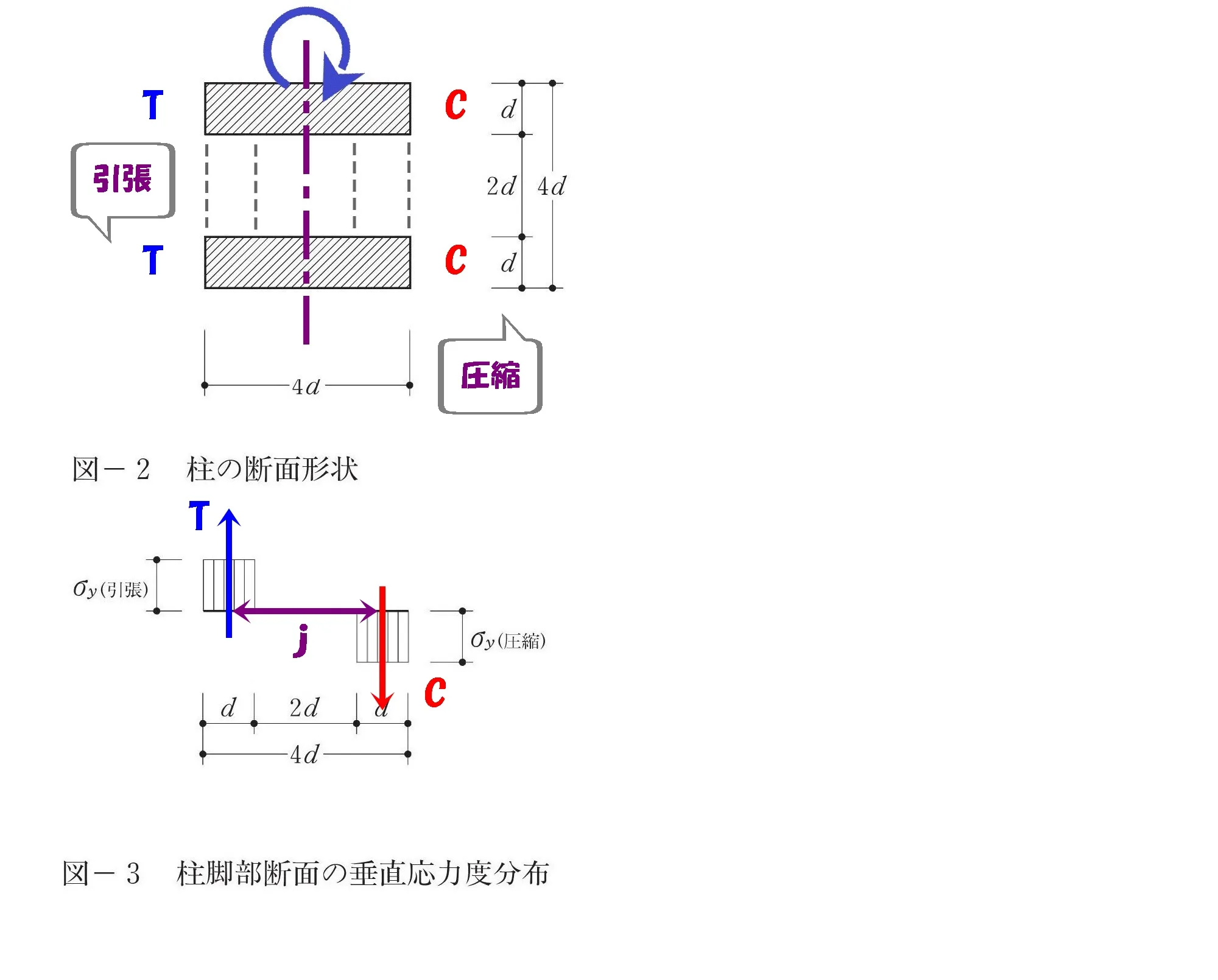

モーメント=力×距離
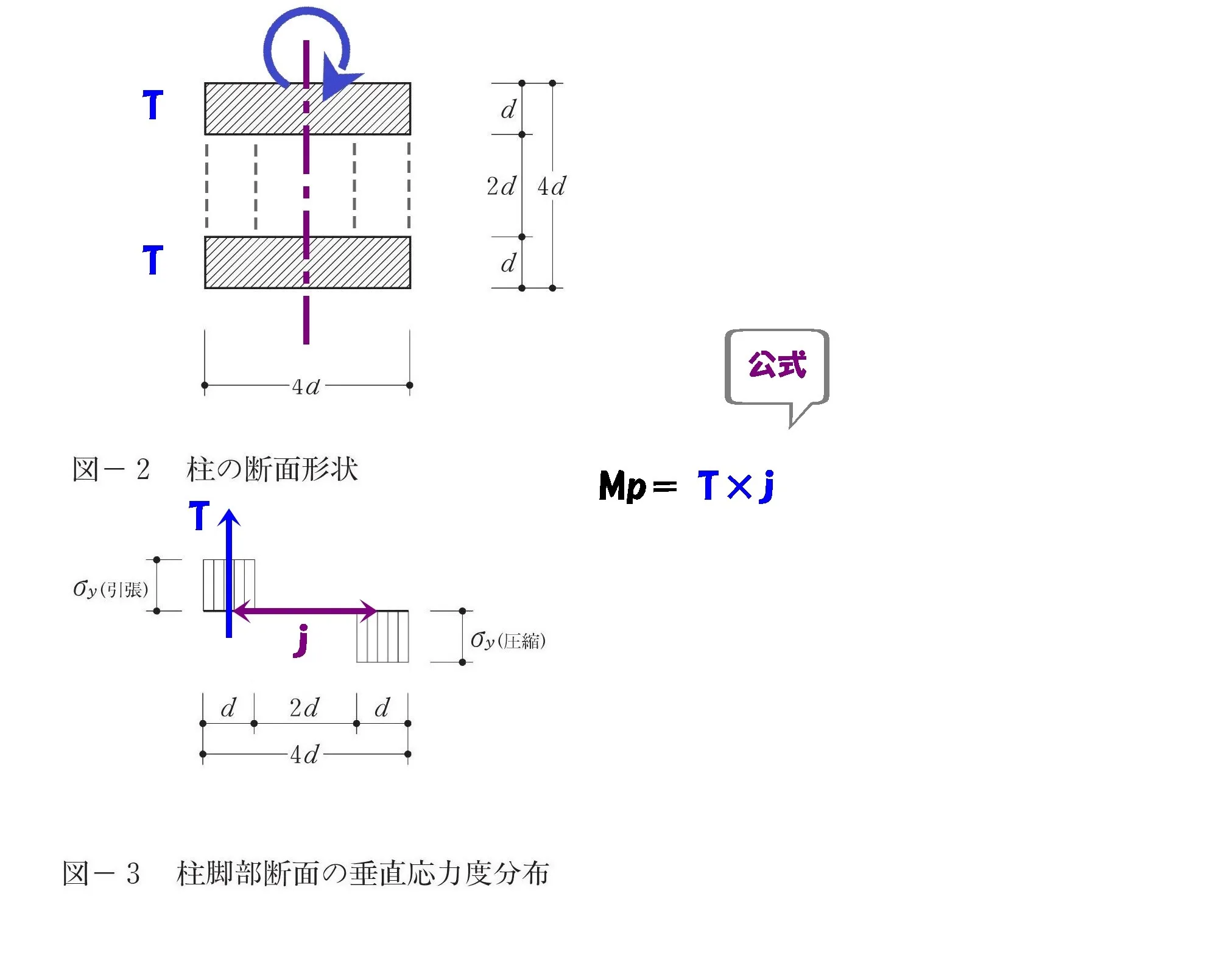

$$モーメント=T*j$$
モーメント=力×距離
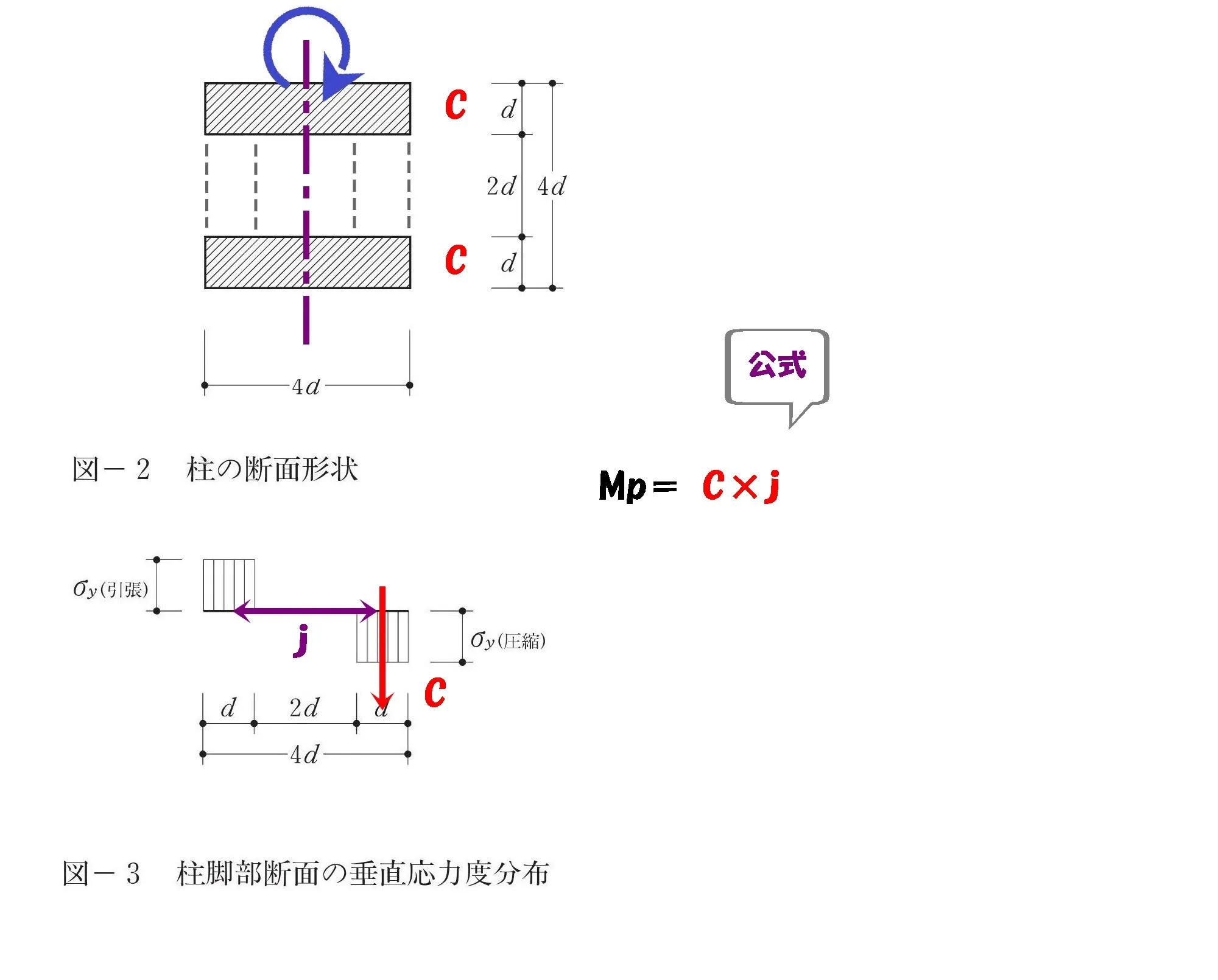

$$モーメント=C*j$$
モーメント=力×距離
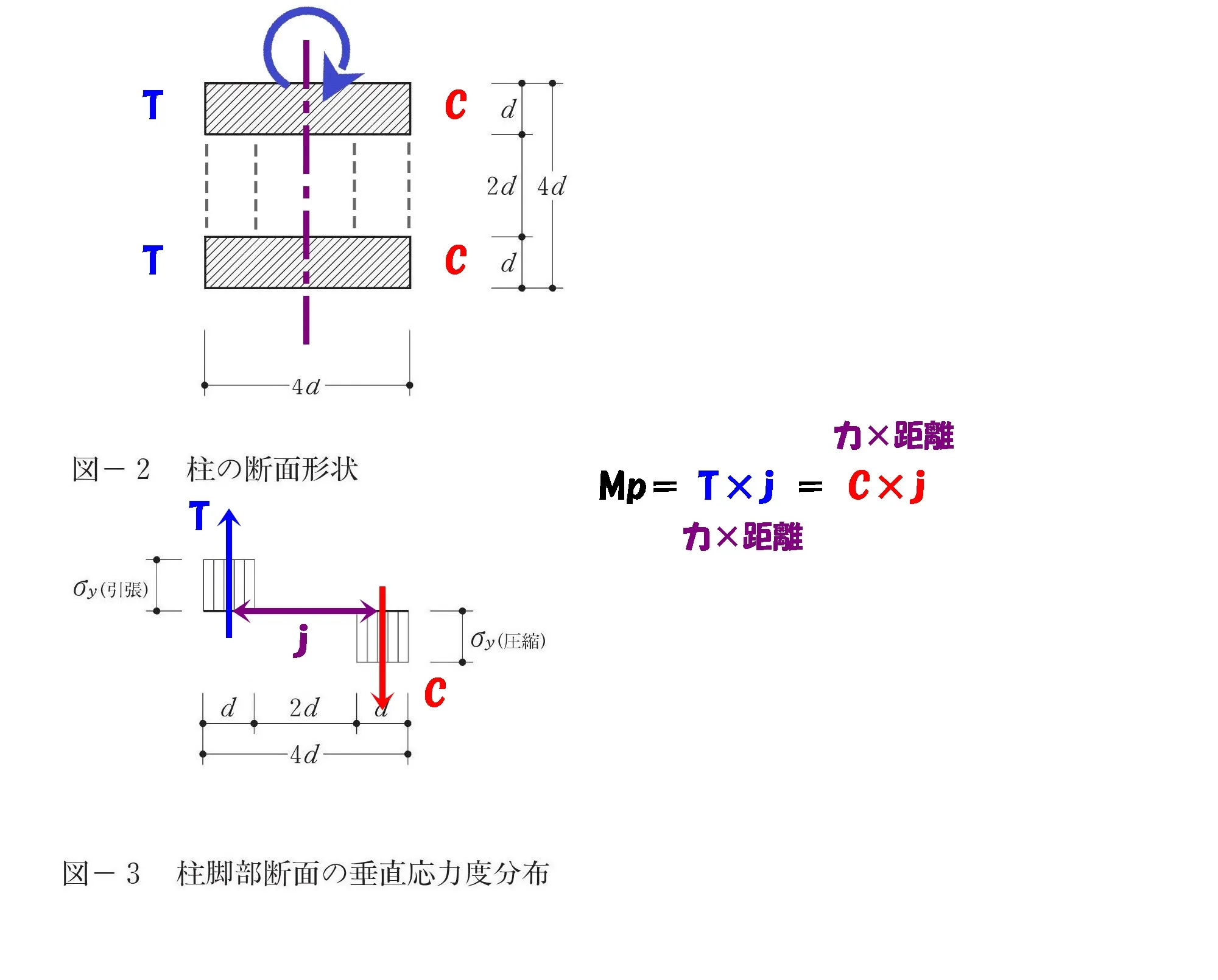

$$モーメント=T*j=C*j$$
これが偶力の関係となります。



TとCのどちらで
解いても答えは同じ。
公式
$$モーメント=力(面積)×距離×σ$$
断面積を求める
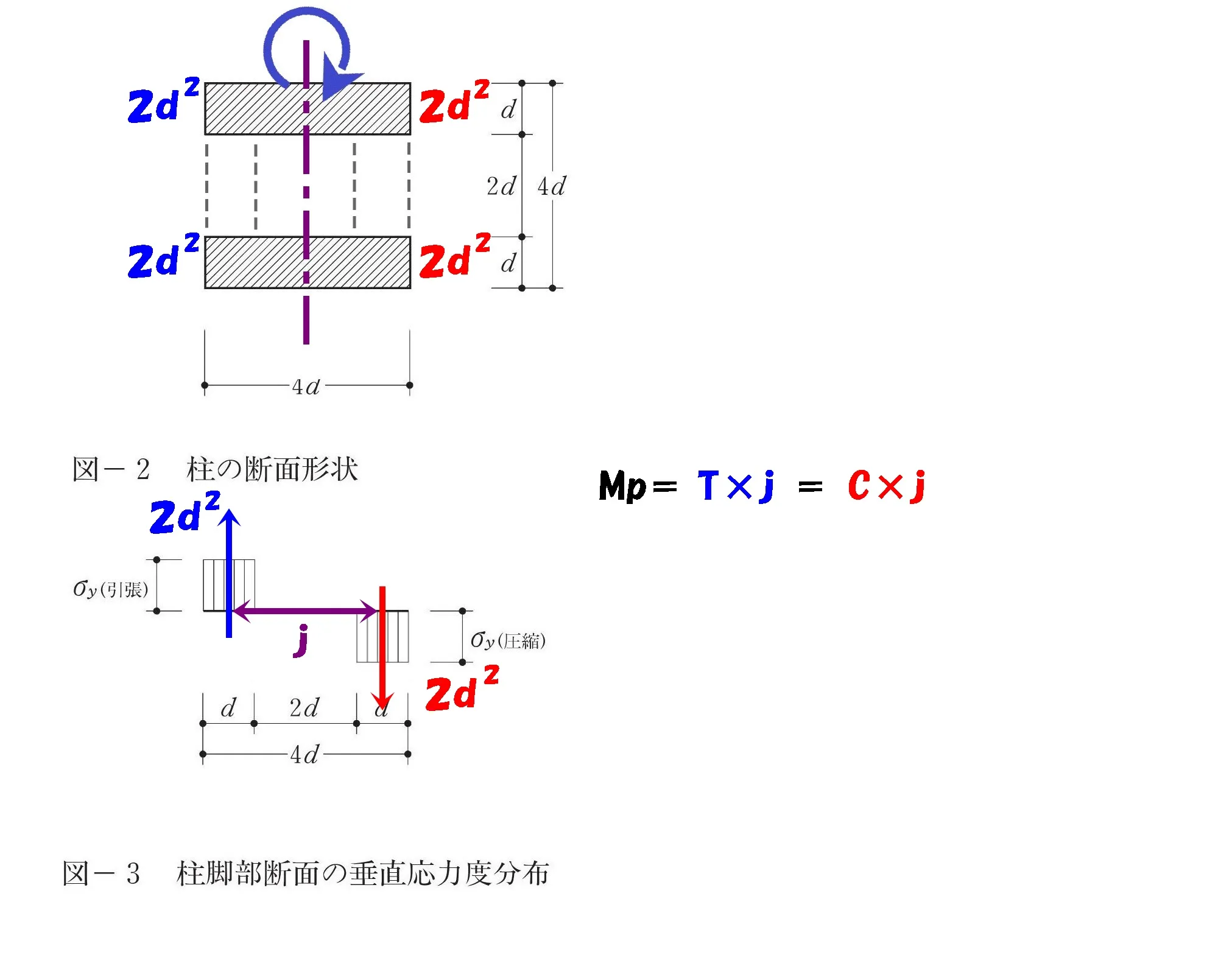

$$曲げ応力度の断面積=2d*d+2d*d=4d^2$$
モーメント=力×距離
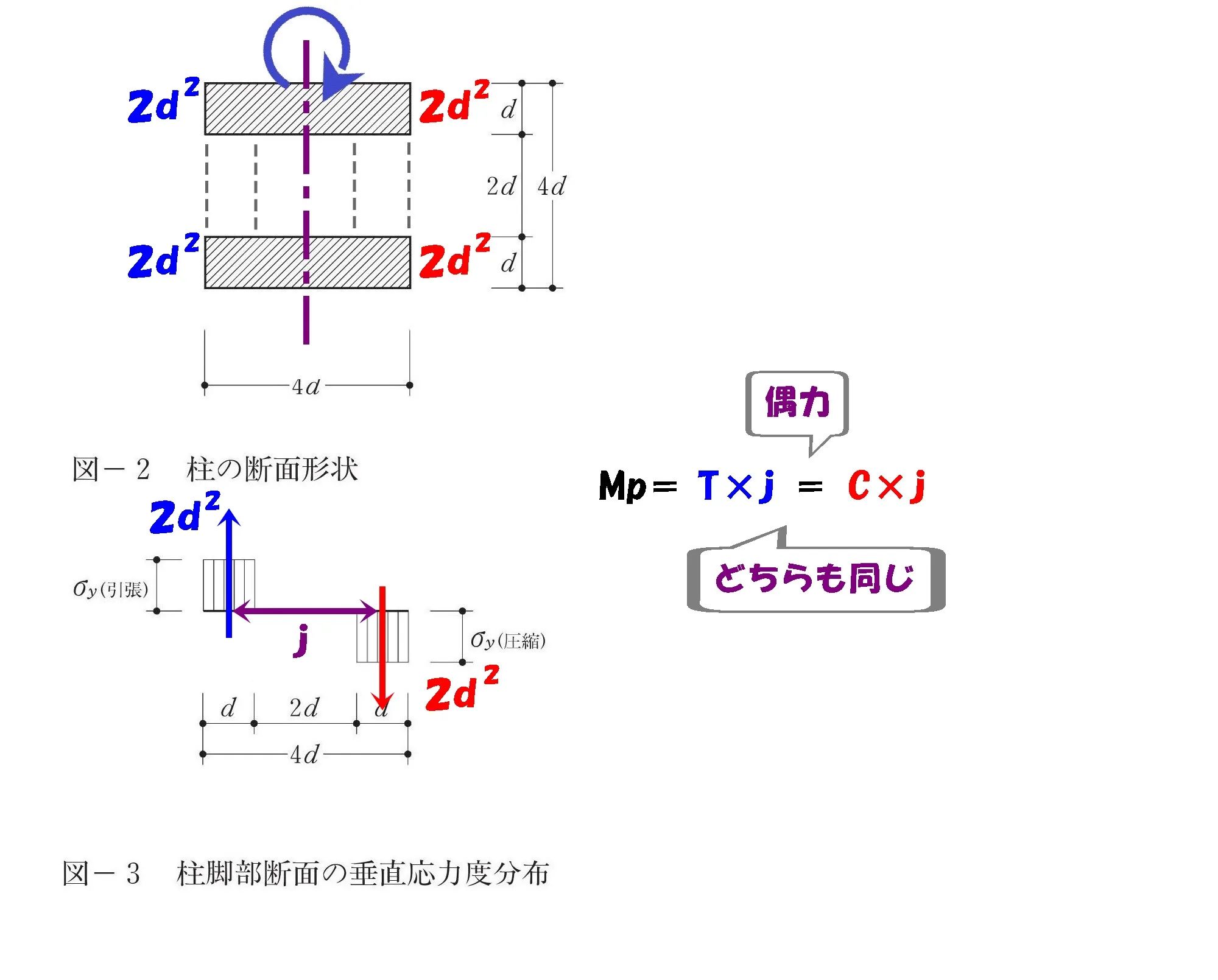

$$モーメント=T*j=C*j$$
モーメント=「T×j」、「C×j」どちらを使っても同じ答えになります。
モーメントを求める
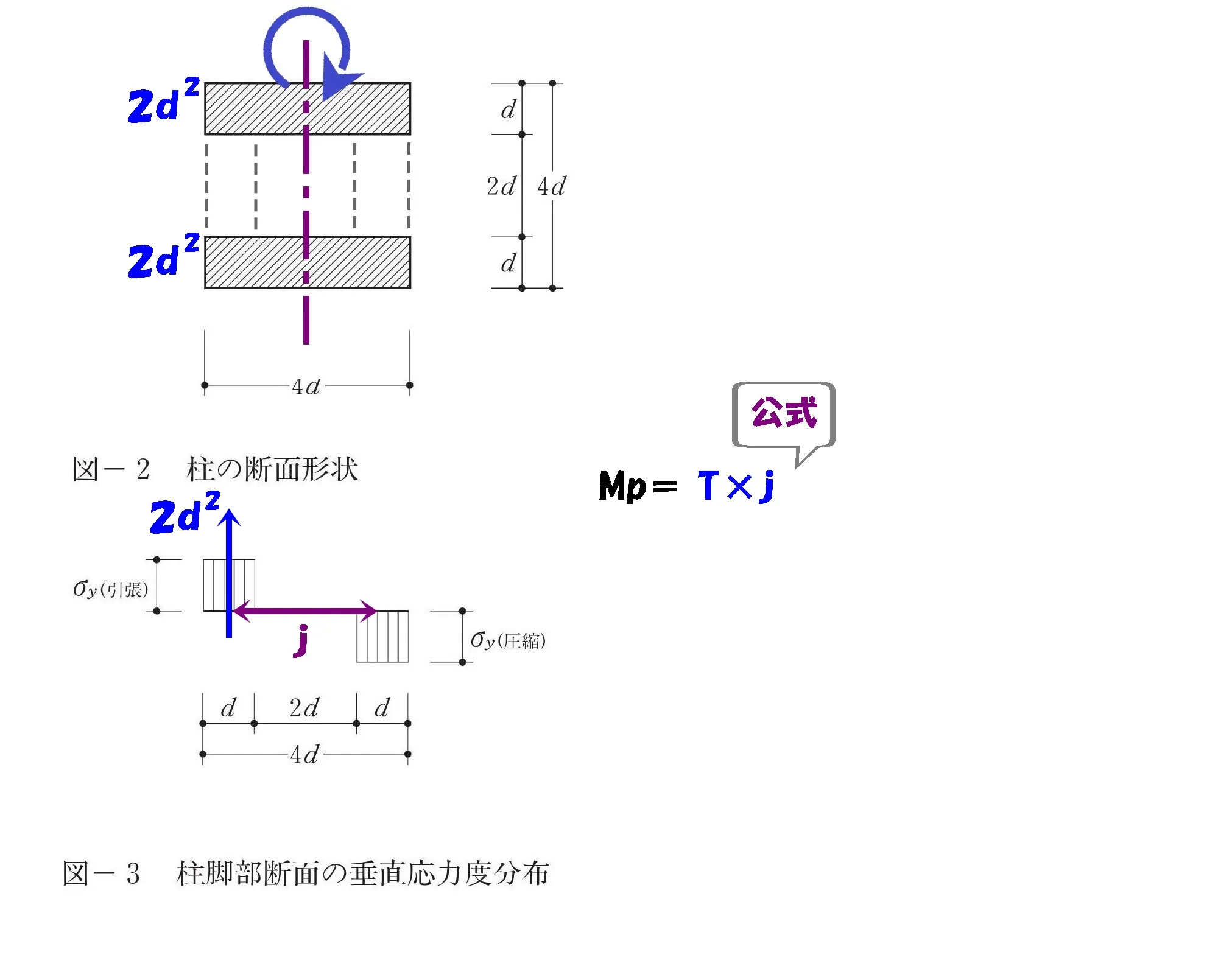

j:応力中心距離



Lとかdとかjまで
使い分けがややこしい。
モーメント=力×距離
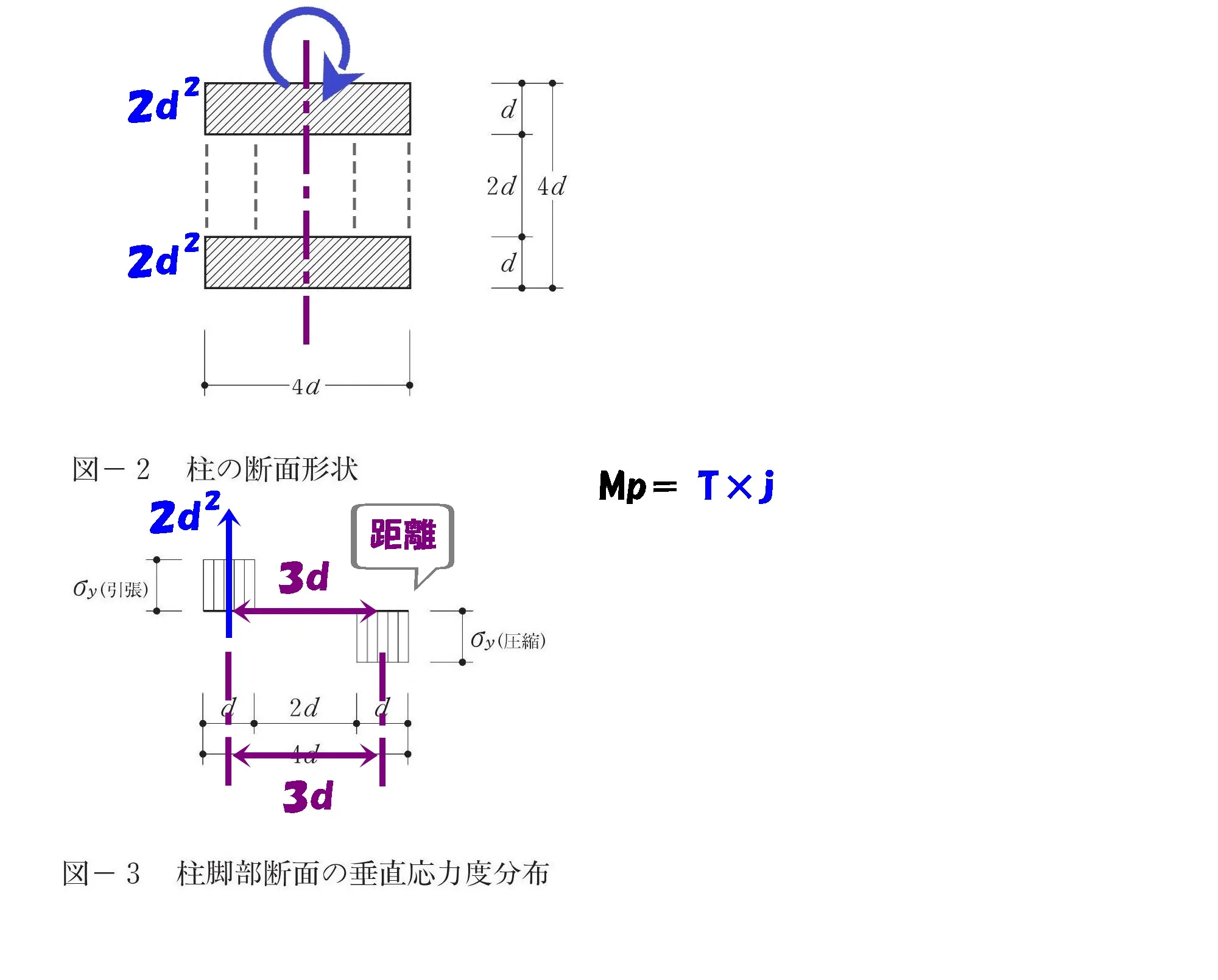

$$力×距離$$$$⇨曲げ応力度の断面積×偶力の間隔$$
$$偶力の間隔=圧縮Tと引張りCの応力中心距離:j$$
$$応力中心距離:j=0.5d+2d+0.5d=3d$$
モーメント=力×距離


$$モーメント=(2d^2+2d^2)*3d$$
圧縮応力度はσ
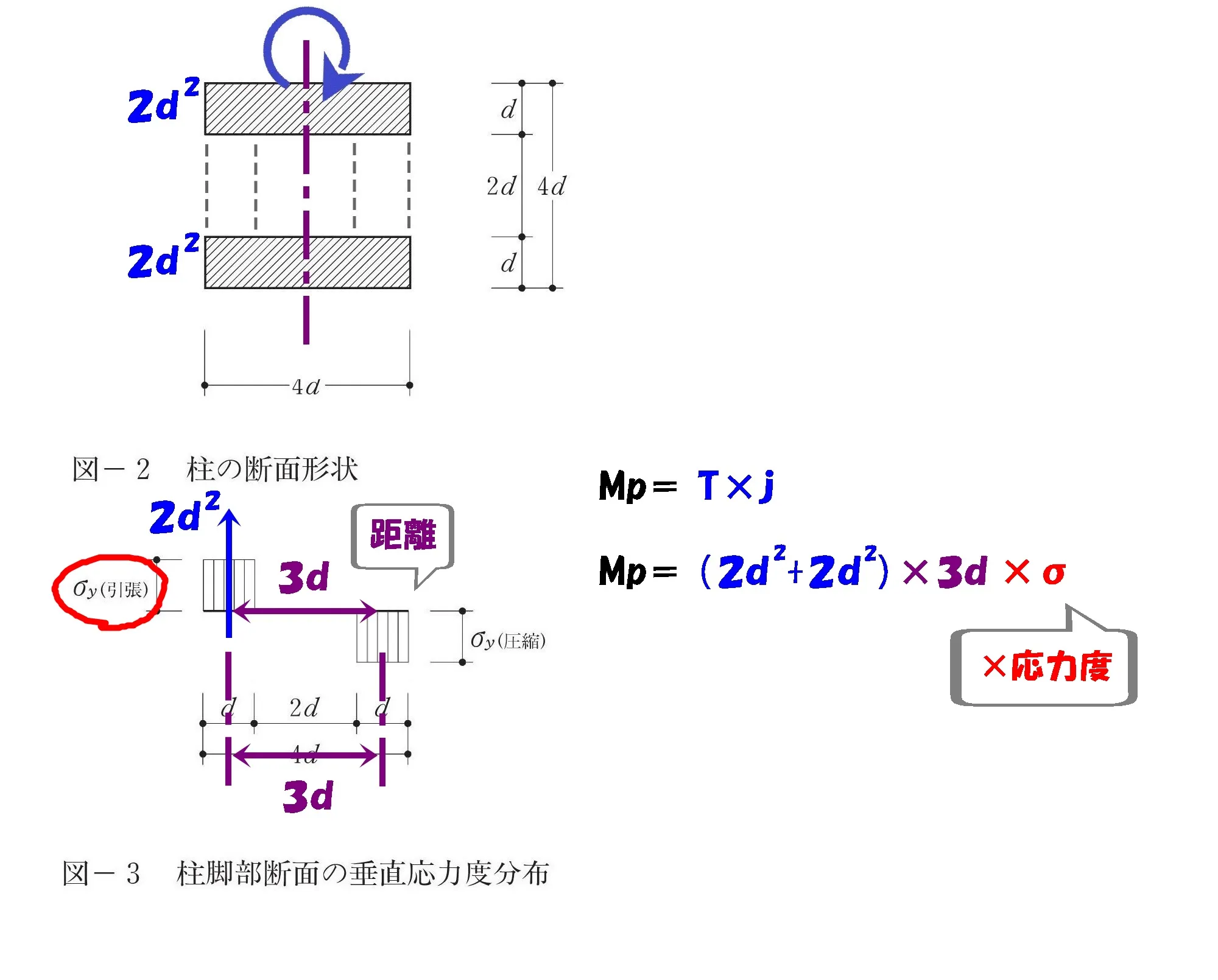

$$モーメント=力(面積)×距離×σ$$
$$(2d^2+2d^2)*3d*\sigma=12d^3\sigma$$



応力度の問題では
力が面積に置き換わる。
公式
$$モーメント=力(面積)×距離×σ$$
水平荷重Qを求める

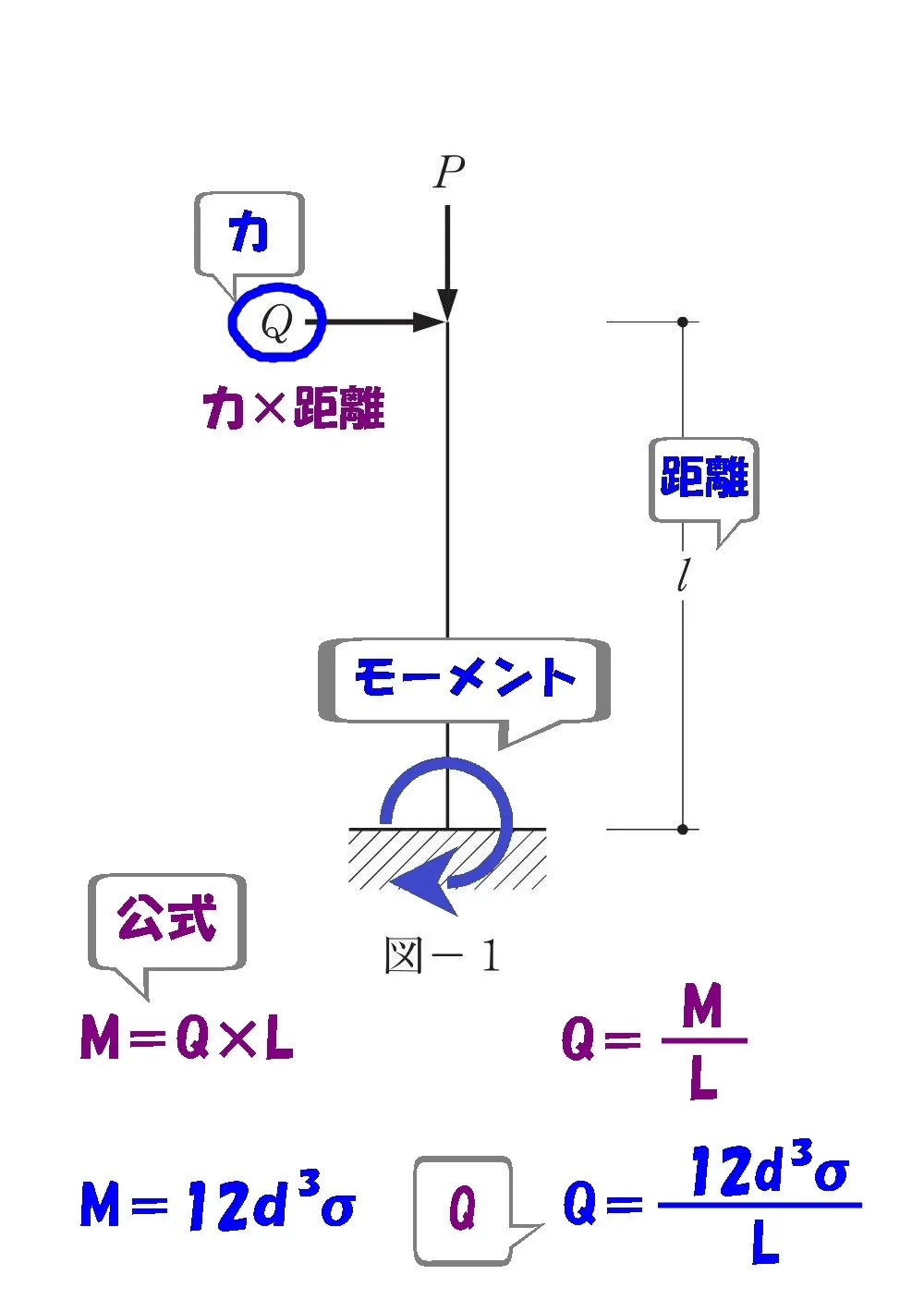

$$M=Q*Lより,Q=\frac{ M }{ L }$$$$\frac{ M }{ L }=\frac{ 12d^3\sigma }{ L }$$
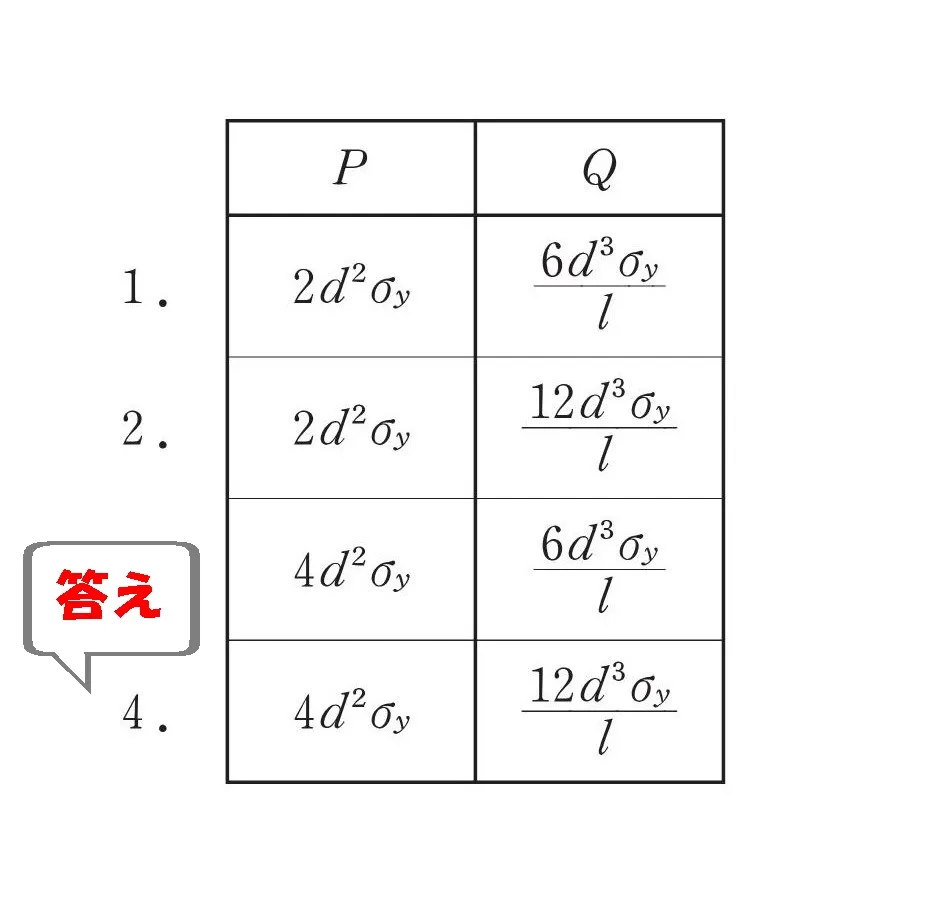
$$鉛直荷重:P=4d^2\sigma,水平荷重:Q=\frac{ 12d^3\sigma }{ L }$$
答え.4

攻略ポイント
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める


この動画を YouTube で視聴
断面二次モーメント
難易度:★★★☆☆
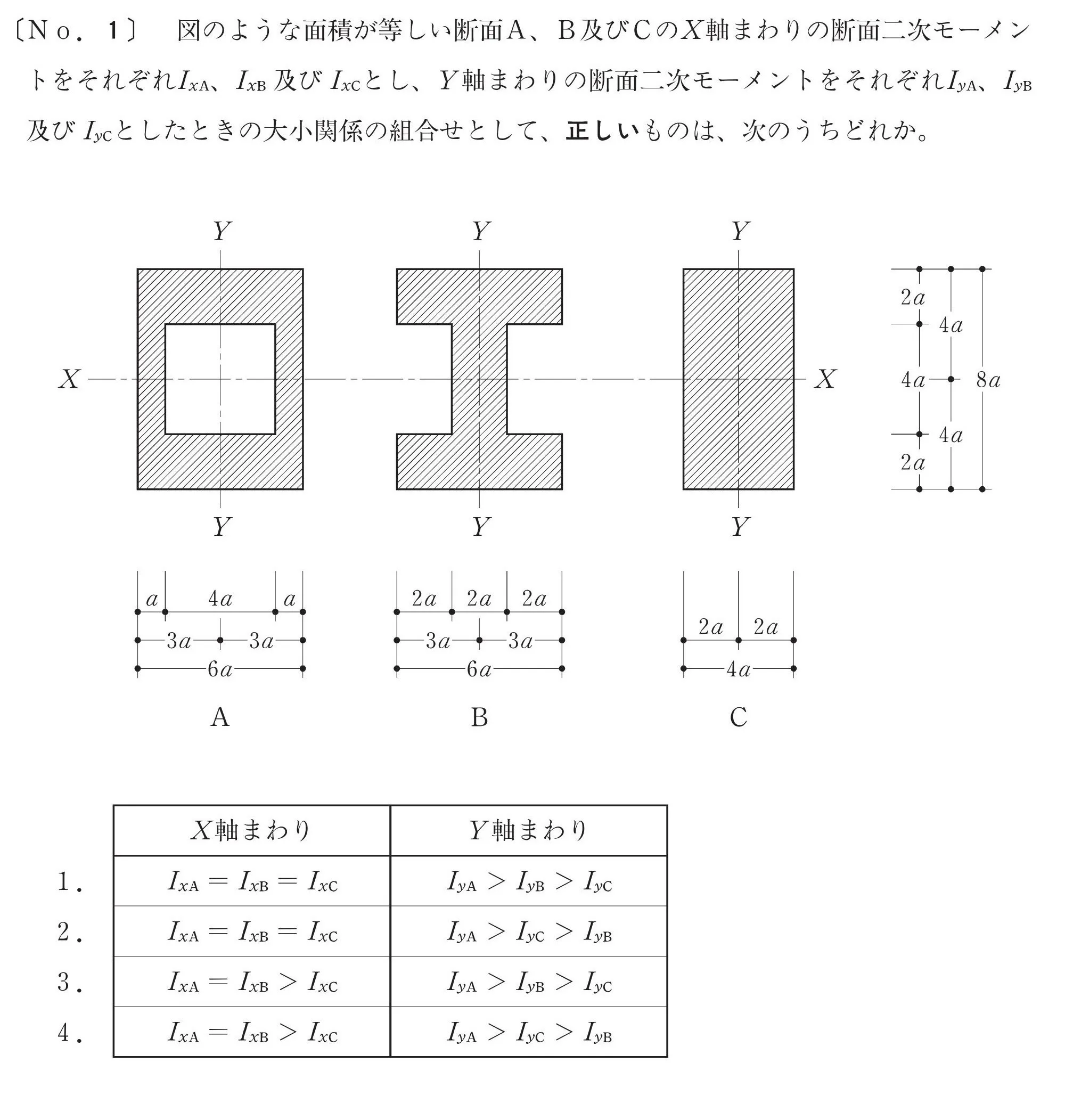
断面二次モーメントを比較する問題です。
解き方というよりは「計算がめんどくさい」というイメージがあるかもしれません。
正解を導くには、公式を組み立て「桁数の多い計算式を効率良く処理する力」を必要とします。



何だかとても
いやな予感がするよ。

公式
$$断面二次モーメントI=\frac{ bh^3 }{ 12 }$$
攻略ポイント
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
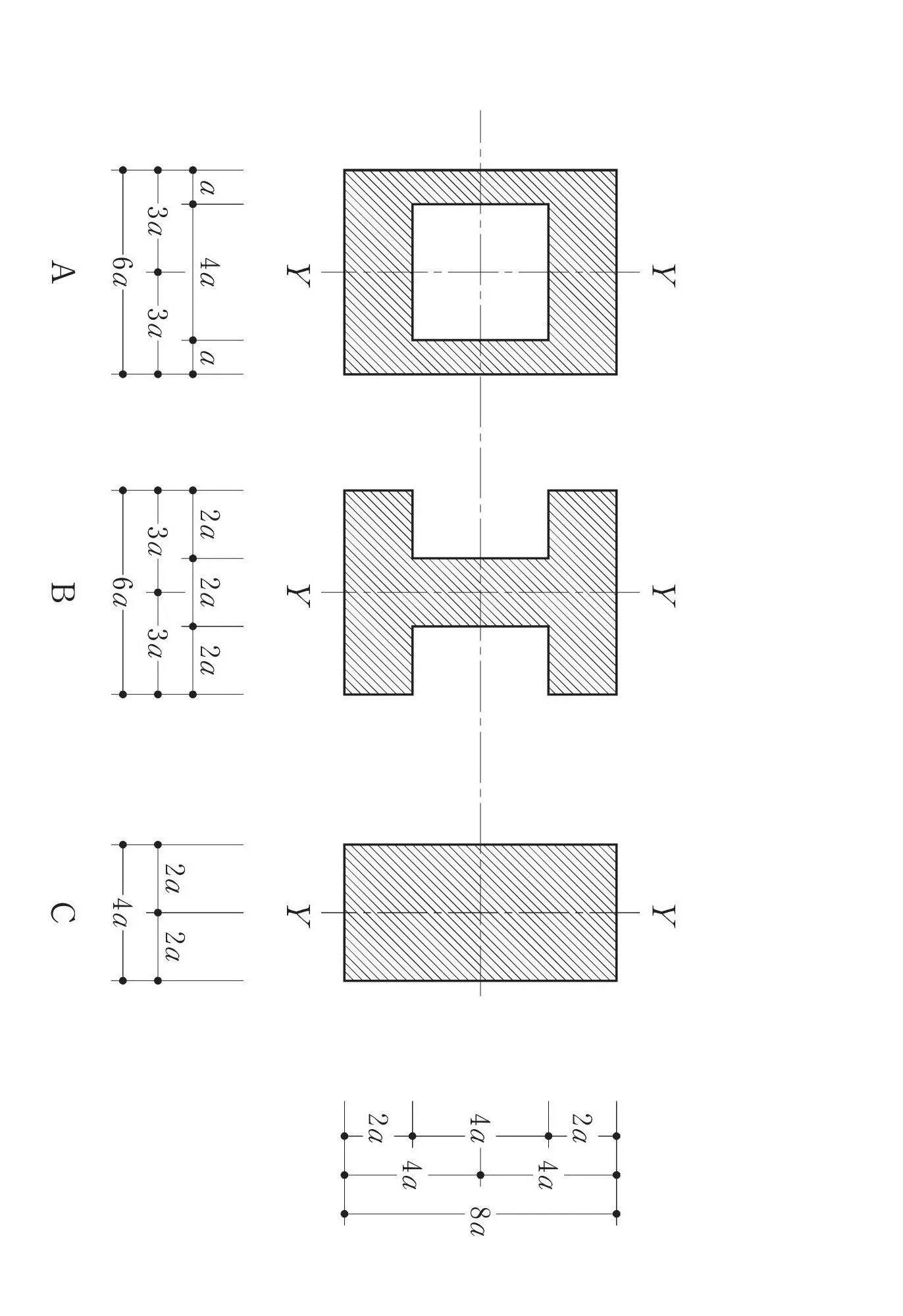
問題

記号の見分け方

- X方向を軸にする
- 断面二次モーメント「Ix」
- Y方向を軸にする
- 断面二次モーメント「Iy」
- 断面形状ABCに対して
- 「Ixa」「Ixb」「Ixc」
- 「Iya」「Iyb」「Iyc」



X方向とY方向
どちらを軸にするか?


この動画を YouTube で視聴
1.選択肢の共通部分に注目する
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
選択肢の共通部分に注目!
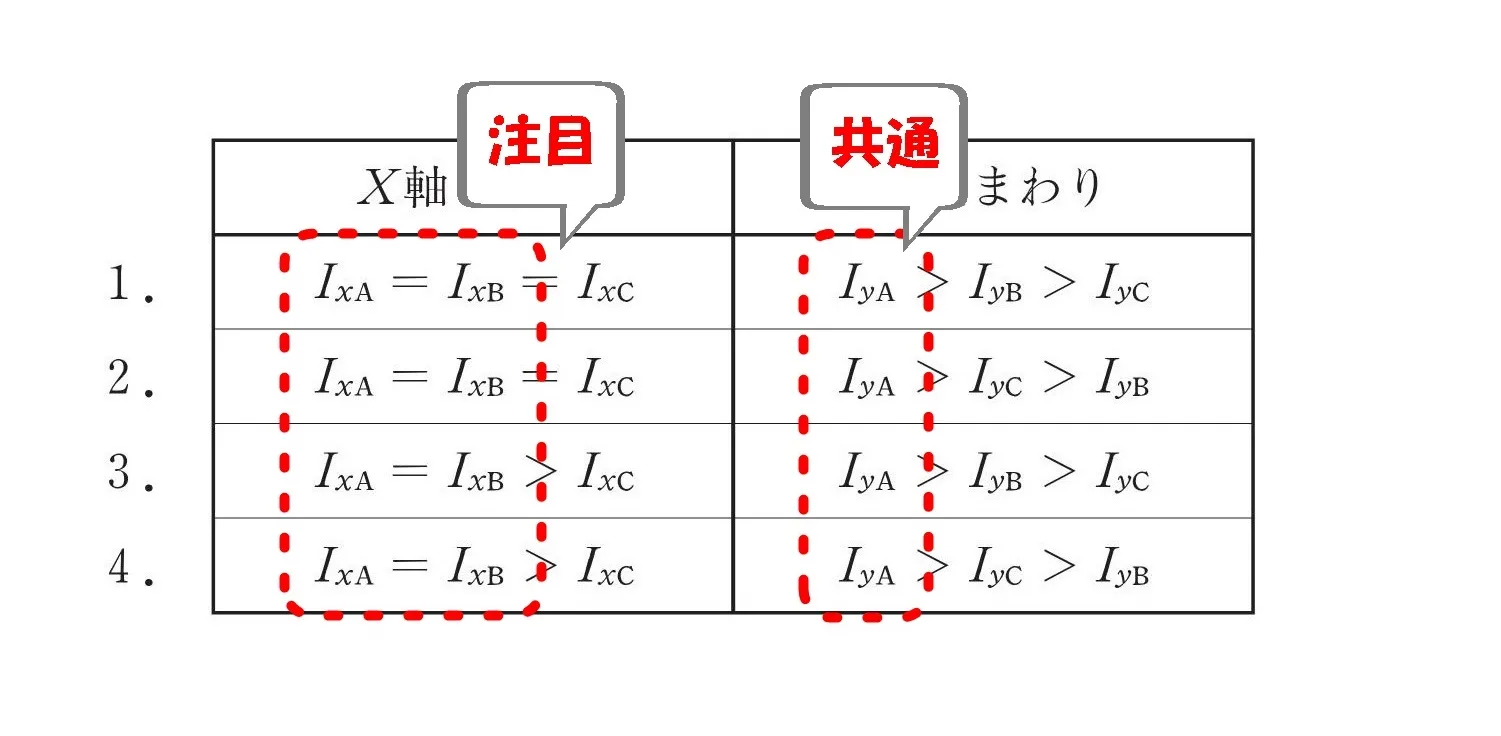

選択肢の共通部分
- 1.2.3.4.のすべての選択肢に「Ixa=Ixb」
- 1.2.3.4.のすべての選択肢に「Iya>」
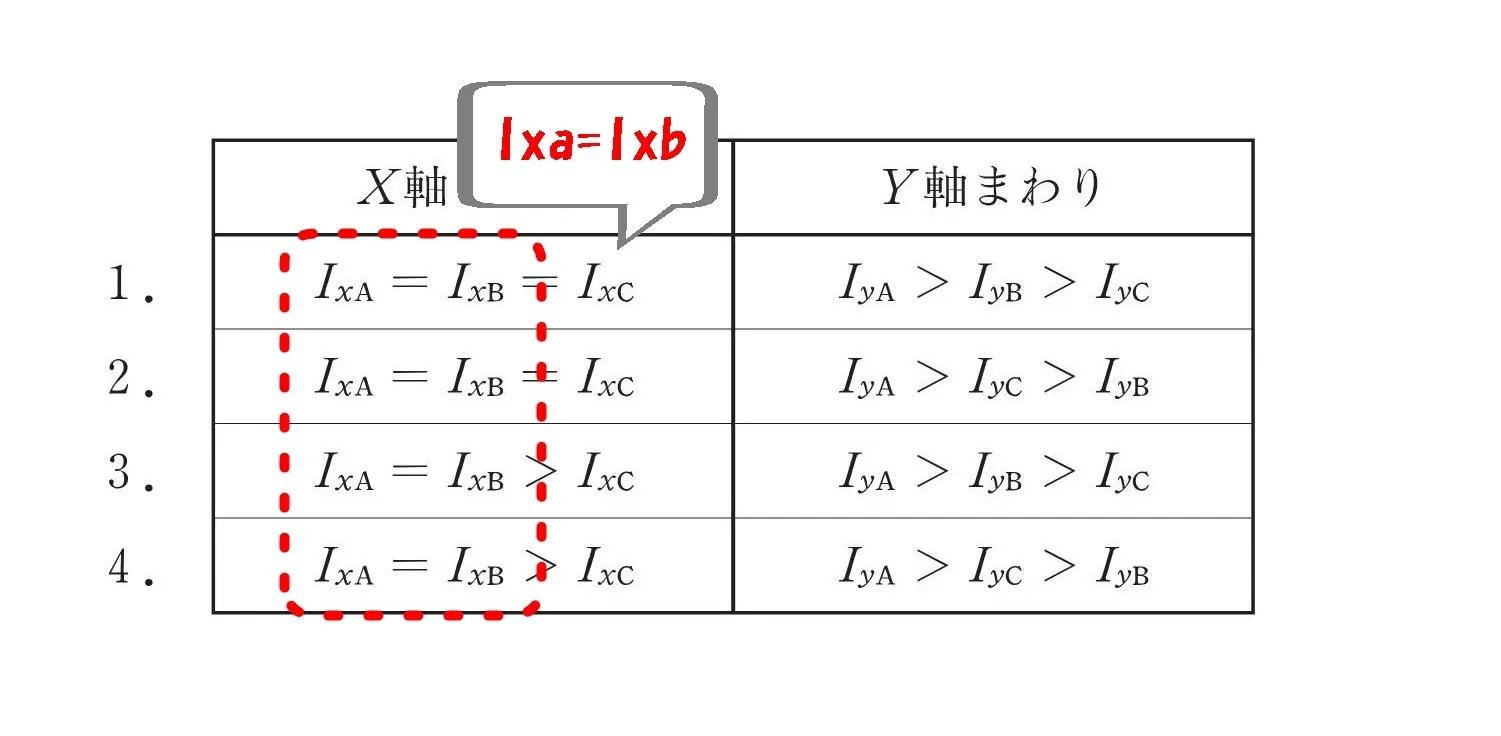

「Ixa=Ixb」について、断面二次モーメントの公式に照らして確認しておきましょう。
(時間制限のある本試験においては、作業を省いても構いません。)
確認する

公式
$$断面二次モーメント=\frac{ bh^3 }{ 12 }$$$$⇨\frac{ 1 }{ 12 }*\{bh^3(外形部分)-bh^3(空洞部分)\}$$
公式から読み取れること
- 断面二次モーメントは幅に比例する。
- 断面二次モーメントは高さの3乗に比例する。
- 断面二次モーメントは部材の断面形状に左右される。
「Ixa=Ixb」
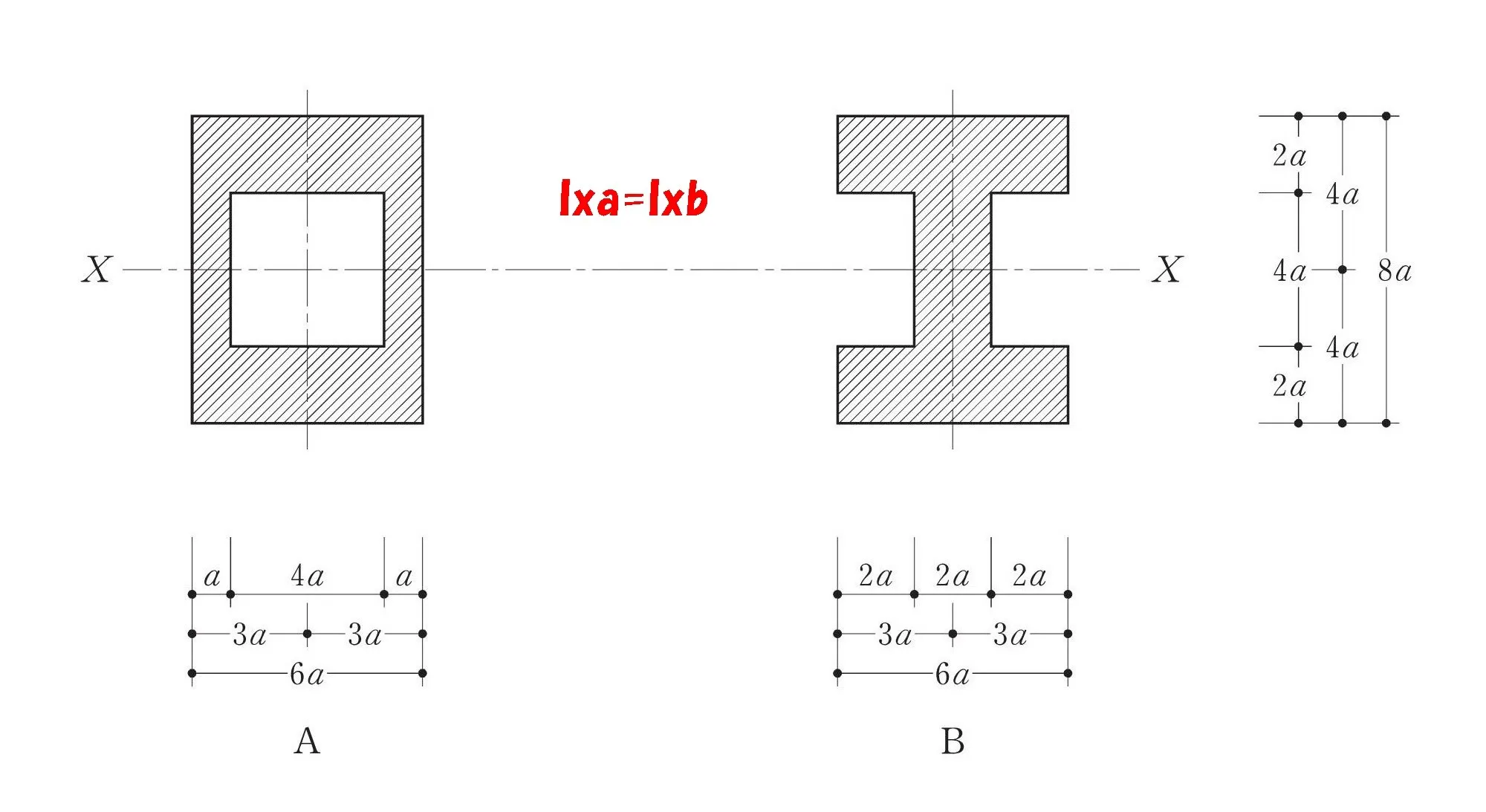

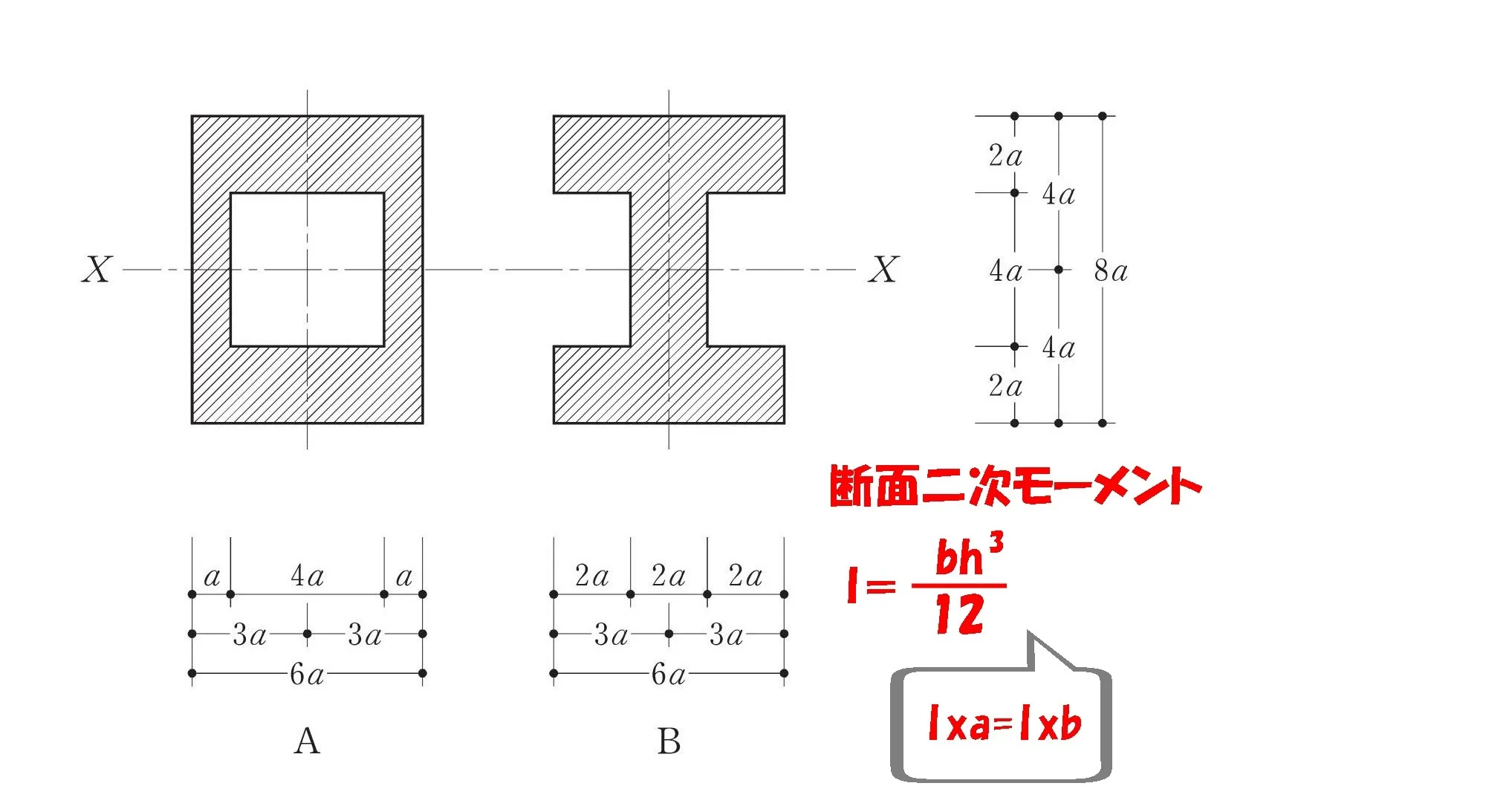
外形寸法は同じ
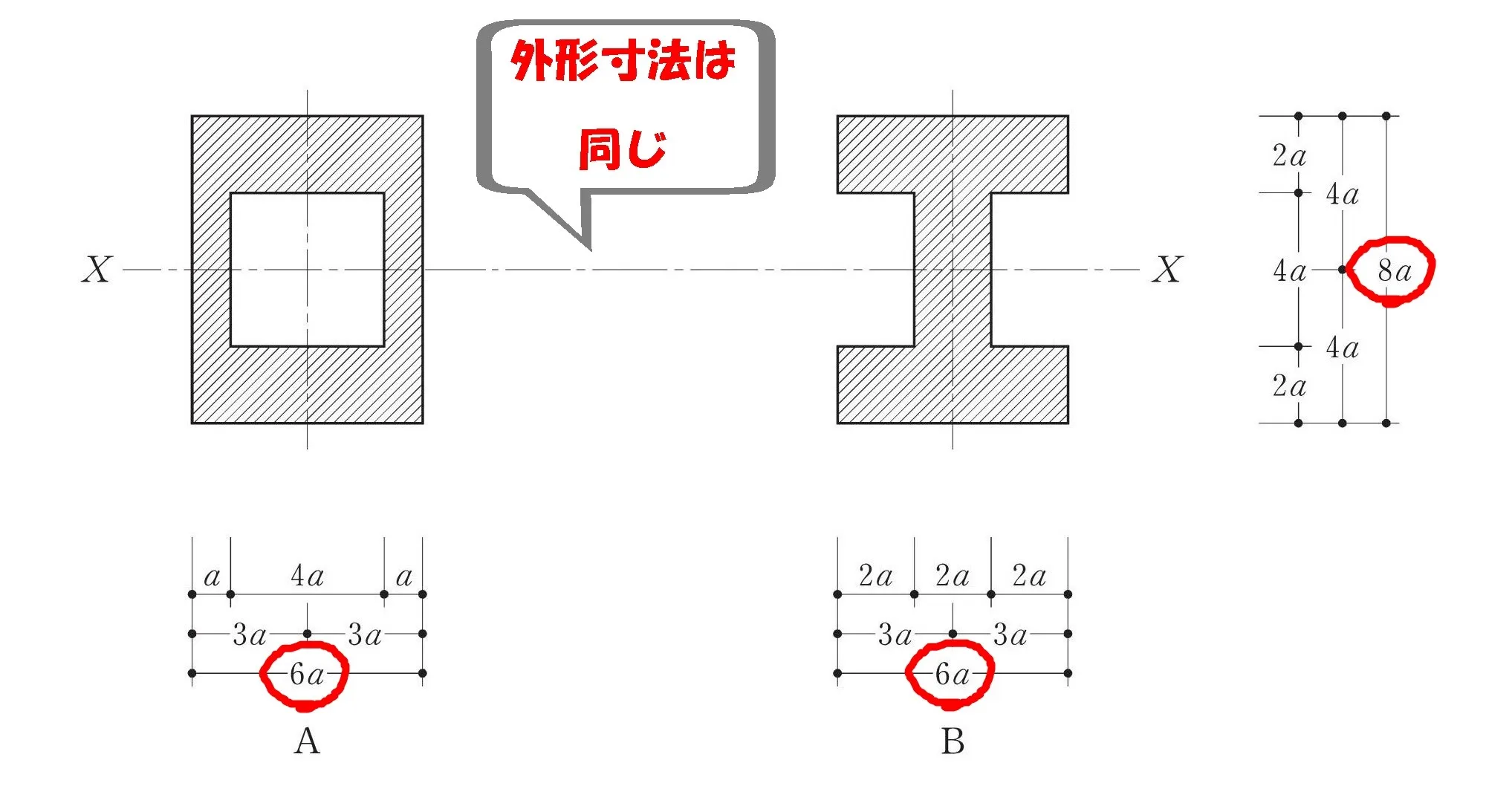

$$部材ABの幅=6a・部材ABの高さ=8a$$
空洞部分の寸法は同じ
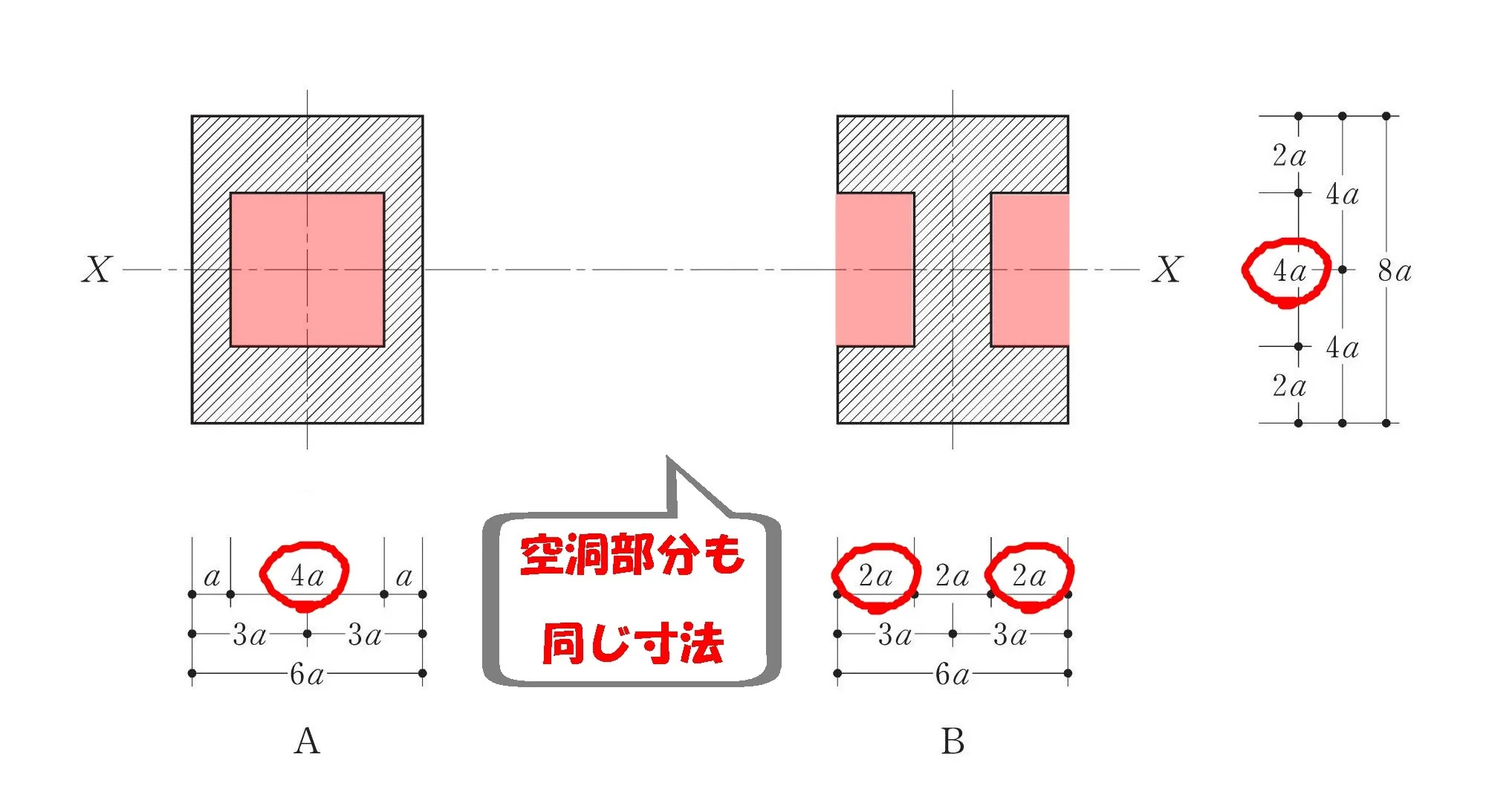

$$部材Aの空洞の幅=4a,空洞の高さ=4a$$$$部材Bの空洞の幅=2a,空洞の高さ=4a(空洞は2ヵ所)$$
空洞部分を比較してみる
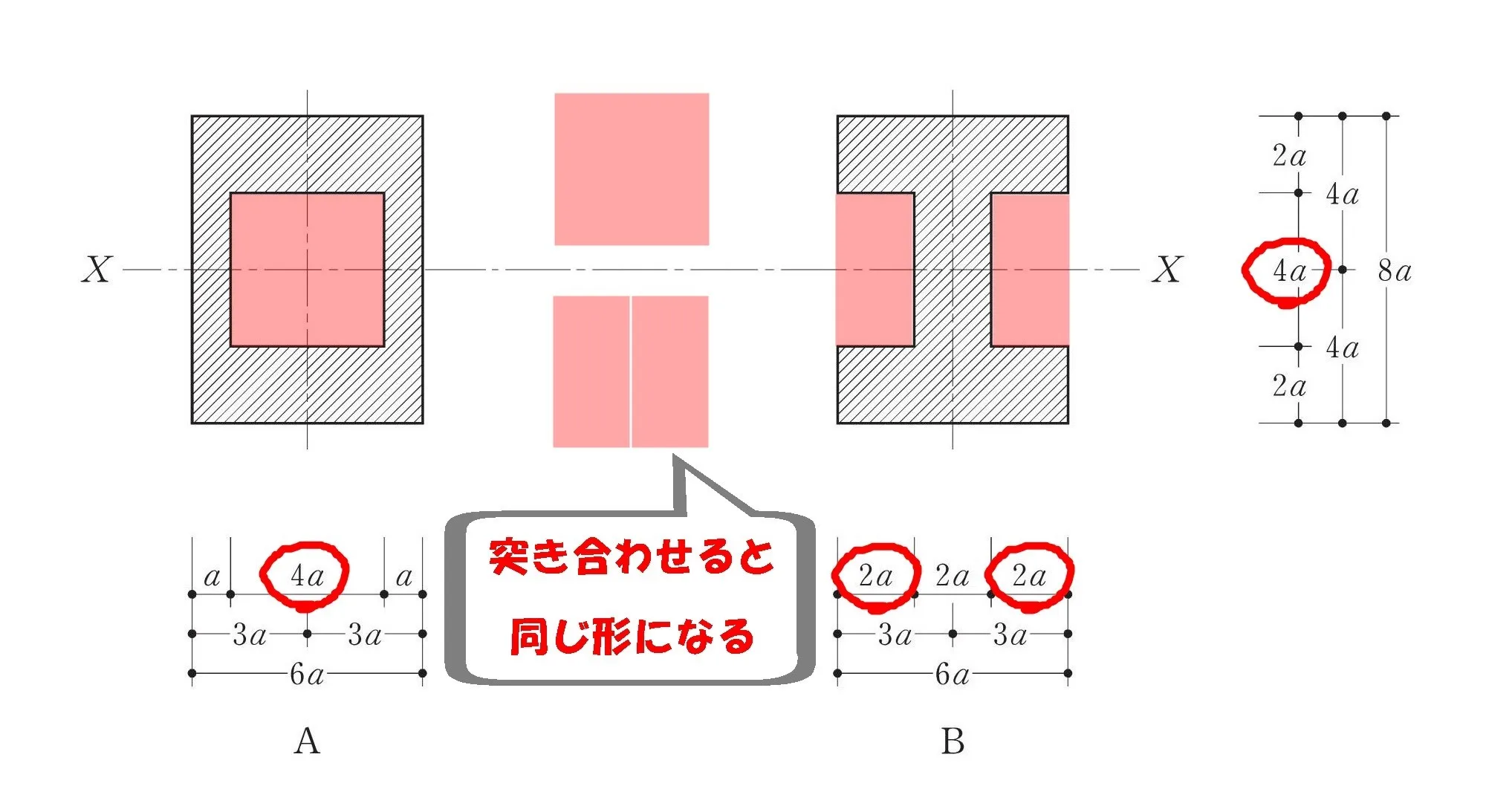

$$部材Aの空洞の寸法:4a*4a$$$$部材Bの空洞の寸法:(2a+2a)*4a$$
断面二次モーメントを比較
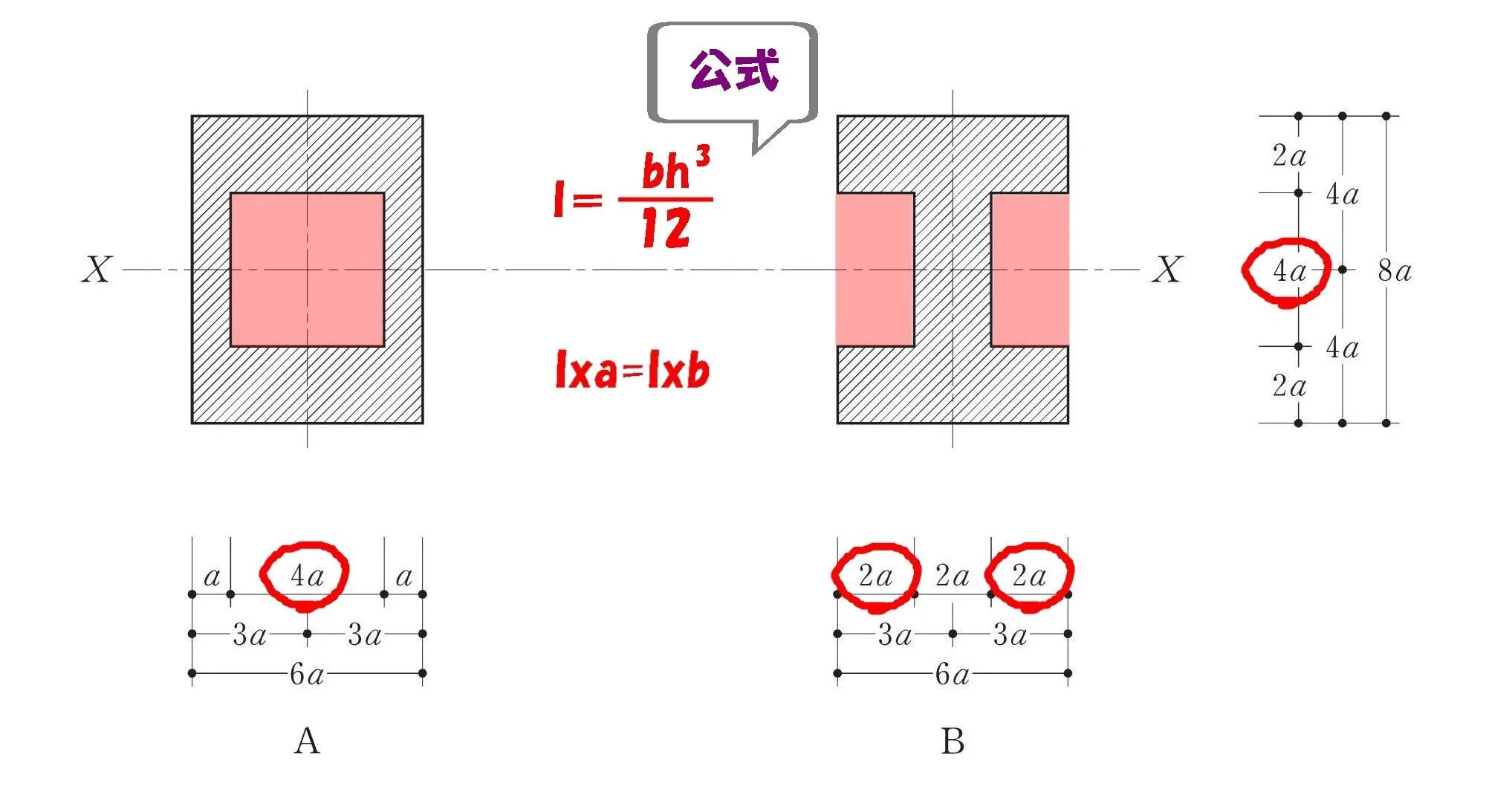

$$Ixa=\frac{ 1 }{ 12 }*\{6a*8a^3(外形部分)-4a*4a^3(空洞部分)\}$$
$$Ixb=\frac{ 1 }{ 12 }*\{6a*8a^3(外形部分)-2*2a*4a^3(空洞部分)\}$$$$=\frac{ 1 }{ 12 }*\{6a*8a^3(外形部分)-4a*4a^3(空洞部分)\}$$
$$式の数値が同じなので、Ixa=Ixb$$
・・・公式を比較すれば、計算するまでもないですよね?
公式
$$断面二次モーメント=\frac{ bh^3 }{ 12 }$$$$⇨\frac{ 1 }{ 12 }*\{bh^3(外形部分)-bh^3(空洞部分)\}$$
公式から読み取れること
- 断面二次モーメントは幅に比例する。
- 断面二次モーメントは高さの3乗に比例する。
- 断面二次モーメントは部材の断面形状に左右される。
Ixa=Ixbは共通


共通部分の比較について
共通部分となるIxaとIxbの比較は不要。
試験問題は4者択一の選択方式です。
「IxaとIxb」を比較しても選択肢を減らすことは出来ません。
選択肢を絞り込むには「何と何を比較すればよいか?」という視点を持ちましょう。
そうすることで、解答に要する時間とエネルギーを節約することができます。



Ixa=Ixbは確定だね。
2.共通部分を除き、残り2つを比較する
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
IxbとIxcを比較する
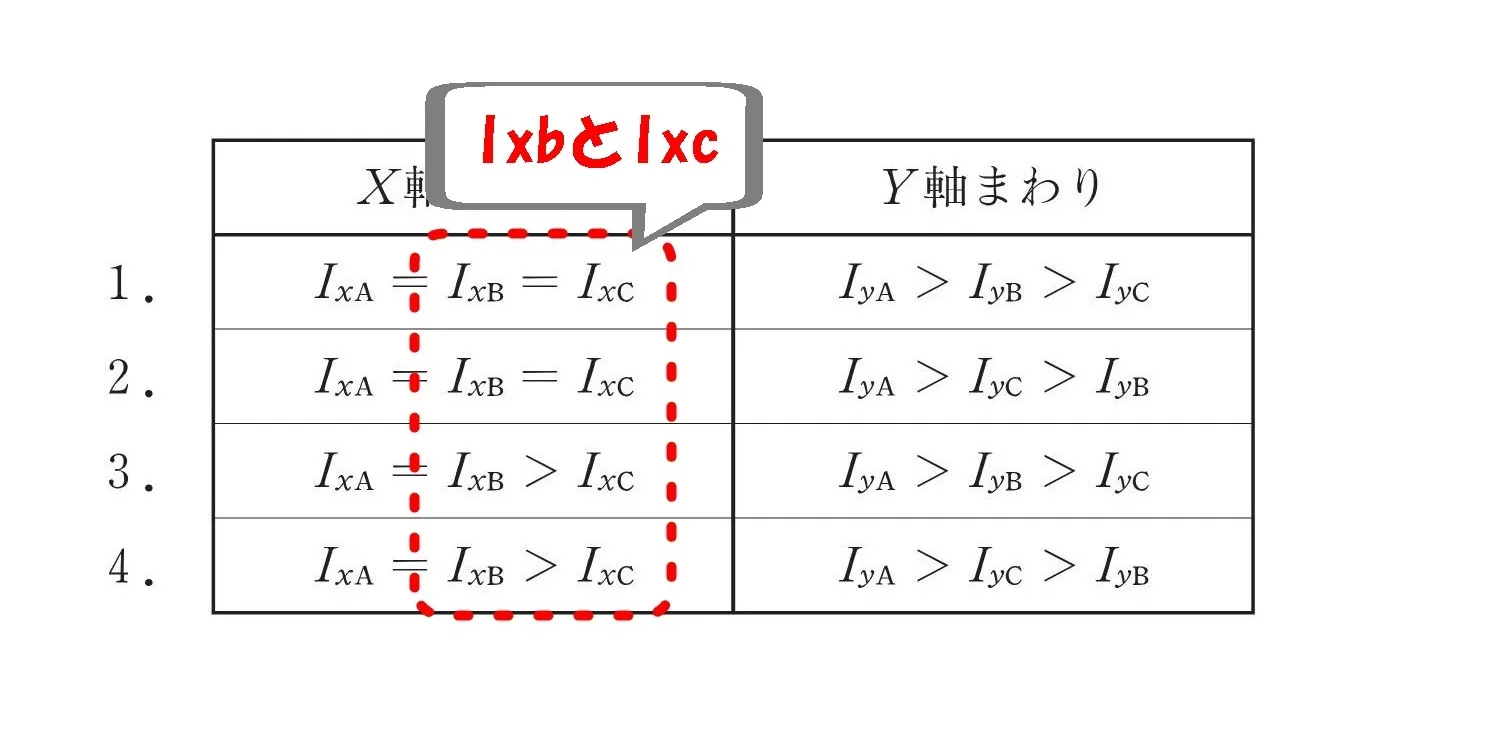

それでは本格的に問題の解答へと話を進めましょう。
断面二次モーメントの計算は桁数の多い掛け算なので、その作業だけでも時間が掛かりますよね?
ここでは「計算に費やすエネルギーを出来るだけ減らしたい」という視点も入れつつ、解説していきましょう。
a=1を代入する
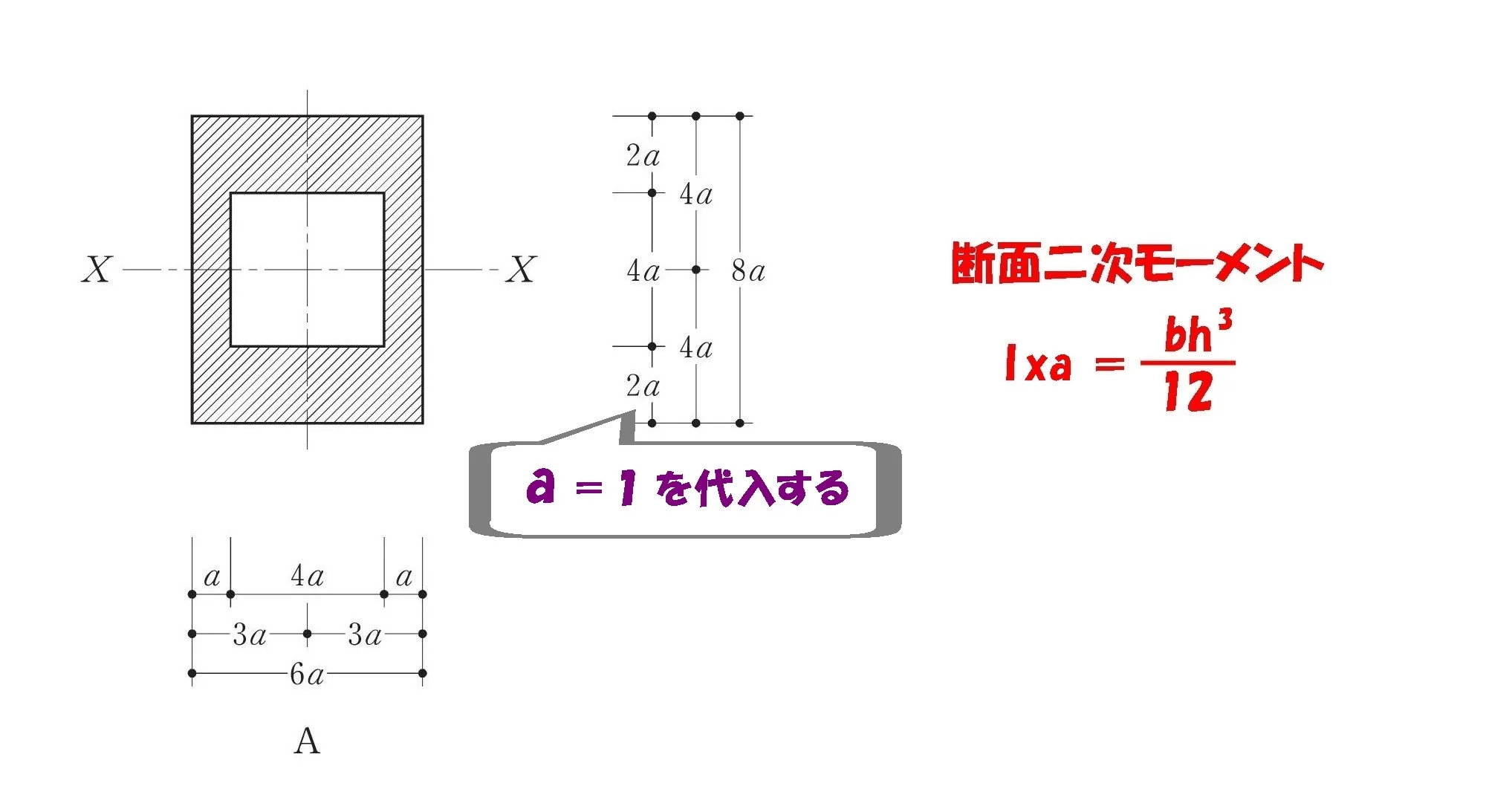

ワンポイント
計算を楽にするには、数式にアルファベットaを入れないようにすること。
この問題は「数値の大小を比較する」だけの解答なので、差し支えはありません。
「a=1」を代入することで、計算式が簡略化して数値の読み間違いリスクを減らせます。



いいね!
3.部材を成形なパーツに分解し、比較しやすくする
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
断面二次モーメント:Ixa
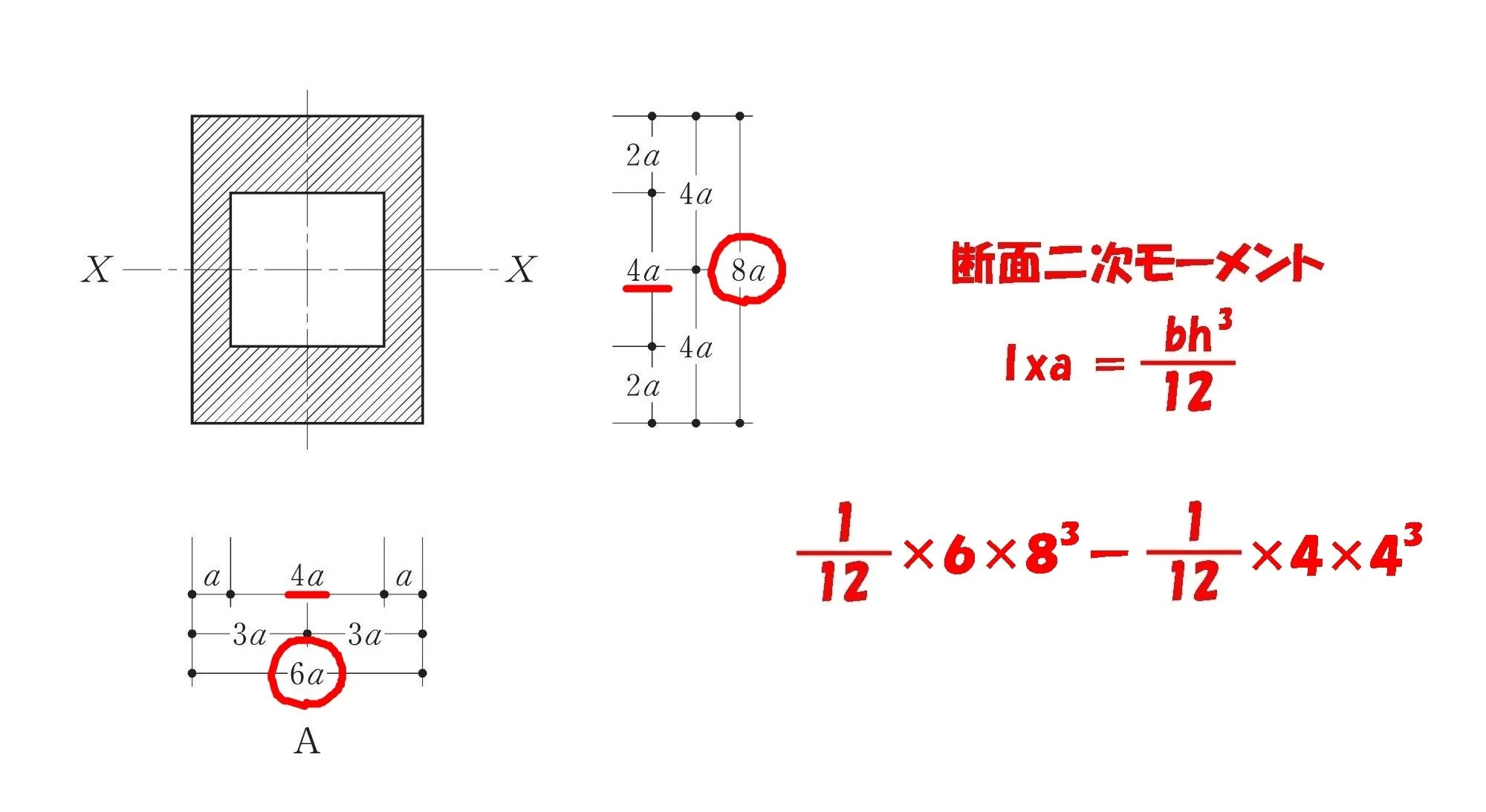

公式
$$断面二次モーメント=\frac{ 1 }{ 12 }*\{bh^3(外形部分)-bh^3(空洞部分)\}$$
$$(計算は省略)$$


A=Bなので、
BとCを比べるだけ。
断面二次モーメント:Ixb
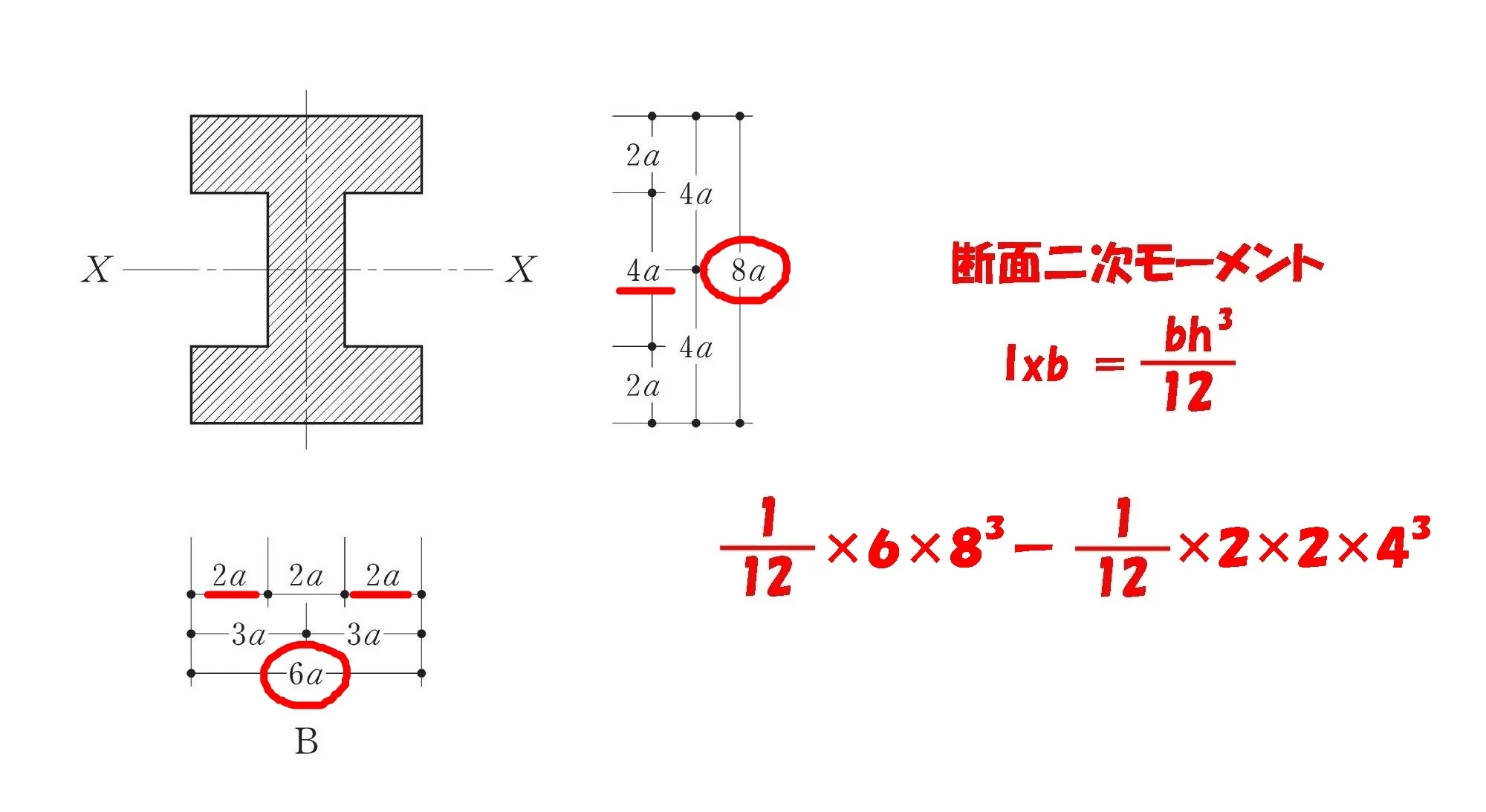

公式
$$断面二次モーメント=\frac{ 1 }{ 12 }*\{bh^3(外形部分)-bh^3(空洞部分)\}$$
$$Ixb=\frac{ 1 }{ 12 }*\{6*8^3(外形部分)-2*2*4^3(空洞部分)\}$$
断面二次モーメント:Ixc
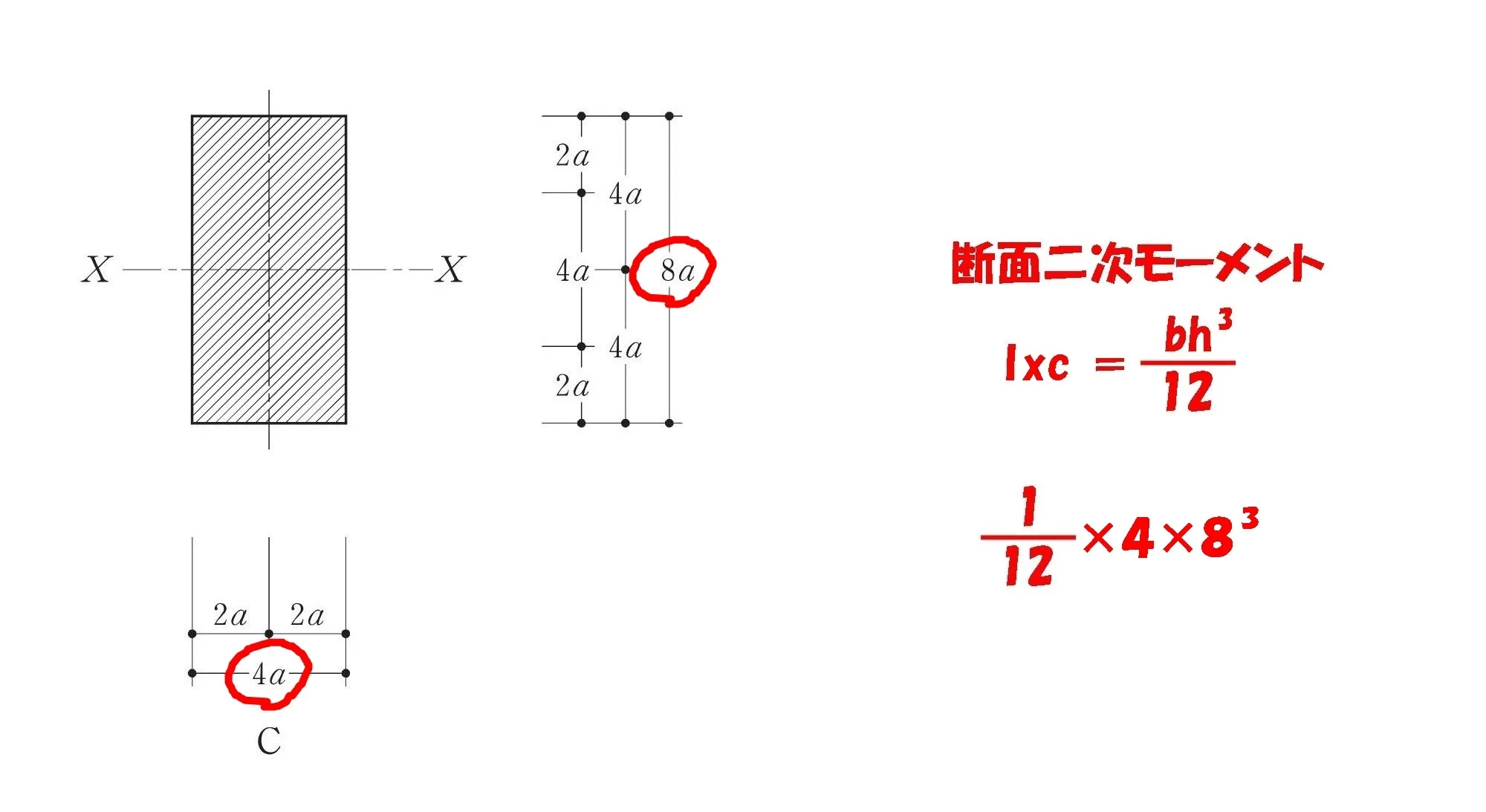

公式
$$断面二次モーメント=\frac{ bh^3 }{ 12 }$$
$$Ixc=\frac{ 1 }{ 12 }* 4*8^3$$



BとCを比べるだけ、
時間を効率良く使おう。
4.計算式は共通項を(・)で束ねて計算式から省く
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
ワンポイント
計算式の書き出しスペースは、問題冊子の表紙を千切って裏面を活用する。
$$Ixb:Ixc$$$$\underline{\frac{ 1 }{ 12 }}*\{6*8^3-2*2*4^3\}:\underline{\frac{ 1 }{ 12 }}* 4*8^3$$
$$(6*\underline{8^3}-2*2*4^3):4*\underline{8^3}$$
$$(6*\underline{2^3*4^3}-4*\underline{4^3}):4*\underline{2^3*4^3}$$
$$\underline{4^3}*(6*2^3-4):\underline{4^3}*4*2^3$$
$$(6*2^3-4):4*2^3⇨(6*2*\underline{2^2}-\underline{2^2}):4*2*\underline{2^2}$$
$$\underline{2^2}*(6*2-1):\underline{2^2}*4*2⇨(6*2-1):4*2$$
$$(6*2-1):4*2⇨11:8=Ixb>Ixc$$
BとCの2つを比較するだけなので、共通項はバシバシ削っていきましょう。



共通の数字で束ねて
バシバシ削っていこう。
ワンポイント
比較するものが3つ以上ある場合も、2つずつ比較して選択肢の数を減らしていく。
1.選択肢の共通部分に注目する
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
選択肢の共通部分に注目!
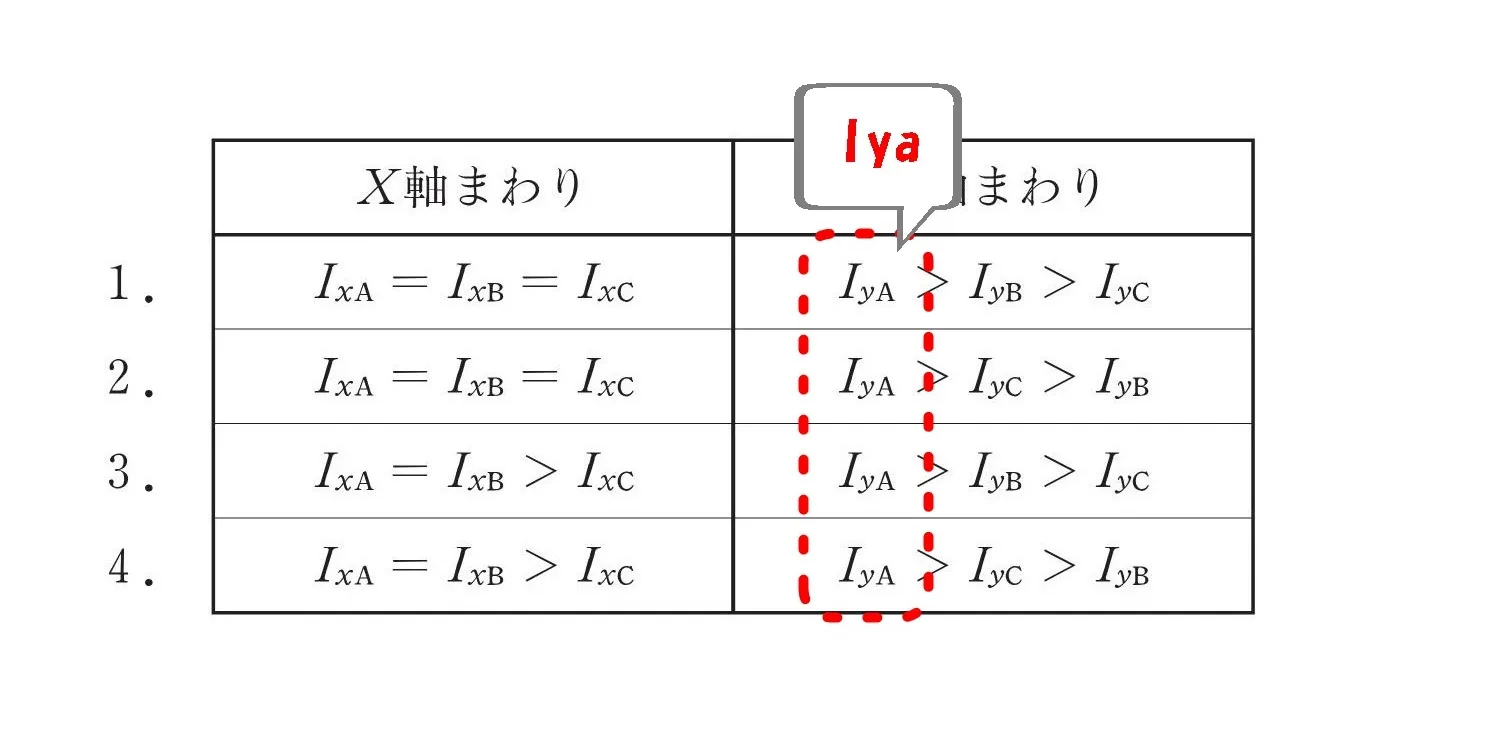

選択肢の共通部分
- 1.2.3.4.のすべての選択肢の最大値に「Iya」
共通部分の比較について
共通部分となる「Iya」の計算は不要。
試験問題は4者択一の選択方式です。(繰り返し)
「Iya」を算出しても選択肢を減らすことは出来ませんよね?
選択肢を絞り込むには「何と何を比較すればよいか?」という視点が大事です。
そうすることで、解答に要する時間とエネルギーを節約しましょう。
2.共通部分を除き、残り2つを比較する
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
IybとIycを比較する
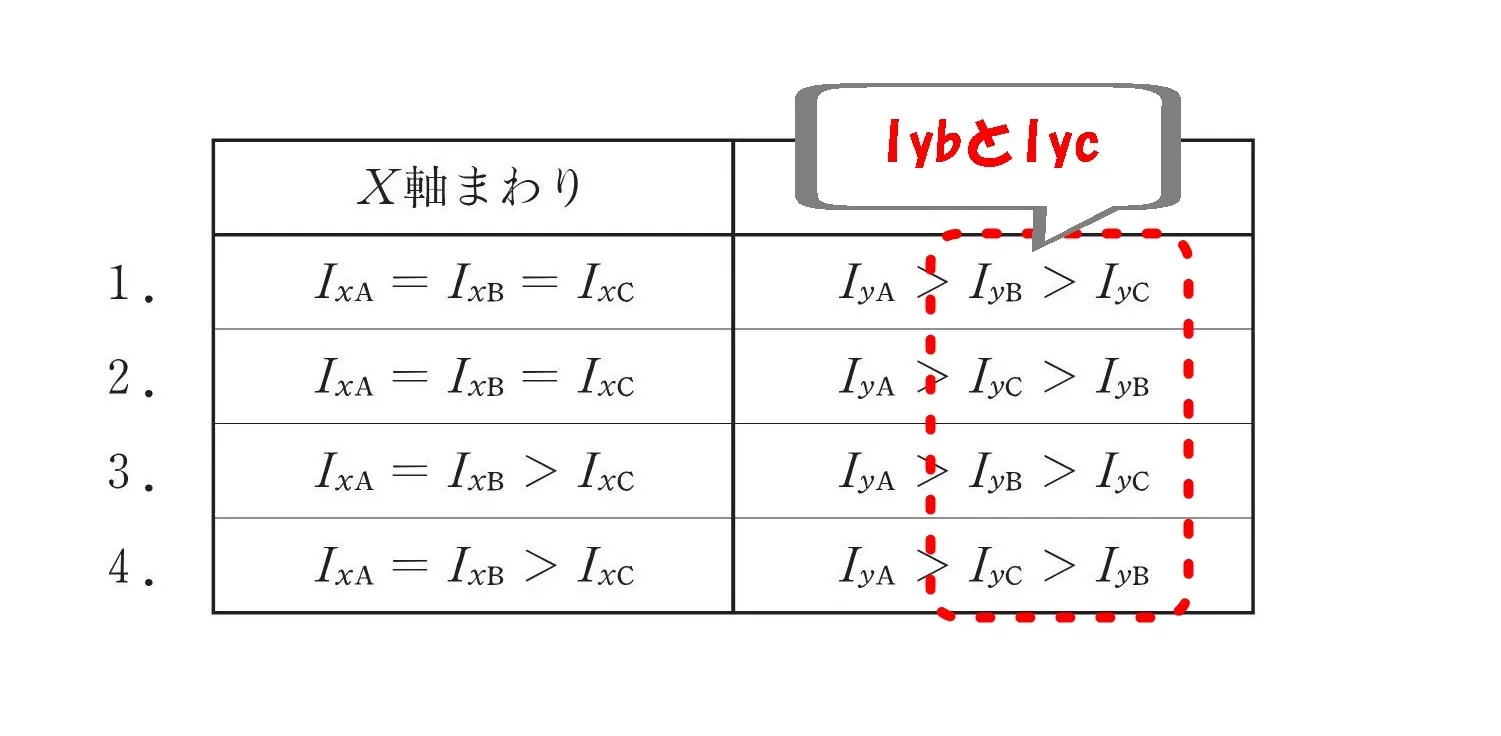

Y軸を水平に向ける

公式
$$断面二次モーメント=\frac{ bh^3 }{ 12 }$$
断面二次モーメントの曲がり軸がY方向に切り変わると、公式のbとhの位置づけが変わります。
Y方向に対応するため、問題用紙を回転させてY軸が水平になるように向けましょう。



問題用紙を
90度回転させる。
IybとIycを比較する
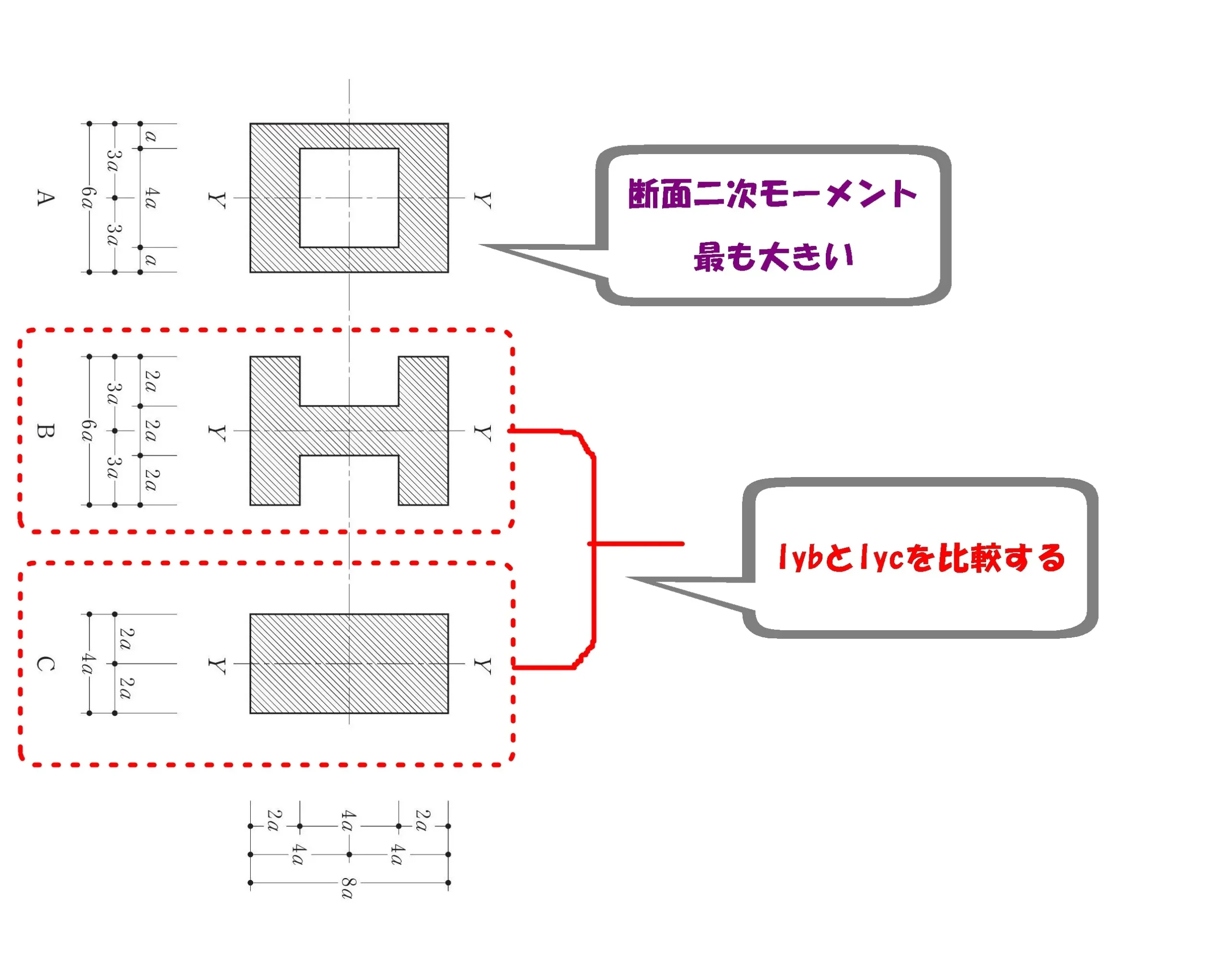

「Iyb」と「Iyc」は形状が異なるので比較するには工夫が必要です。
H型をしている「Iyb」の部材については3つのパーツに分解しましょう。
3.部材を成形なパーツに分解し、比較しやすくする
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
「Iyb」の部材を分解する
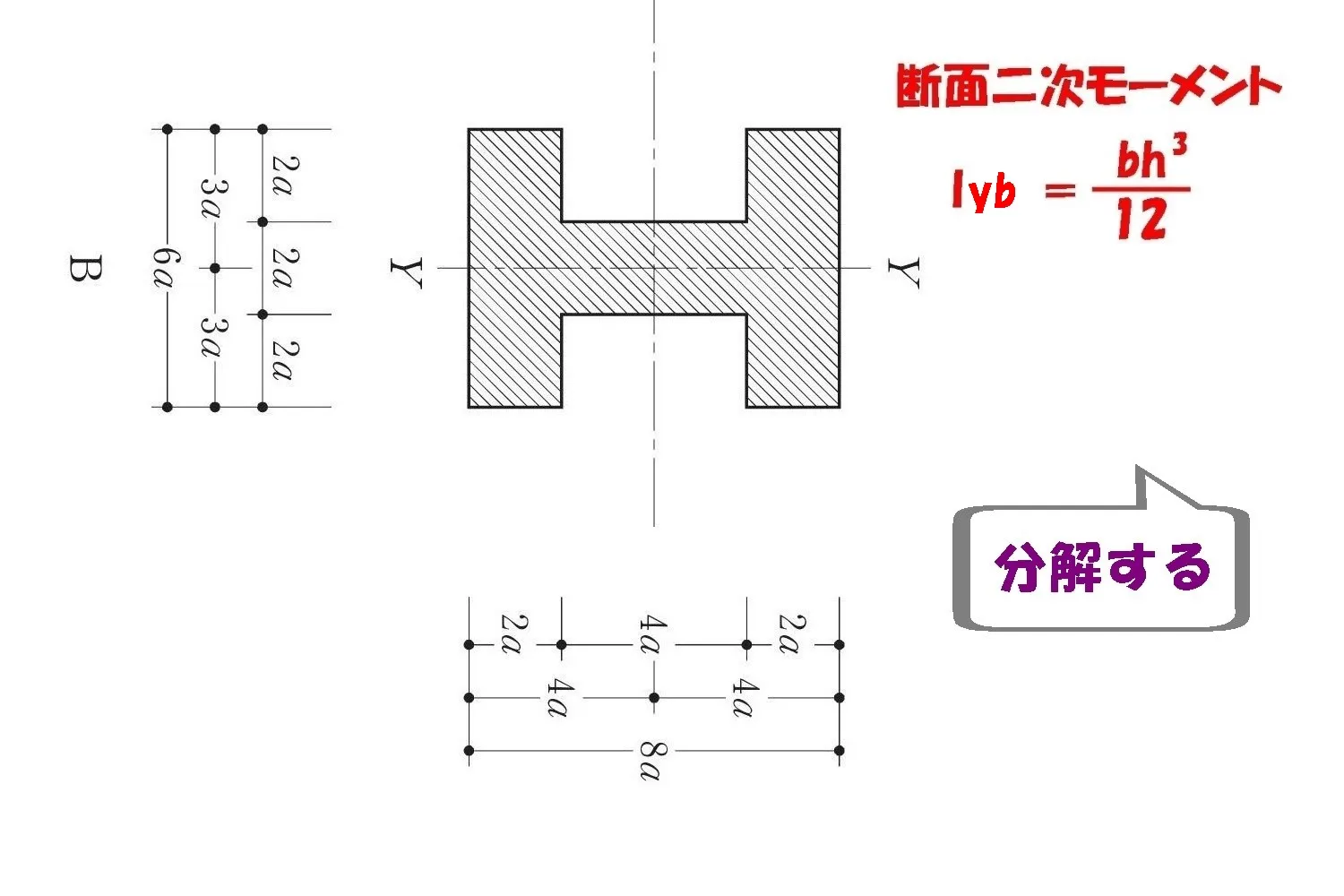

3つのパーツに分解する
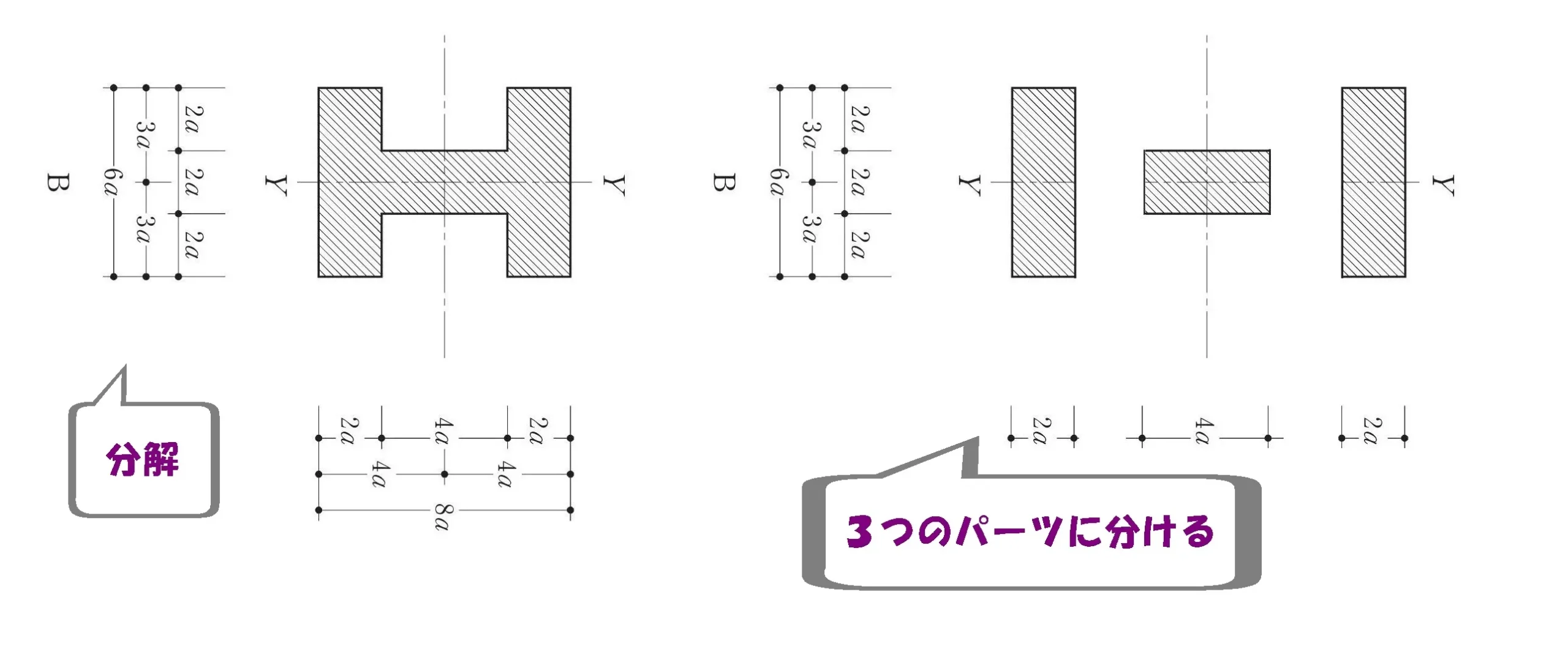

H型の部材を3つの成形なパーツに分解します。
注意!
分解したパーツは、それぞれのパーツの図芯が回転軸のうえにあること。



図芯が回転軸の上に
乗ってないとダメなの?



それが大前提だよ。
まずはそこが出発点です。
a=1を代入する
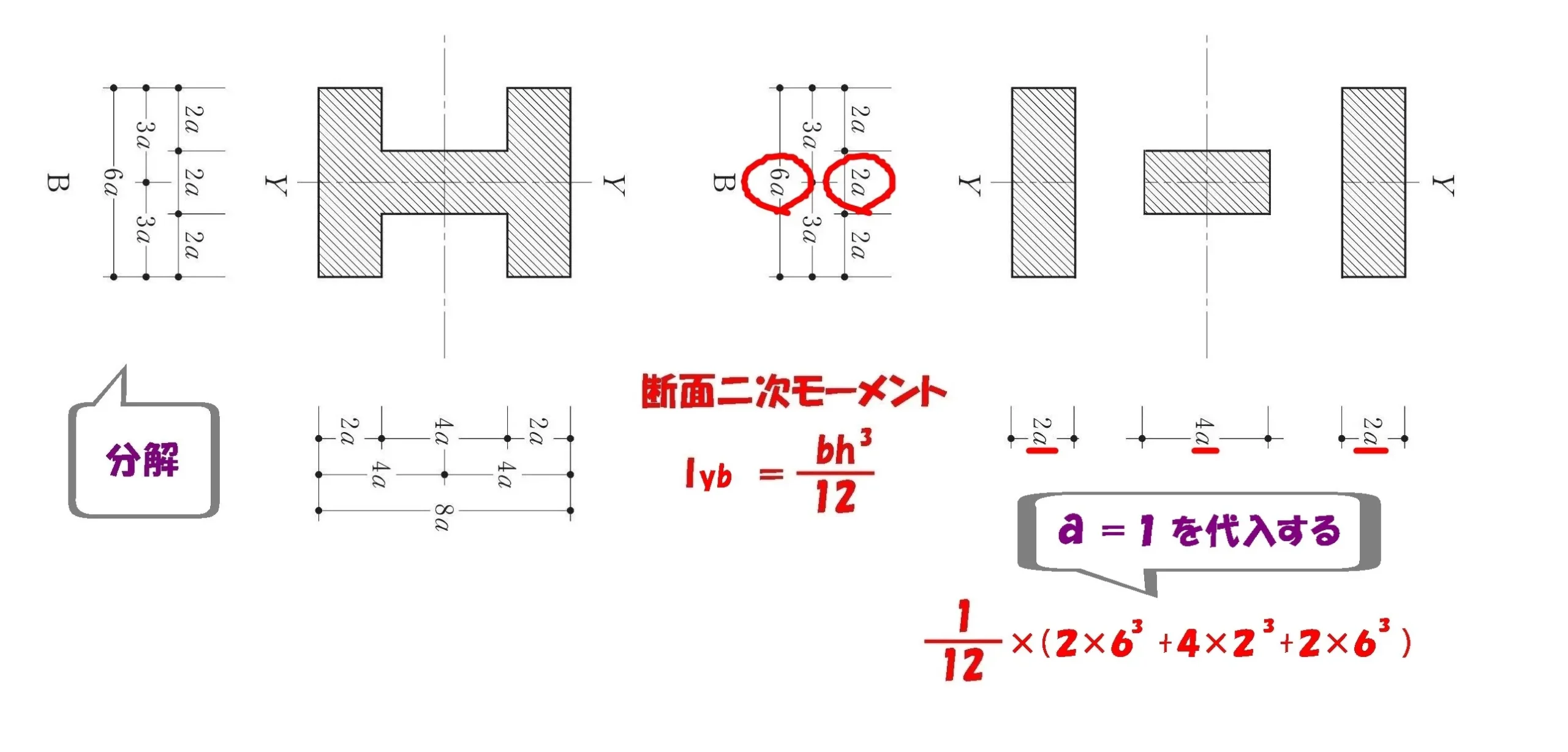

$$a=1を代入する。$$
$$Iyb=\frac{ 1 }{ 12 }*\{bh^3①+bh^3②+bh^3③\}$$
$$Iyb=\frac{ 1 }{ 12 }*\{2*6^3+4*2^3+2*6^3\}$$
4.計算式は共通項を(・)で束ねて計算式から省く
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く
ワンポイント
計算式の書き出しスペースは、問題冊子の表紙を千切って裏面を活用する。
IybとIycの数式
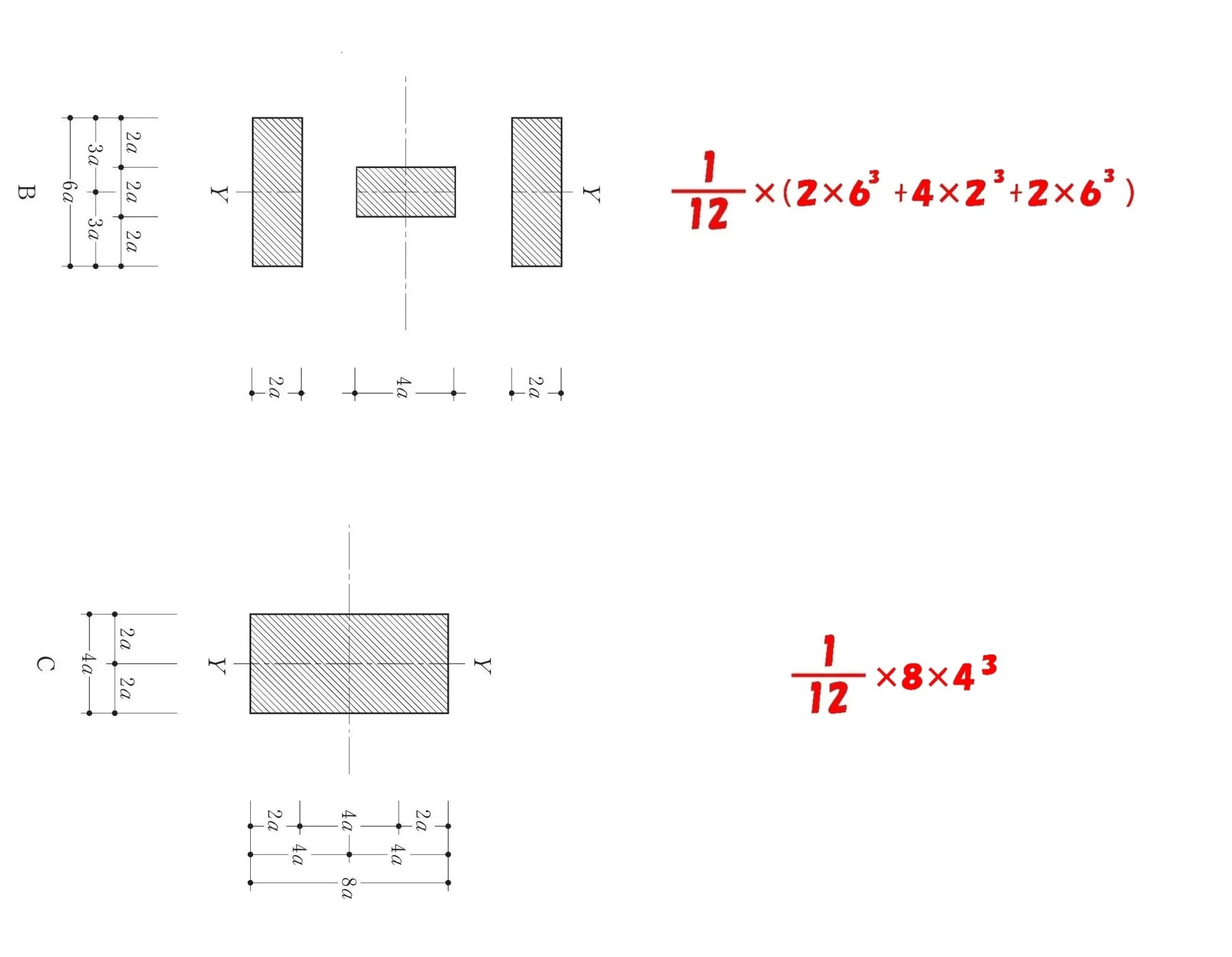

$$Iyb=\frac{ 1 }{ 12 }*\{2*6^3+4*2^3+2*6^3\}$$
$$Iyc=\frac{ 1 }{ 12 }*8*4^3$$
IybとIycを比較する
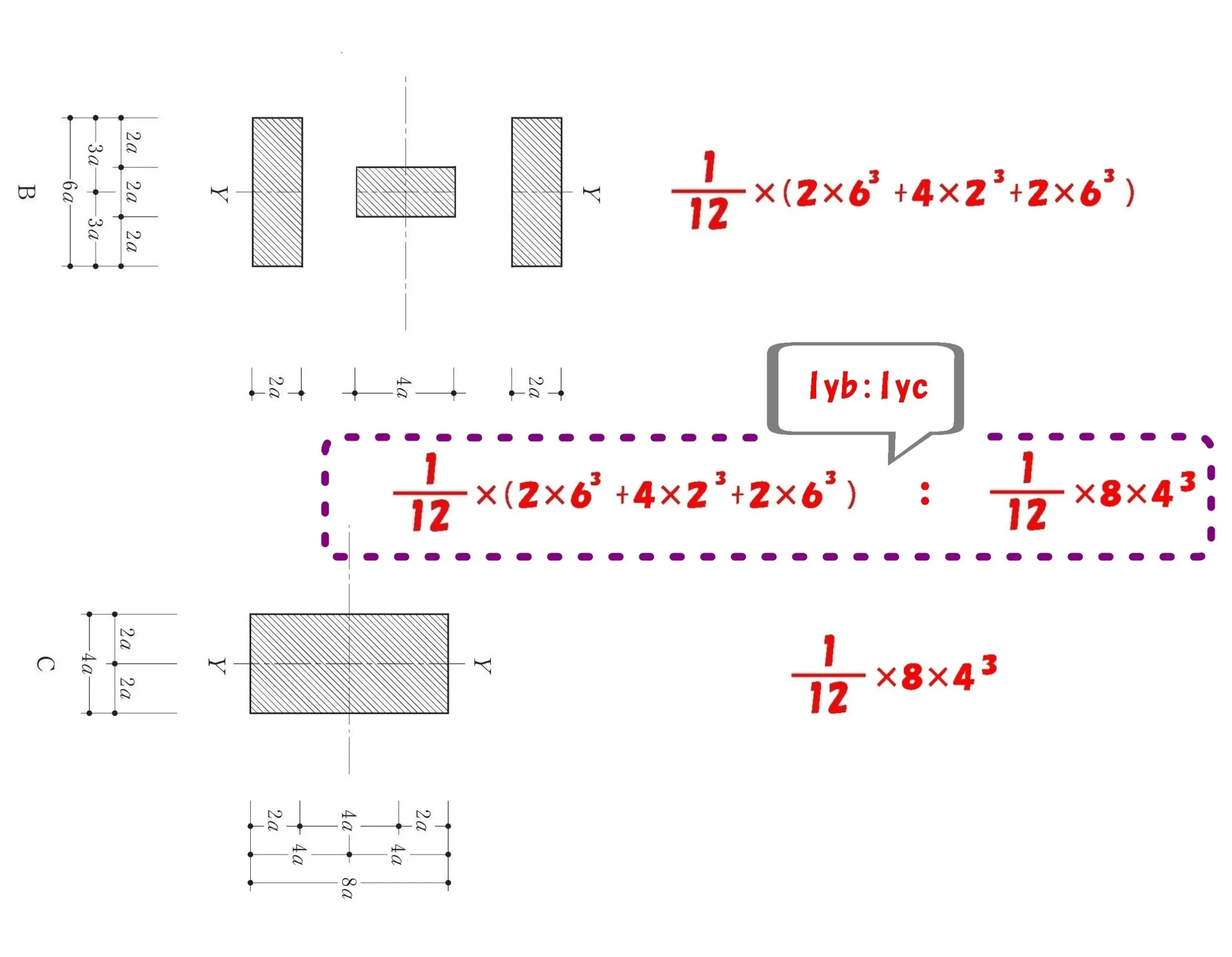

$$Iyb:Iyc$$
$$\underline{\frac{ 1 }{ 12 }}*\{2*6^3+4*2^3+2*6^3\}:\underline{\frac{ 1 }{ 12 }}*8*4^3$$
$$(\underline{2*6^3}+4*2^3+\underline{2*6^3}):8*4^3⇨(\underline{2*2*6^3}+4*2^3):8*4^3$$
$$(\underline{2^2*2^3}*3^3+\underline{2^2*2^3}):\underline{2^3}*\underline{2^3*2^3}$$
$$\underline{2^2*2^3}*(3^3+1):\underline{2^2*2^3}*\underline{2}*2^3$$
$$(3^3+1):2*2^3⇨28:16=7:4⇨Iyb>Iyc$$
$$X軸まわり[Ixb>Ixc],Y軸まわり[Iyb>Iyc]$$
BとCの2つを比較するだけなので、共通項はバシバシ削っていきましょう。



共通の数字で束ねて
バシバシ削っていこう。
ワンポイント
比較するものが3つ以上ある場合も、2つずつ比較して選択肢の数を減らしていく。
答え.3


攻略ポイント
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く


この動画を YouTube で視聴
梁のたわみ
難易度:★★☆☆☆
たわみの公式を使ったシンプルな基本問題です。
まず始めに、単純梁と片持ち梁の公式を確認しましょう。
たわみδとたわみ角θ
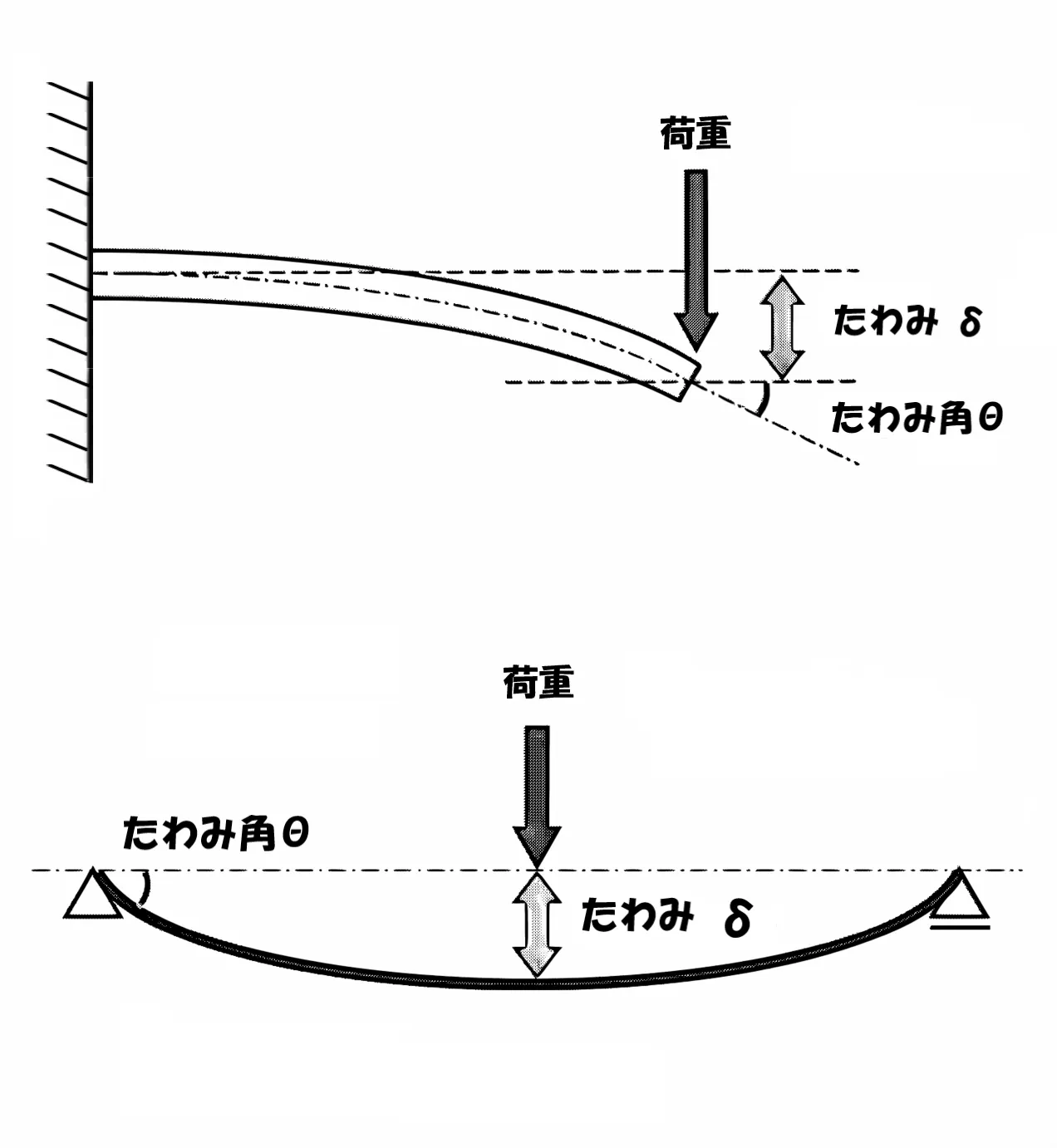

単純梁のイメージ
- たわみδ:梁が受ける荷重により生じる”中央部の下がり”
- たわみ角θ:梁が受ける荷重により生じる”両端の角度(変位)”
単純梁の公式
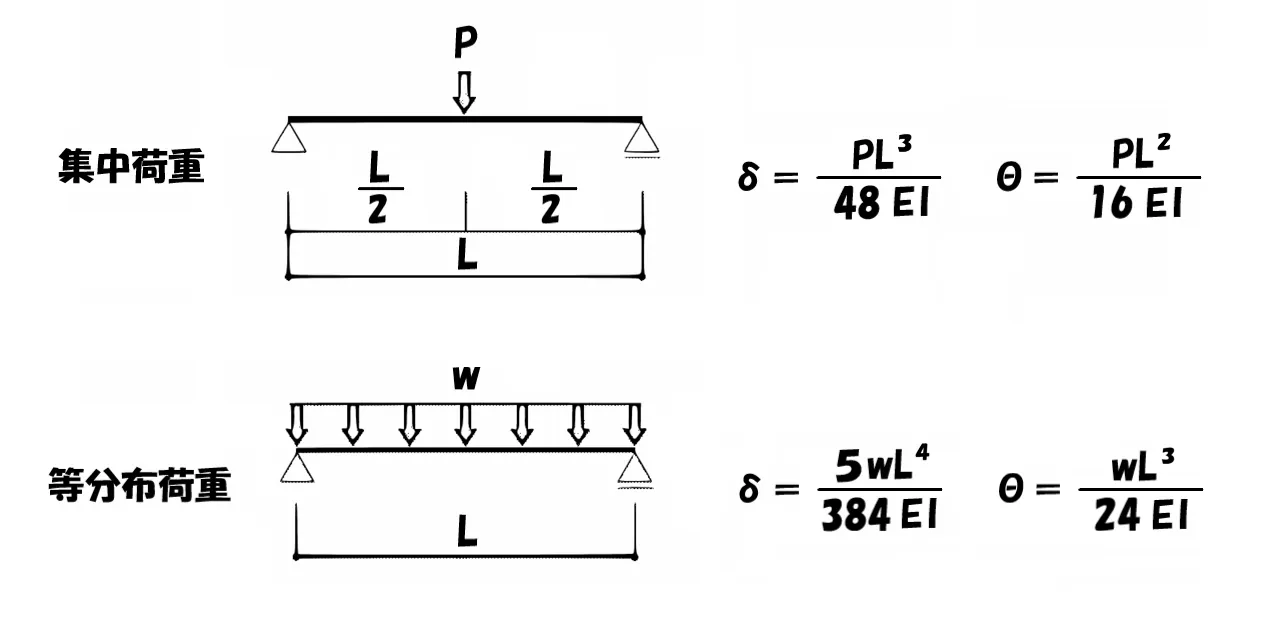

単純梁の公式(集中荷重)
$$たわみ:\delta=\frac{ PL^3 }{ 48EI },たわみ角:\theta=\frac{ PL^2 }{ 16EI }$$
- たわみは長さLの3乗に比例する。
- たわみ角は長さLの2乗に比例する。
片持ち梁の公式
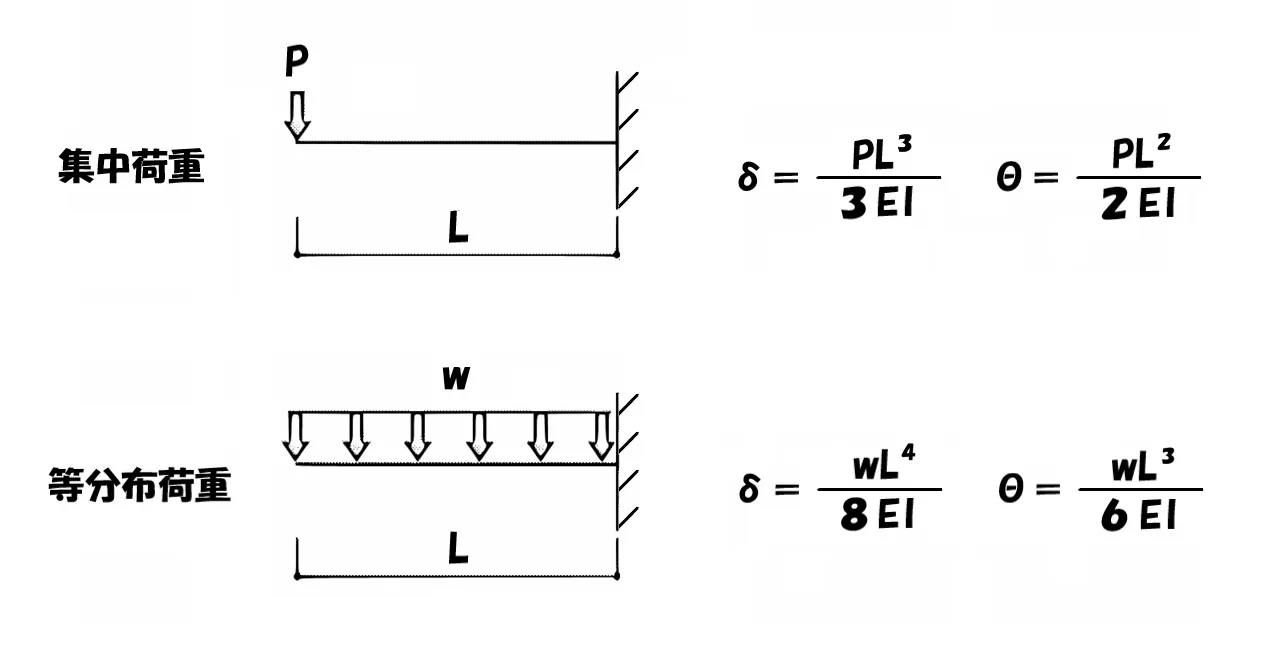

片持ち梁の公式(集中荷重)
$$たわみ:\delta=\frac{ PL^3 }{ 3EI },たわみ角:\theta=\frac{ PL^2 }{ 2EI }$$
攻略ポイント
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める
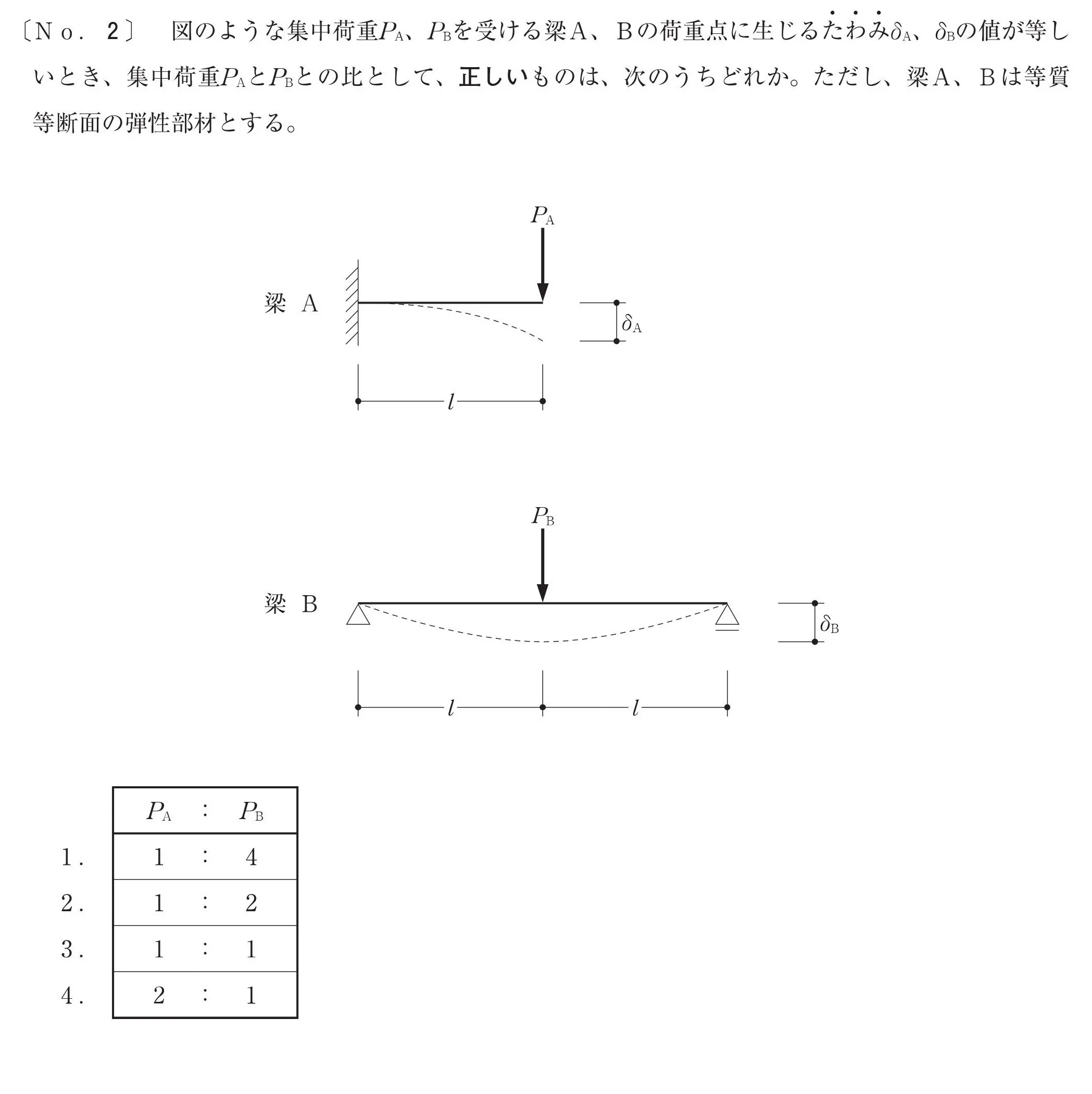
問題



この動画を YouTube で視聴
1.梁の形状と荷重の受ける範囲を読み取る
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める
問題文を読み取る
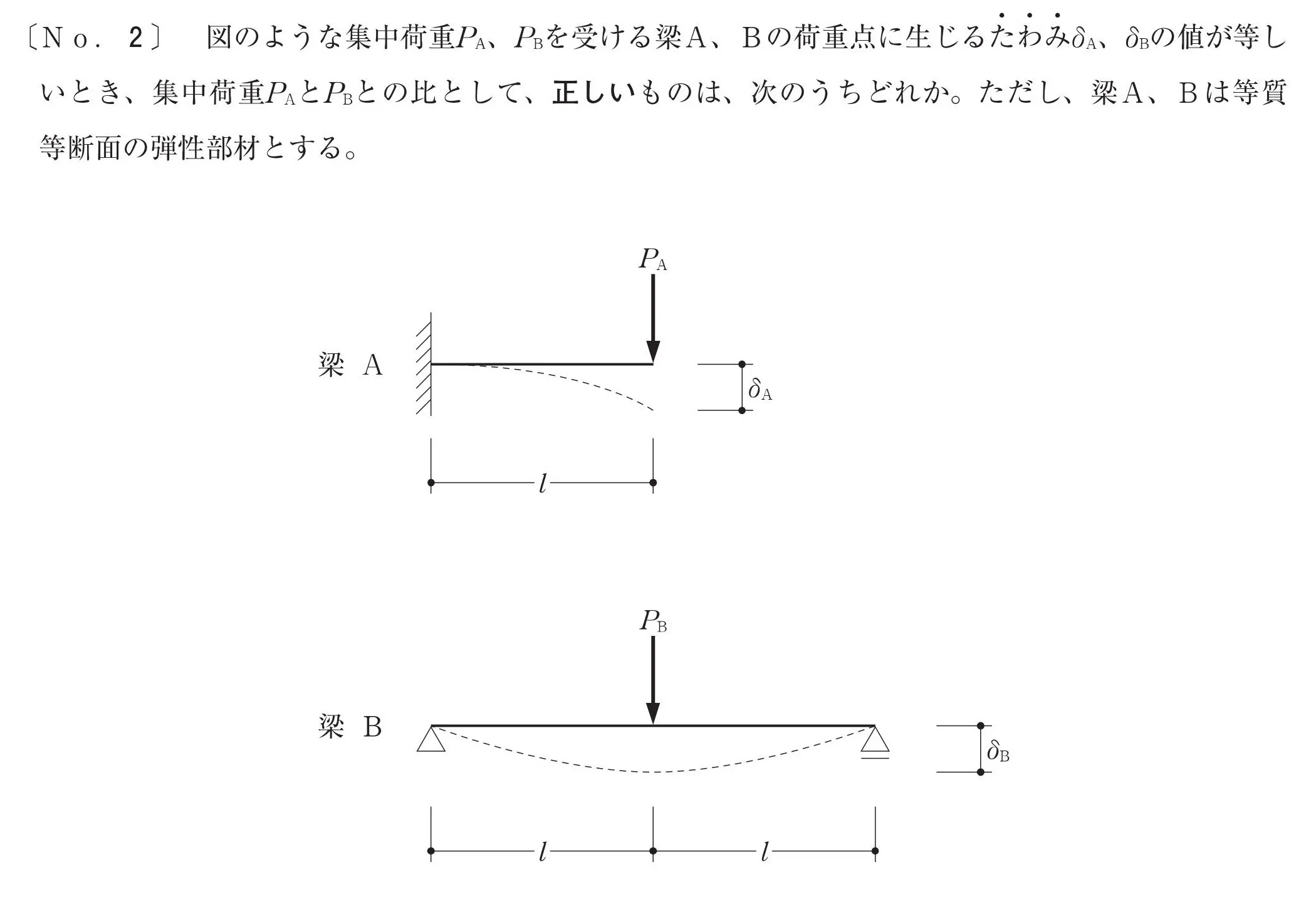

梁の支持方式
- 梁A:片持ち梁
- 梁B:単純梁
アンダーラインに注目!
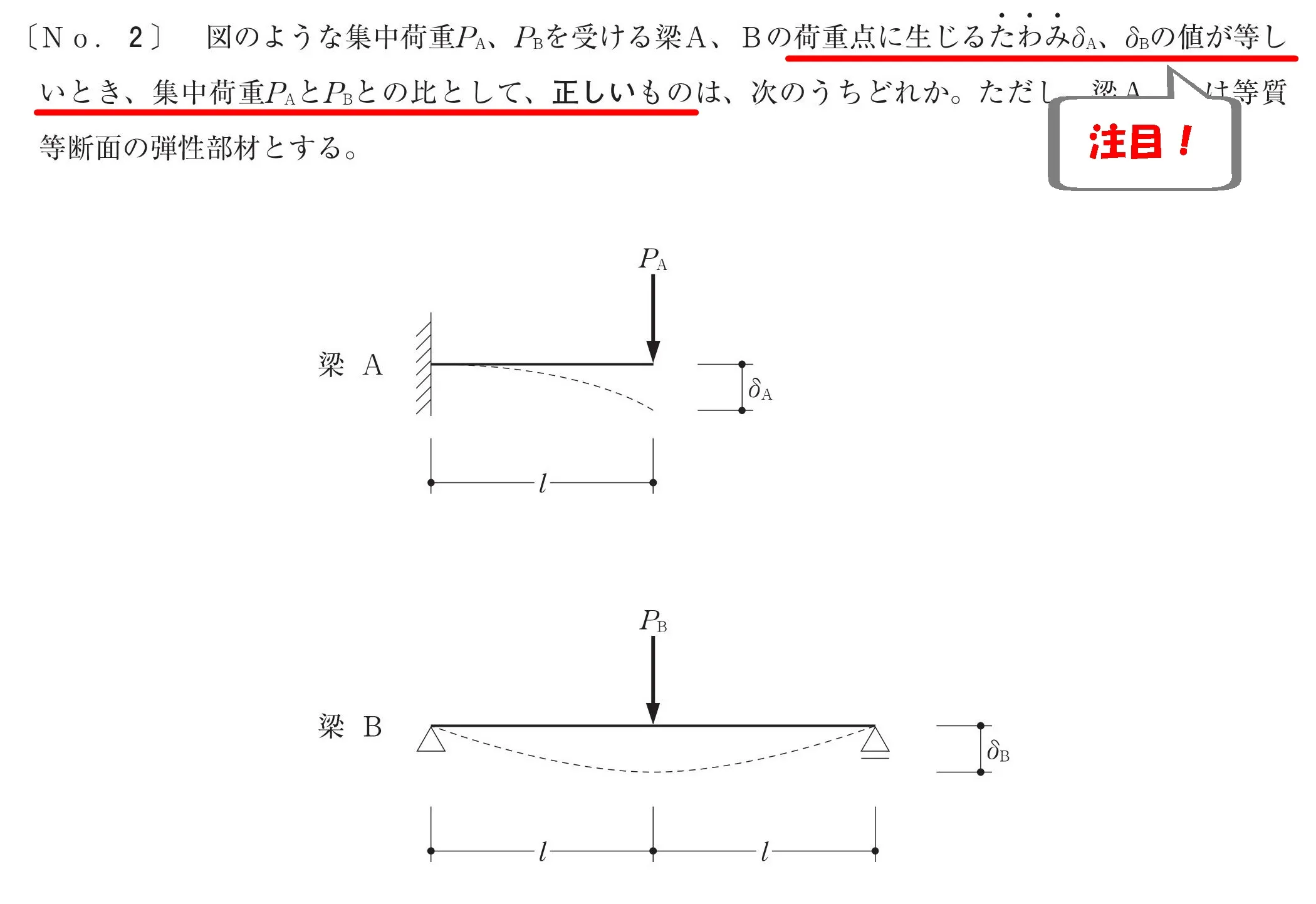

荷重の受ける範囲
- Pa:集中荷重
- Pb:集中荷重
たわみδaとδbが等しい
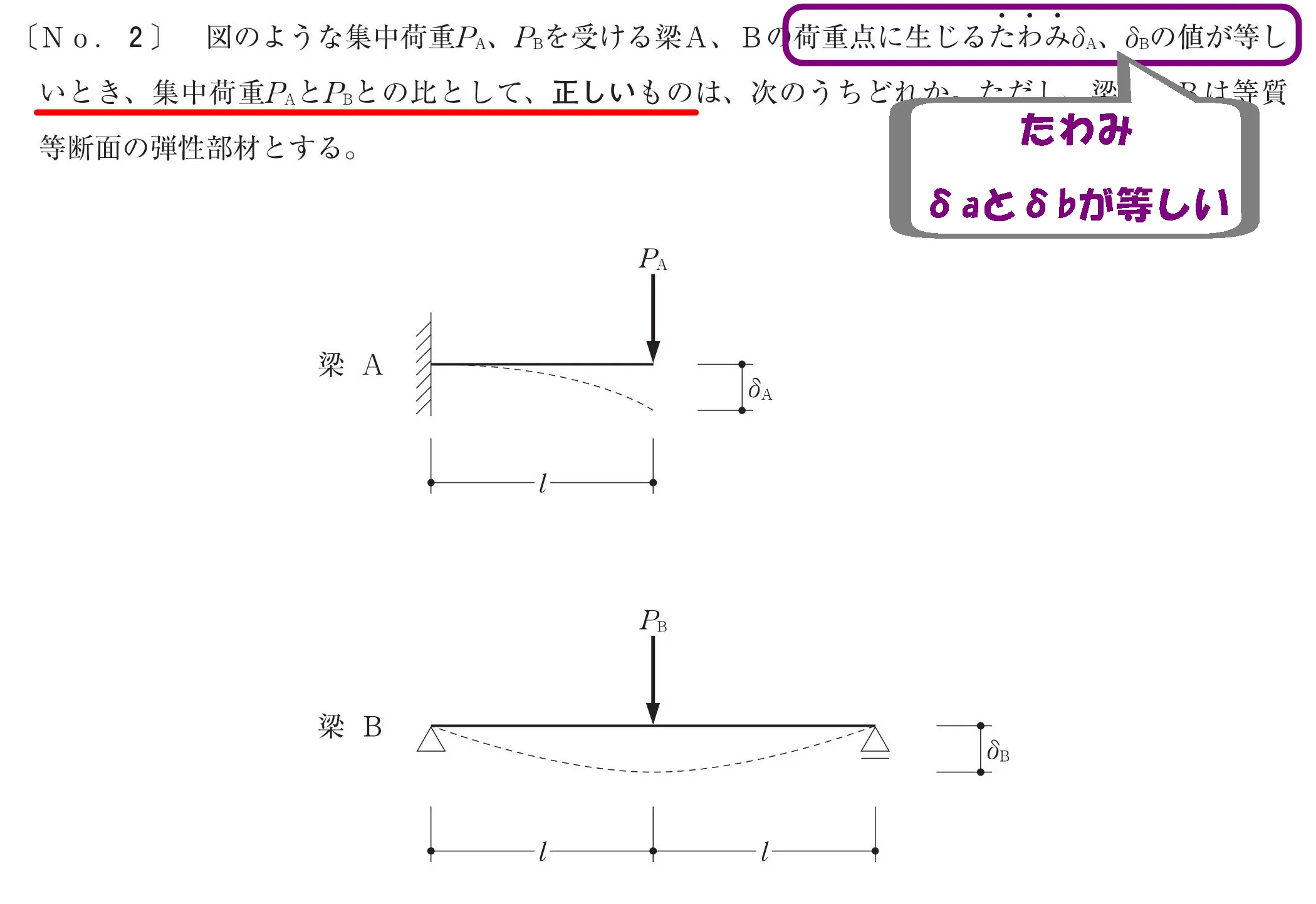

たわみが等しい
- 片持ち梁Aに生じるたわみδa
- 単純梁Bに生じるたわみδb
- 荷重点に生じるδaとδbが等しい
集中荷重PaとPbの比を求める
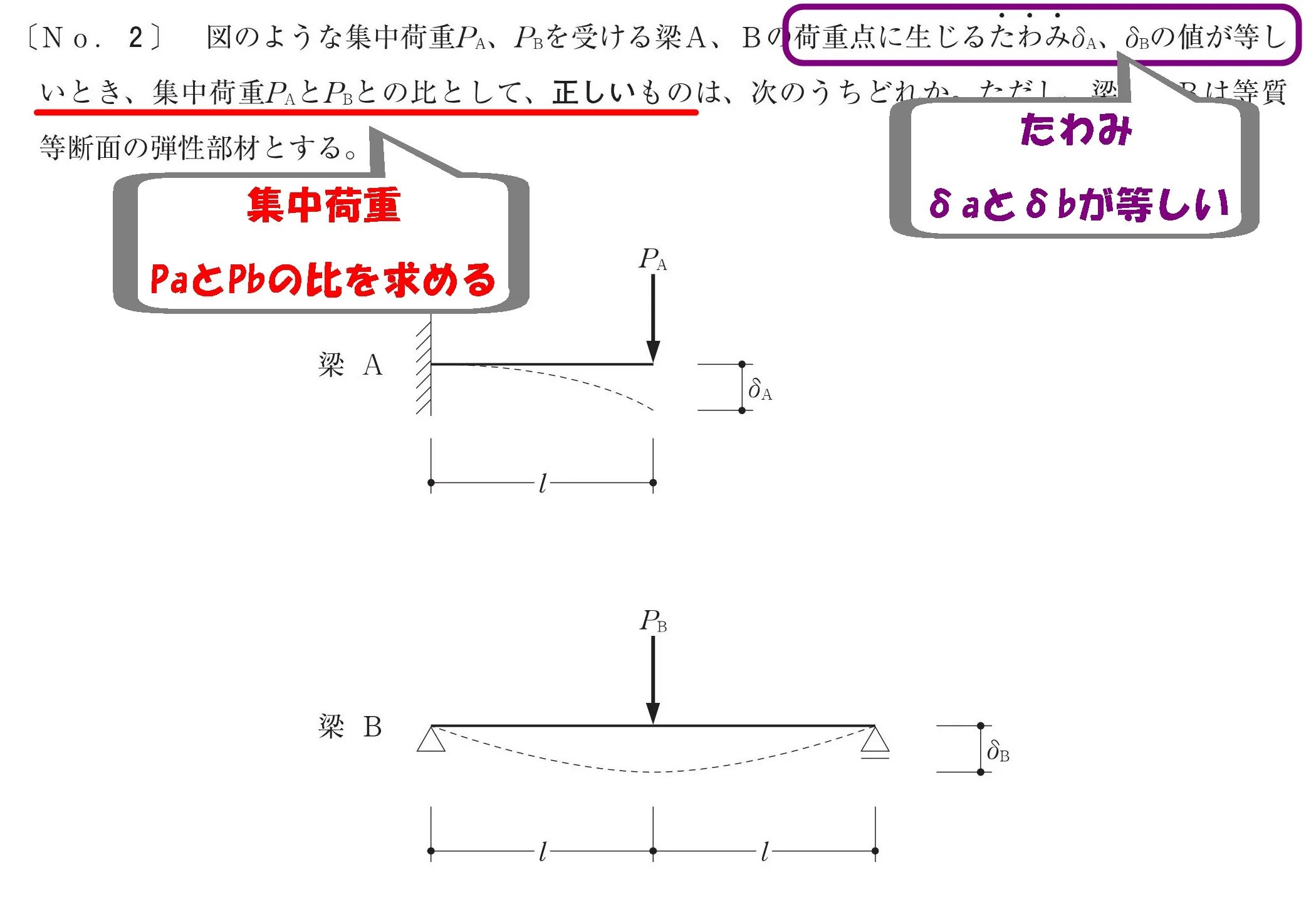

求めるもの
- 片持ち梁Aに加わるPa
- 単純梁Bに加わるPb
- 集中荷重Pa:Pbの比を求める
問題図にメモする
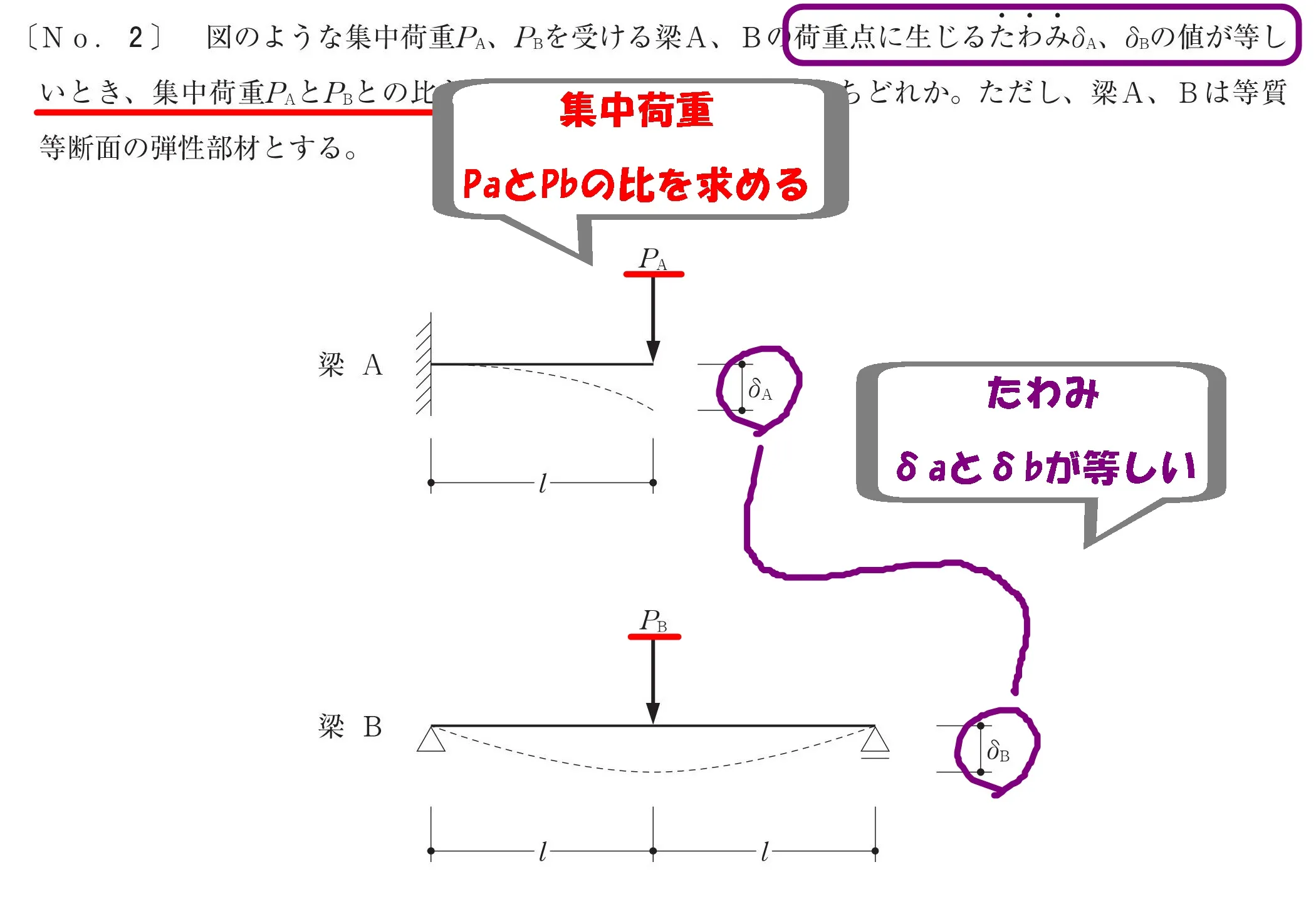

δaとδbはイコールで結ぶ。
2.問題用紙の余白に必要な公式をメモする
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める
荷重Pは集中荷重
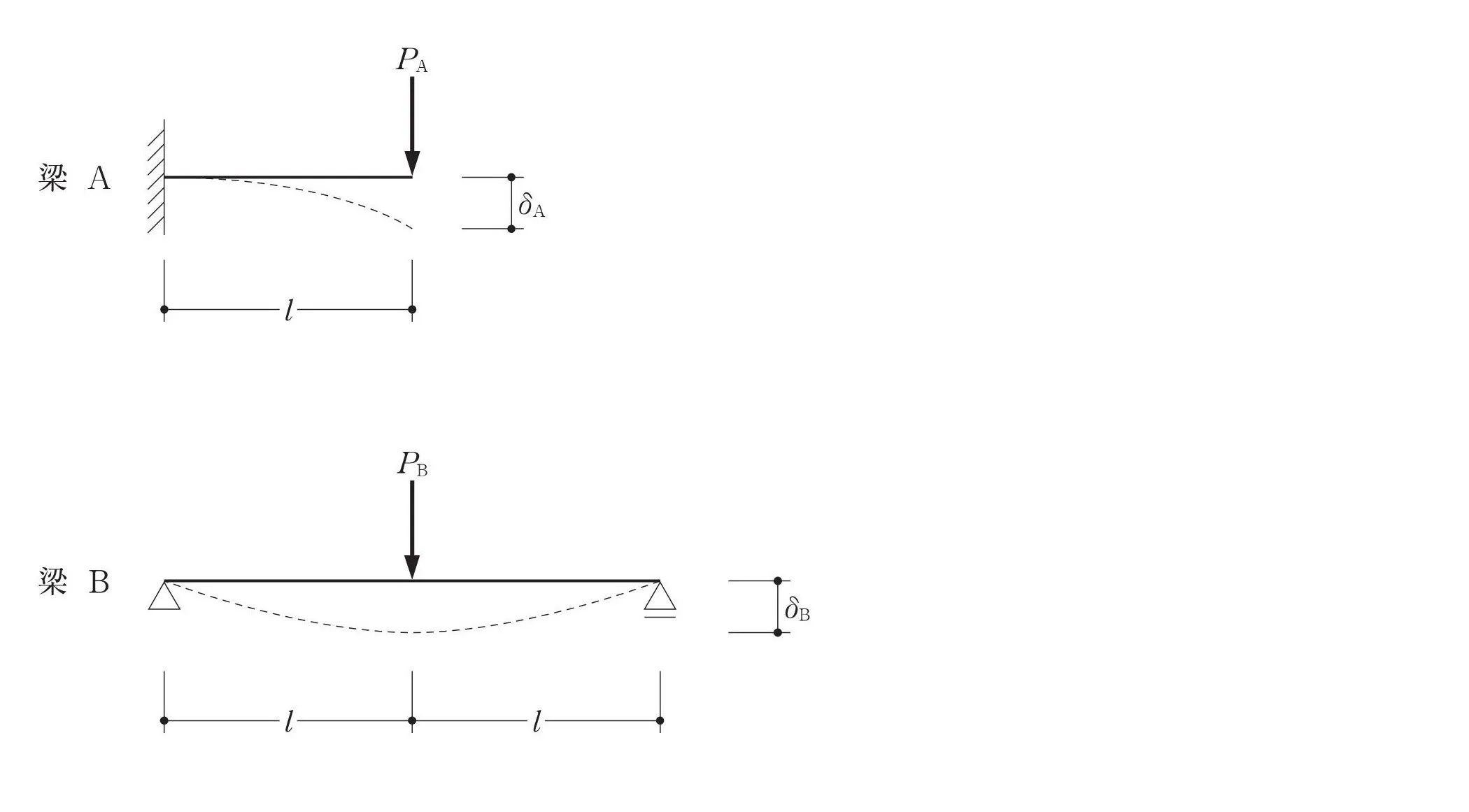

たわみ角θの公式
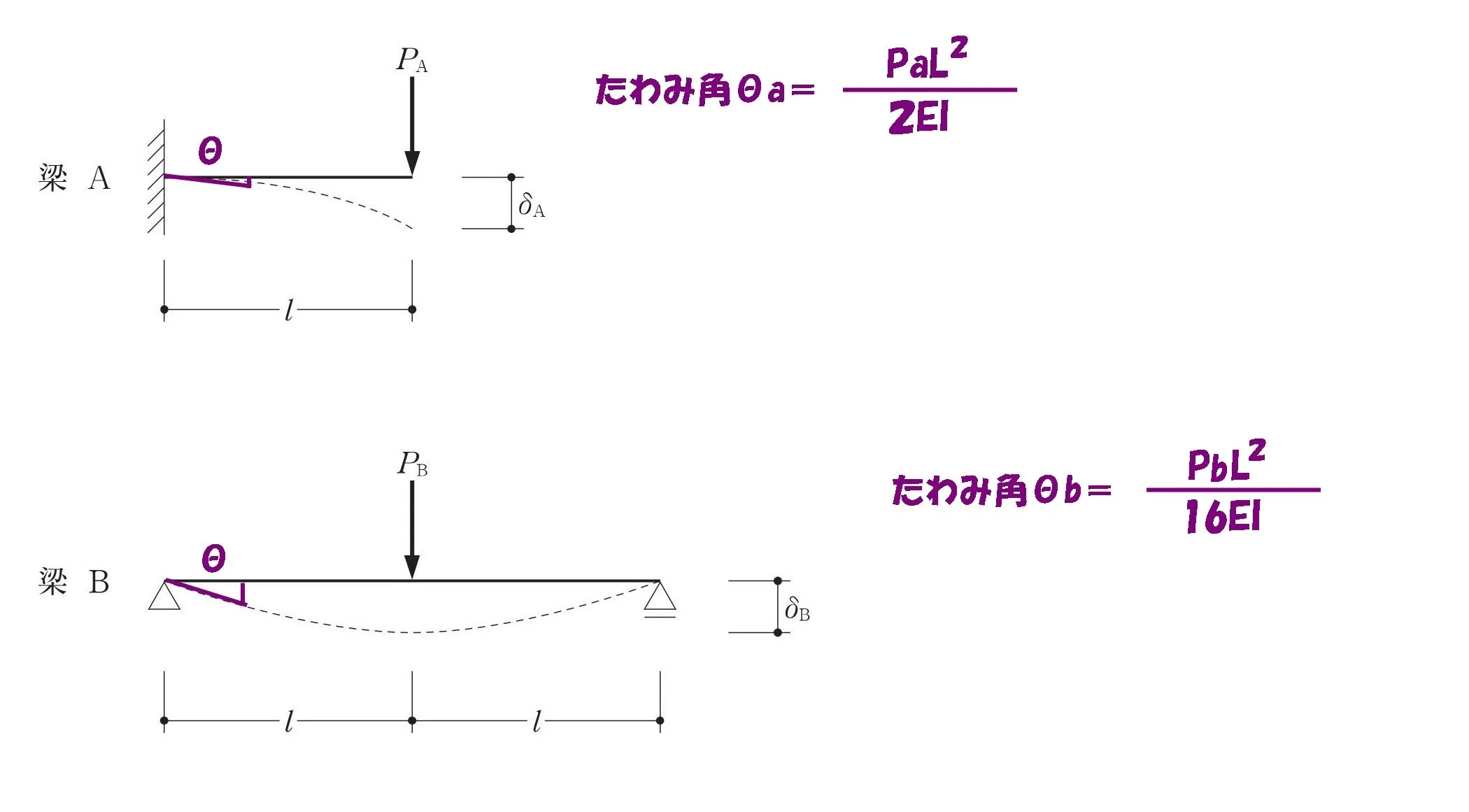

(たわみ角θは参考です。)



たわみ角θは
材長Lの2乗に比例する。
たわみδの公式
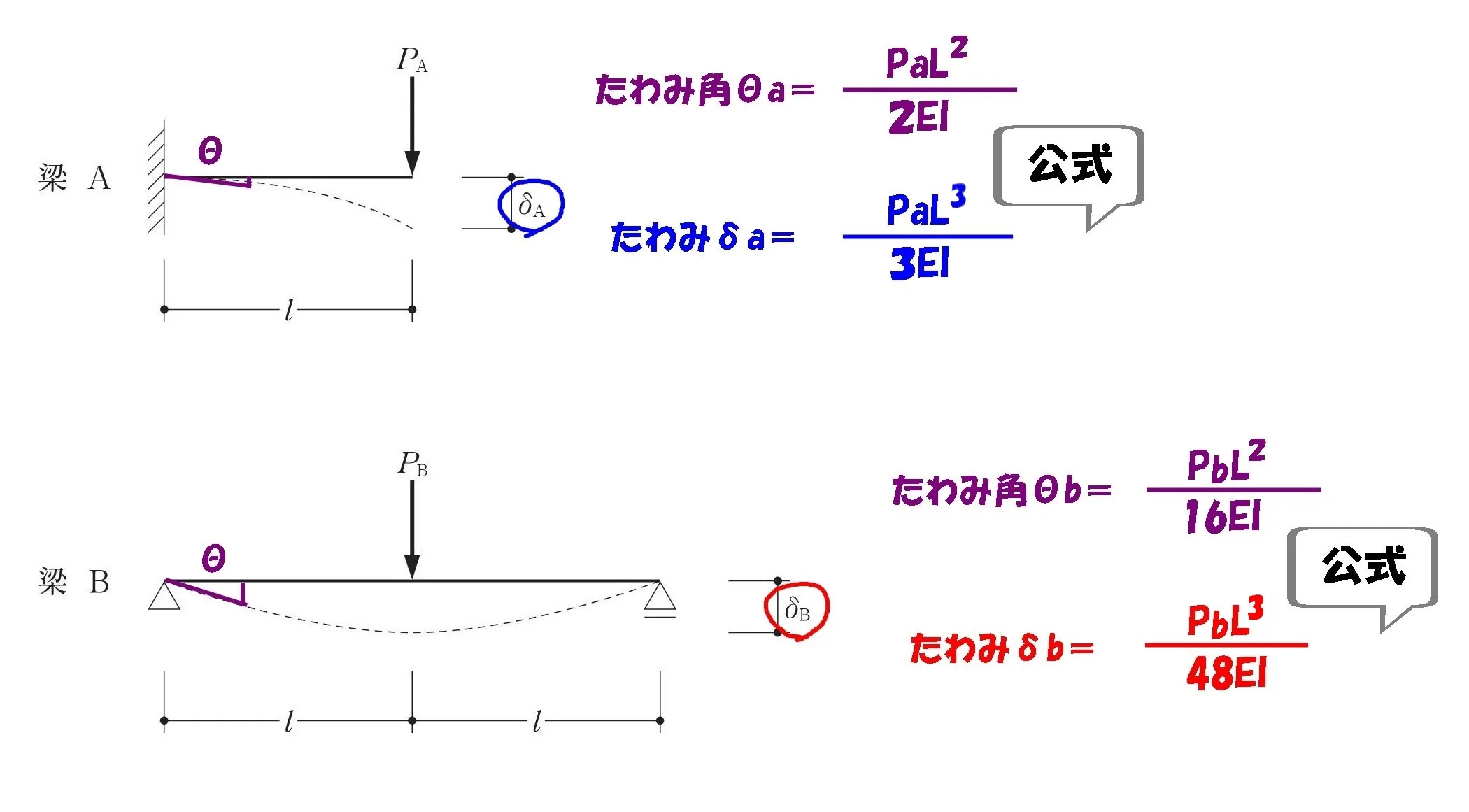




たわみδは
材長Lの3乗に比例する。
片持ち梁のたわみ公式
$$\delta=\frac{ PL^3 }{ 3EI }$$
単純梁のたわみ公式
$$\delta=\frac{ PL^3 }{ 48EI }$$
材長Lの違いに注目!
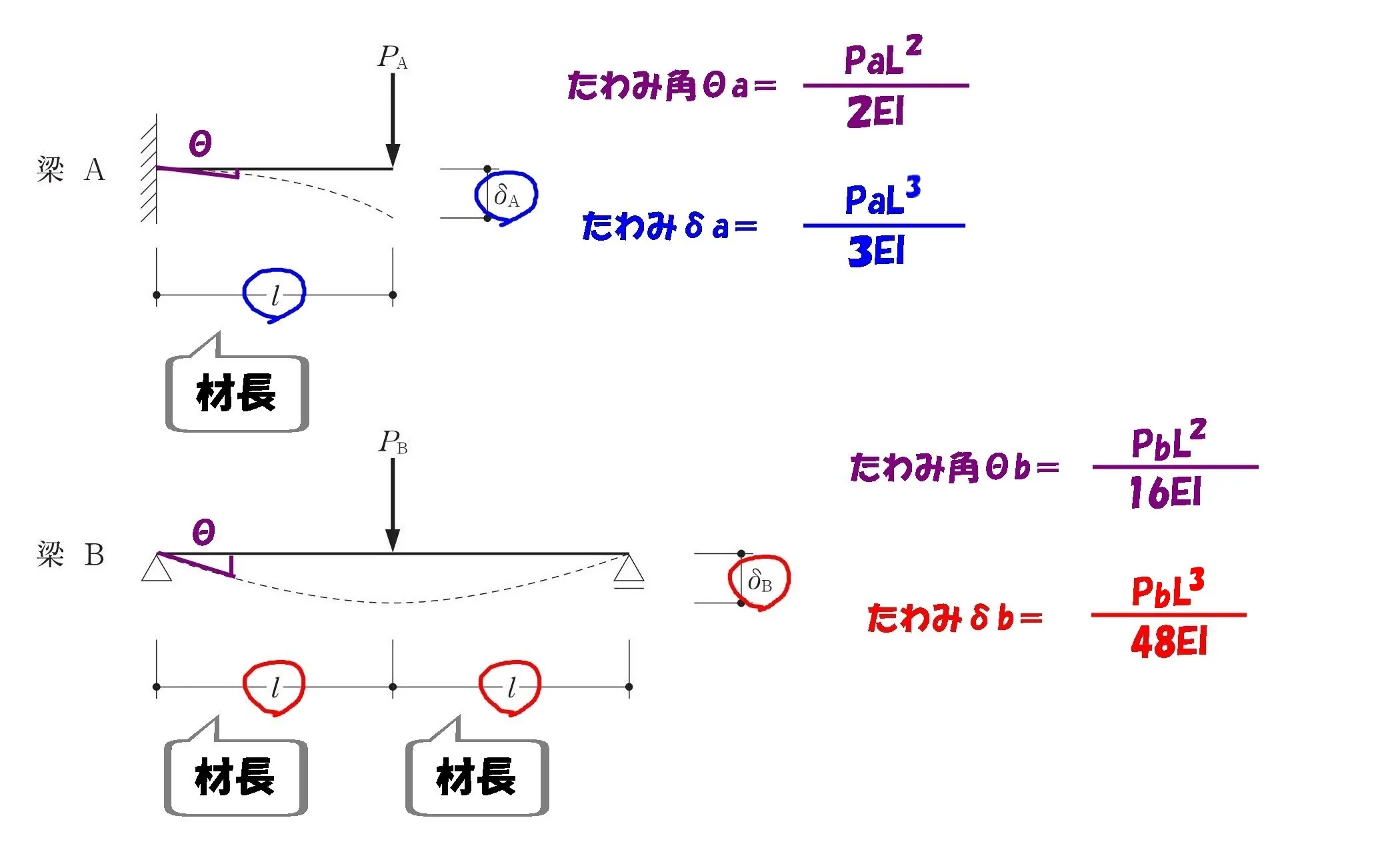




おおおっと!?
この問題の注意ポイント!
$$梁A:片持ち梁の材長=L$$$$梁B:単純梁の材長=L+L=2L$$
この問題の最大のポイントは、材長の違いを読み取れるかどうかです。
3.公式をイコールで結び、Pa:Pbの比を求める
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める
たわみδa=δb
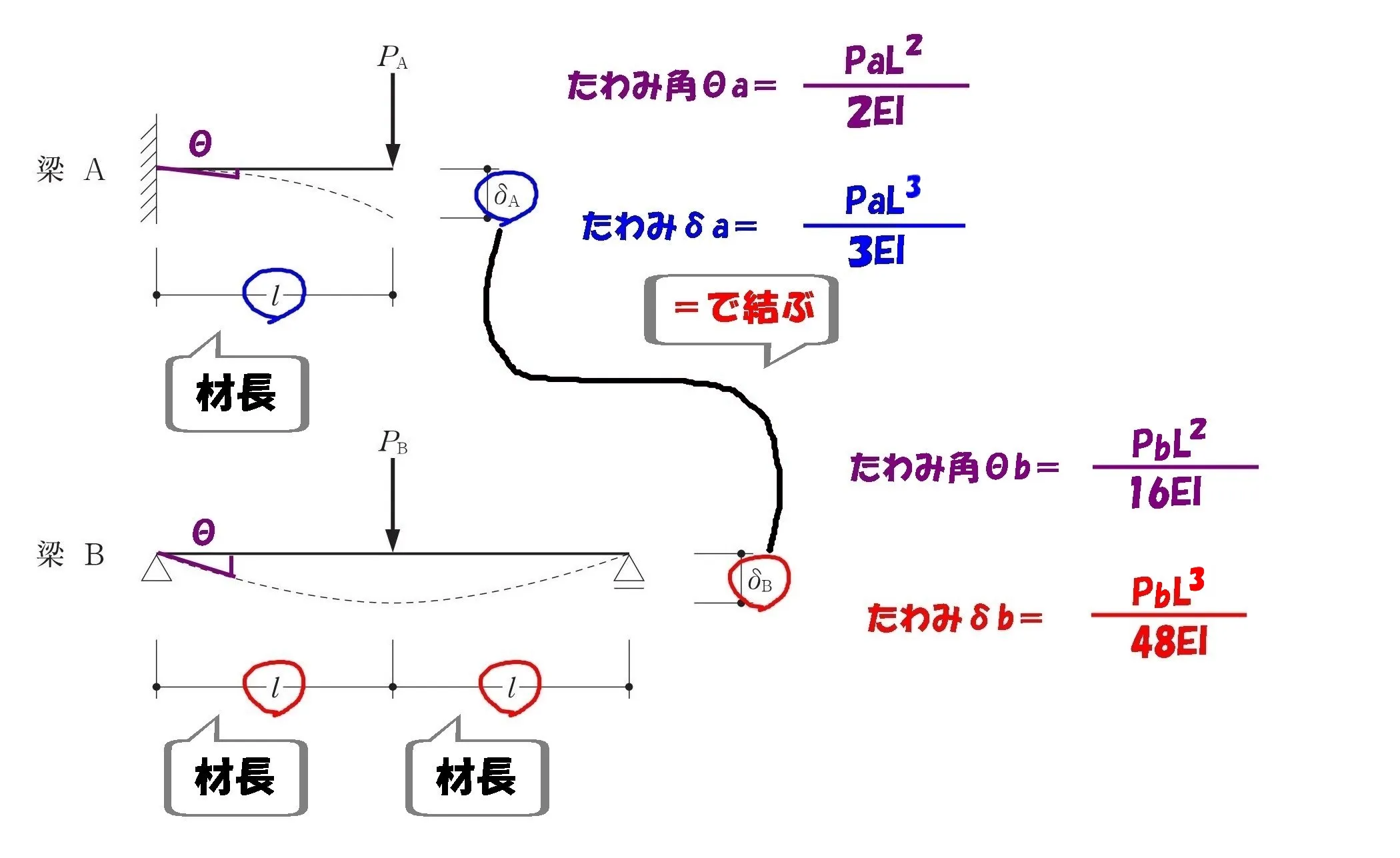

片持ち梁のたわみ公式
$$δa=\frac{ PaL^3 }{ 3EI }$$
単純梁:Bのたわみの式
梁の長さはLではなく2L
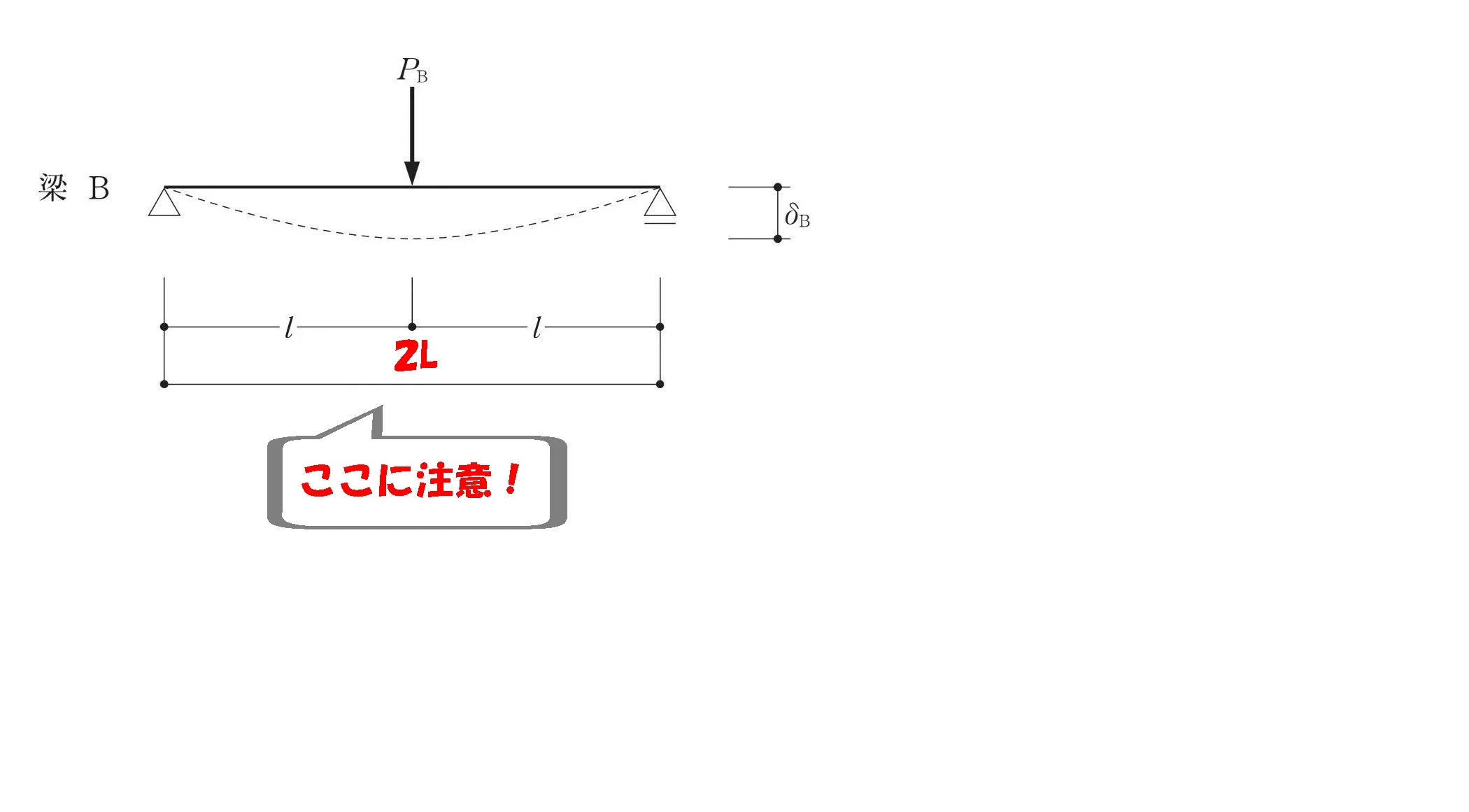

δ=PL³/48EIの公式をそのまま使うと外れを引いてしまいます。
問題図を確認して、長さ=2Lを代入しましょう。



Lが2Lに、こいつは
なかなかのトラップだな。
この問題の注意ポイント!
$$梁B:単純梁の材長=L+L=2L$$
梁の長さに2Lを代入する
$$δb=\frac{ Pb(2L)^3 }{ 48EI }$$
Pa:Pbを求める
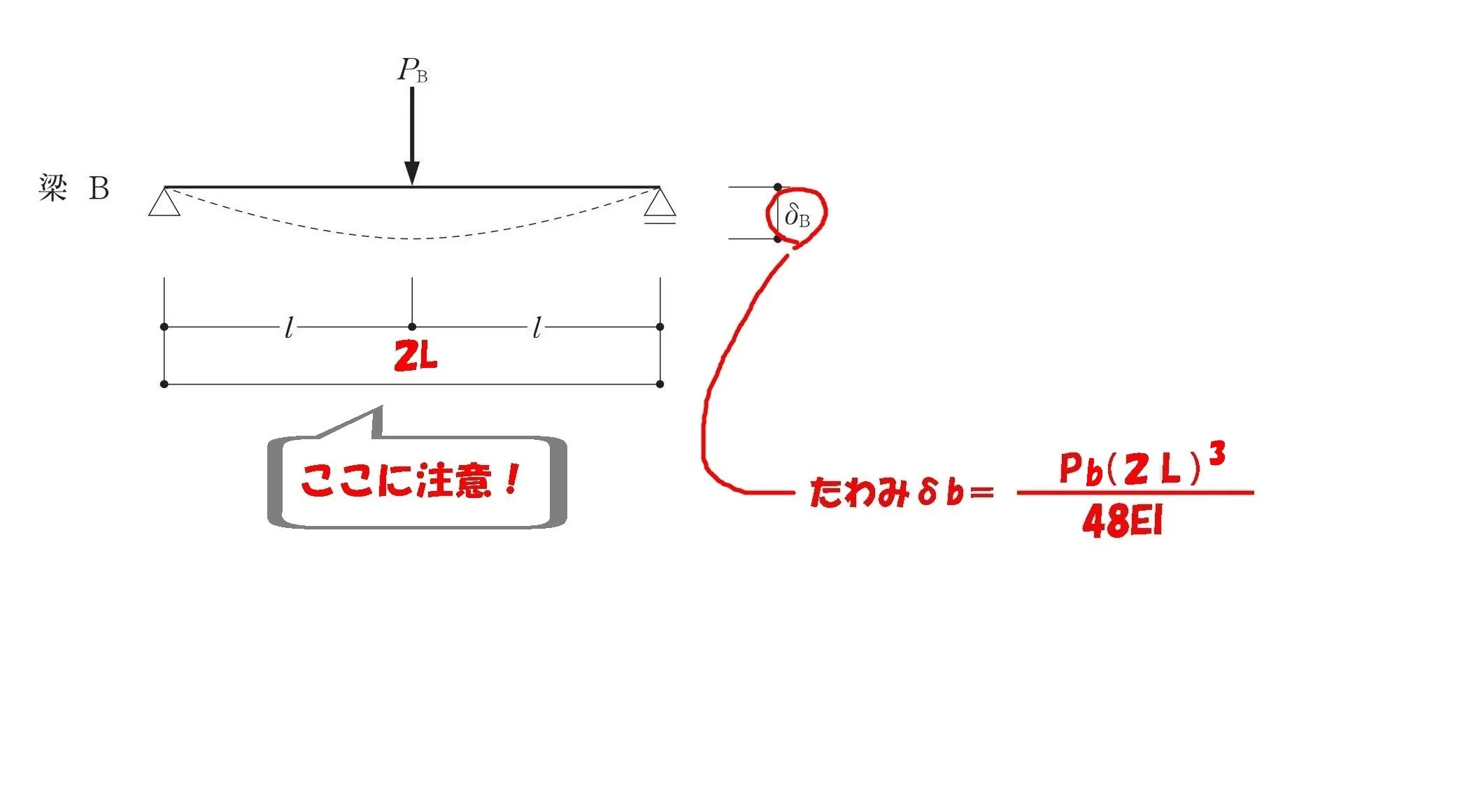

$$δa=\frac{ PaL^3 }{ 3EI }$$
$$δb=\frac{ Pb(2L)^3 }{ 48EI }$$
$$問題文より,たわみδa=δb$$$$(イコールで結ぶ)$$
$$δa=δbより$$
$$\frac{ Pa\underline{L}^3 }{ 3\underline{EI} }=\frac{ Pb(2\underline{L})^3 }{ 48\underline{EI} }$$$$\frac{ Pa*1^3 }{ 3 }=\frac{ Pb*2^3 }{ 48 }$$
$$\frac{ Pa }{ Pb }=\frac{ \underline{3*2^3} }{ \underline{3*2^3}*2 }⇨\frac{ 1 }{ 2 }$$$$Pa:Pb=1:2$$
答え.2




Lが2Lだったなんて
やられたよ。(涙)
攻略ポイント
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める


この動画を YouTube で視聴
力の吊り合い
難易度:★★★★★
力の吊り合いを使って、部材に作用する力を求める問題です。
反力、モーメント、せん断力を読み解くうえで、正しい理解が必要となる教材ともいえるでしょう。



この問題は
少し手強いぞ!
この問題には、構造力学の重要な要素がたくさん詰まっています。
イメージ図

攻略ポイント
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
問題
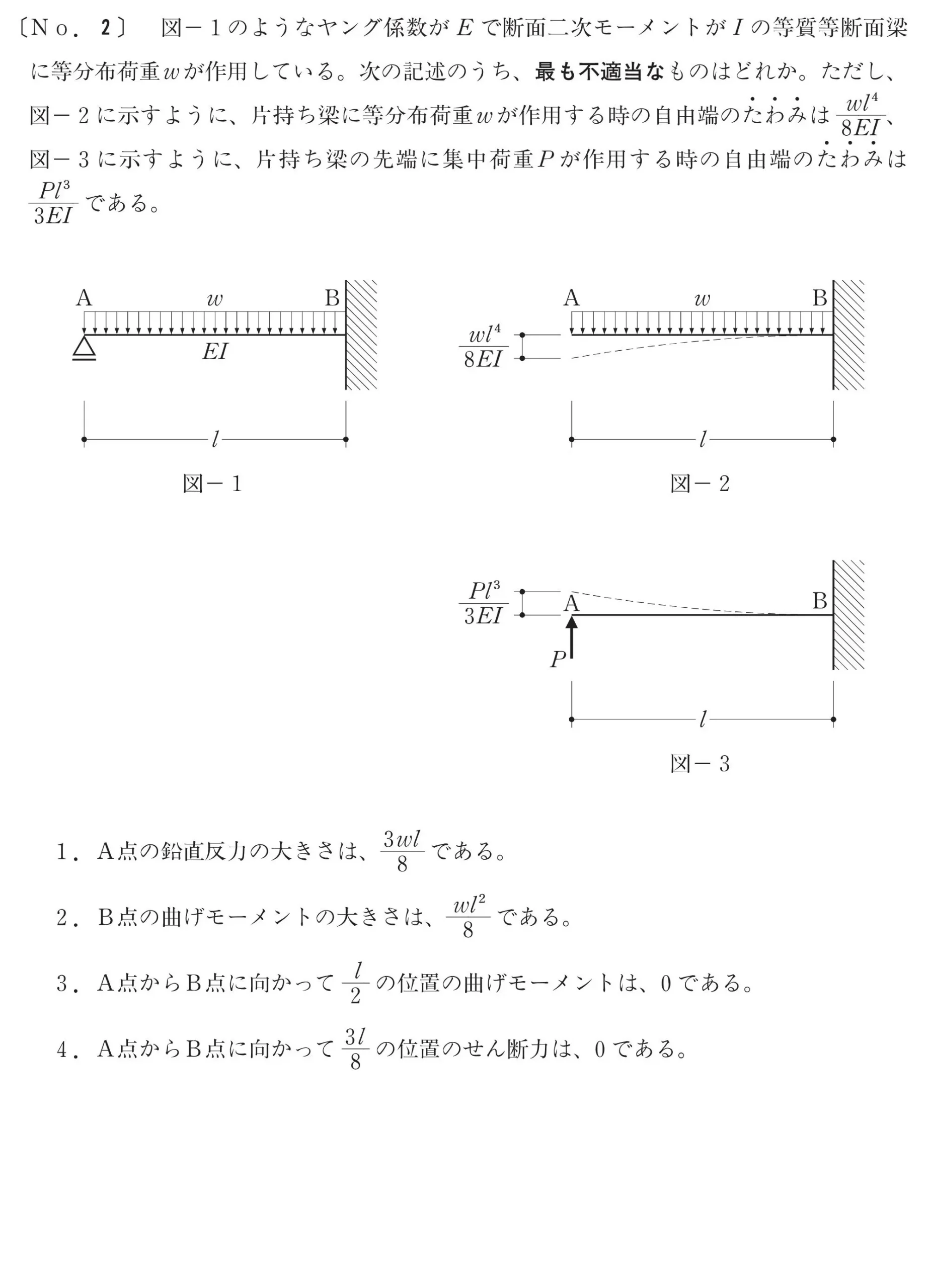

攻略のポイント
集中荷重のたわみと等分布荷重のたわみをイコールで結ぶ
アンダーラインに注目!


アンダーライン
- 片持ち梁に等分布荷重wが作用するときのたわみ
- 片持ち梁に集中荷重Pが作用するときのたわみ
A点のたわみ
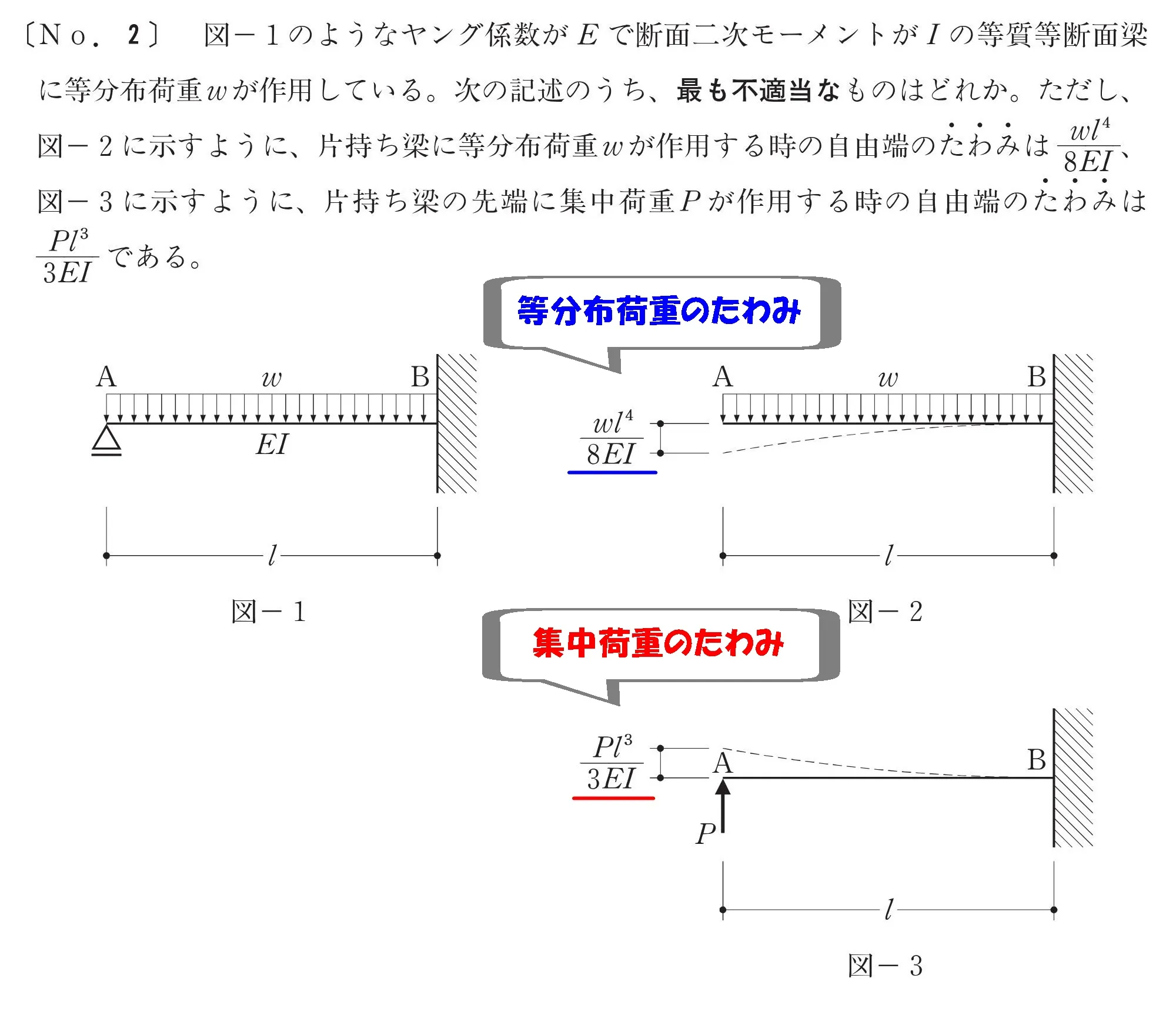

等分布荷重wのA点(図-2)のたわみ$$\frac{ wL^4 }{ 8EI }$$
集中荷重PのA点(図-3)のたわみ$$\frac{ PL^3 }{ 3EI }$$



たわみの公式が
すでに定義されている。
図-1、図-2、図-3
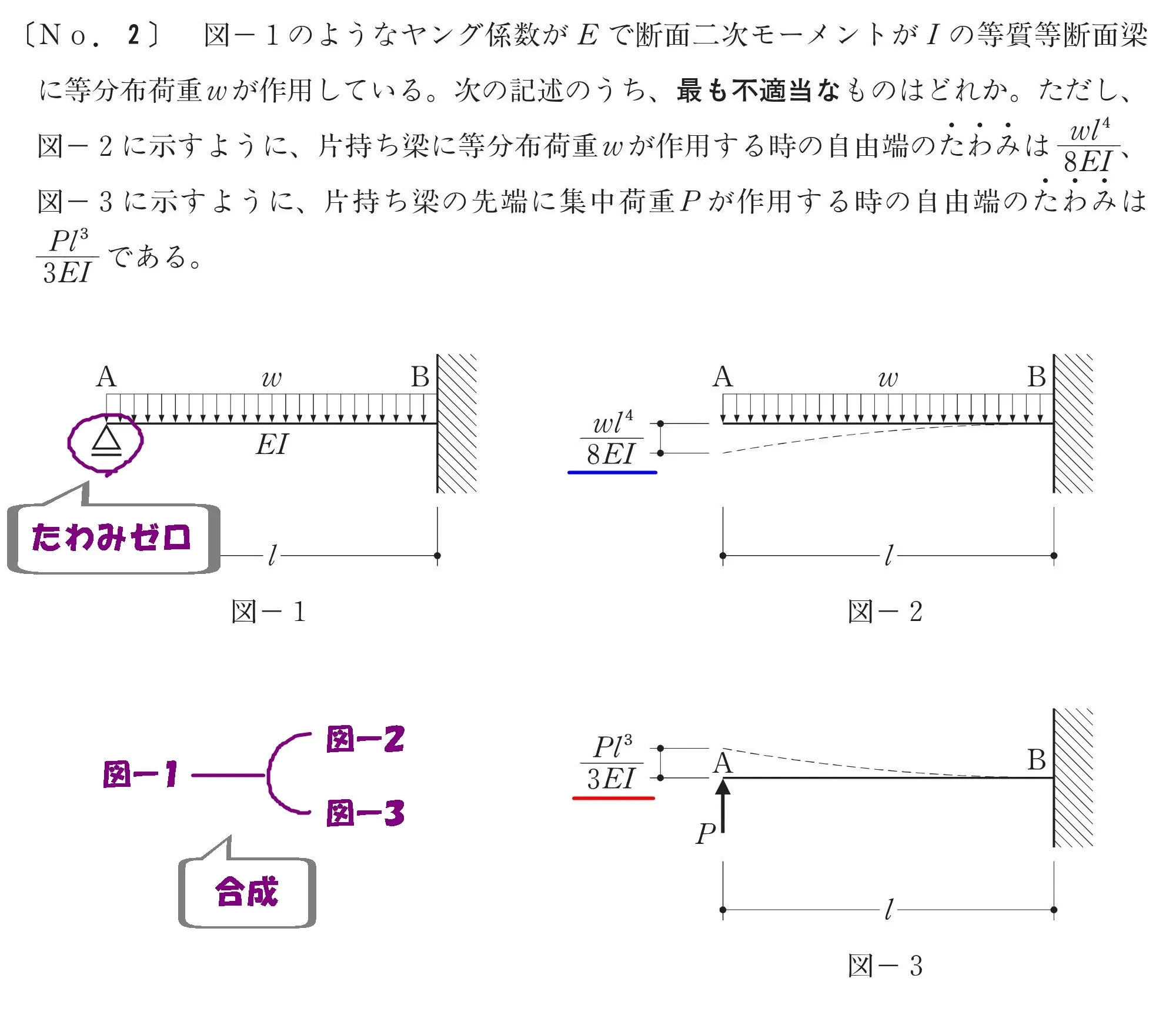

読み取りポイント
- 図-1の梁は、図-2と図-3の梁に分解できる
- 図-2の荷重wと図-3の荷重Pを合成すると、図-1になる
- 図-2のたわみと図-3のたわみを合成するとゼロ(図-1の支点)になる
たわみをイコールで結ぶ
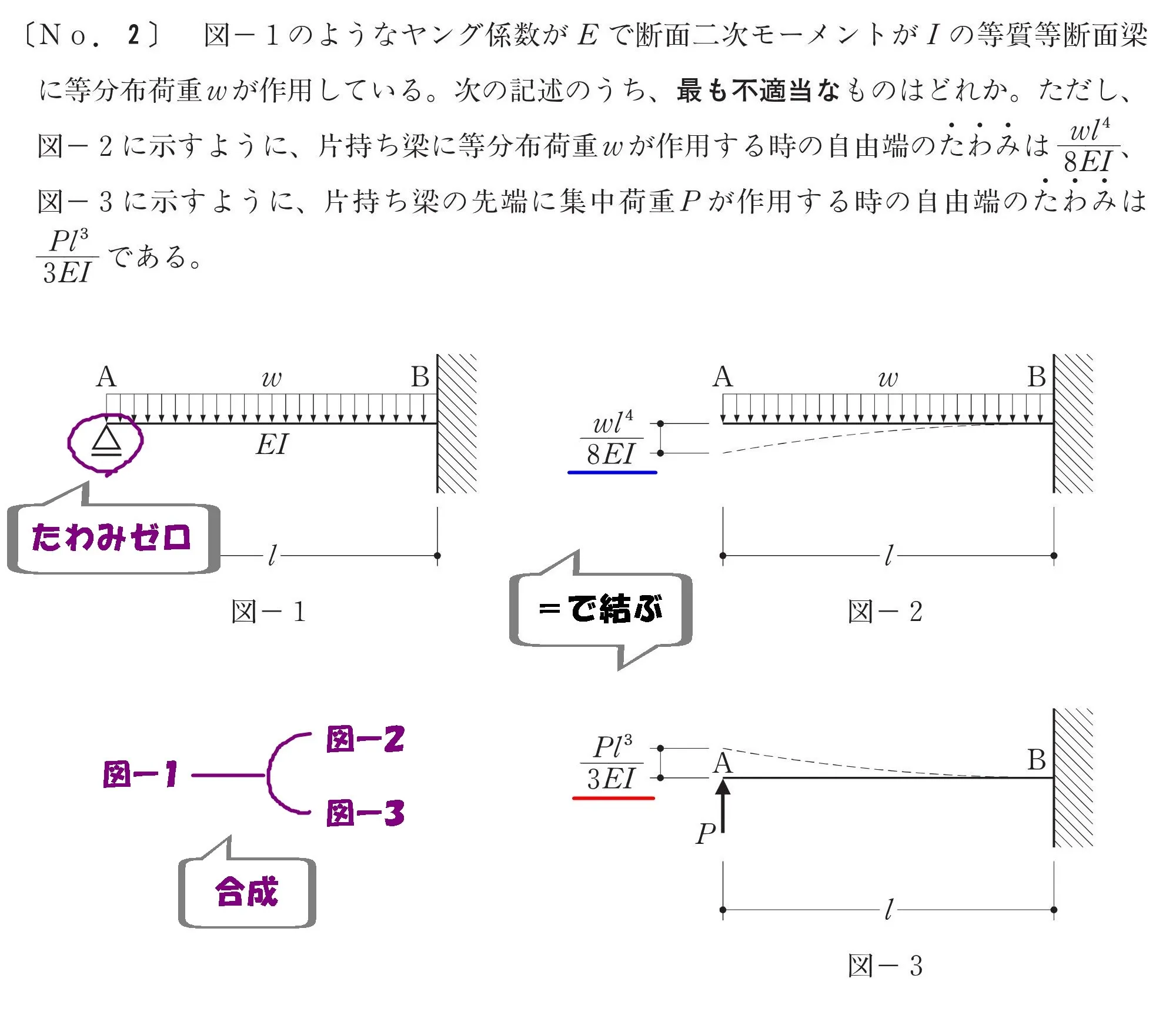

$$\frac{ wL^4 }{ 8EI }-\frac{ PL^3 }{ 3EI }=0より、\frac{ wL^4 }{ 8EI }=\frac{ PL^3 }{ 3EI }$$



A点を起点にして
吊り合い式が成り立つ。
攻略のポイント
集中荷重のたわみと等分布荷重のたわみをイコールで結ぶ
枝.1


$$1.[A点の鉛直反力の大きさは、\frac{ 3wL }{ 8 }である。]$$
A点のたわみはゼロ(図-1)
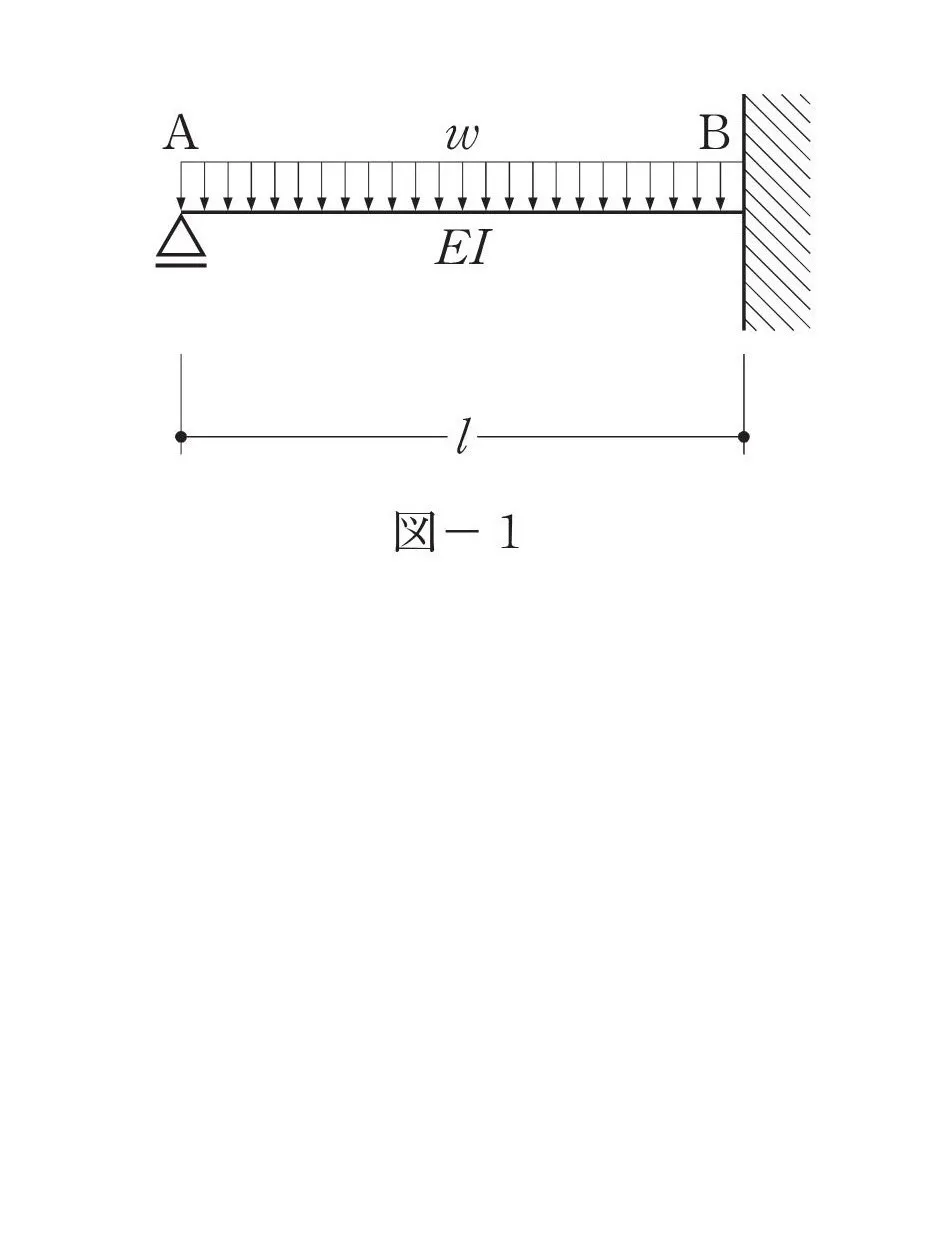

イコールで結ぶ
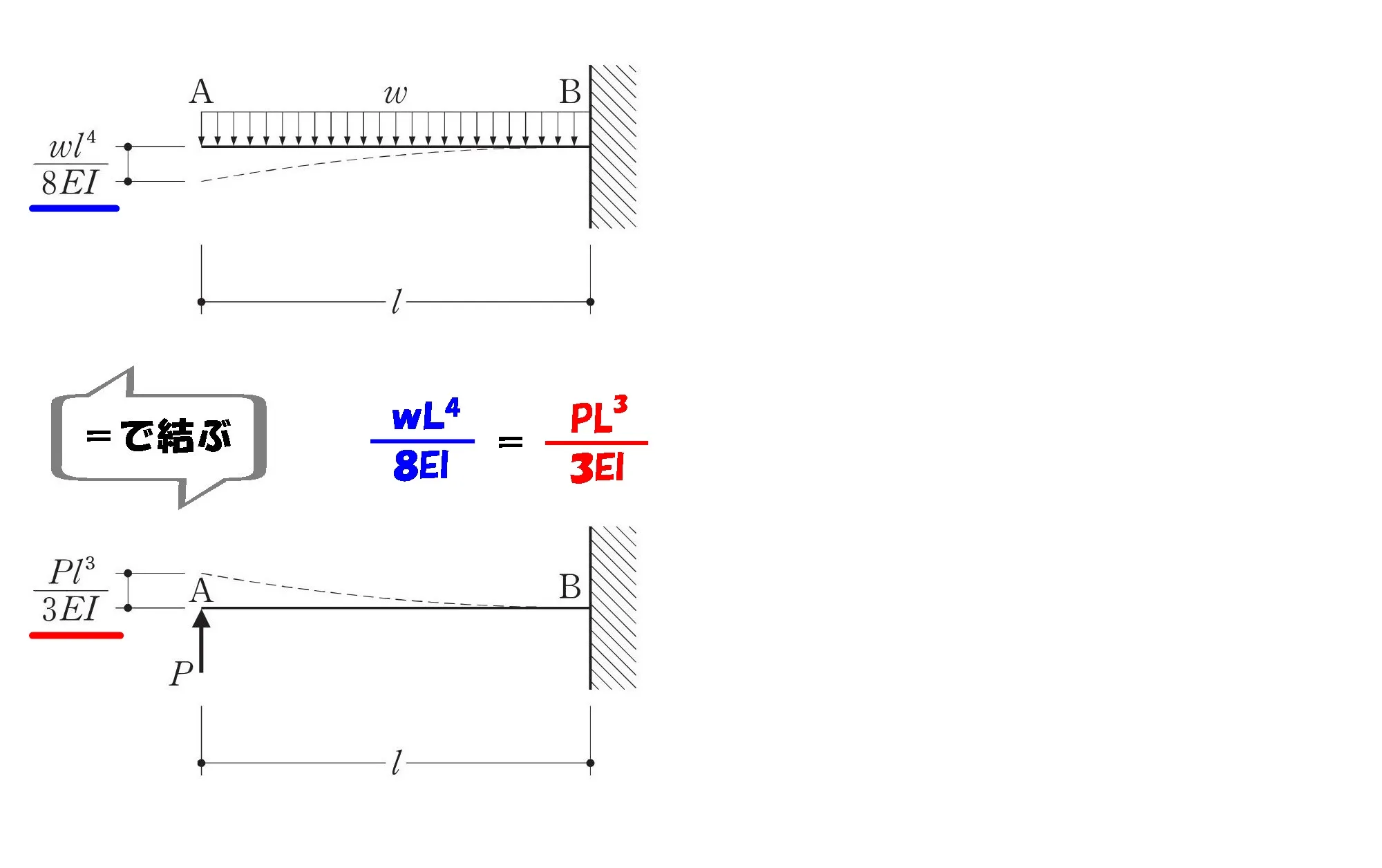

$$\frac{ wL^4 }{ 8EI }-\frac{ PL^3 }{ 3EI }=0より、\frac{ wL^4 }{ 8EI }=\frac{ PL^3 }{ 3EI }$$



たわみを「=」で結び、
鉛直反力P=の式にする。
鉛直反力Pを求める
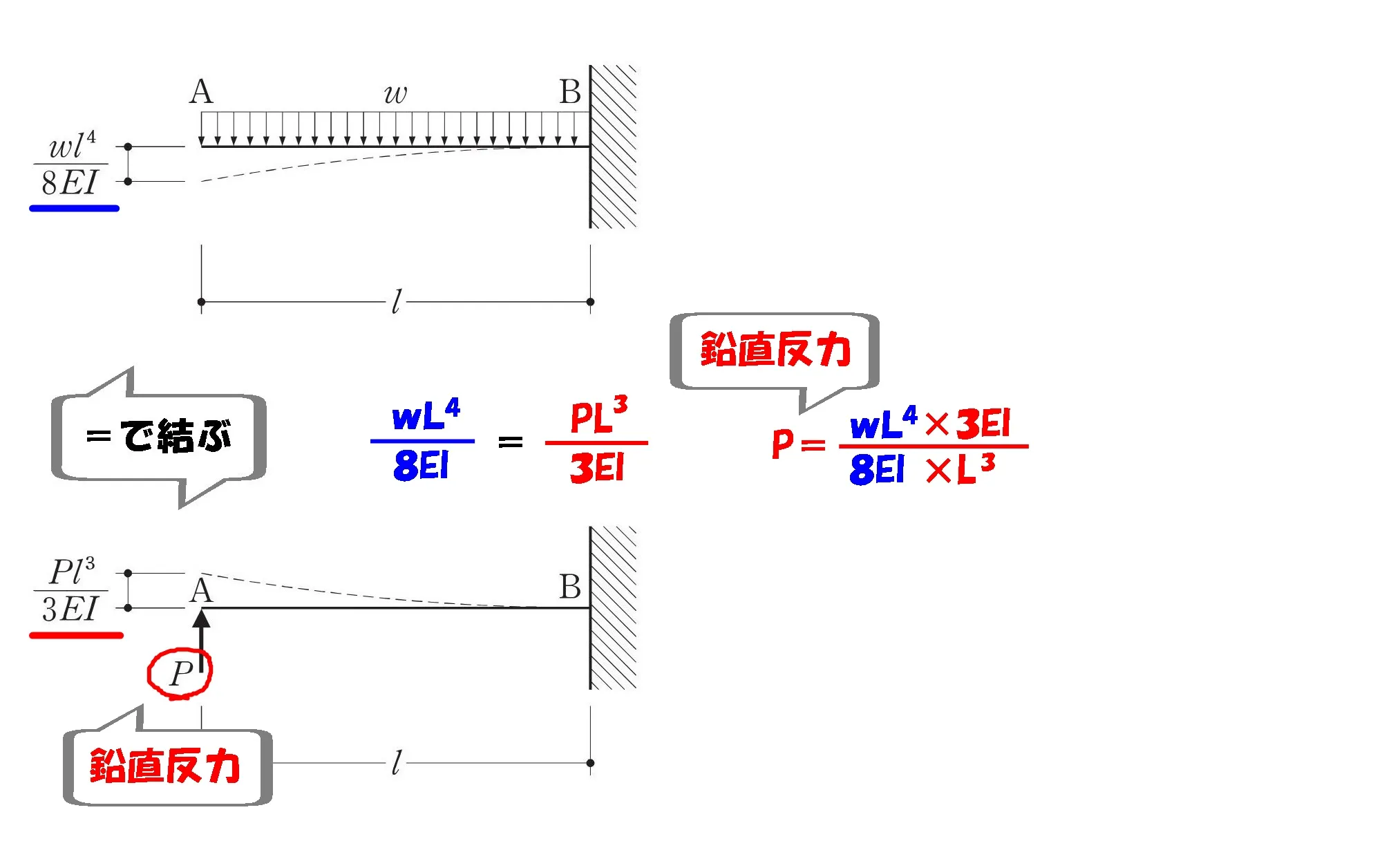

$$\frac{ wL^4 }{ 8EI }=\frac{ PL^3 }{ 3EI }より、P=\frac{ wL^4*3EI }{ 8EI*L^3 }$$
$$P=\frac{ w\underline{L^4}*3\underline{EI} }{ 8\underline{EI}*\underline{L^3} }⇨P=\frac{ 3wL }{ 8 }$$
攻略のポイント
集中荷重のたわみと等分布荷重のたわみをイコールで結ぶ
攻略ポイント
- 文章を読み取る
- モーメント=力×距離
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
枝.2


1.文章を読み取る
$$2.[B点の曲げモーメントの大きさは、\frac{ wL^2 }{ 8 }である。]$$
モーメントの合成
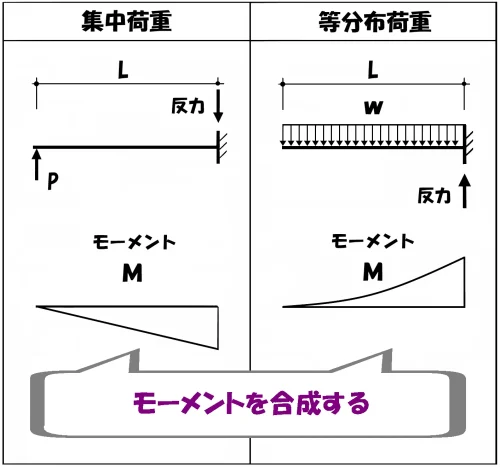

枝.1で求めた鉛直反力を使って、図-2と図-3のモーメントを合成します。
2.モーメント=力×距離
- 文章を読み取る
- モーメント=力×距離
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
集中荷重のモーメント
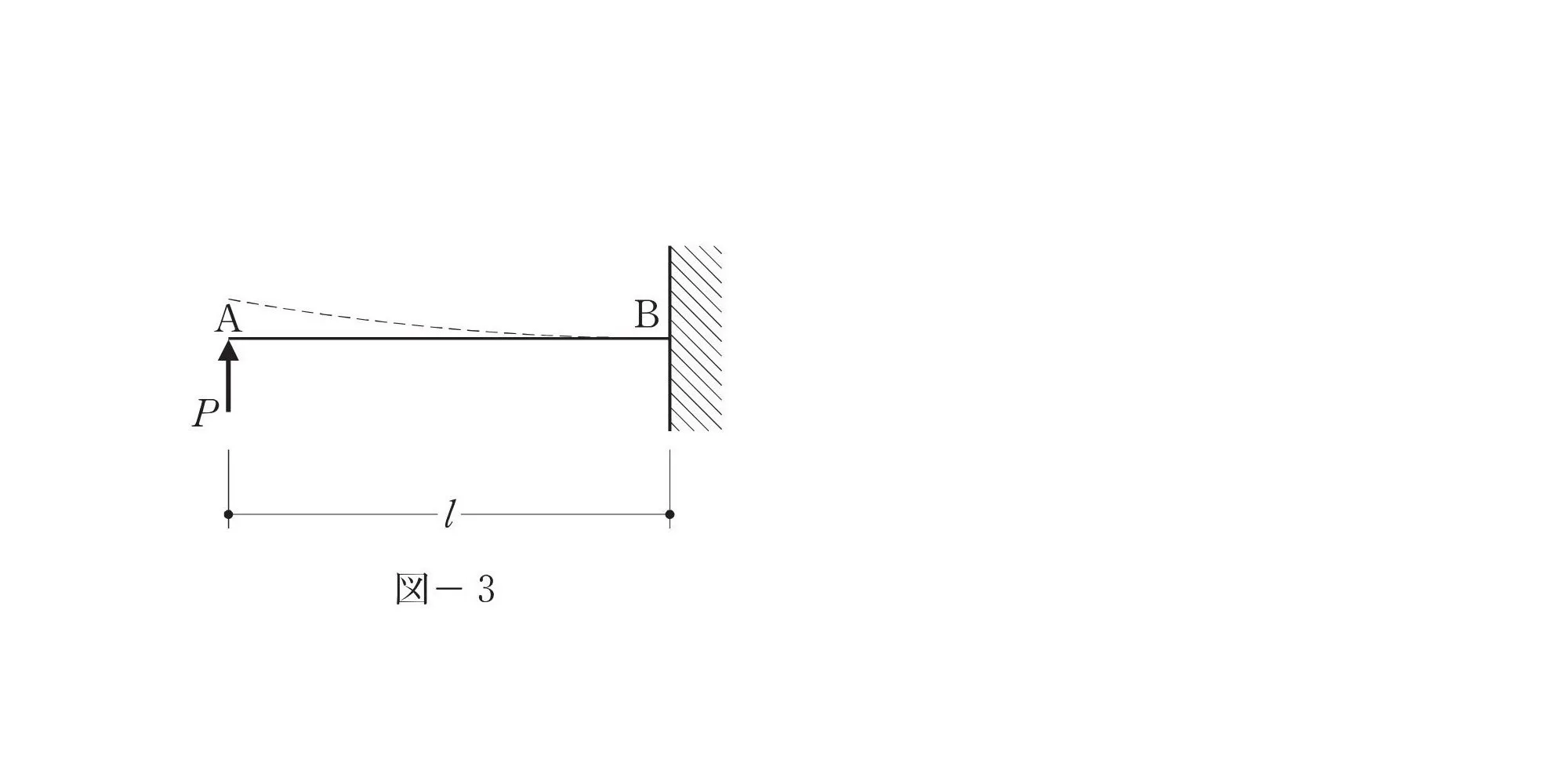

モーメント=力×距離
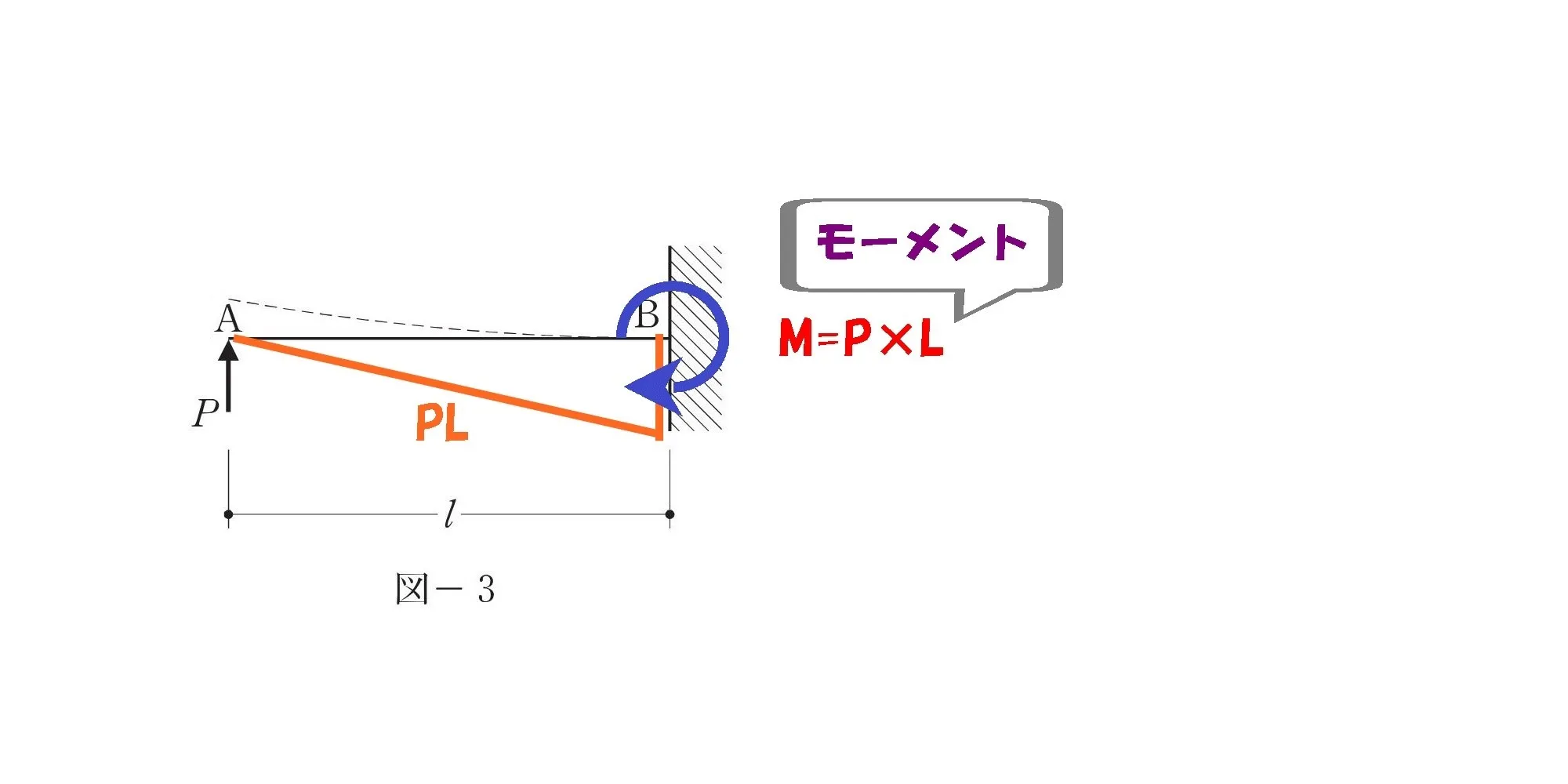

$$M=P*L$$
Pに3wL/8を代入する
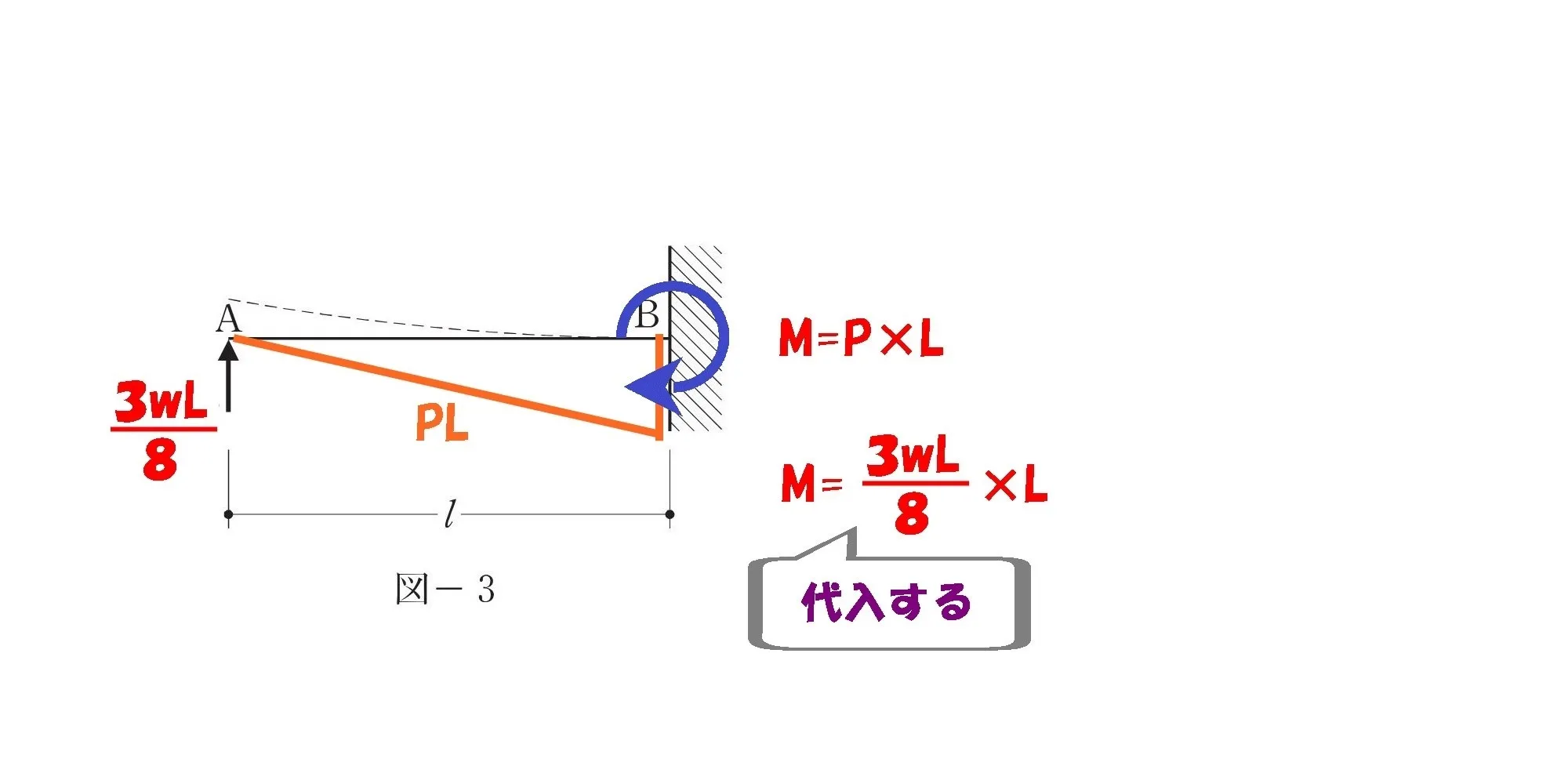

$$M=P*Lより、M=\frac{ 3wL }{ 8 }*L$$$$M=\frac{ 3wL^2 }{ 8 }$$



1.で求めた鉛直反力Pを
ここで使うのがポイント。
3.w×Lを集中荷重に置き換える
- 文章を読み取る
- モーメント=力×距離
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
等分布荷重のモーメント
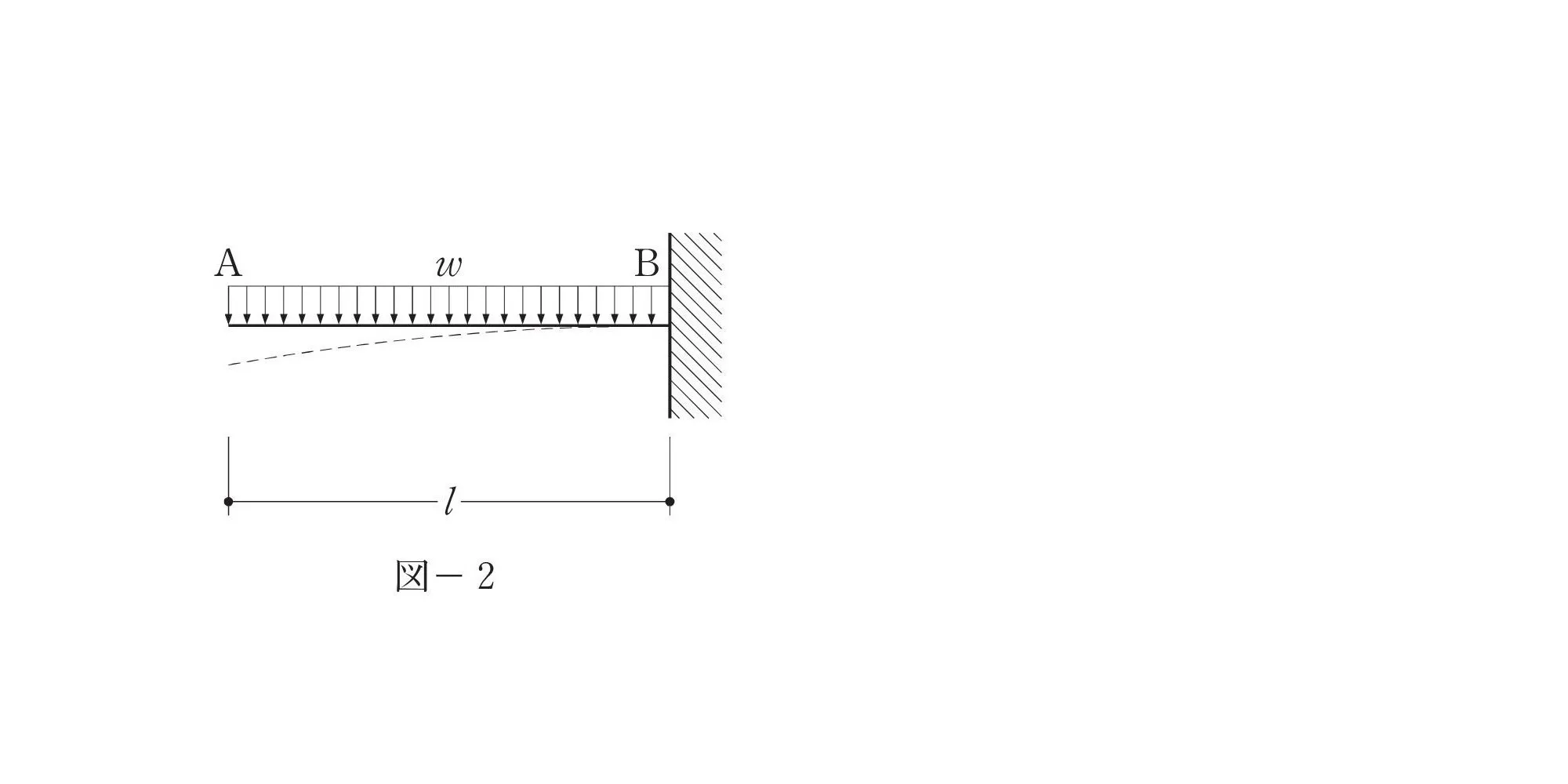

w×L
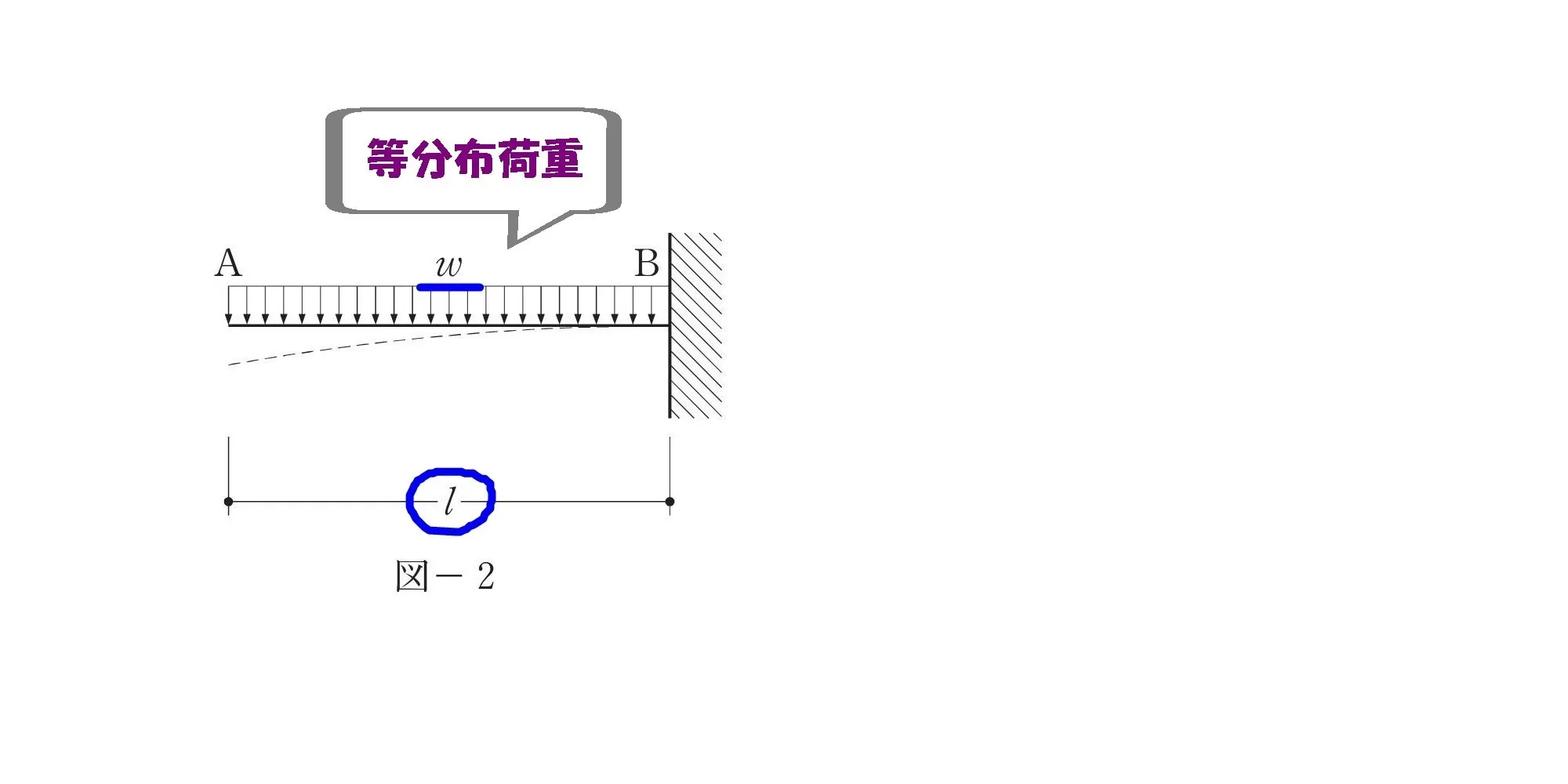

集中荷重wLに置き換える
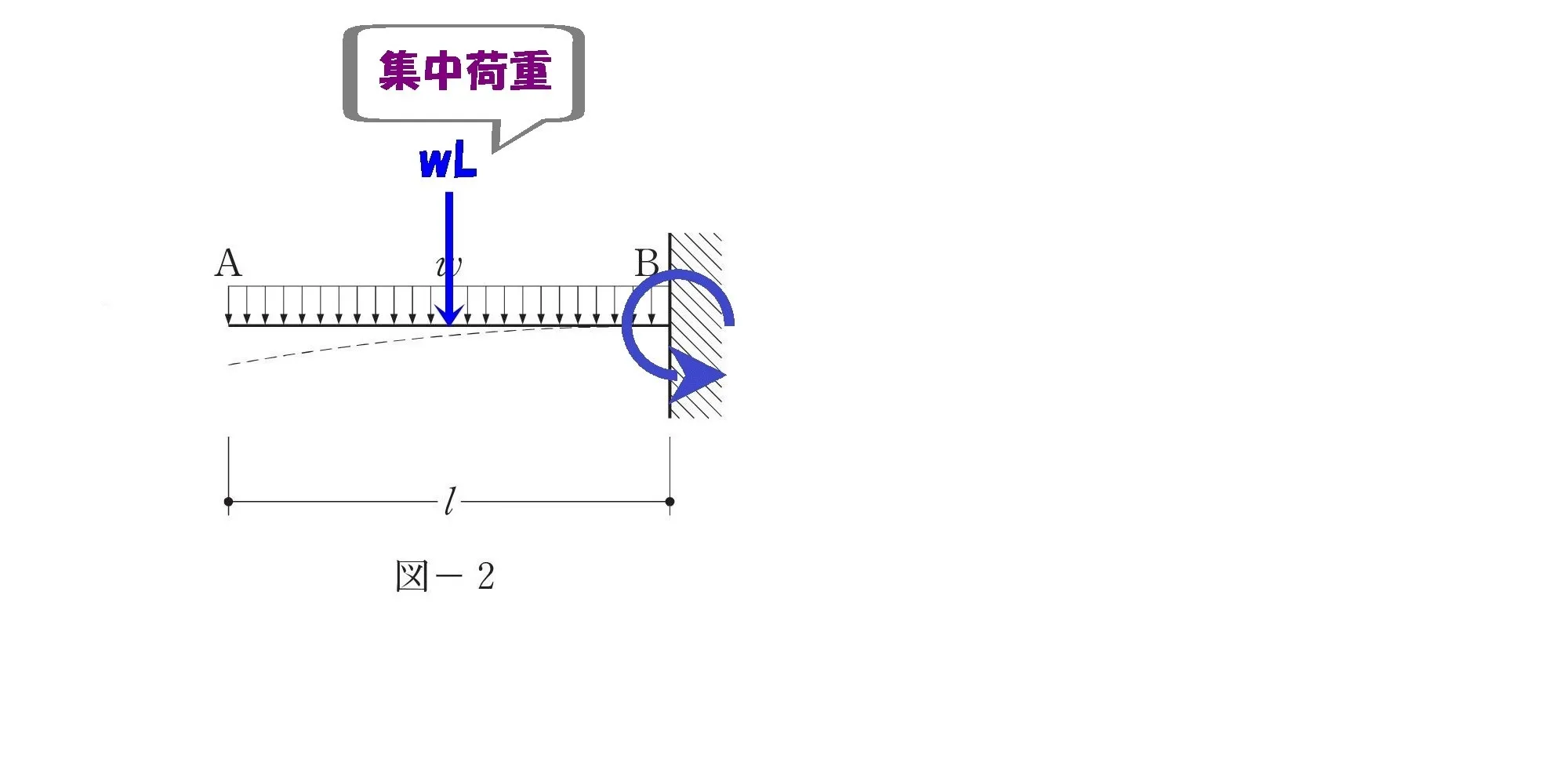

距離はL/2になる
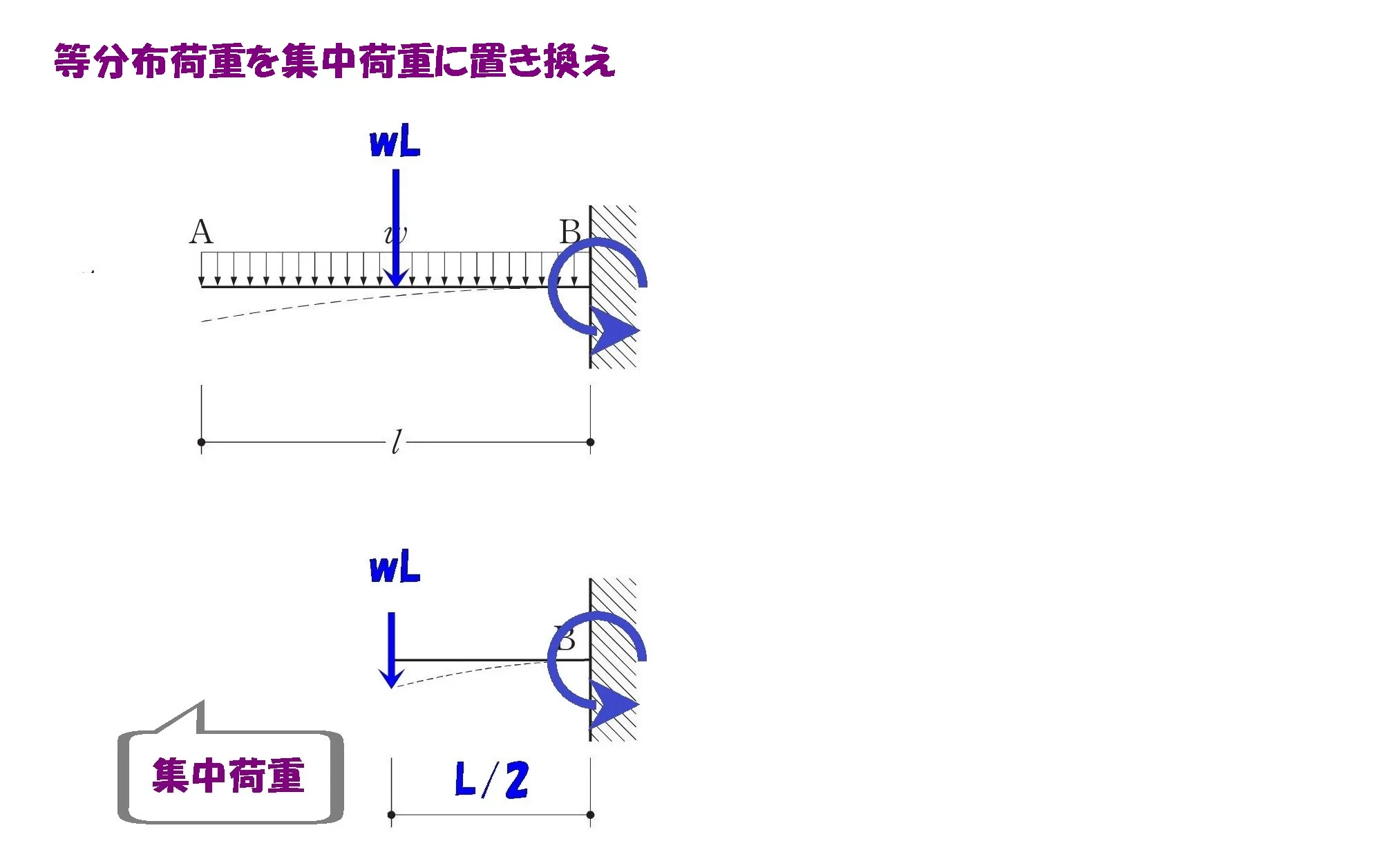

等分布荷重:wLを集中荷重に置き換えた場合は、力の作用点はLの”中心”になる。



ここも重要なポイント!
4.それぞれのモーメントを合成する
- 文章を読み取る
- モーメント=力×距離
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
モーメント=力×距離
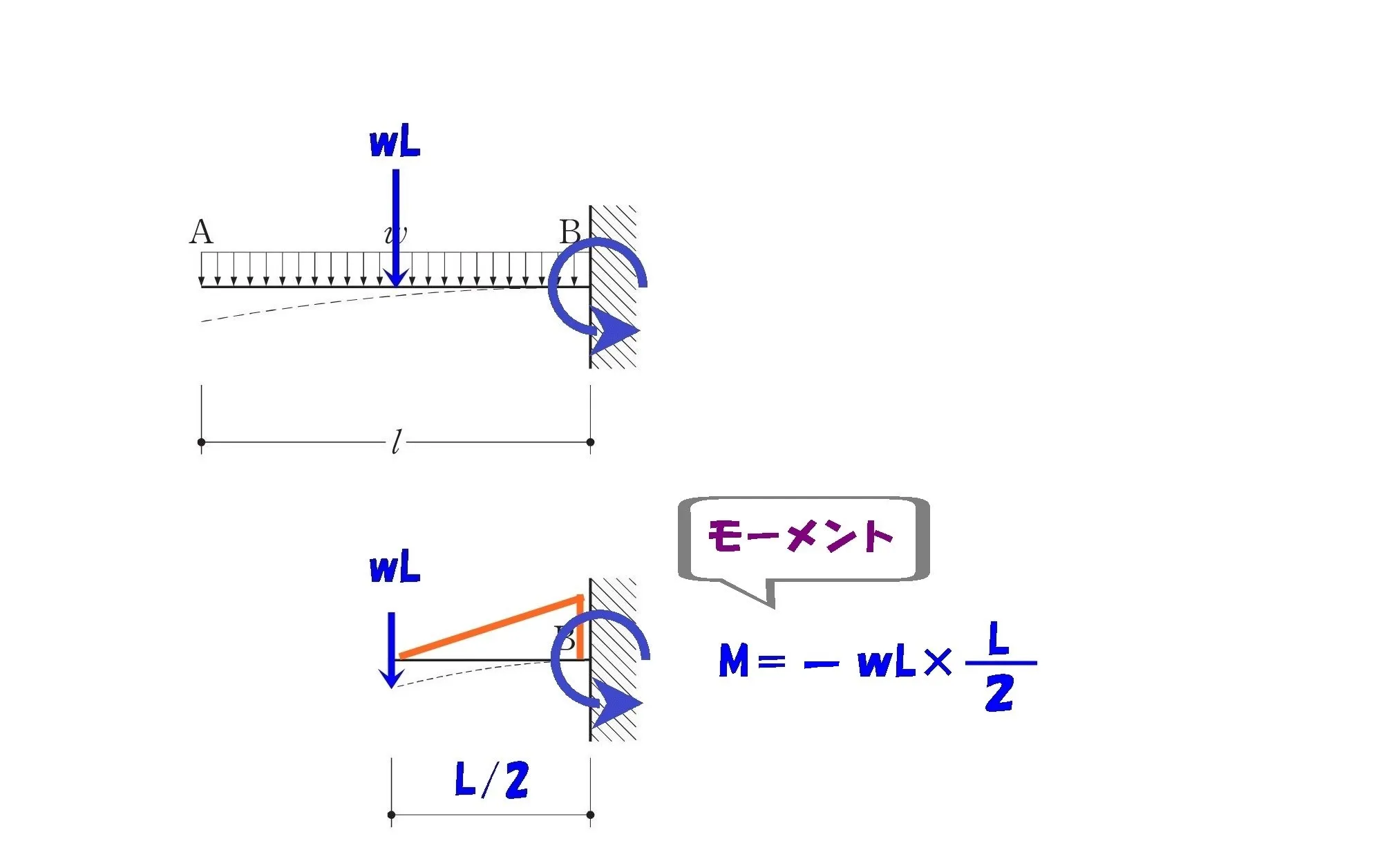

$$M=-wL*\frac{ L }{ 2 }⇨M=-\frac{ wL^2 }{ 2 }$$
$$モーメントの合成=\frac{ 3wL^2 }{ 8 }(集中荷重)-\frac{ wL^2 }{ 2 }(等分布荷重)$$
$$\frac{ 3wL^2 }{ 8 }-\frac{ 4wL^2 }{ 8 }=-\frac{ wL^2 }{ 8 }⇨モーメントの大きさ:\frac{ wL^2 }{ 8 }$$
攻略ポイント
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
枝.3


1.文章を読み取る
$$3.[A点からB点に向かって\frac{ L }{ 2 }の位置の曲げモーメントは、0である。]$$
モーメントの合成





モーメント図を合成して
L/2の位置を確かめる。
A点からB点に向かってL/2の位置
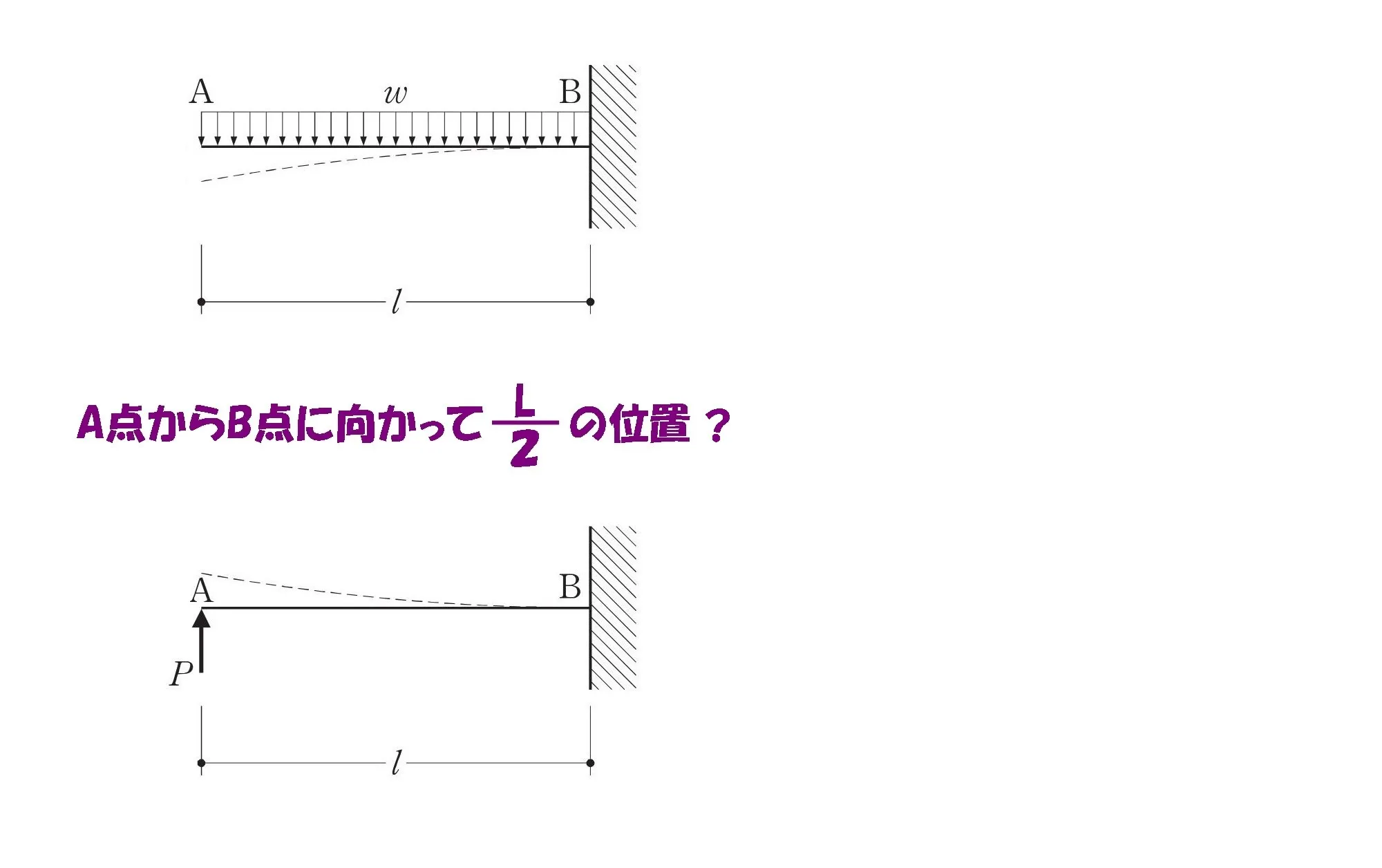

2.部材を切断してパーツを取り出す
A点からB点に向かってL/2の位置を取り出します。
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
L/2の位置で切断する
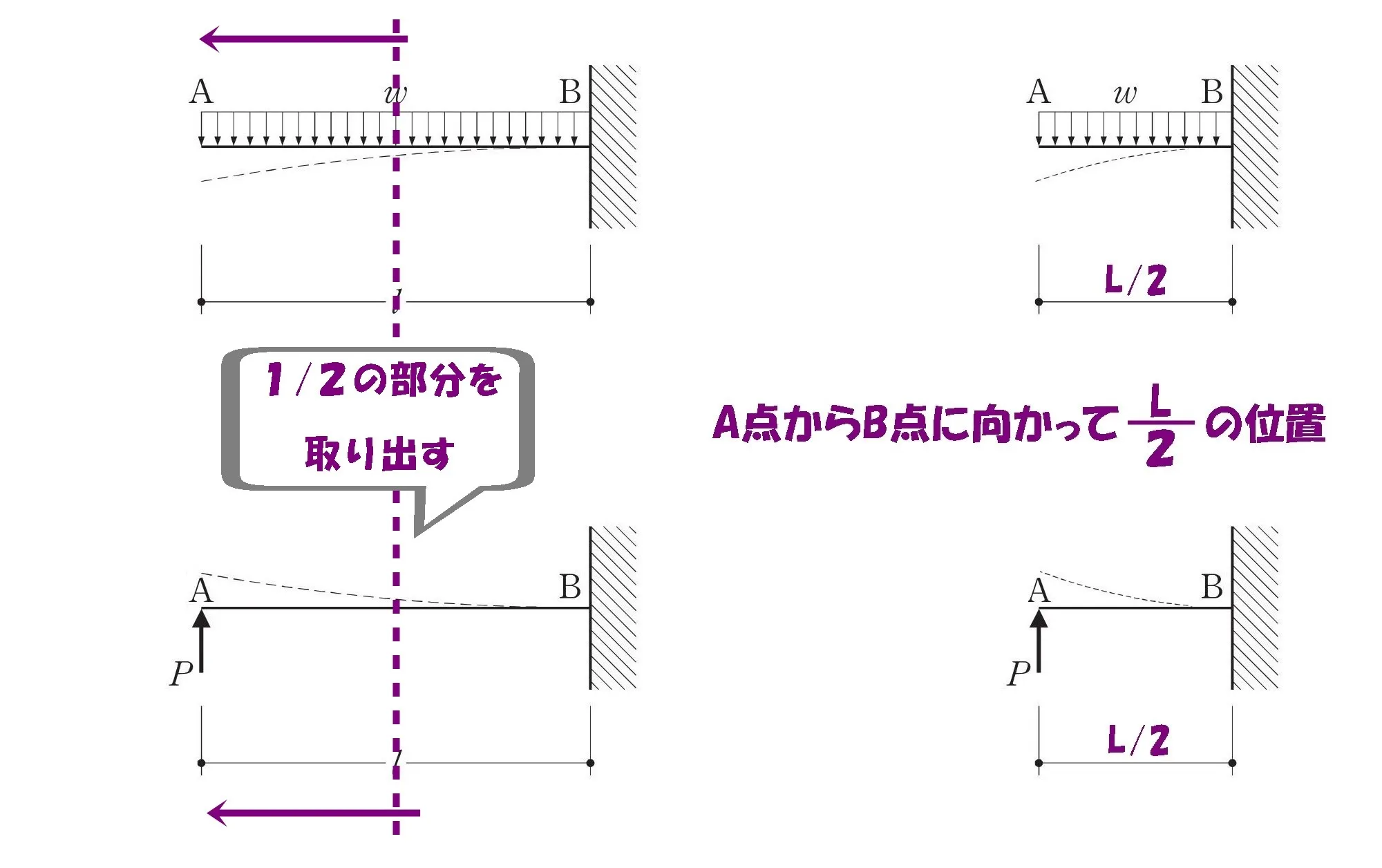




準備は良いか?
L/2の位置に回転軸を置く




1/2斬り!
A点からB点に向かってL/2の位置が固定端となる片持ち梁を取り出しましょう。
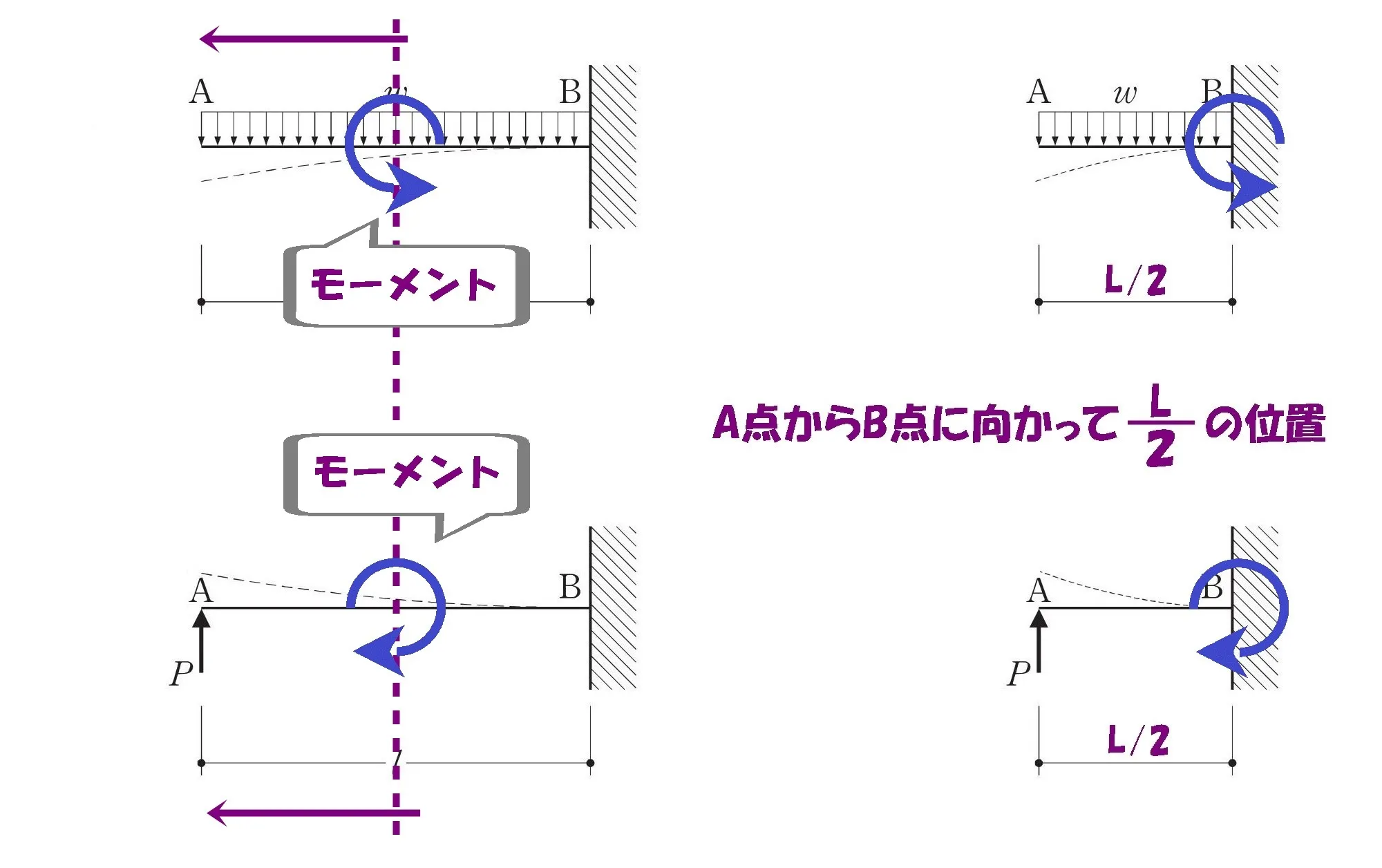
L/2の片持ち梁
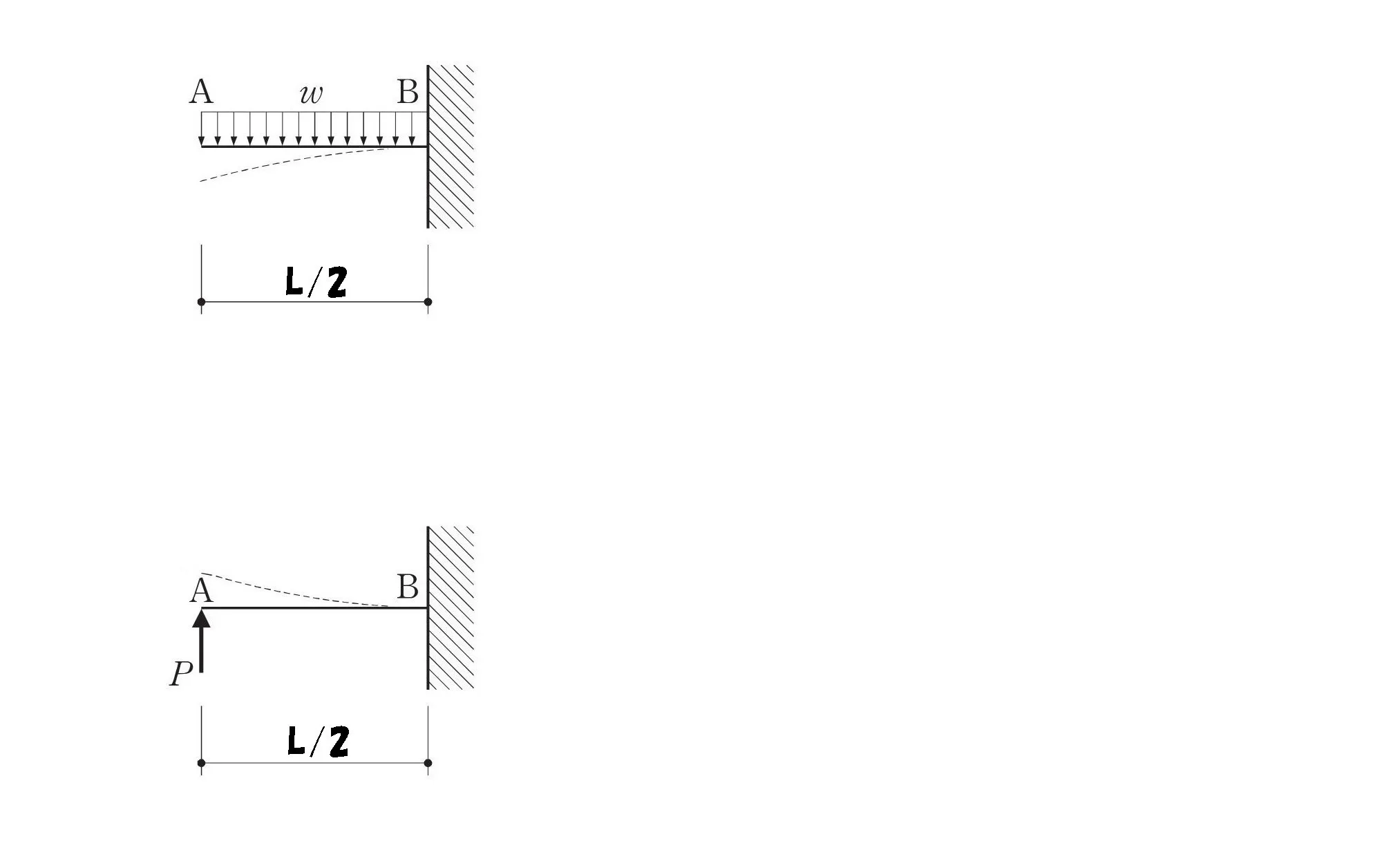

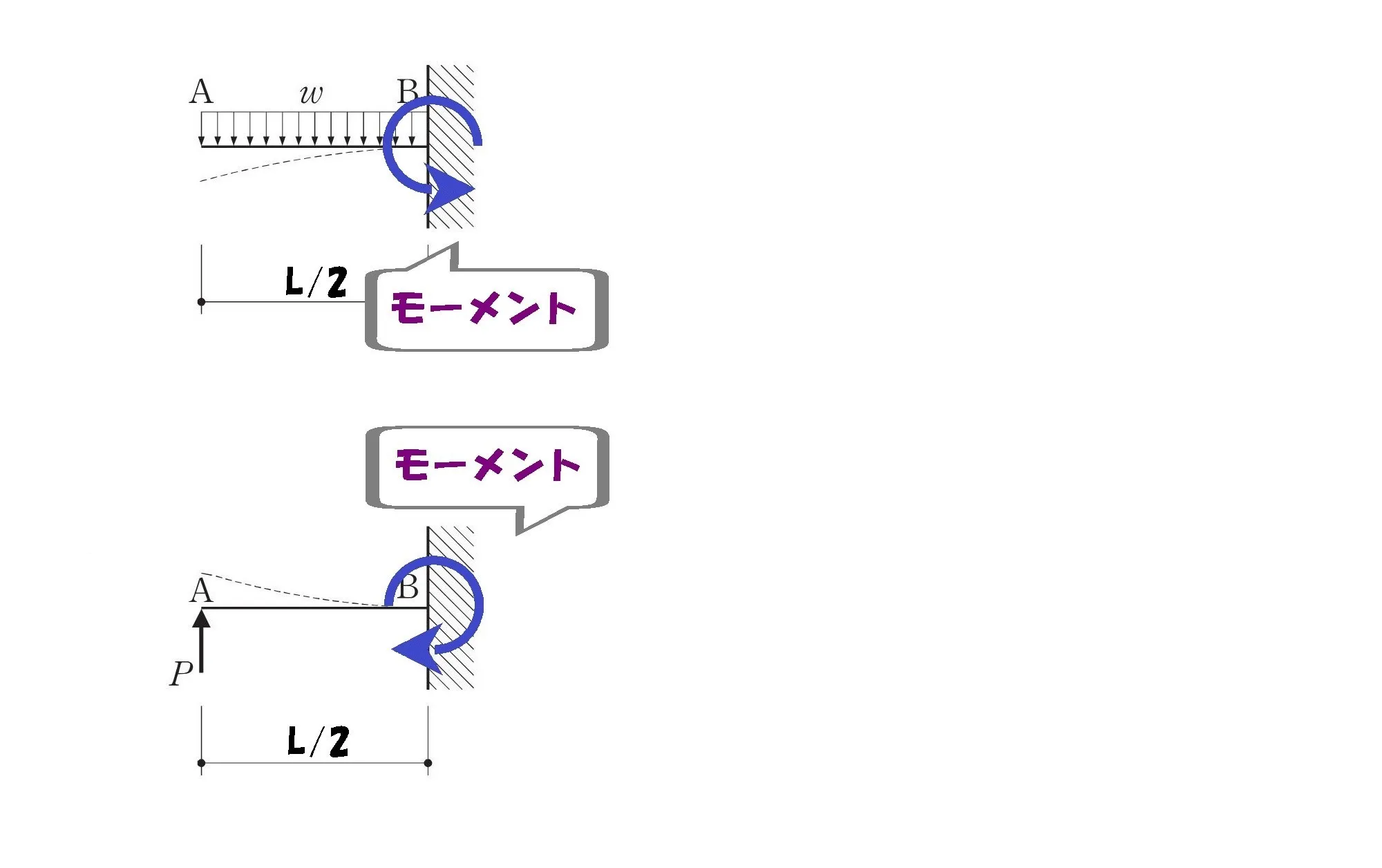

L/2の位置にモーメントの回転軸を置きます。
3.w×Lを集中荷重に置き換える
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
梁に掛かる荷重を書き込む
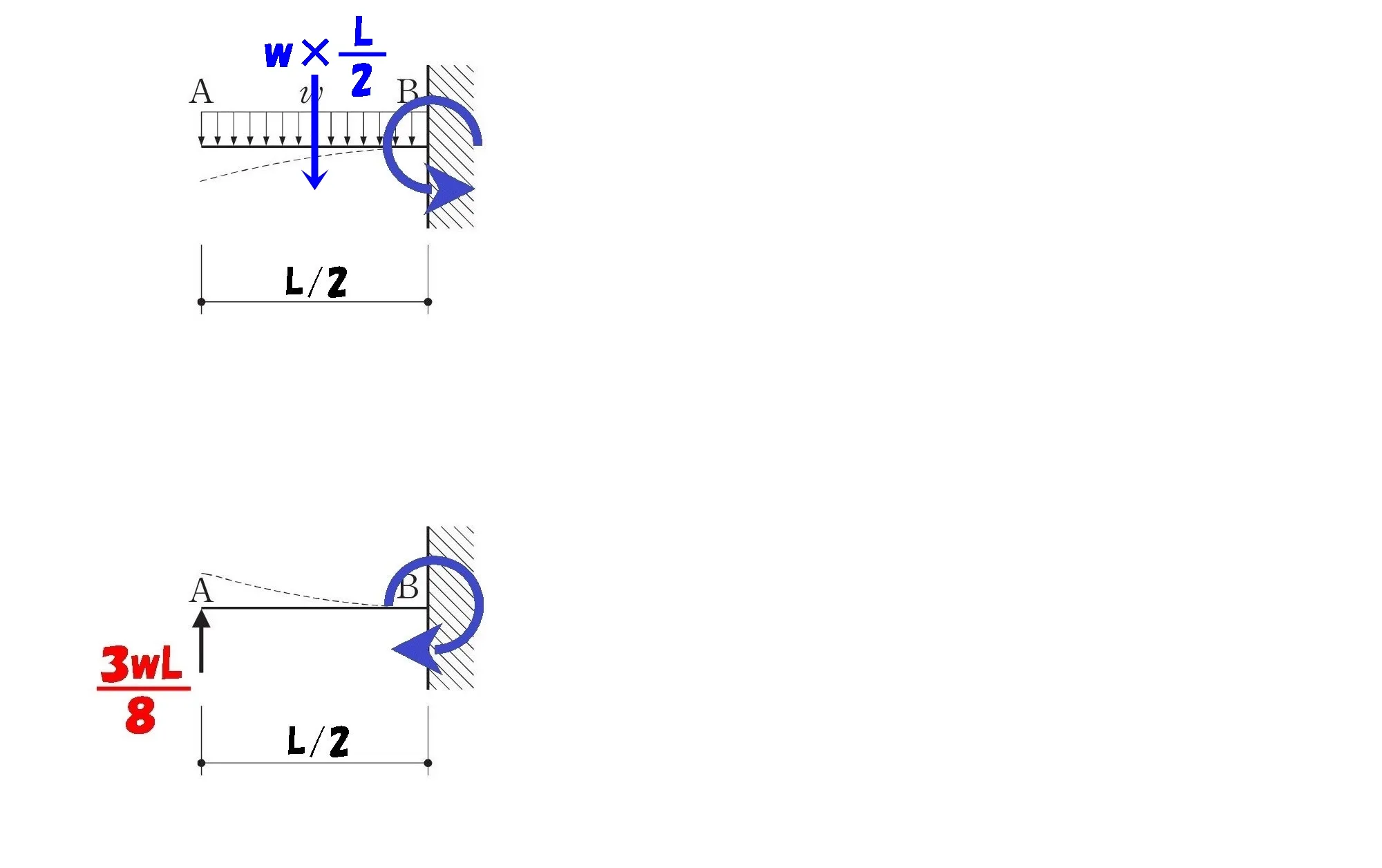

$$梁に掛かる荷重はそれぞれ$$
$$等分布荷重:w*\frac{ L }{ 2 }=\frac{ wL }{ 2 }$$$$集中荷重:鉛直反力より\frac{ 3wL }{ 8 }$$
wL/2を集中荷重に置き換える
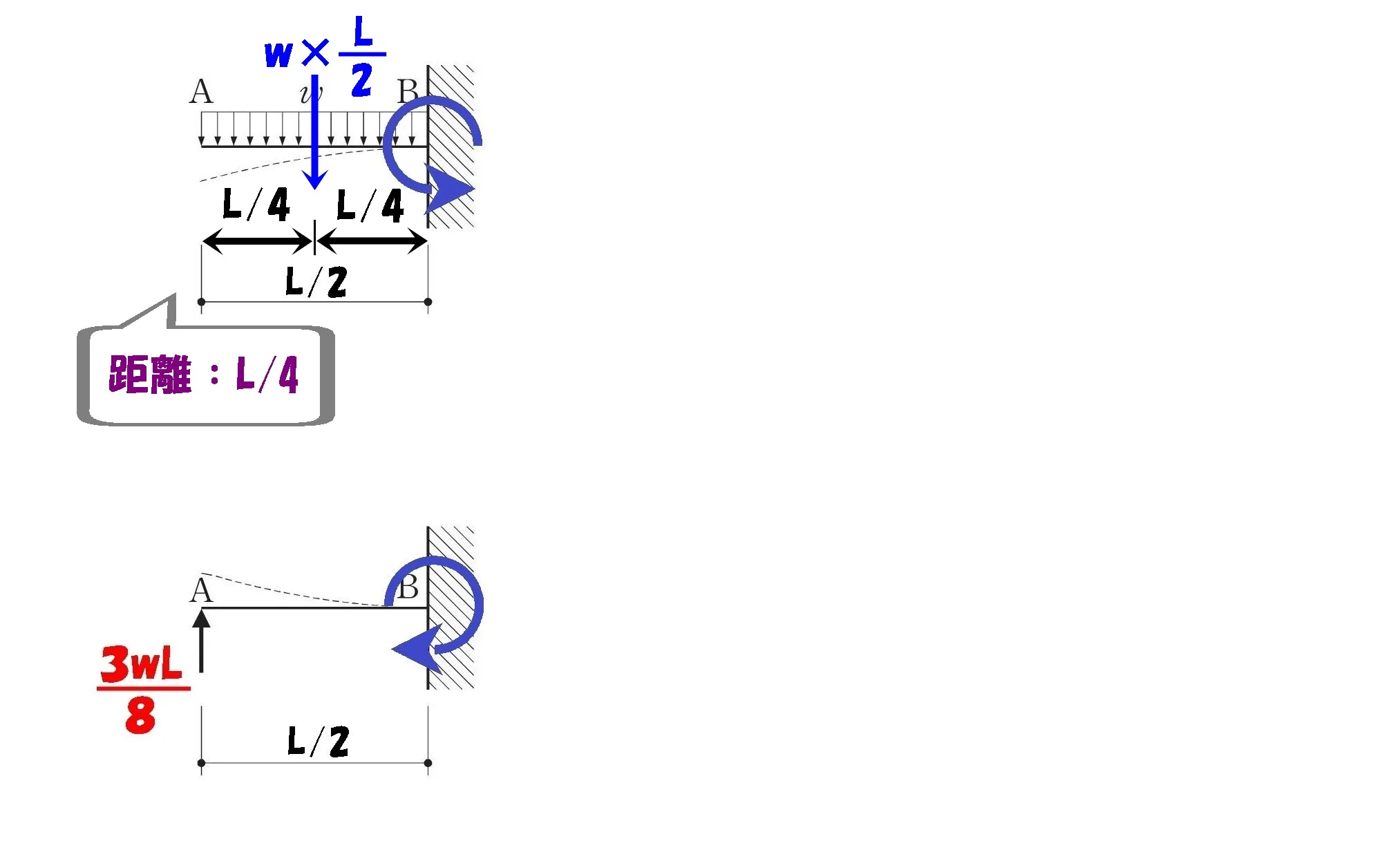

攻略ポイント
等分布荷重:wL/2を集中荷重に置き換えた場合は、力の作用点はL/2の”中心”になる。



L/2の中心までの距離は
さらに半分のL/4になる。
L/4の片持ちに置き換える
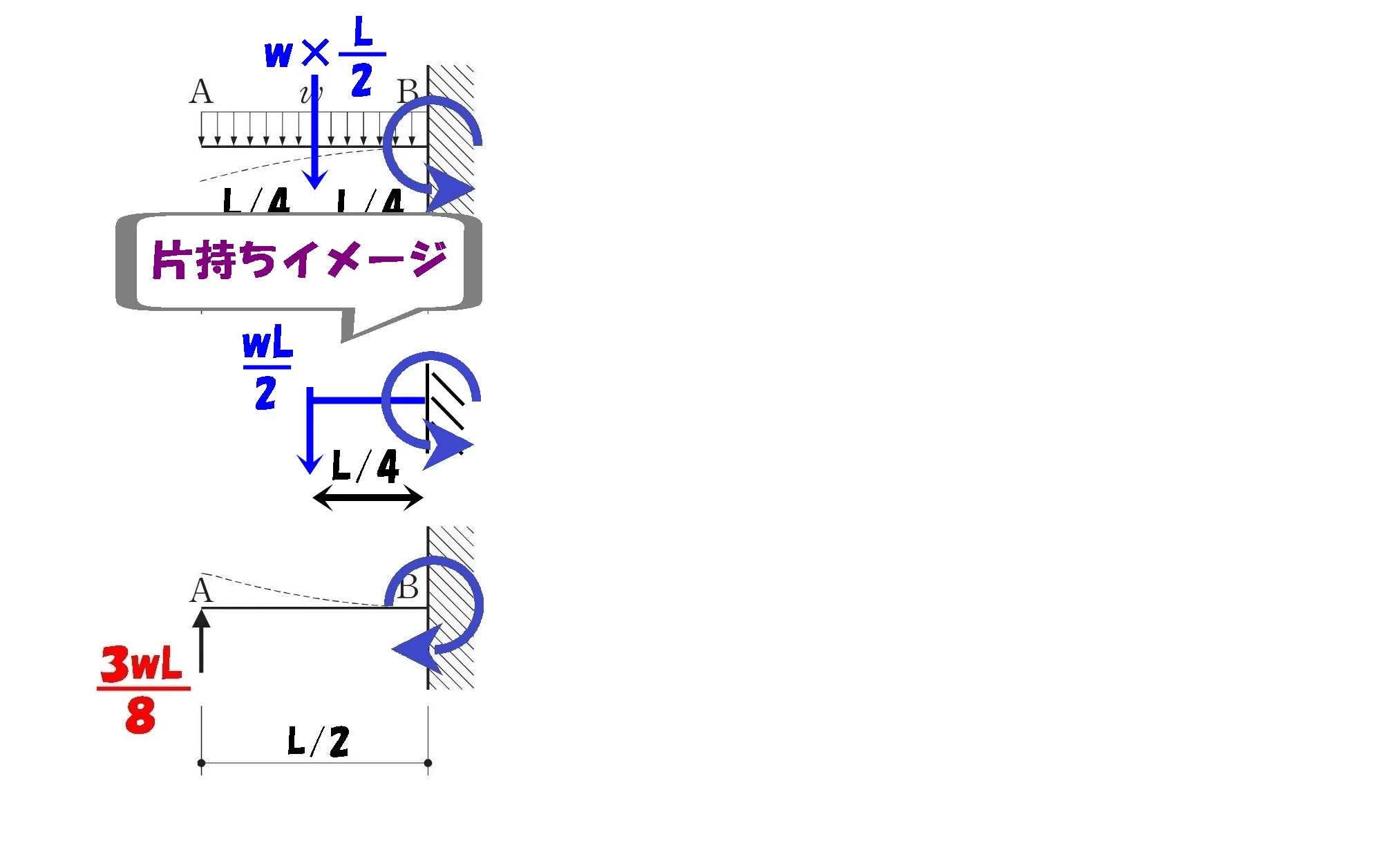

$$等分布荷重におけるモーメントの力と距離$$
$$力:\frac{ wL }{ 2 },距離:\frac{ L }{ 4 }$$
4.それぞれのモーメントを合成する
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
モーメント=力×距離
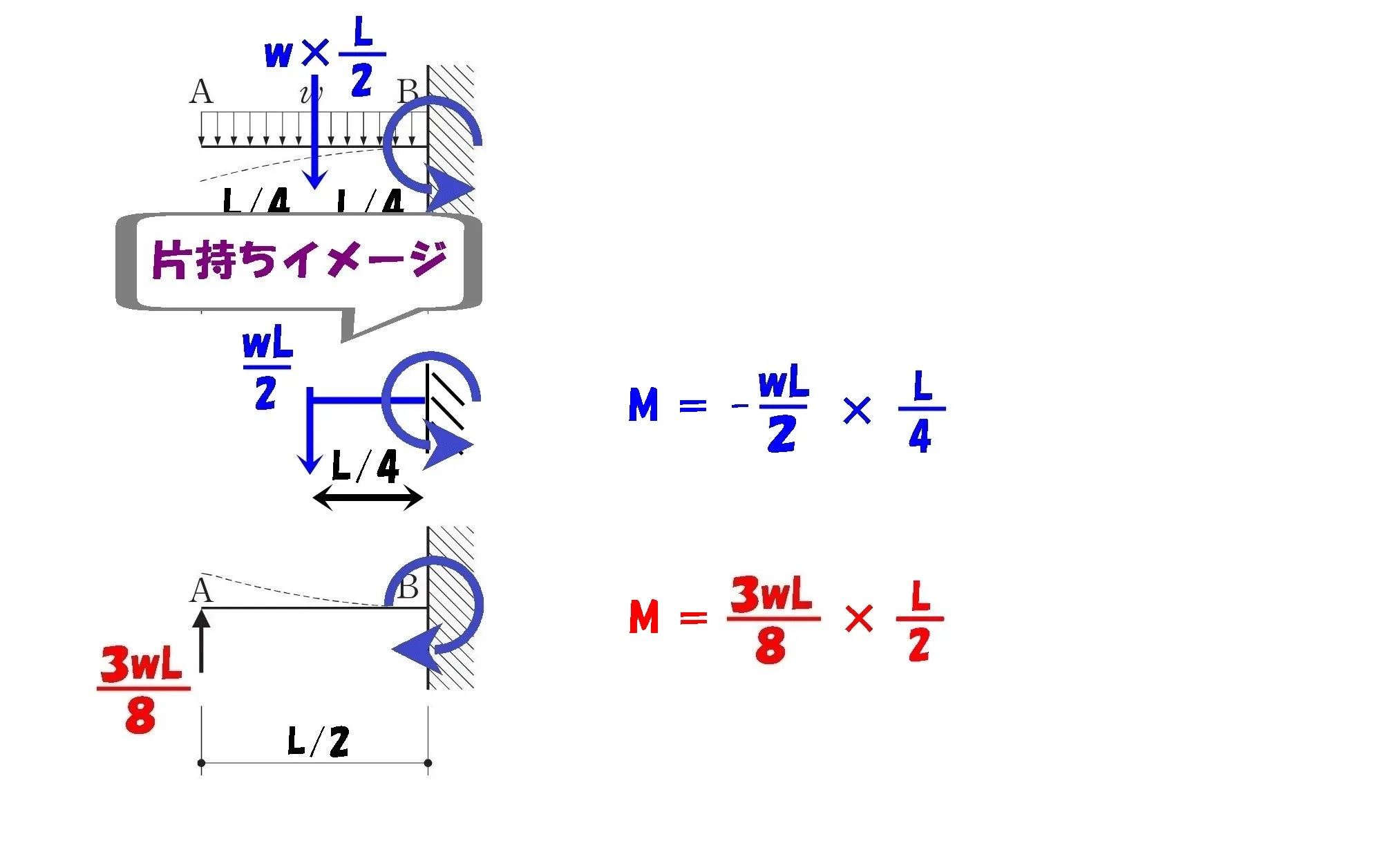

$$M(等分布荷重):-\frac{ wL }{ 2 }*\frac{ L }{ 4 }=-\frac{ wL^2 }{ 8 }$$
$$M(集中荷重):\frac{ 3wL }{ 8 }*\frac{ L }{ 2 }=\frac{ 3wL^2 }{ 16 }$$
$$モーメントの合成=-\frac{ wL^2 }{ 8 }+\frac{ 3wL^2 }{ 16 }$$
$$=-\frac{ 2wL^2 }{ 16 }+\frac{ 3wL^2 }{ 16 }=\frac{ wL^2 }{ 16 }(\neq0)$$
攻略ポイント
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのせん断力を合成する
枝.4


1.文章を読み取る
$$4.[A点からB点に向かって\frac{ 3L }{ 8 }の位置のせん断力は、0である]$$
せん断力の合成
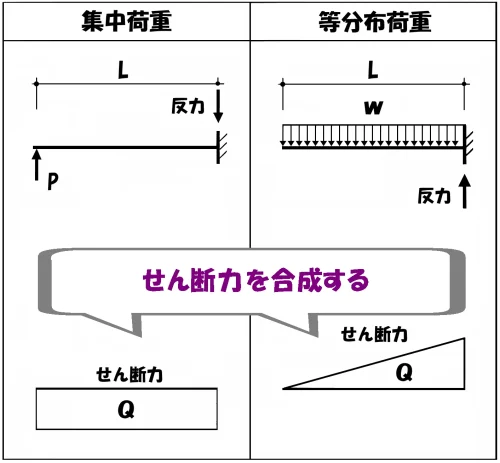




せん断力図を合成して
3L/8の位置を確かめる。
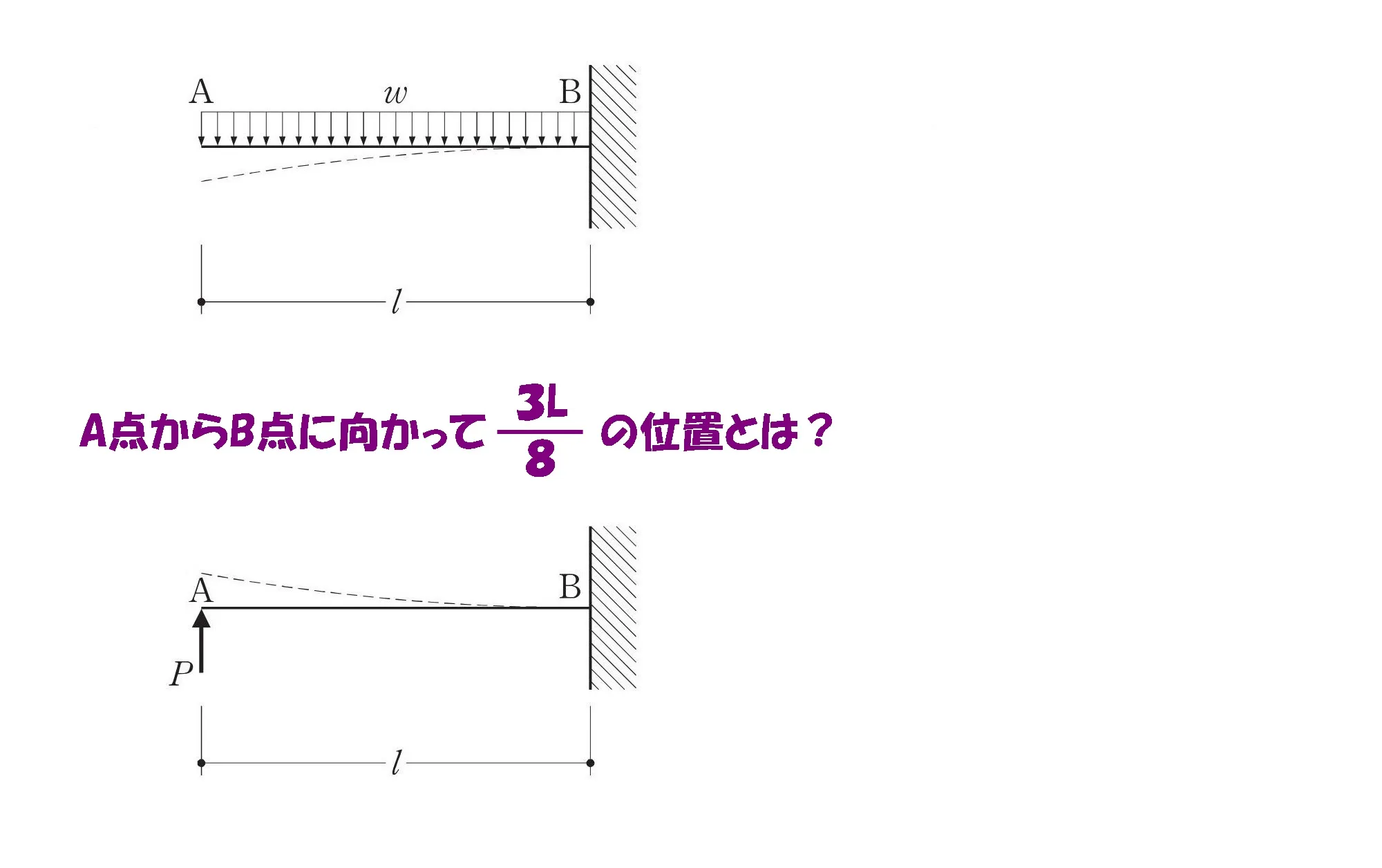
2.部材を切断してパーツを取り出す
A点からB点に向かって3L/8の位置を取り出します。
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのせん断力を合成する
A点からB点に向かって3L/8の位置




準備は良いか?
3L/8の位置で切断する
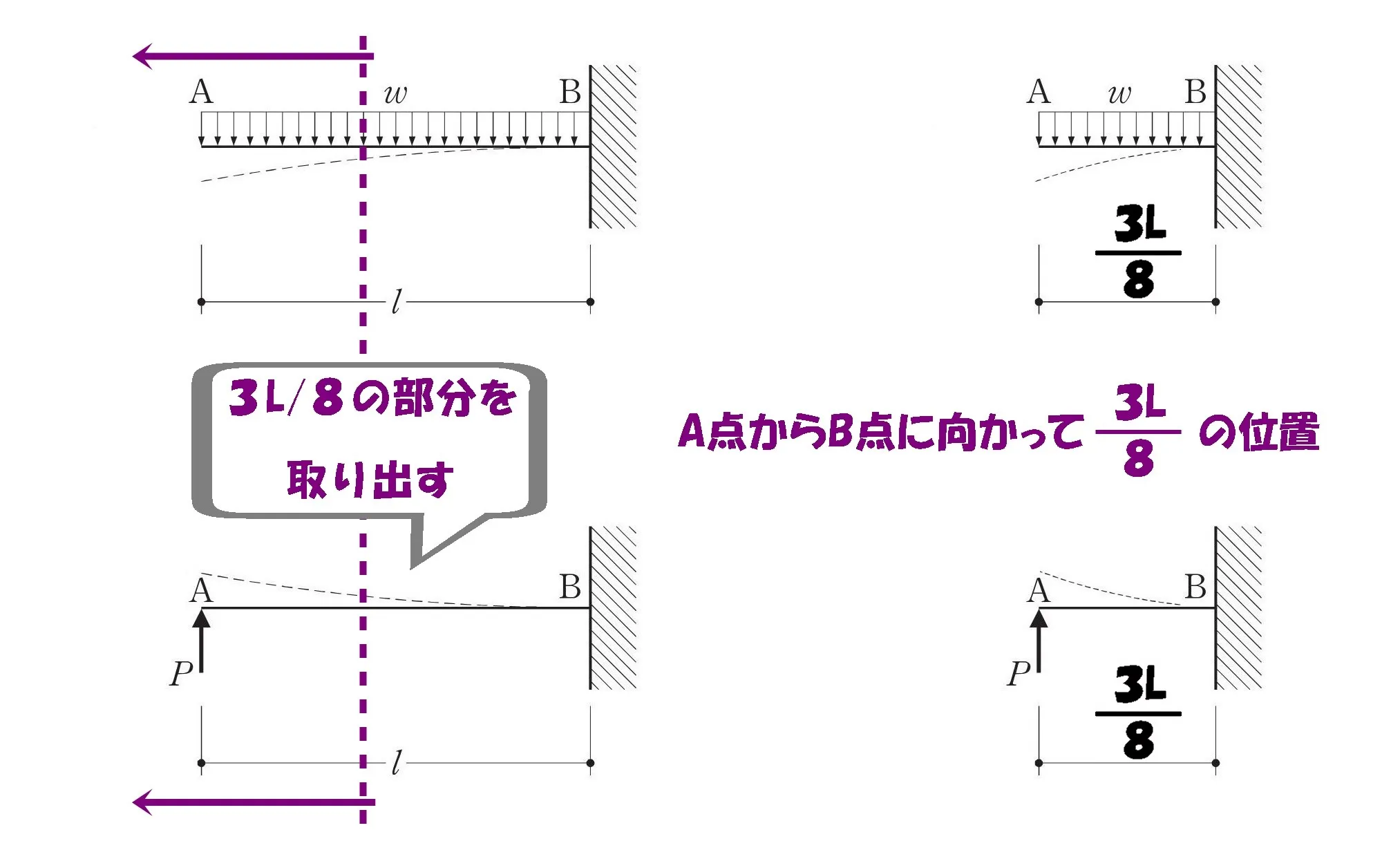




3/8斬り!
A点からB点に向かって3L/8の位置が固定端となる片持ち梁を取り出しましょう。
3L/8の片持ち梁
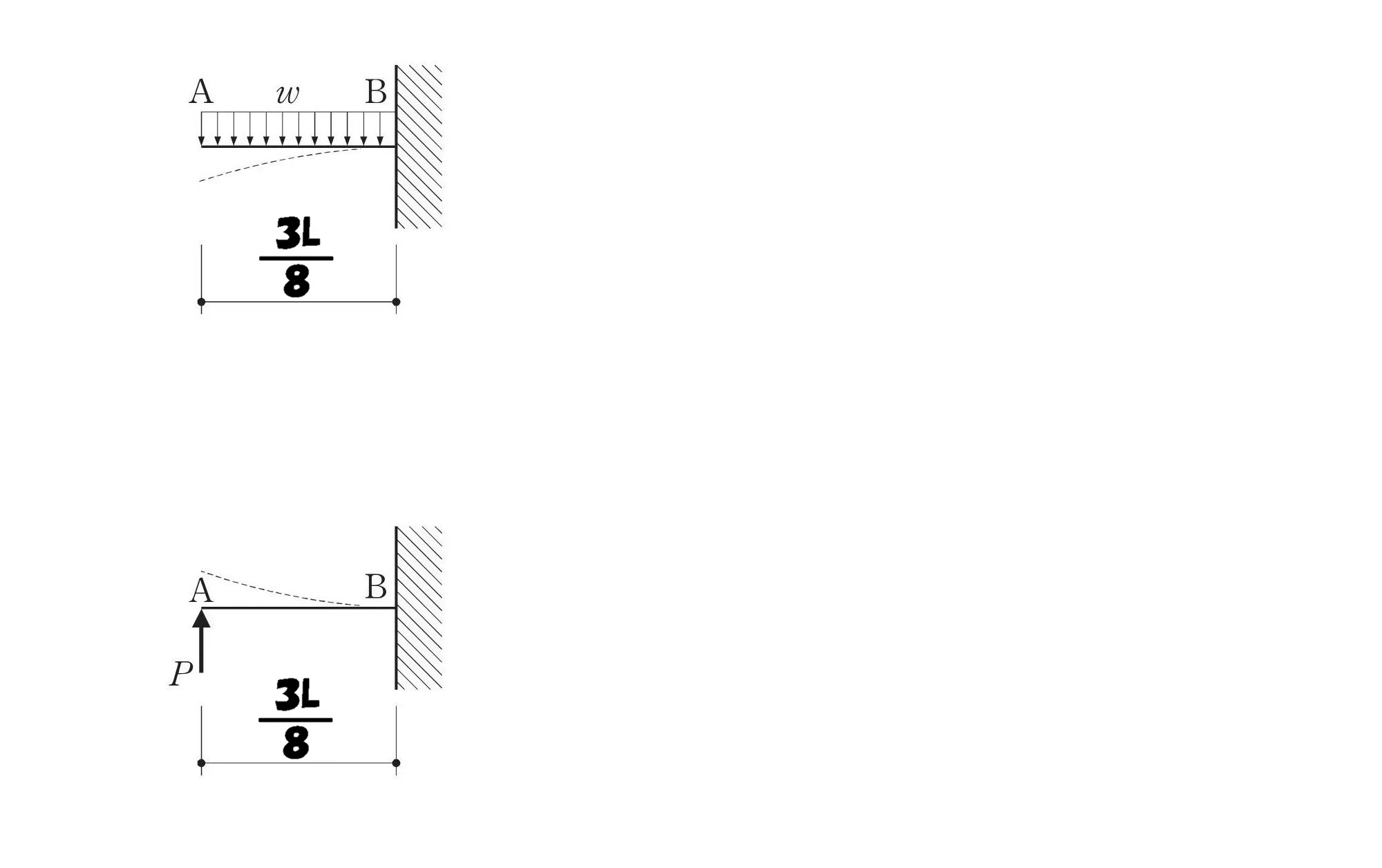

3.w×Lを集中荷重に置き換える
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのせん断力を合成する
3wL/8を集中荷重に置き換える
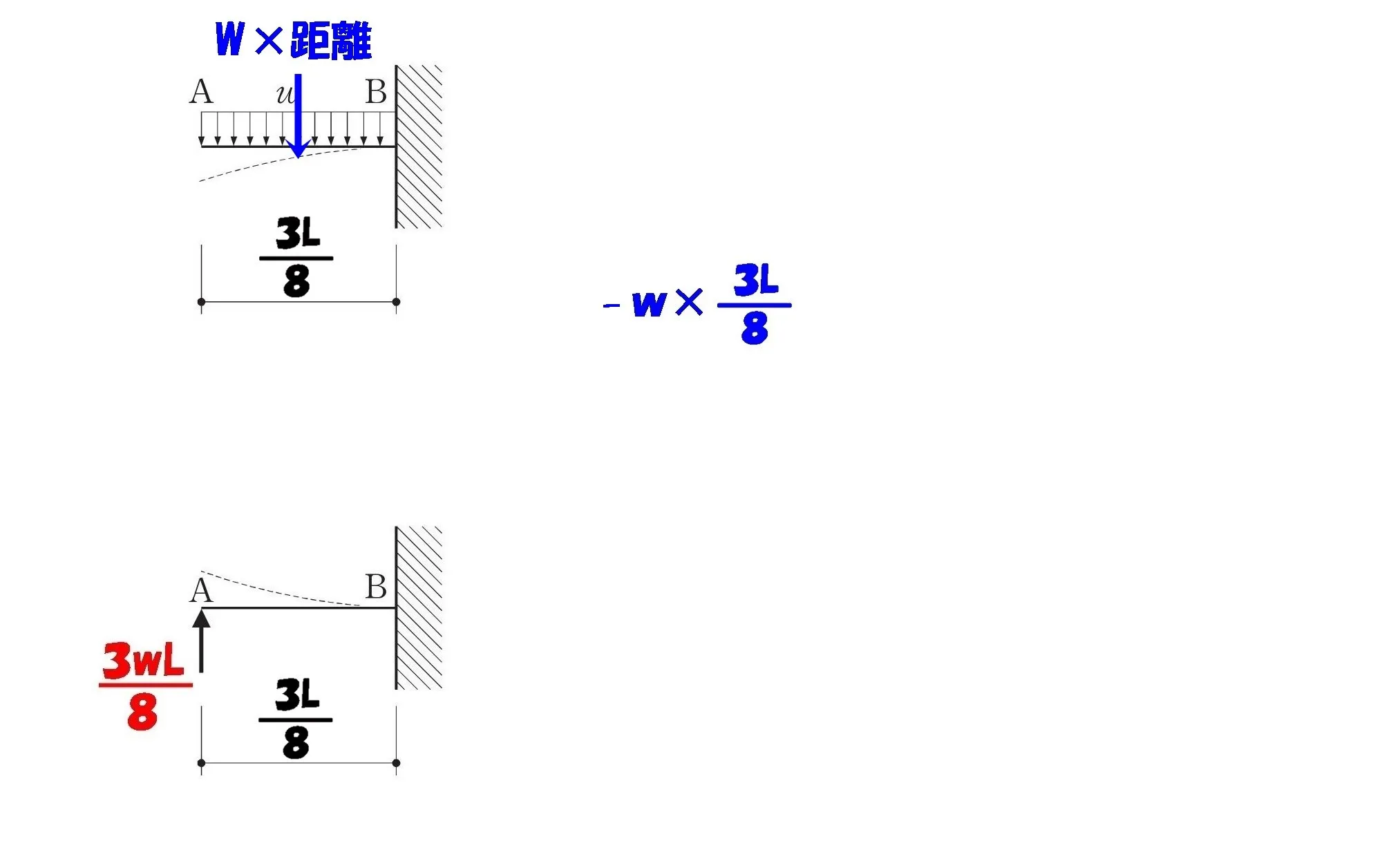

$$Q(等分布荷重)=-w*\frac{ 3L }{ 8 }=-\frac{ 3wL }{ 8 }$$
せん断力の単位は[N]なので、等分布荷重[N/m]×距離[m]=せん断力[N]とする。



単位は合わせる。
これが公式の基本です。
4.それぞれのせん断力を合成する
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのせん断力を合成する
せん断力を合成する
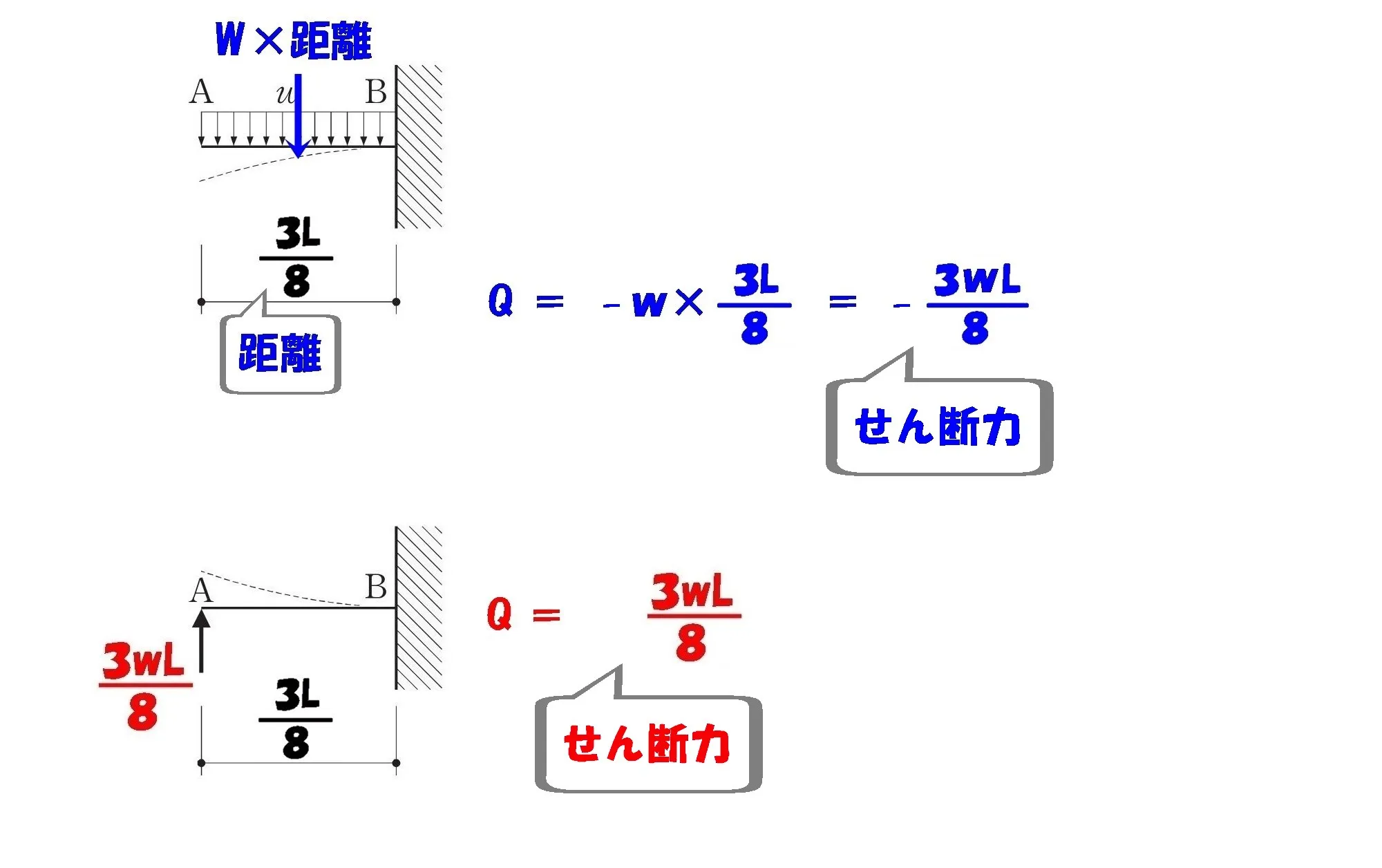

$$Q(等分布荷重)=-\frac{ 3wL }{ 8 }$$$$Q(集中荷重)=\frac{ 3wL }{ 8 }$$
$$せん断力の合成=-\frac{ 3wL }{ 8 }+\frac{ 3wL }{ 8 }=0$$
答え.3(誤り)





拙者もまだまだ
修行が必要でござる。
攻略ポイント
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する
トラス-1
難易度:★★★☆☆
トラスの攻略は「切断法」が基本です。
過去問を通して、解き方を完全マスターしていきましょう。
トラスを攻略



トラス100本ノック!


この動画を YouTube で視聴
攻略ポイント
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める
問題
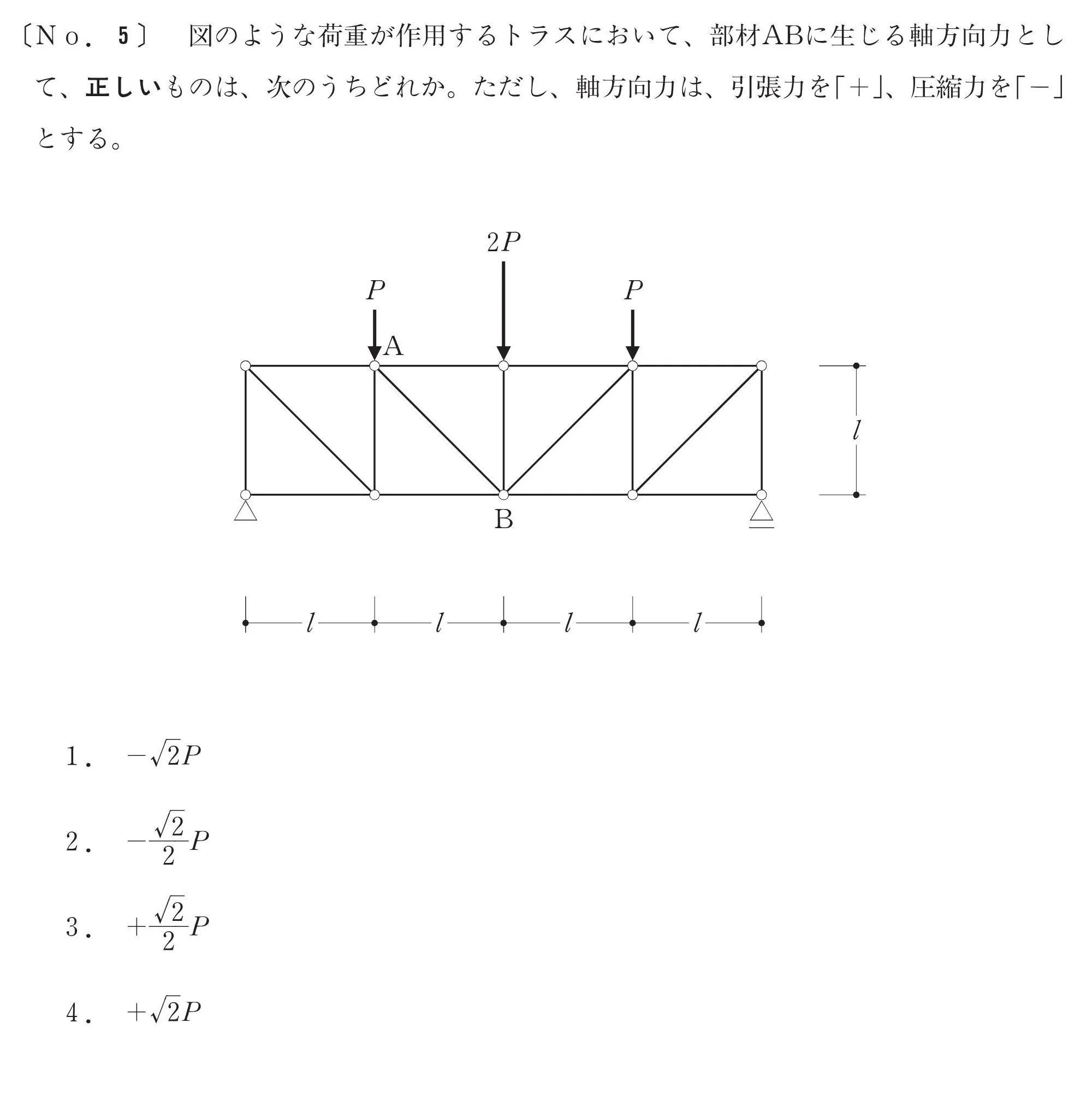

求める部材をチェックする
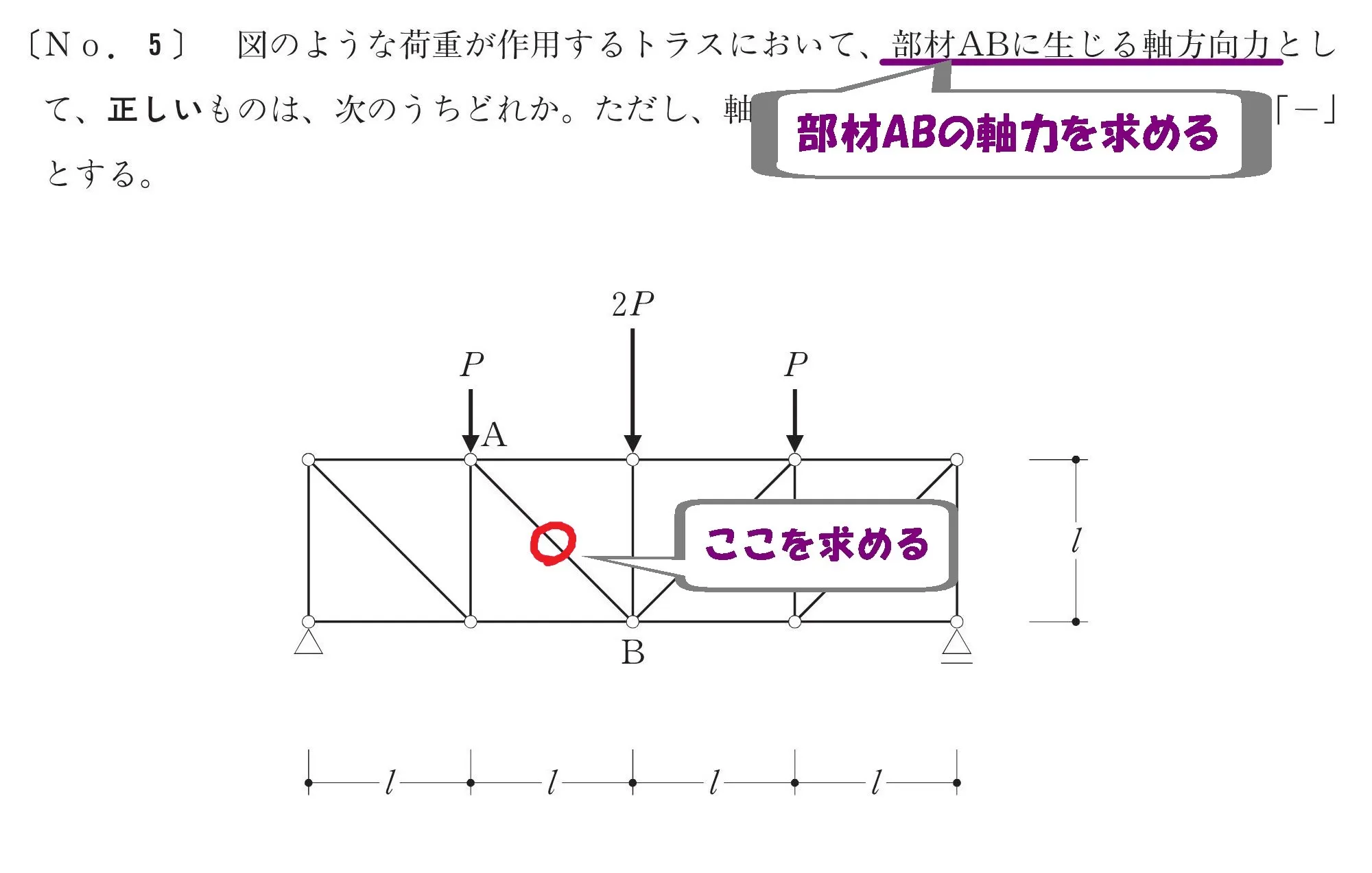

「部材ABに生じる軸力を求める」ことから、対象物に印を付けておきましょう。



斜め部材に
〇印をつけておこう。
1.支点反力を求める
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める
支点反力を求める
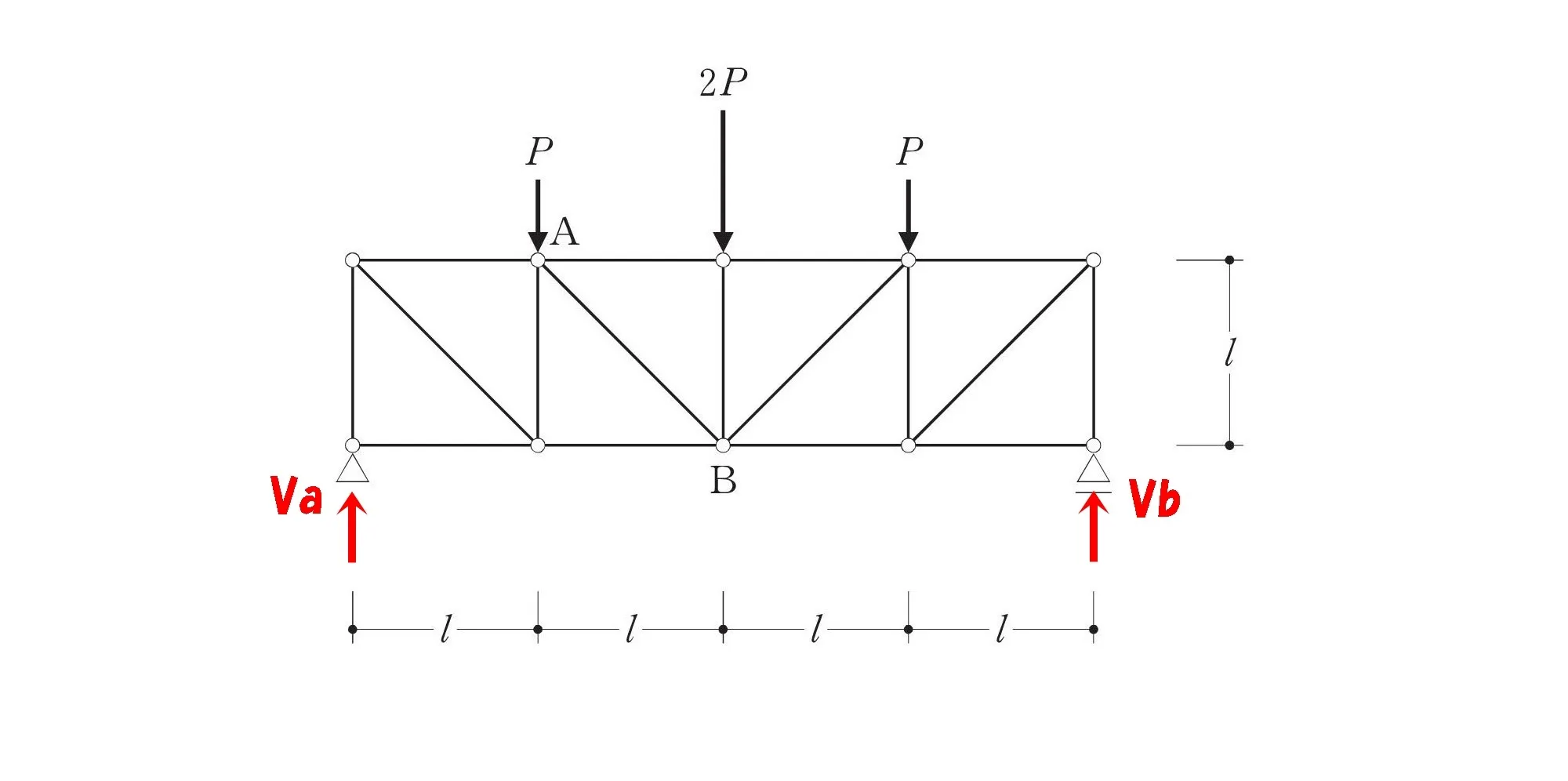

左:ピン支点
右:ローラー支点
ピン支点を起点にΣM=0
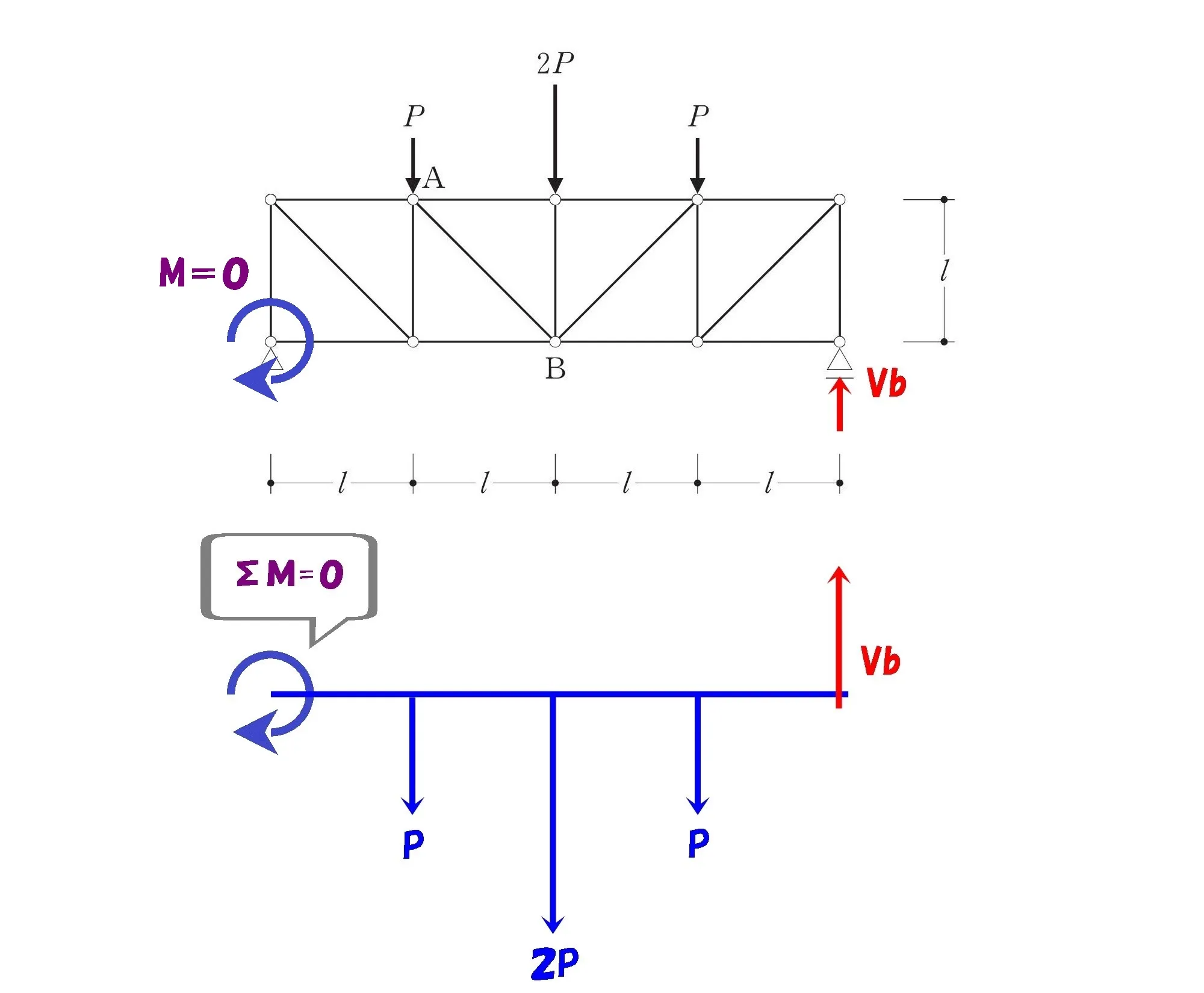

$$L=1を代入,\Sigma M=0より$$$$P*1+2P*2+P*3-Vb*4=0$$
$$4Vb=8Pより,Vb=2P$$
$$\Sigma Y=0より$$$$P+2P+P-Va-2P=0⇨Va=2P$$
公式
$$\Sigma M=0$$



Σエム!
鉛直反力は2P
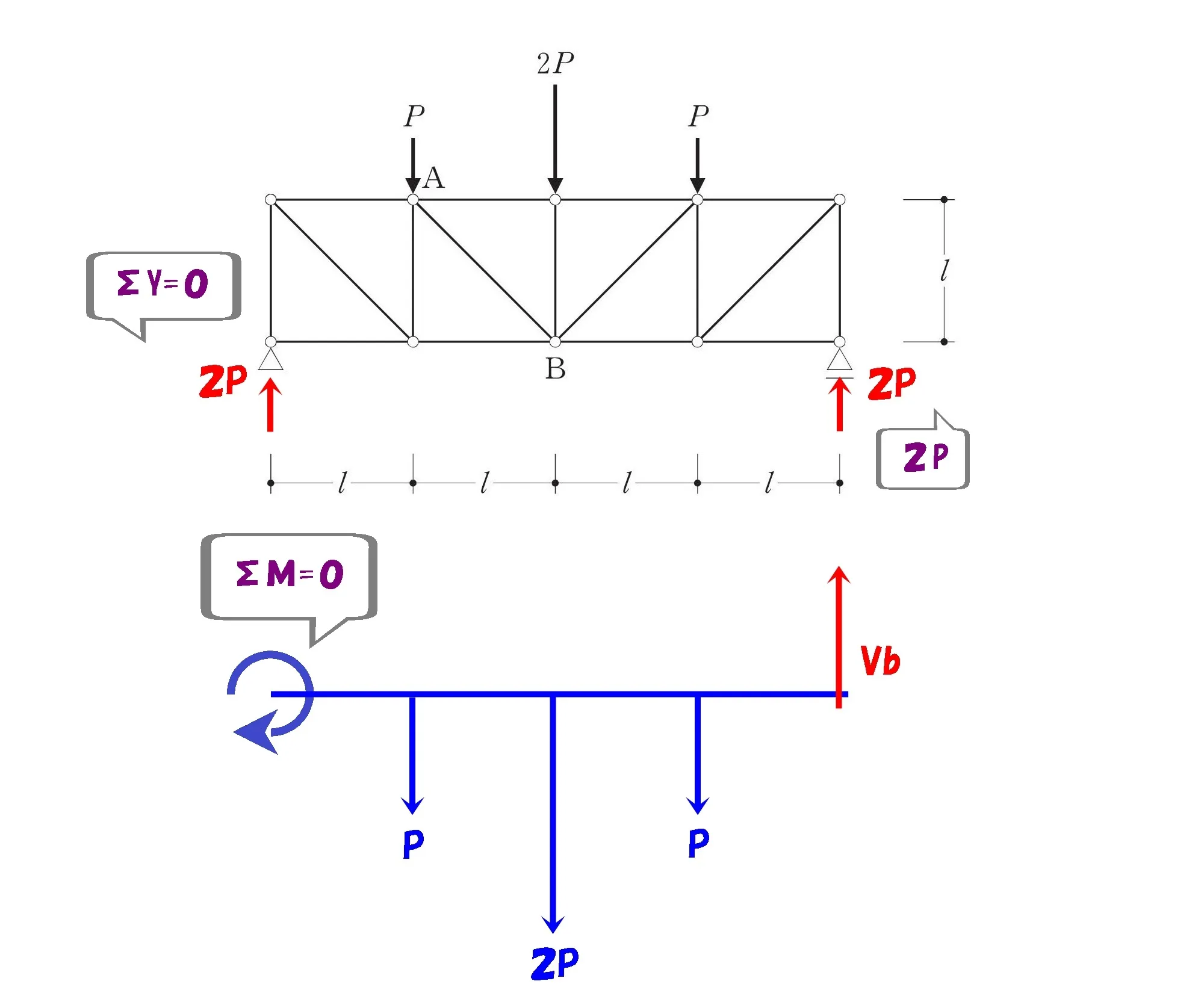

$$Va=2P,Vb=2P$$
2.斜め部材を切断する(切断法)
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める
部材ABの軸力を求める
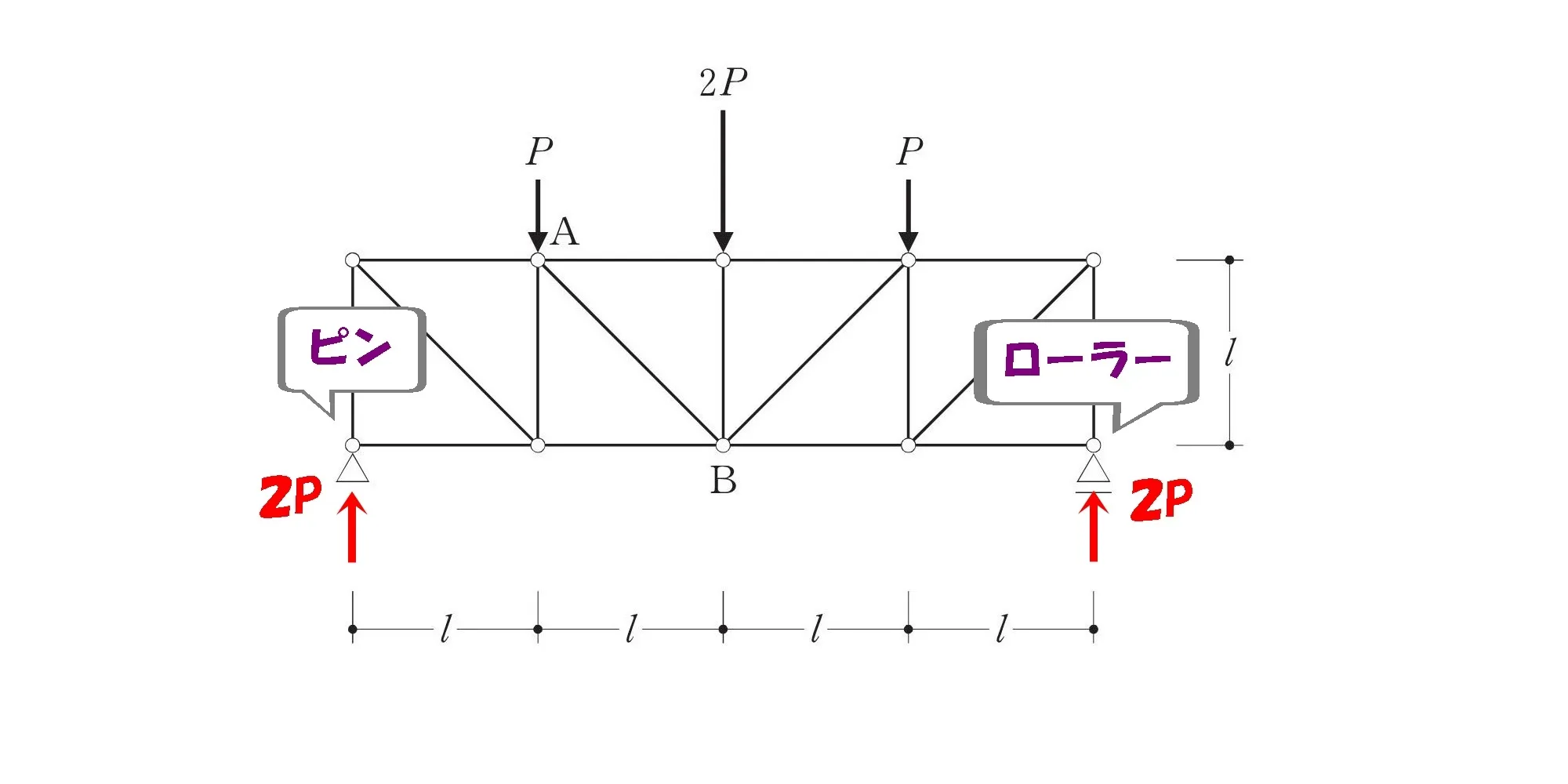

左:ピン支点
右:ローラー支点
部材を切断する
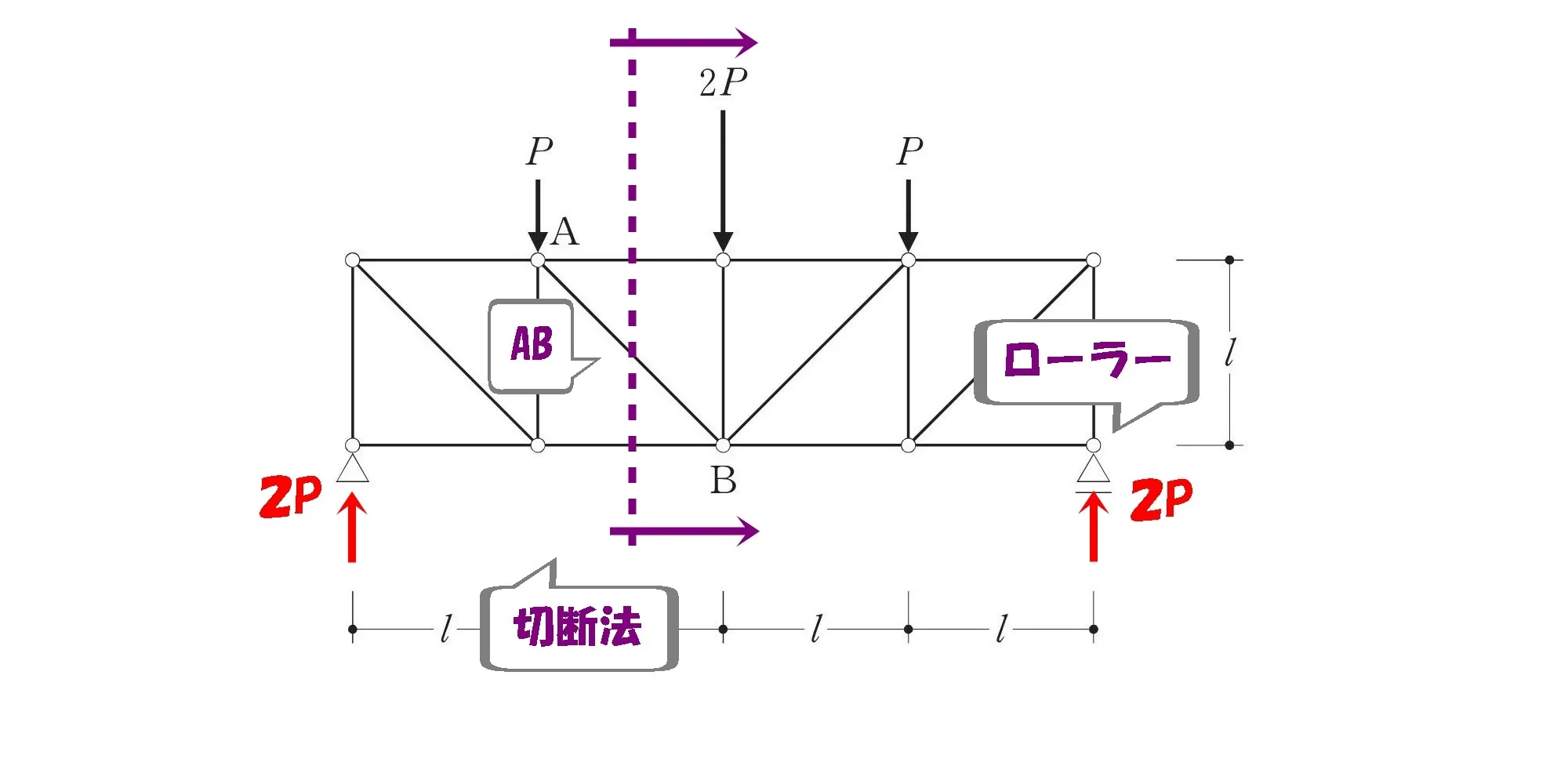

切断法のポイント
- 支点反力は先に求めておく。
- 対象となる部材ABを含む位置で切断する。
- ピン支点より反力の少ないローラー支点の部材を取り出す。



準備は良いか?
部材を取り出す
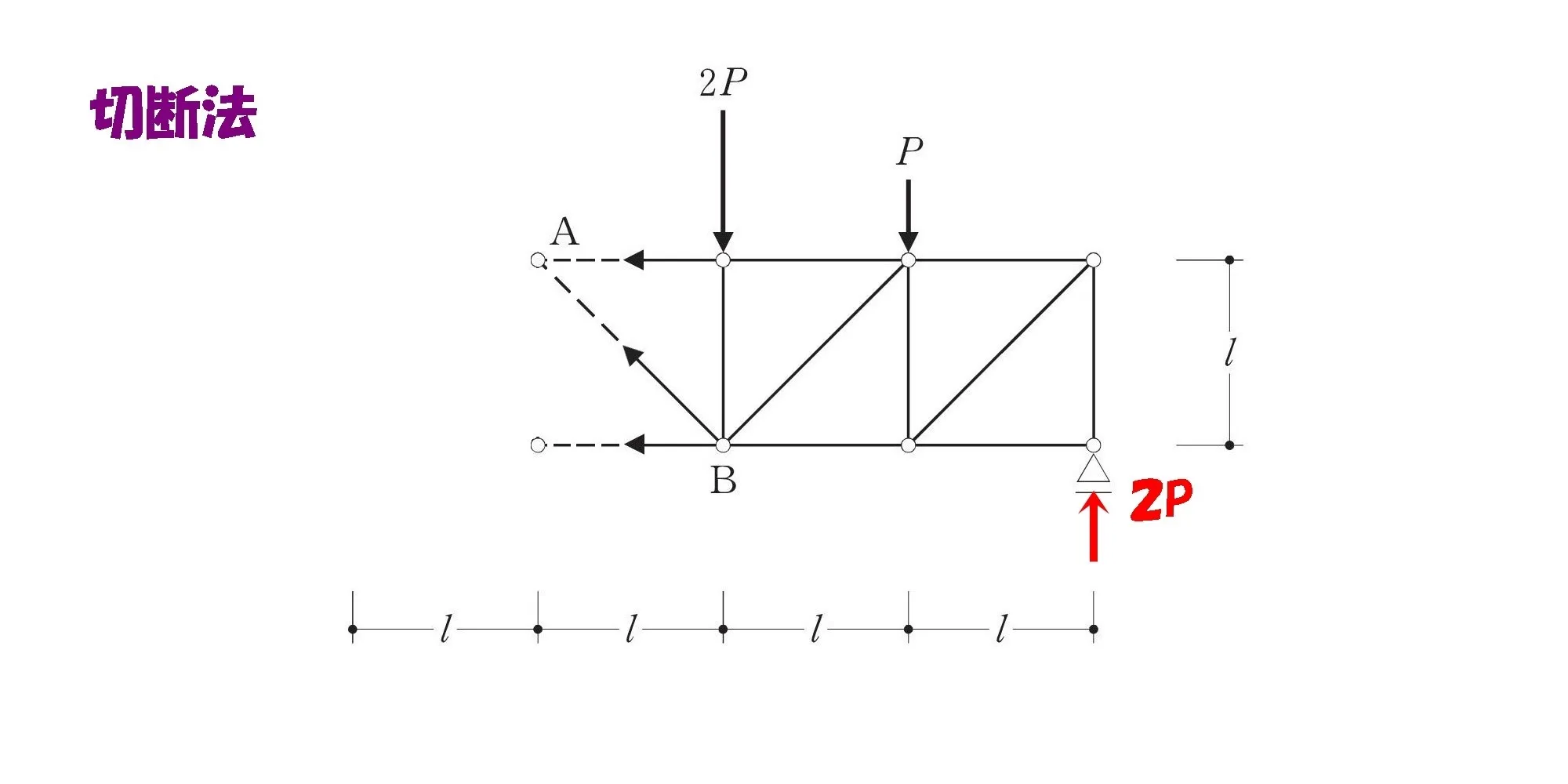

切断した部材は引張り方向(+)を仮定して、ベクトルを伸ばします。



トラス切断!
部材ABの角度は45度
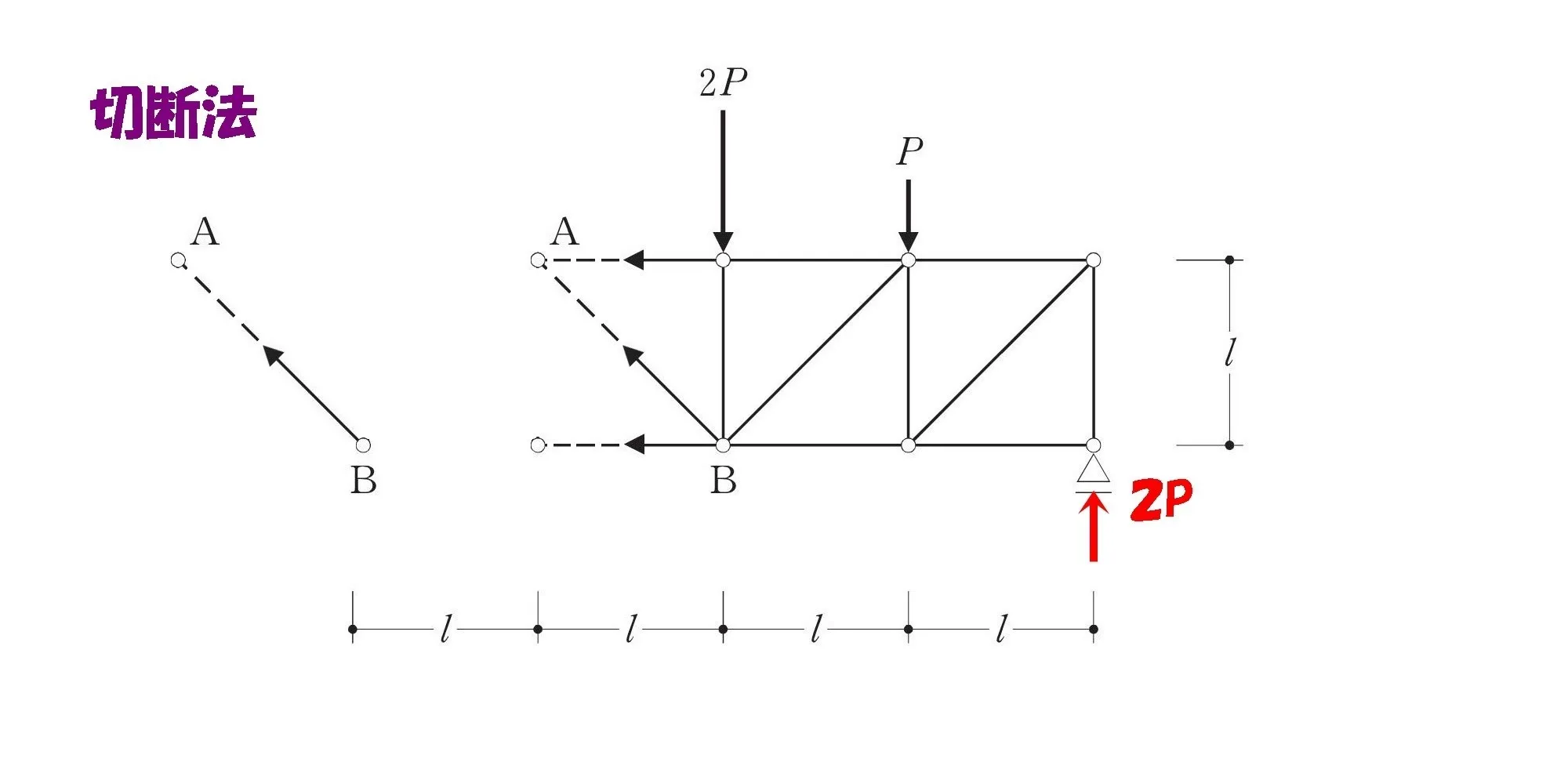

$$45度の直角三角形の辺の比=1:1:\sqrt{2}$$
ベクトルを分解する
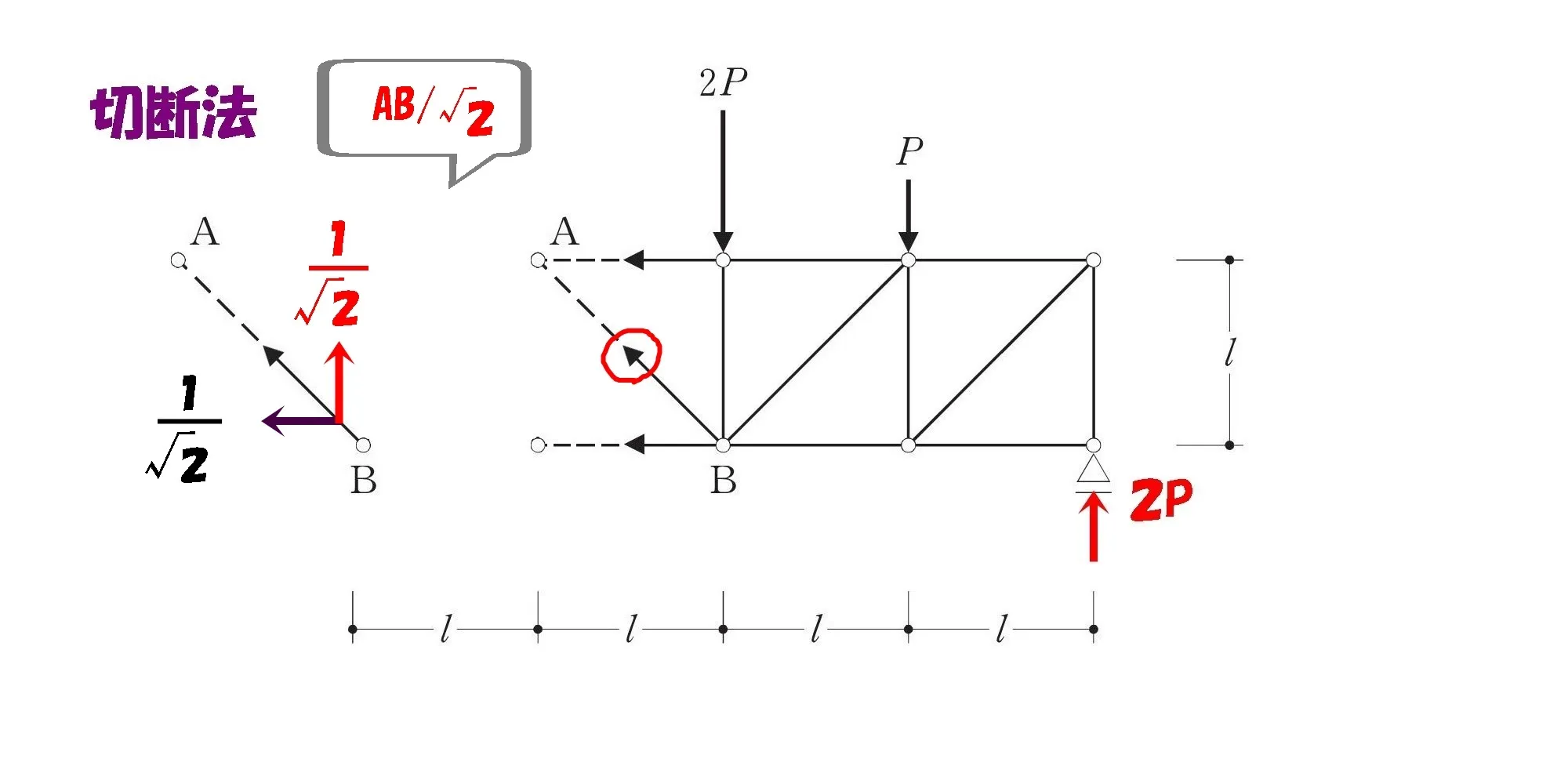

$$AB:ABx:ABy=1:\frac{ 1 }{ \sqrt{2} }:\frac{ 1 }{ \sqrt{2} }$$
$$タテ部材とヨコ部材の軸力ABは,AB*\frac{ 1 }{ \sqrt{2} }$$
3.ΣY=0の吊り合い式より軸力を求める
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める
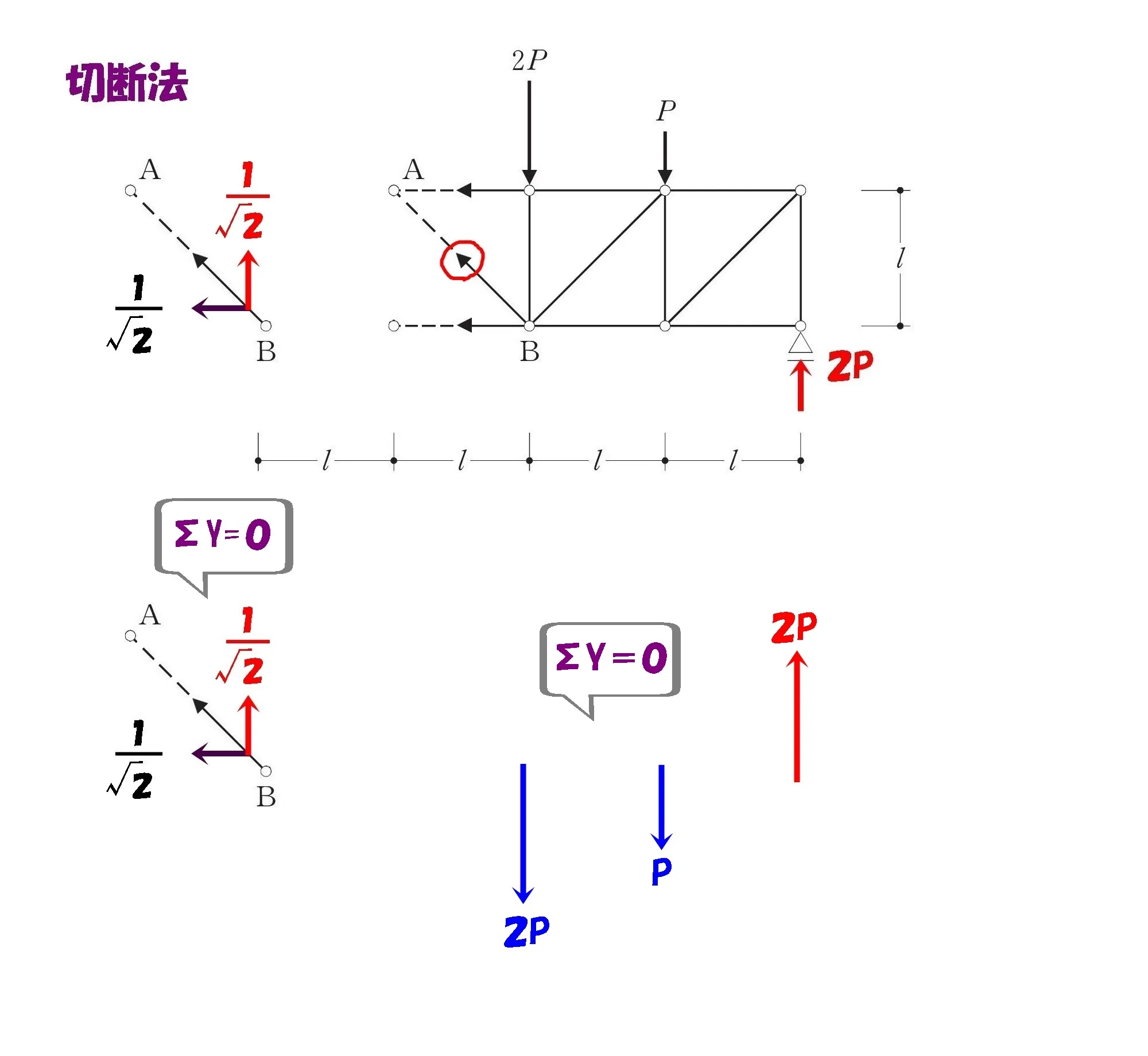
ΣY=0

公式
$$\Sigma Y=0$$



Σワイ!
軸力ABを求める
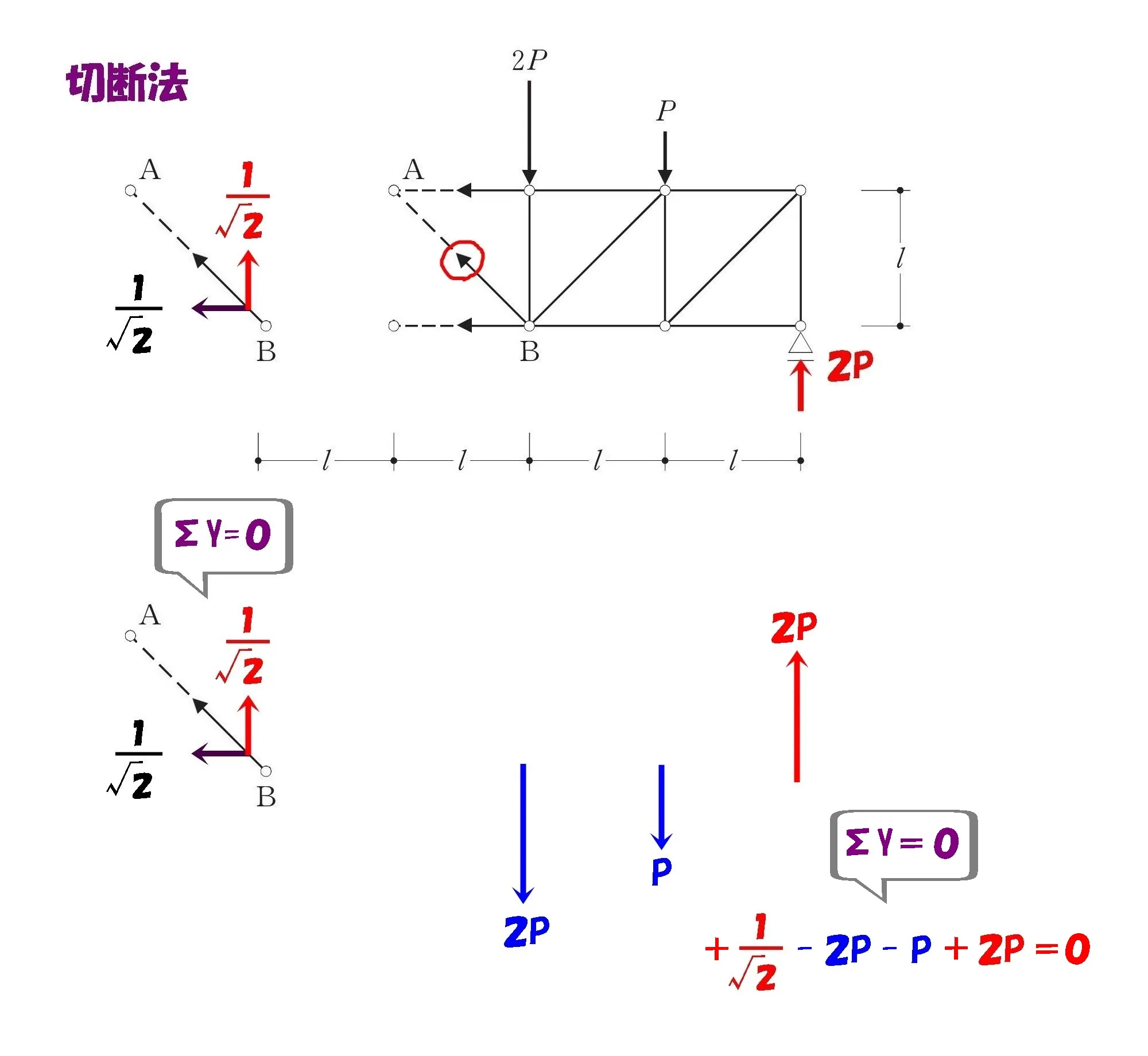

$$\Sigma Y=0より$$$$+AB*\frac{ 1 }{ \sqrt{2} }-2P-P+2P(反力)=0$$
$$AB=+{ \sqrt{2} }*P=+{ \sqrt{2} }P$$


この動画を YouTube で視聴
モーメントの吊り合い式:ΣM=0の活用法
ΣM=0の活用法
- 斜め部材のラインを延長する。
- 斜め部材と他の部材との交点に注目する。
- 斜め部材との交点を起点にしてΣM=0の式を作る。
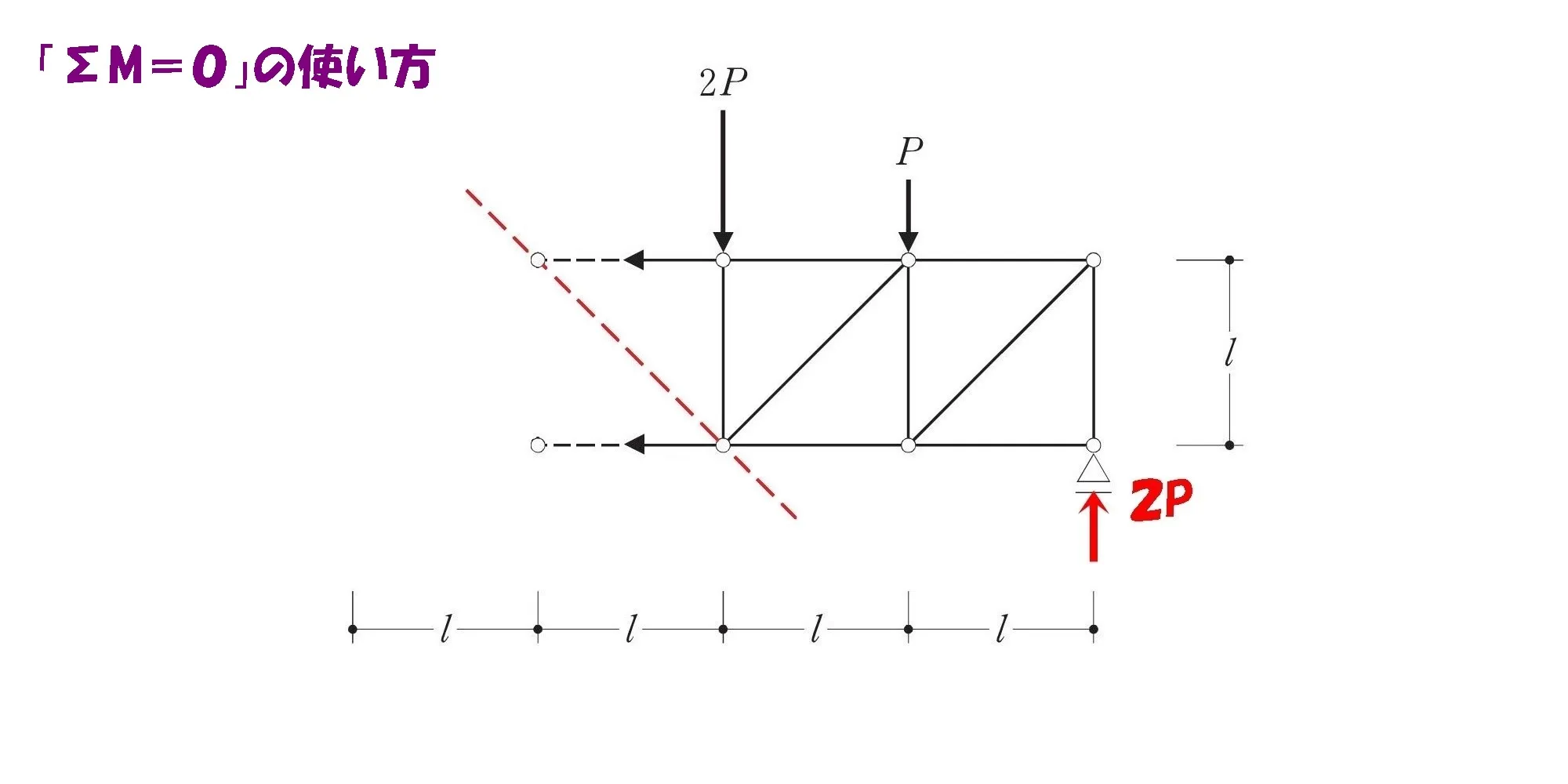

ΣM=0により軸力を求める方法は知っているものの「どこを起点にすれば良いのか?」
モーメントの吊り合い式を立てるうえで、その起点となる位置の決め方についてお伝えします。



それが知りたい!
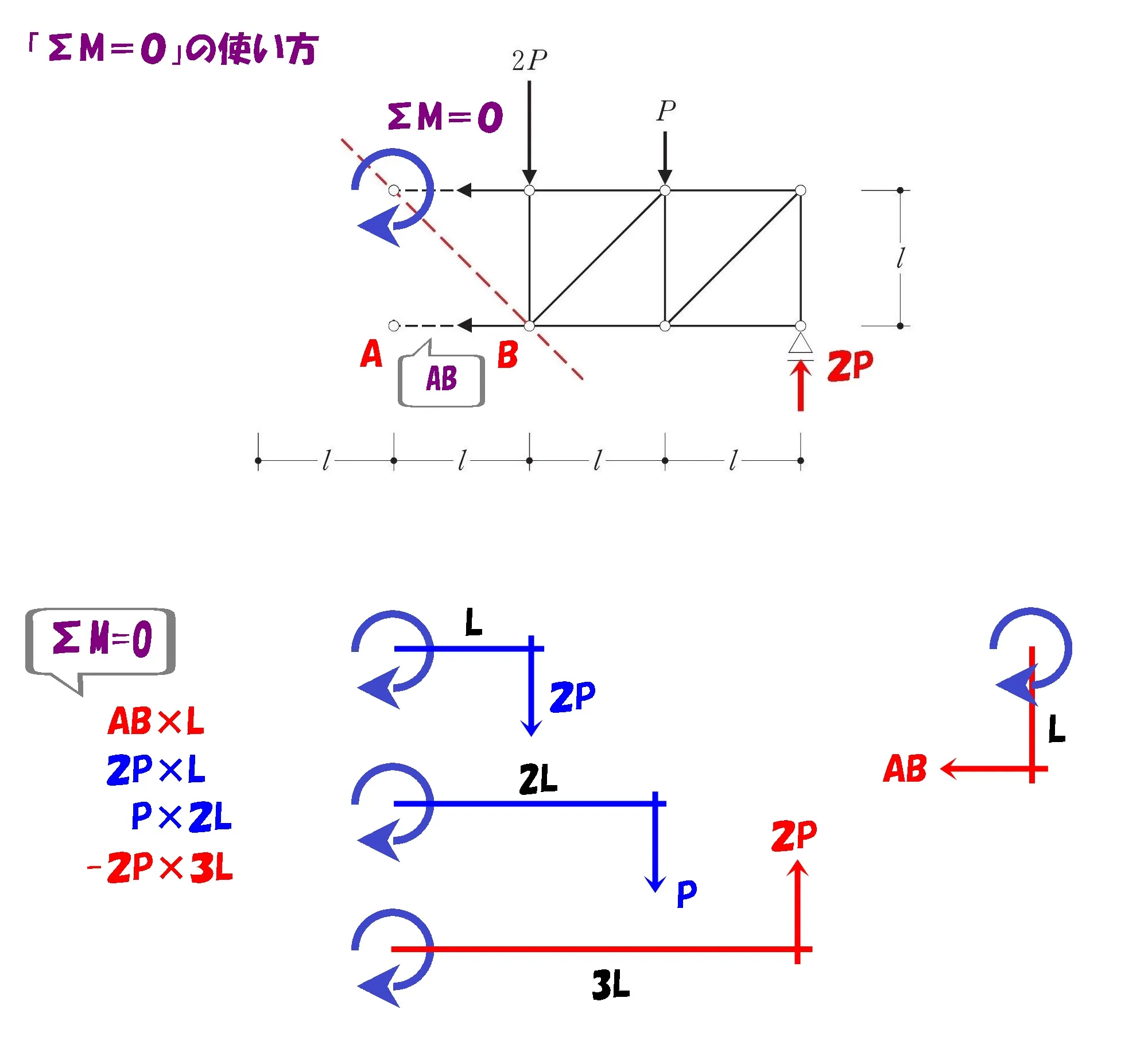
斜め部材のラインを延長する
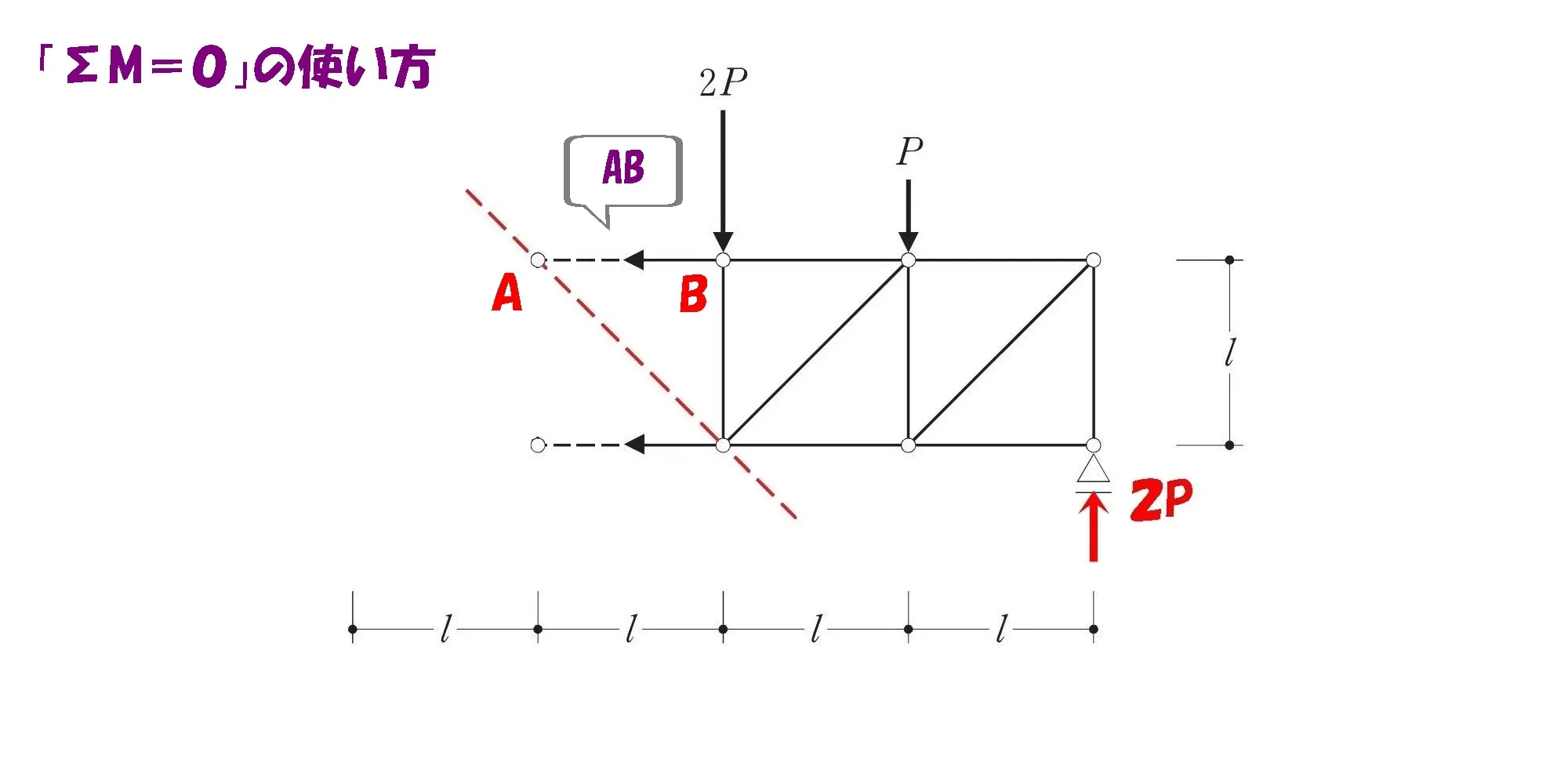

ケース①:ヨコ部材(上)の軸力を求める。
1.斜め部材のラインを延長する。
斜め部材との交点に注目する
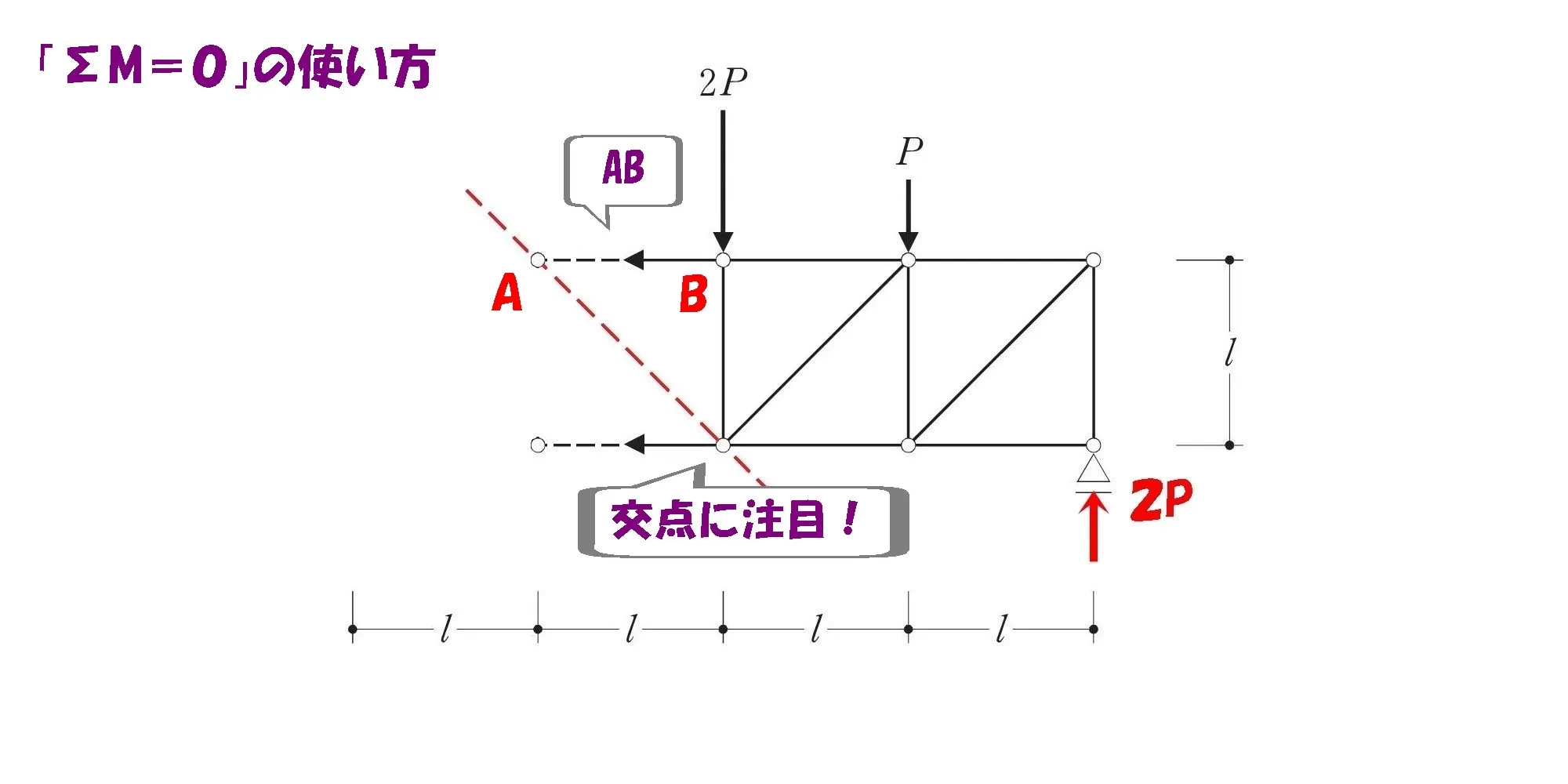

2.斜め部材と他の部材との交点に注目する。
斜め部材との交点を起点にする
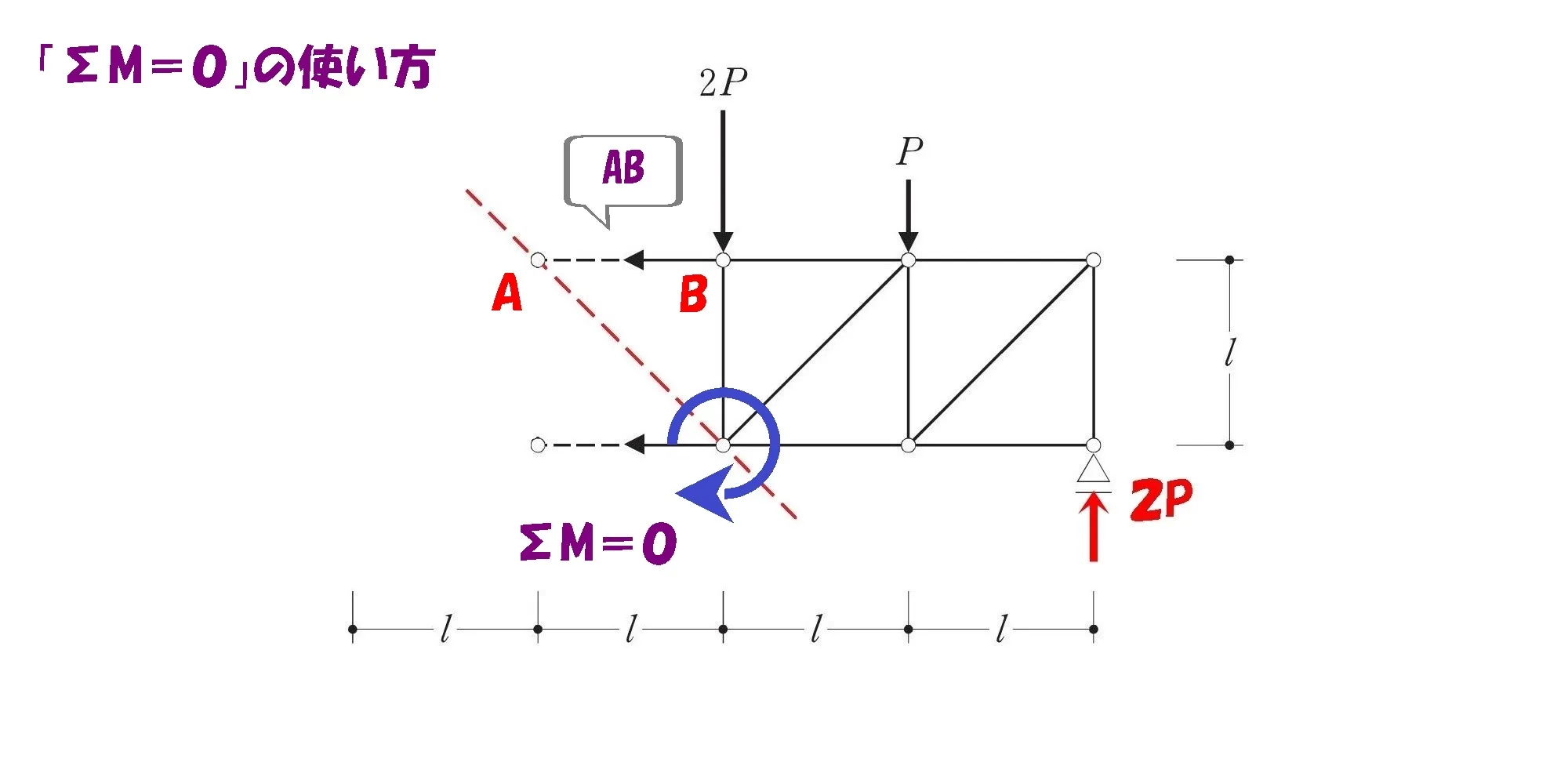

3.斜め部材との交点を起点にしてΣM=0の式を作る。
モーメントの吊り合い式の起点=ヨコ部材と斜め部材との交点。
求める軸力がヨコ部材(上)であれば、ヨコ部材(下)と斜め部材との交点になります。
モーメントの吊り合い式
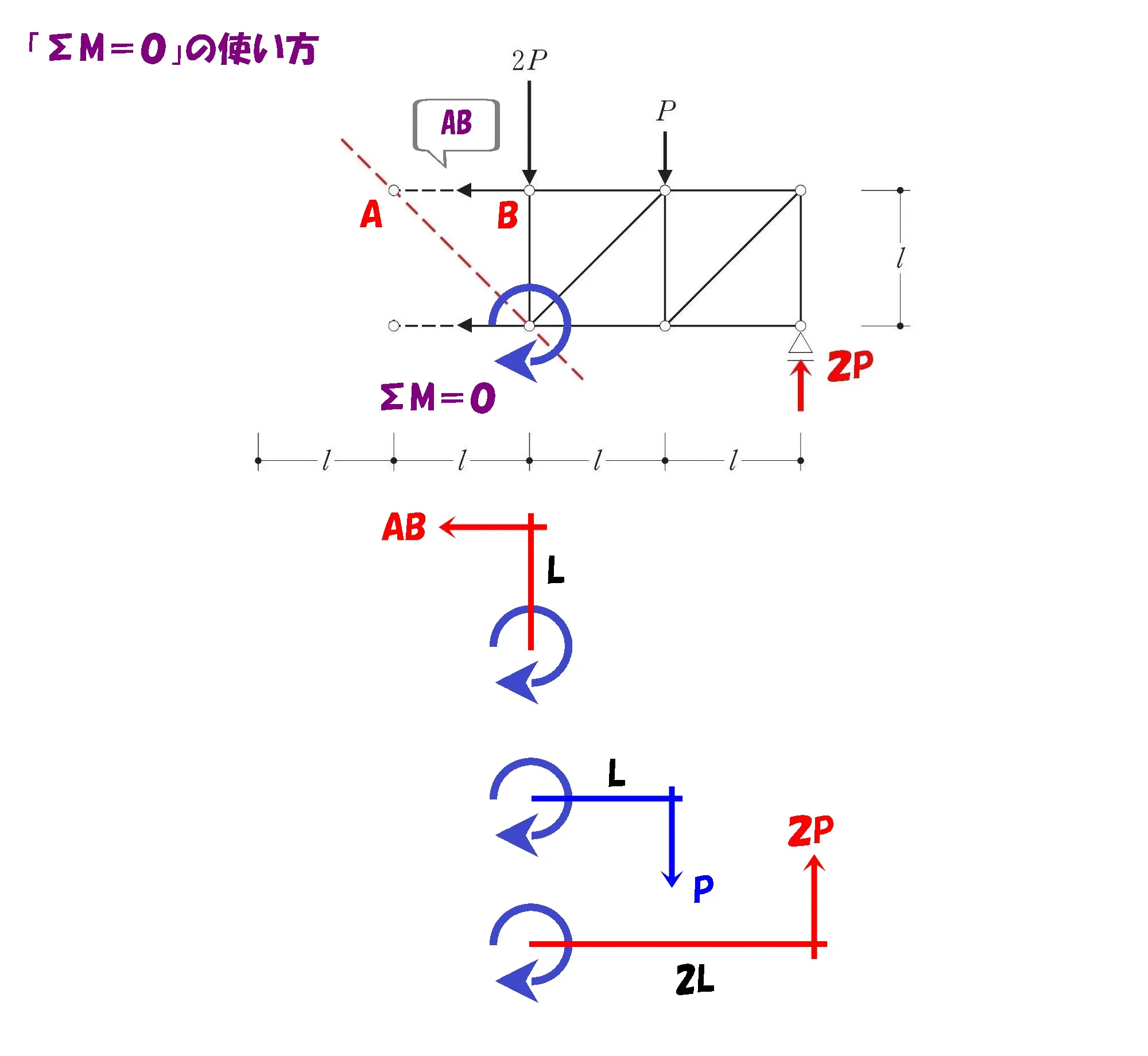

モーメント=力×距離
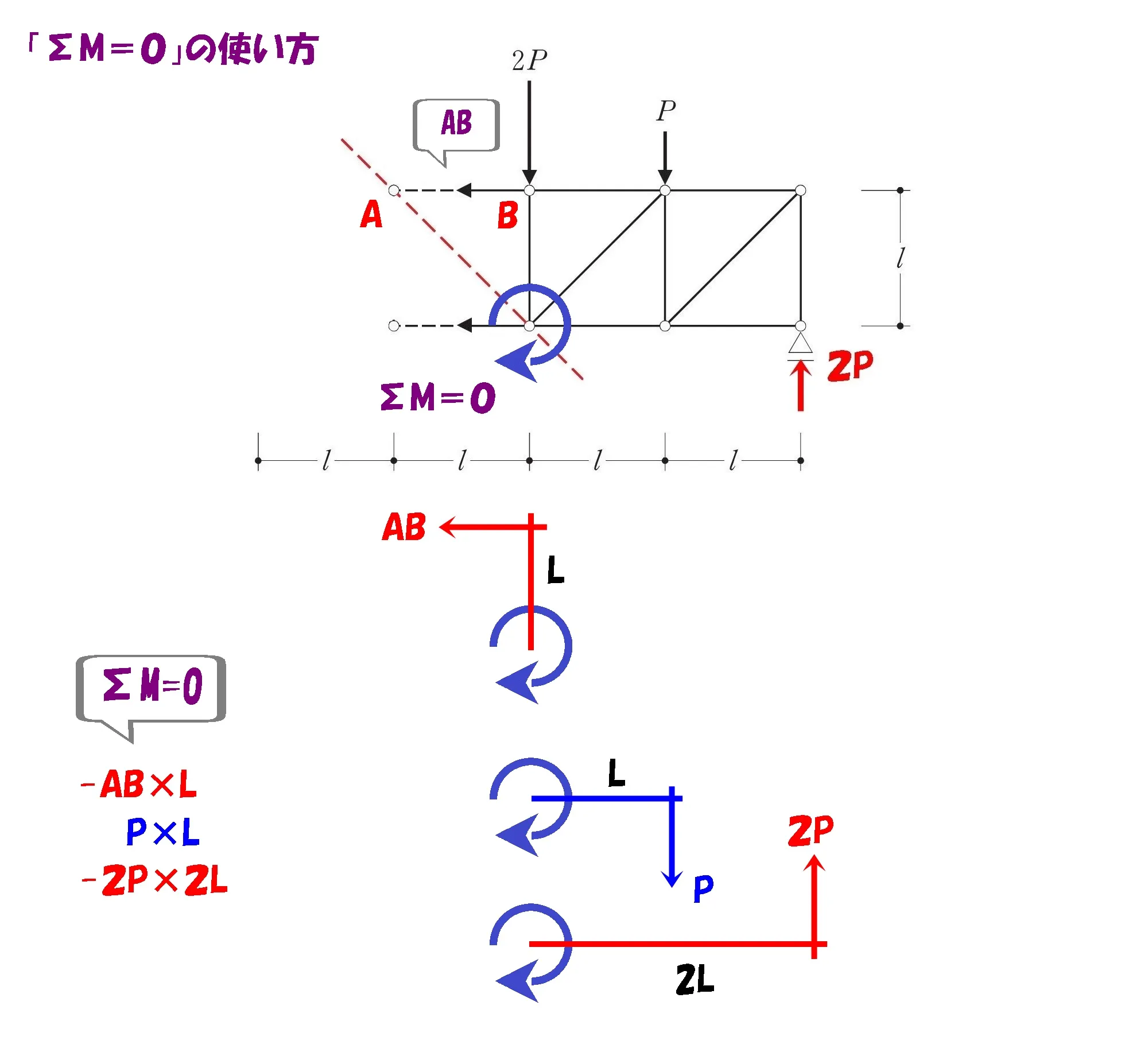

$$\Sigma M=0より,$$$$-AB*L+P*L-2P(反力)*2L=0$$
ΣM=0の活用法
- 斜め部材のラインを延長する。
- 斜め部材と他の部材との交点に注目する。
- 斜め部材との交点を起点にしてΣM=0の式を作る。
斜め部材のラインを延長する
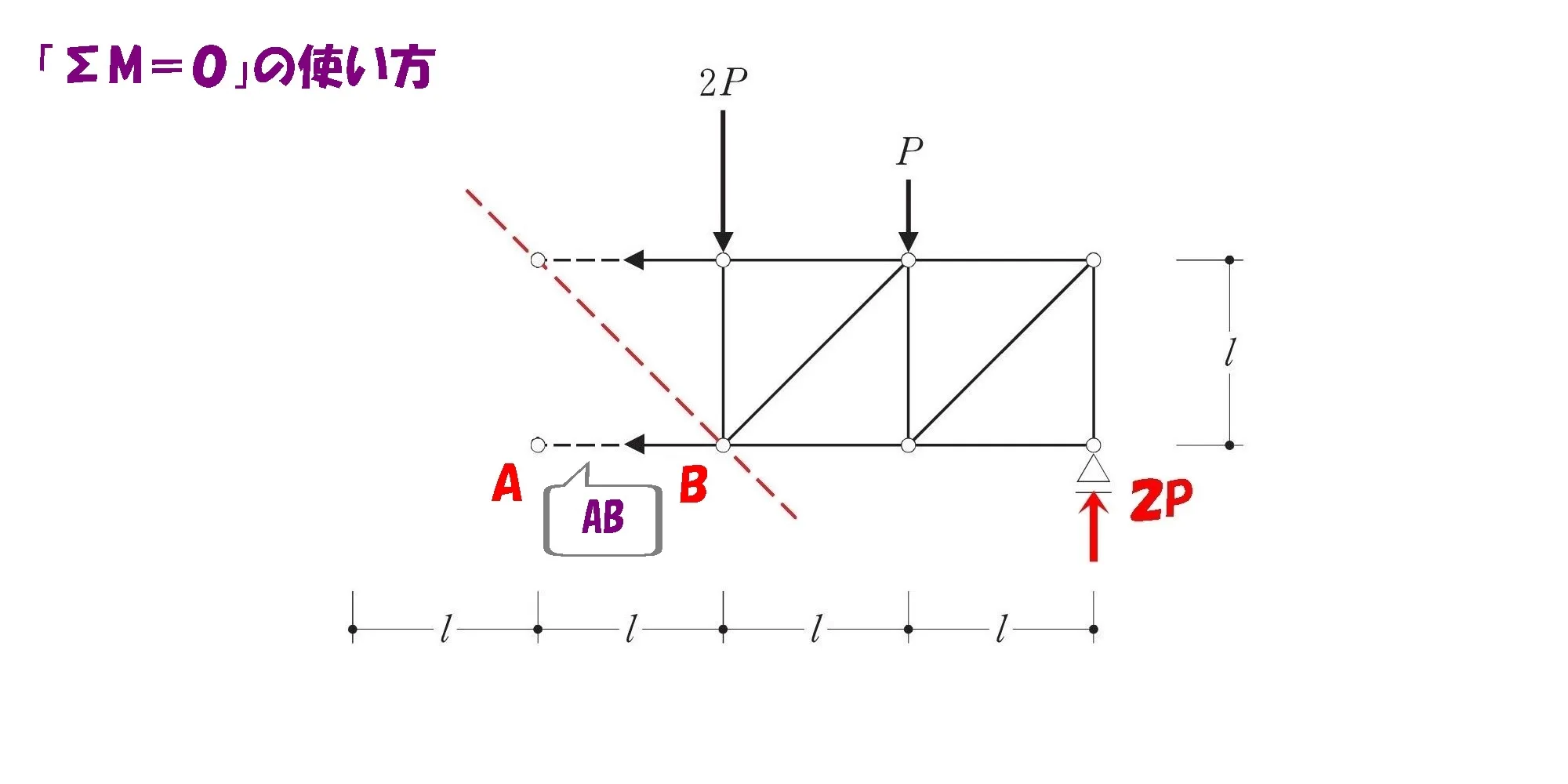

ケース②:ヨコ部材(下)の軸力を求める。
1.斜め部材のラインを延長する。
斜め部材との交点に注目する
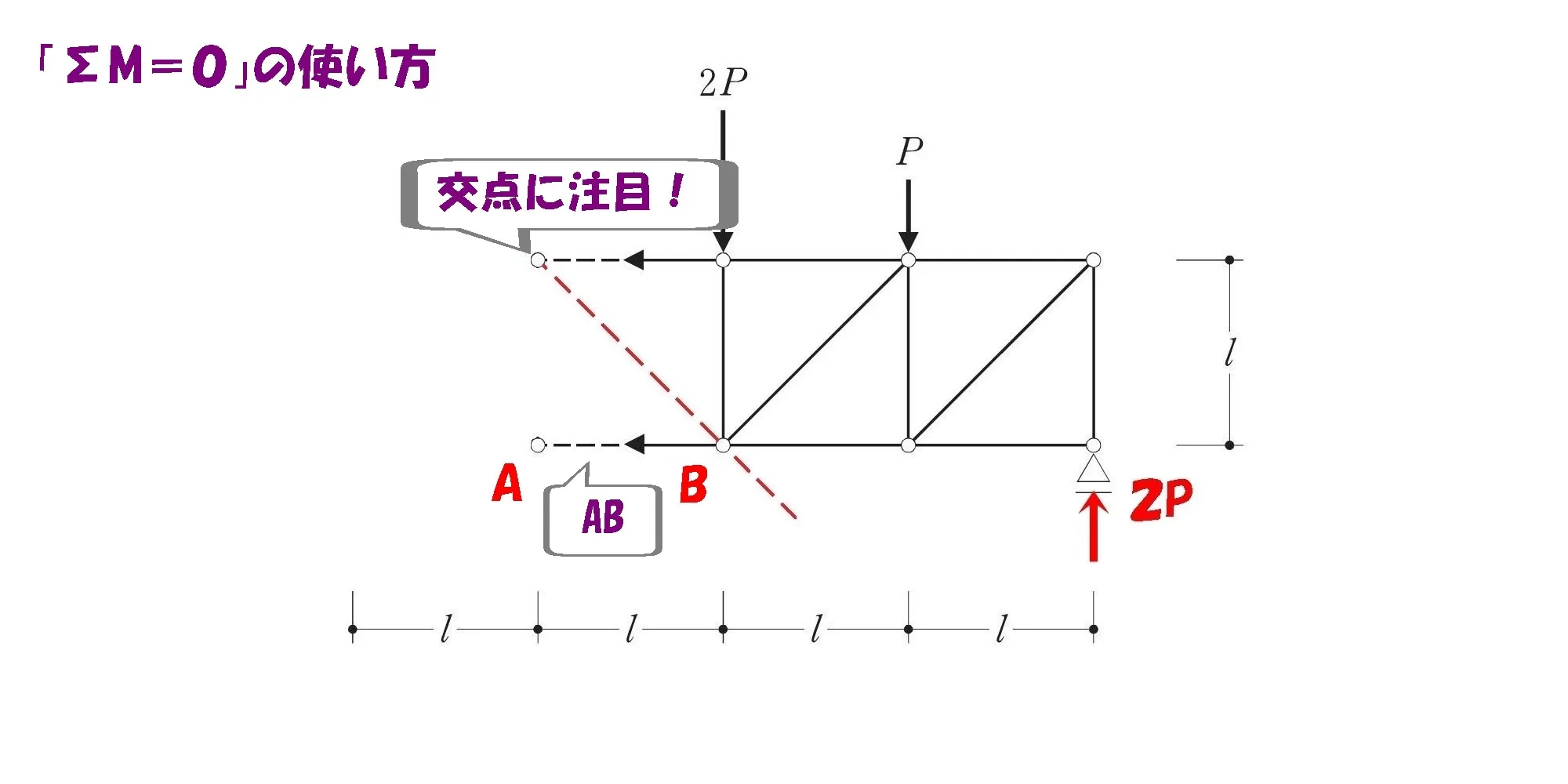

2.斜め部材と他の部材との交点に注目する。
斜め部材との交点を起点にする
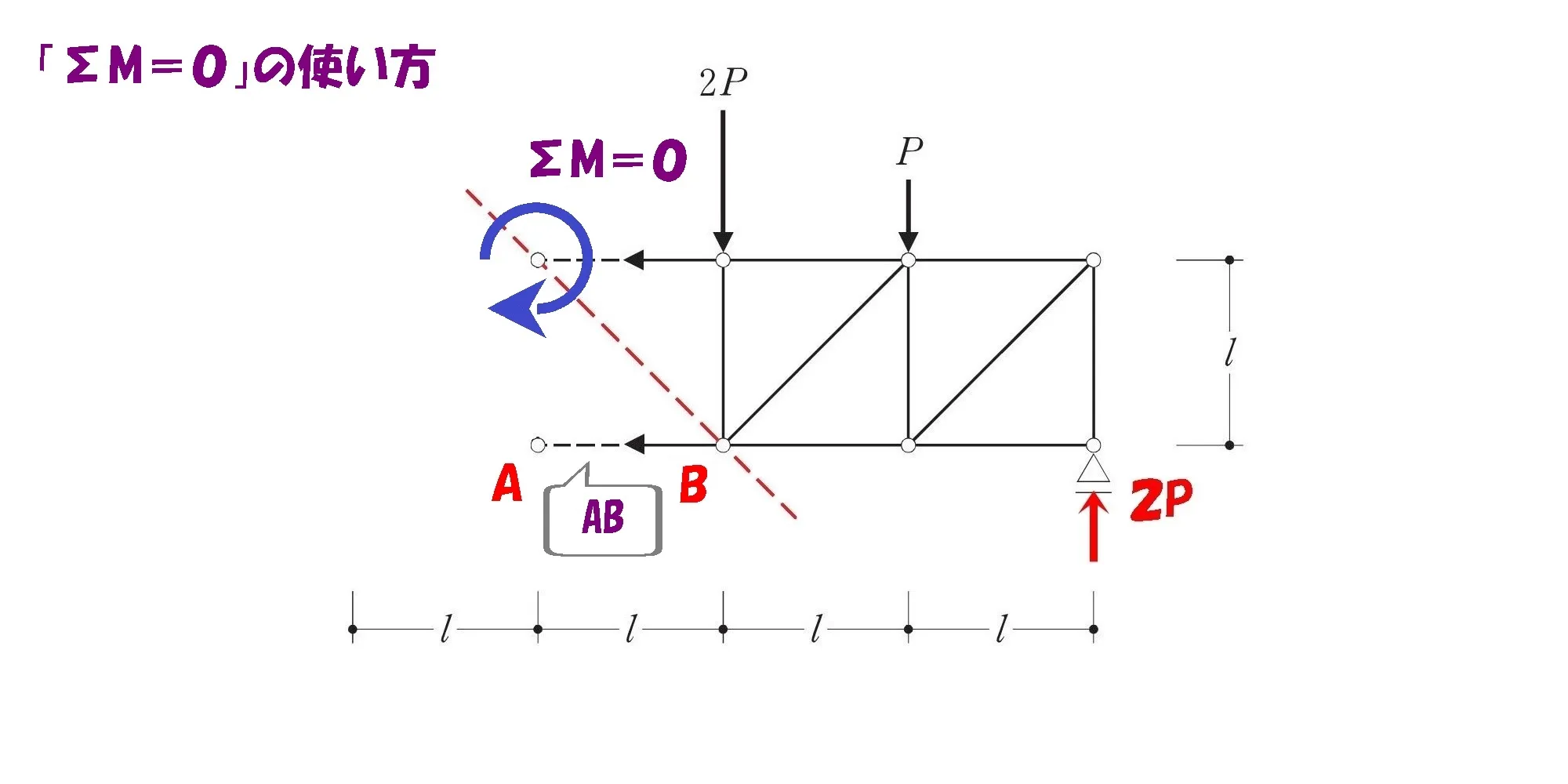

3.斜め部材との交点を起点にしてΣM=0の式を作る。
モーメントの吊り合い式の起点=ヨコ部材と斜め部材との交点。
求める軸力がヨコ部材(下)であれば、ヨコ部材(上)と斜め部材との交点になります。
モーメントの吊り合い式
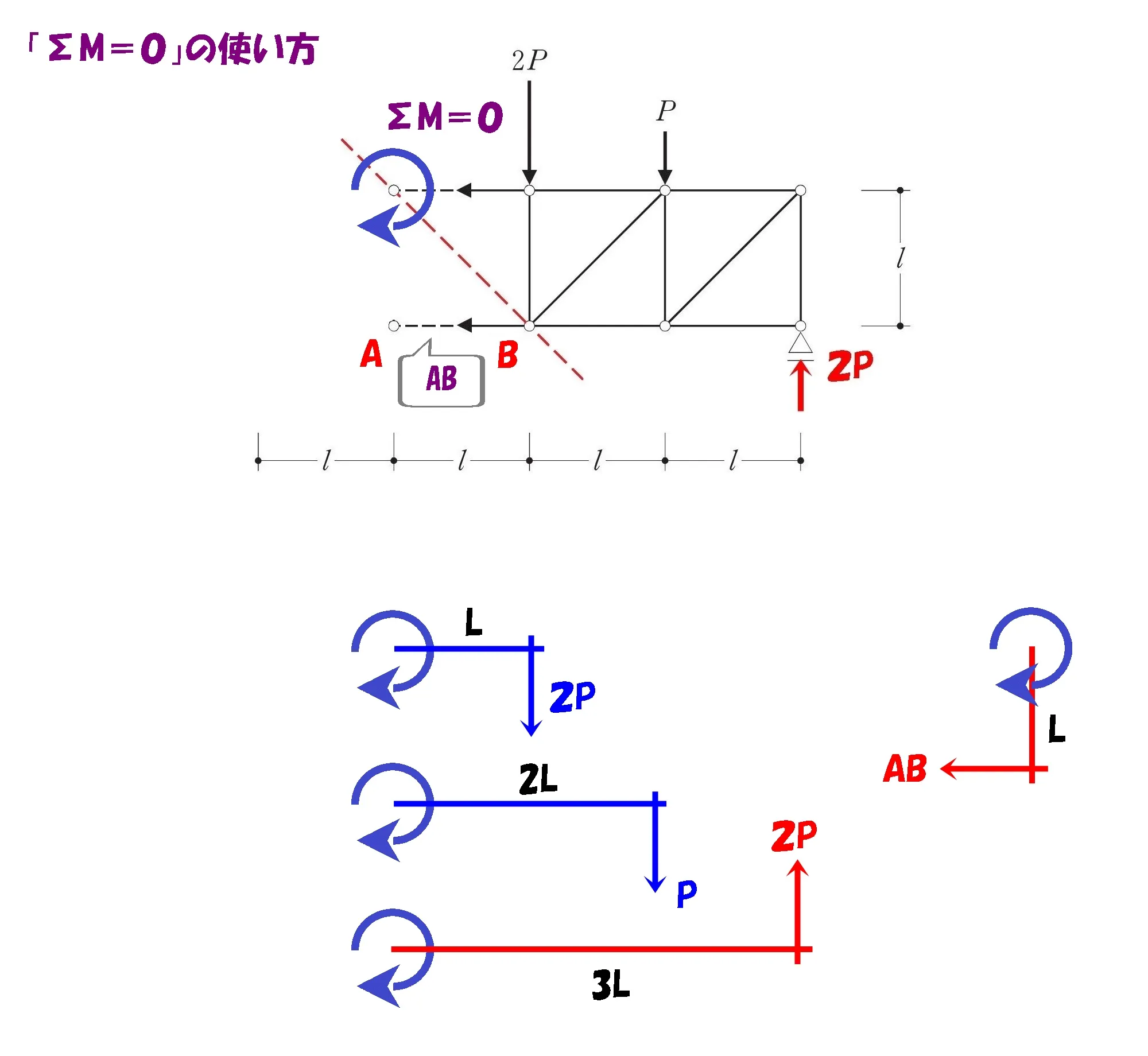

モーメント=力×距離


$$\Sigma M=0より,$$$$AB*L+2P*L+P*2L-2P(反力)*3L=0$$
ΣM=0の活用法
- 斜め部材のラインを延長する。
- 斜め部材と他の部材との交点に注目する。
- 斜め部材との交点を起点にしてΣM=0の式を作る。
ヨコ部材の軸力を求める
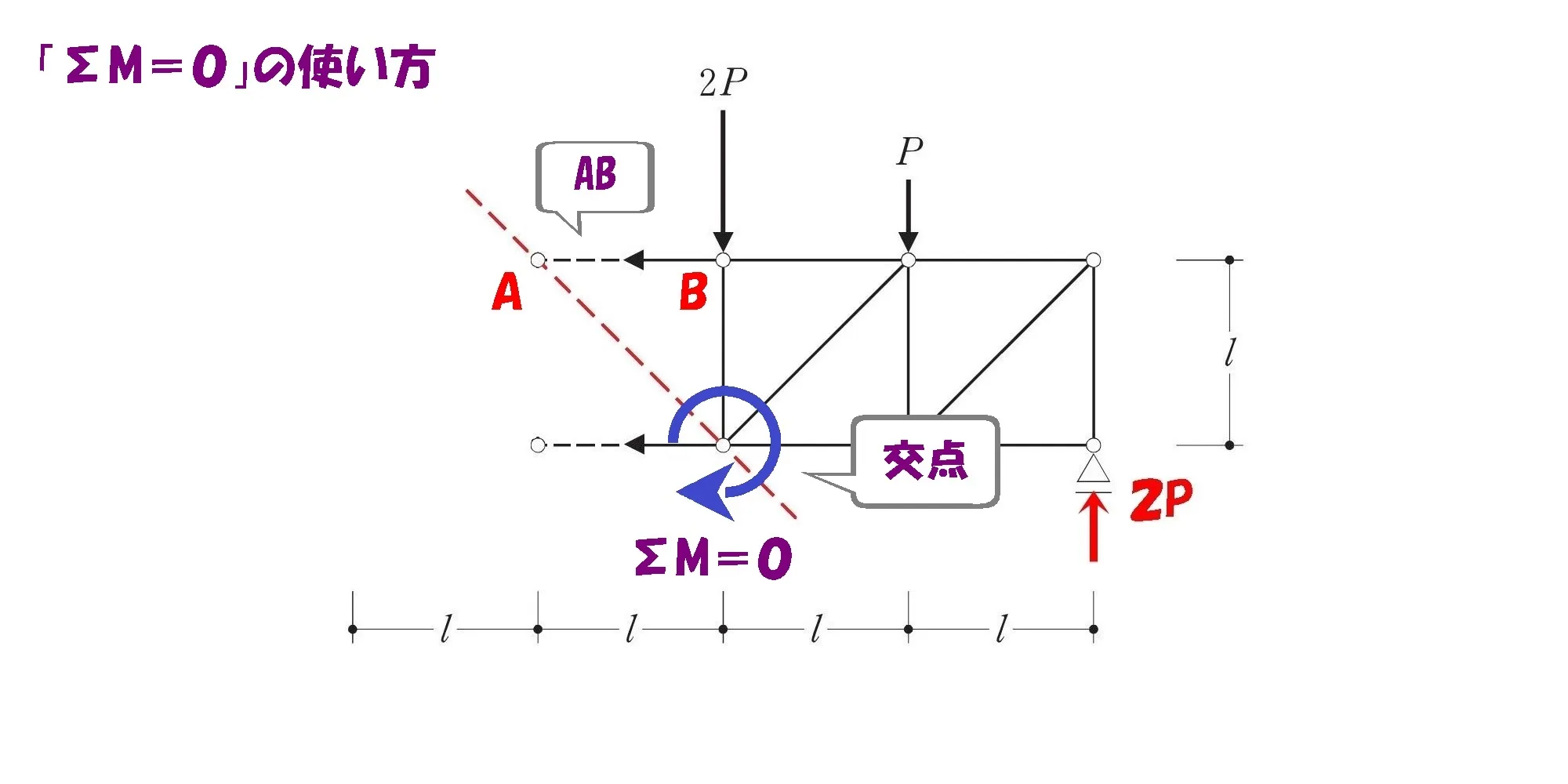

ケース①:ヨコ部材(上)の軸力を求める。
ΣM=0の起点
求める軸力がヨコ部材(上)であれば、ヨコ部材(下)と斜め部材との交点。
ヨコ部材の軸力を求める
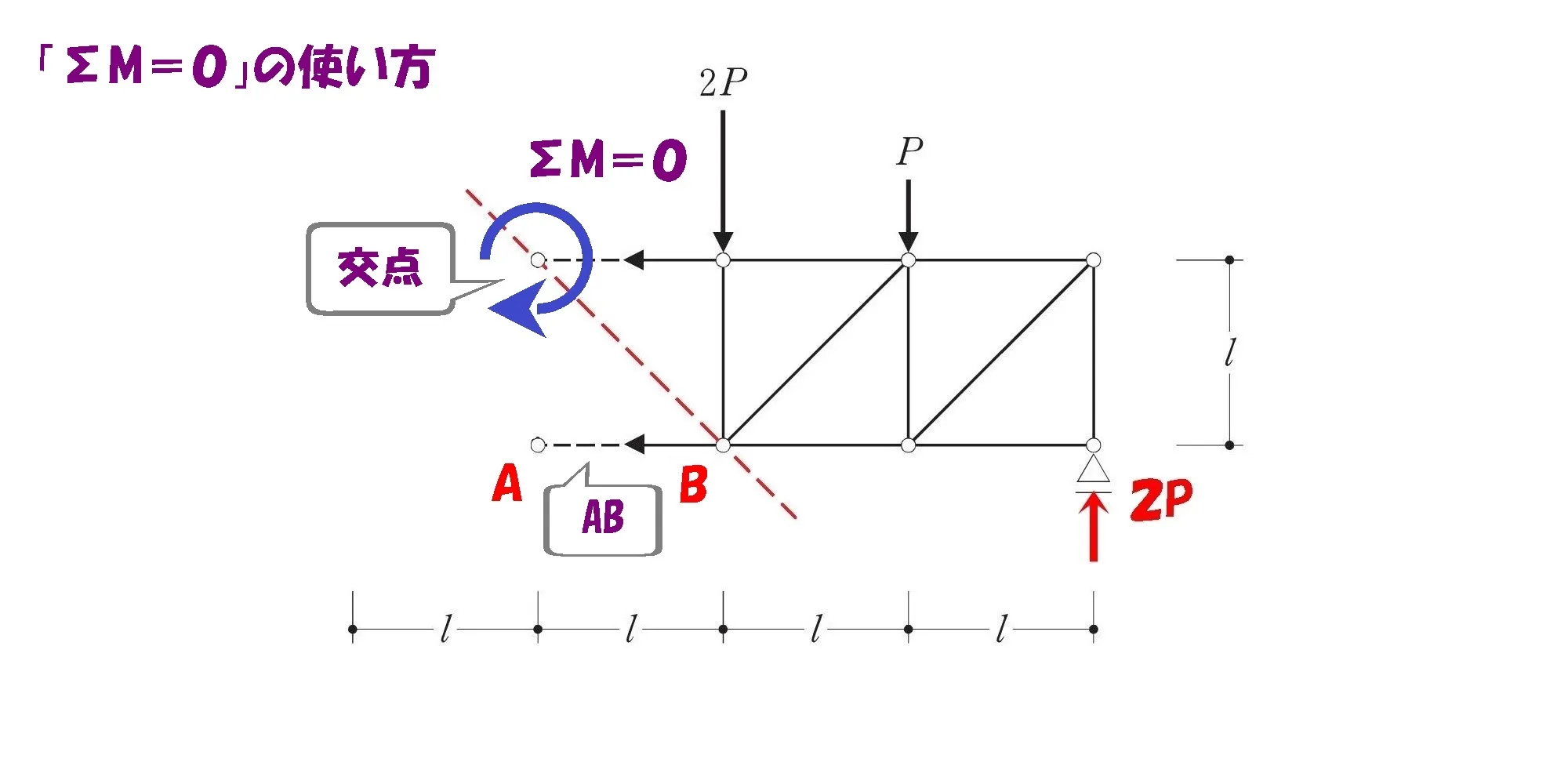

ケース②:ヨコ部材(下)の軸力を求める。
ΣM=0の起点
求める軸力がヨコ部材(下)であれば、ヨコ部材(上)と斜め部材との交点。
斜め部材の軸力を求める
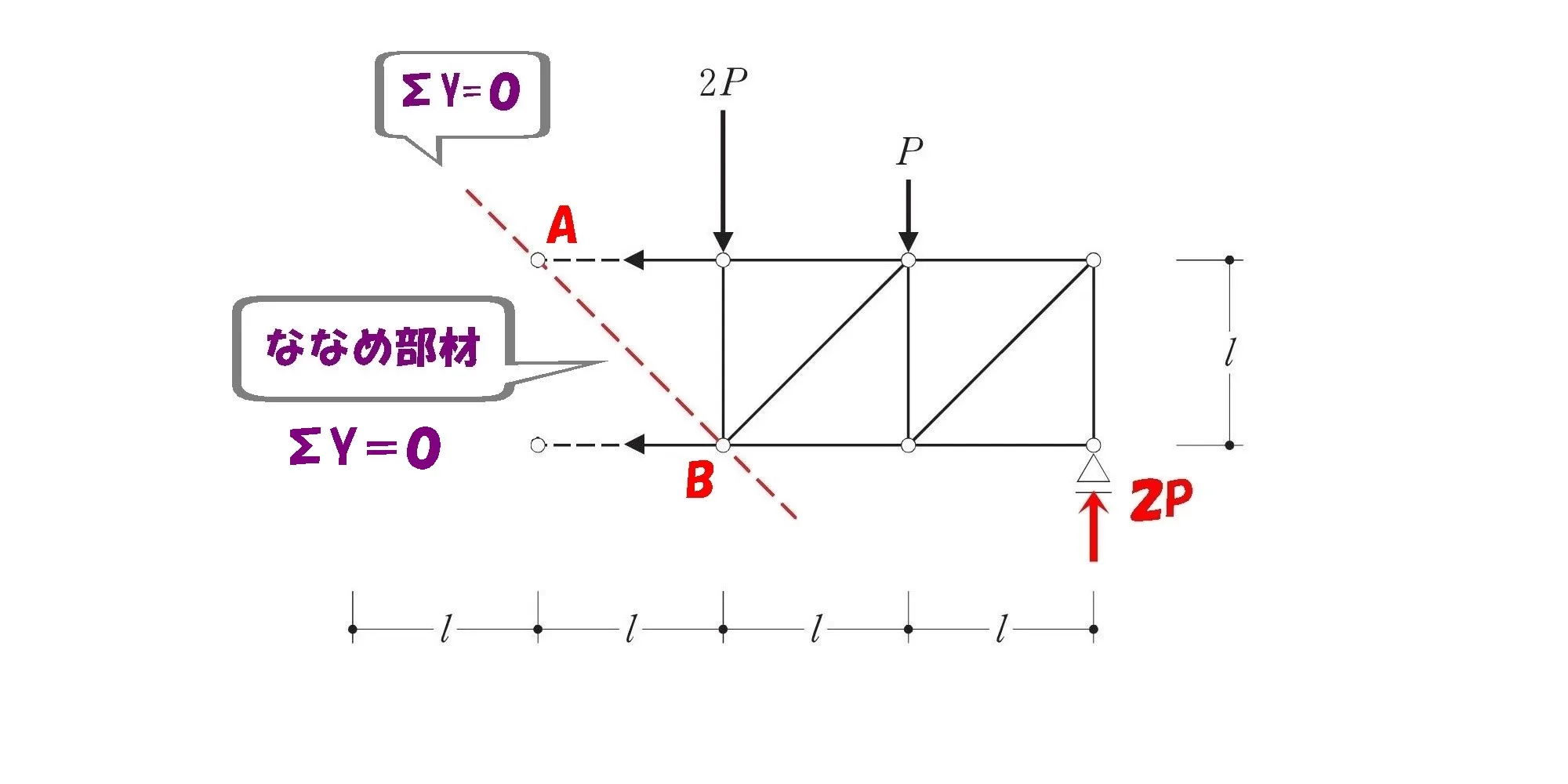

ケース③:斜め部材の軸力を求める。
斜め部材はΣY=0より、外力と反力の吊り合い式より求める。



切断法をモノに出来れば
トラスはもう怖くない!
答え.4





つまらぬモノを
斬ってしまった。
攻略ポイント
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める
トラス-2
難易度:★★★★☆
2度目の対決です。トラスを極めてしまいましょう。
トラスを攻略



トラス100本ノック!
(2回目)
攻略ポイント
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
問題
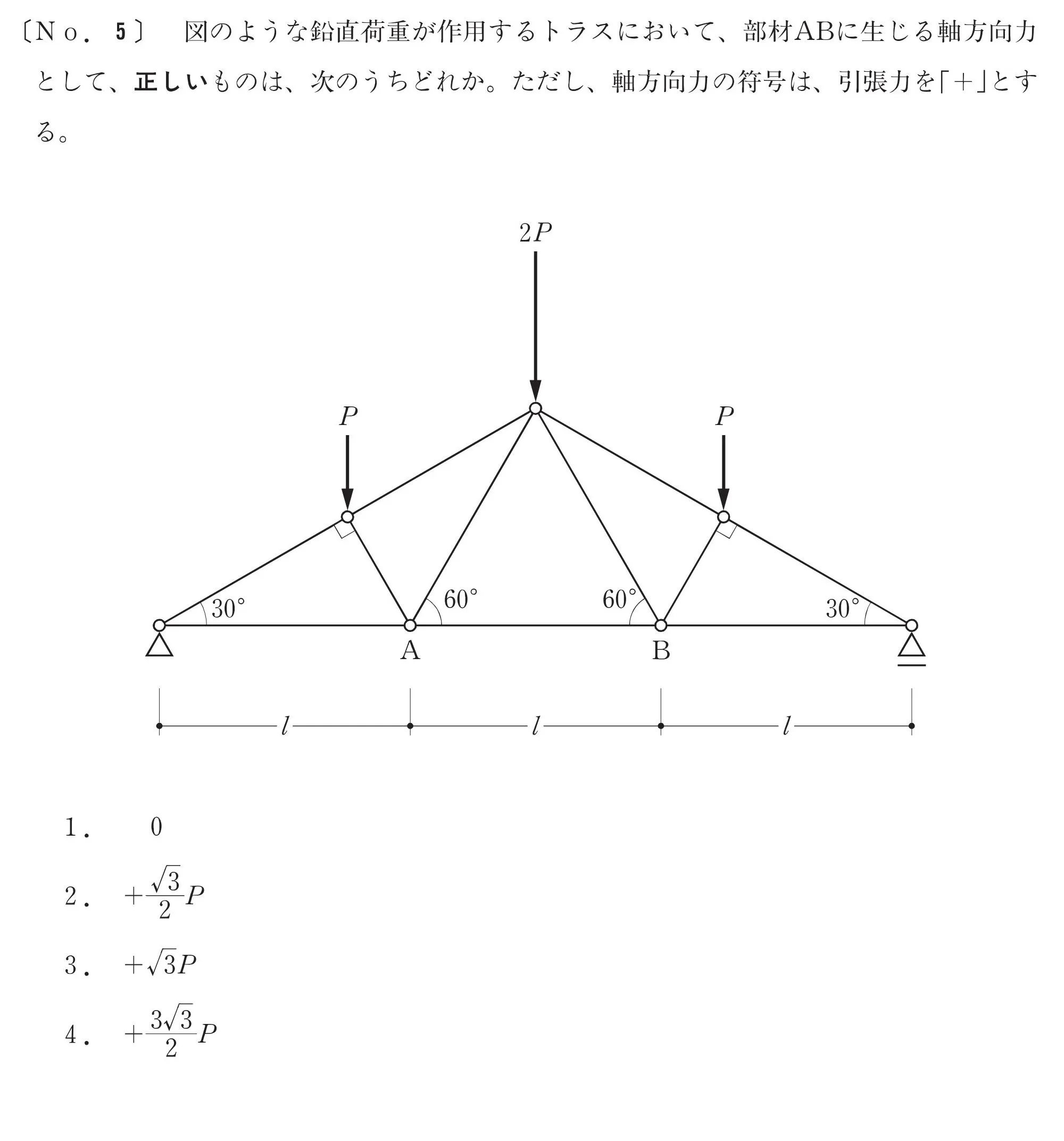

求める部材をチェックする
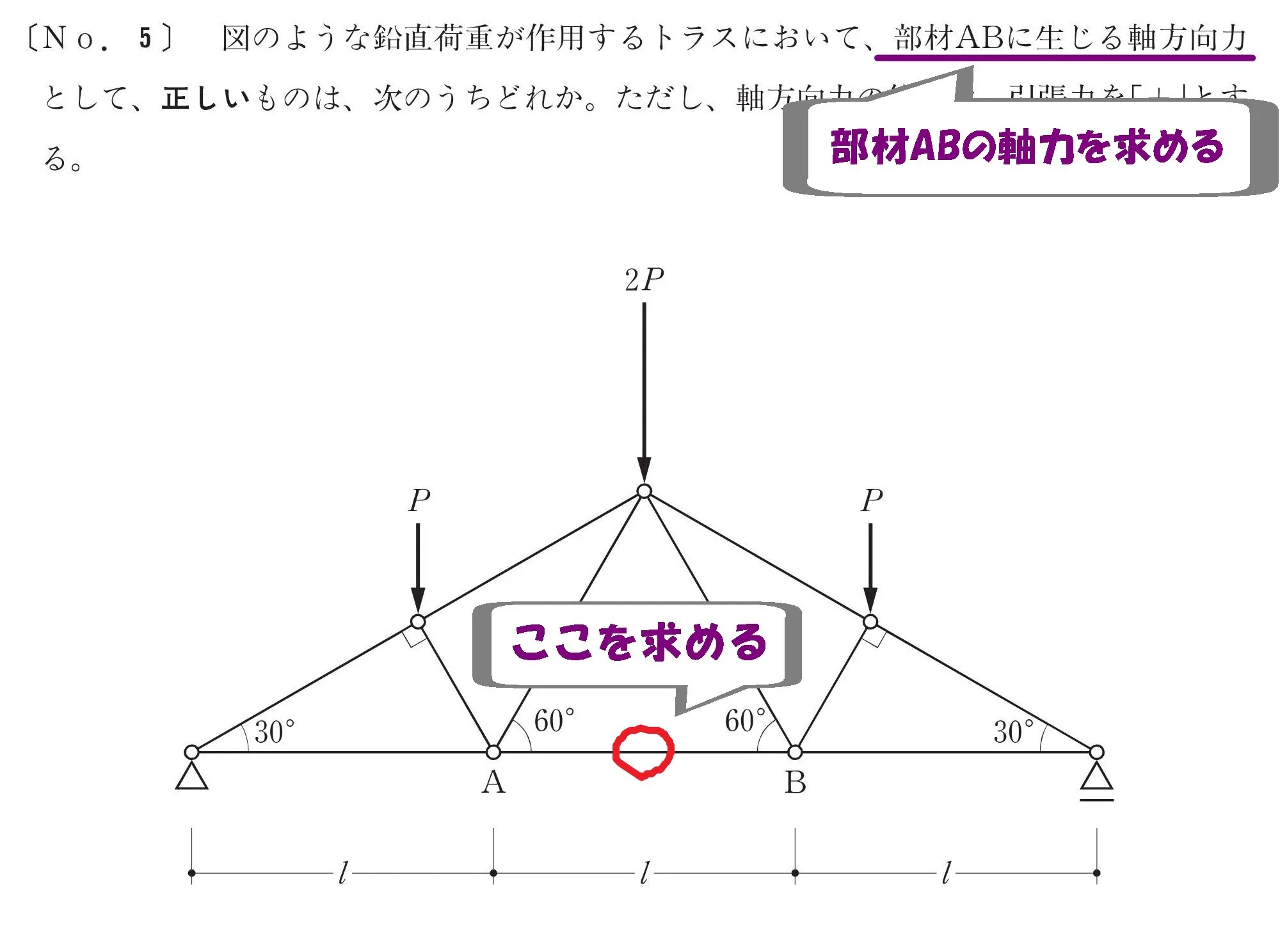

「部材ABに生じる軸力を求める」ことから、対象物に印を付けておきましょう。



この組み方は
何となく、手強そう。
1.支点反力を求める
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
支点反力を求める
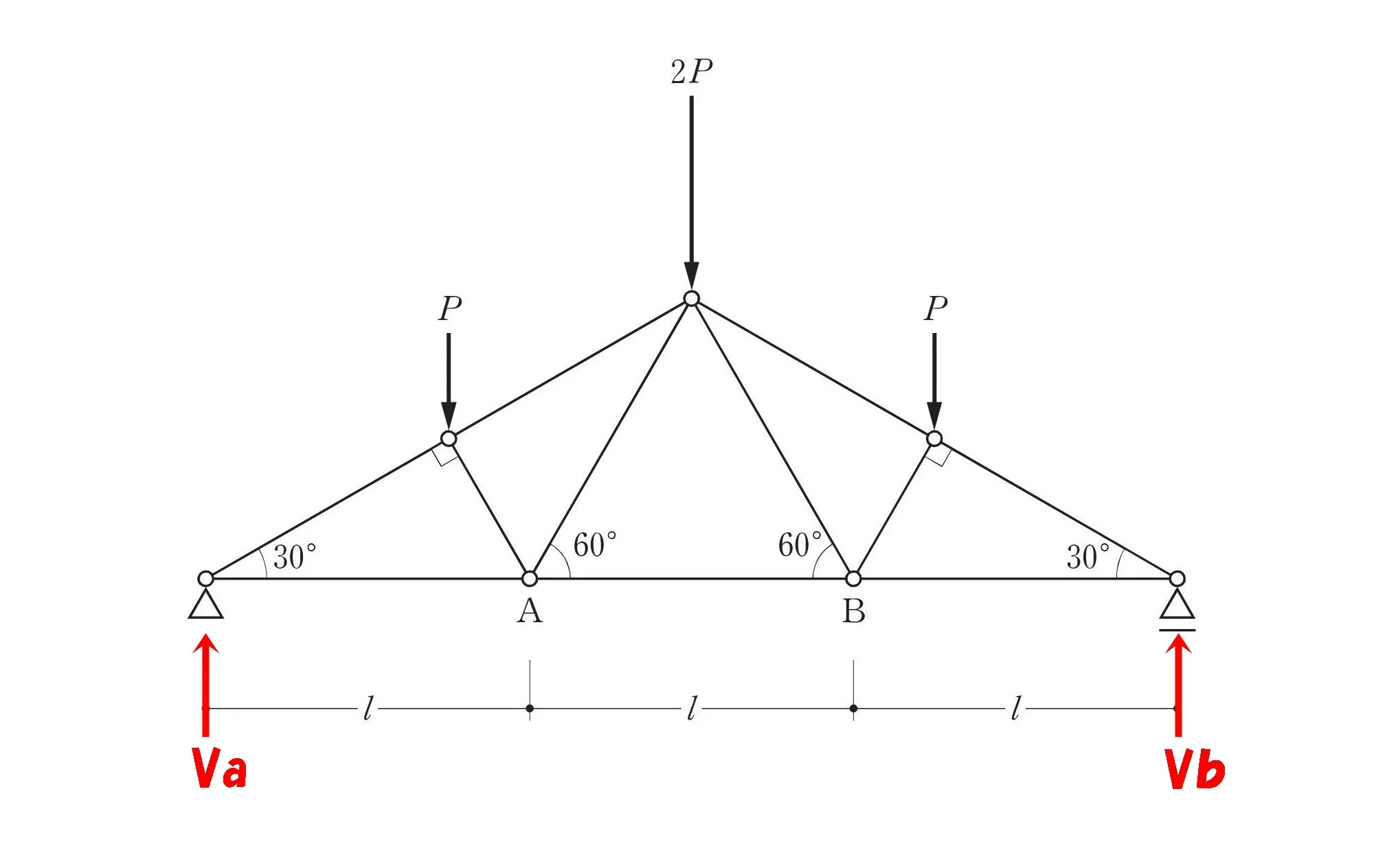

左:ピン支点
右:ローラー支点
ピン支点を起点にΣM=0
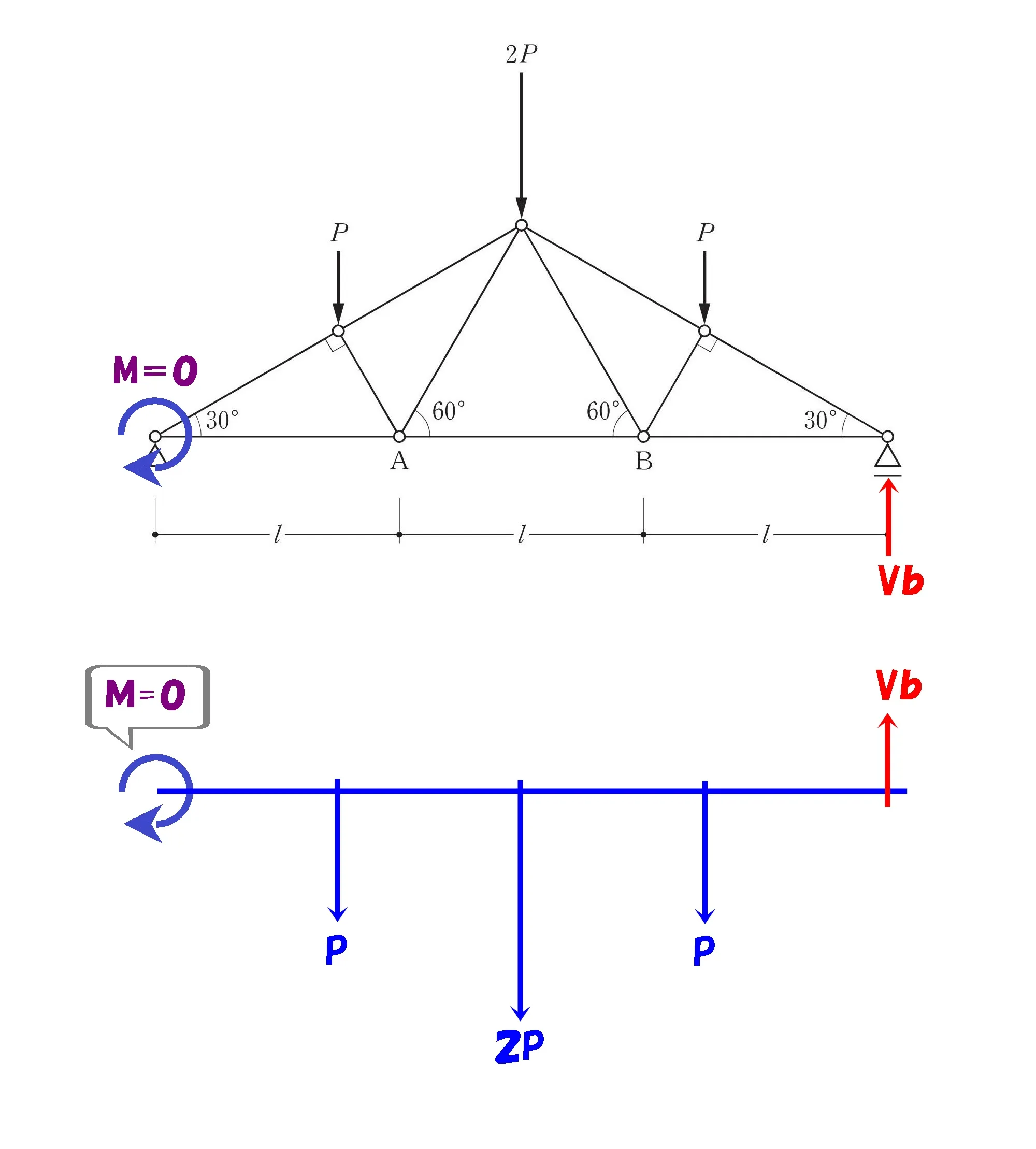

L=4/3を代入する
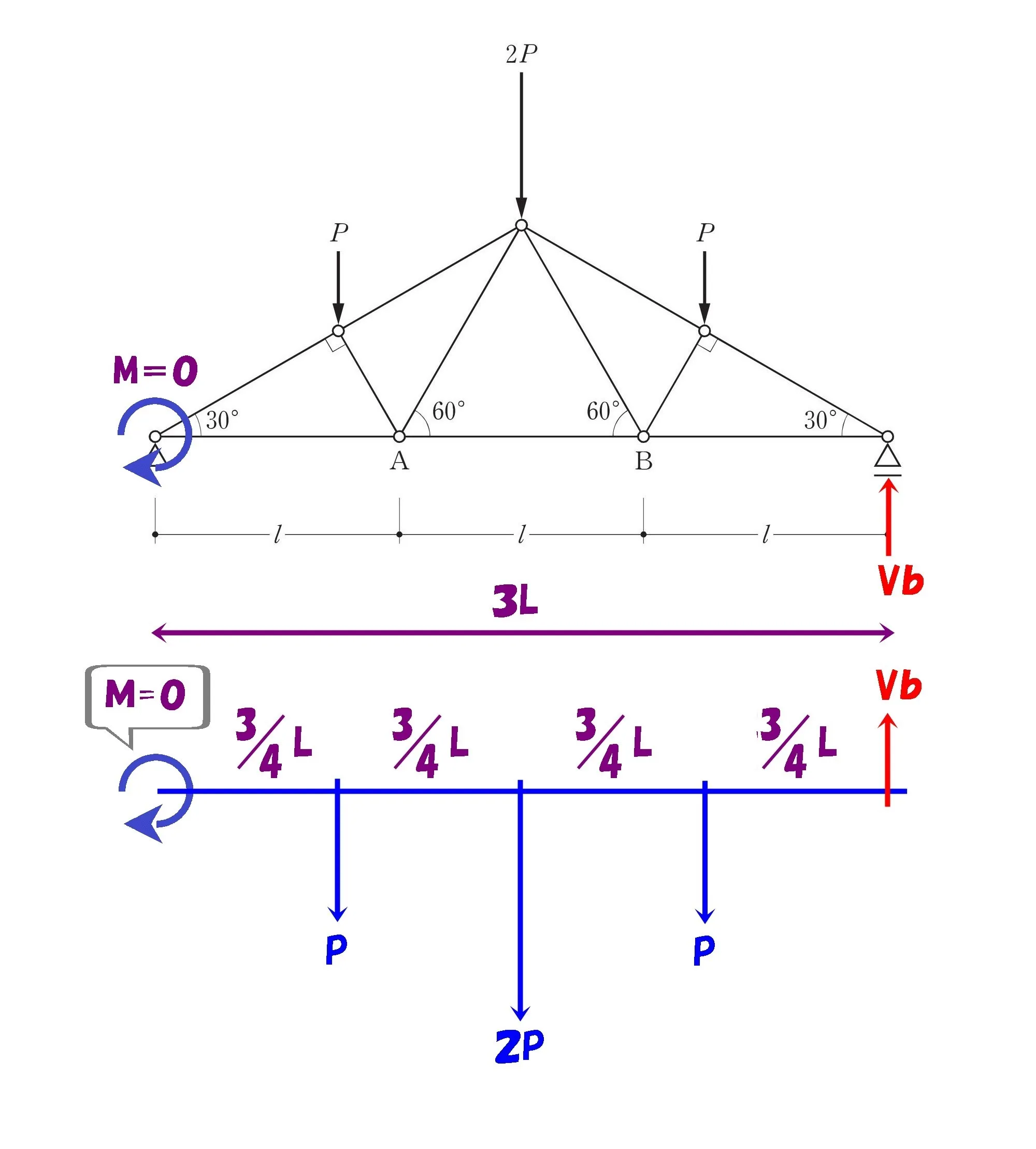

トラスの全長3Lを4分割すると、モーメントの中心からPまでの距離は3/4L



式から3/4を消したいので
L=4/3を代入する。
$$L=\frac{ 4 }{ 3 }を代入,\Sigma M=0より$$$$P*1+2P*2+P*3-Vb*4=0$$
$$4Vb=8Pより,Vb=2P$$
$$\Sigma Y=0より$$$$P+2P+P-Va-2P=0⇨Va=2P$$
鉛直反力は2P
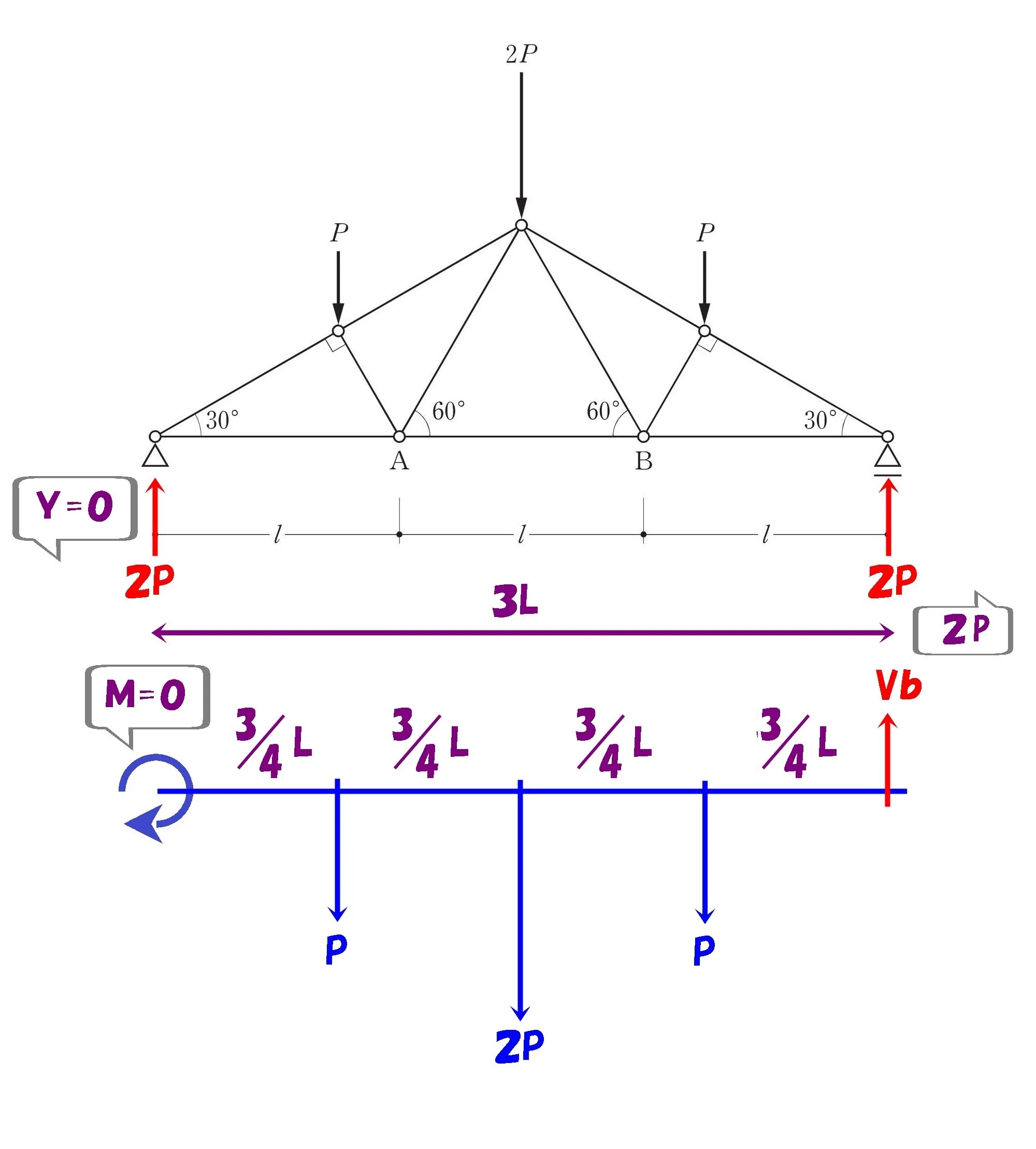

2.対象となる部材を切断する
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
部材ABの軸力を求める
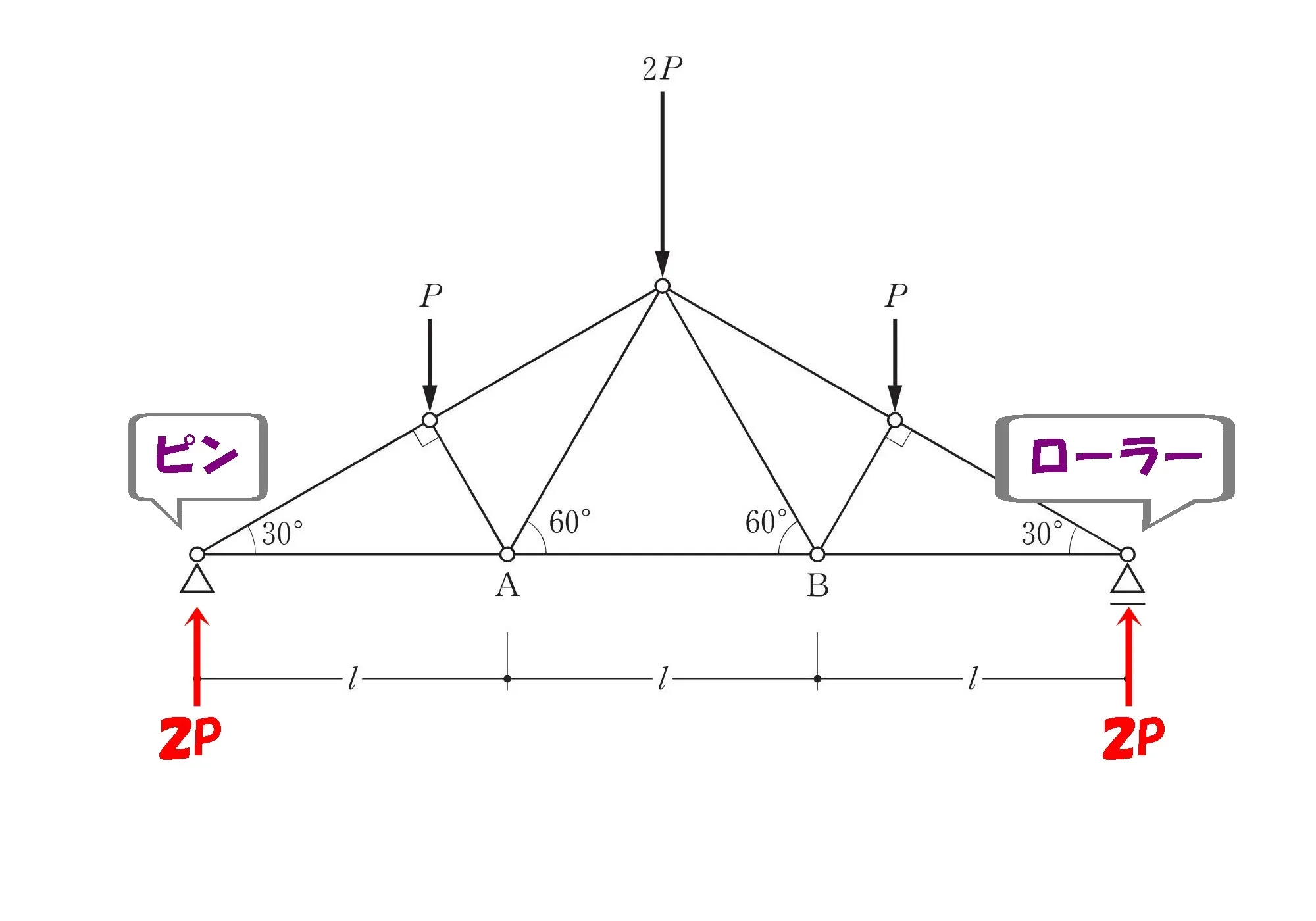

左:ピン支点
右:ローラー支点
部材を切断する
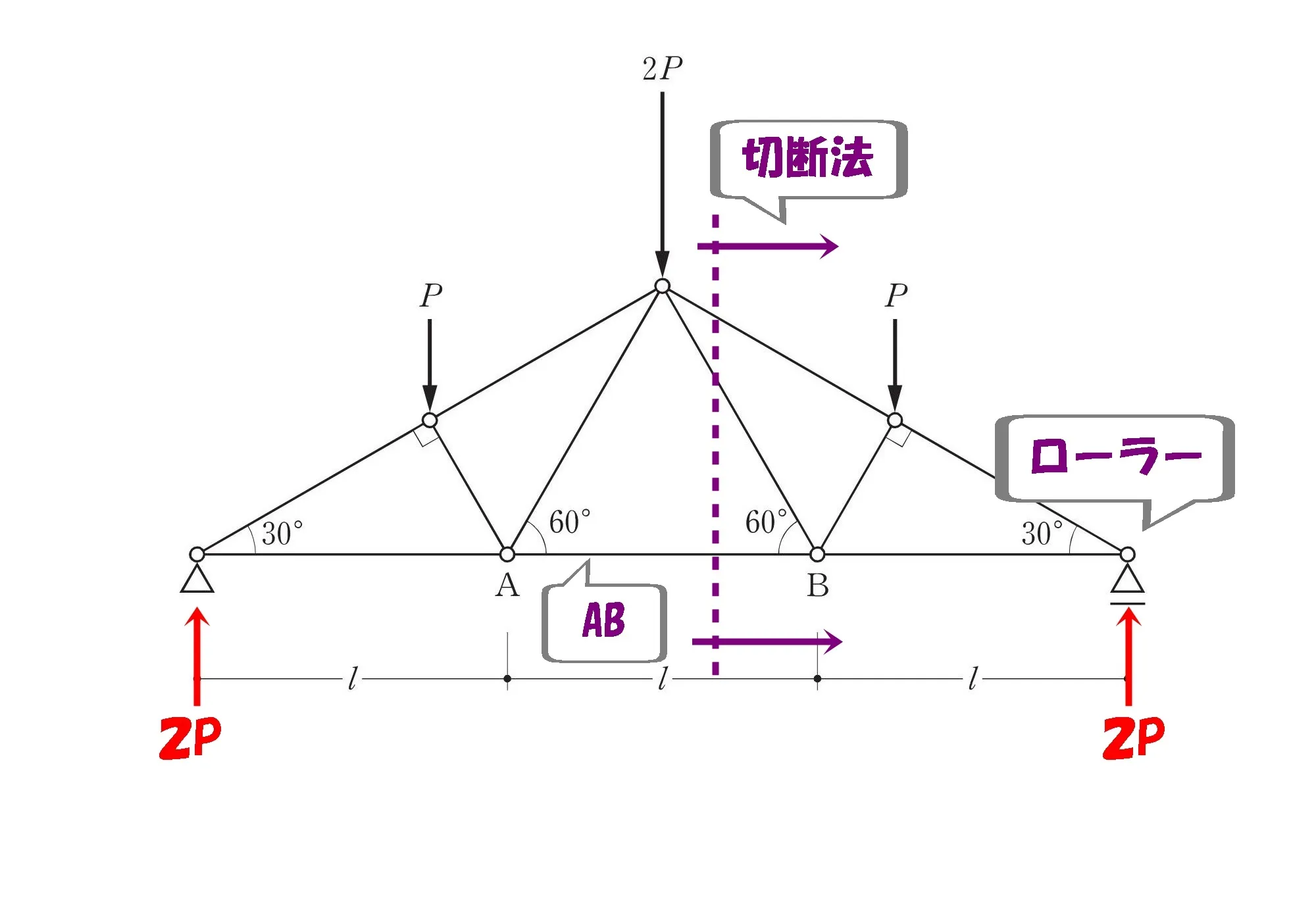

切断法のポイン
- 支点反力は先に求めておく。
- 対象となる部材ABを含む位置で切断する。
- ピン支点より反力の少ないローラー支点の部材を取り出す。



準備は良いか?
部材を取り出す
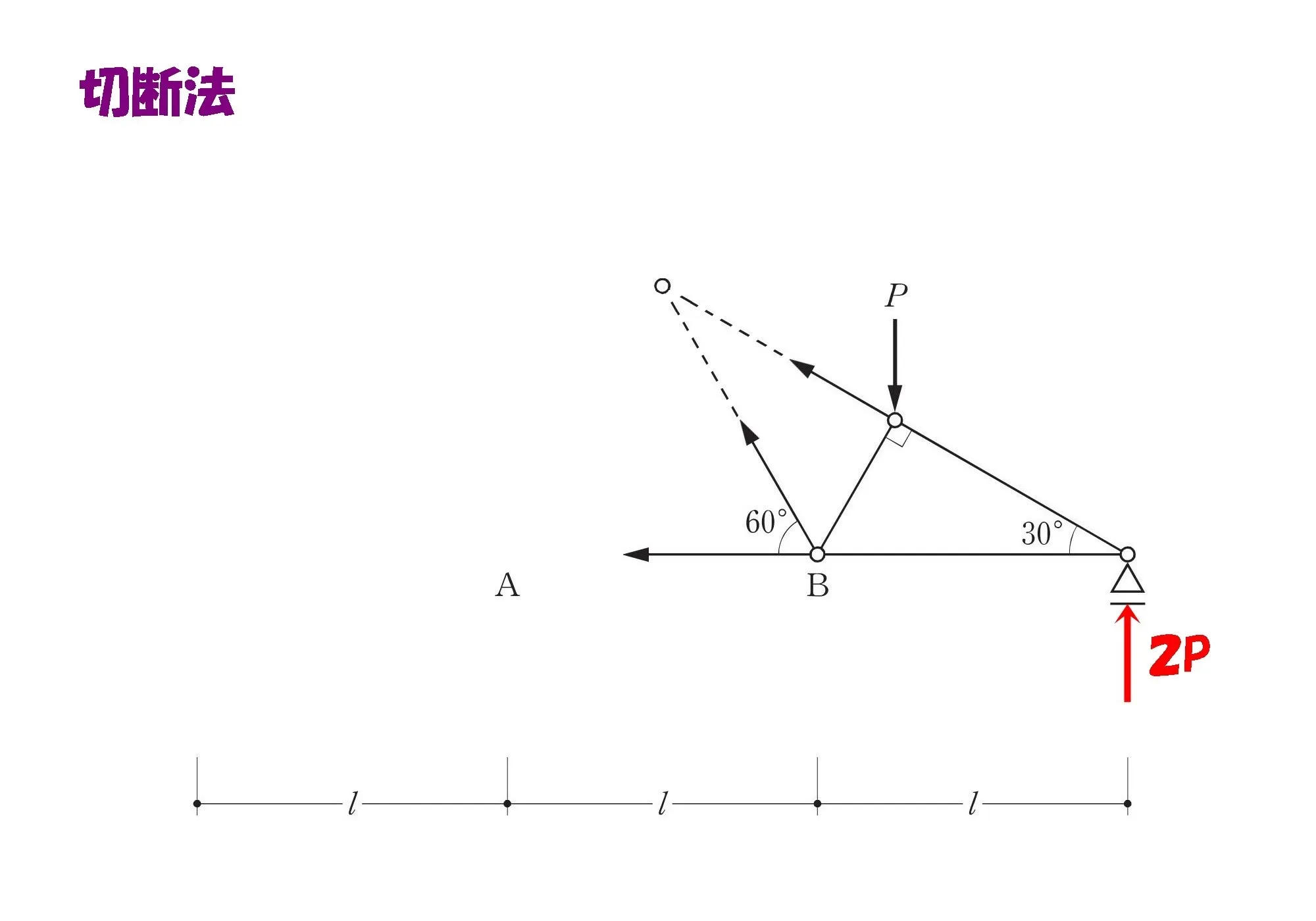




トラス切断!
公式
$$\Sigma M=0$$



Σエム!
3.斜材の延長ラインの交点に注目する
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
斜め部材の交点に注目する
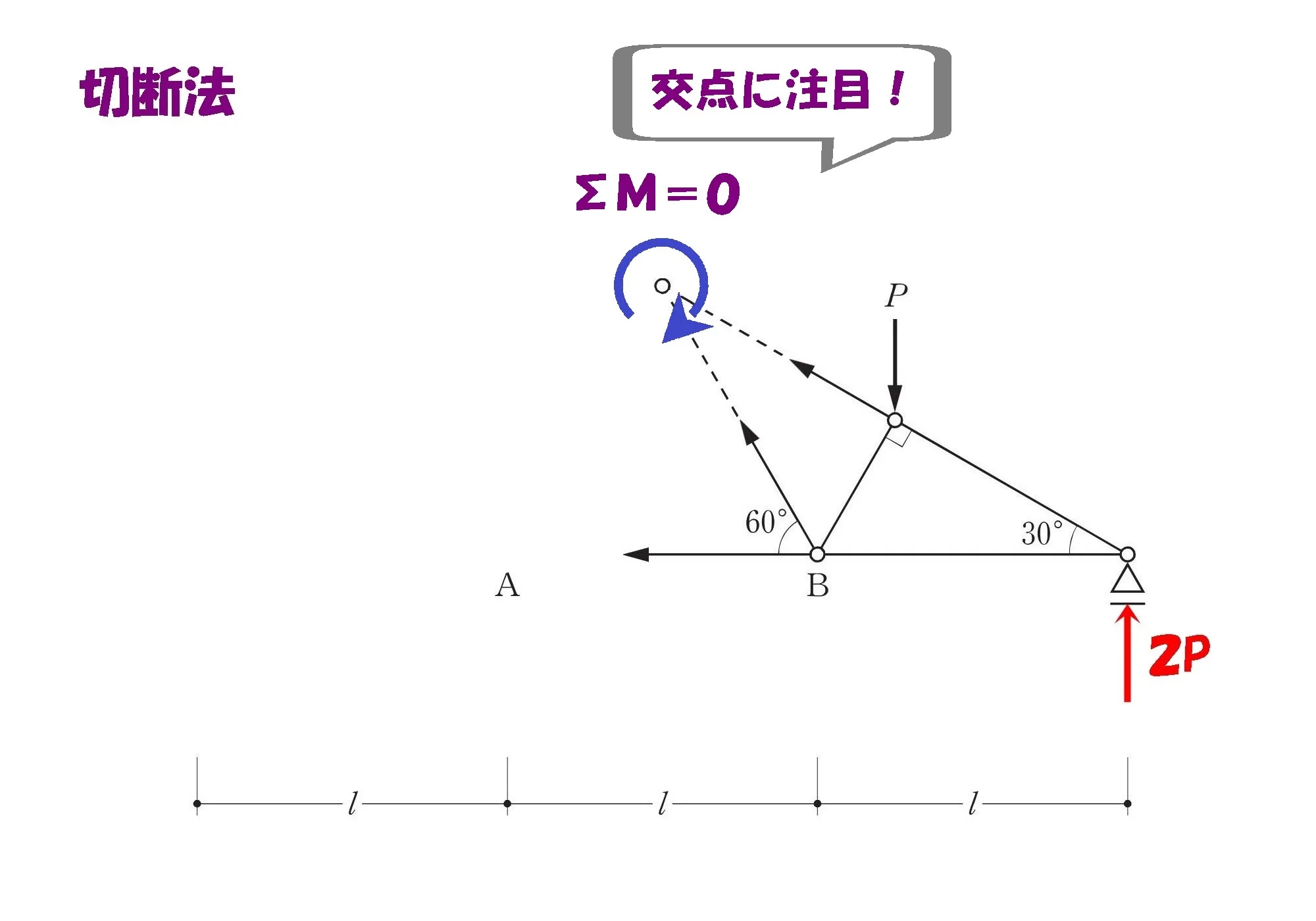

切断した部材から延長ラインを引き、その交点に注目しましょう。



交点に注目する!
モーメントの吊り合い式
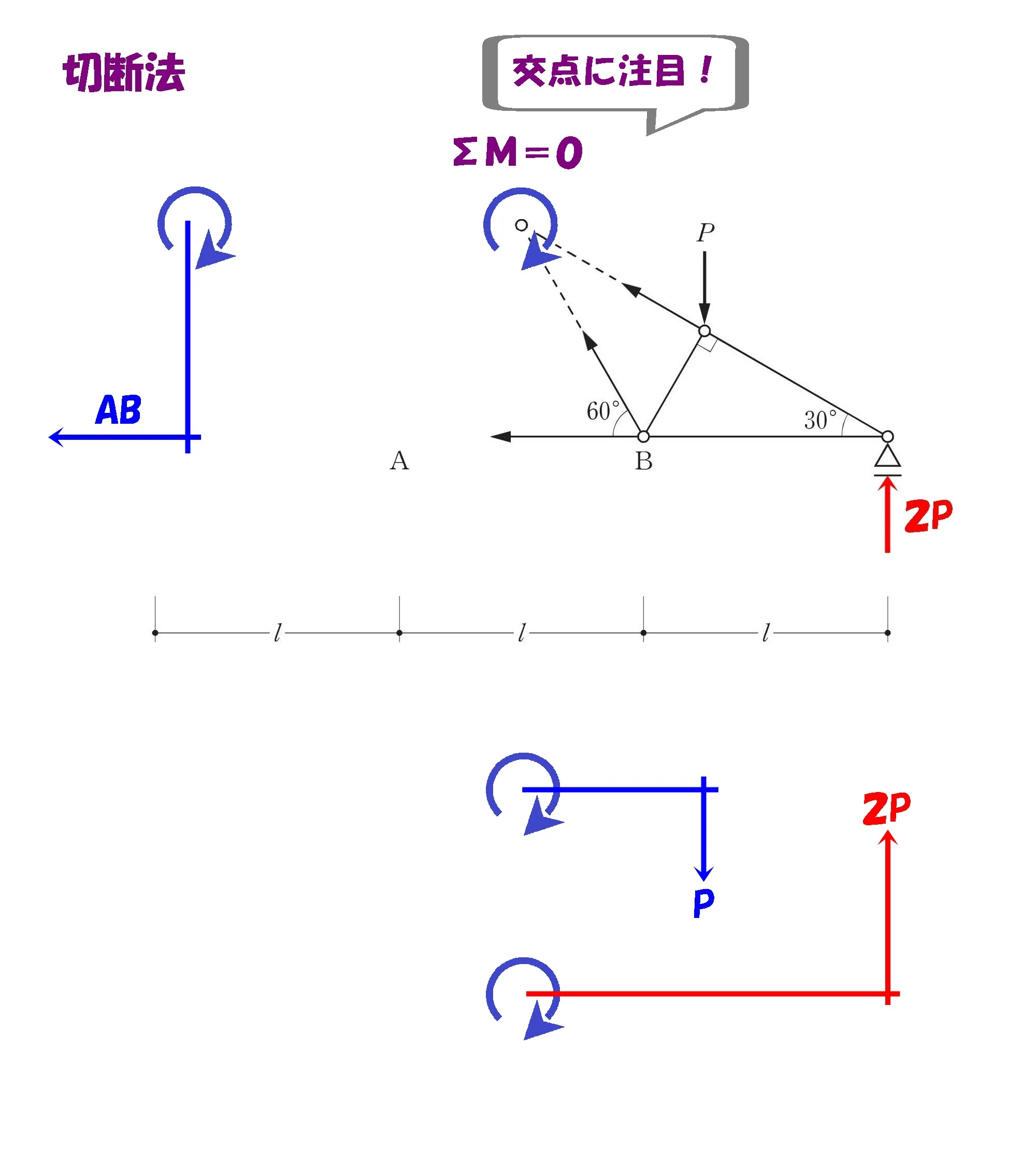

「斜め部材の交点」を中心にしたモーメントの吊り合い式が成立します。
4.三角形の辺の比を使って距離を求める
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
トラスの全長を4分割する
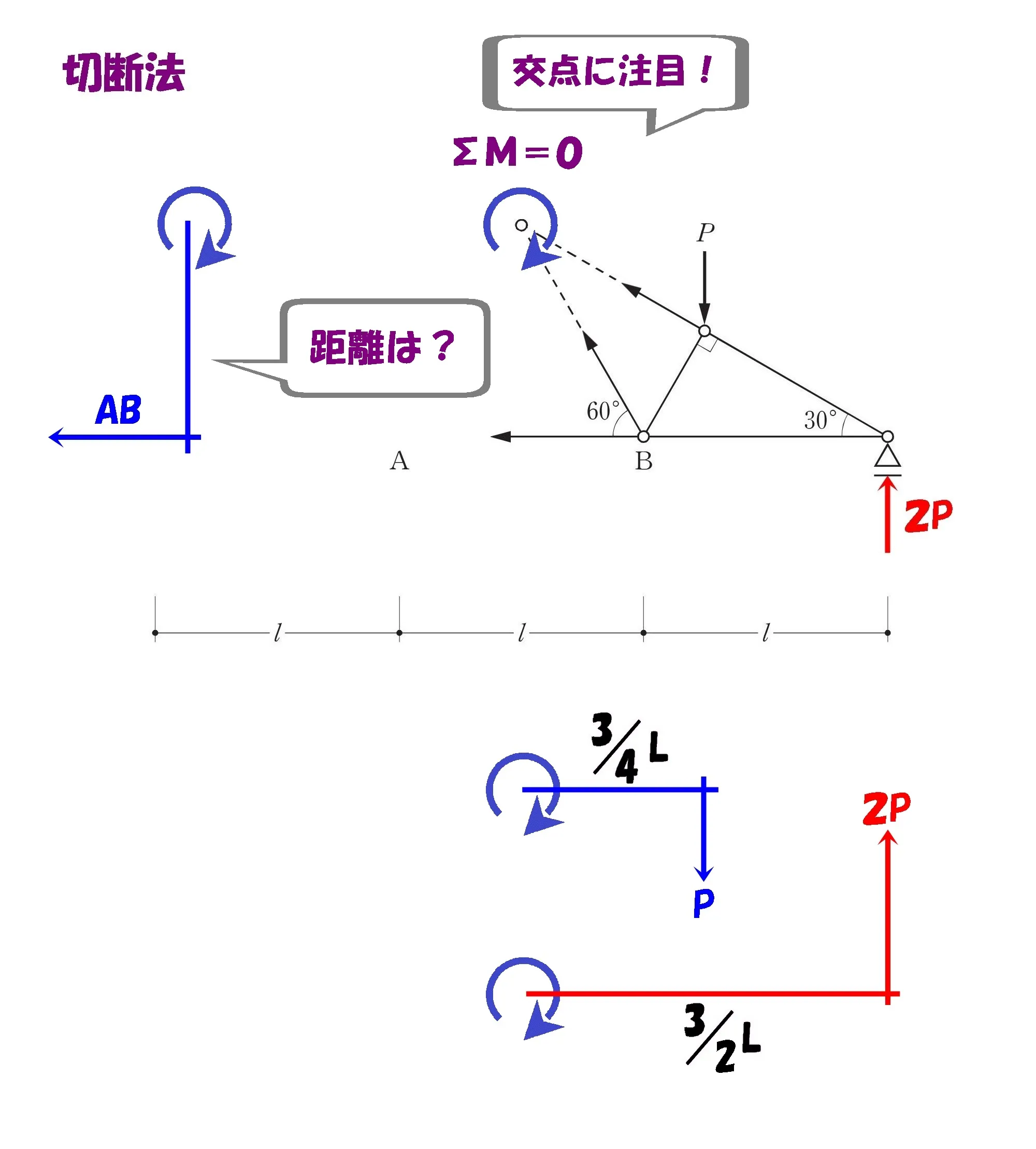

トラスの全長3Lを4分割すると、モーメントの中心からPまでの距離は3/4L
トラスの梁せいを求める
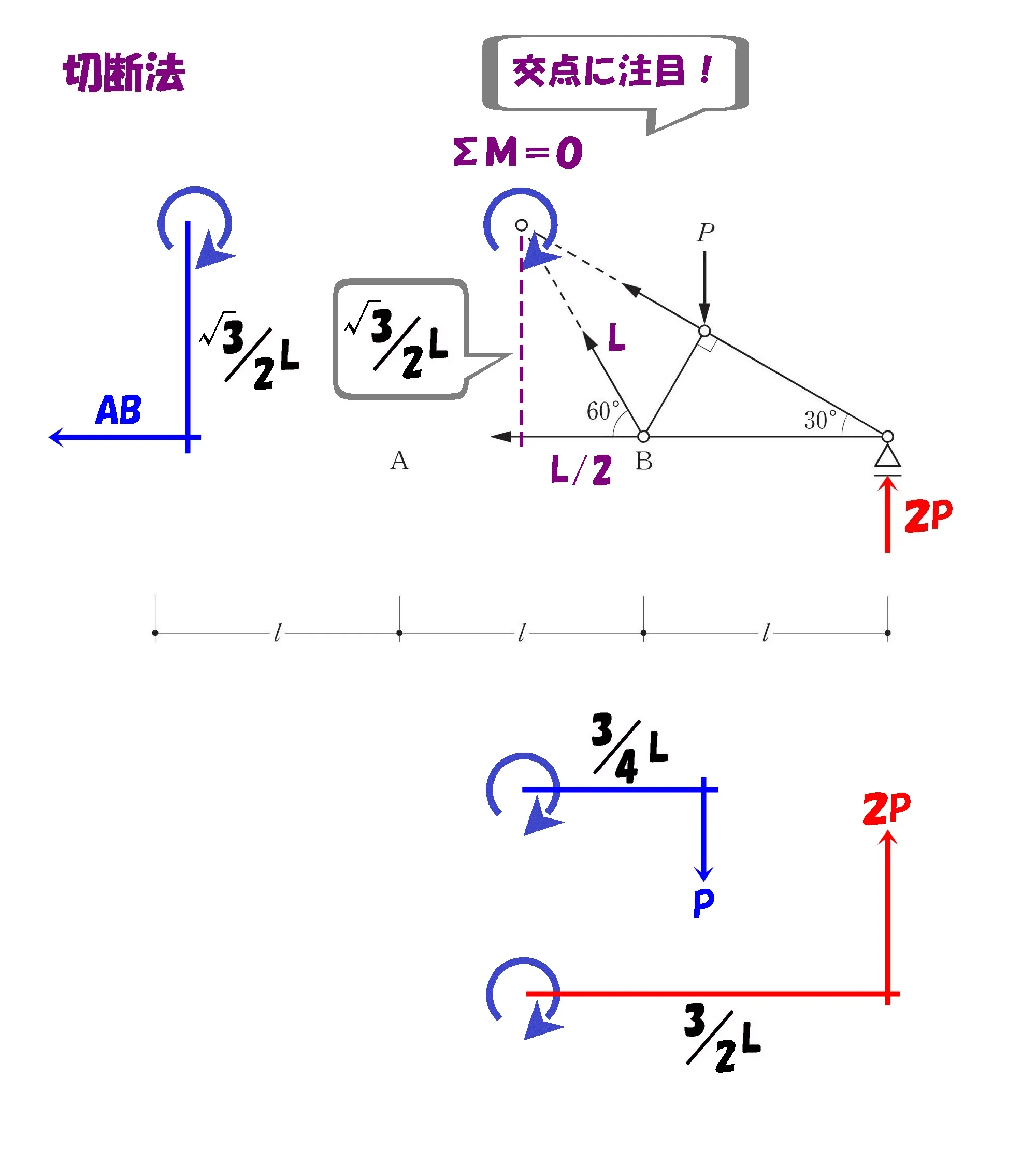

$$60度の直角三角形の辺の比=2:1:\sqrt{3}$$
$$2:1:\sqrt{3}=L:\frac{ L }{ 2 }:\frac{ \sqrt{3} }{ 2 }$$
5.ΣM=0の吊り合い式より軸力を求める
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める
モーメント=力×距離
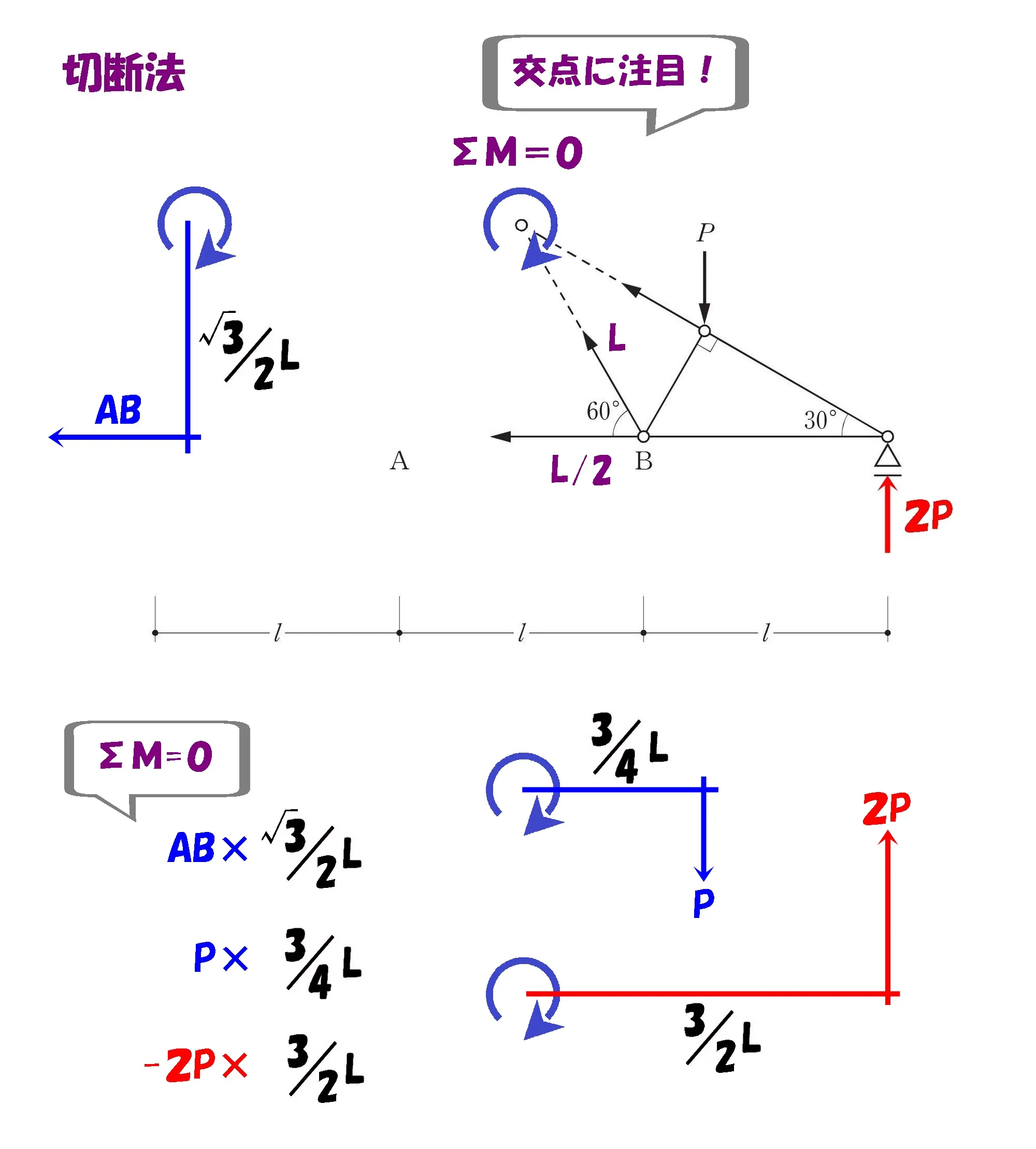

$$L=1を代入。\Sigma M=0より,$$$$+AB*\frac{ \sqrt{3} }{ 2 }+P*\frac{ 3 }{ 4 }-2P*\frac{ 3 }{ 2 }=0$$
$$\frac{ \sqrt{3} }{ 2 }AB=\frac{ 2*3 }{ 2 }P-\frac{ 3 }{ 4 }P$$
両辺に×4
$$2\sqrt{3}AB=(2*2*3) P-3P⇨2\sqrt{3}AB=9P$$
$$AB=\frac{ 9P }{ 2\sqrt{3} }⇨\frac{ 9P*\sqrt{3} }{ 2\sqrt{3} *\sqrt{3}}=\frac{ 9P*\sqrt{3} }{ 2*3 } $$
$$\frac{ \underline{3}*3P*\sqrt{3} }{ 2*\underline{3} }=\frac{ 3\sqrt{3} }{ 2 }P$$$$AB=+\frac{ 3\sqrt{3} }{ 2 }P$$
答え.4





成仏!
攻略ポイント
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める


この動画を YouTube で視聴
ブレース付き架構
難易度:★★☆☆☆
ブレース付き架構の攻略は、トラスの「切断法による解き方」を応用することが出来ます。
トラスを攻略



トラス切断法を
思い出すのだ!
攻略ポイント
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
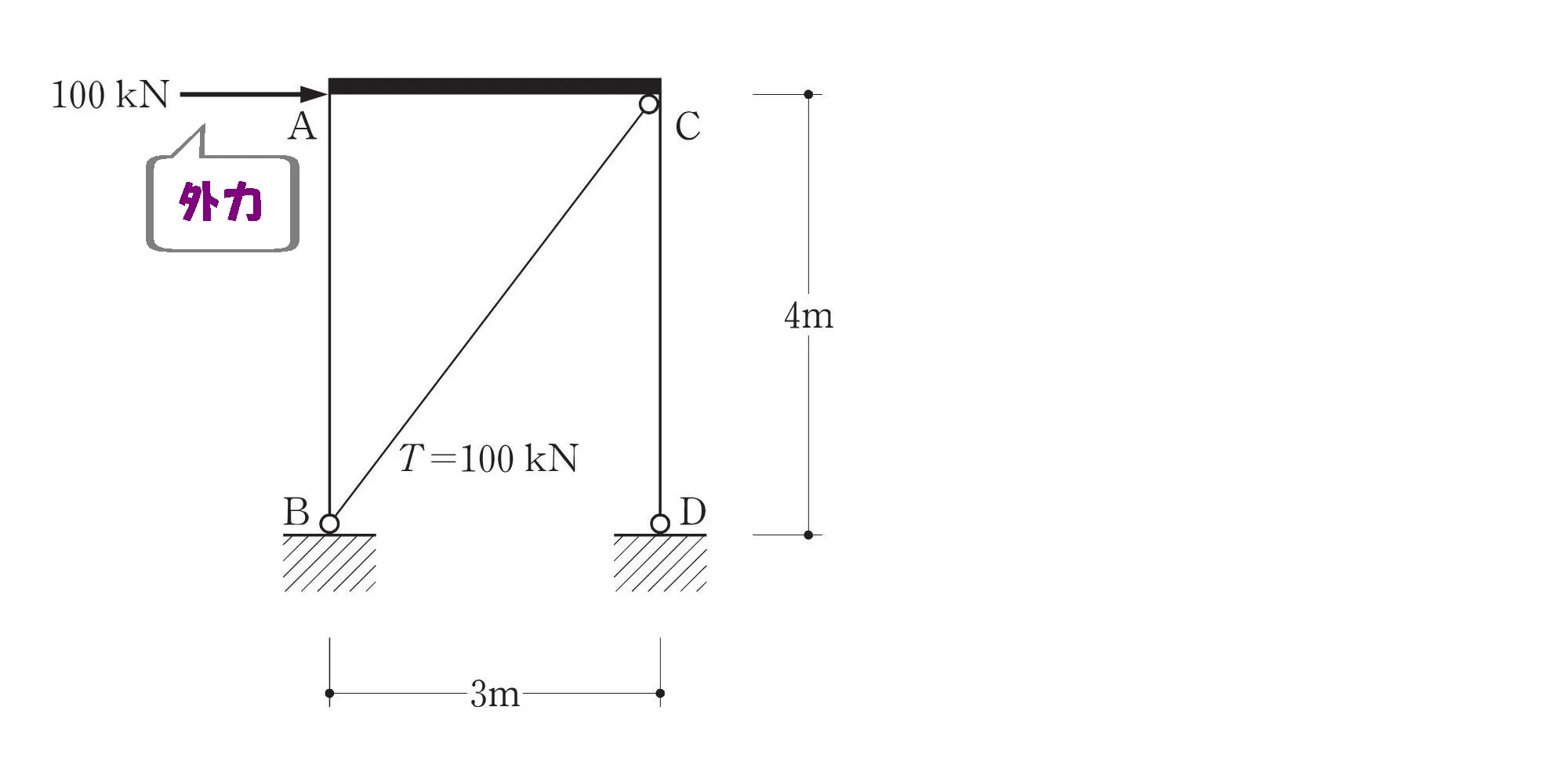
問題
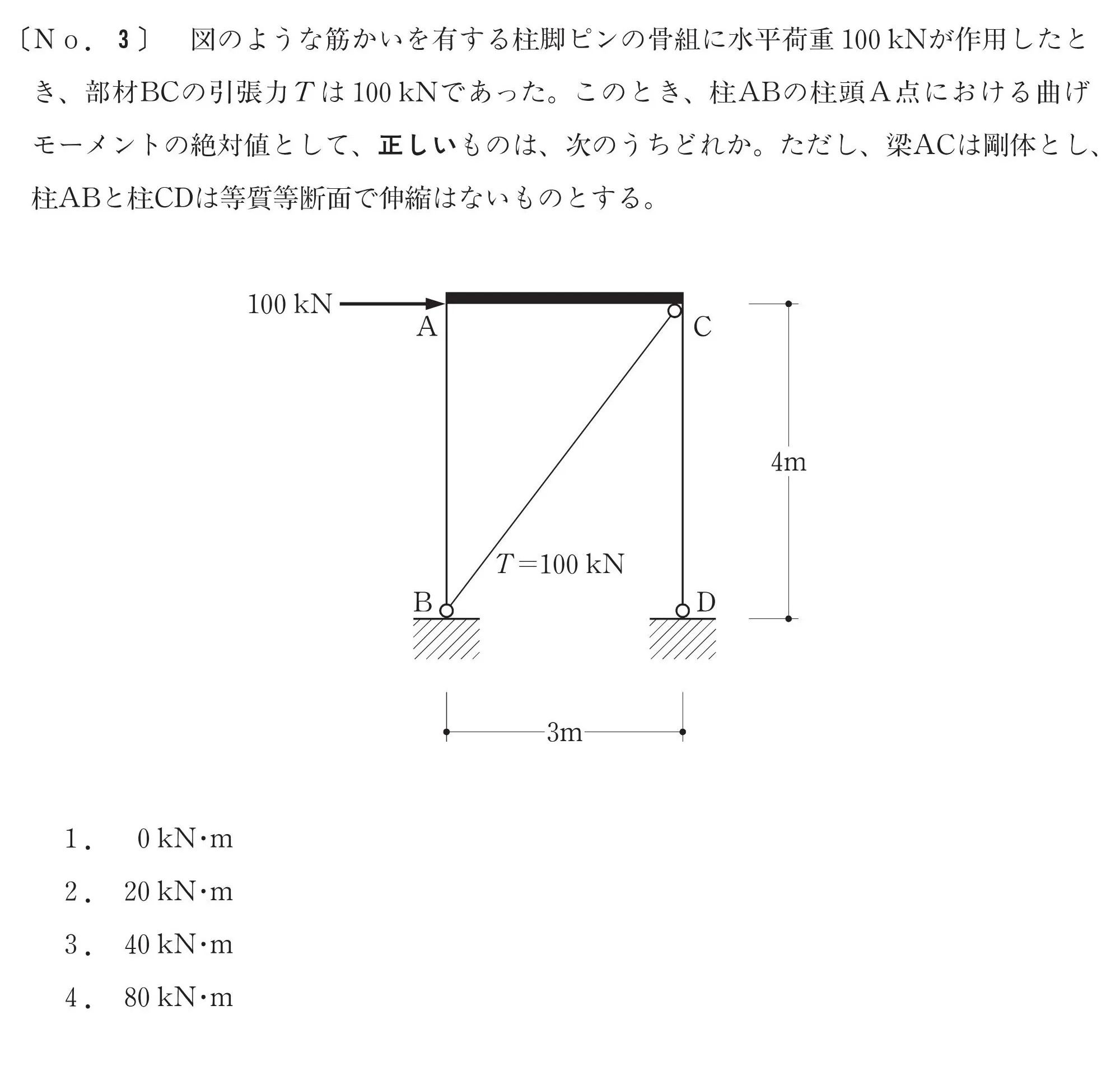

1.問題文を読み取り、求める物を定める
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
問題文を読み取る
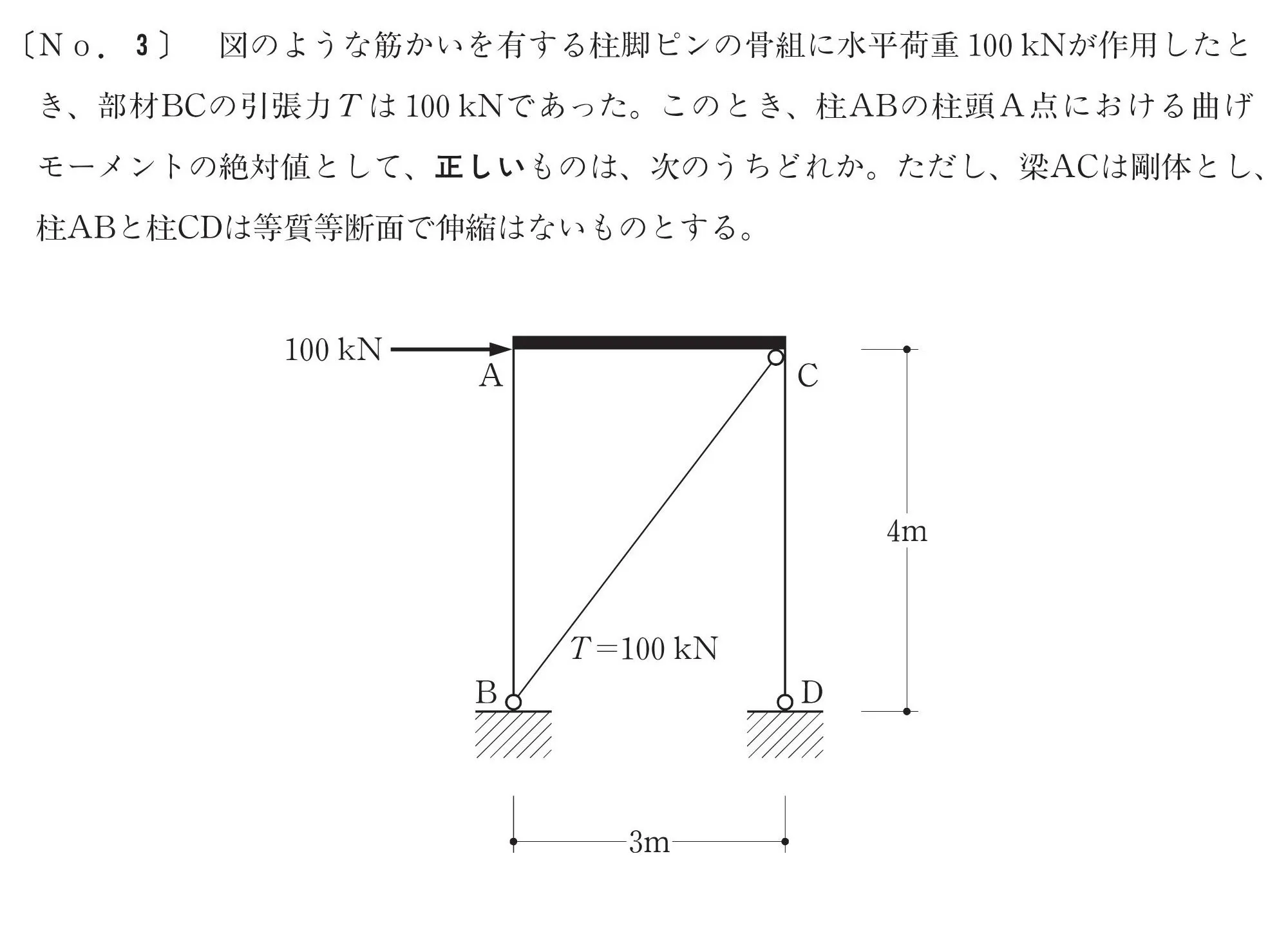

A点のモーメントを求める
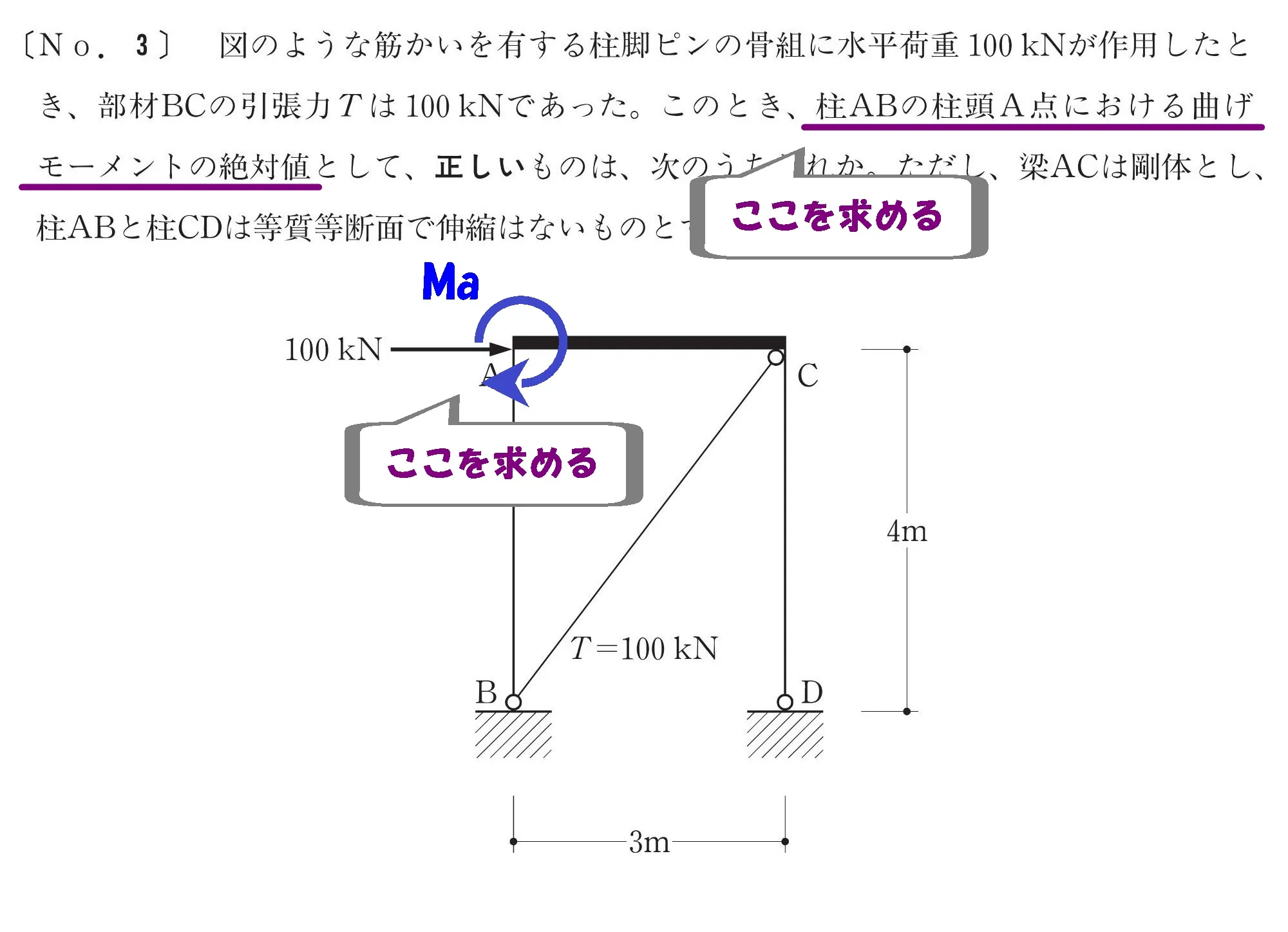

「柱ABの柱頭A点における曲げモーメント(絶対値)」を求める。
柱脚の支持条件
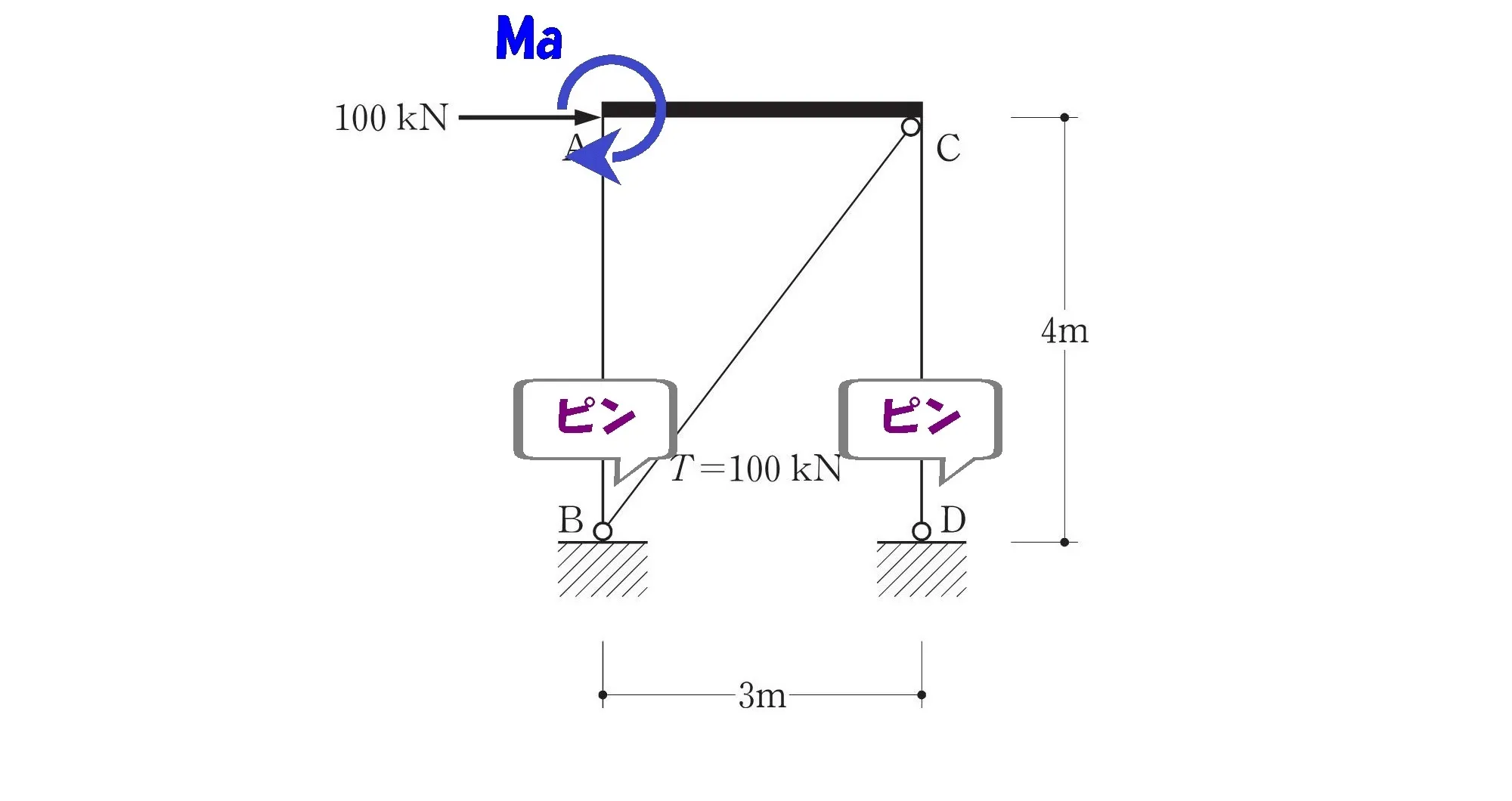

左:ピン支点
右:ピン支点
モーメント図を描く
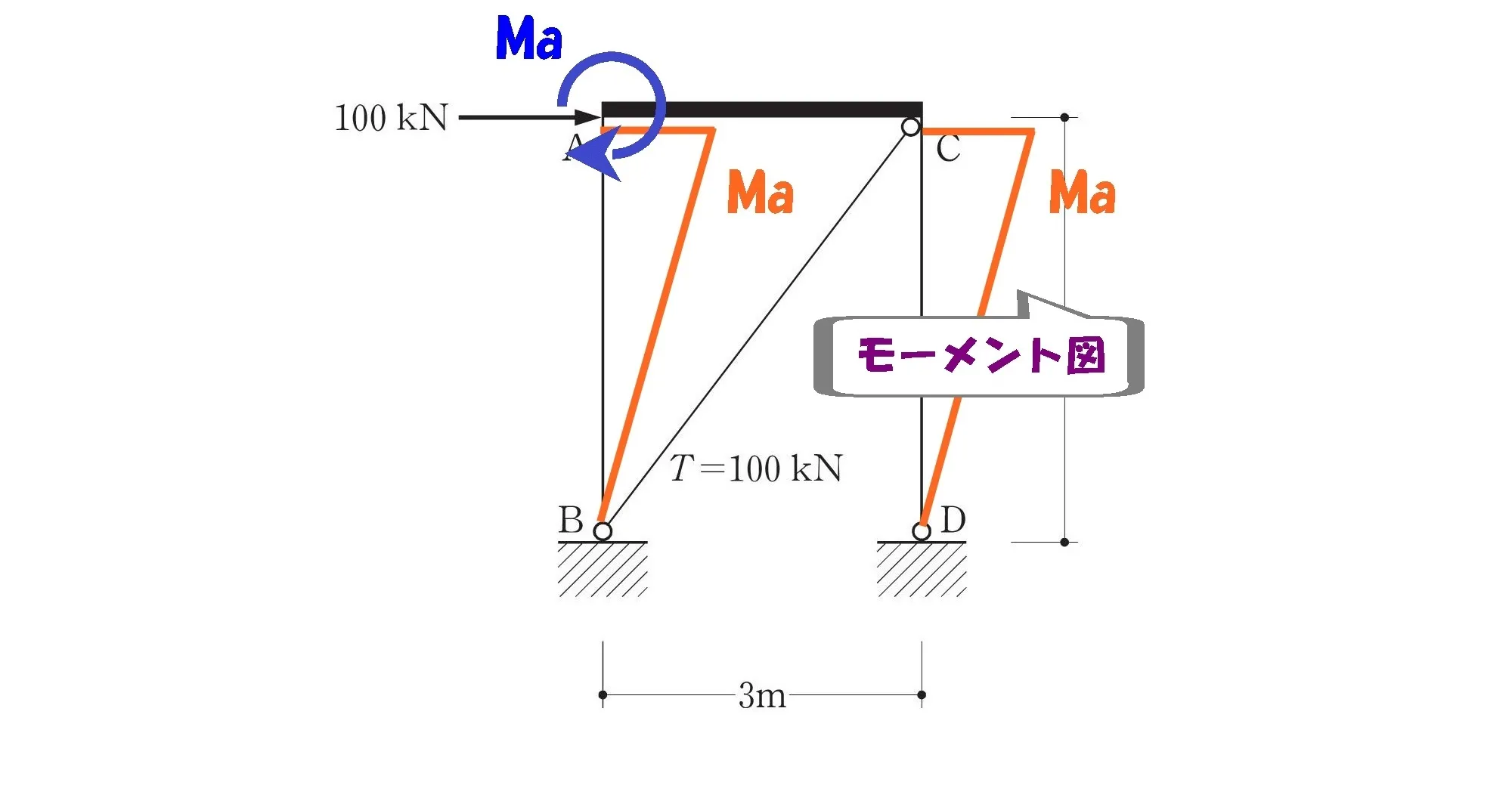

ピン支点のモーメントはゼロ(負担しない)に考慮して、モーメント図を描きましょう。
せん断力を書き込む
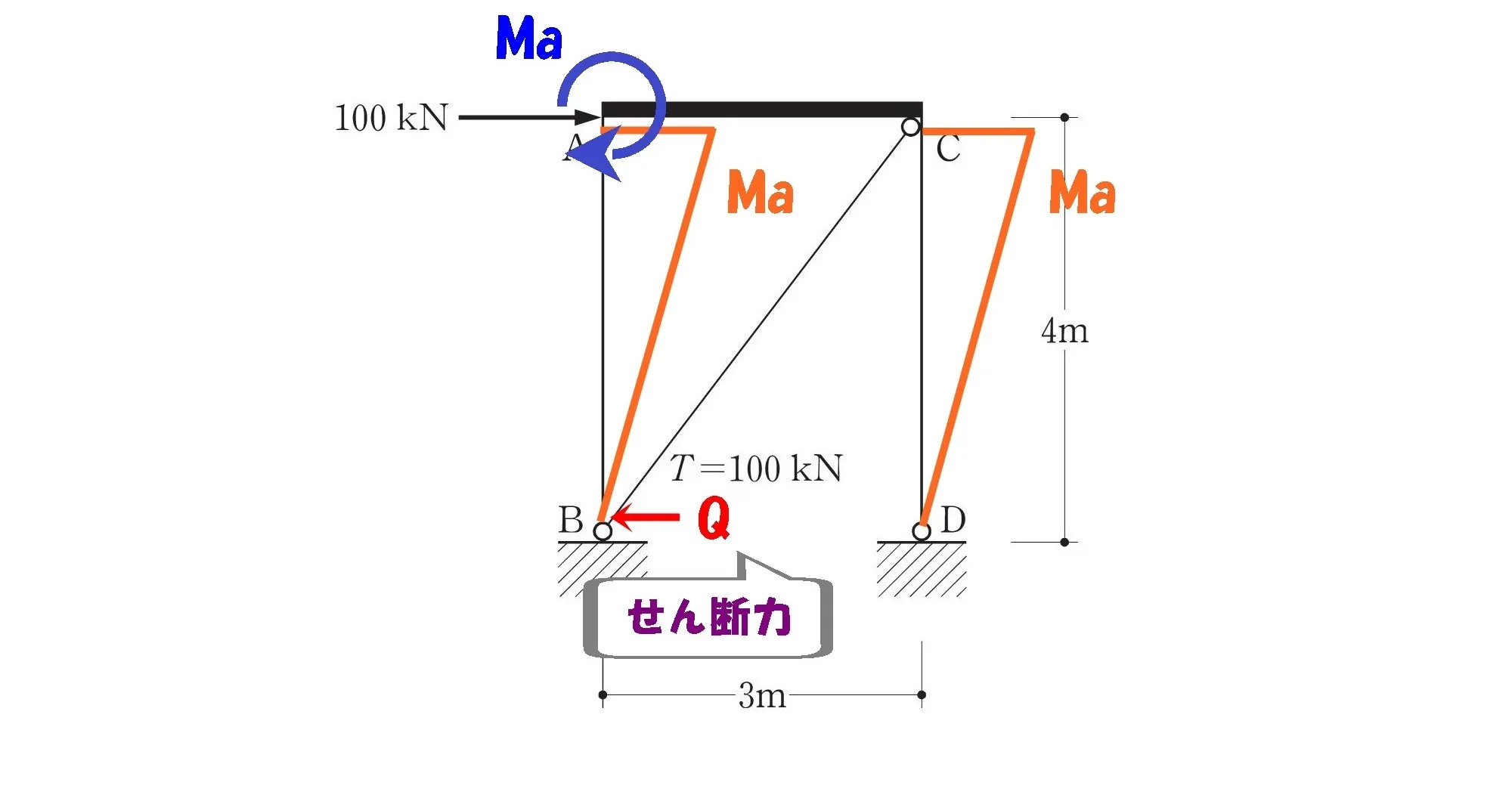

モーメント=力×距離
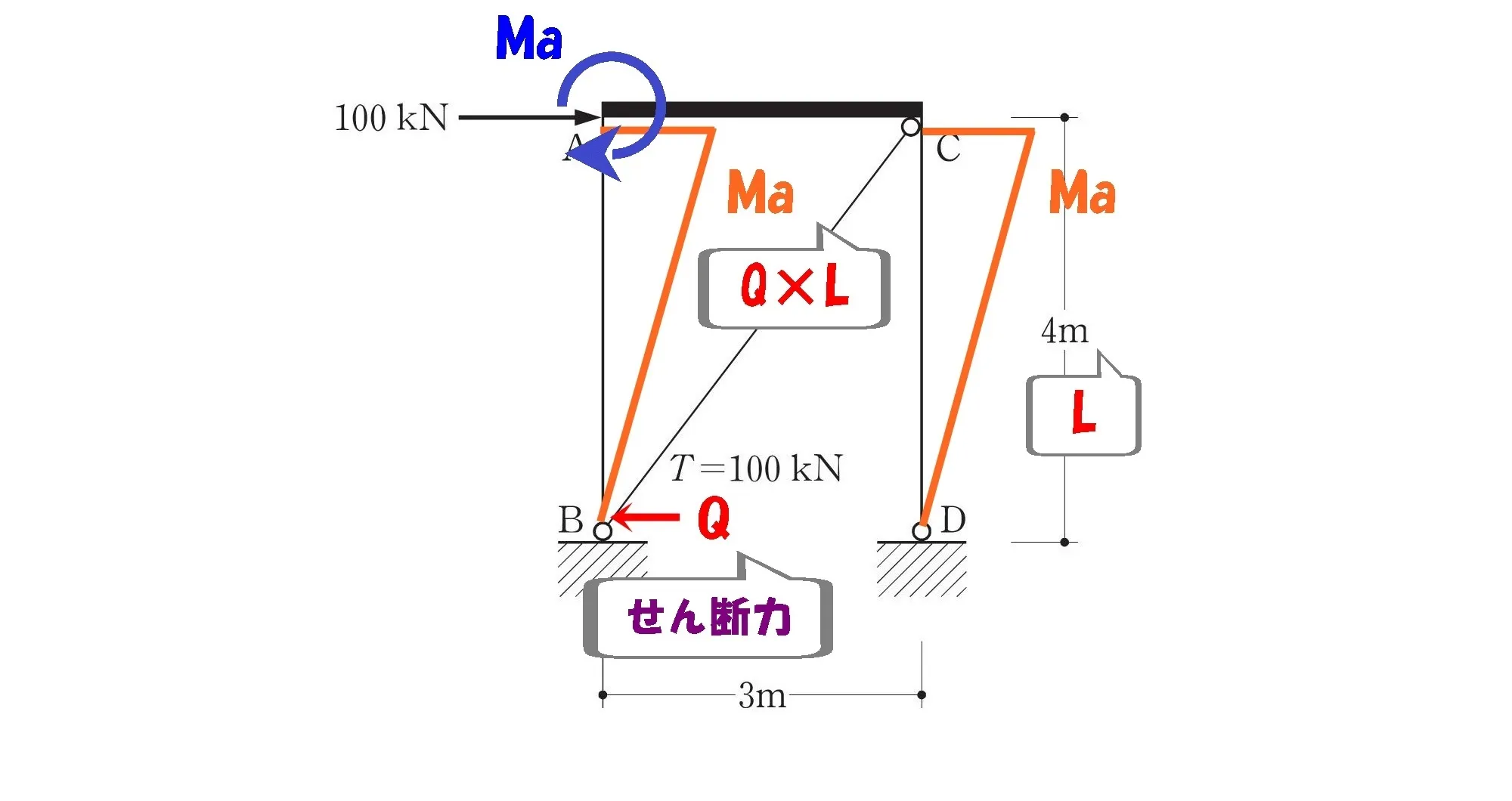

$$「モーメント=力×距離」$$$$「力」=せん断力、「距離」=4m$$
梁ACは剛体
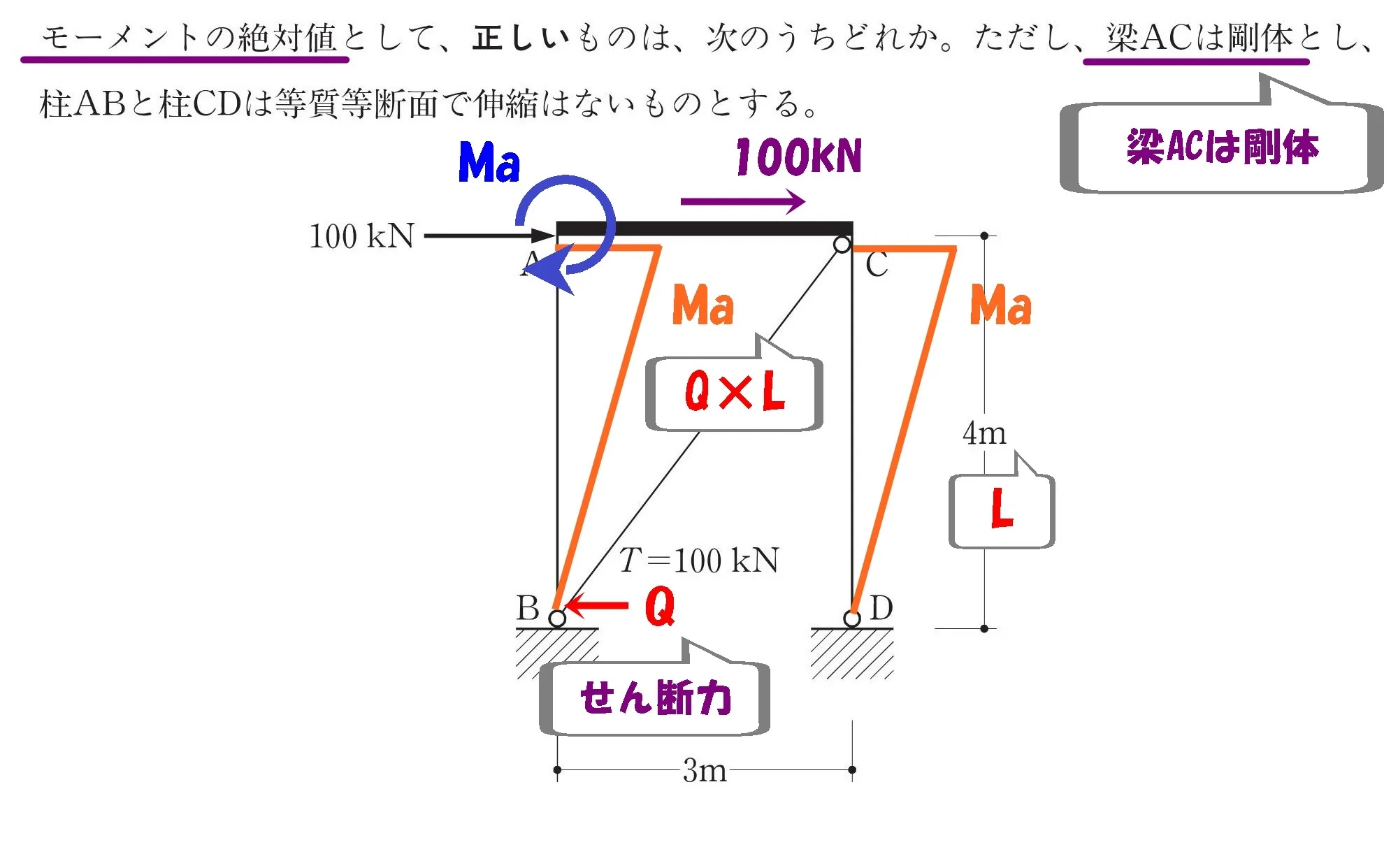

「梁ACは剛体」
梁ACの内部応力は、均一に100kNを負担していることを意味します。



モーメントの力は
せん断力に置き換わる。
2.ブレースを含む部材を切断して取り出す
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
水平荷重100kN

ブレースの引張り力
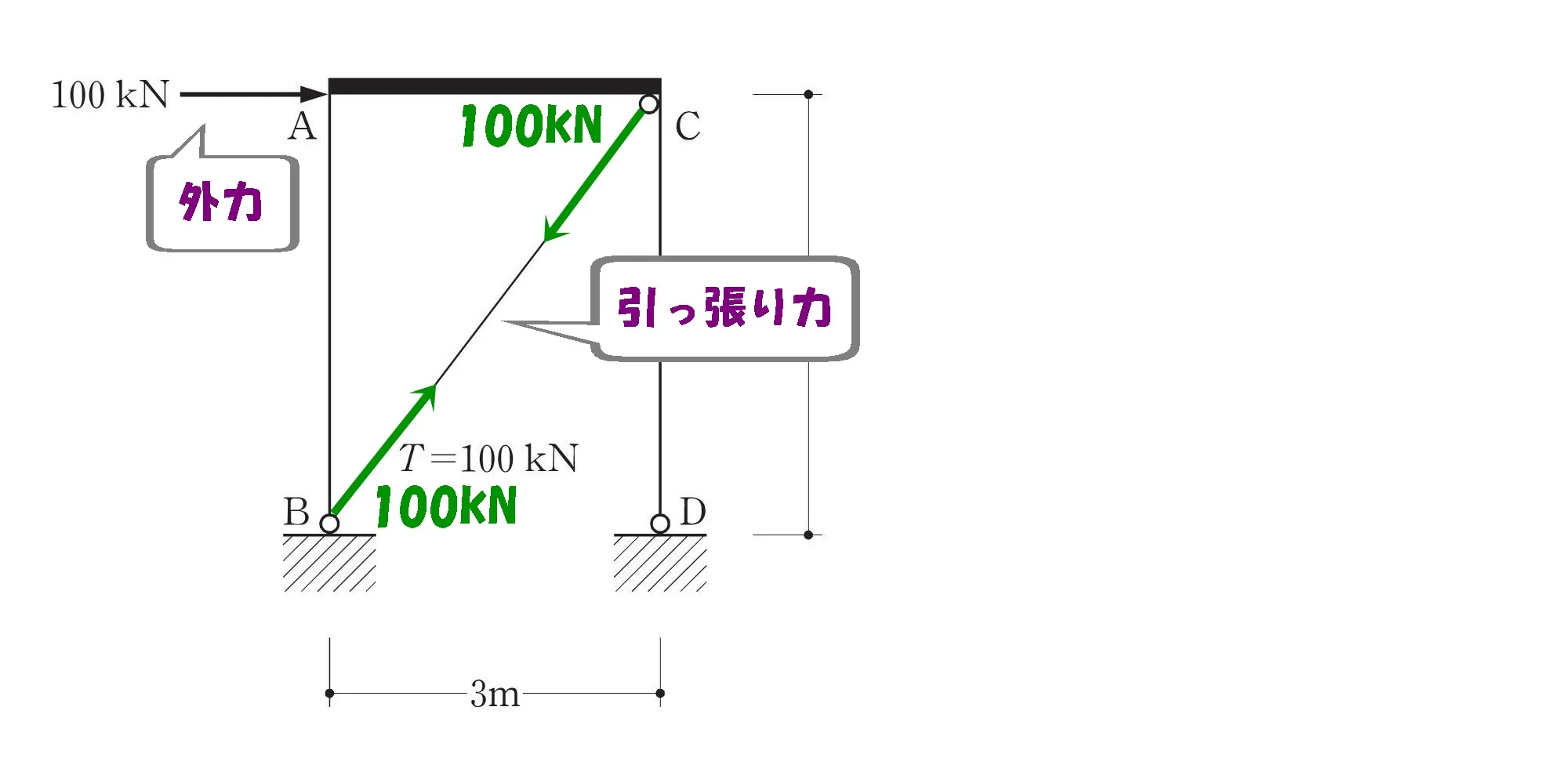

問題図より、ブレースに掛かる引張り力は100kN。
水平荷重の100kNとは別物なので、混同しないようにしましょう。



ブレースは
引張り力を負担する部材
ブレースを切断する
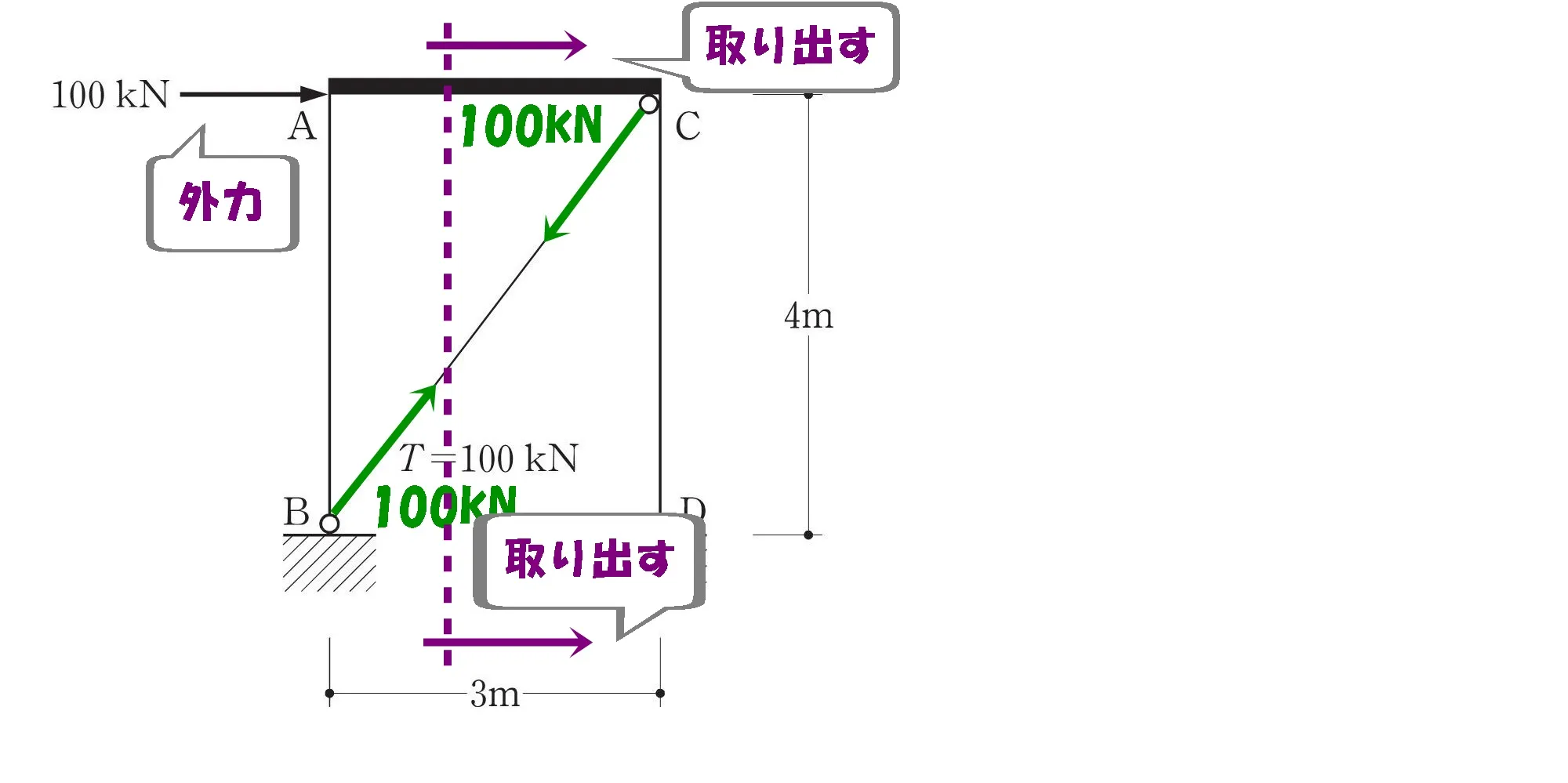

部材AB(左側)のモーメントを求めるにはブレースの応力が必要になります。
この場合、ブレースを含む位置を切断してCD(右側)の部材を取り出しましょう。



ラーメン斬り!
部材CDを取り出す。
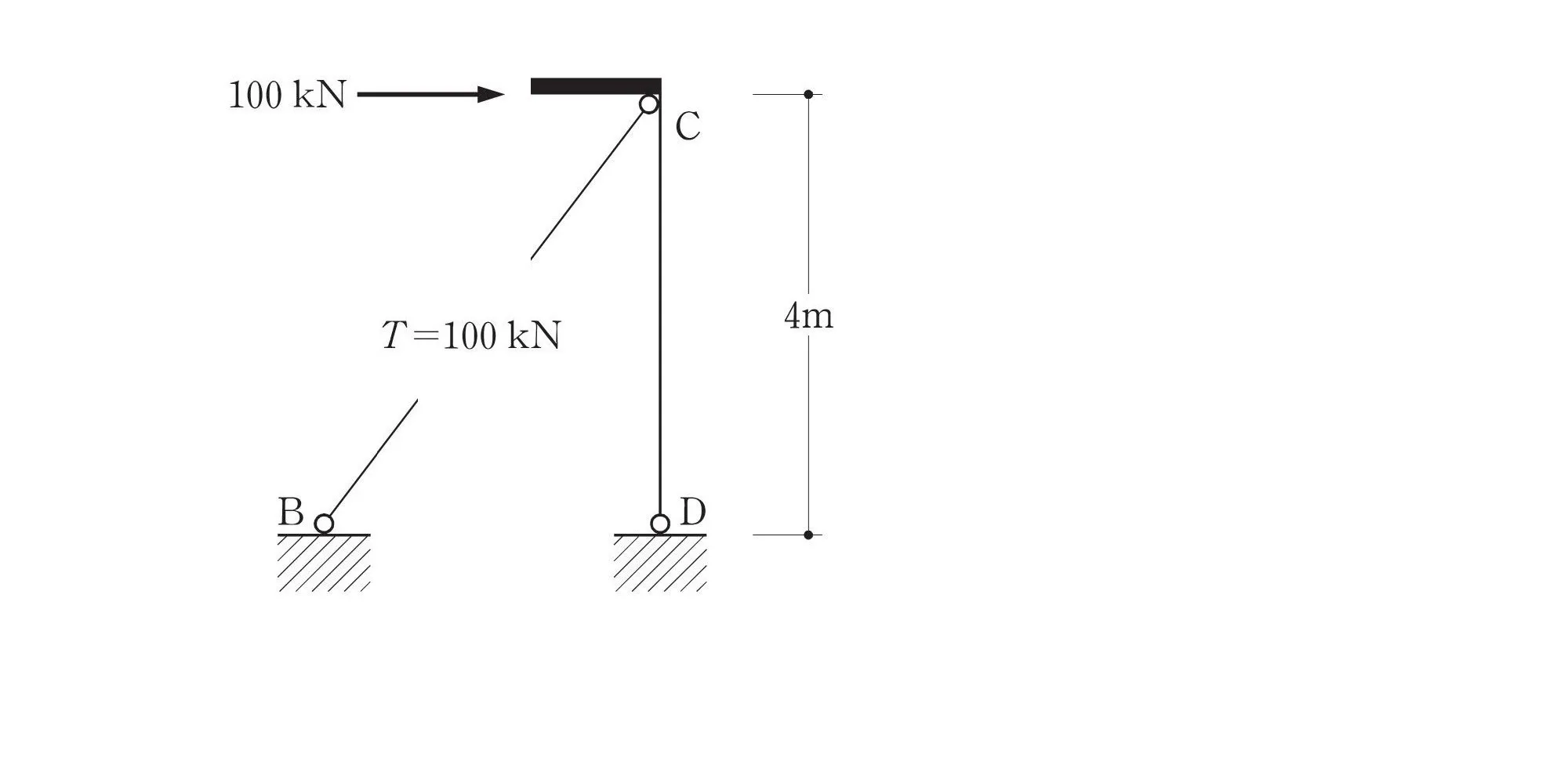

梁ACは剛体
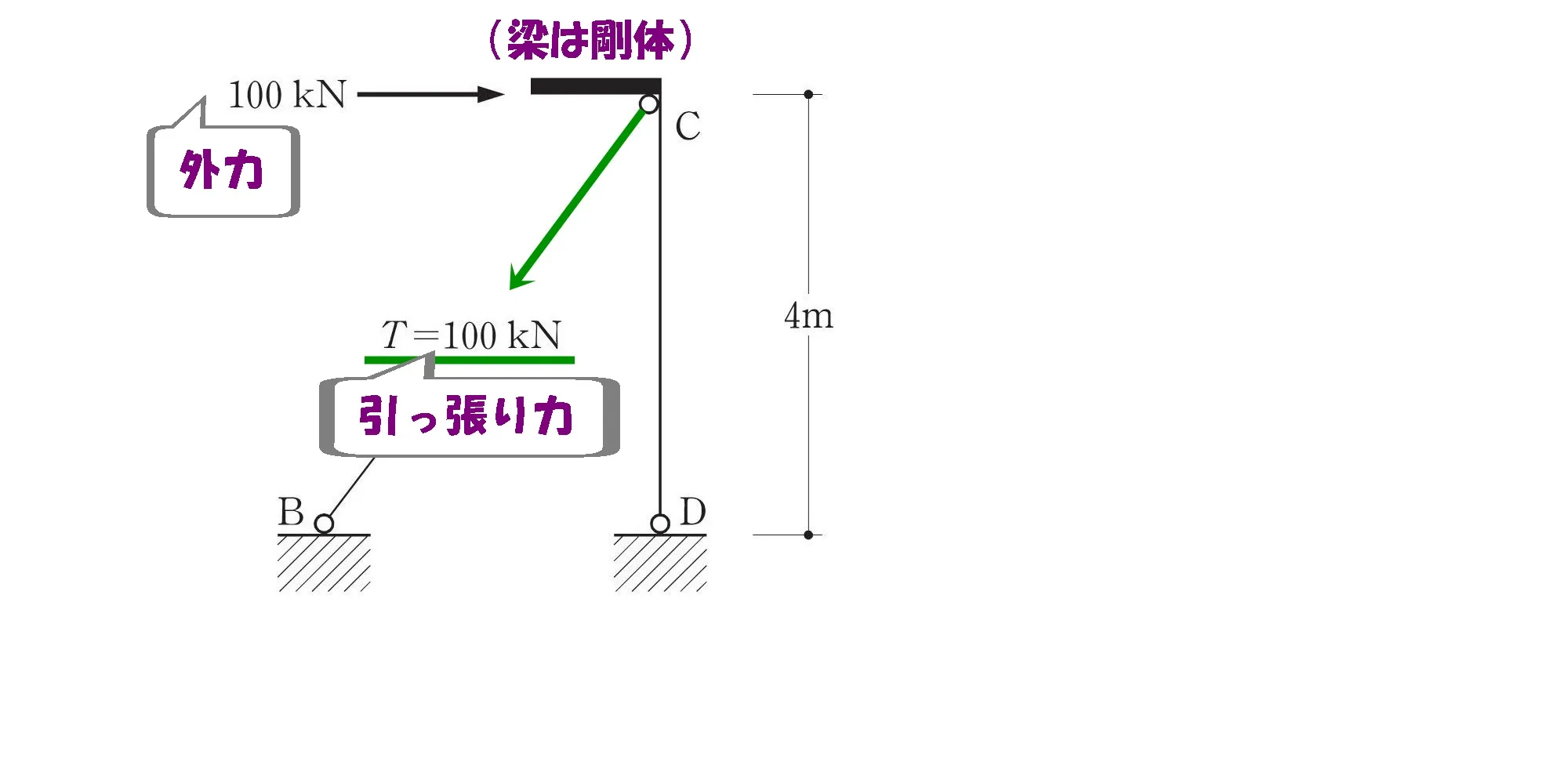

「梁ACは剛体」なので、切断部においても水平荷重100kNは梁に作用します。
せん断力を書き込む
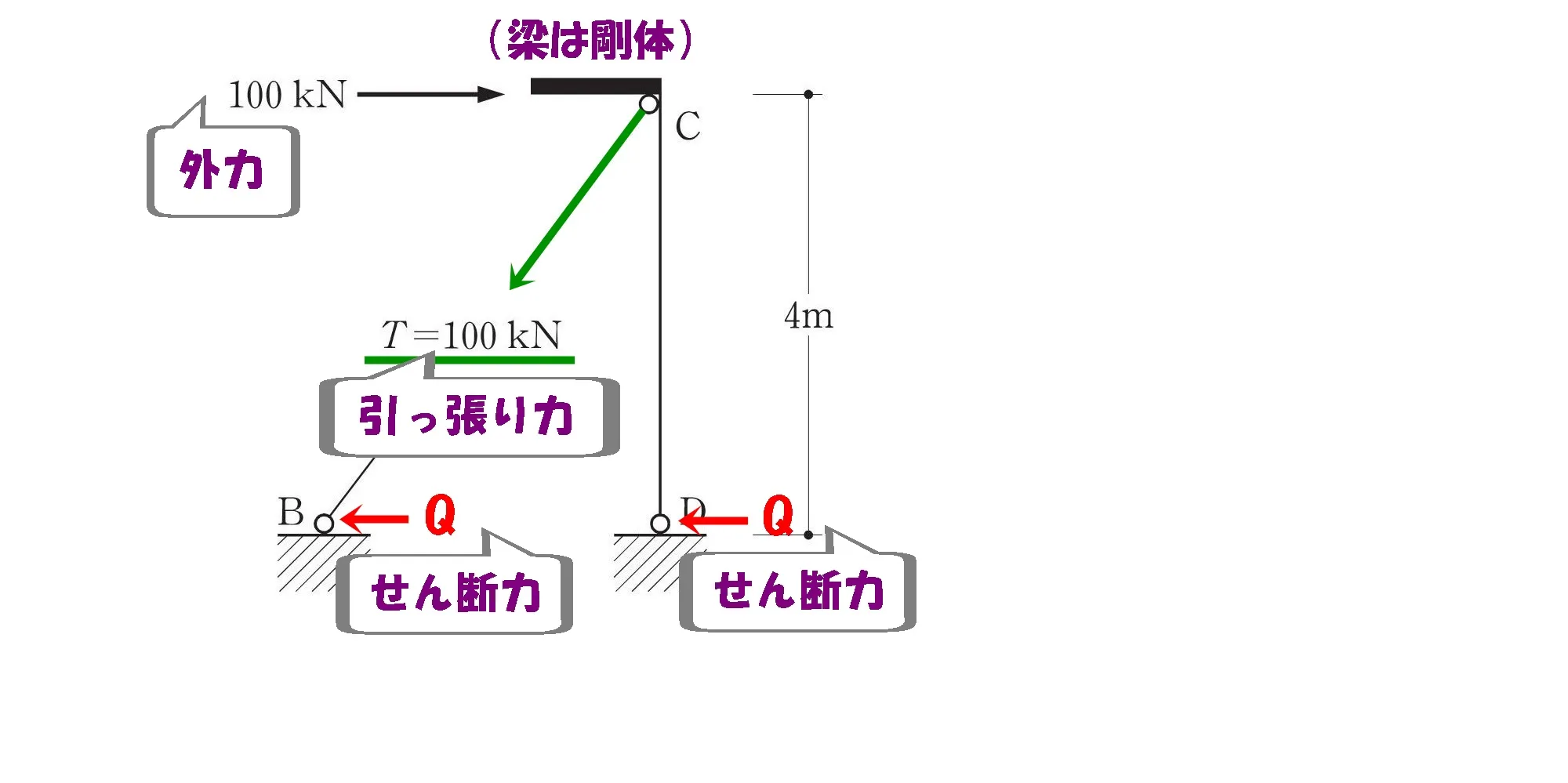

ここで注意するべきことは、せん断力は「柱ABと柱CDの2ヵ所」あるということ。



柱脚は2つあるので
せん断力Qも2つある。
3.ΣX=0により、2つのせん断力を求める
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
ΣX=0
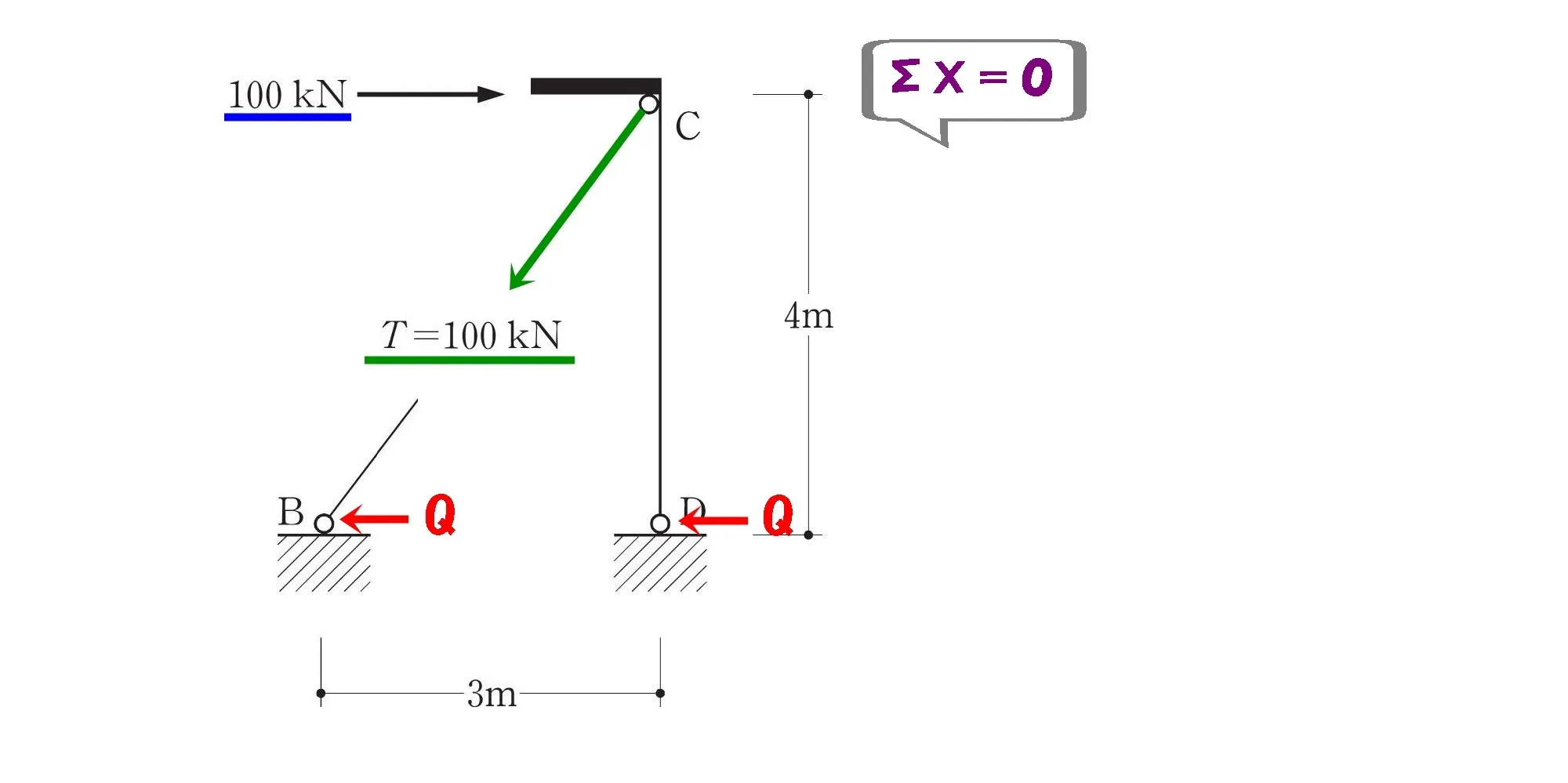

この切断図により、「水平方向の吊り合い式:ΣX=0」が成立します。
ブレースの傾きに注目する
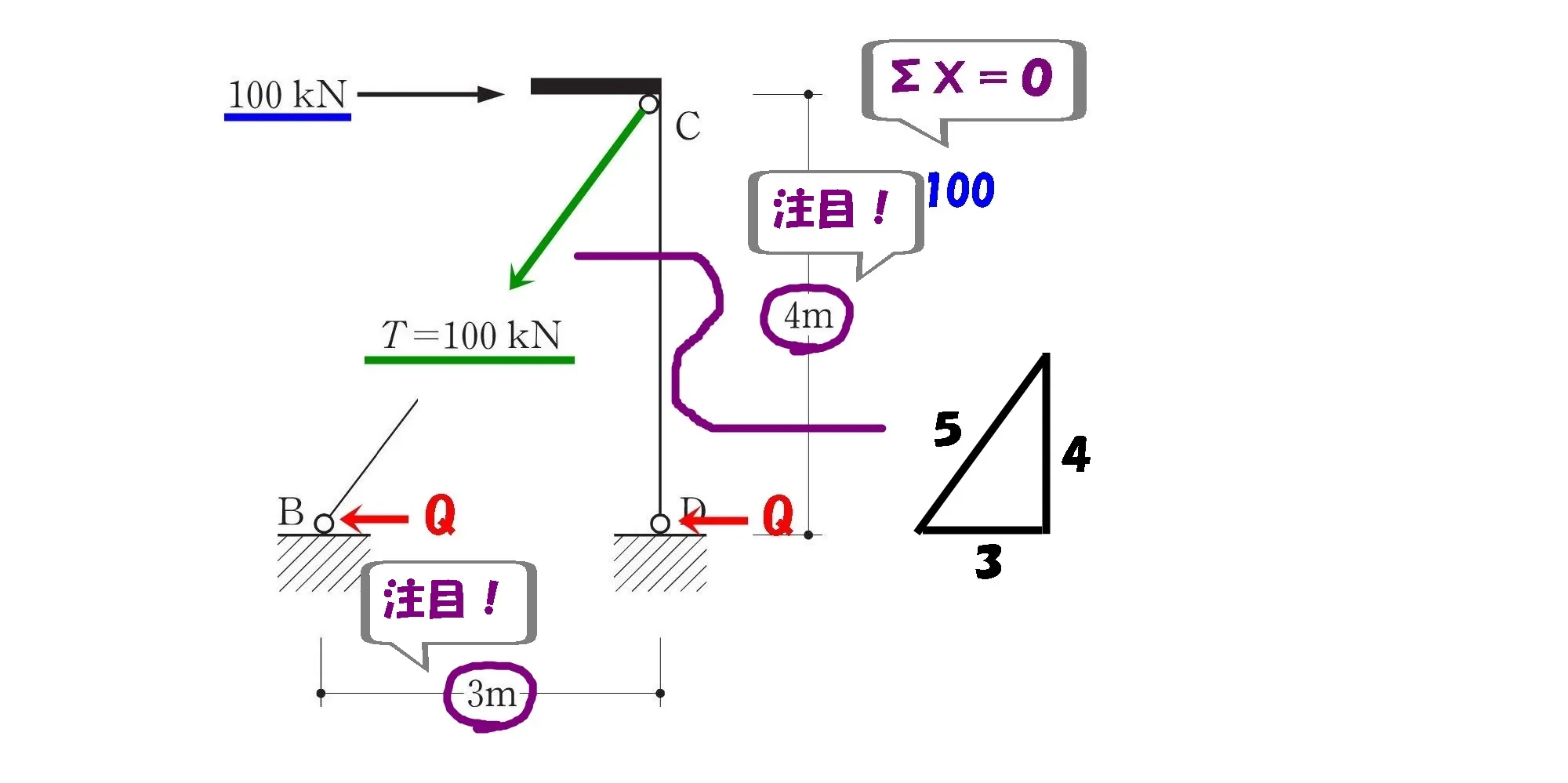

$$柱の間隔BD:3m,柱の高さCD:4mより$$$$直角三角形の辺の比=3:4:5が成り立つ。$$
直角三角形の辺の比
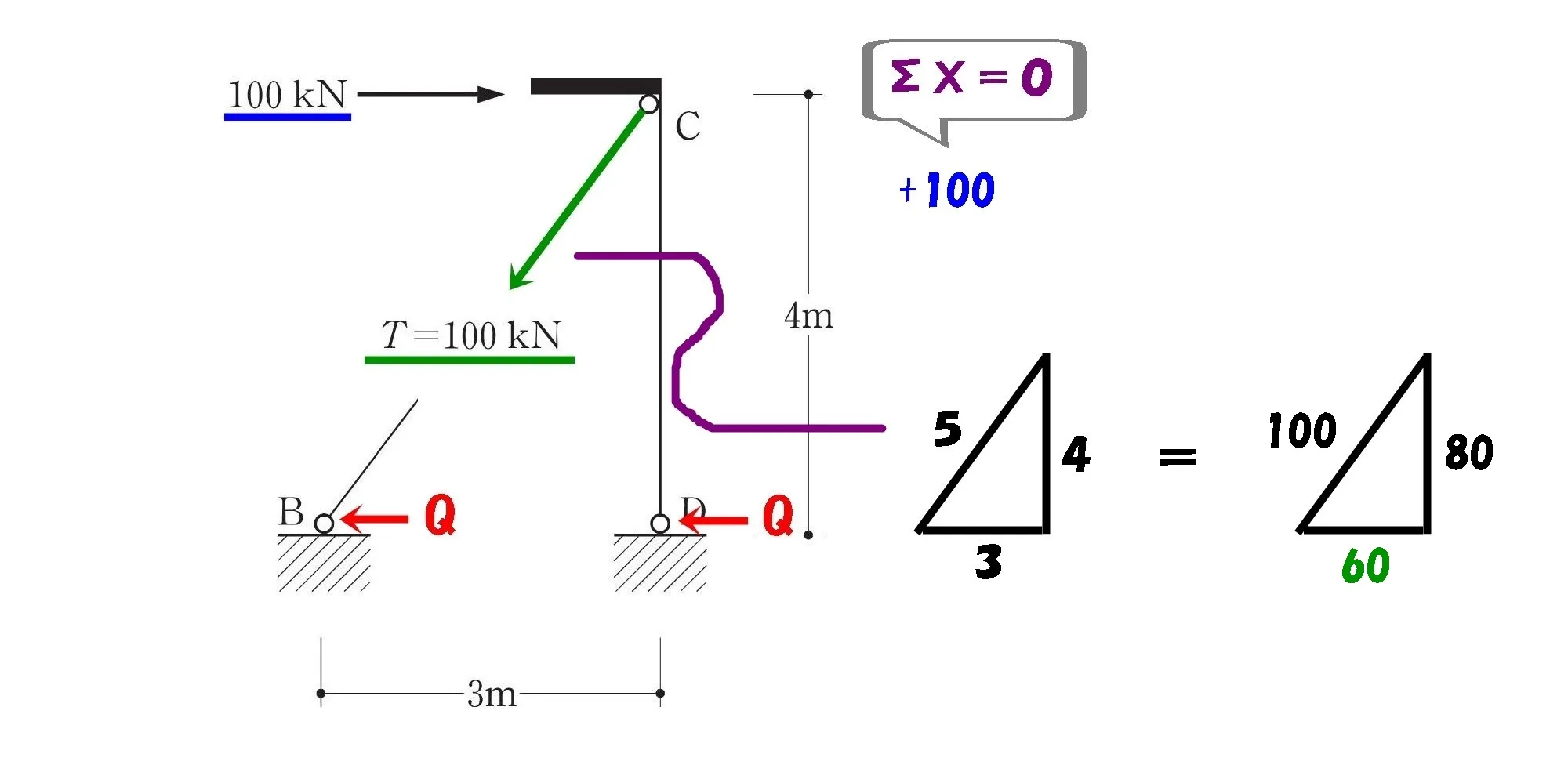

$$直角三角形の辺の比=3:4:\underline{5}=60kN:80kN:\underline{100kN}$$
ベクトルを分解する
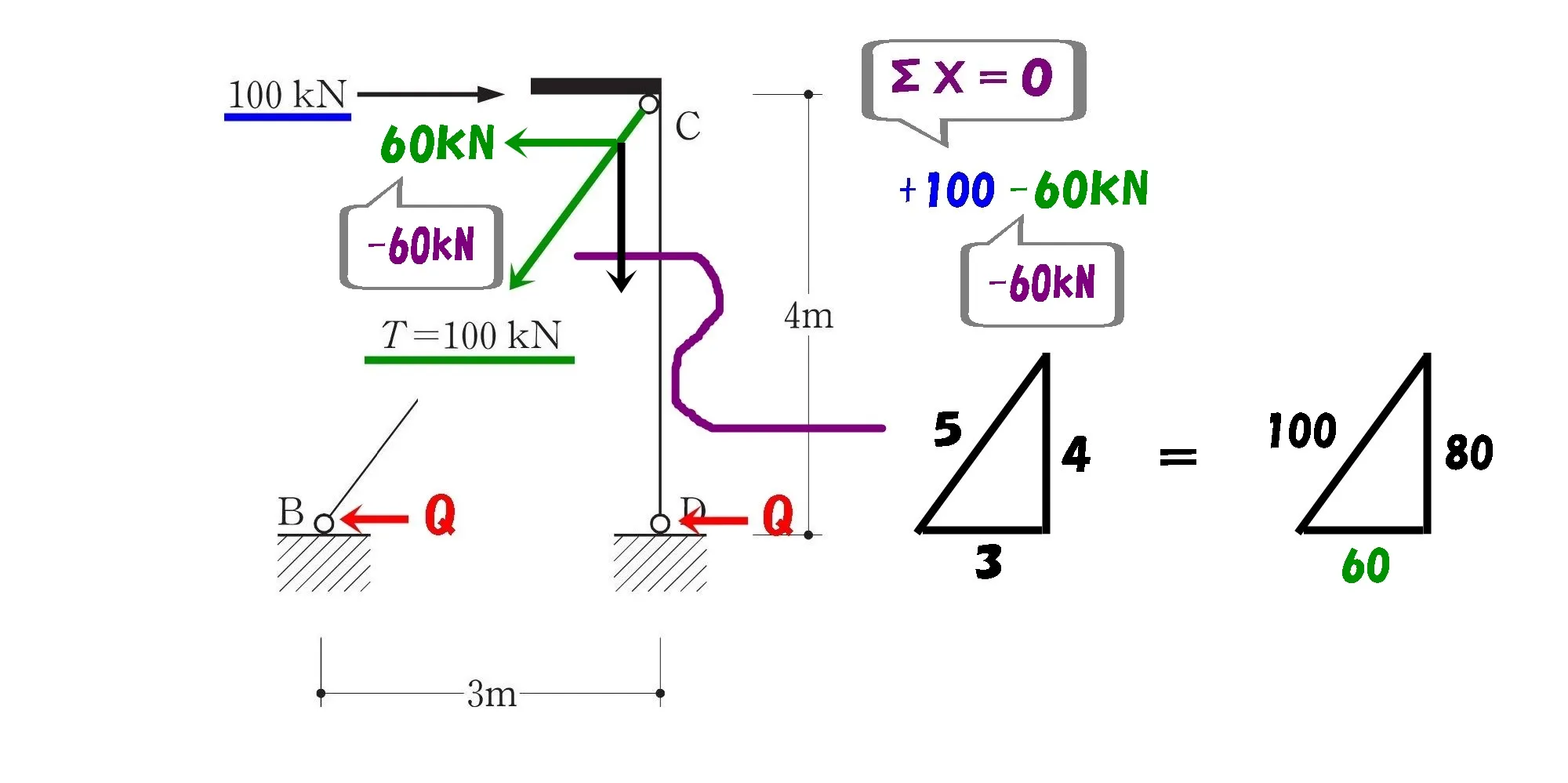

$$[ブレースに作用する力のX方向]$$$$直角三角形の辺の比=\underline{3}:4:5=\underline{60kN}:80kN:100kN$$
せん断力=Q+Q
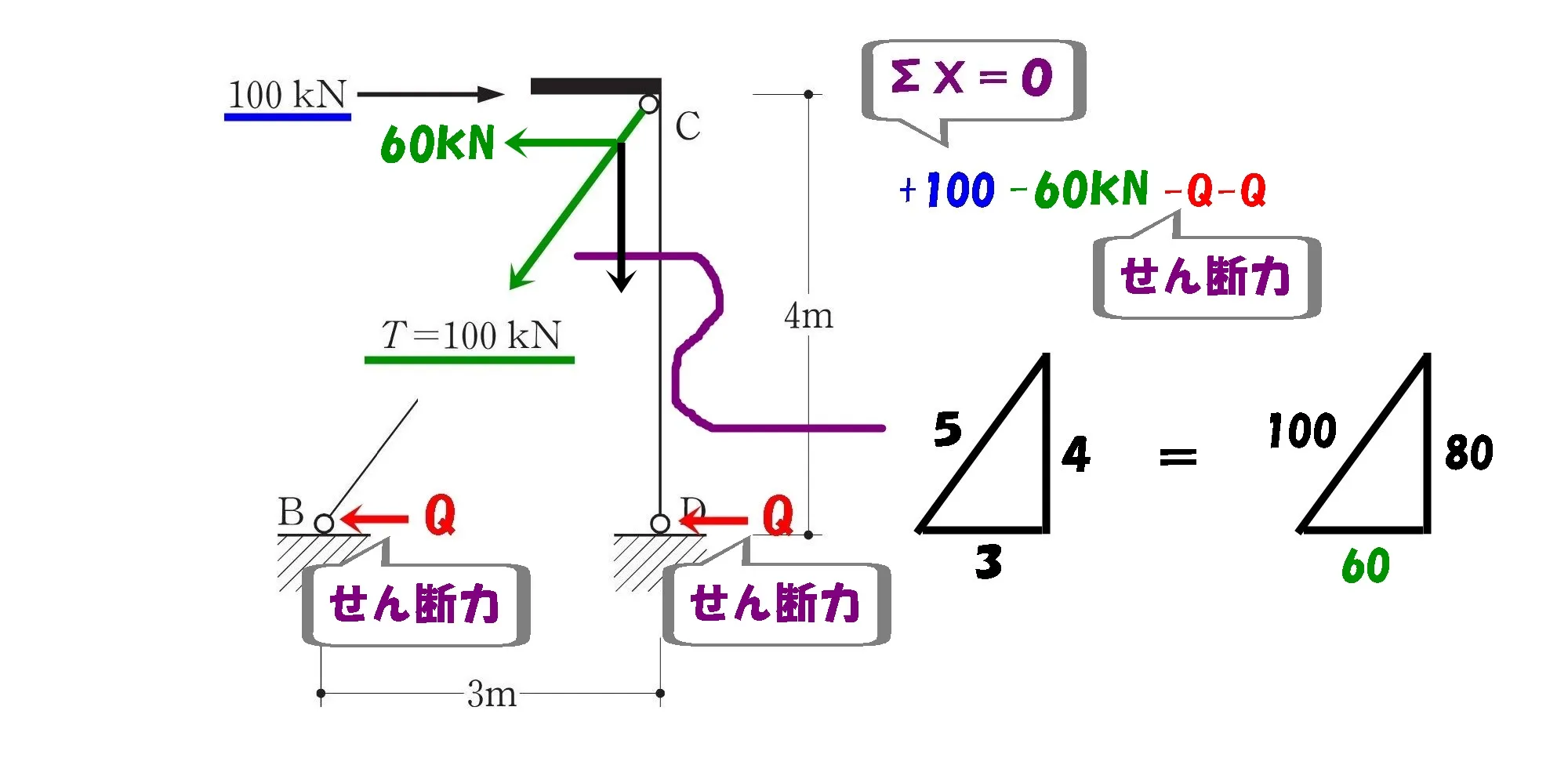

水平荷重100kNをプラスに定義した場合、60kNはマイナス方向となることに注意しましょう。
水平方向の吊り合い式
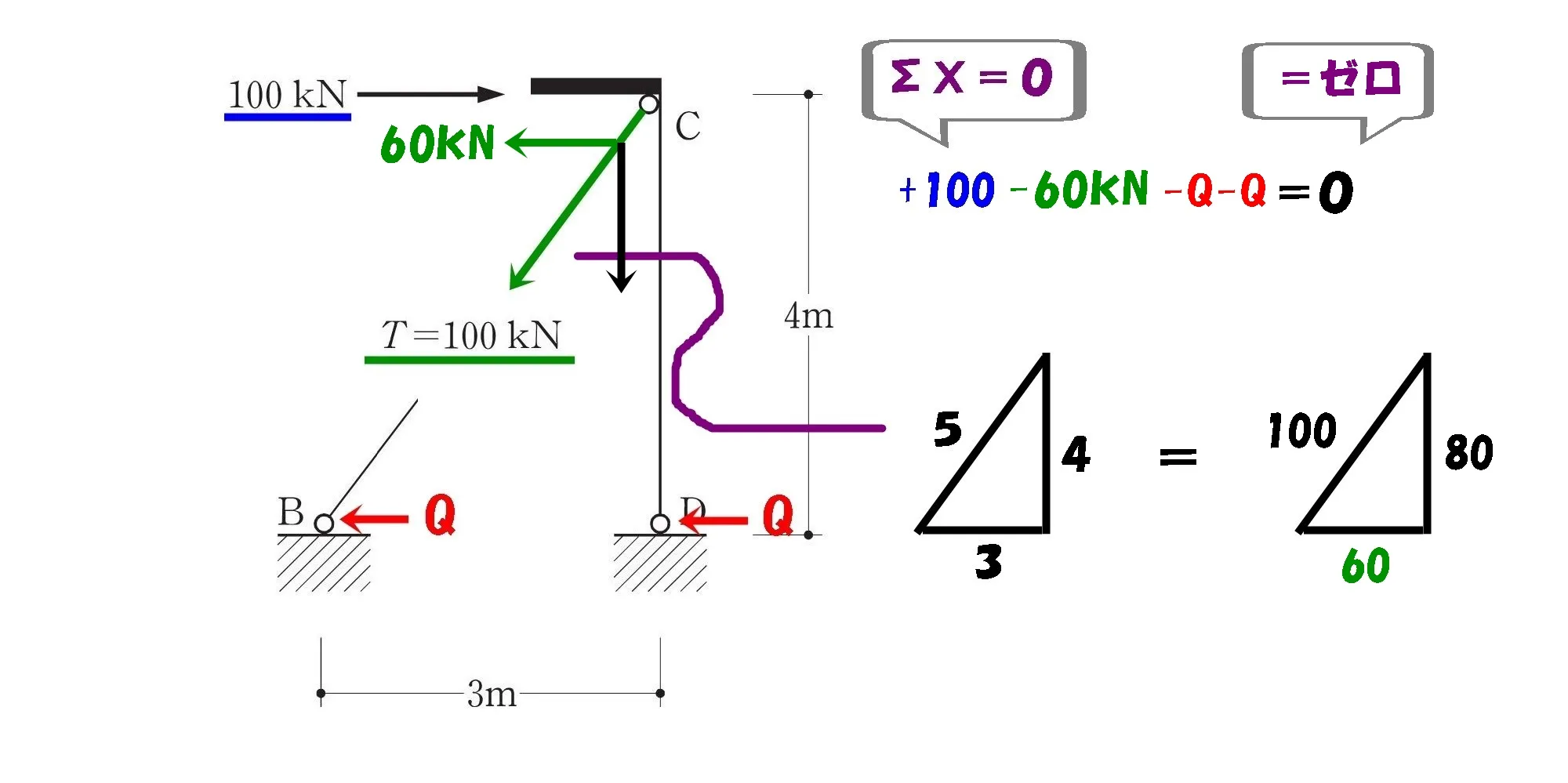

公式
$$\Sigma X=0$$



Σエックス!
ΣX=0
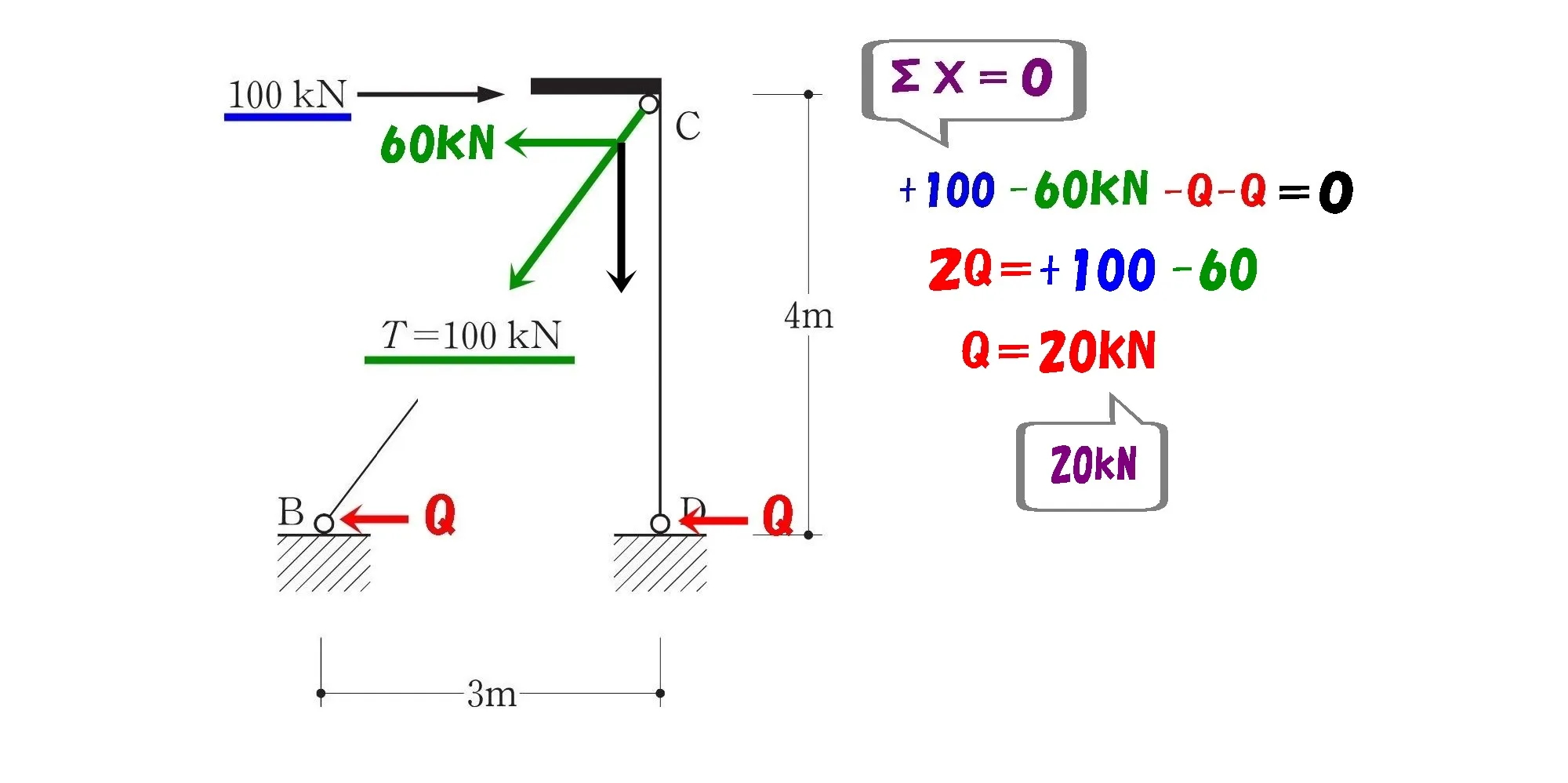

$$\Sigma X=0より,+100-60-Q-Q=0$$$$2Q=40⇨Q=20kN$$
4.せん断力×距離により、モーメントを求める
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
せん断力=20kN
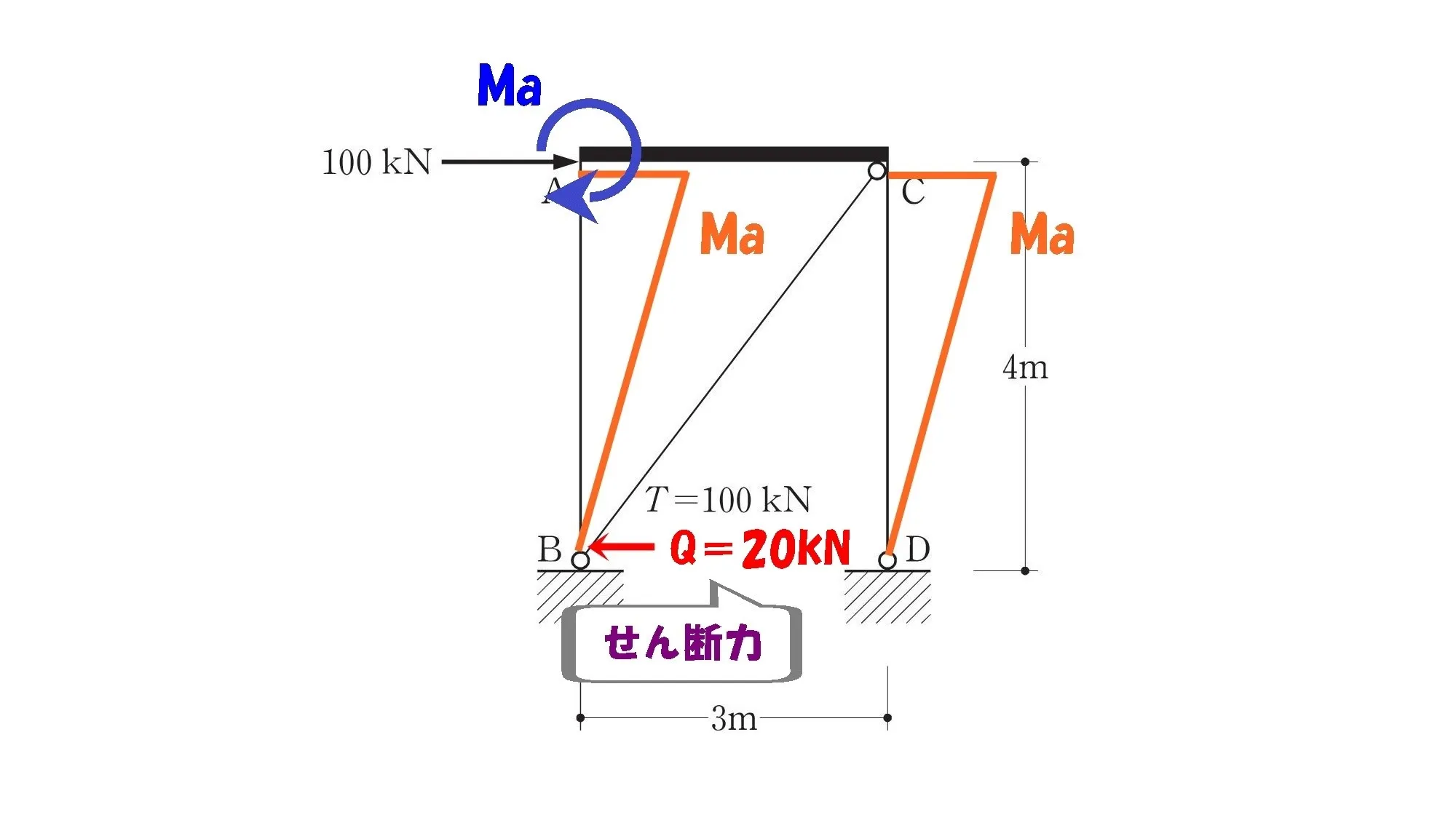

モーメント=力×距離
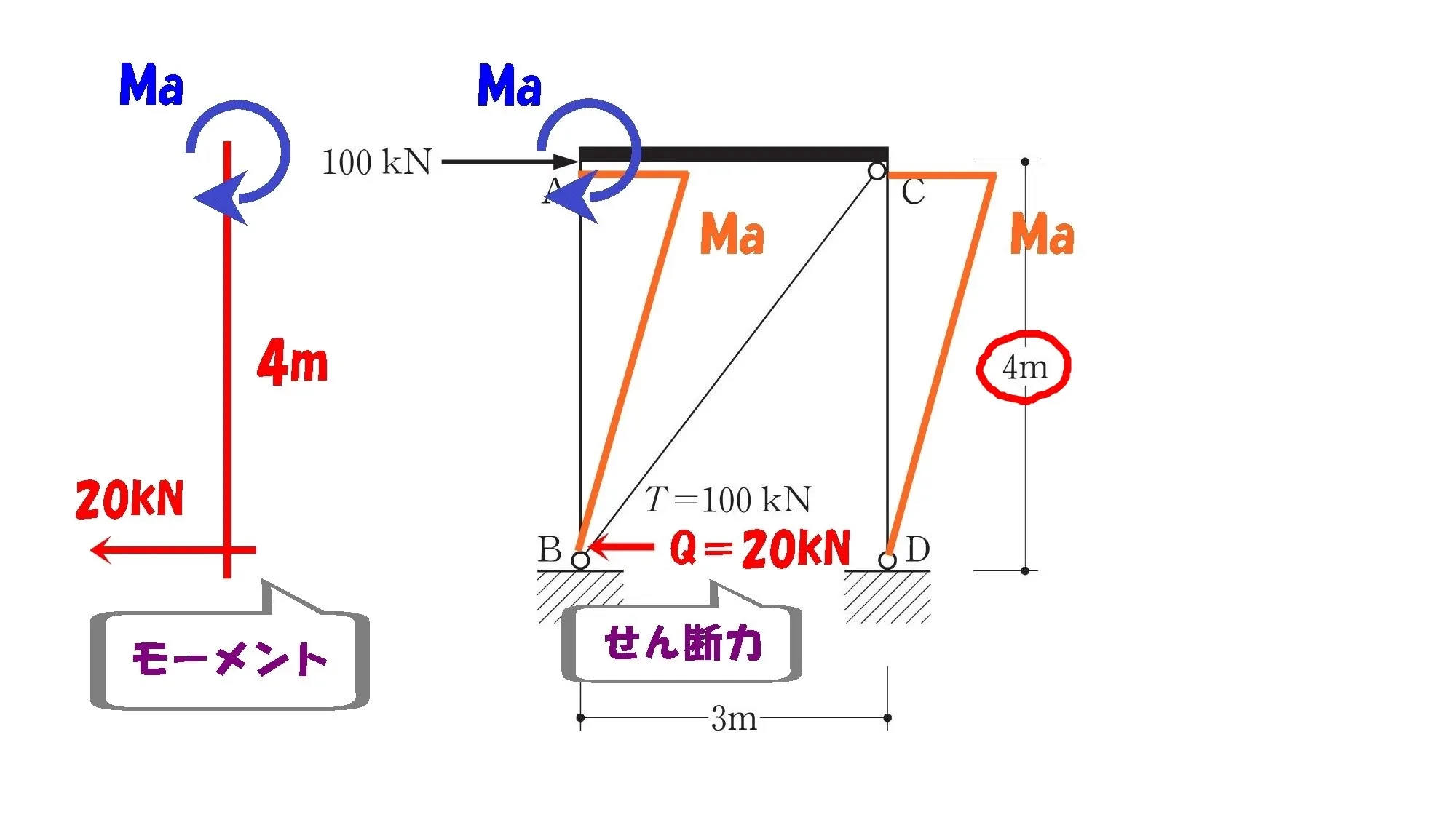

$$「モーメント=力×距離」$$$$「力」=20kN、「距離」=4m$$
A点のモーメントを求める
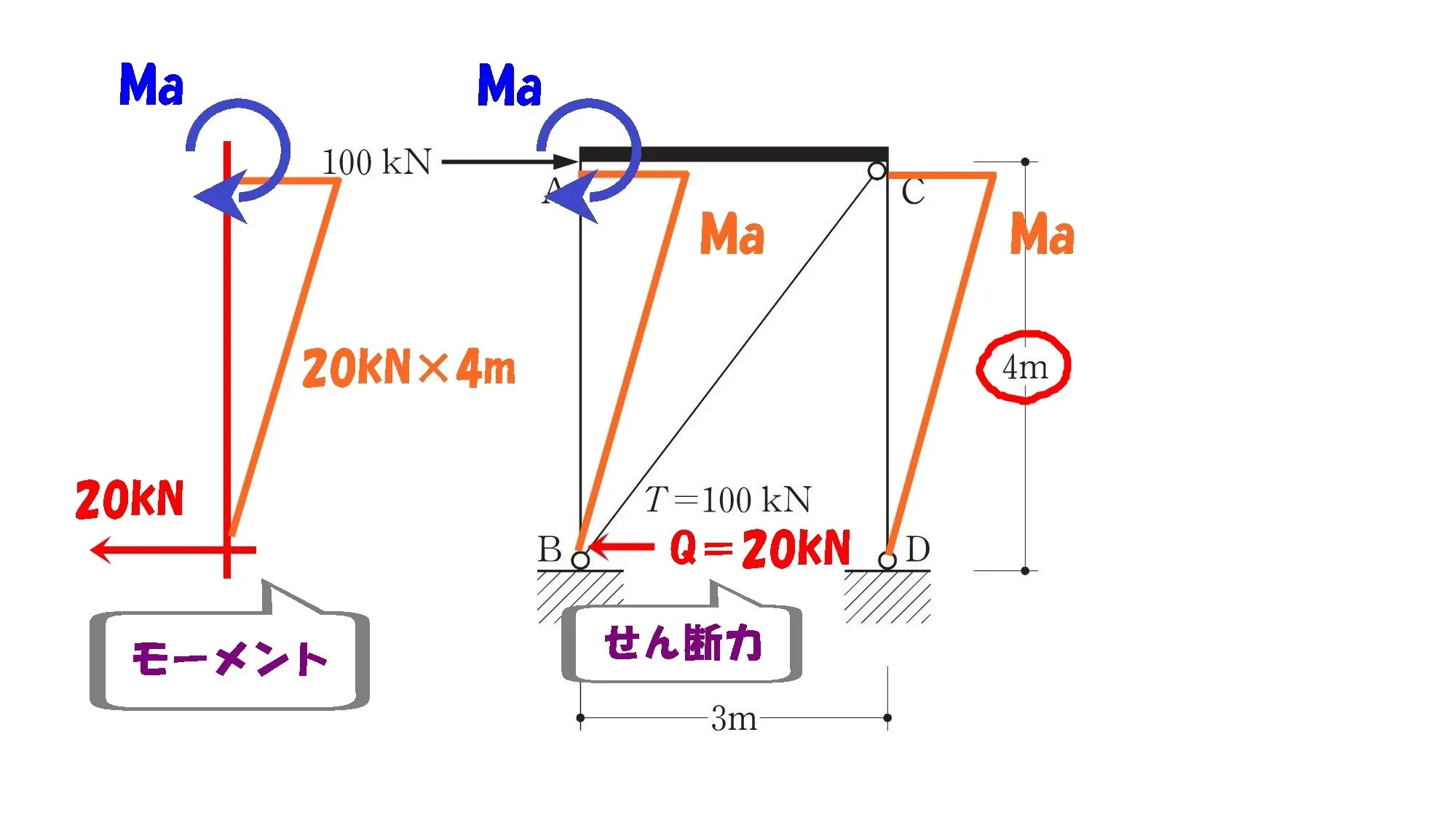

$$モーメントA=20kN*4m=80kN.m$$
答え.4


攻略ポイント
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める
座屈荷重
難易度:★★☆☆☆
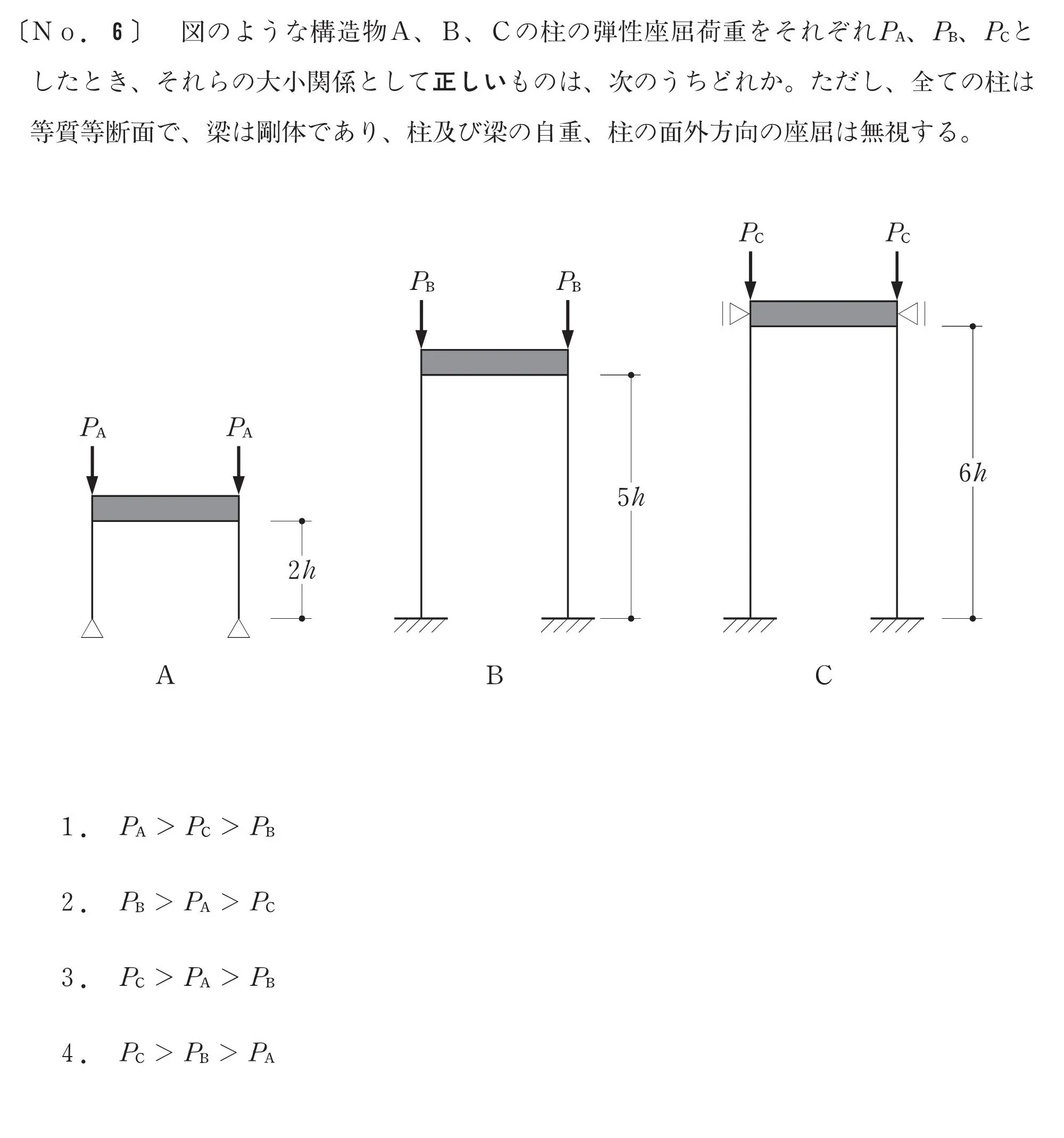
柱の支持条件の違いによる、弾性座屈荷重の比較問題です。
ポイントは「座屈長さ」を求めた後に、弾性座屈荷重の大小関係を求めるところにあります。
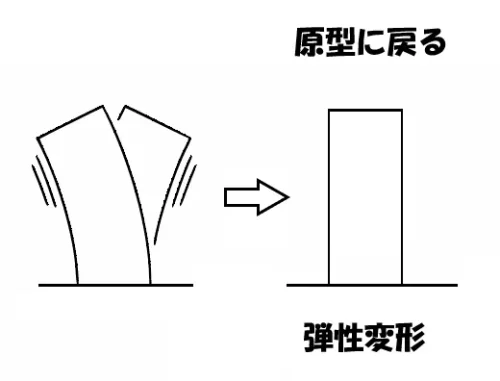
弾性座屈とは?
弾性イメージ




- 建物+外力→建物が変形する。
- 建物-外力(外力を取り除く)→建物が原形に戻る状態。
建物に及ぼす外力を取り除いたときに、建物が原形に戻る性質を「弾性」といいます。
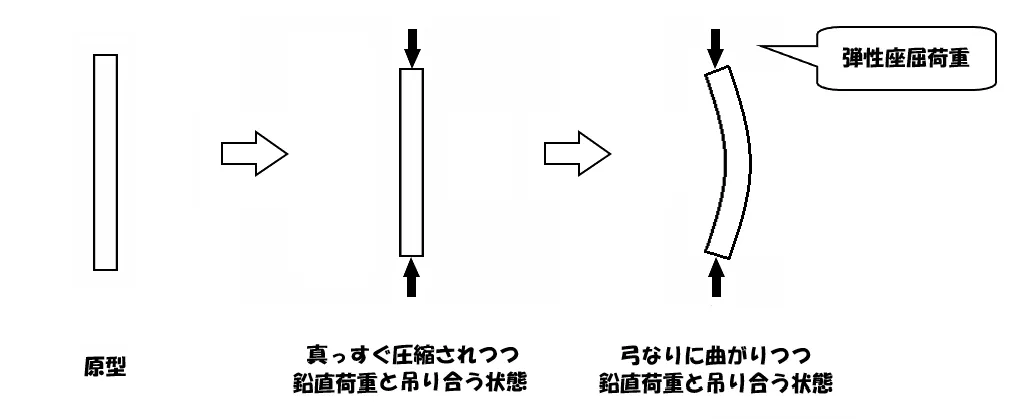

柱部材に鉛直荷重が加わり、その力が増すことで柱は弓なりに曲がり始めます。
弓なりに曲がる柱が「弾性」状態を保ちつつ、鉛直荷重と吊り合う状態を「弾性座屈」と呼ぶのです。
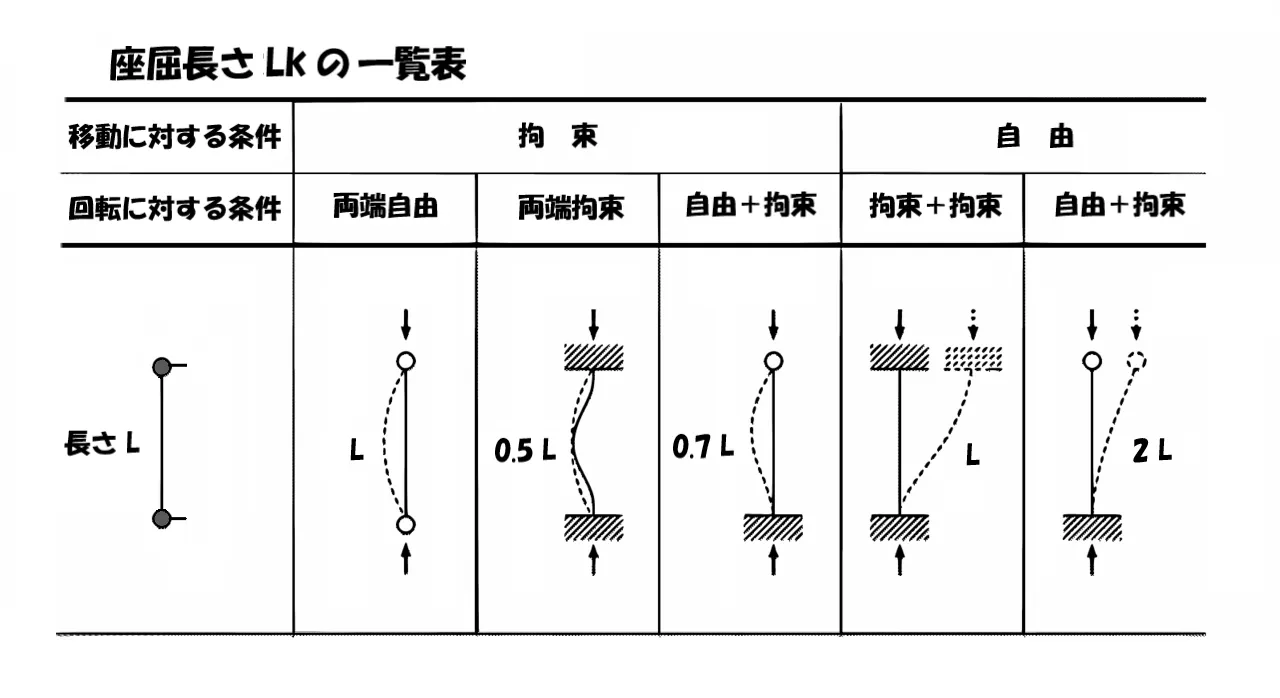
覚えておくべきもの



この動画を YouTube で視聴
攻略ポイント
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める
問題

1.弾性座屈荷重に比例するもの、反比例するものを把握する
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める
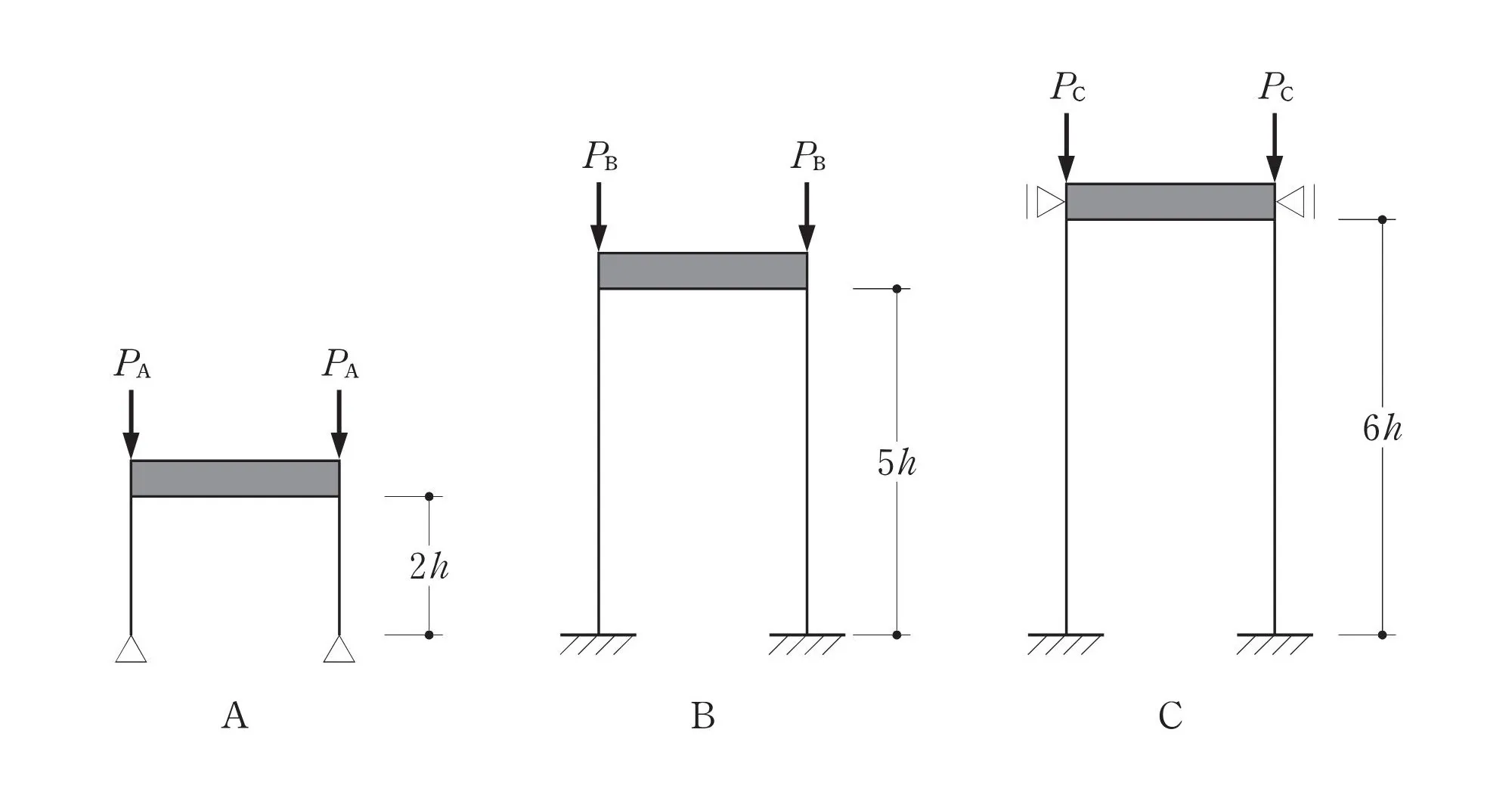

柱梁の支持条件
| A | B | C | |
|---|---|---|---|
| 梁 | 自由 | 自由 | 拘束 |
| 柱脚 | 拘束(ピン) | 拘束(固定) | 拘束(固定) |
問題文を読み取る
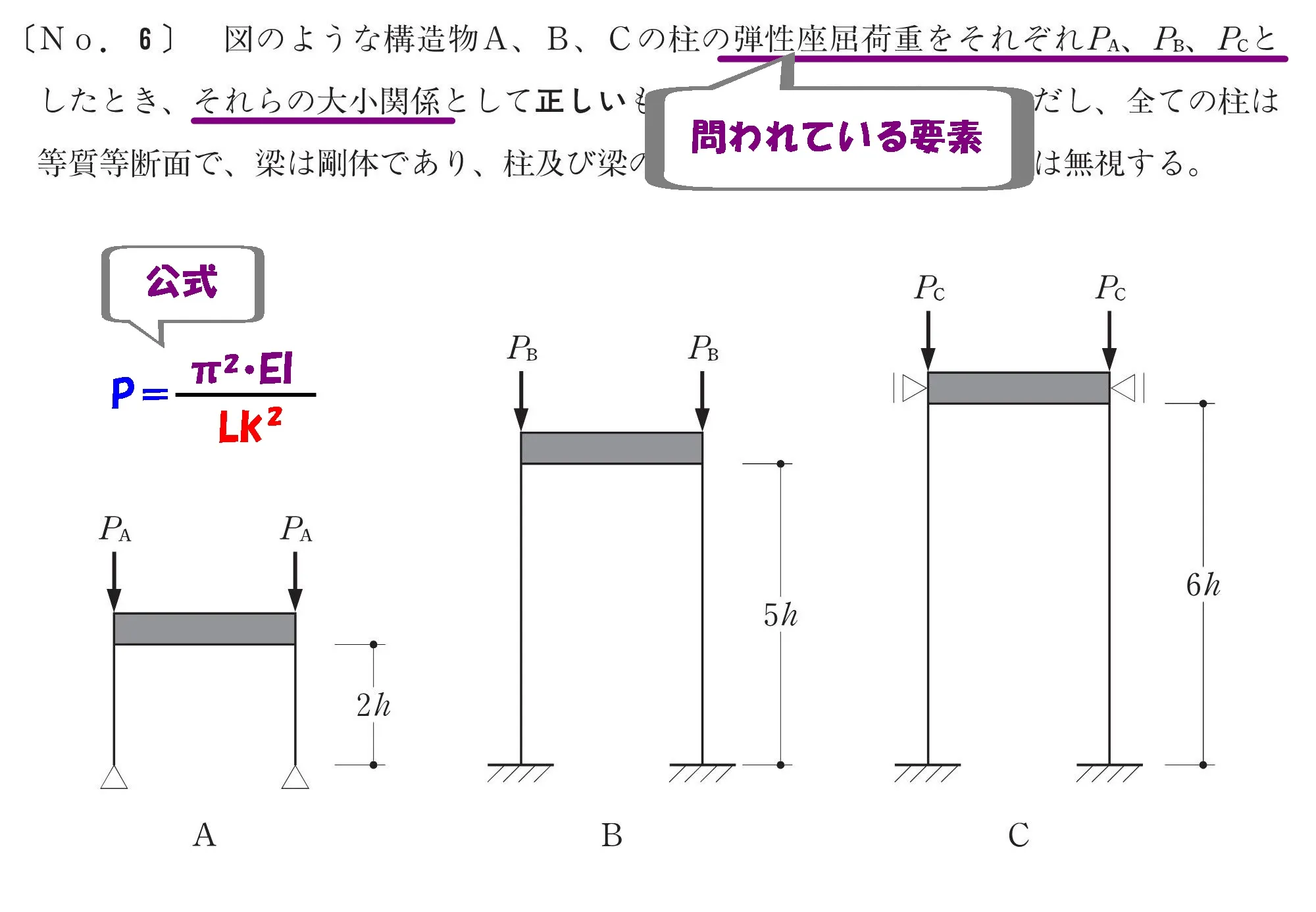

$$[弾性座屈荷重の公式]$$$$P=\frac{ \pi^2*EI }{ Lk^2 }$$
比例、反比例の関係
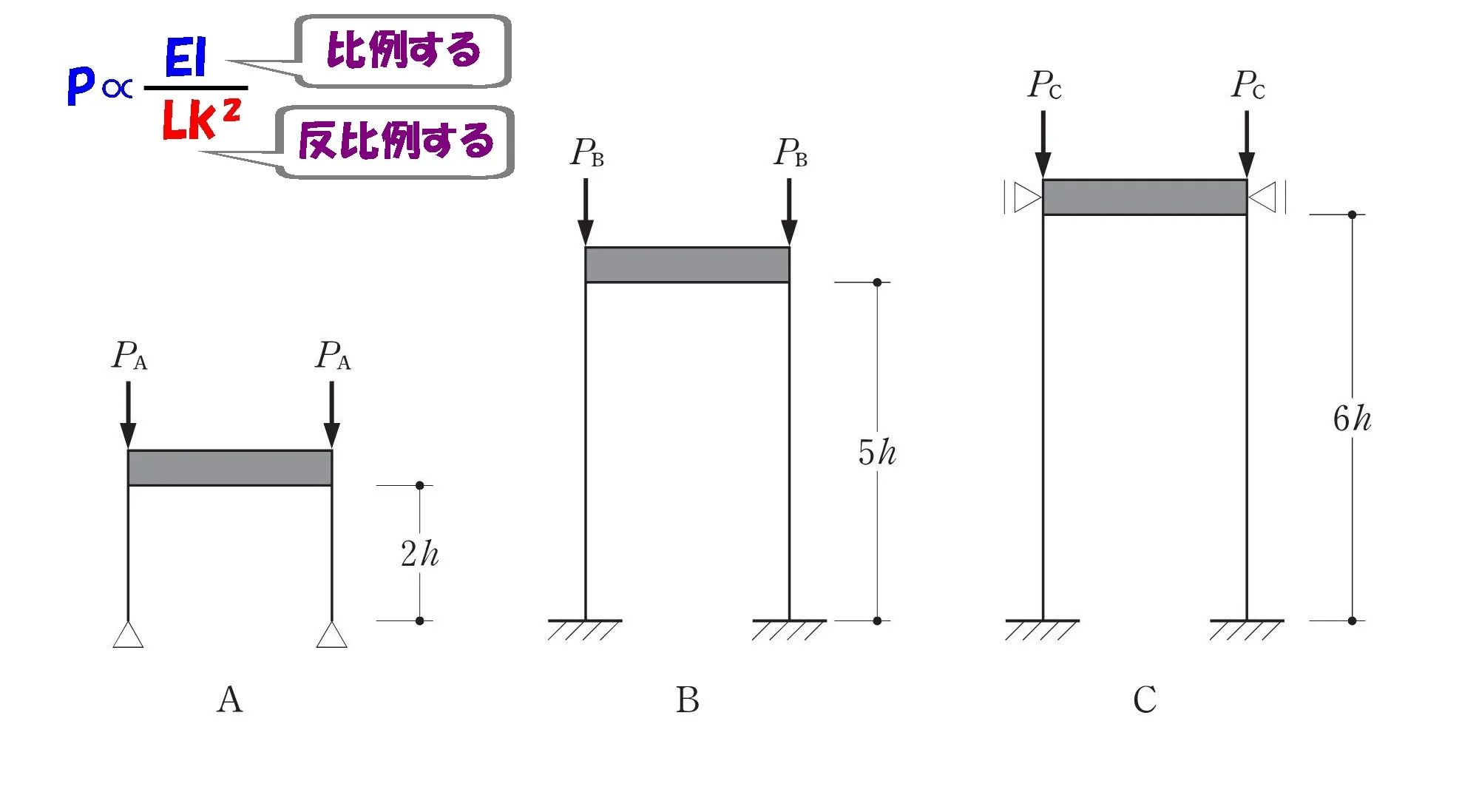

$$P\propto\frac{ EI }{ Lk^2 }$$$$弾性座屈荷重Pは曲げ剛性EIに比例し、座屈長さLkの2乗に反比例する。$$
全ての柱は等質等断面
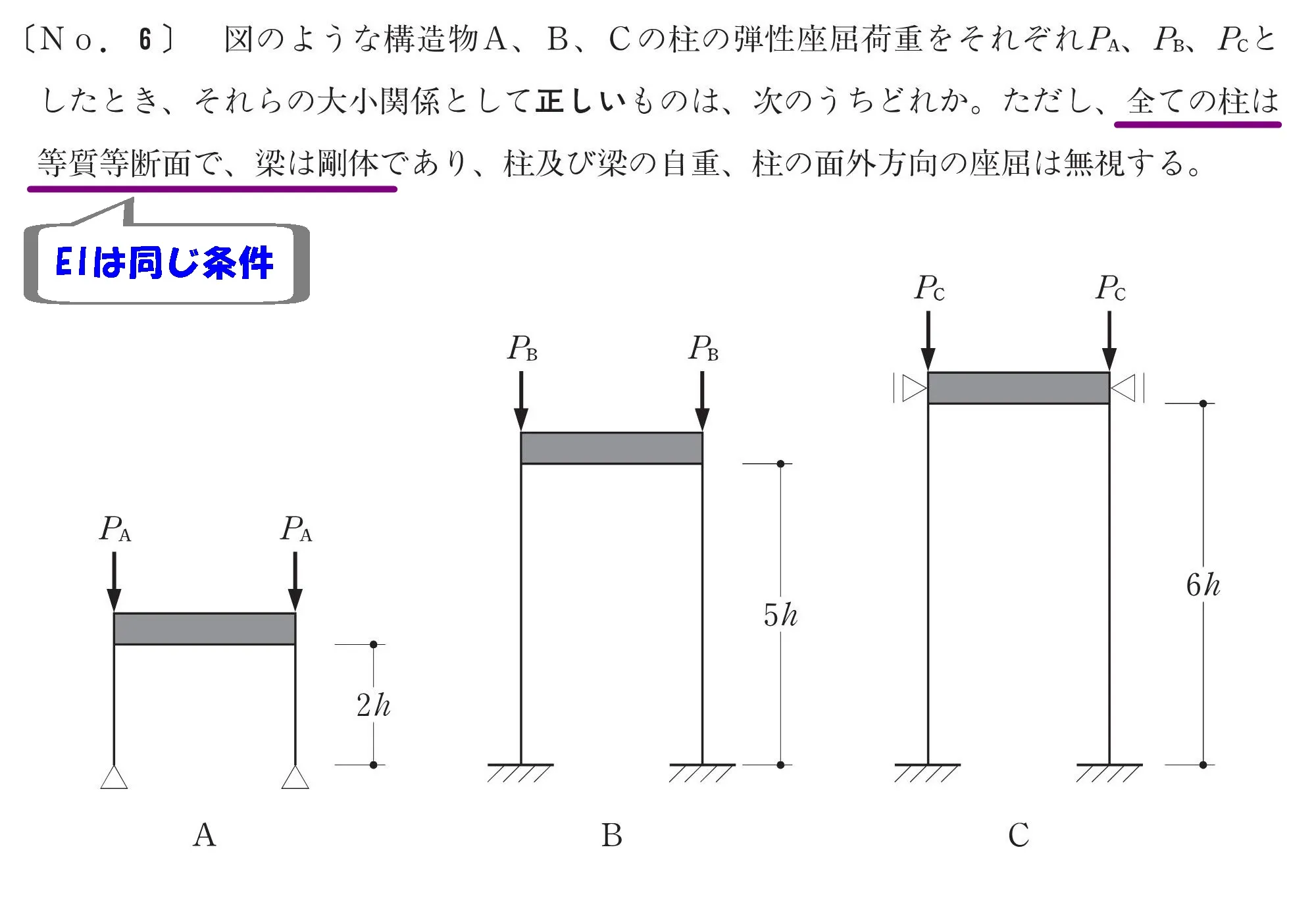

全ての柱は「等質」「等断面」
- 等質:ヤング係数Eが同じ
- 等断面:断面二次モーメントIが同じ
- 等質等断面:曲げ剛性EIが同じ



条件が同じものは
公式から省いていこう。
PはLkの2乗に反比例する
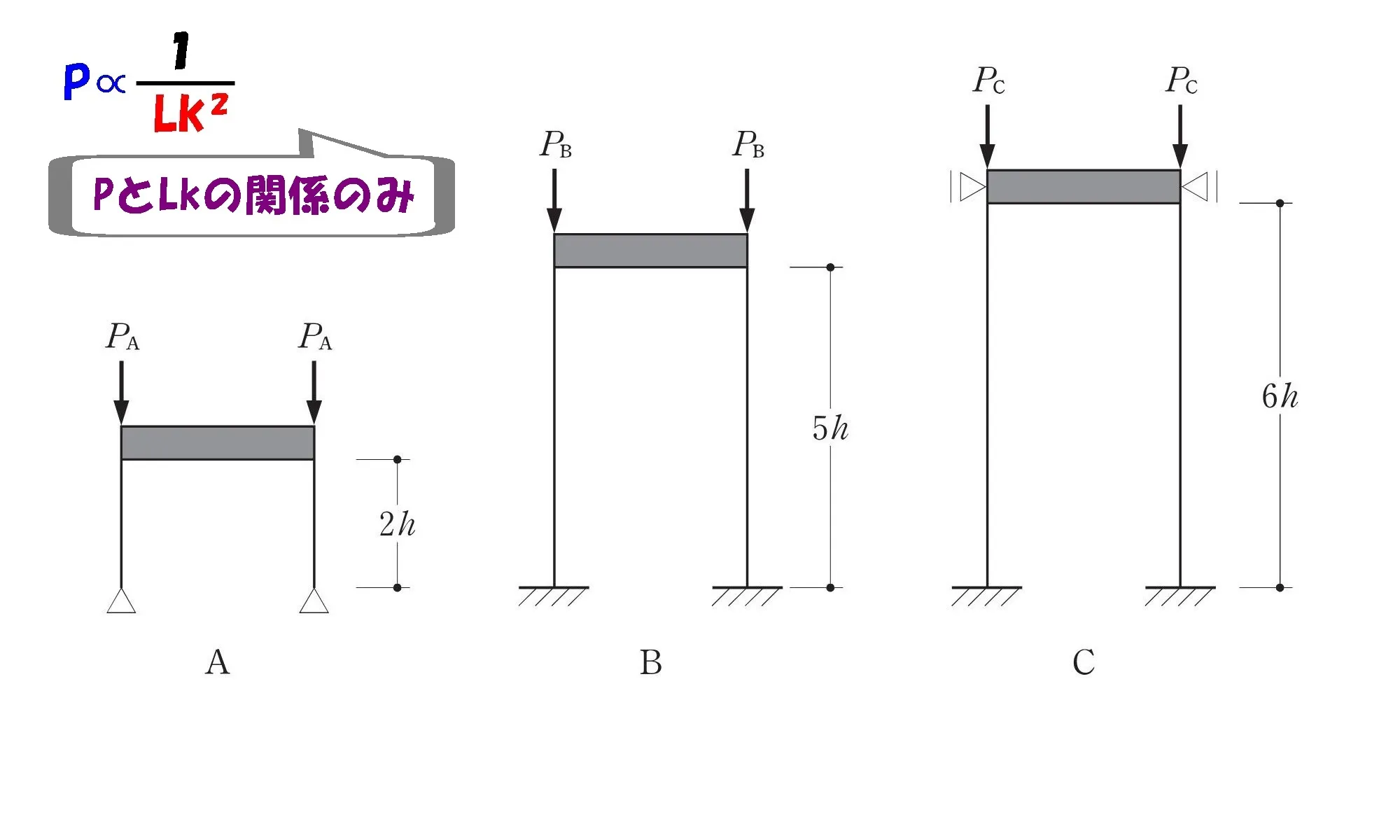

$$P\propto\frac{ EI }{ Lk^2 }$$
$$EIが同じ条件であることから,P\propto\frac{ 1 }{ Lk^2 }$$
$$弾性座屈荷重Pは、座屈長さLkの2乗に反比例する。$$$$(Lkは部材の支持条件により異なる)$$
柱梁の支持条件
| A | B | C | |
|---|---|---|---|
| 梁 | 自由 | 自由 | 拘束 |
| 柱脚 | 拘束(ピン) | 拘束(固定) | 拘束(固定) |
2.柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める
柱の曲がり図を描く
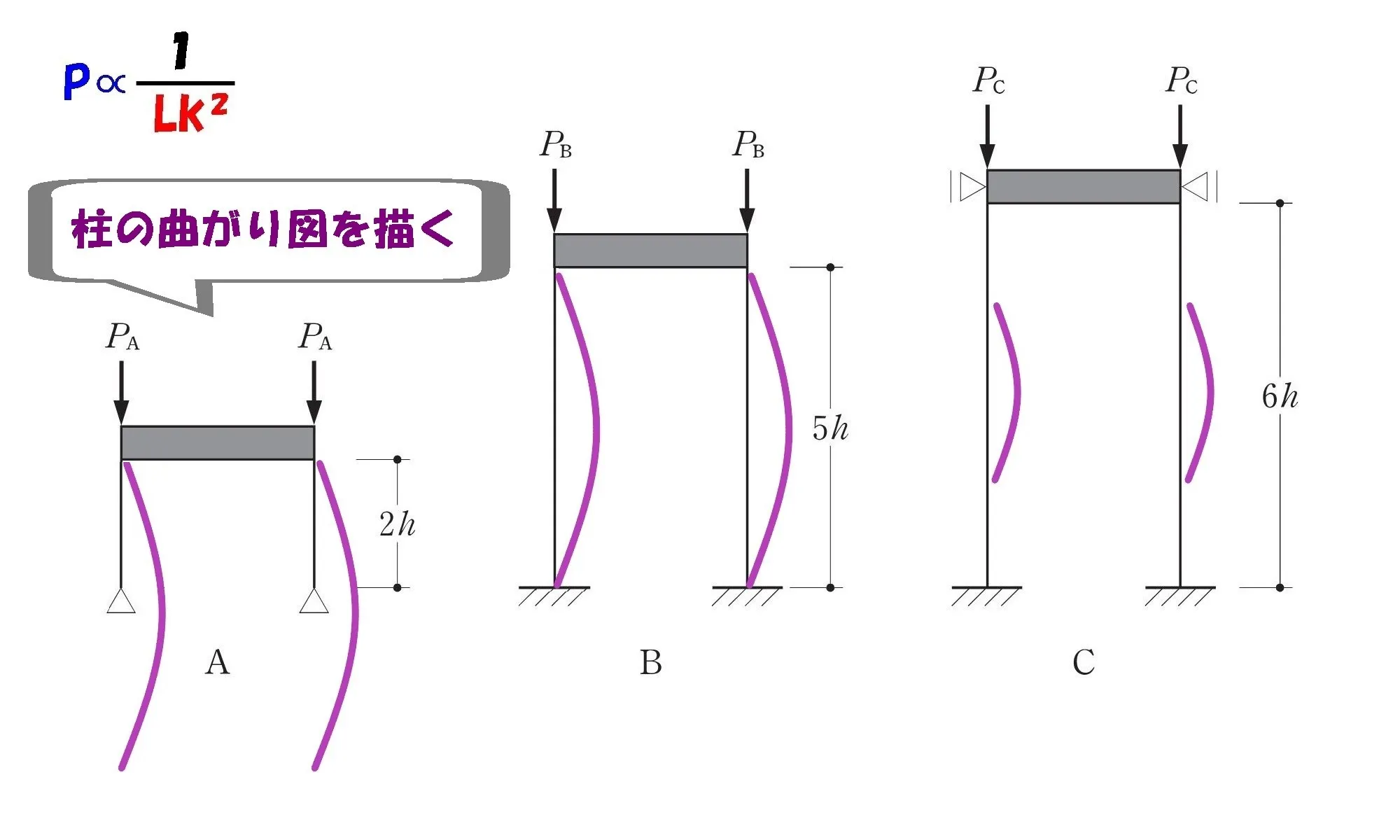

柱の曲がり
| A | B | C | |
|---|---|---|---|
| 梁 | 自由 | 自由 | 拘束 |
| 柱脚 | 拘束(ピン) | 拘束(固定) | 拘束(固定) |
| 曲がり | 柱の長さより 大きく曲がる | 柱の長さと 同じだけ曲がる | 柱の真ん中の 部分だけ曲がる |
座屈長さの係数を書き込む
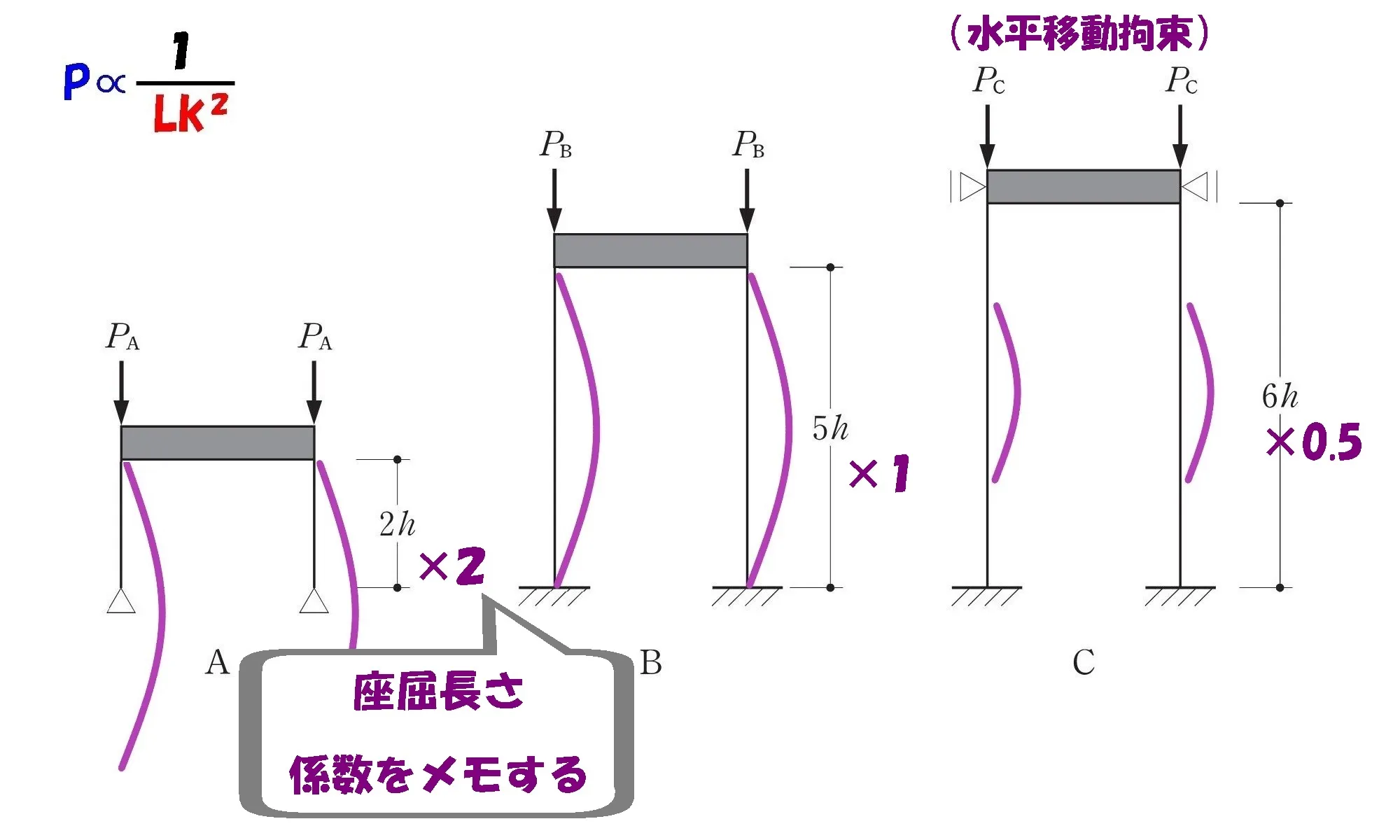

柱の支持条件の違いにより、部材の長さに掛ける係数は異なります。
その係数は覚えておき、問題図の柱の長さの表記「2h・5h・6h」のとなりに書き込みましょう。
係数
| A | B | C | |
|---|---|---|---|
| 梁 | 自由 | 自由 | 拘束 |
| 柱脚 | 拘束(ピン) | 拘束(固定) | 拘束(固定) |
| 係数 | ×2 | ×1 | ×0.5 |



条件と数値は
その都度、覚えていこう。
参考


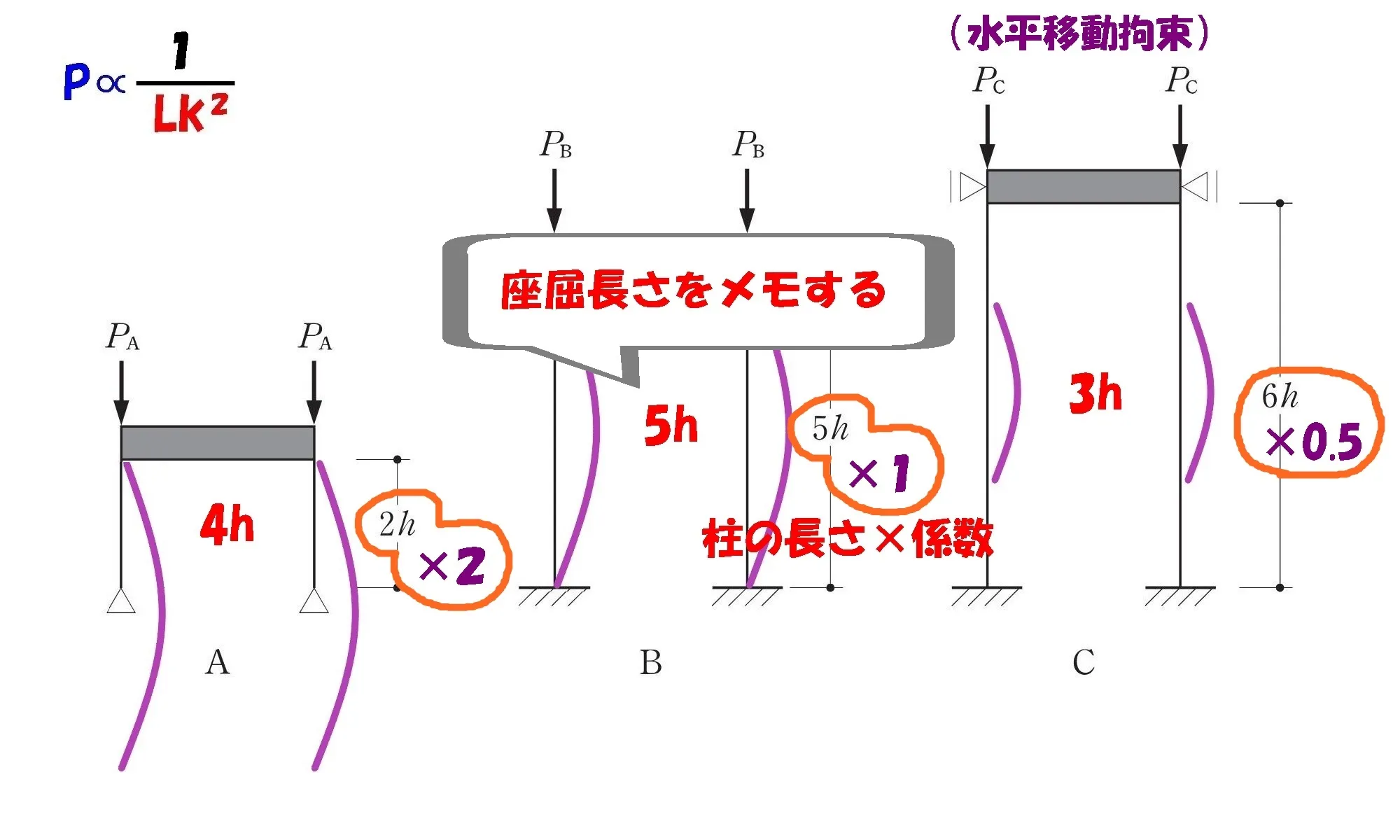
座屈長さをメモする

公式
$$柱の座屈長さ=柱の長さ×係数$$
- $$Lka=2h*2=4h$$
- $$Lkb=5h*1=5h$$
- $$Lkc=6h*0.5=3h$$
計算した座屈長さLka・Lkb・Lkcを問題図に書き込む。
3.柱の座屈長さより、弾性座屈荷重の大小関係を求める
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める
数値の大きさ順に並べる
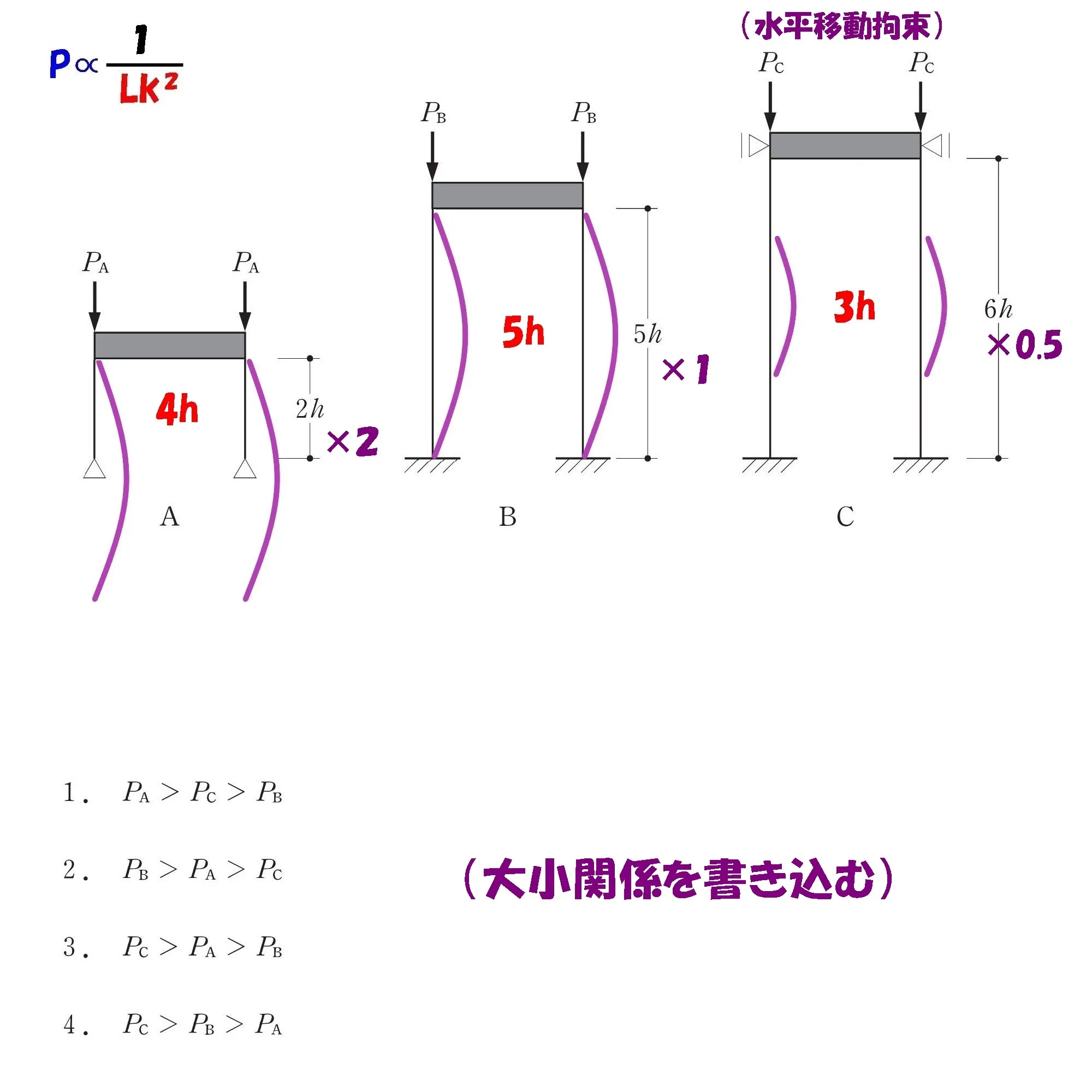

$$P\propto\frac{ 1 }{ Lk^2 }より,$$
$$弾性座屈荷重Pは、座屈長さLkの2乗に反比例する。$$
$$(Pの大小関係とLkの大小関係は逆になる)$$



答えを導くときに
ここは間違えやすい!
不等号を書く
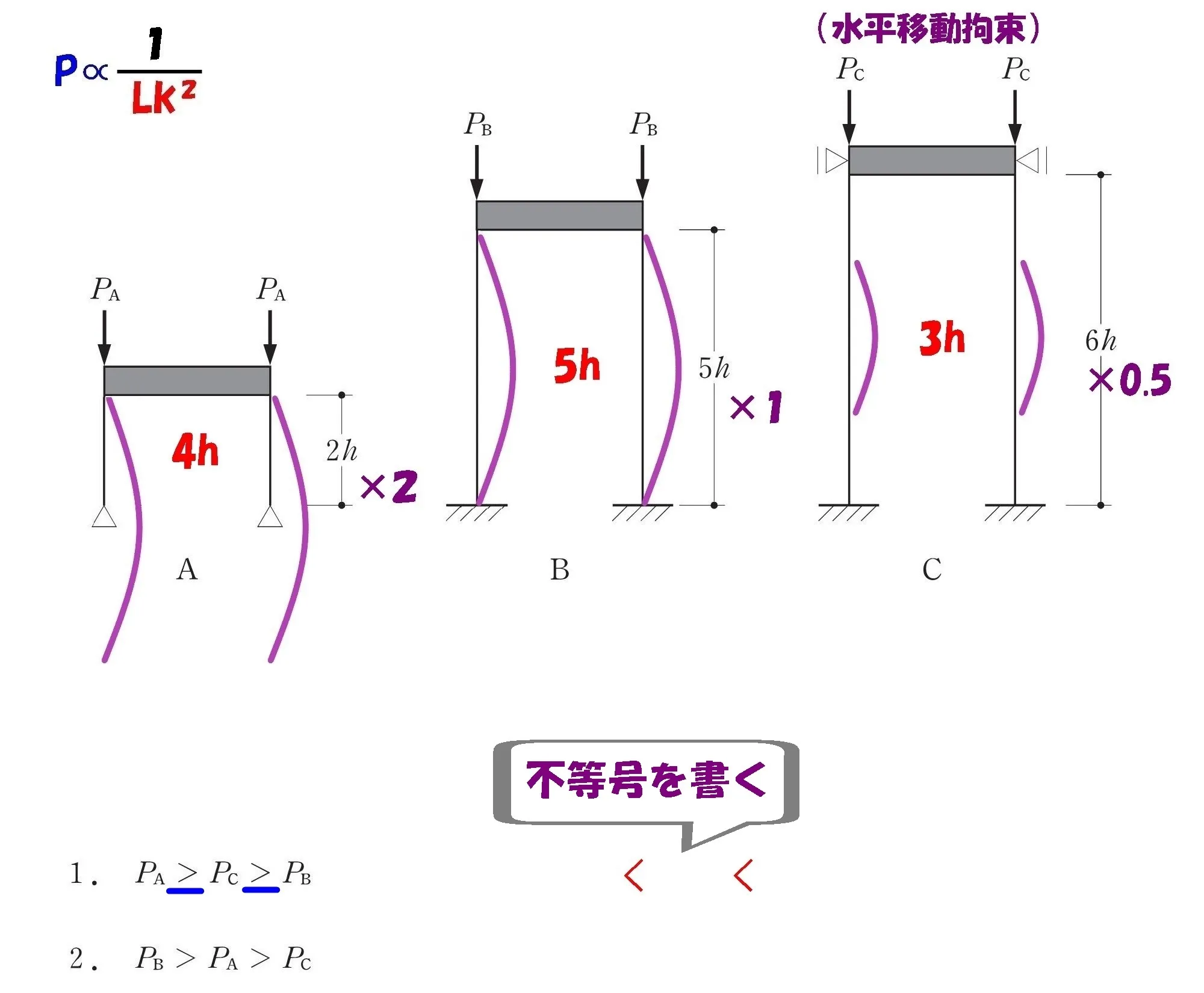

注意点
Pの大小関係とLkの大小関係は逆になる。
これを踏まえて、解答の不等号「>」とは逆の「<」方向の不等号を書いておく。



PはLkに逆比例する。



不等号の向きも
解答とは逆にしておく。
数値を並べる
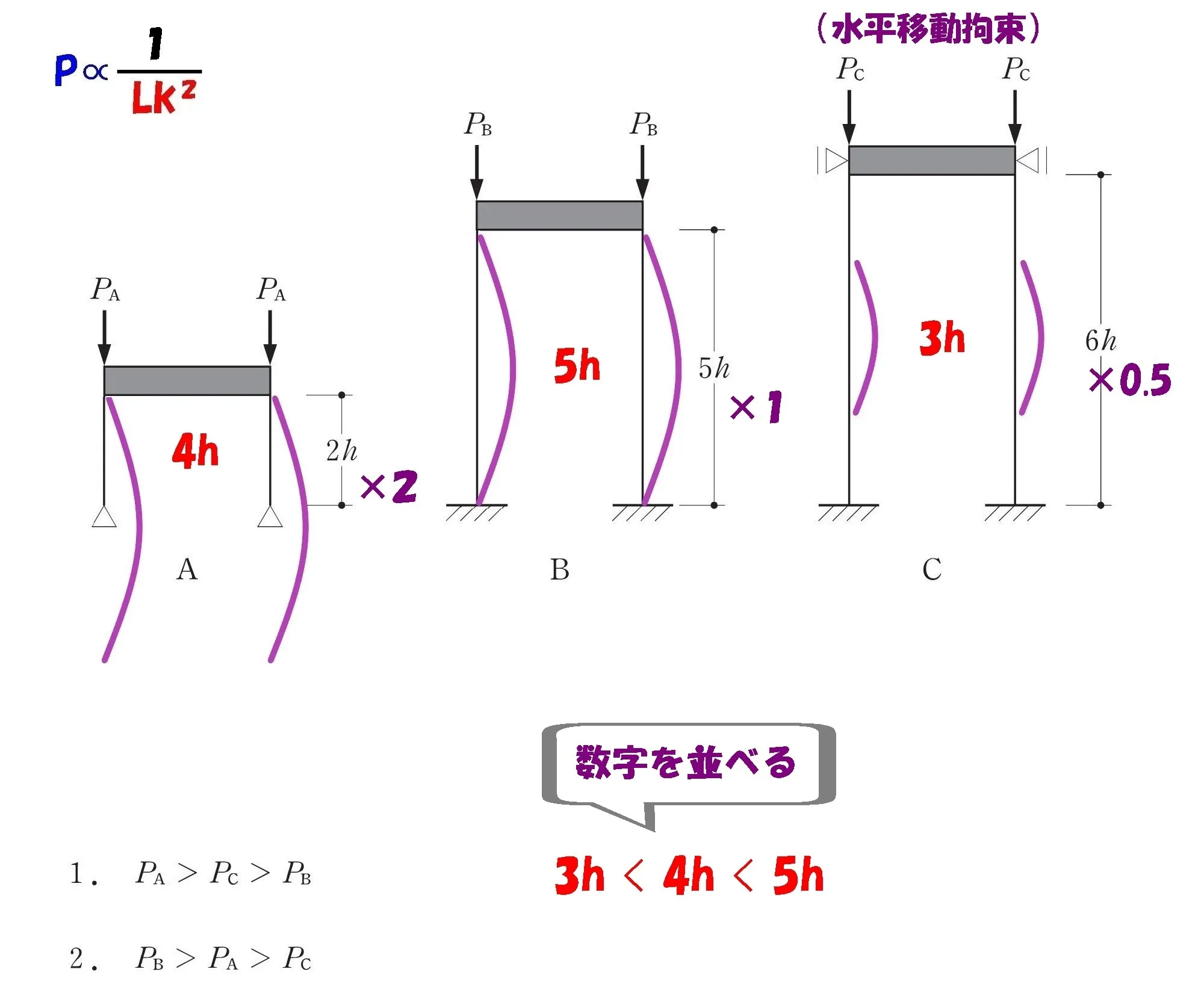

求めたABCのそれぞれの座屈長さの数値を「<」に習って並べましょう。
対応する選択肢を並べる
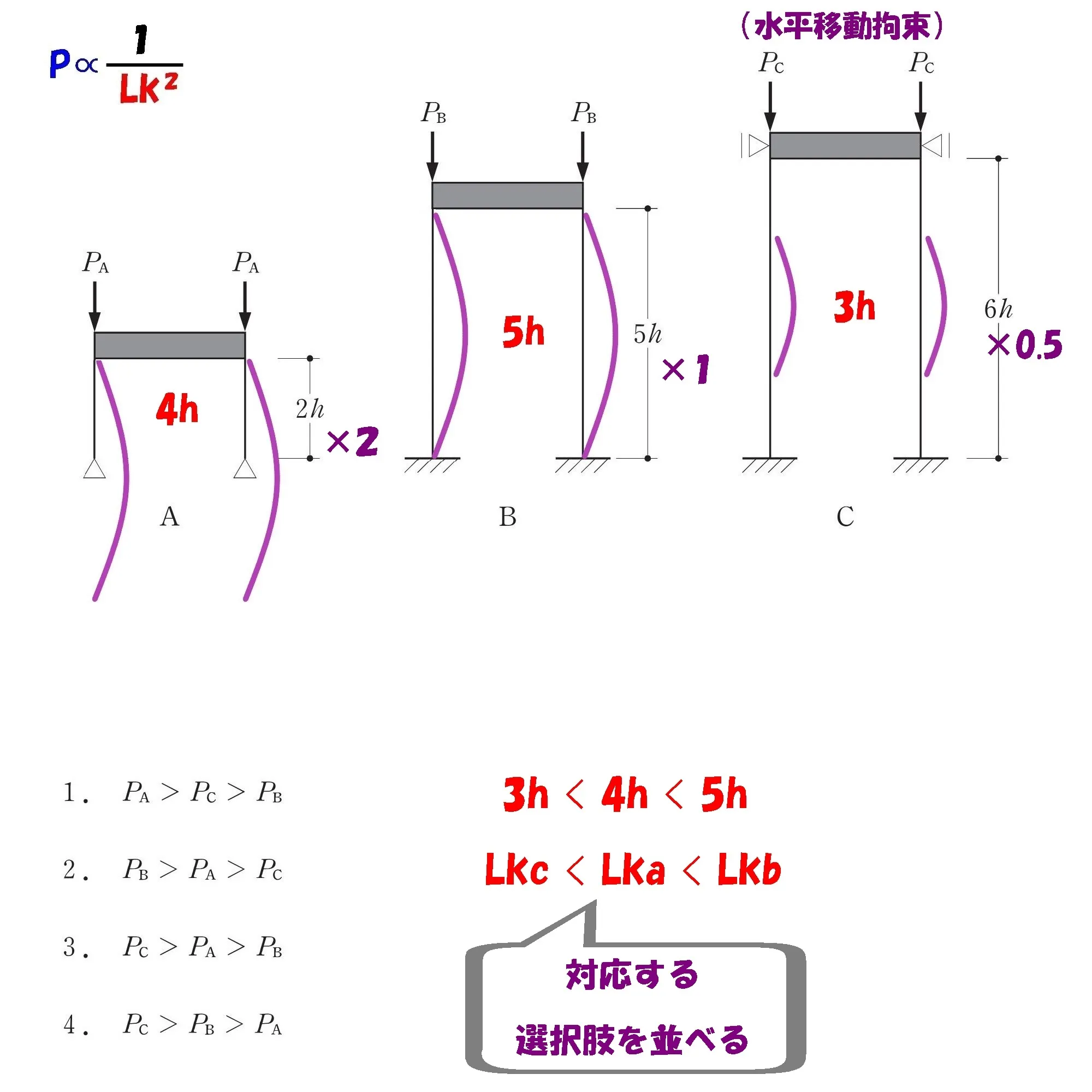

問題図を確認しながら、数値に対応したアルファベット「Lka・Lkb・Lkc」を書きましょう。



数値を並べて記号を書く
これが間違えない手法。
対応する選択肢を並べる
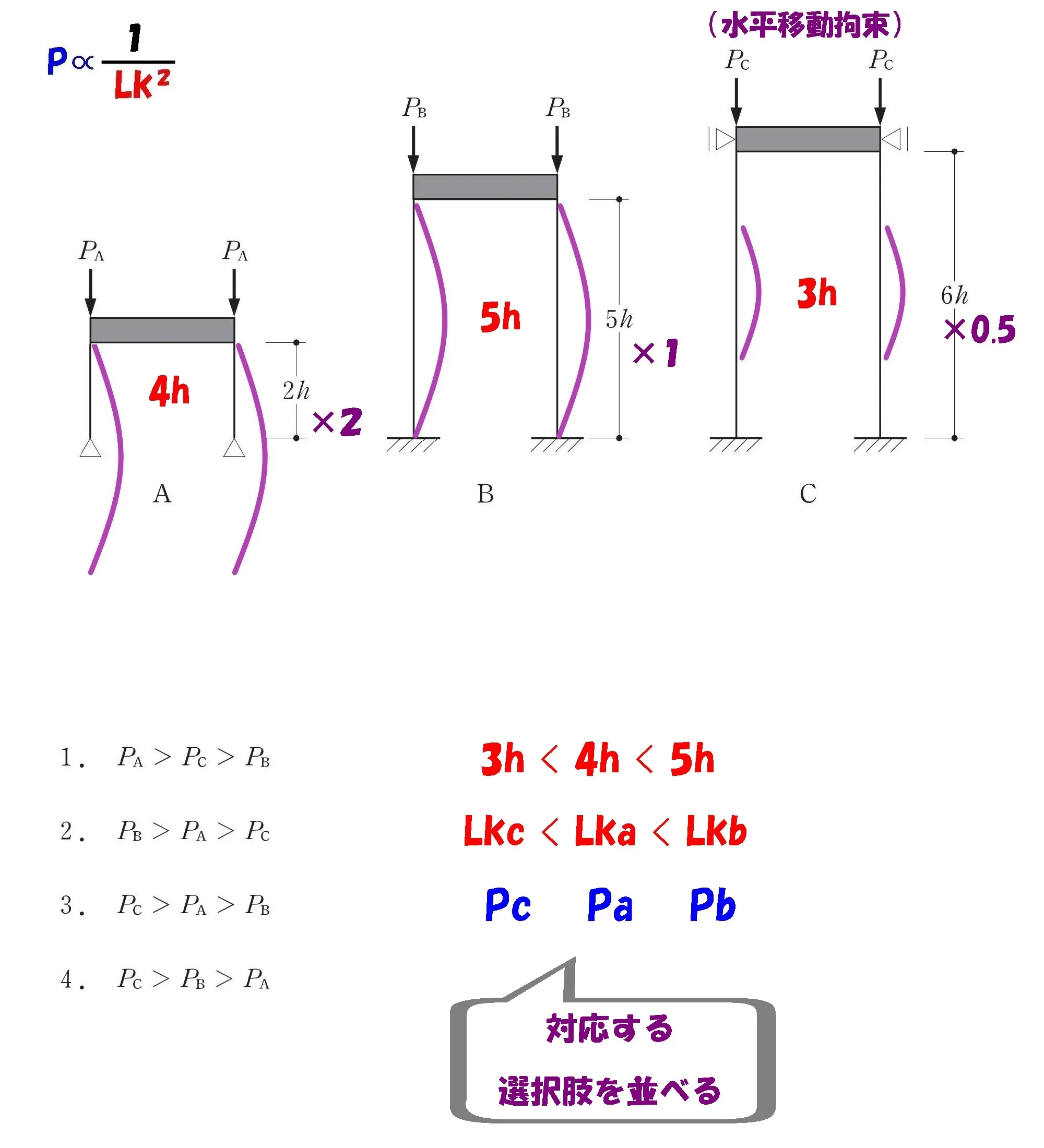

「Lka・Lkb・Lkc」に対応したアルファベット「Pa・Pb・Pc」を書きましょう。
不等号を逆向きに書き込む
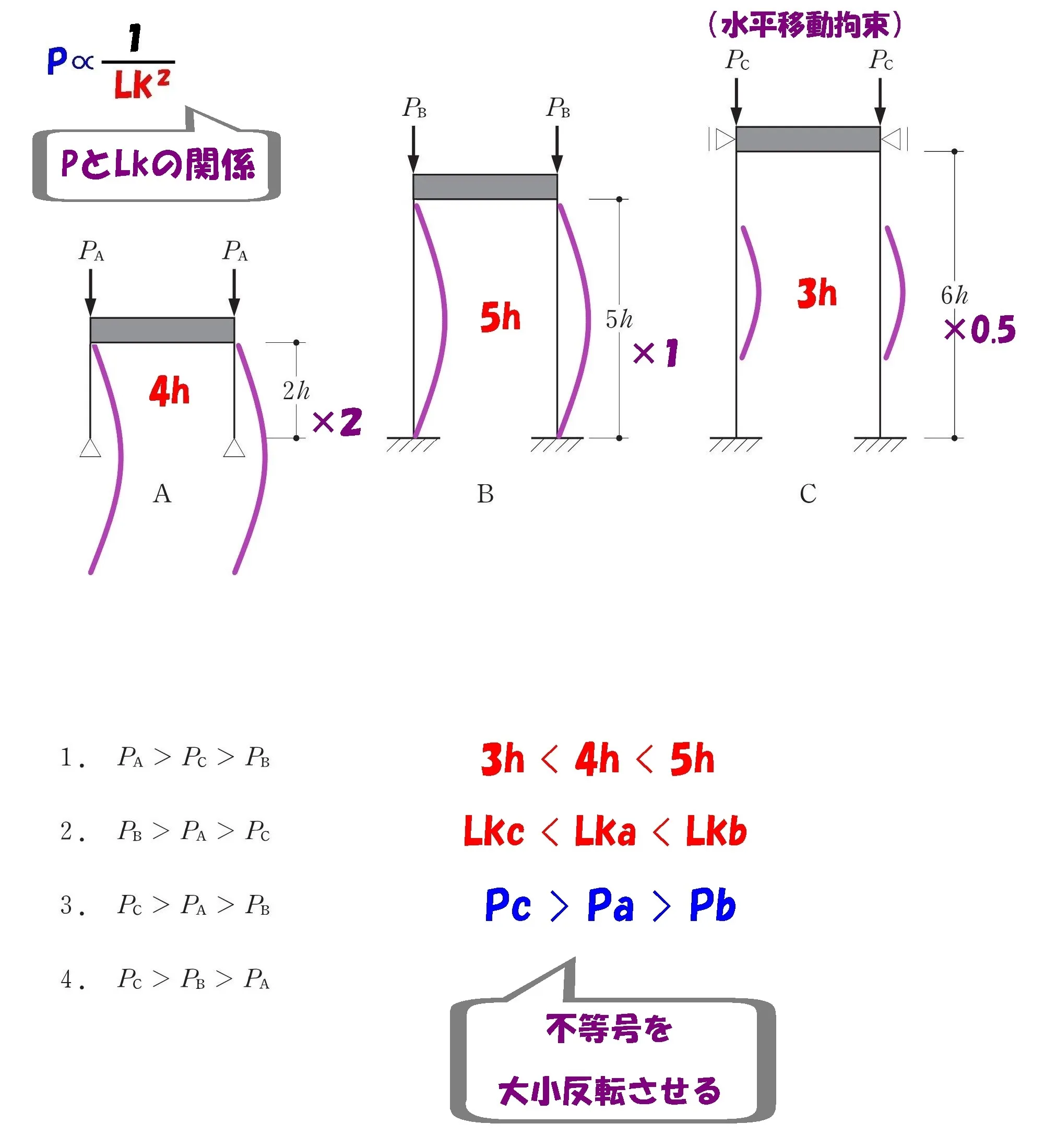

注意点
Pの大小関係とLkの大小関係は逆になる。
これを踏まえて、Lkの「<」の不等号とは逆向きの「>」の不等号を書き込む。
答え.3
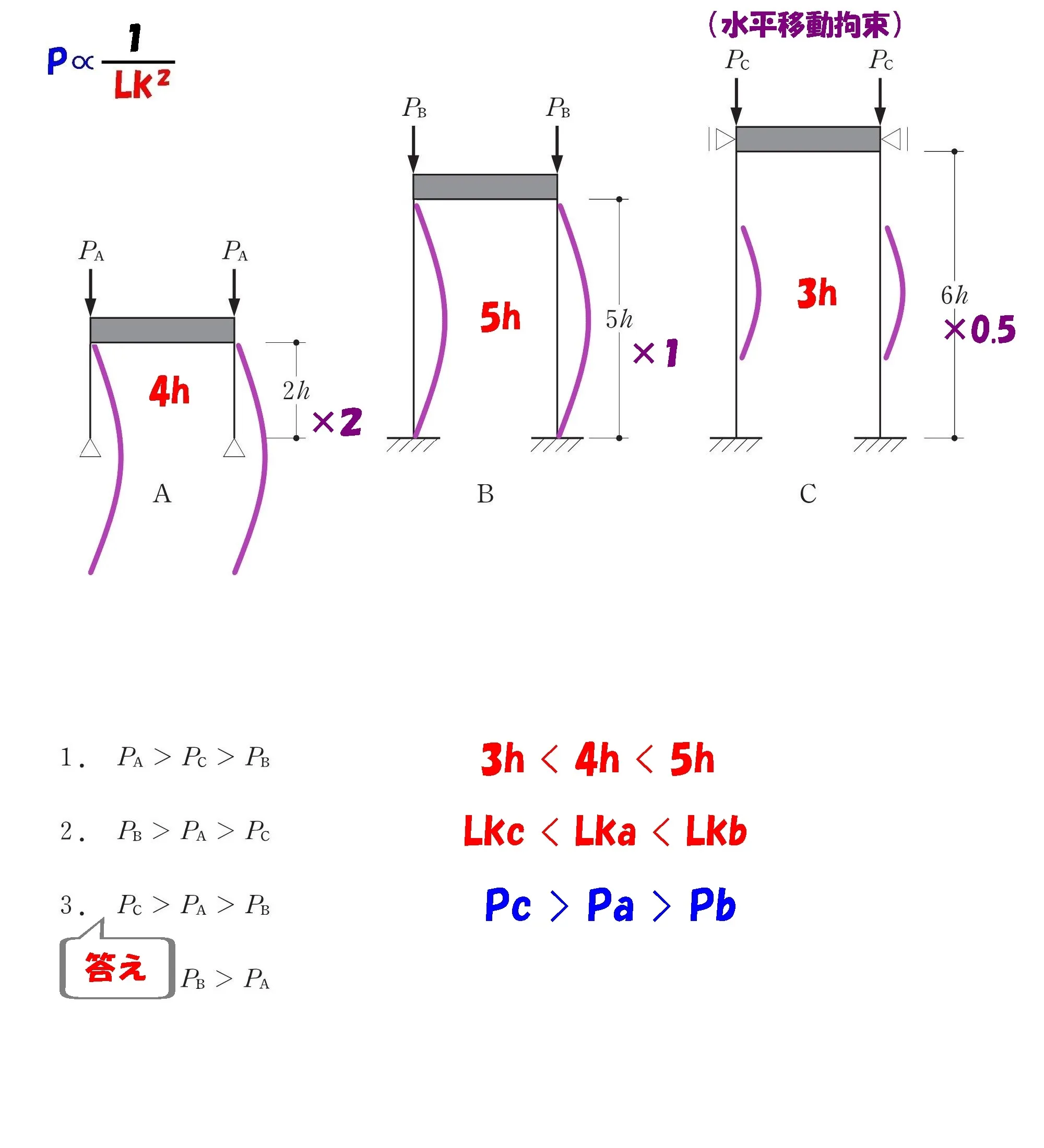

攻略ポイント
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める


この動画を YouTube で視聴
水平剛性
難易度:★★☆☆☆
水平剛性の違いによるせん断力の比較問題です。
せん断力を「部材の剛比で振り分ける」という考え方を身につけておきましょう。
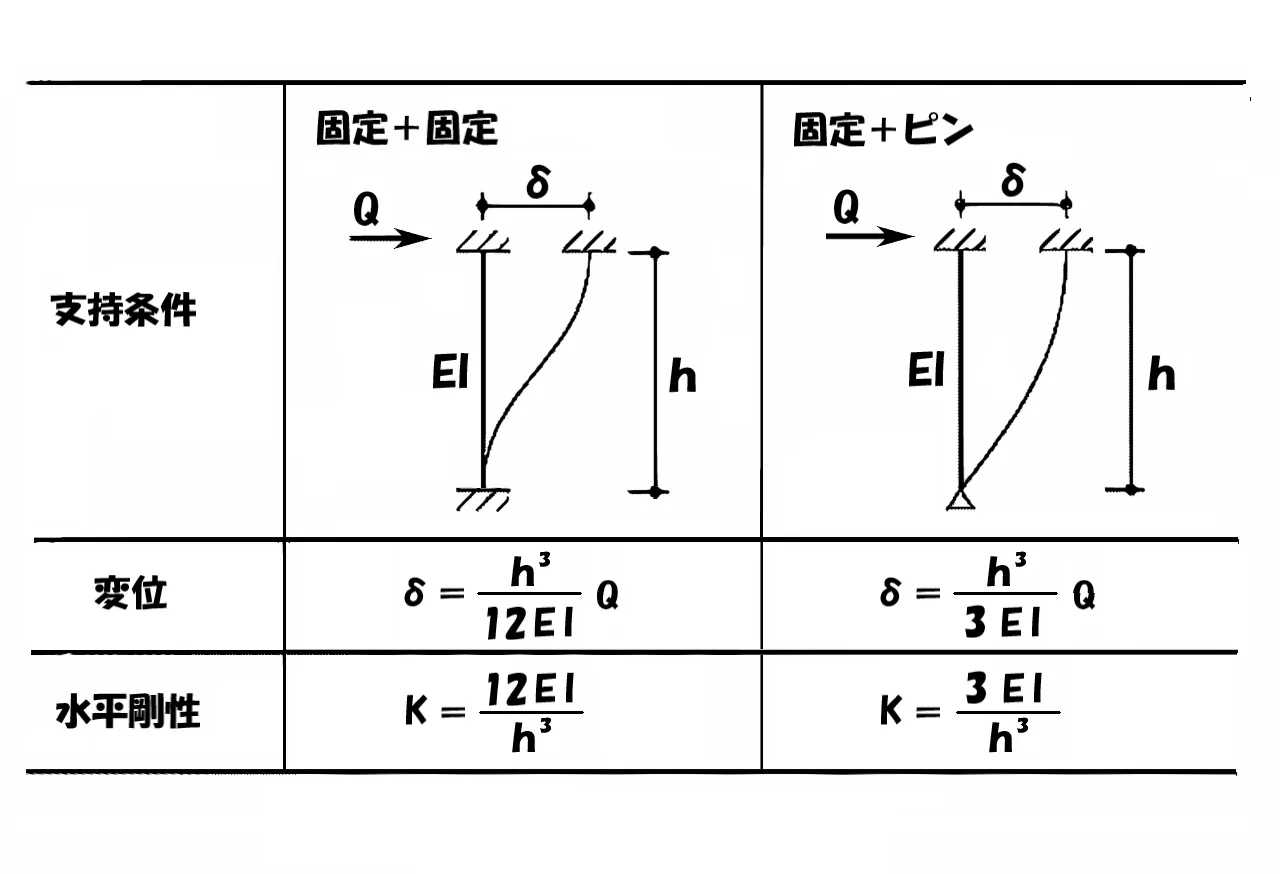
変位と水平剛性の公式

攻略ポイント
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める
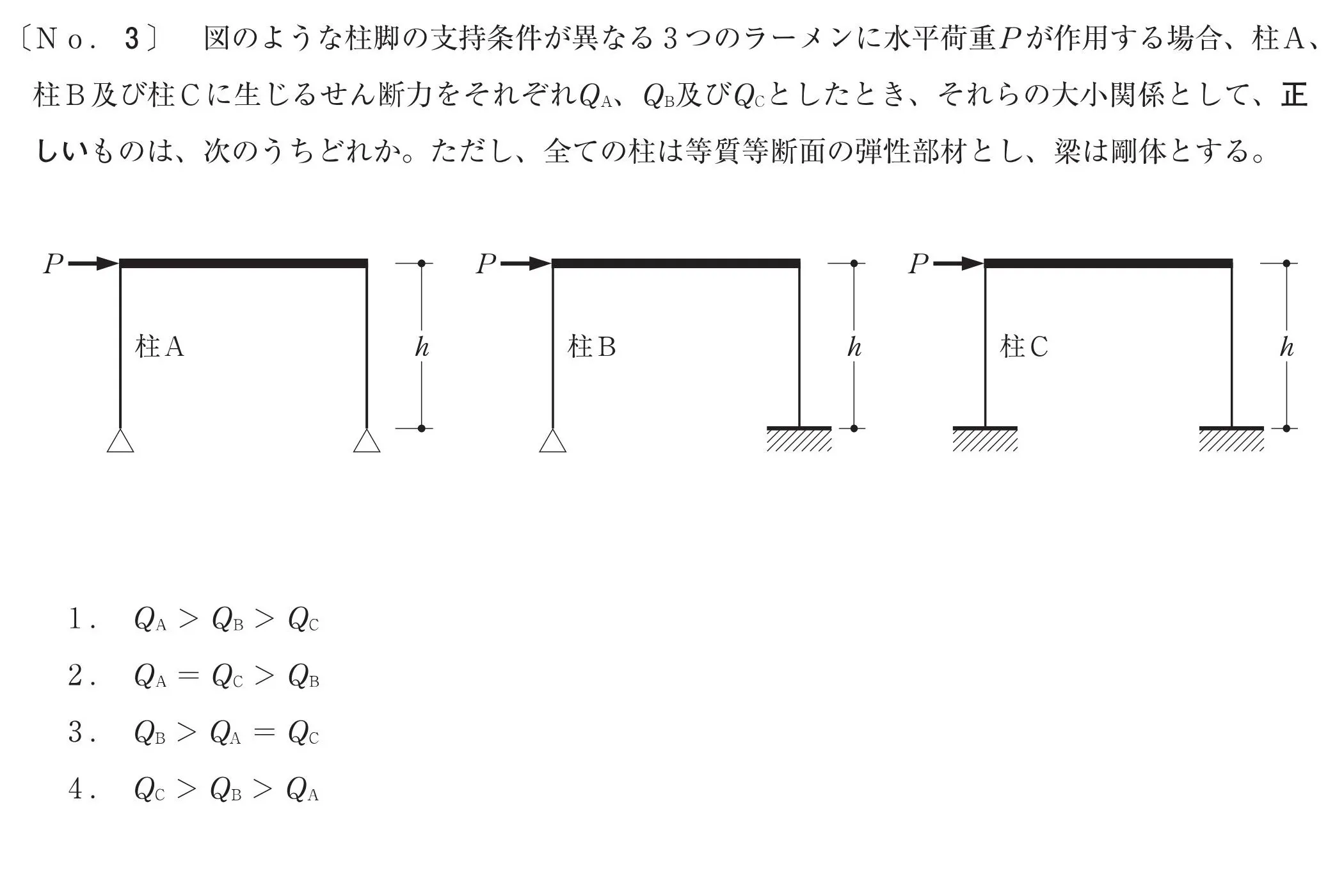
問題

1.せん断力に比例するもの、反比例するものを把握する
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める
問題文の読み取り
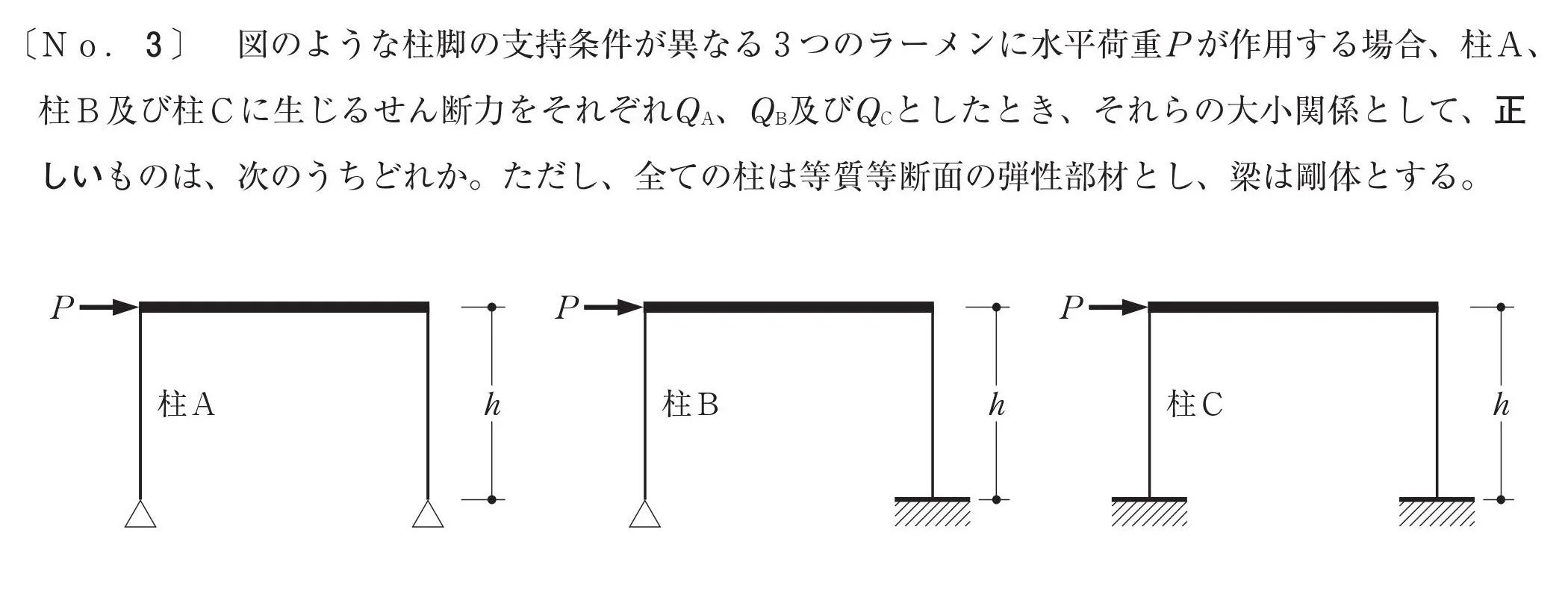

せん断力を比較する
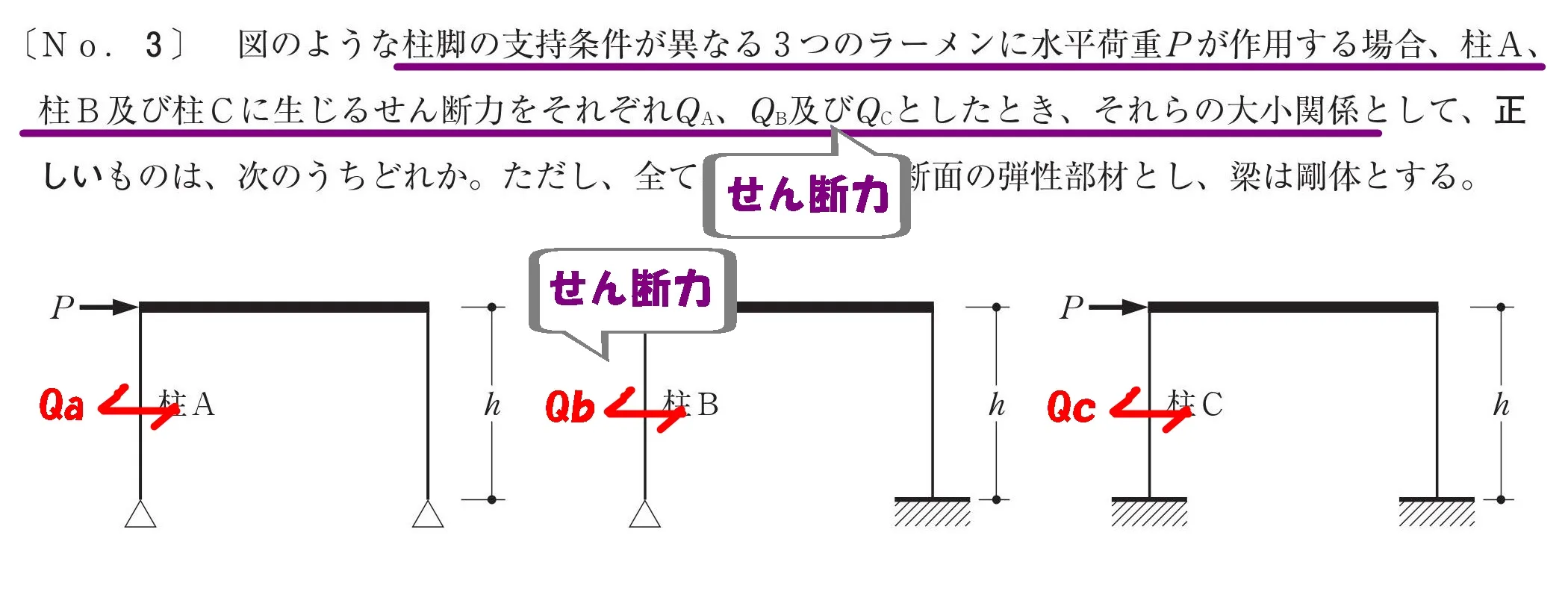

柱A・柱B・柱Cのせん断力Qa・Qb・Qcを求める問題となります。



3つのラーメンの
せん断力を比べる。
梁は剛体
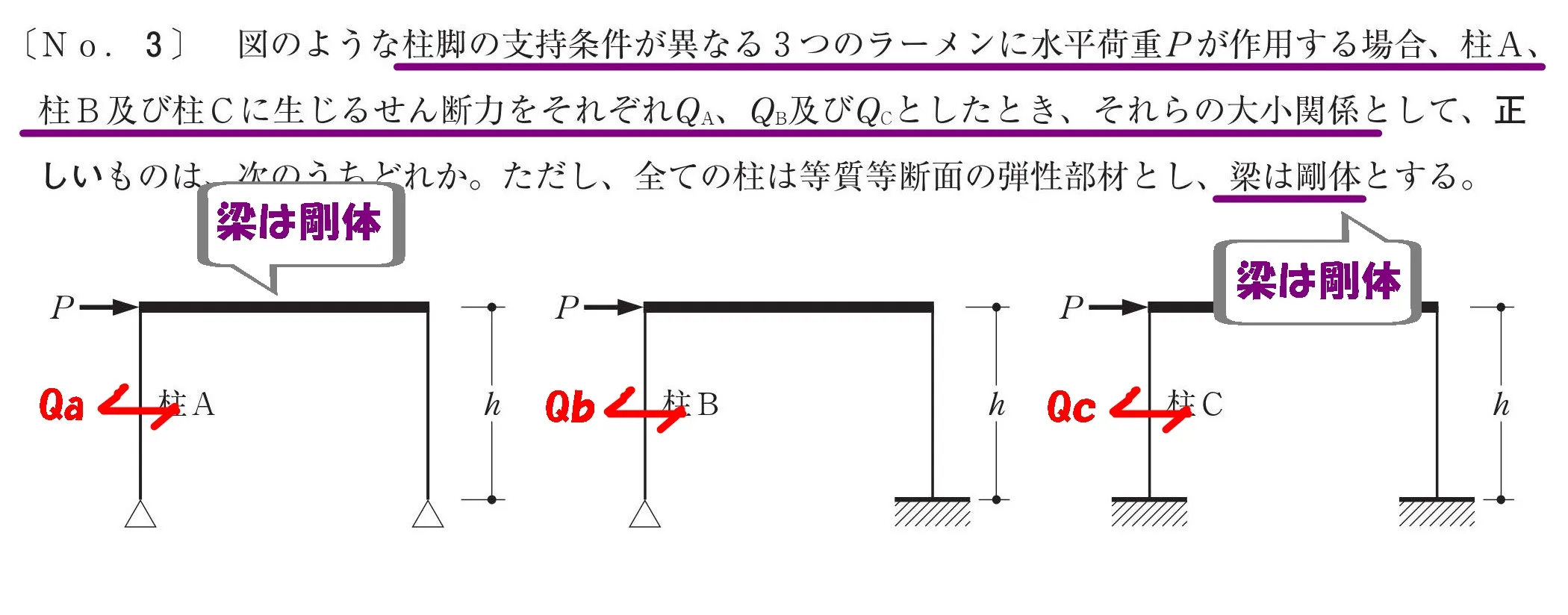

「梁は剛体」とはどう影響するのか?
たわみが等しくなる
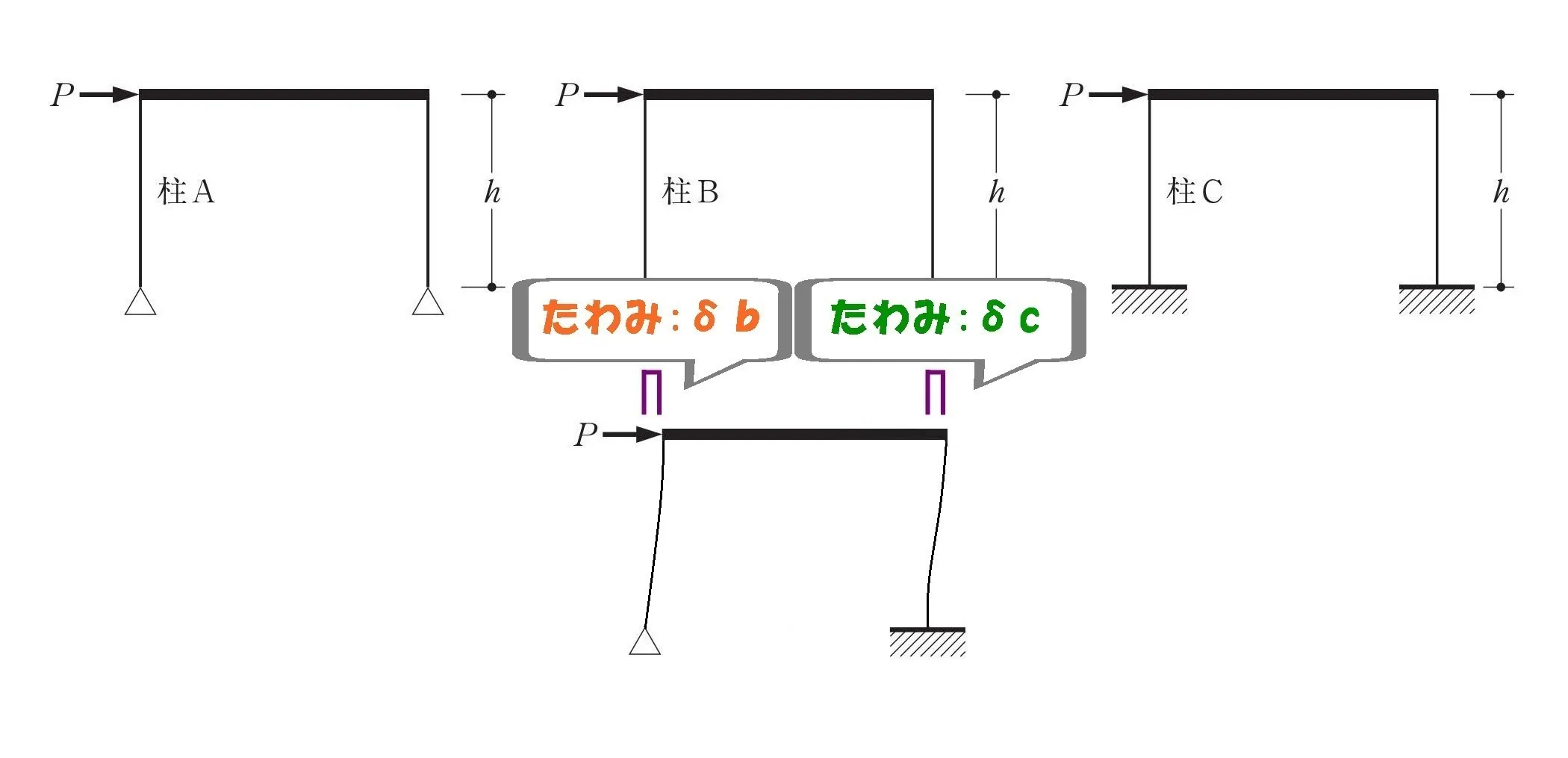

「梁は剛体」の場合、梁に接続している2つの柱(頭)が一緒に動きます。
そのため柱脚の支持条件に関わらず、2つの柱の変位が等しくなるのです。



梁と2本の柱が
一体となって動く。
たわみの公式
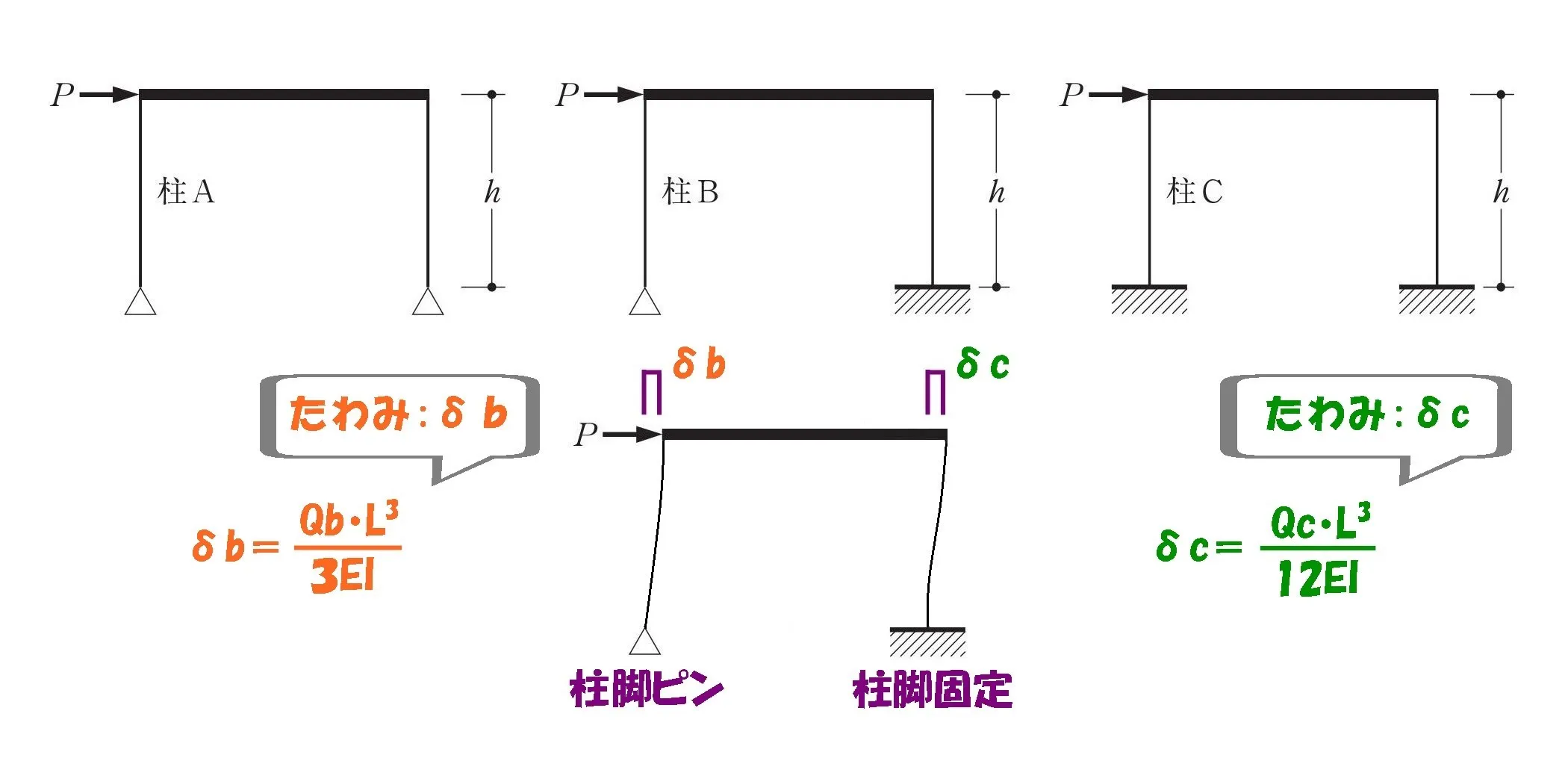

$$ピン支点のたわみ:\delta b=\frac{ Qb*L^3 }{ 3EI }$$$$固定端のたわみ:\delta c=\frac{ Qc*L^3 }{ 12EI }$$
$$\delta b=\delta cより,\frac{ Qb*L^3 }{ 3EI }=\frac{ Qc*L^3 }{ 12EI }$$
$$Qb=\frac{ Qc }{ 4 }⇨\frac{ Qb }{ Qc }=\frac{ 1 }{ 4 }$$$$剛比=Qb:Qc=1:4$$
せん断力の公式
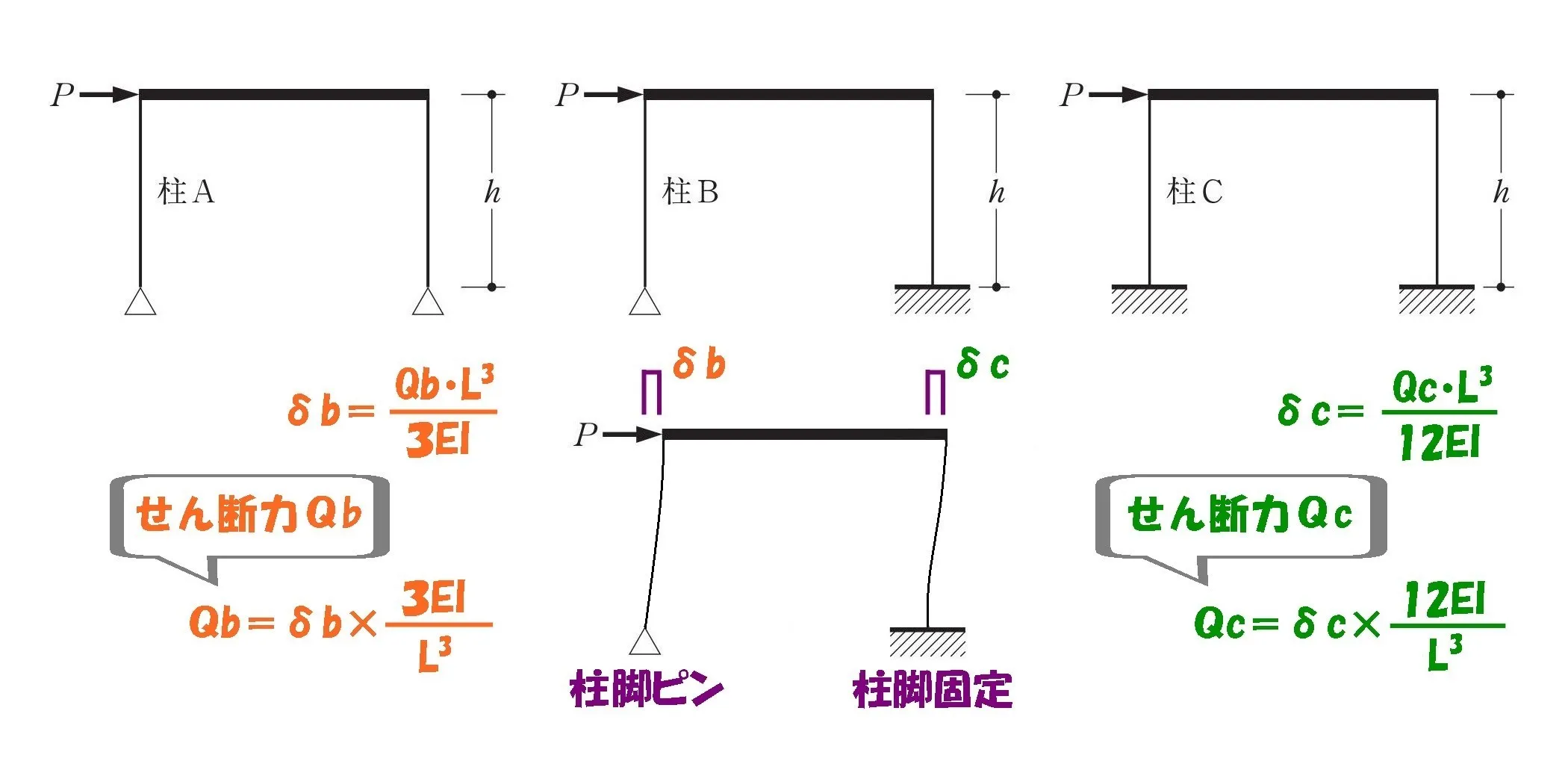

$$ピン支点のたわみ:\delta b=\frac{ Qb*L^3 }{ 3EI }より,$$$$せん断力:Qb=\delta b*\frac{ 3EI }{ L^3 }$$
$$固定端のたわみ:\delta c=\frac{ Qc*L^3 }{ 12EI }より,$$$$せん断力:Qc=\delta c*\frac{ 12EI }{ L^3 }$$
$$\delta b=\delta cより,Qb:Qc=1:4となる。$$



ピンと剛接合の剛比は
1:4の比になる。
せん断力に比例するもの
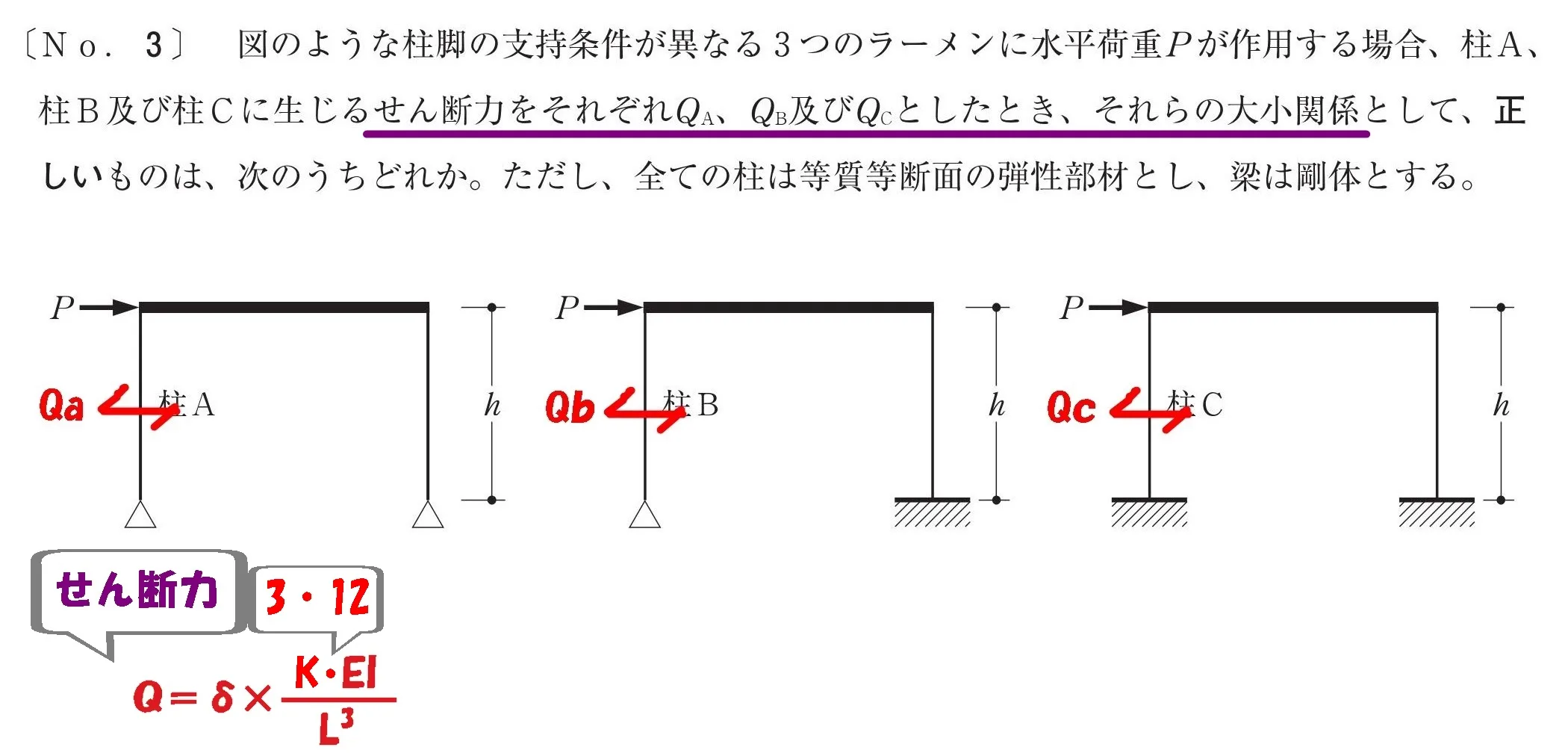

$$せん断力:Q=\delta*\frac{ k*EI }{ L^3 }より,$$
$$せん断力Qは,たわみ\deltaと曲げ剛性EIに比例する。$$
$$(k=ピン又は固定端により,3又は12)$$
全ての柱は等質等断面
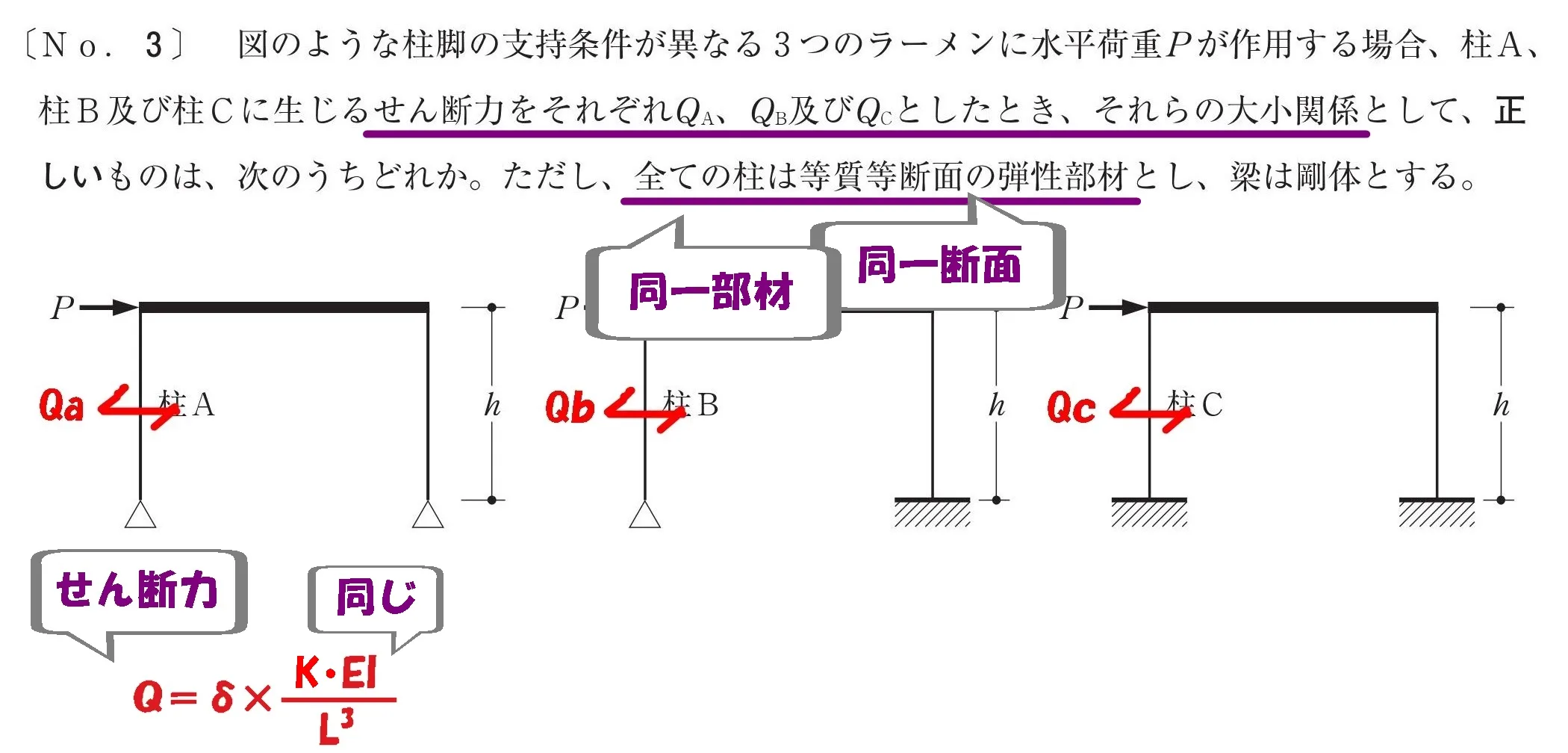

全ての柱は「等質」「等断面」よりEIは同じ。
- 等質:ヤング係数Eが同じ
- 等断面:断面二次モーメントIが同じ
- 等質等断面:曲げ剛性EIが同じ



条件が同じものは
式から省いていこう。
梁は剛体
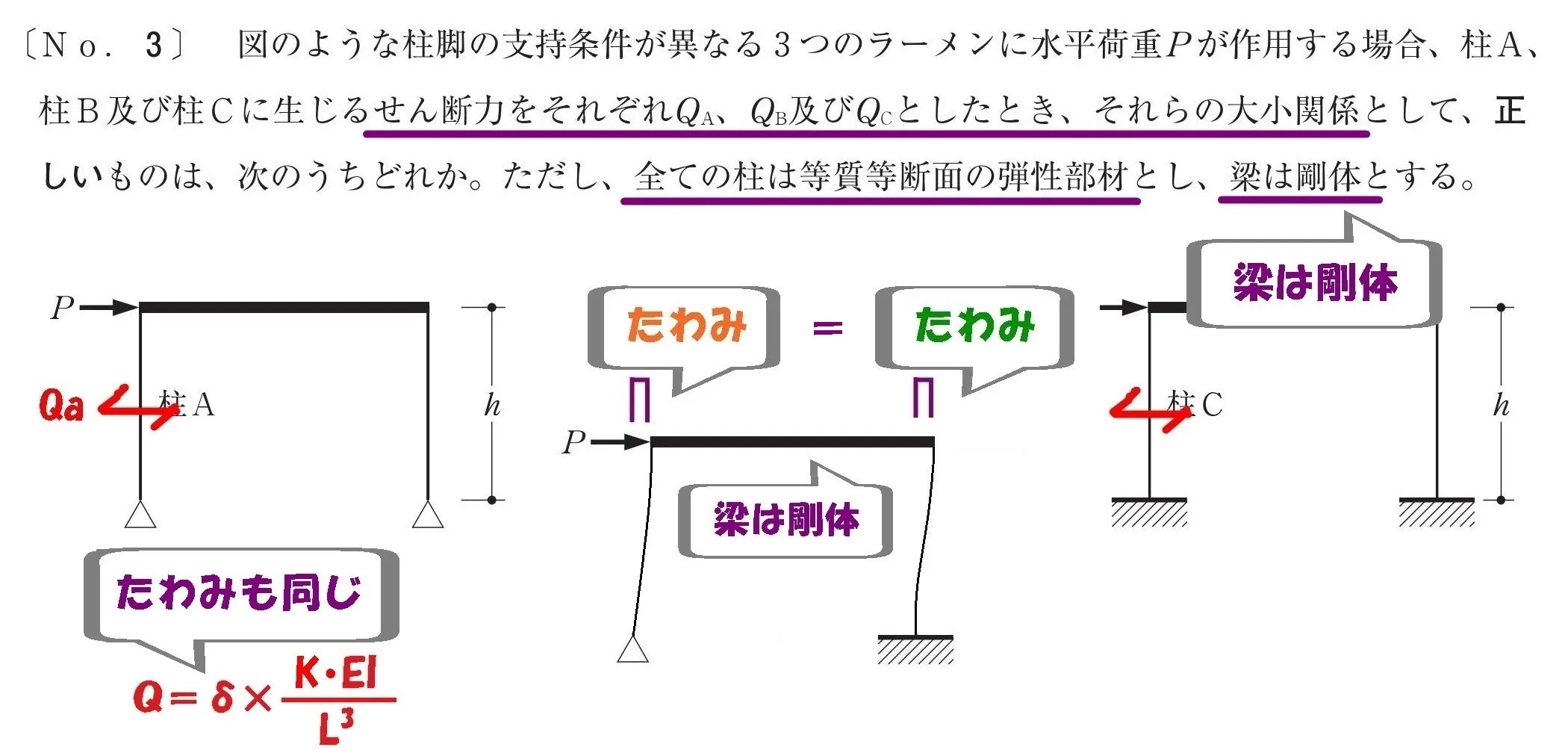

「梁は剛体」ということから、たわみδも同じ。
せん断力に反比例するもの
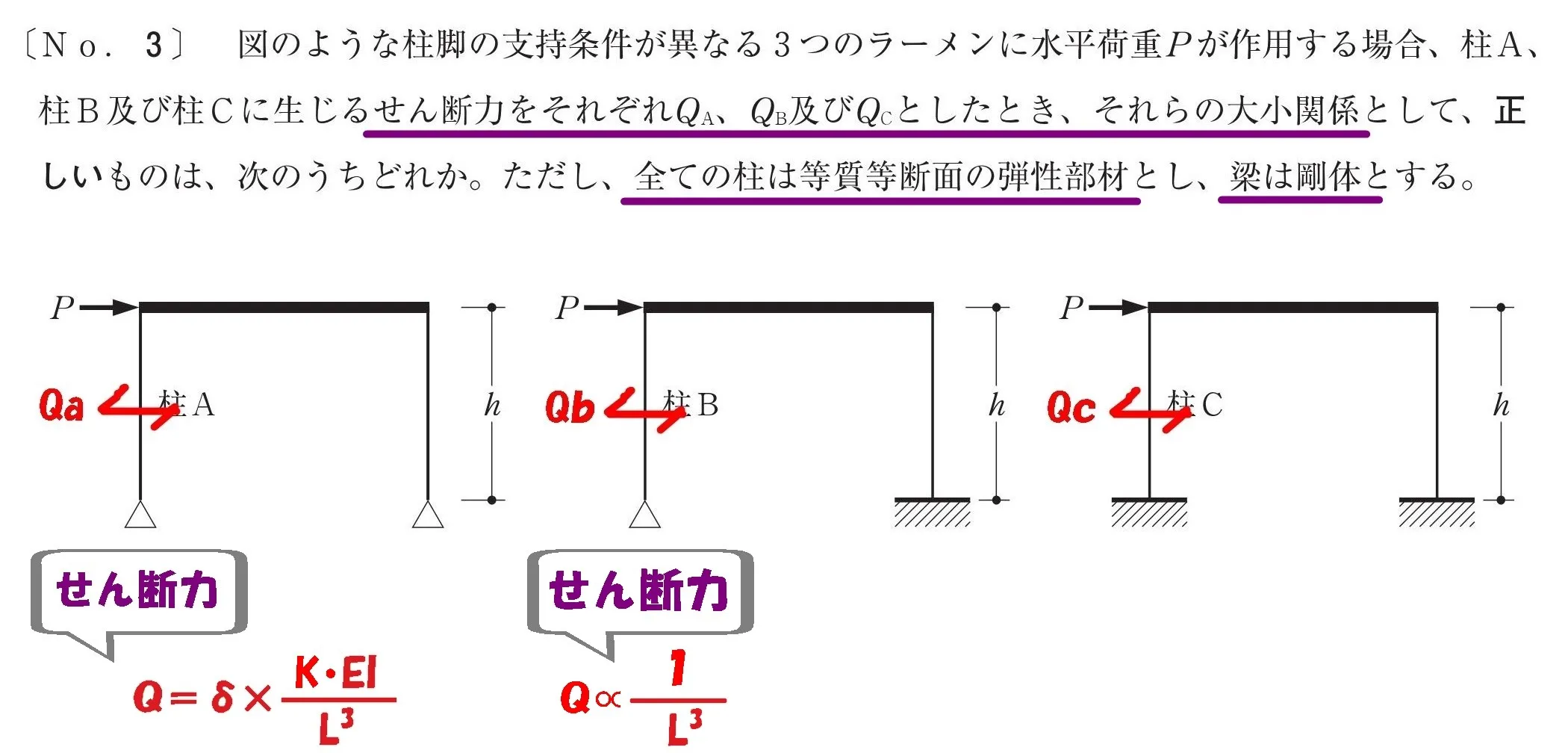

$$せん断力:Q=\delta*\frac{ k*EI }{ L^3 }より,$$
$$せん断力Qは,柱の長さh(L)の3乗に反比例する。$$
柱の長さも同じ
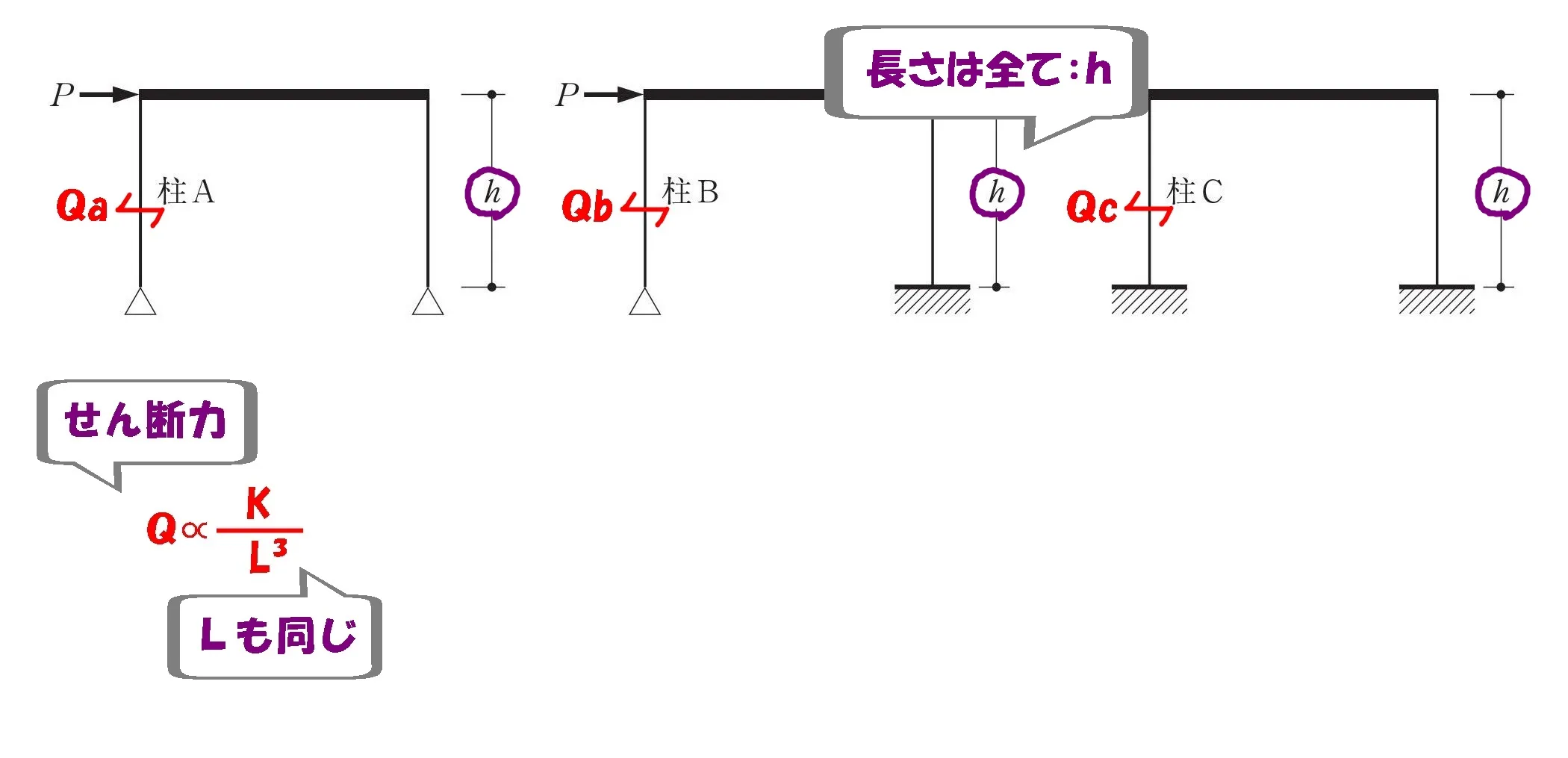

「柱の長さはすべてh」ということなので、せん断力は定数:kによってのみ左右される。
$$せん断力:Q\propto 定数:k$$$$定数:k=\{ピン又は固定端により,3又は12\}$$
読み取りポイント
せん断力は、ラーメン架構の柱脚の支持条件によってのみ比較できる。
柱脚の支持条件の違いを読み取り、剛比を求める
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める
柱脚に注目する
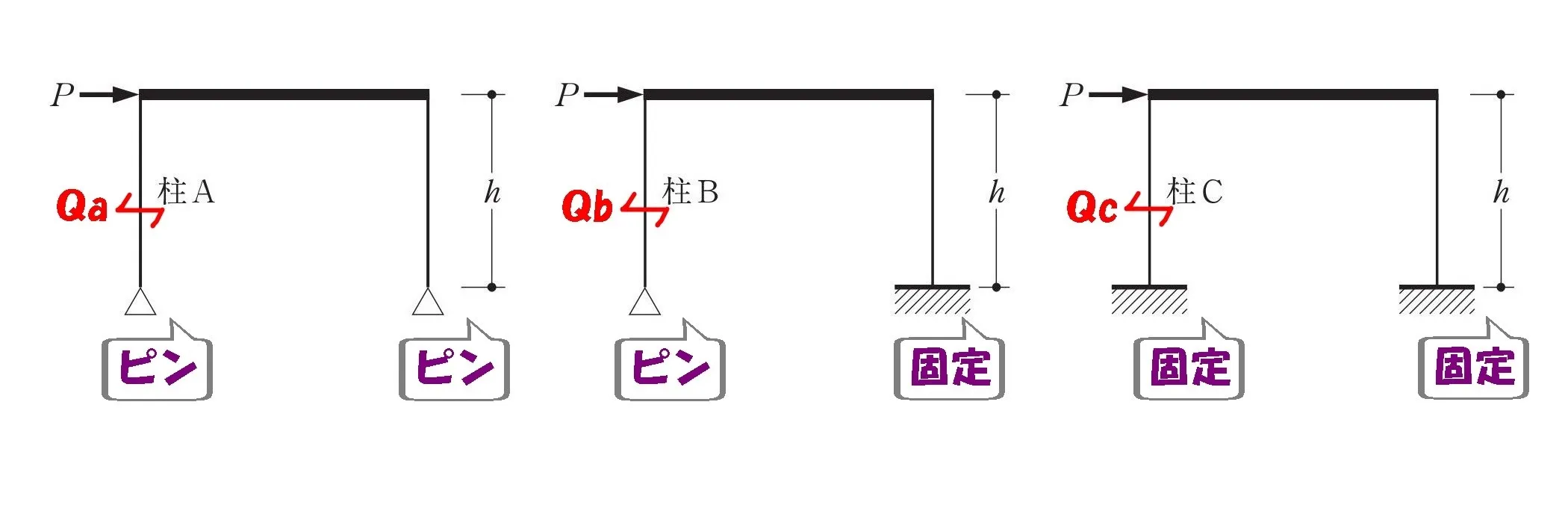

| A | B | C |
|---|---|---|
| ピン:ピン | ピン:固定 | 固定:固定 |



ピンと固定の違いを
書き出していきましょう。
柱の剛比
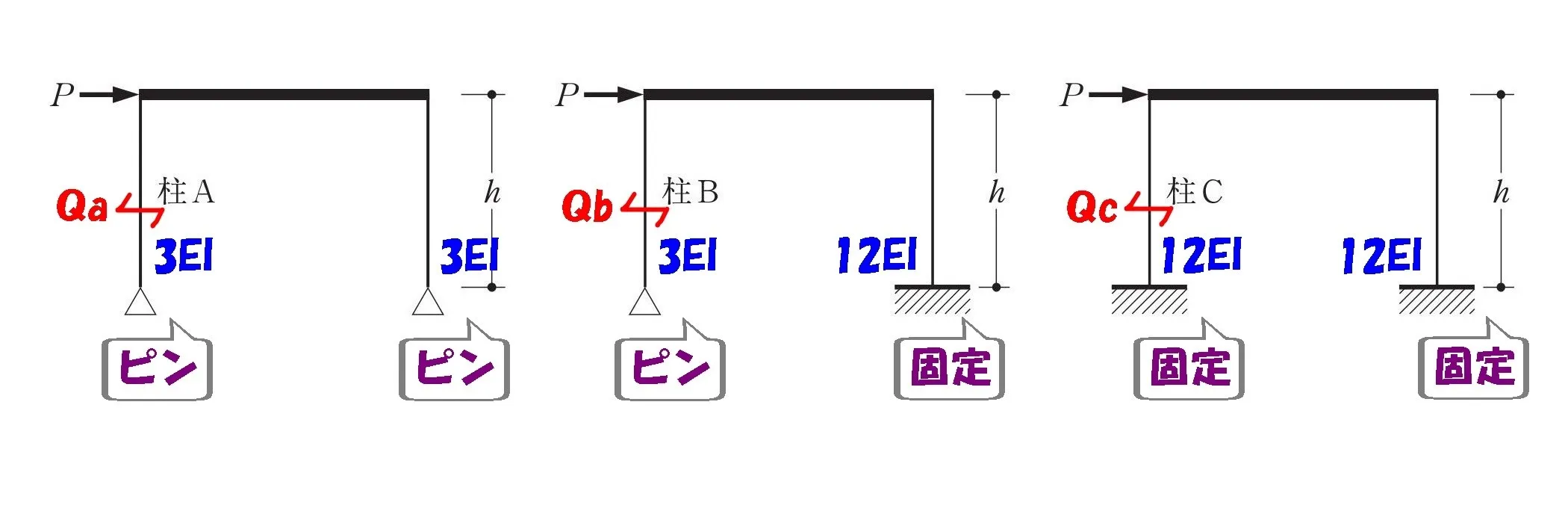

| A | B | C |
|---|---|---|
| ピン:ピン | ピン:固定 | 固定:固定 |
| 3EI:3EI | 3EI:12EI | 12EI:12EI |
柱の剛比
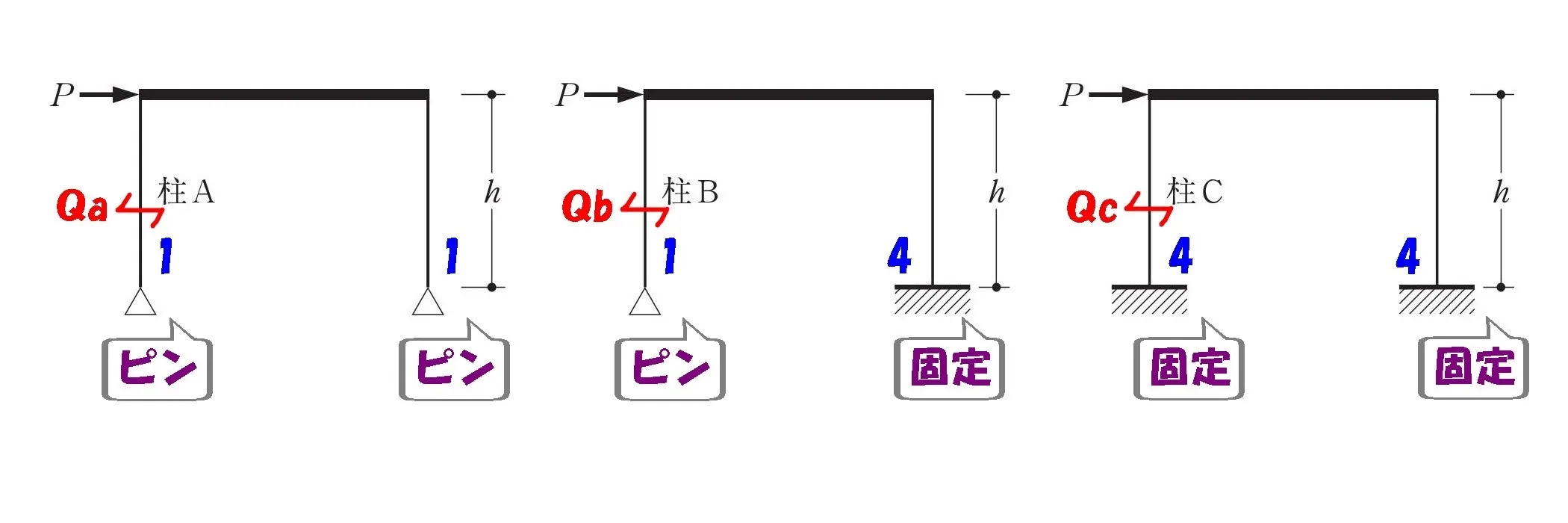

| A | B | C |
|---|---|---|
| ピン:ピン | ピン:固定 | 固定:固定 |
| 1:1 | 1:4 | 4:4 |
3.柱の剛比から、せん断力の大小関係を求める
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める
柱A・柱Cのせん断力
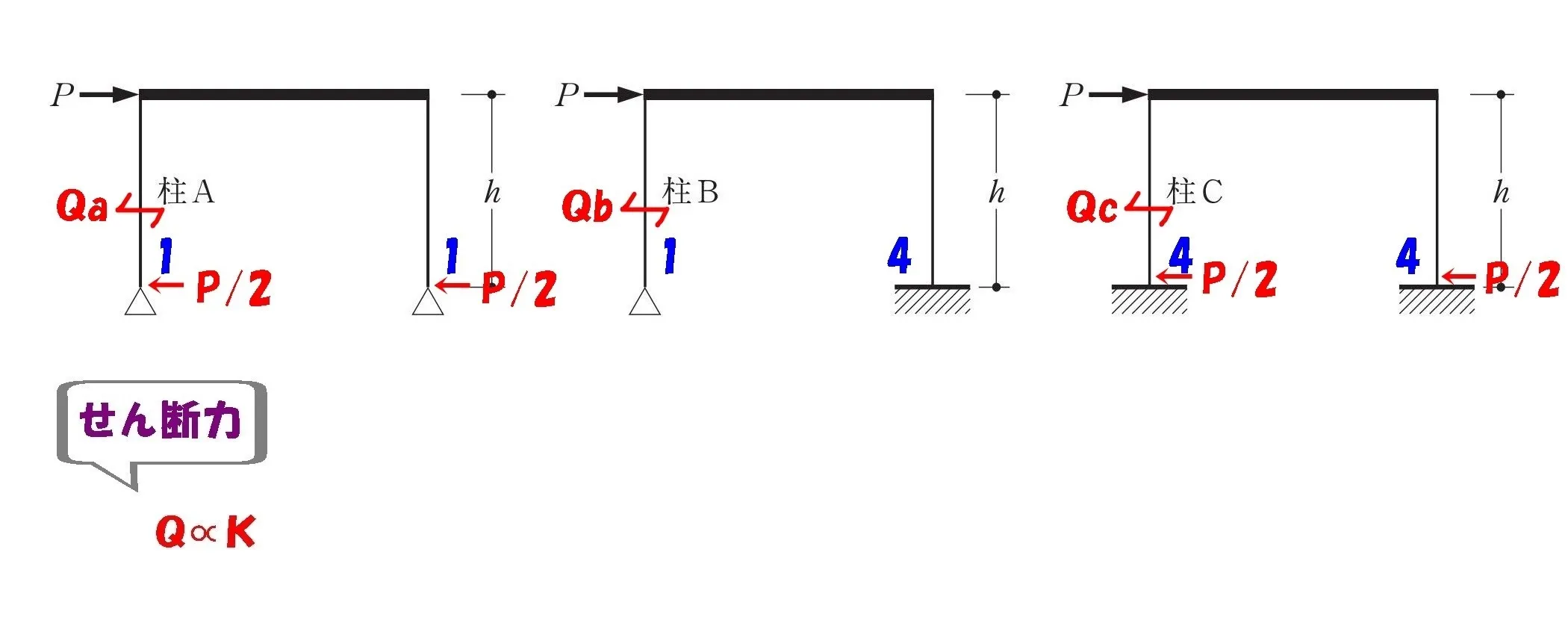

$$Qa=P*\frac{ 1 }{ 1+1 }=\frac{ P }{ 2 }$$$$Qc=P*\frac{ 4 }{ 4+4 }=\frac{ P }{ 2 }$$
架構Aと架構Cは柱の支持条件が両側の柱とも同じため、柱の剛比は1:1(4:4)。
せん断力Qa・Qcは水平荷重Pに対して両側の柱に2分されるので、せん断力はP/2となる。
柱Bのせん断力は?
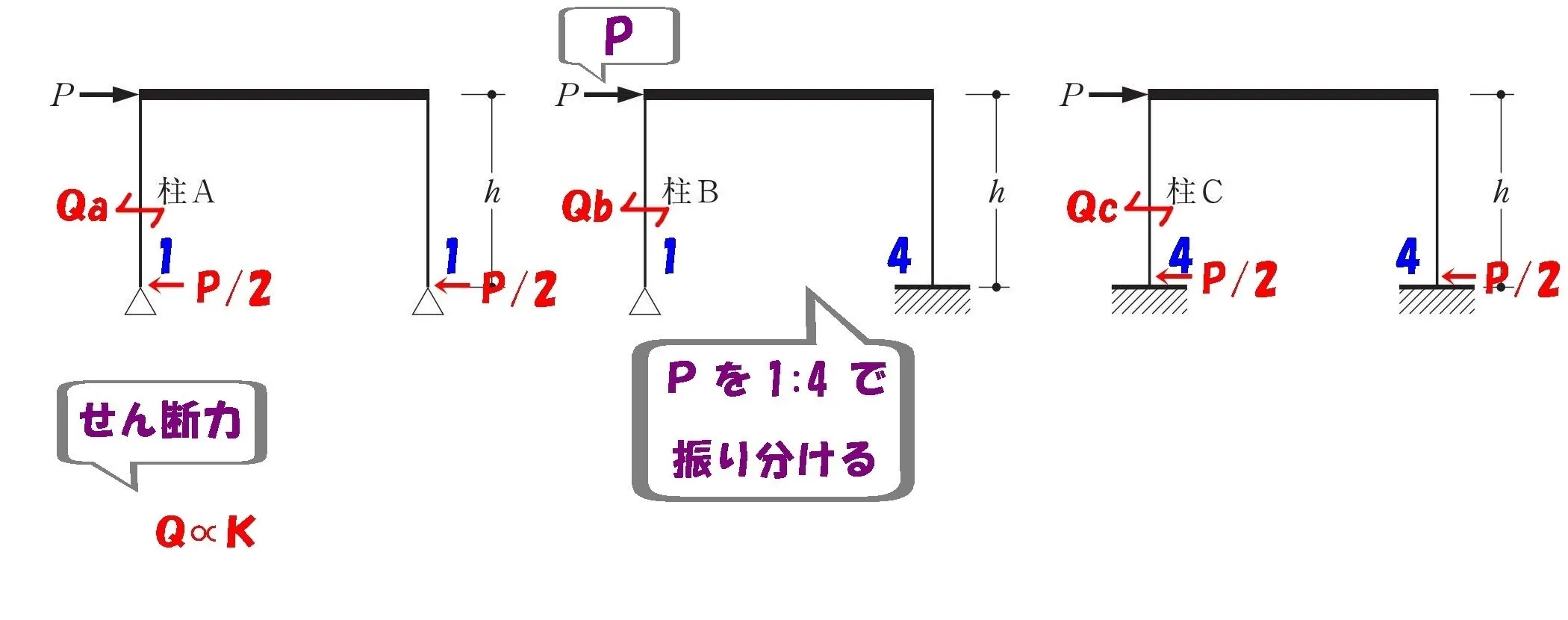

$$せん断力Qb=P*\frac{ 1 }{ 1+4}=\frac{ P }{ 5 }$$
架構Bのせん断力:Qbは、水平荷重Pに対して柱の剛比(1:4)で振り分けられます。



水平荷重Pを
柱の剛比で振り分ける。
Qb=P/5
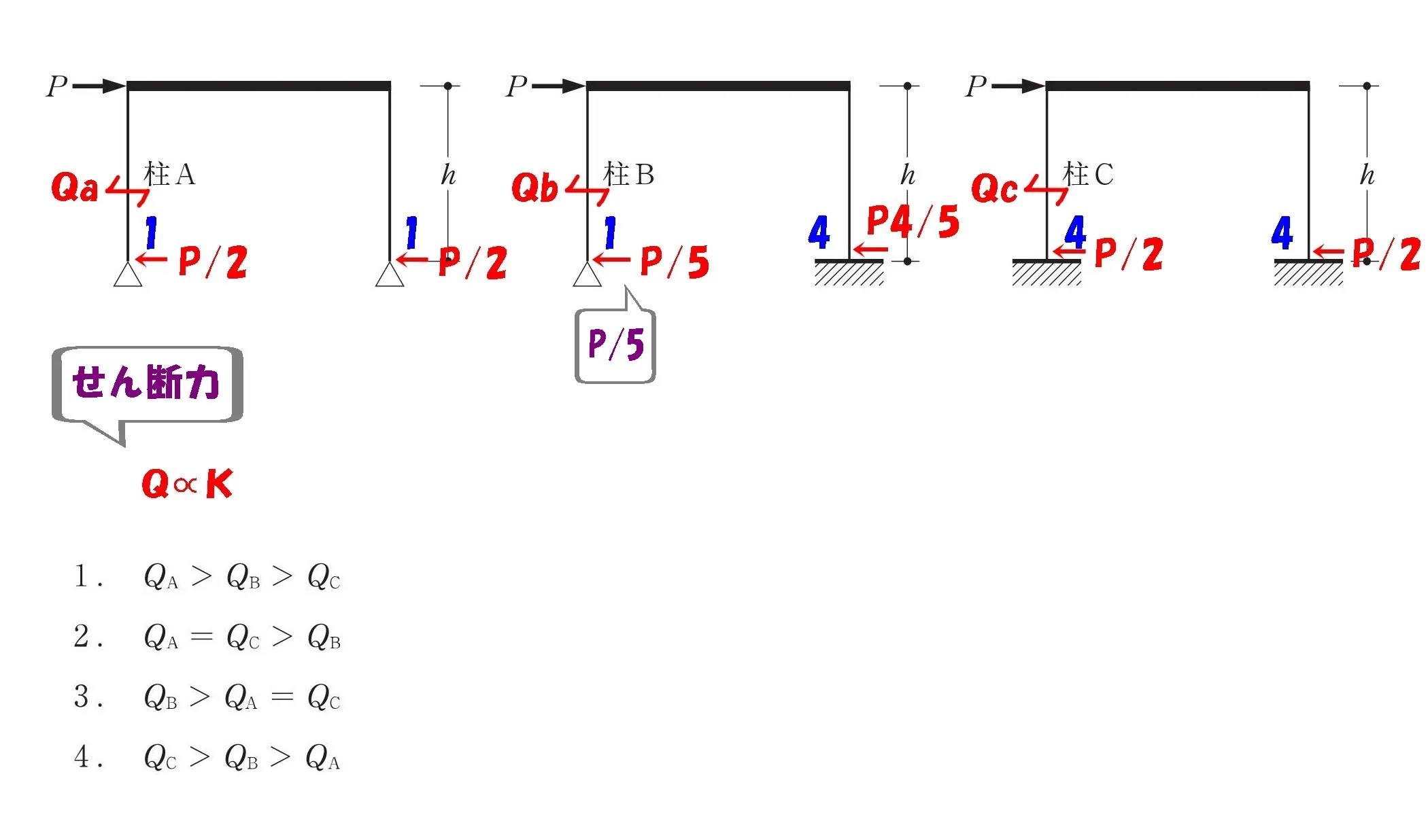

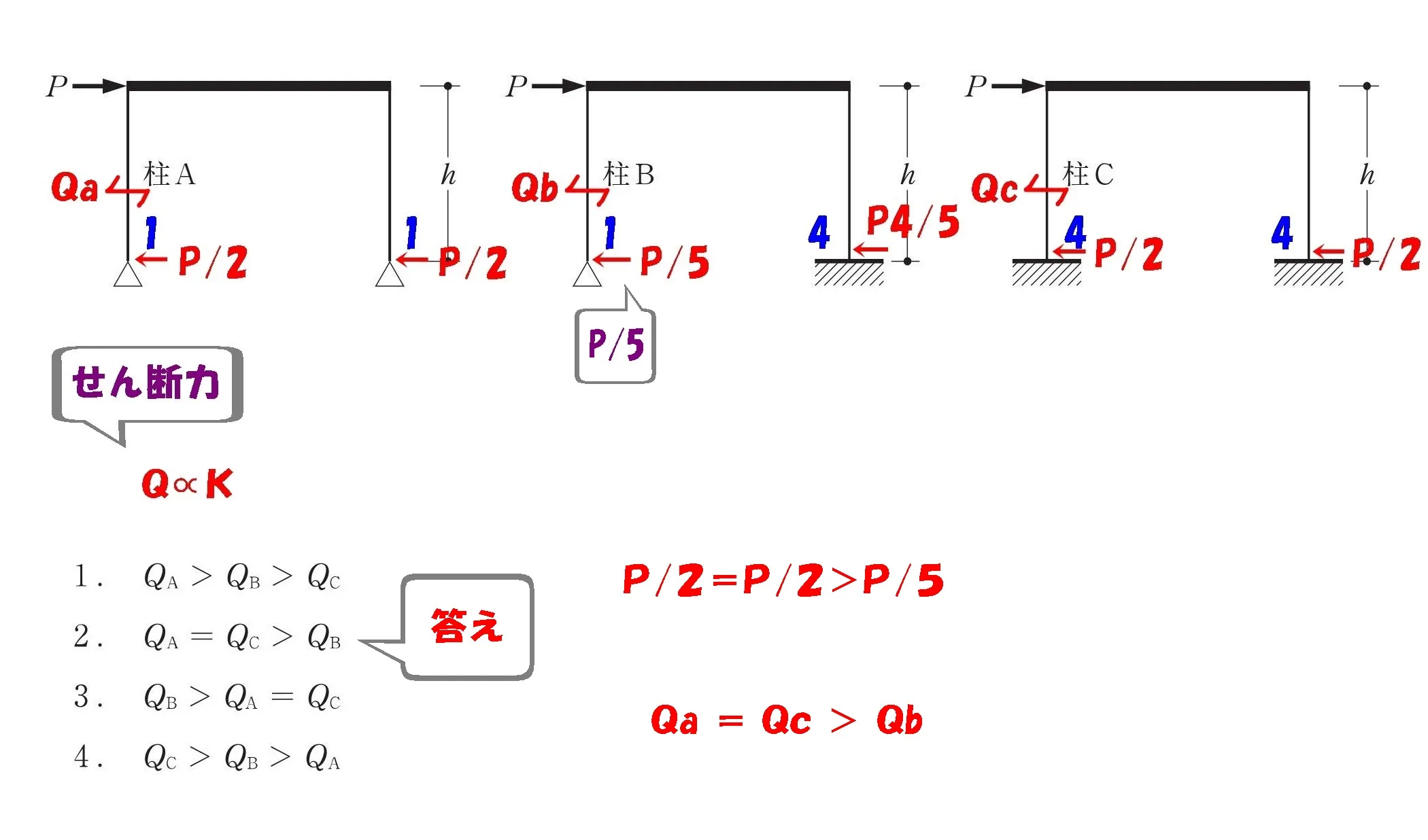
数値を大きさ順に並べる
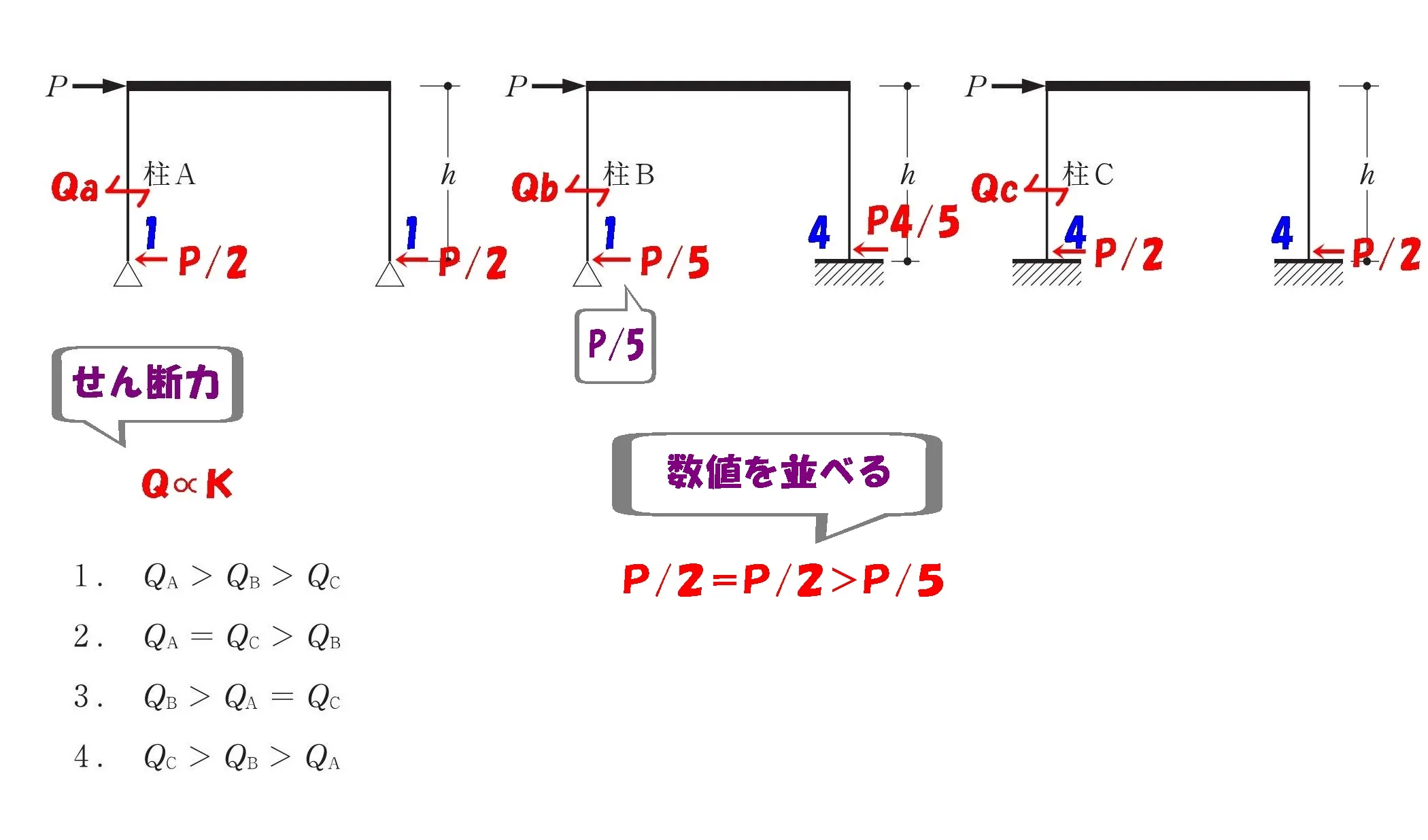

求めた数値、P/2・P/2・P/5を大きさ順に並べます。
対応する記号を書き込む
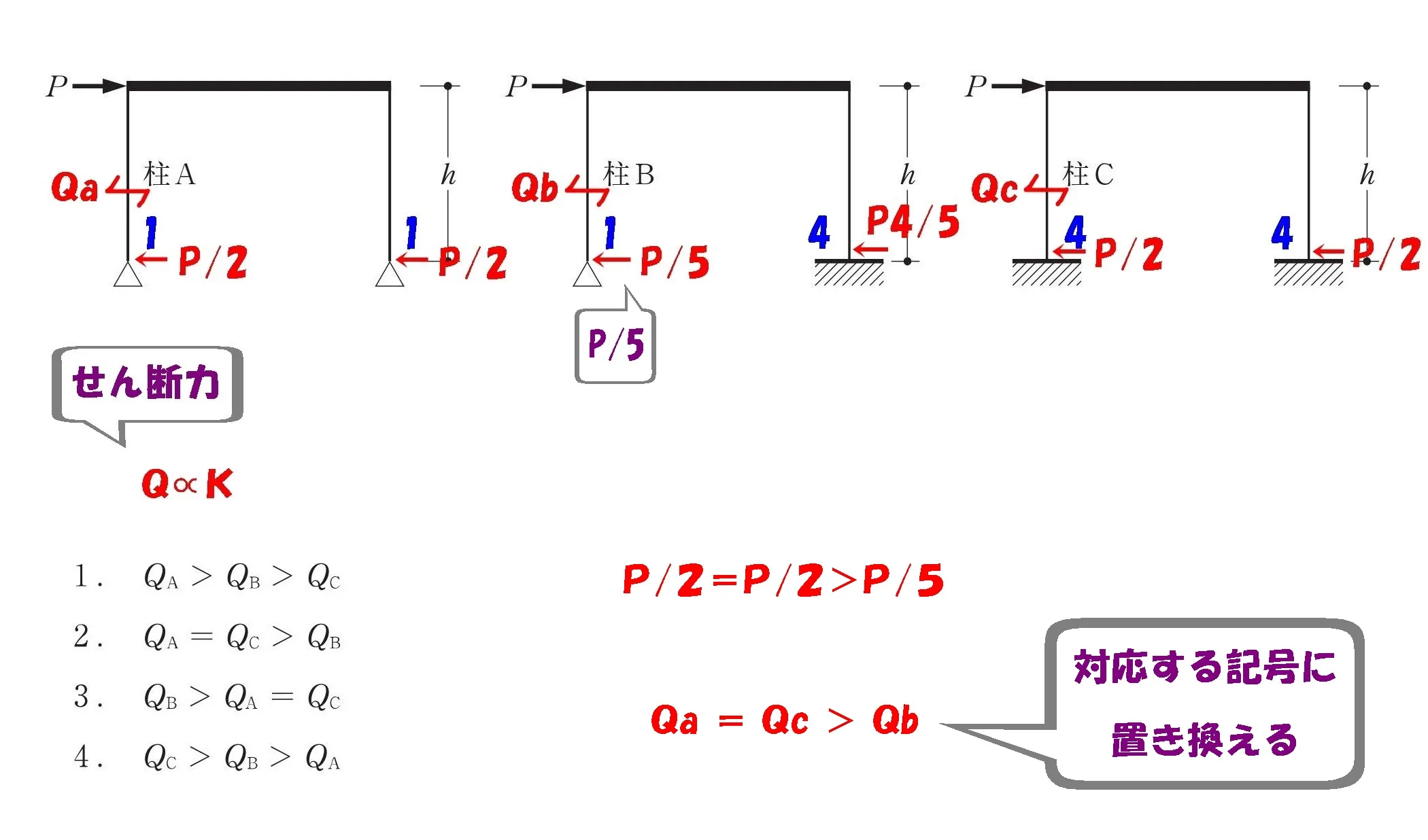

対応するアルファベット:Qa・Qb・Qcを書き込み、不等号を付けましょう。



数値を並べて記号を書く。
これが間違えない手法。
答え.2

攻略ポイント
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める
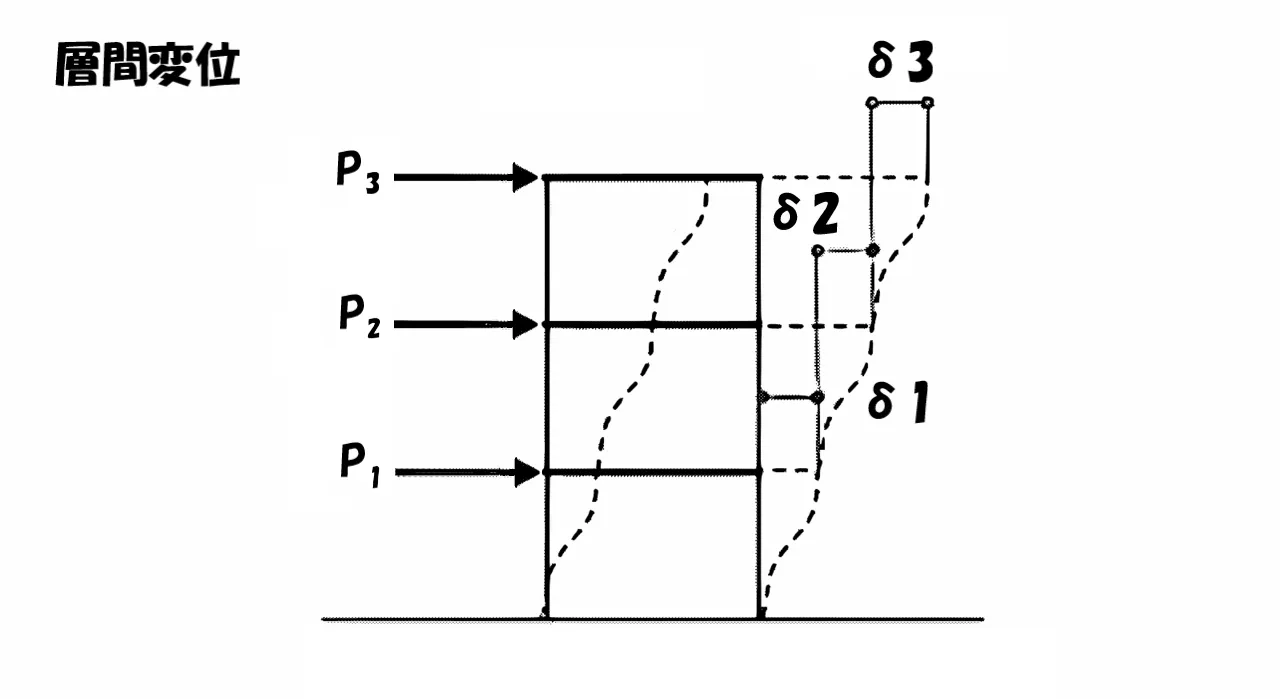
層間変位
難易度:★★☆☆☆
層間変位は何に比例し、何に反比例するのか?
他の要素との関係は「公式から読み取ること」を身につけておきましょう。
層間変位のイメージ図

攻略ポイント
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
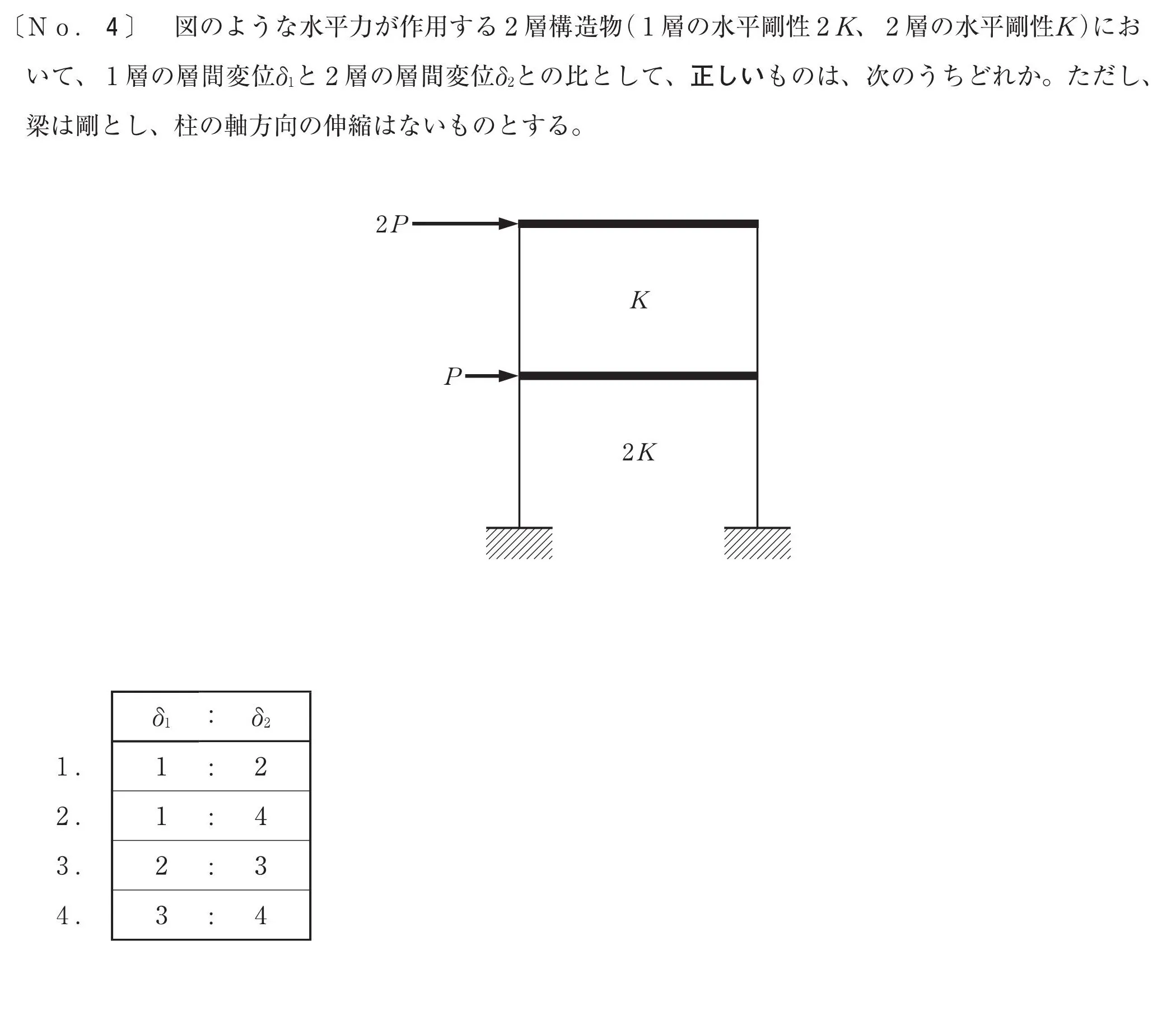
問題



この動画を YouTube で視聴
1.層間変位に比例するもの、反比例するものを把握する
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
層間変位の比を求める
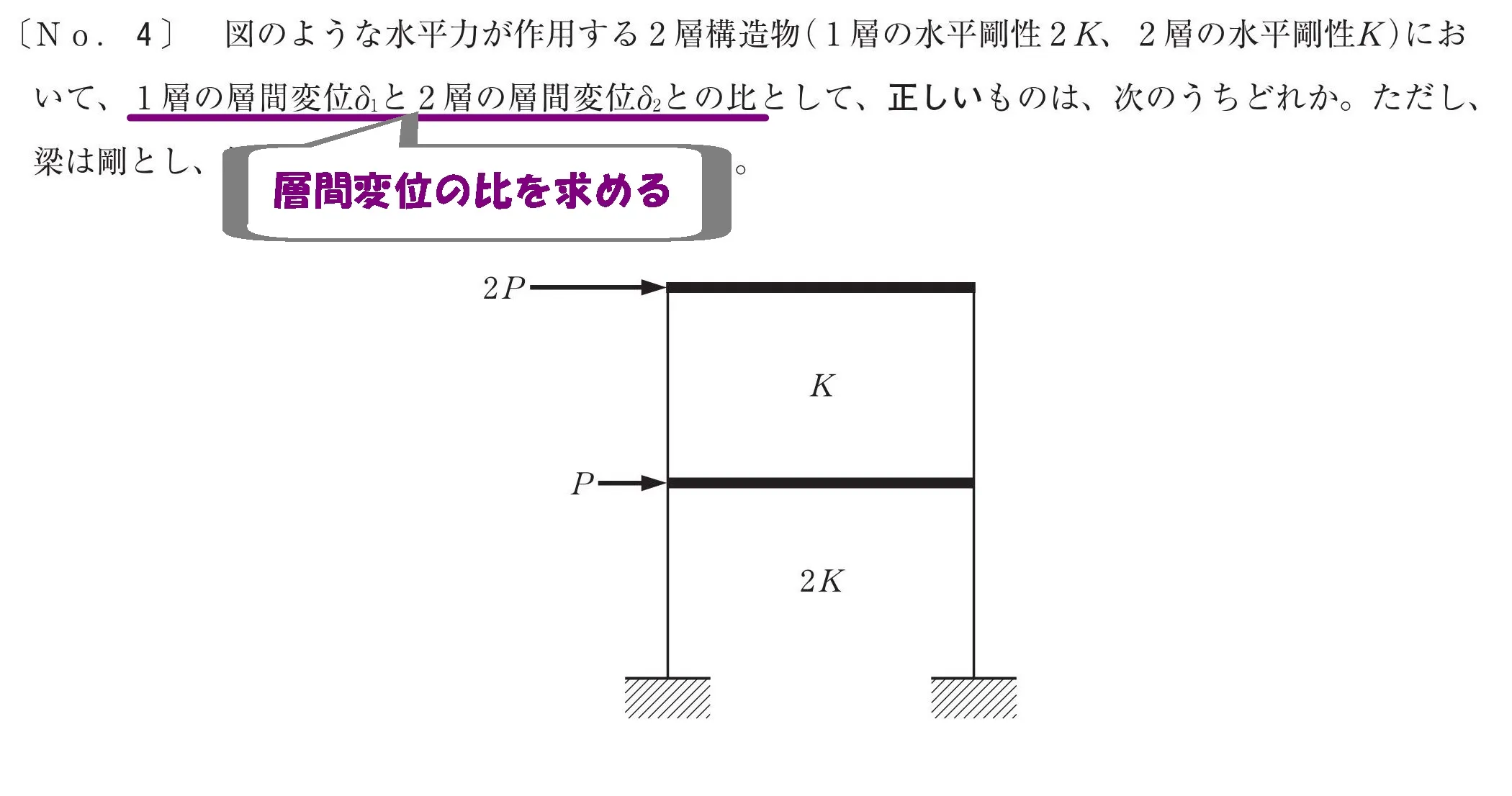

1階と2階の層間変位の比「δ1:δ2」を求める問題です。
層間変位のイメージ図
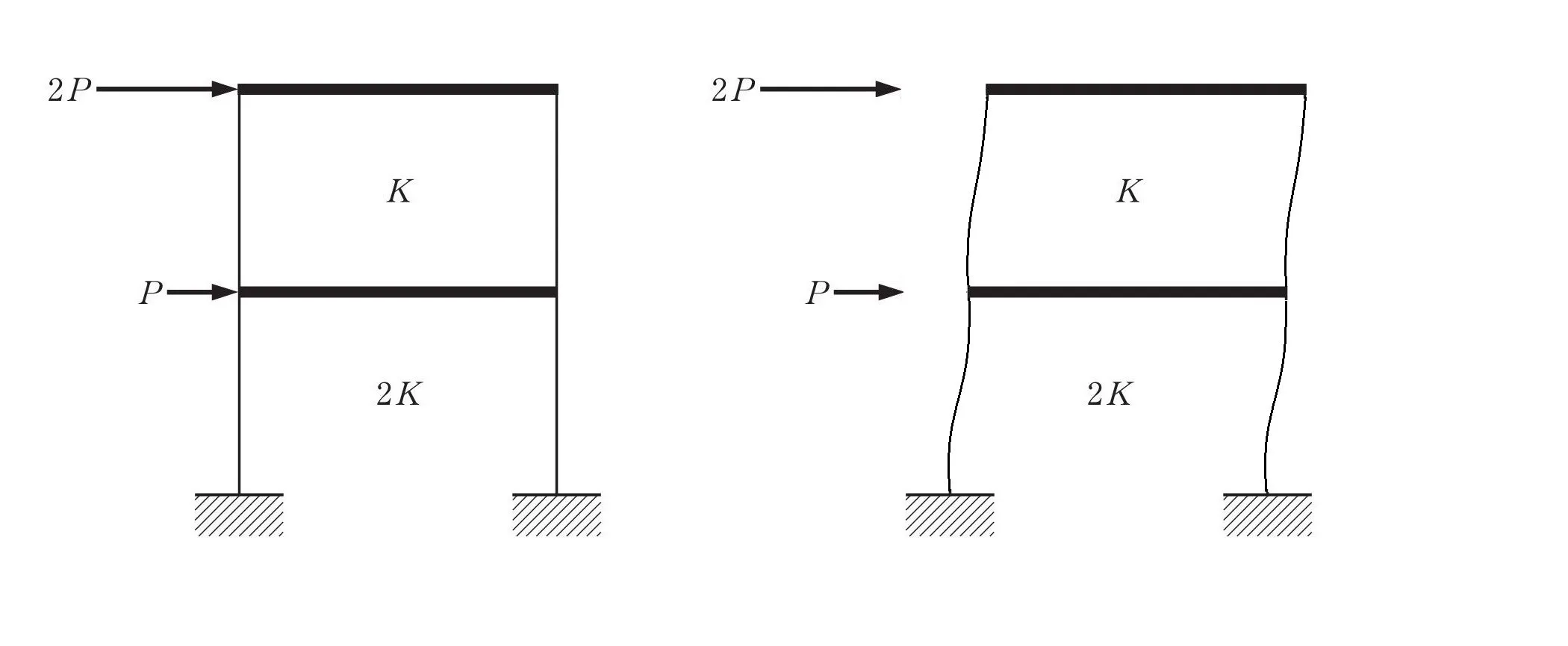

層間変位とは?
- 1層フロアと2層フロアとの間に生じる変位
- 2層フロアと3層フロアとの間に生じる変位
層間変位に影響するもの
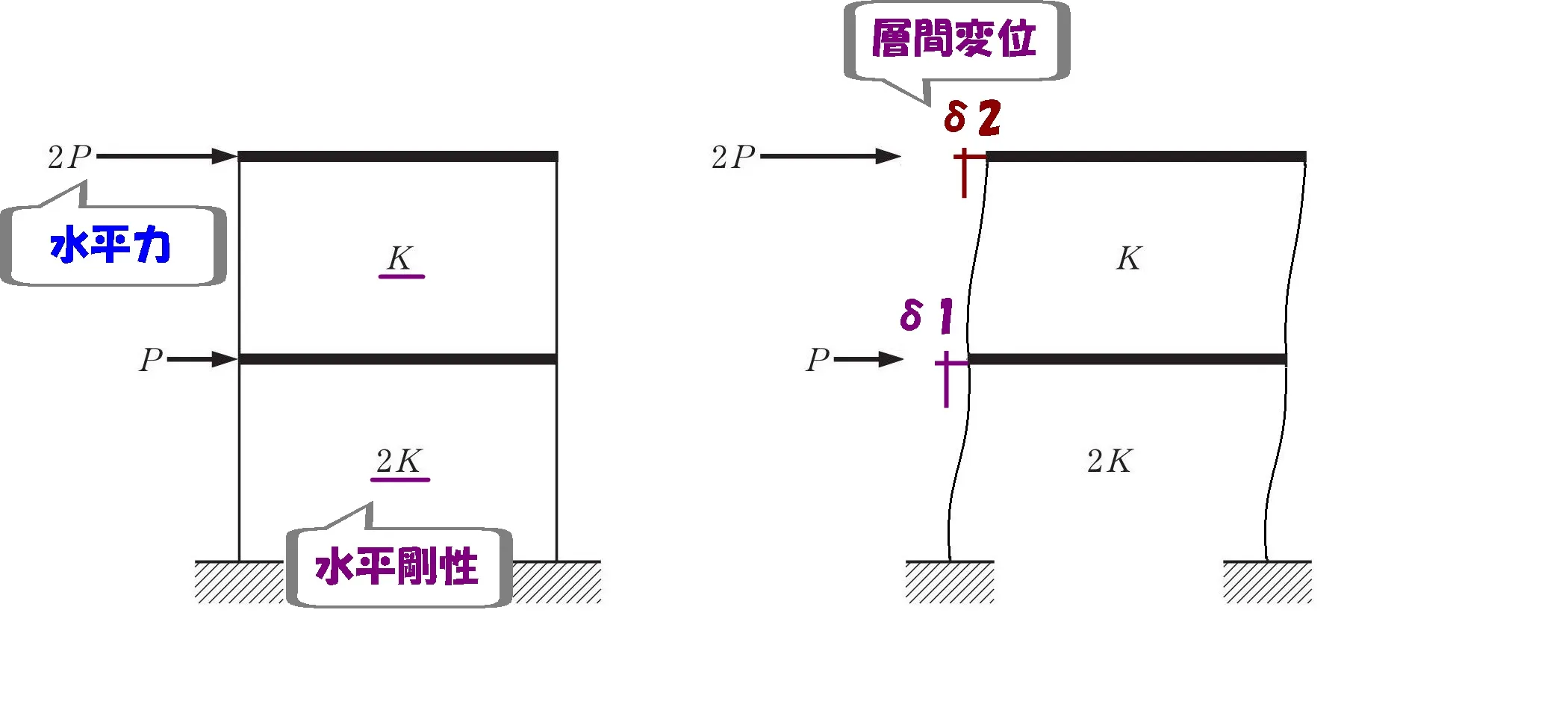

層間変位の大きさに影響をあたえるもの。
- 建物の「水平剛性」
- 建物に及ぼす「水平力」
層間せん断力の公式
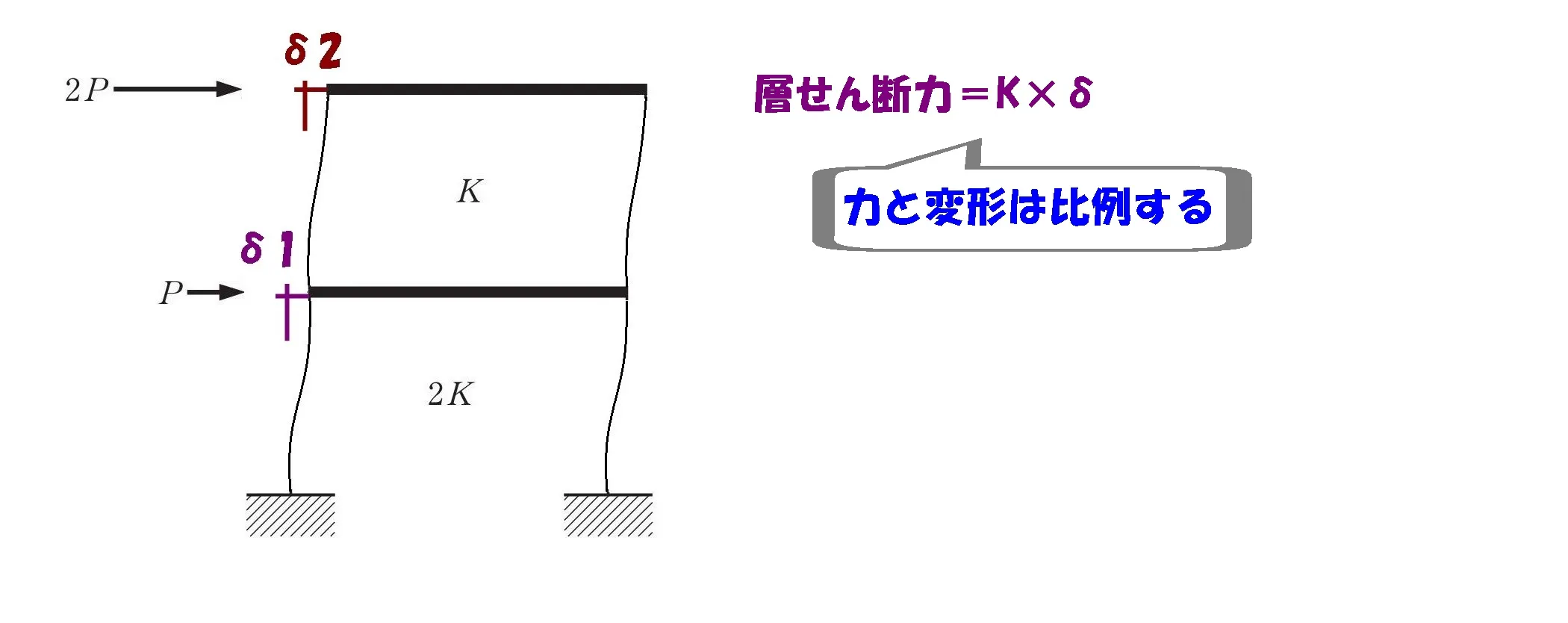

公式 ①
$$層せん断力Q=K*\delta$$
$$層せん断力Qは、水平剛性Kと変位量δに比例する。$$
公式 ②
$$水平剛性:K=\frac{ 12EI }{ h^3 }より,K\propto \frac{ EI }{ h^3 }$$
$$水平剛性Kは、曲げ剛性EIに比例し、柱の長さhの3乗に反比例する。$$
層間変位に比例するもの
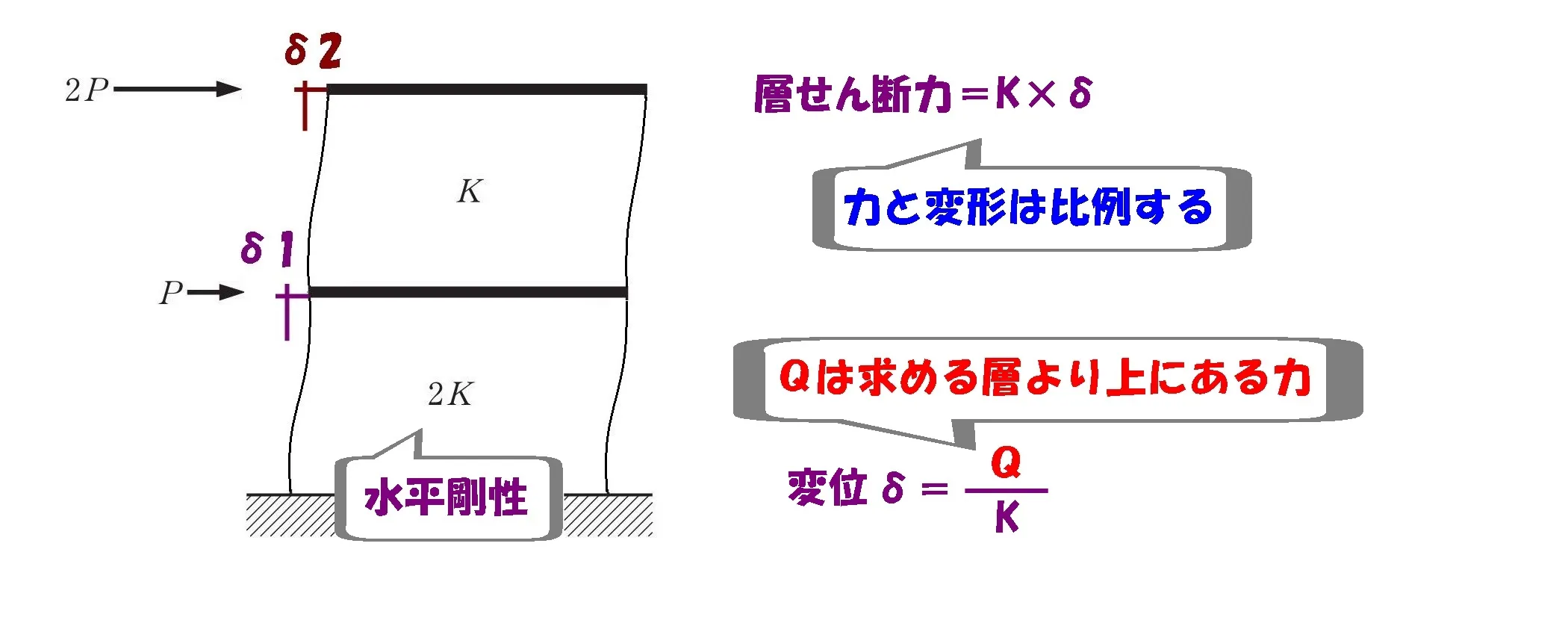

$$Q=K*\deltaより,\delta=\frac{ Q }{ K }$$
公式 ③
$$\delta=\frac{ Q }{ K }$$
$$\underline{層間変位δは、層せん断力Qに比例し、水平剛性Kに反比例する。}$$
2.柱脚のラインで部材を切断して、上部の架構を取り出す
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
柱脚を切断する
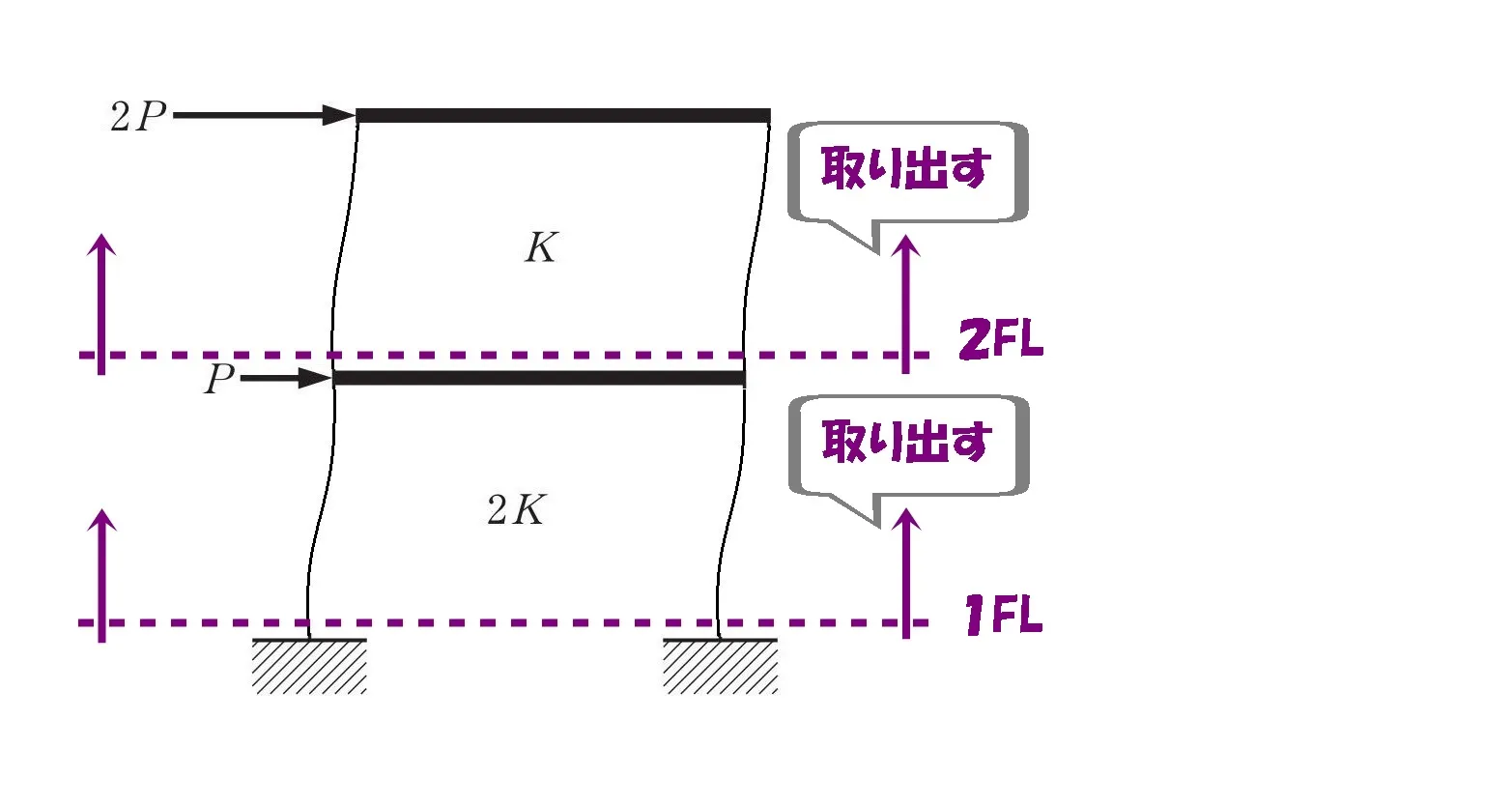




伝家の宝刀、部材斬り!
切断して部材を取り出す
- 2層目の柱脚から上部を取り出す。
- 1層目の柱脚から上部を取り出す。
上部の架構を取り出す
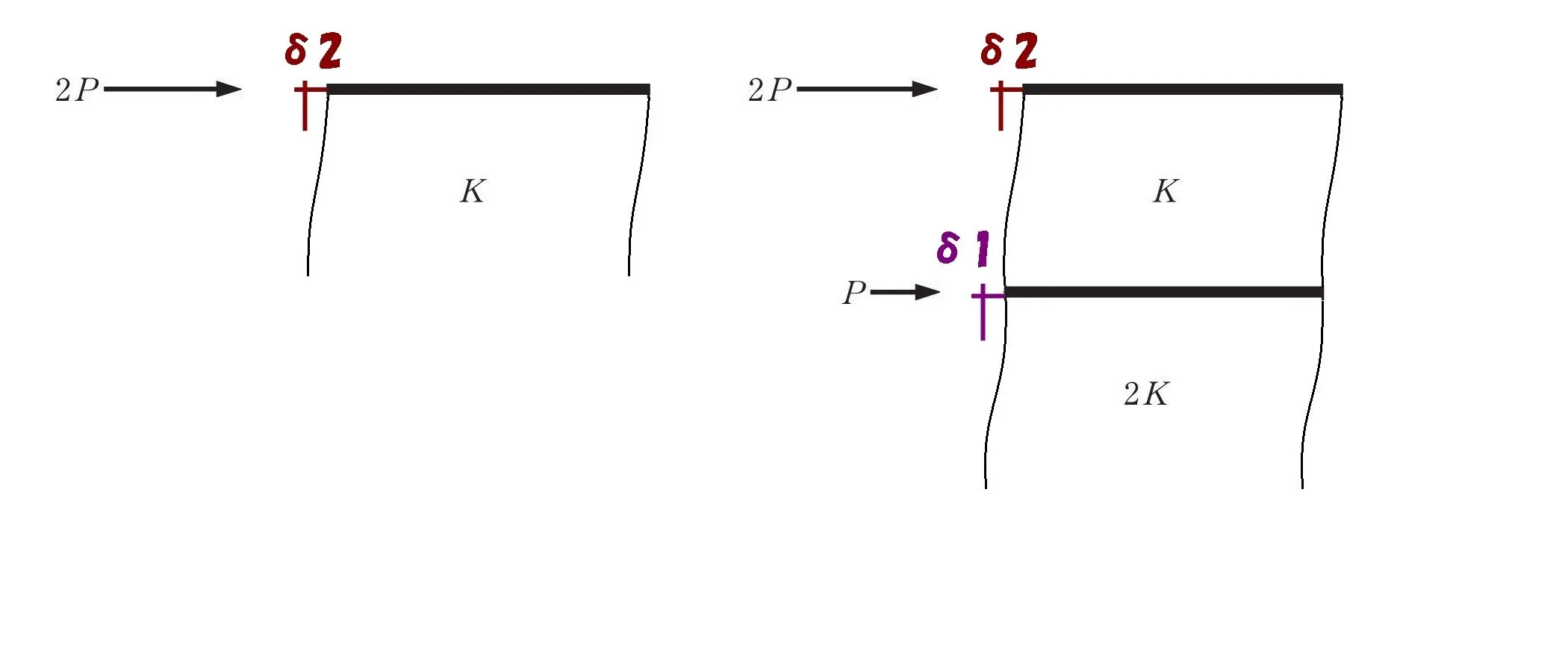

- 2層目の柱脚から上部を取り出す。
- 1層目の柱脚から上部を取り出す。
方程式を作るための準備として、それぞれの図を書き出しておく。
3.水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
層せん断力を求める
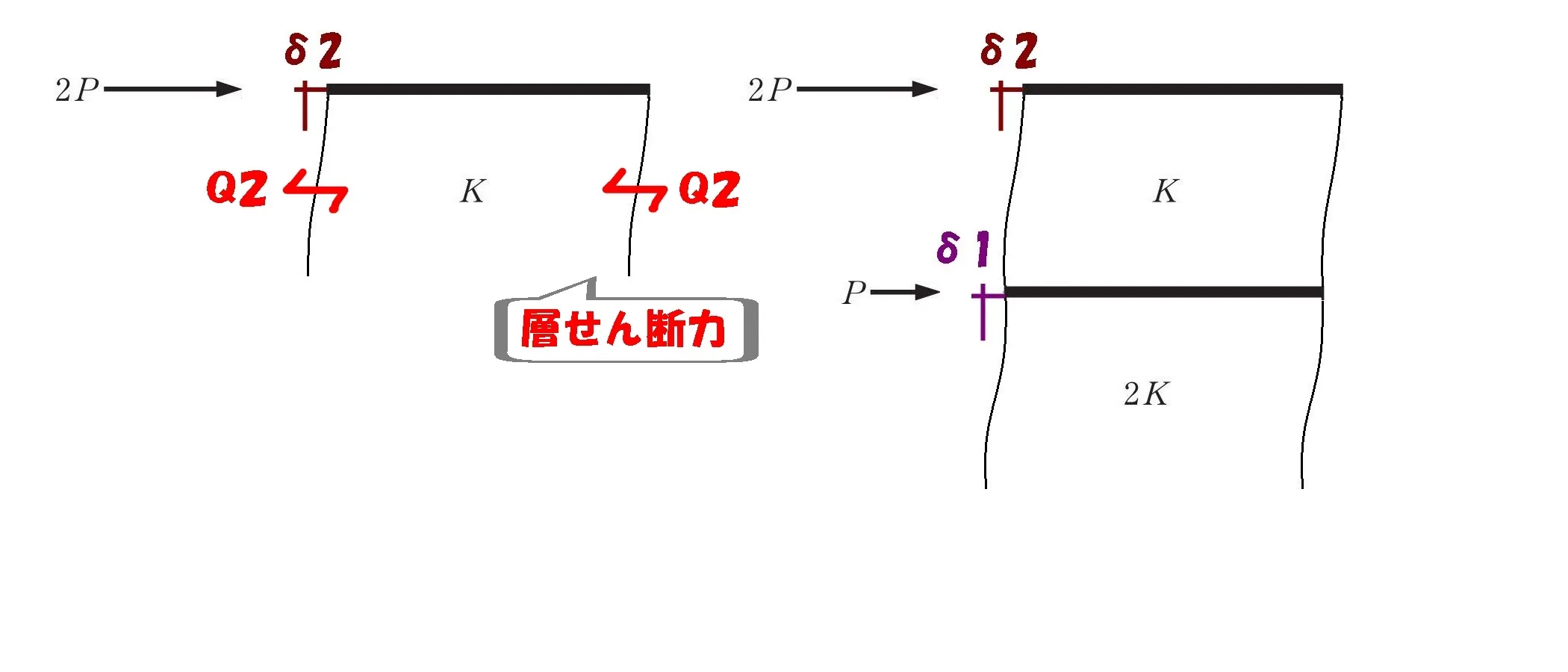

層せん断力は”上の層”から、順に求めていきます。
先に求めるものは、2層目の層せん断力「Q2」
せん断力Q2を求める
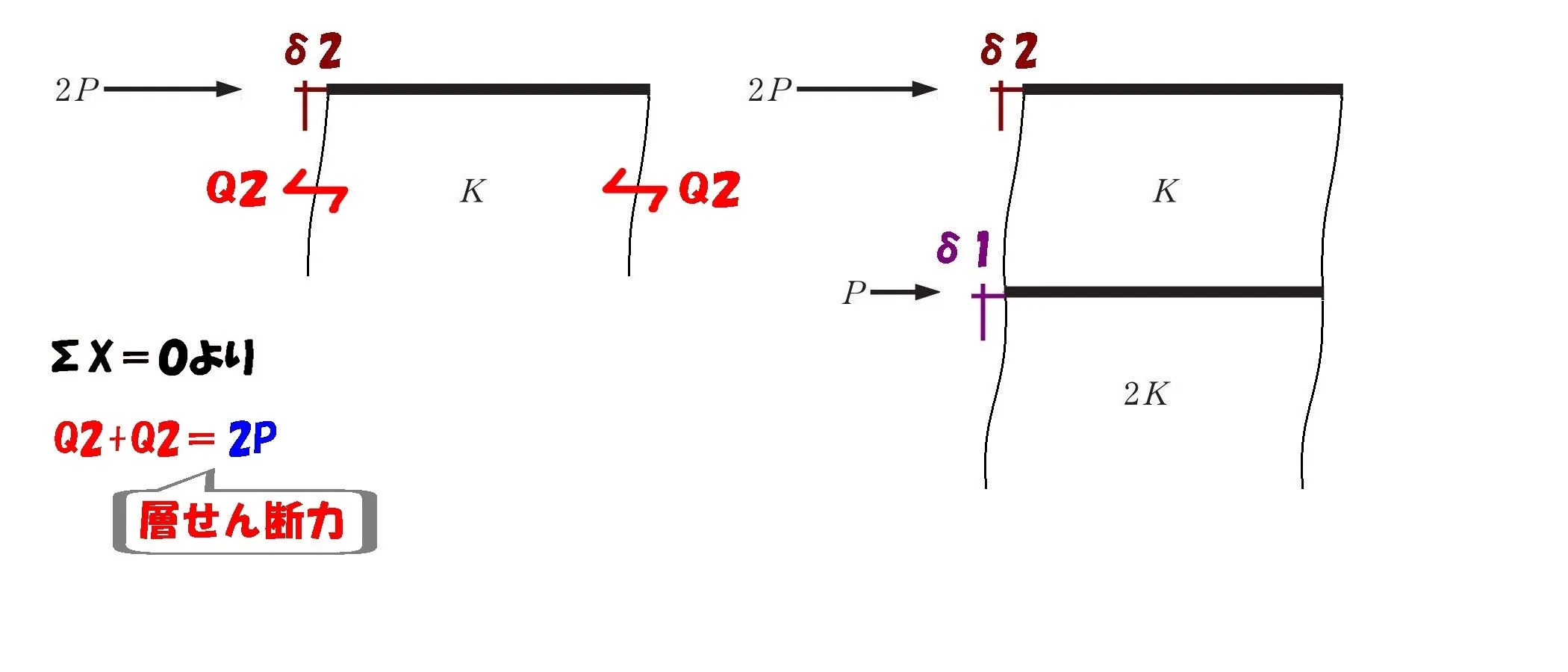

$$\Sigma X=0より,$$$$2P-Q2-Q2=0$$$$⇨Q2+Q2=2P$$
$$(水平力との吊り合い式が成立する)$$
公式
$$\Sigma X=0$$



Σエックス!
1層目の層せん断力
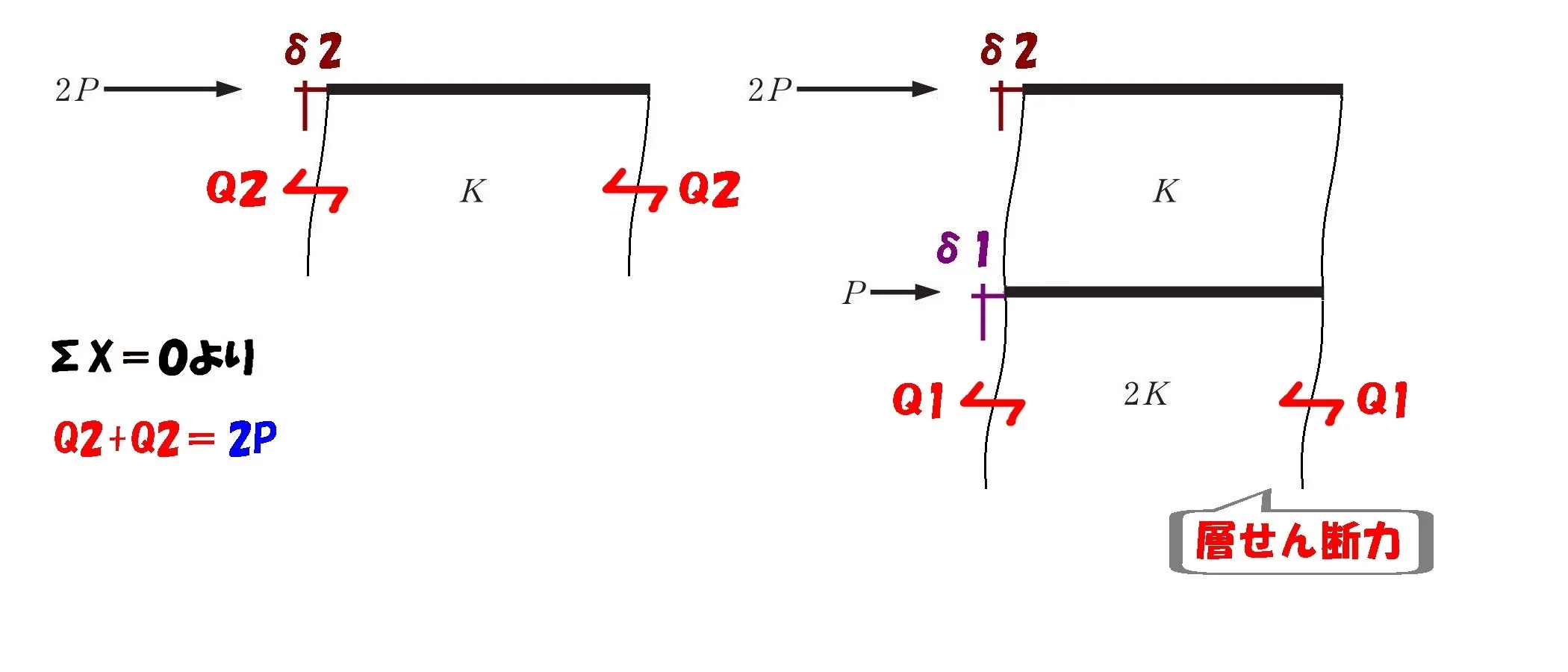

1層目の層せん断力「Q1」を求めます。
水平力との吊り合いを取る
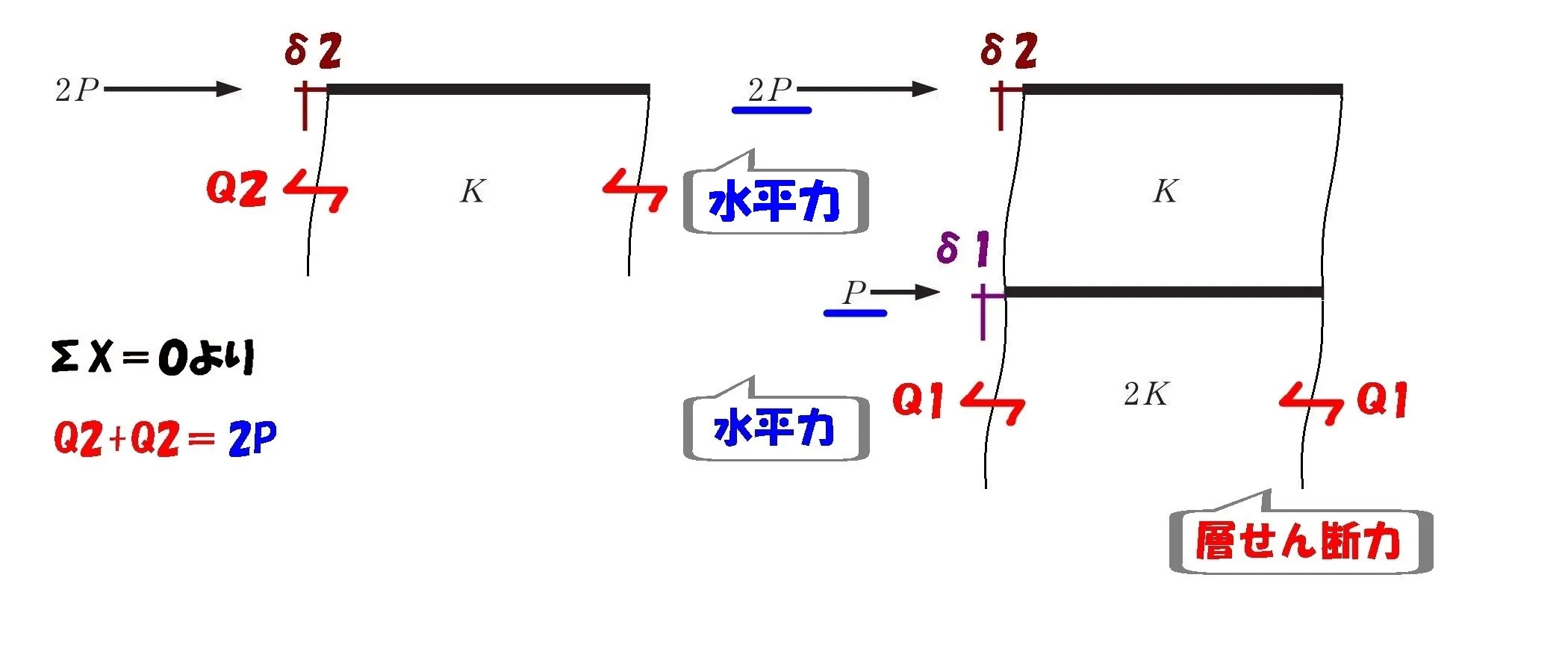

「水平力と層せん断力は吊り合う」
注意点
水平力は1層目、2層目(上部に図示してあるもの全て)をΣX=0に含める
せん断力Q1を求める
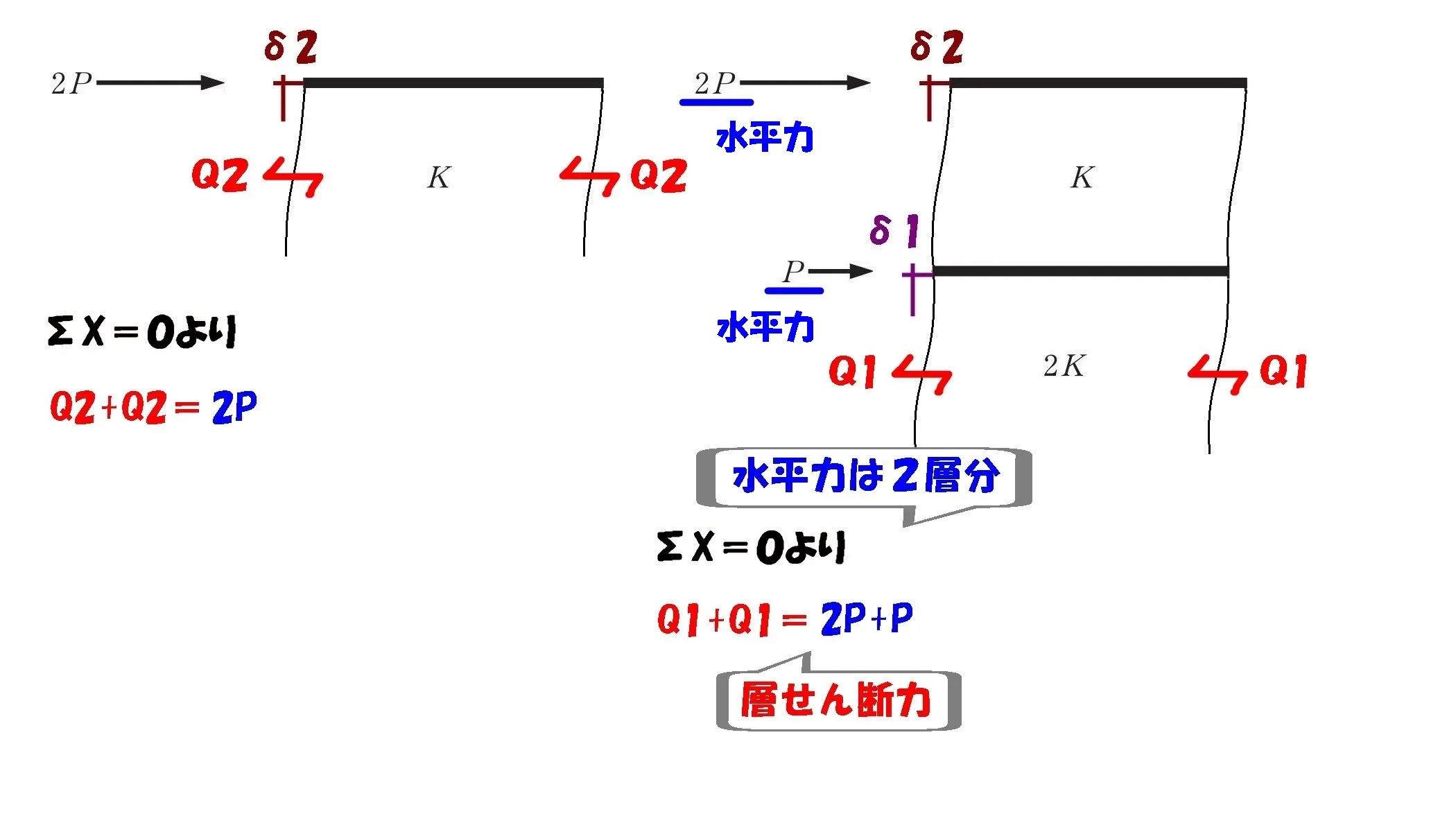

$$\Sigma X=0より,$$$$2P+P-Q1-Q1=0$$$$⇨Q1+Q1=3P$$
$$(水平力との吊り合い式が成立する)$$
公式
$$\Sigma X=0$$



Σエックス!
4.層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める
層間変位の公式
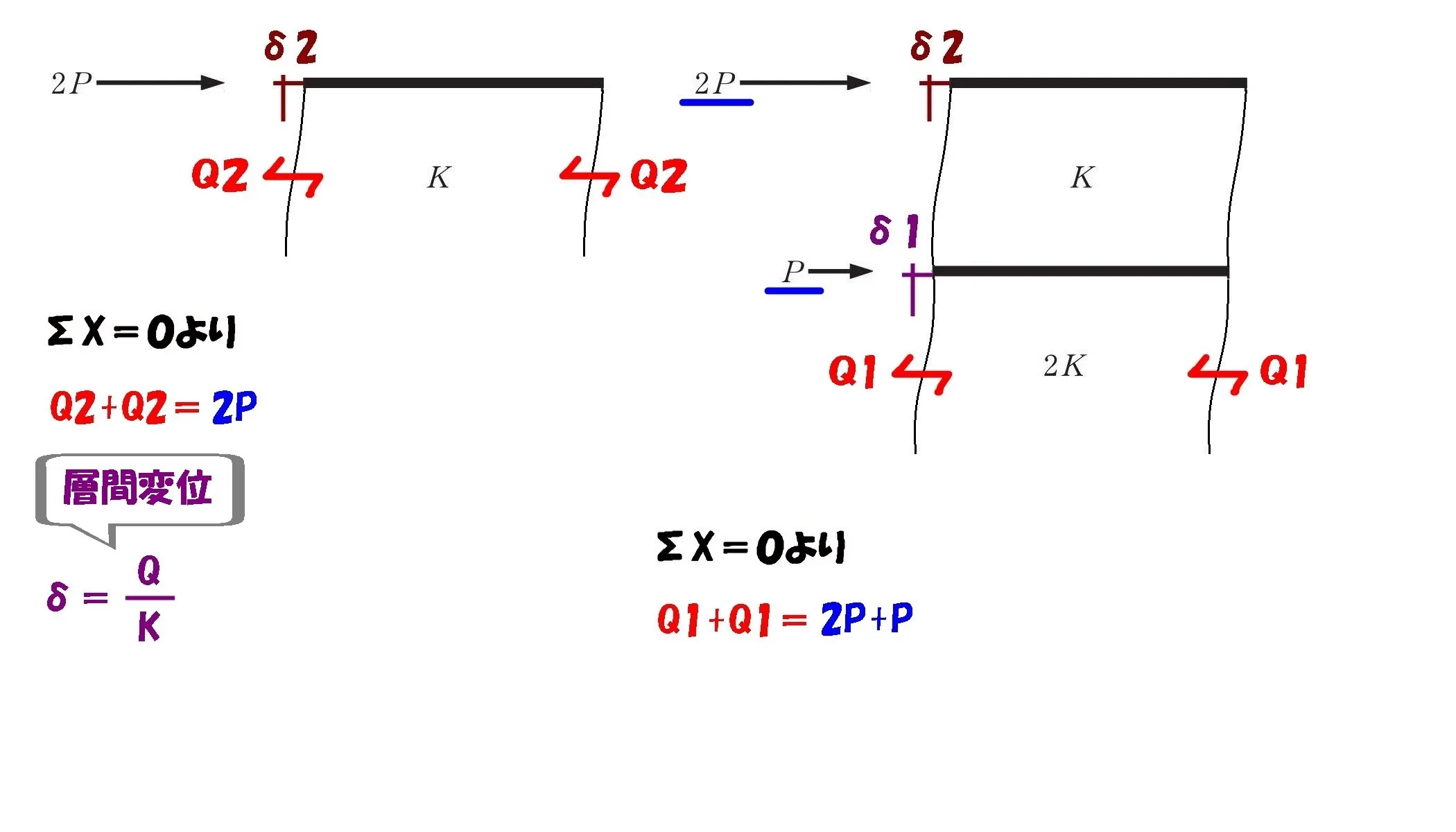

$$層間変位:\delta=\frac{ Q }{ K }$$
層せん断力Q/水平剛性Kの関係より、1階と2階の層せん断力の比(δ1:δ2)を求めましょう。
1F:2Fを比較する
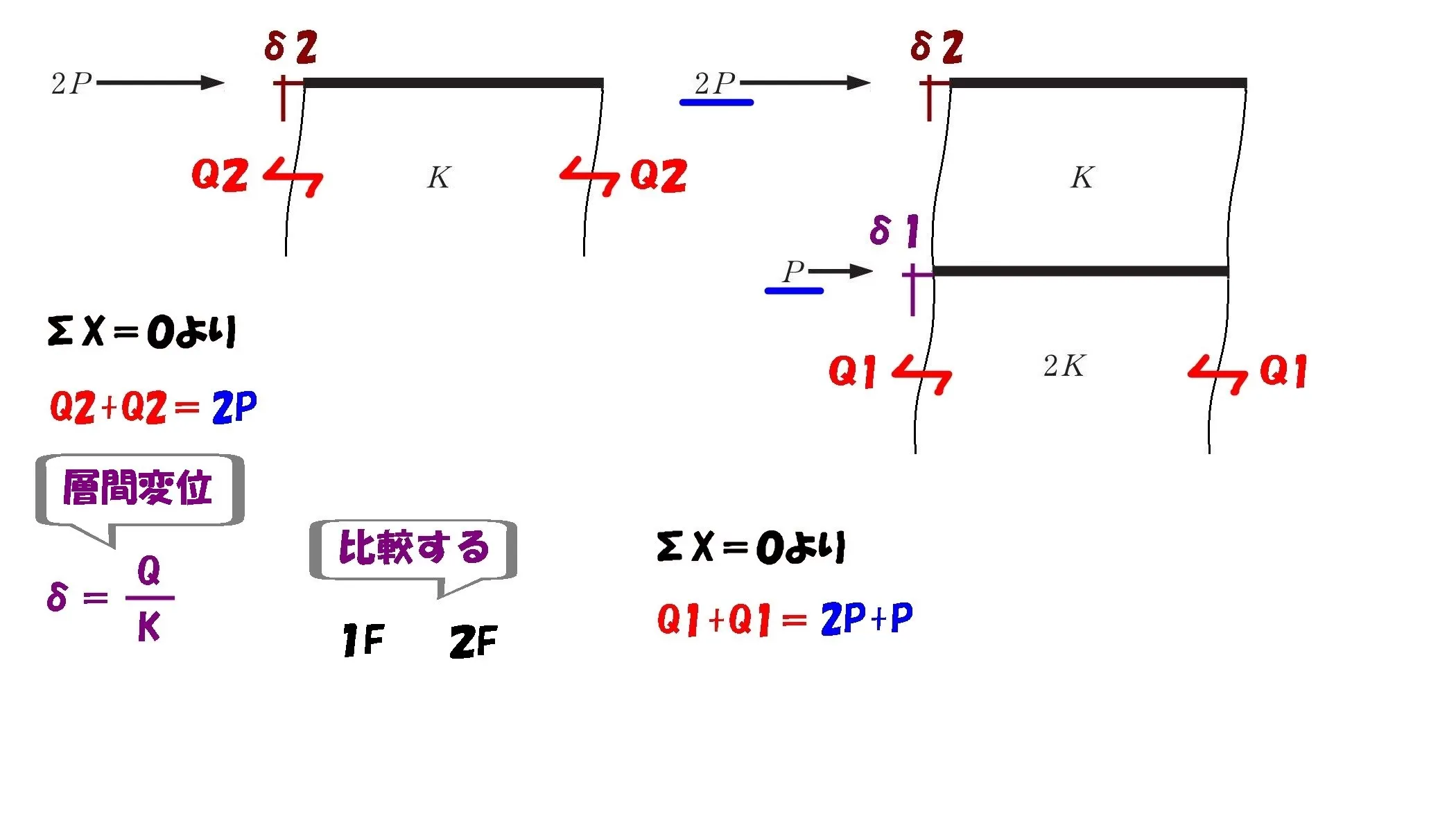

問題用紙の余白に「1F:2F」と並べて書きます。
$$\{\delta 1:\delta 2=1F:2F\}$$
層せん断力の比
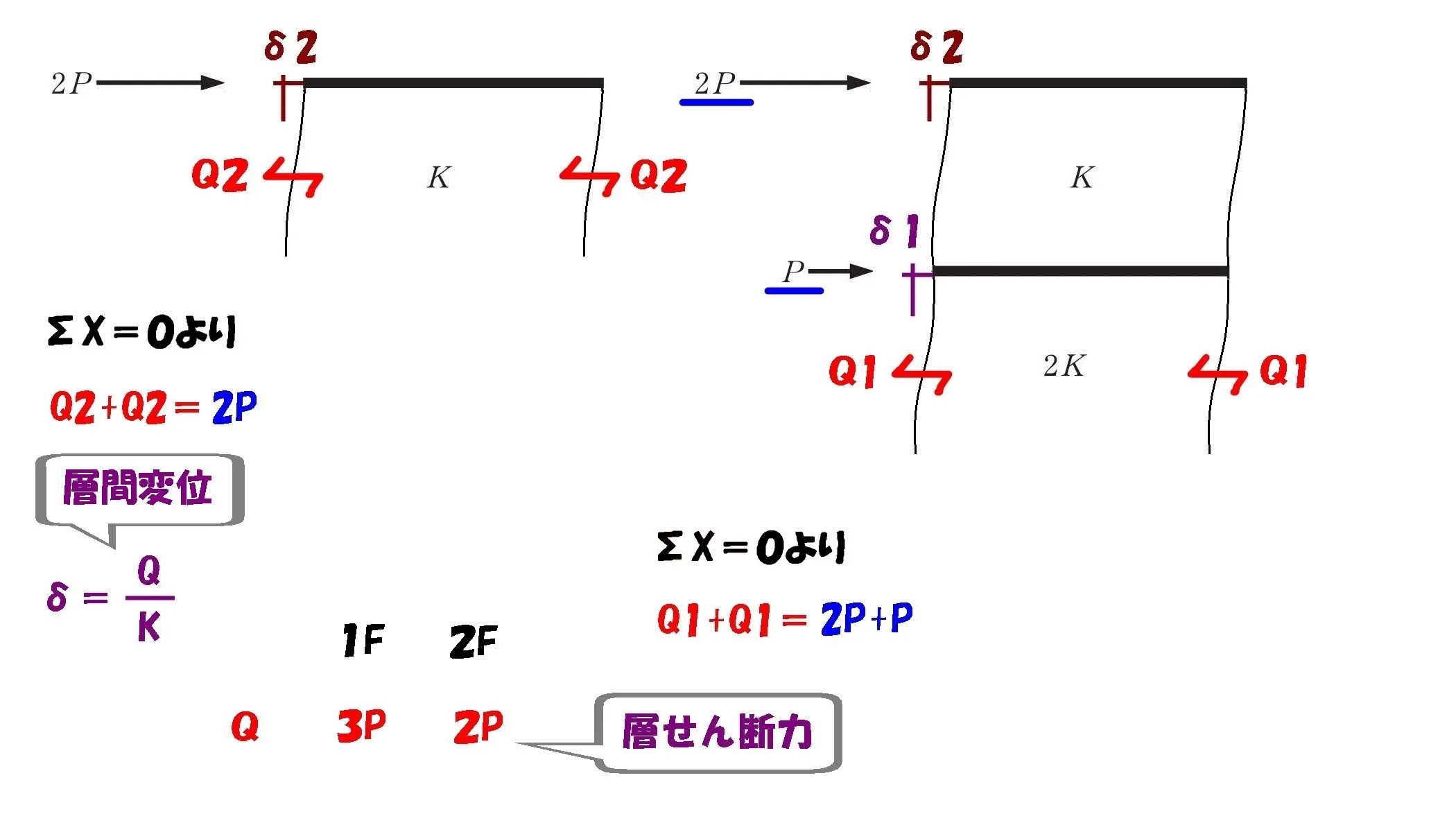

$$\{層せん断力の比=3P:2P\}$$
水平剛性の比
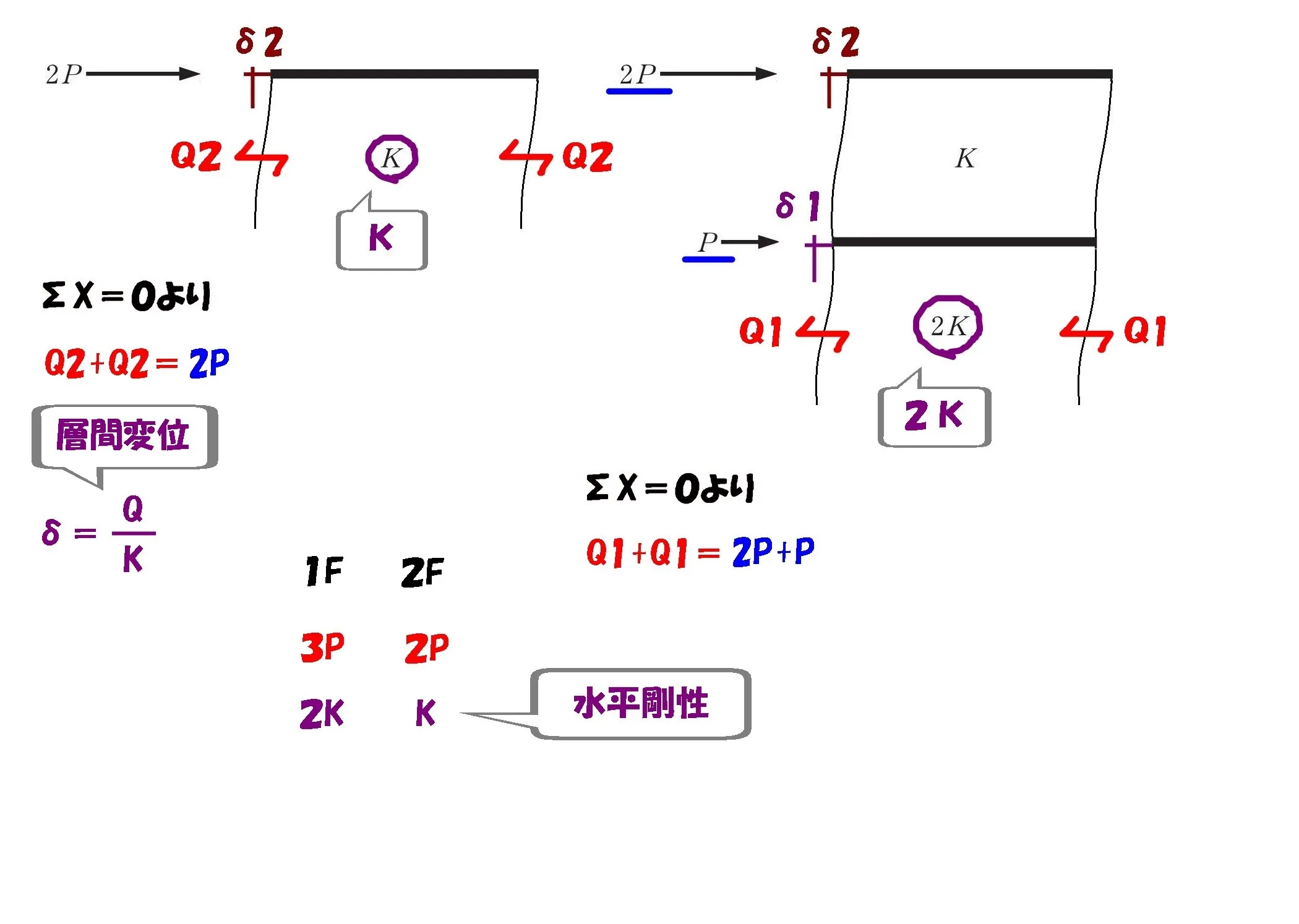

$$\{水平剛性の比=2K:K\}$$



比べる要素を
左右に書き出していく。
Q/Kの比
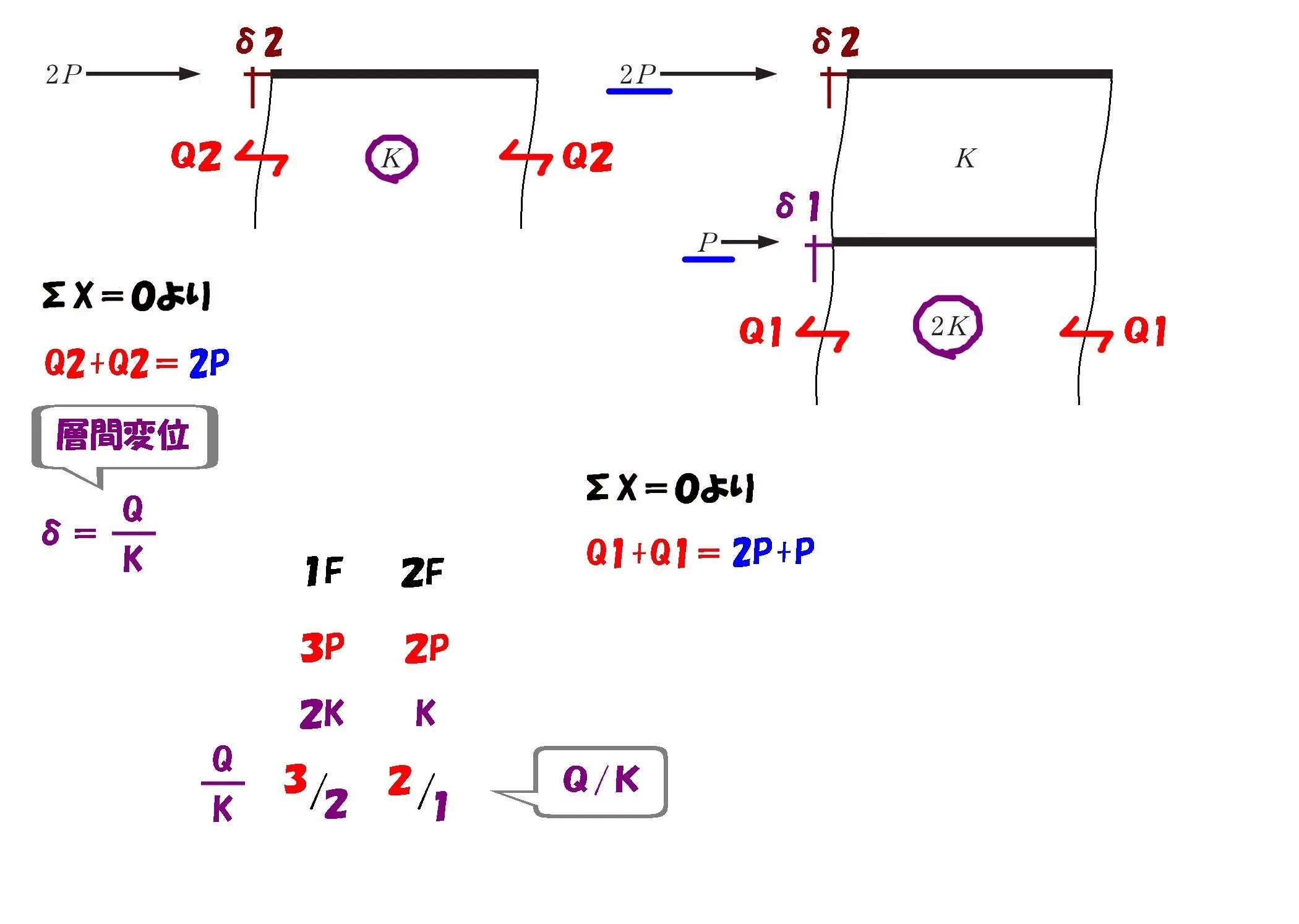

$$\{\frac{ Q }{ K }の比=\frac{ 3P }{ 2K }:\frac{ 2P }{ K }\}$$
層間変位の比
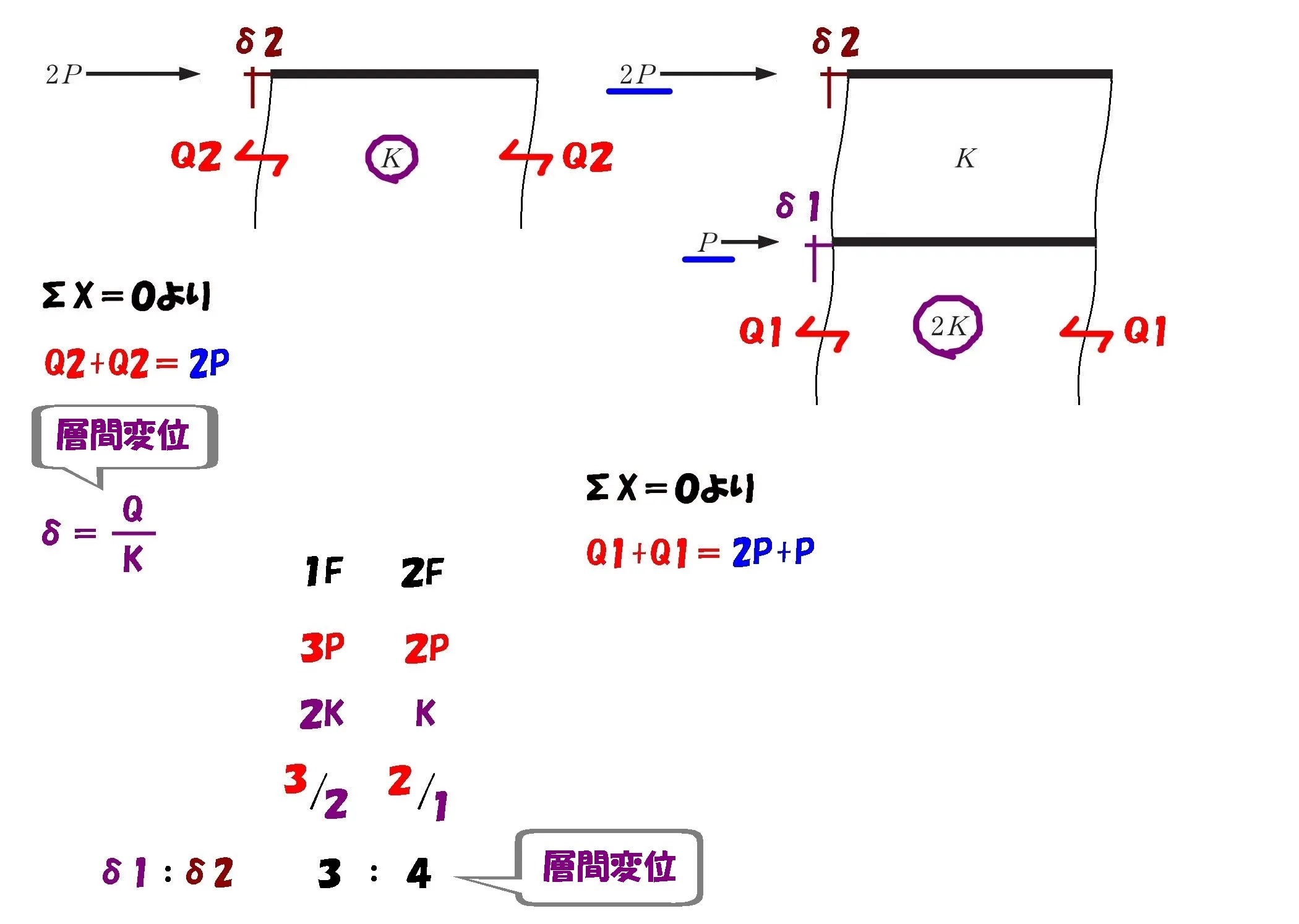

$$\{\frac{ 3P }{ 2K }:\frac{ 2P }{ K }=3:4\}$$
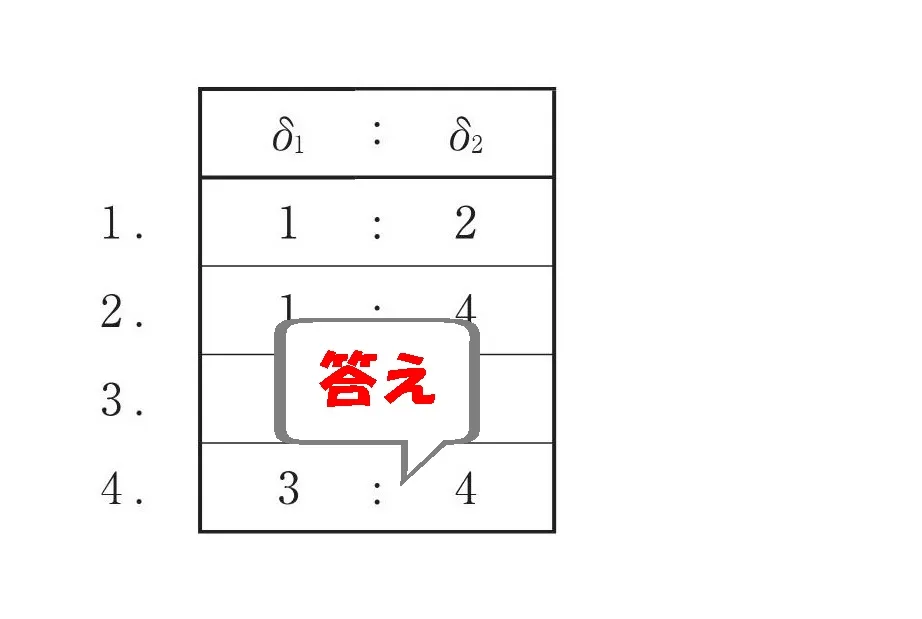
$$\delta 1:\delta 2=1F:2F=3:4$$



比べる要素を
左右に書き出していこう。
答え.4

攻略ポイント
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める


この動画を YouTube で視聴
2層構造物
難易度:★★★★★
2層構造物は、構造力学における基本的な考え方をすべて試される問題です。
反力・軸力・モーメント・せん断力など、部材に作用する力を様々な切り口で出題されます。
どのパーツを問われても解き方の手順は決まっているので、必ずマスターしておきましょう。



攻略法を押さえれば
2層構造物も怖くない。



ラーメンを食うな!


この動画を YouTube で視聴
考え方
せん断力は「モーメント図の傾き」として捉える。
攻略ポイント
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
問題
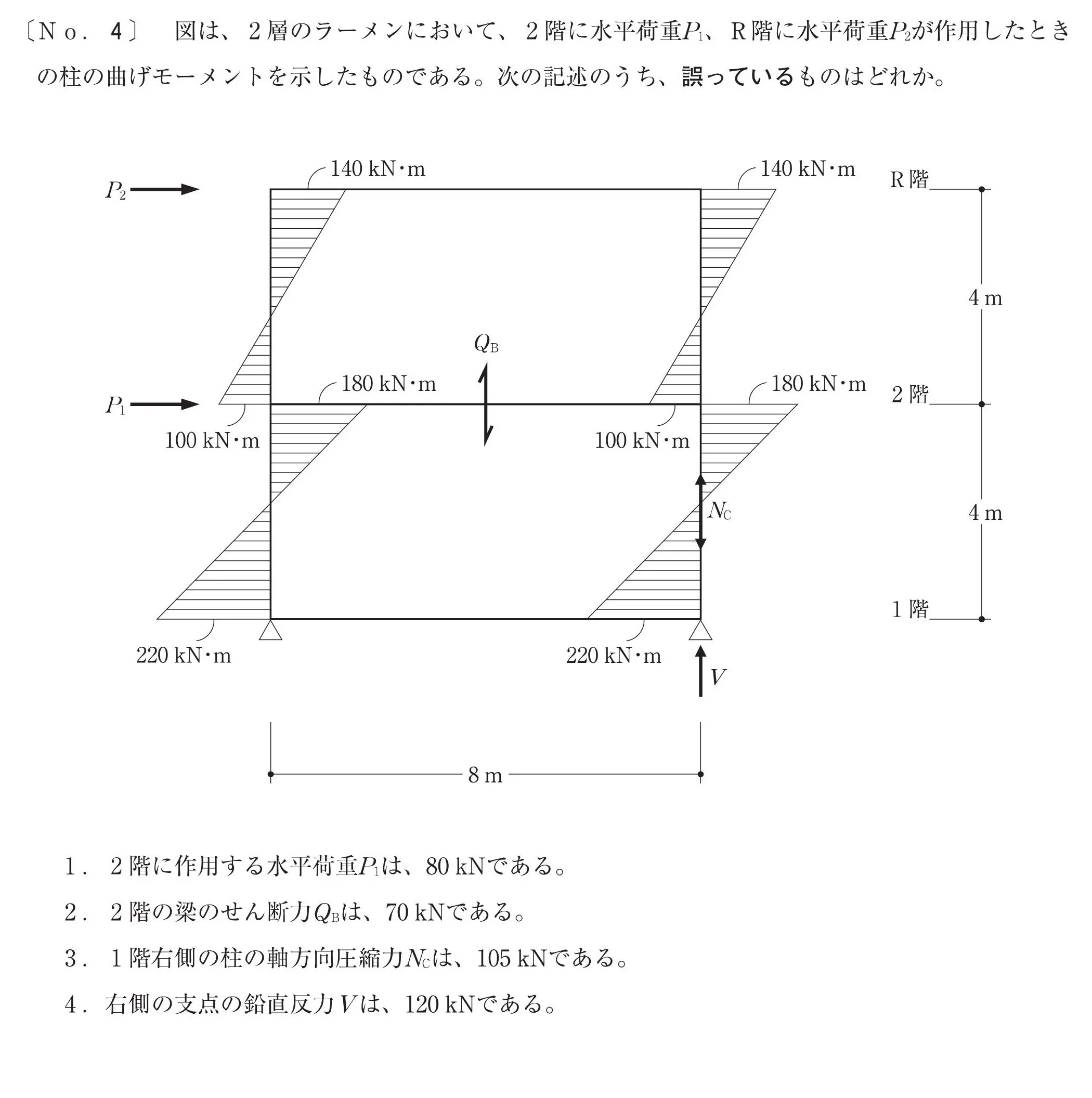

枝.1


$$1.[2階に作用する水平荷重P1は、80kNである。]$$
1.部材を切断して取り出す
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
層を切断する
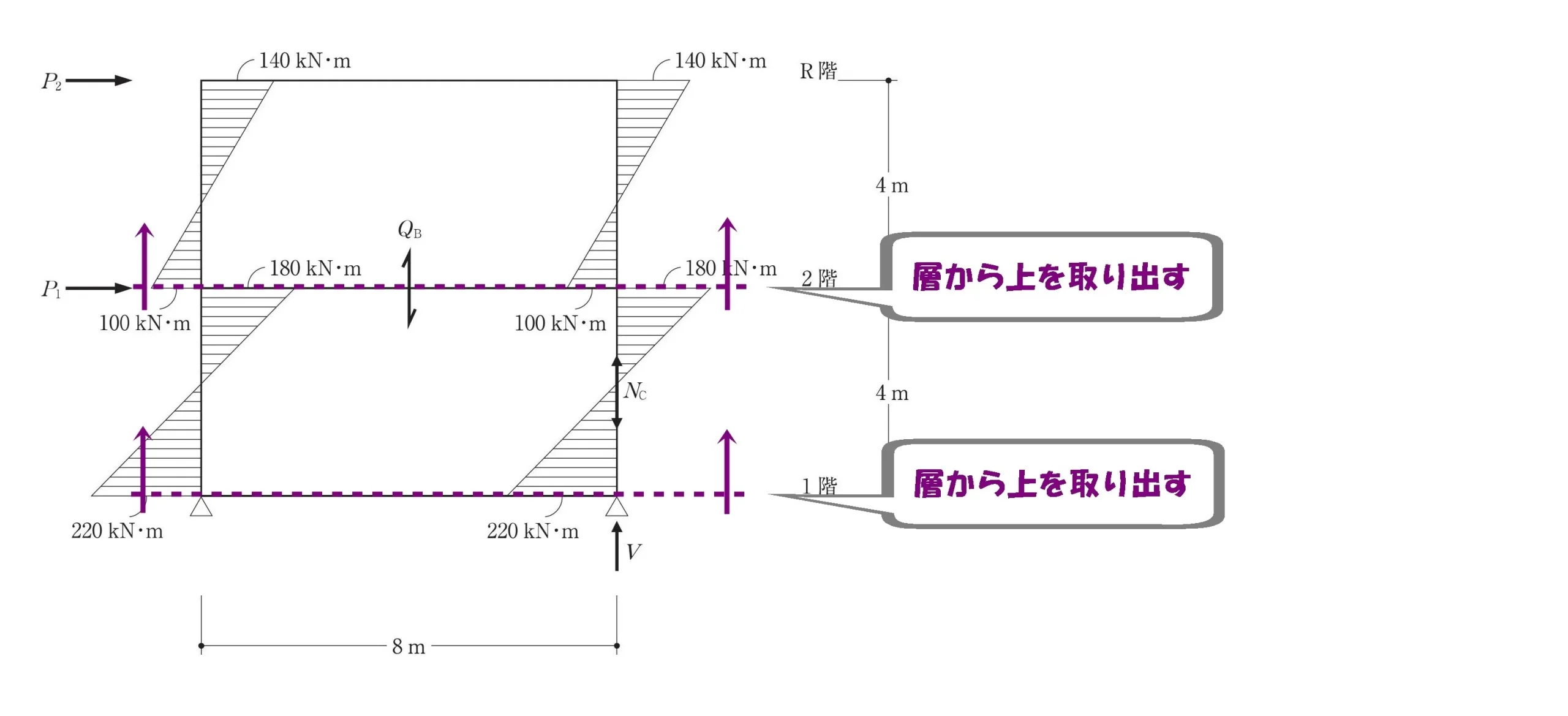

切断して部材を取り出す
- 2層目から上部を取り出す。
- 1層目から上部を取り出す。



伝家の宝刀、部材斬り!
2層目から上部を取り出す
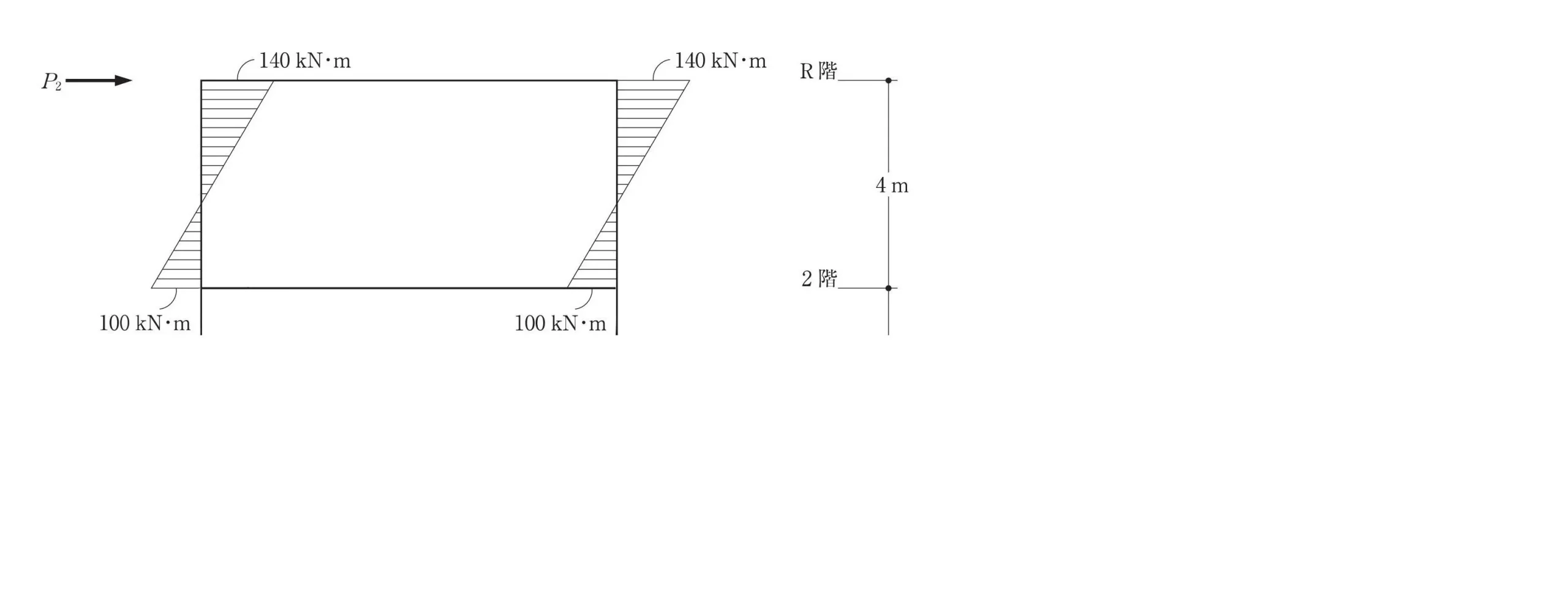

水平方向の力の吊り合い式ΣX=0を使って、せん断力を求めます。
モーメント=力×距離
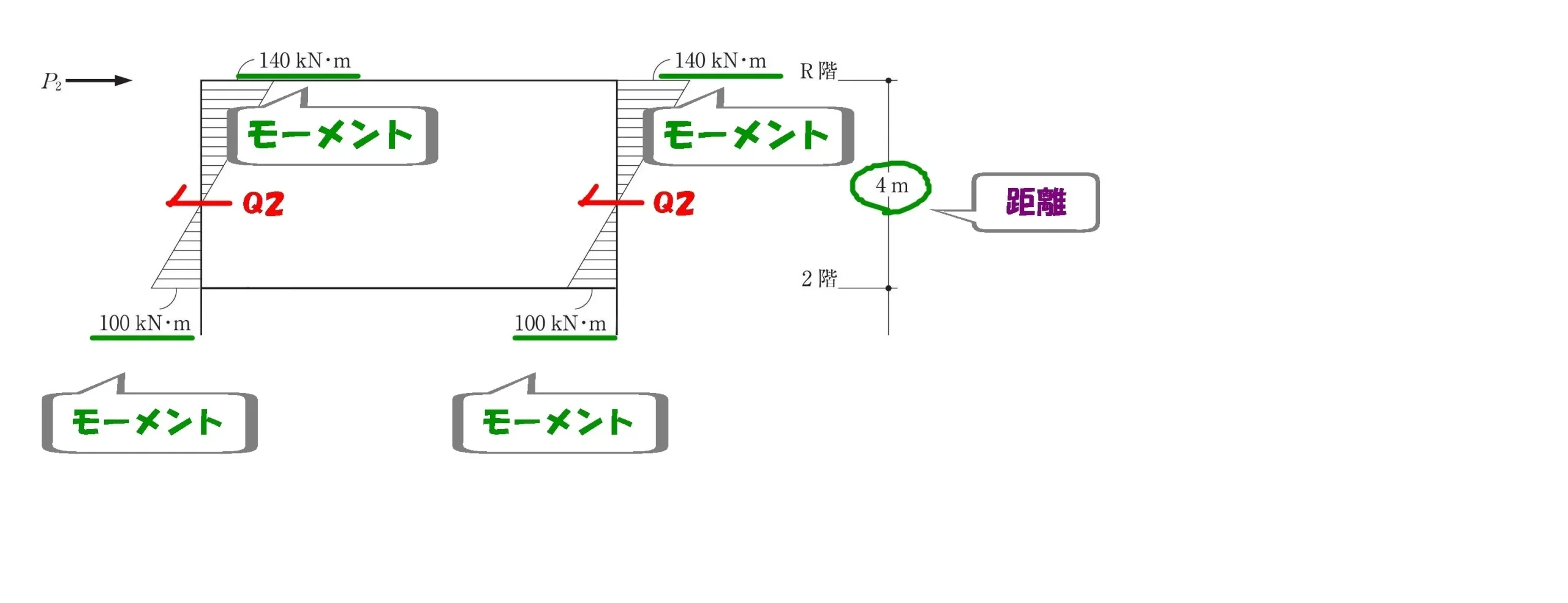

$$モーメント=力×距離$$$$モーメント=(140kN+100kN)$$$$力=Q2・距離=4m$$
3.柱(2階)のせん断力を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
モーメント図の傾き
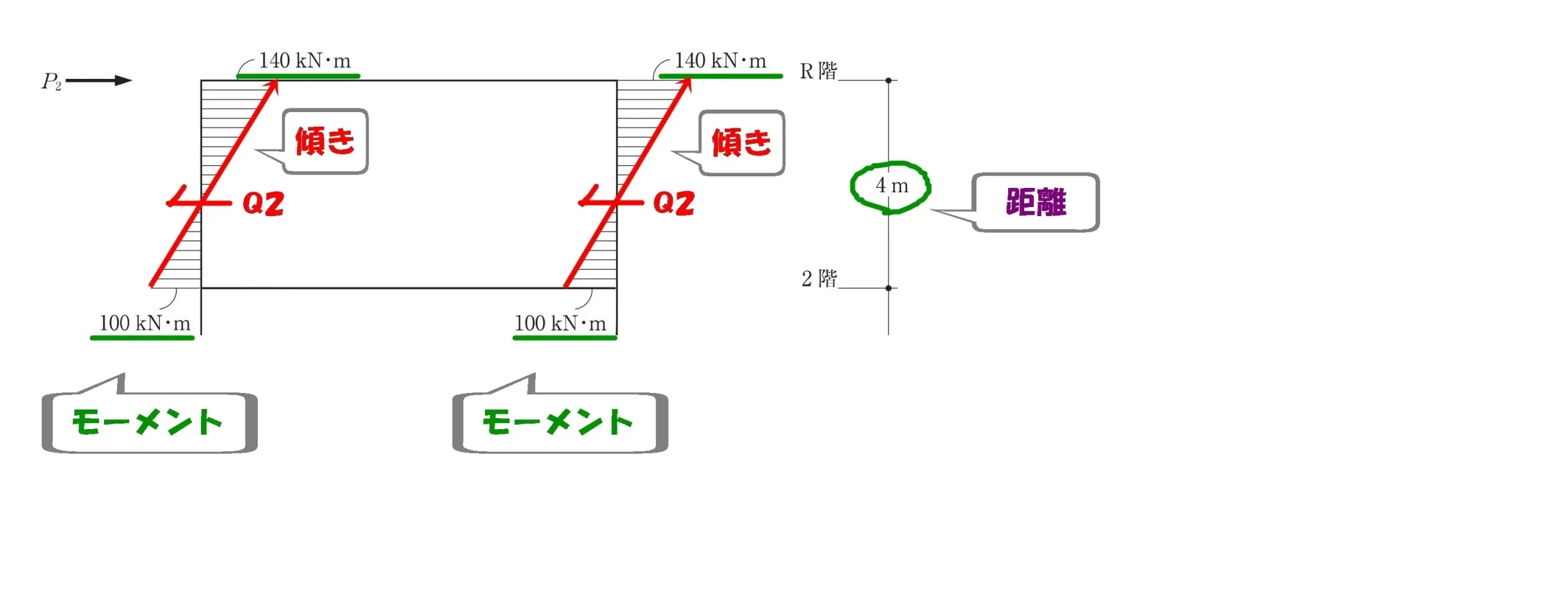

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
考え方
せん断力は「モーメント図の傾き」として捉える。



この考え方は覚えておこう。
せん断力Q2を求める
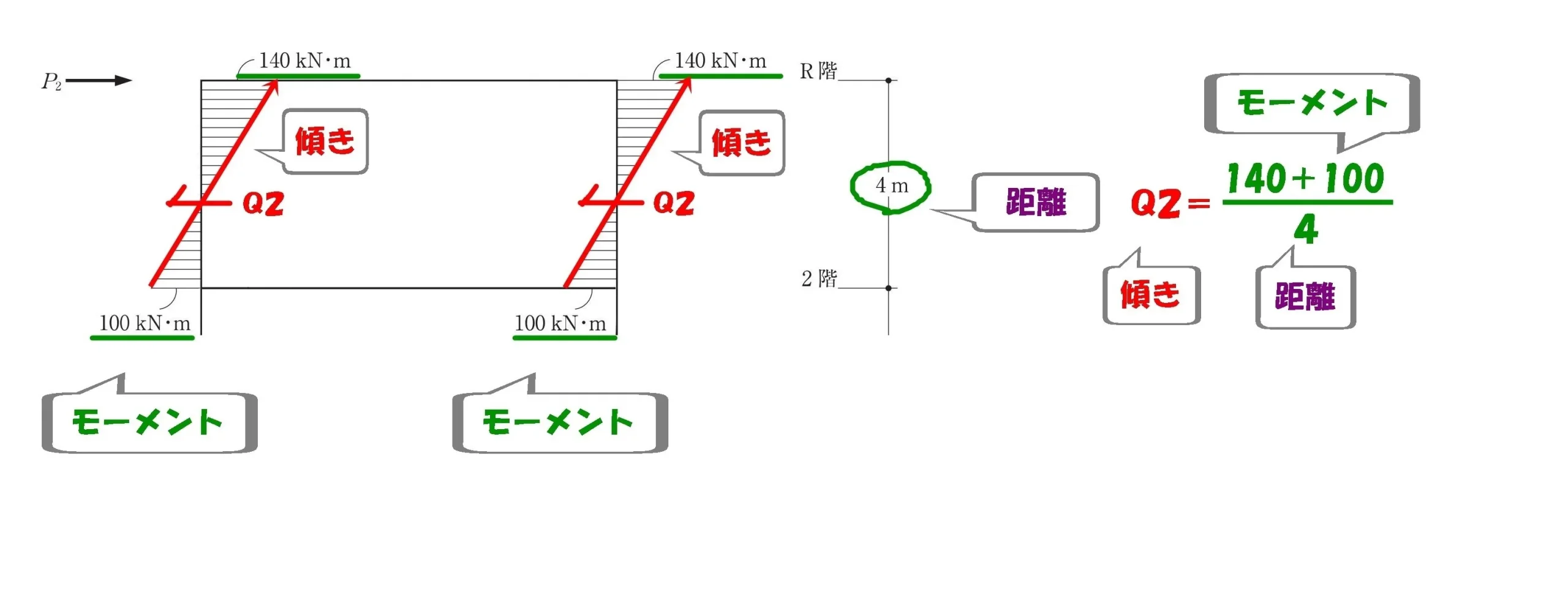

$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }より,$$
$$せん断力:Q2=\frac{ 140+100 }{ 4 }=60kN$$
4ΣX=0から未知数を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
吊り合い式ΣX=0
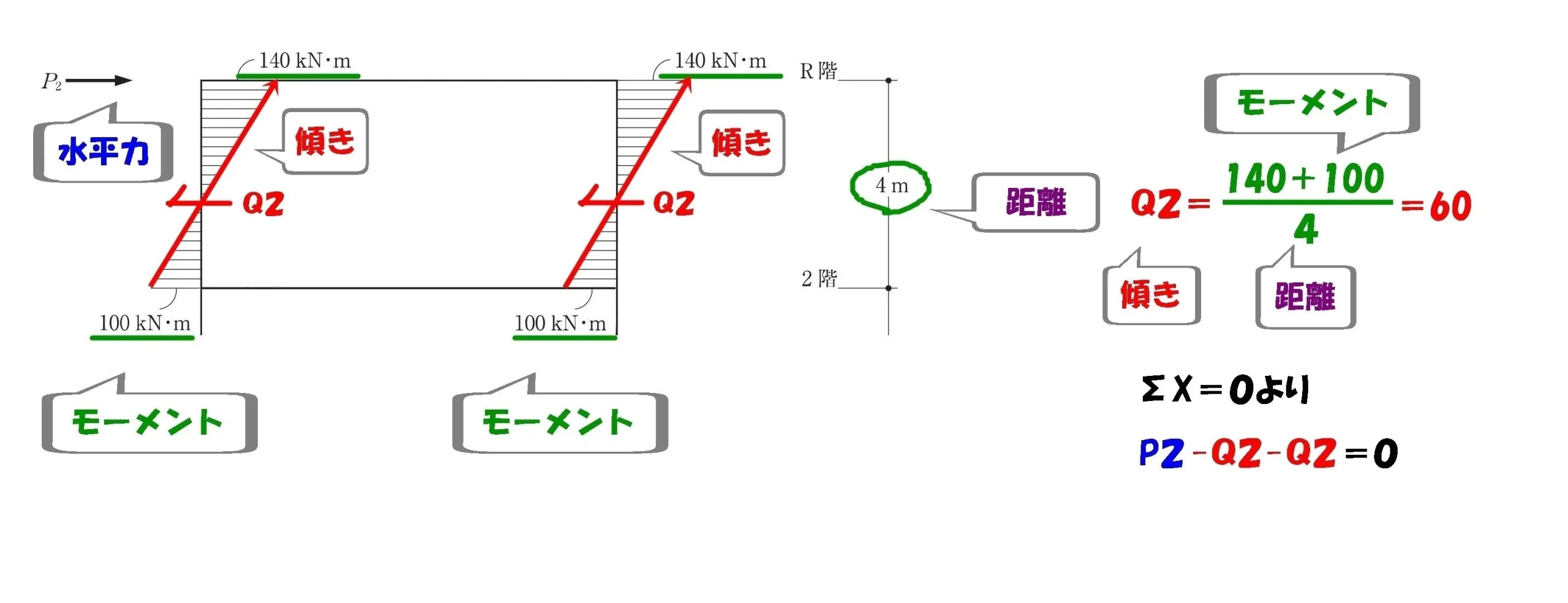

$$\Sigma X=0より,$$$$P2-Q2-Q2=0が成り立つ$$
水平荷重P2を求める
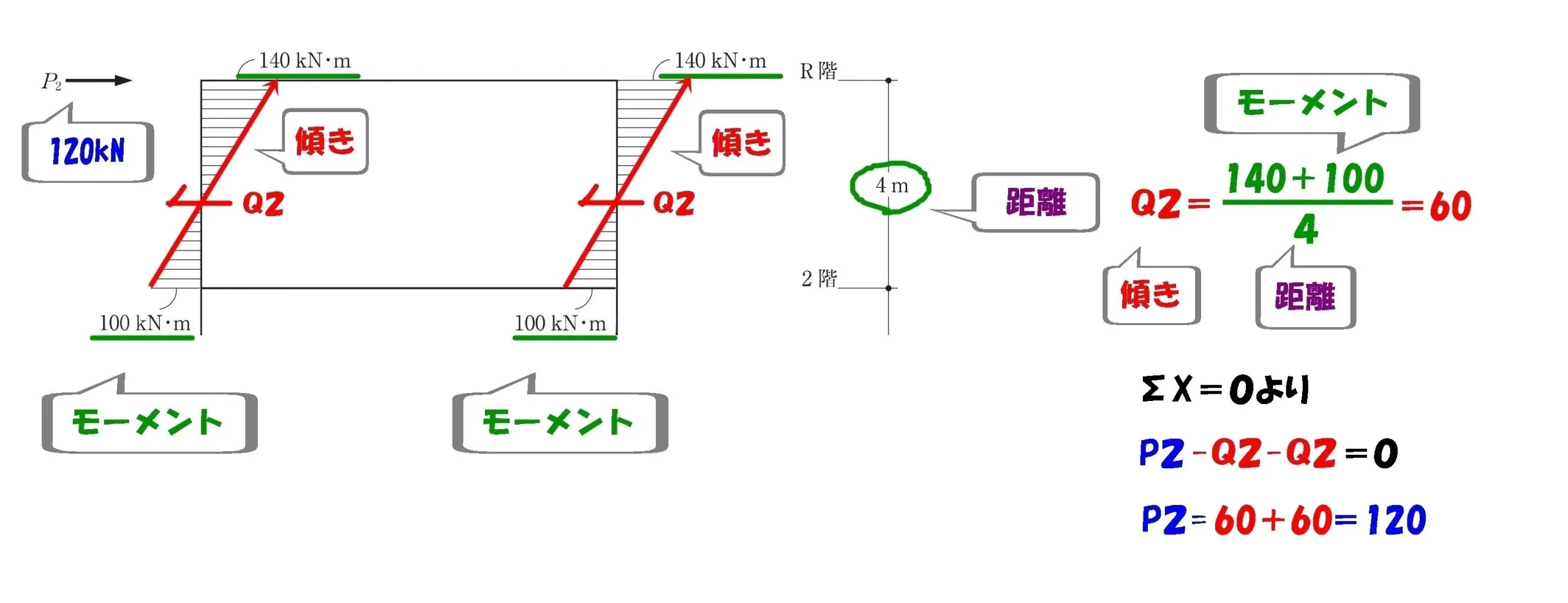

$$P2-Q2-Q2=0より,$$$$P2=Q2+Q2=60+60=120kN$$
公式
$$\Sigma X=0$$



Σエックス!
3.柱(1階)のせん断力を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
せん断力Q1を求める
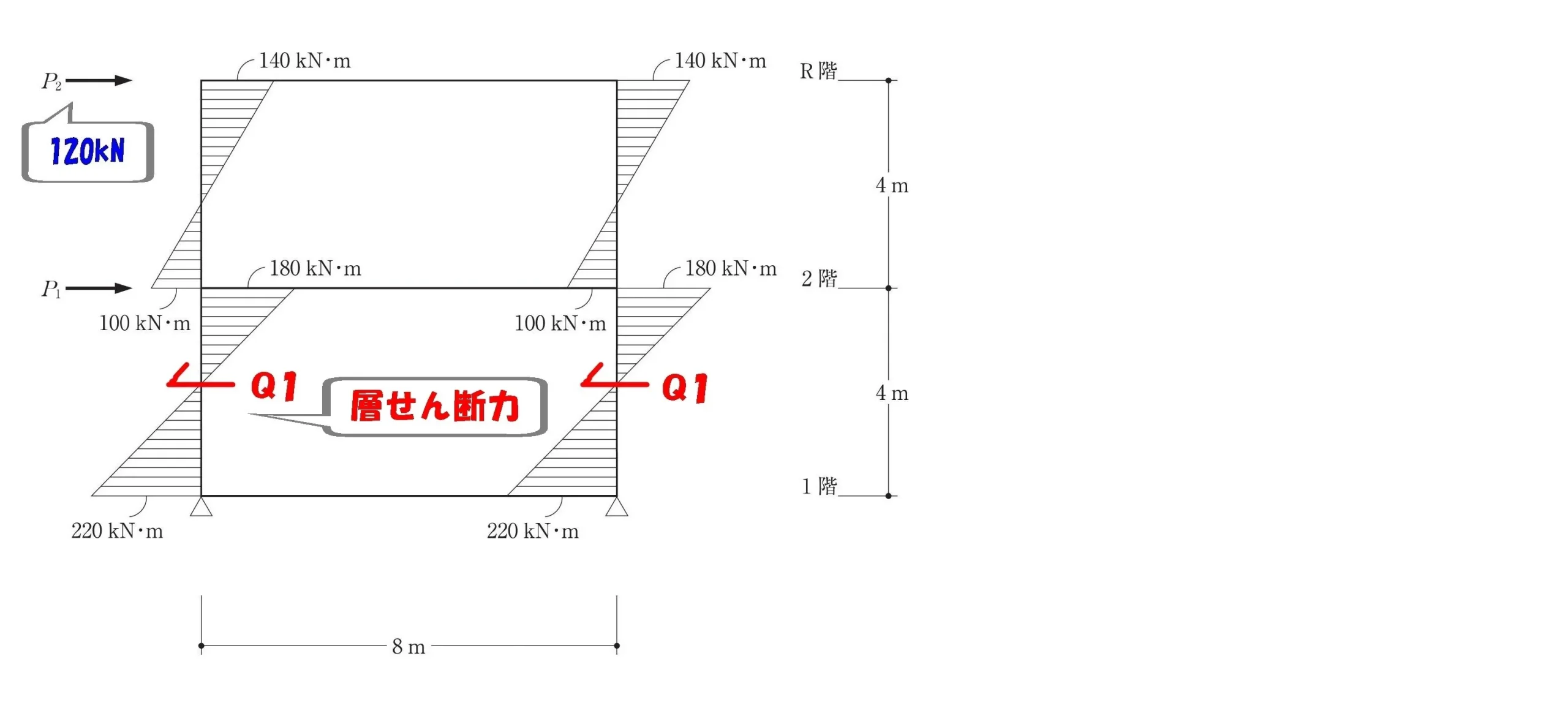

水平方向の力の吊り合い式ΣX=0を使って、せん断力を求めます。
モーメント=力×距離
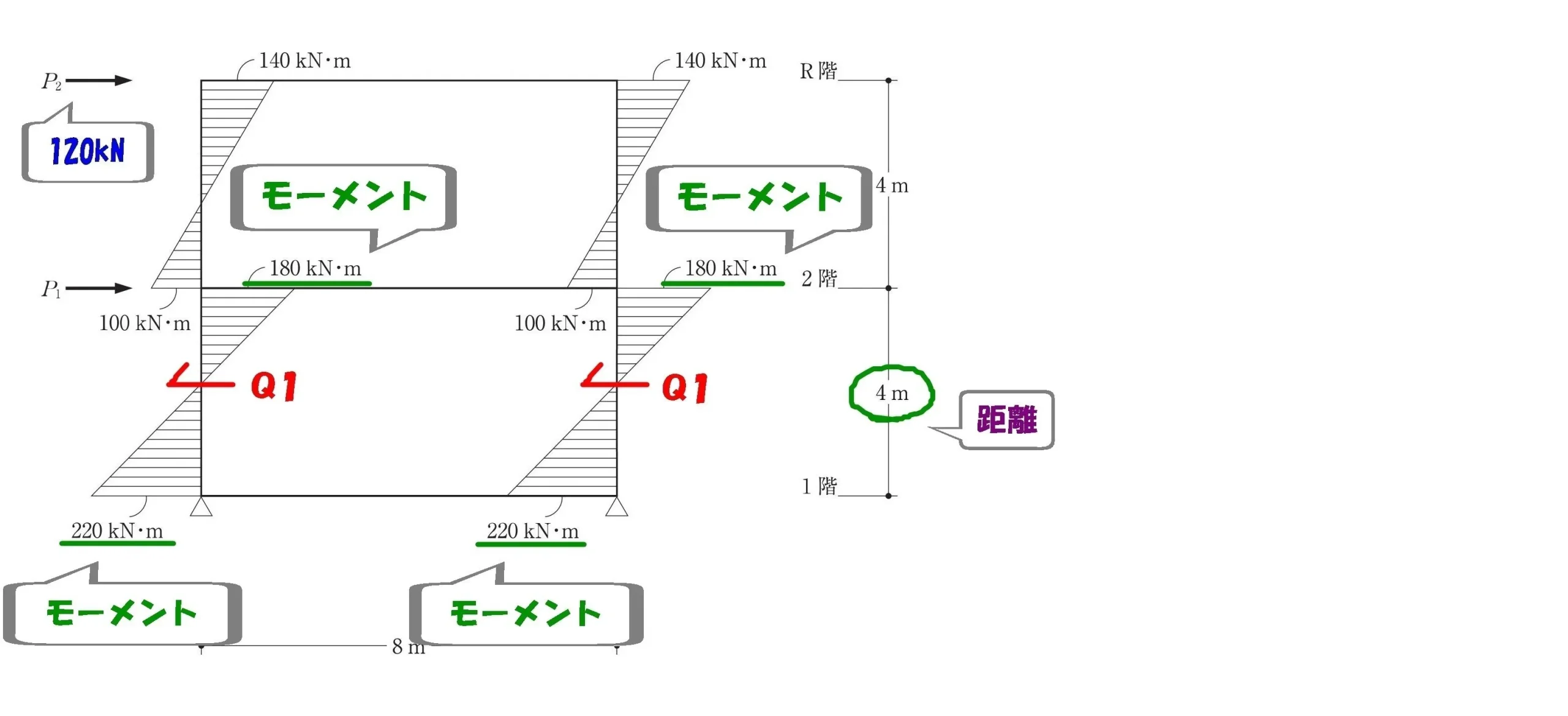

$$モーメント=力×距離$$$$モーメント=(180kN+220kN)$$$$力=Q1・距離=4m$$
考え方
せん断力は「モーメント図の傾き」として捉える。
モーメント図の傾き
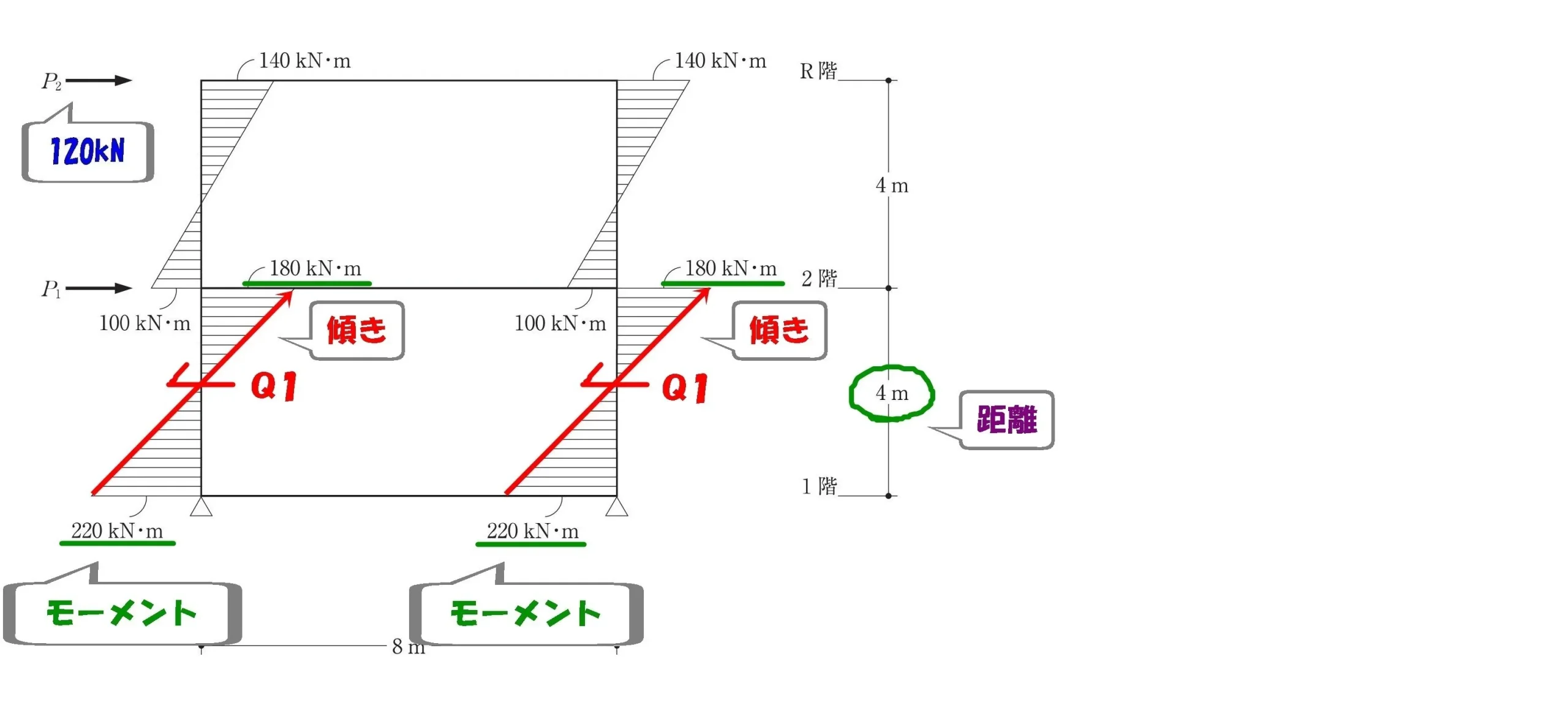

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
せん断力Q1を求める
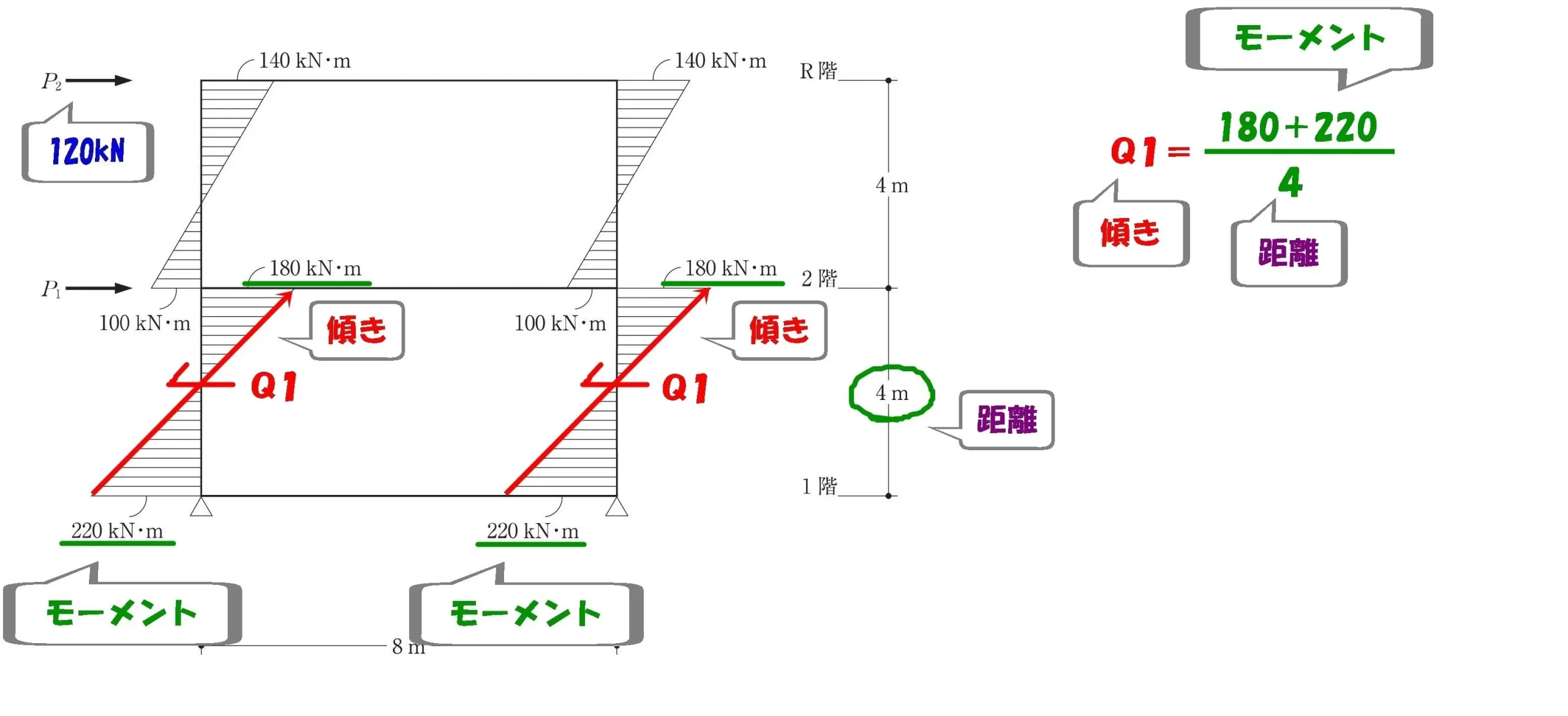

$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }より,$$
$$せん断力:Q1=\frac{ 180+220 }{ 4 }=100kN$$



せん断力は
モーメントの傾き。
4.ΣX=0から未知数を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
吊り合い式ΣX=0
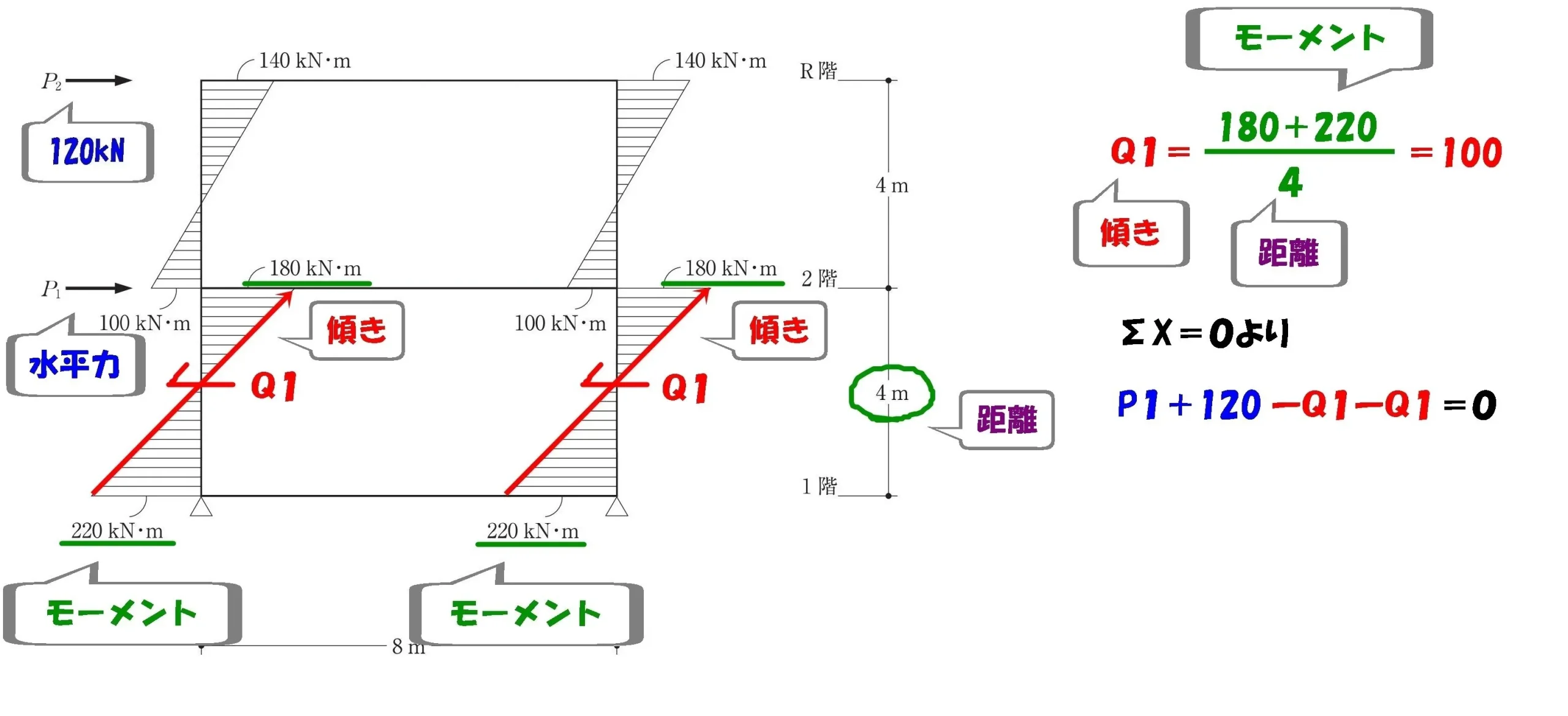

$$\Sigma X=0より,$$$$P1+P2(120kN)-Q1-Q1=0が成り立つ$$
水平荷重P1を求める
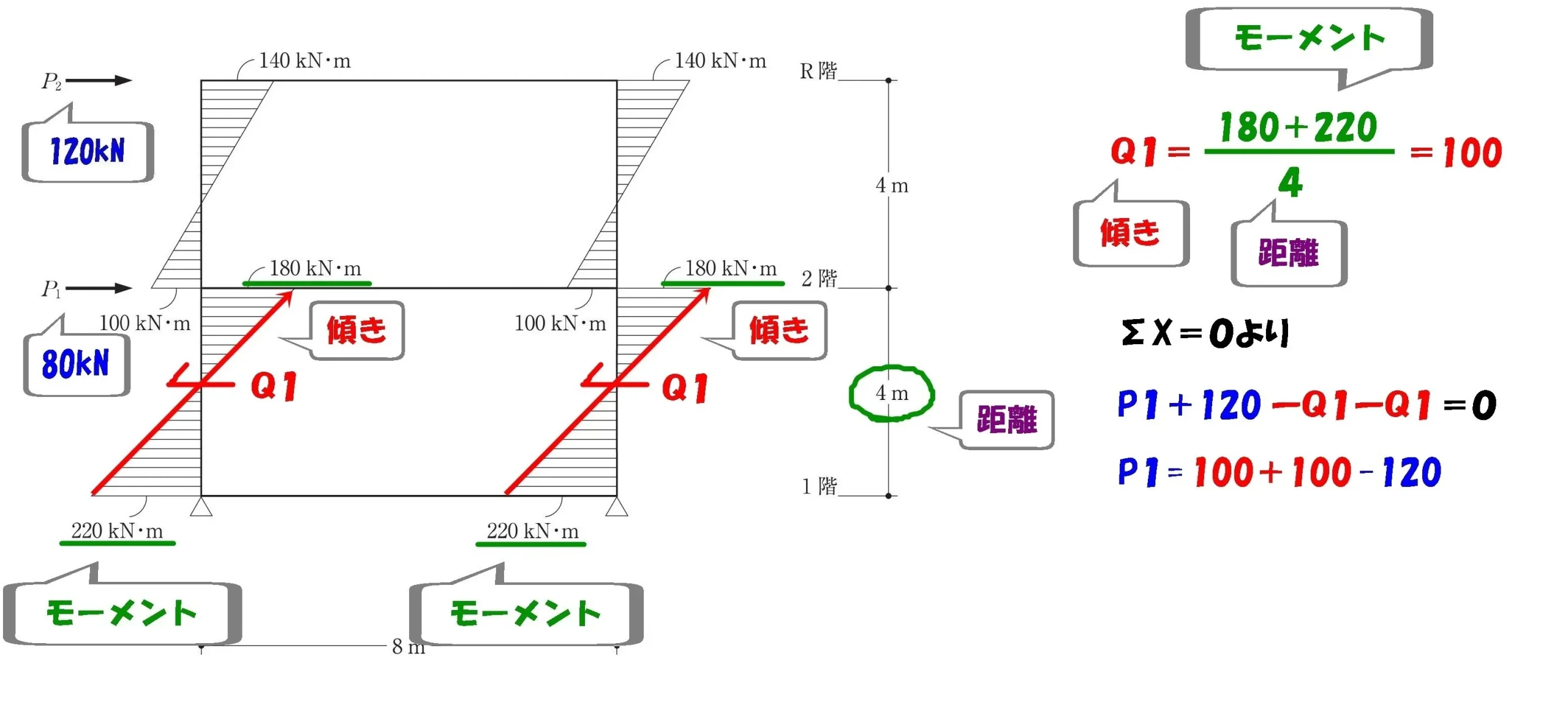

$$P1+P2-Q1-Q1=0より,$$
$$P1=Q1+Q1-P2=100+100-120=80kN$$$$水平荷重P1=80kN$$
公式
$$\Sigma X=0$$



Σエックス!
枝.2


$$2.[2階の梁のせん断力Qbは、70kNである。]$$
1.部材を切断して取り出す
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
柱を切断する
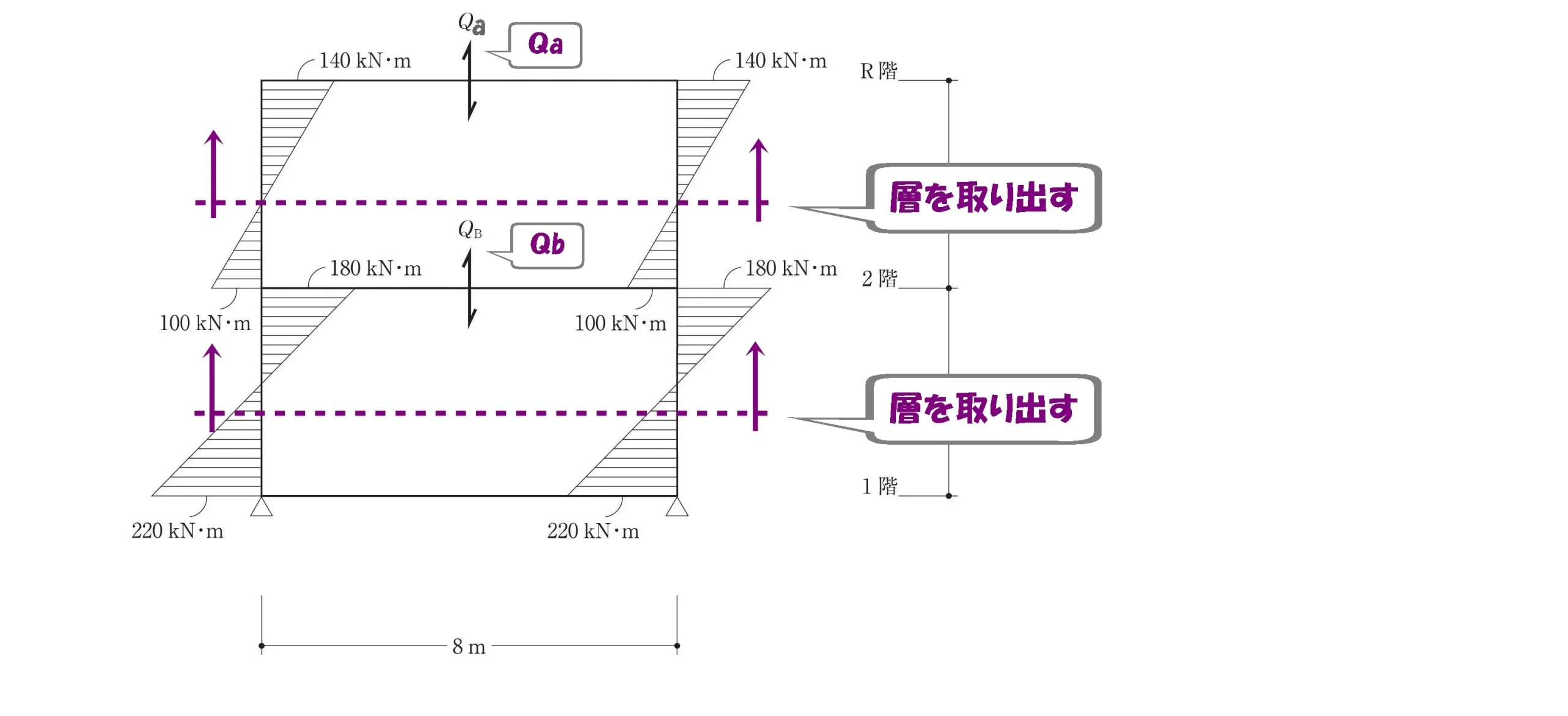

切断して部材を取り出す
- 2層目の柱から上部を取り出す。
- 1層目の柱から上部を取り出す。



伝家の宝刀、部材斬り!
2.モーメント図を描く
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
2層目から上部を取り出す
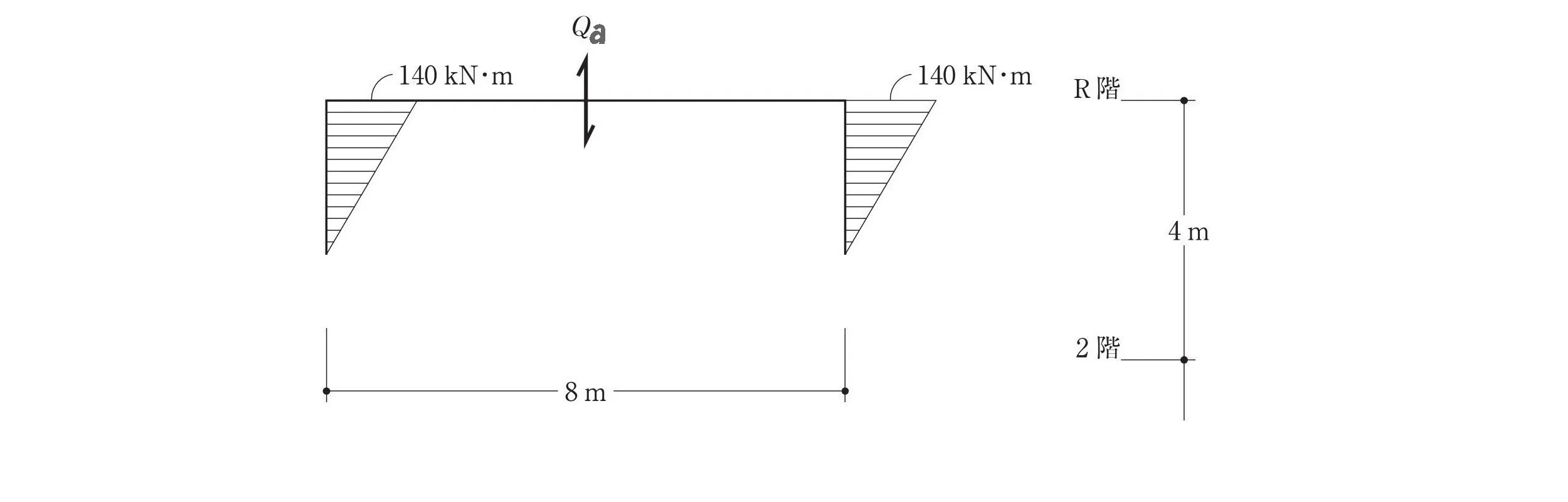

モーメント図を描く
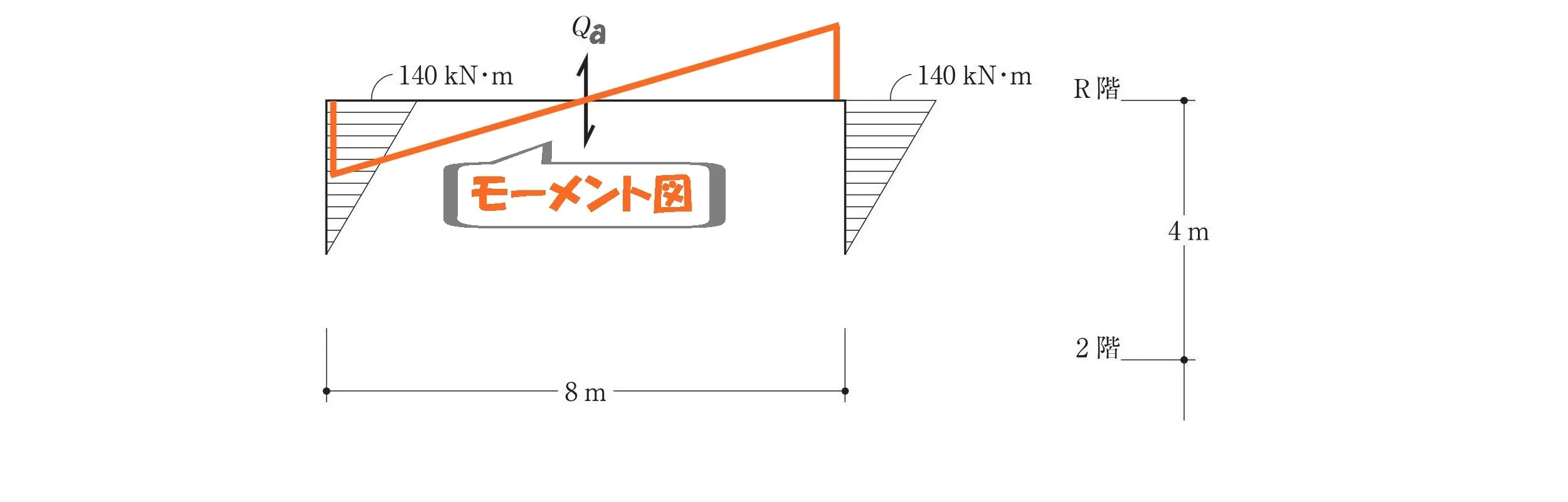

モーメント=力×距離
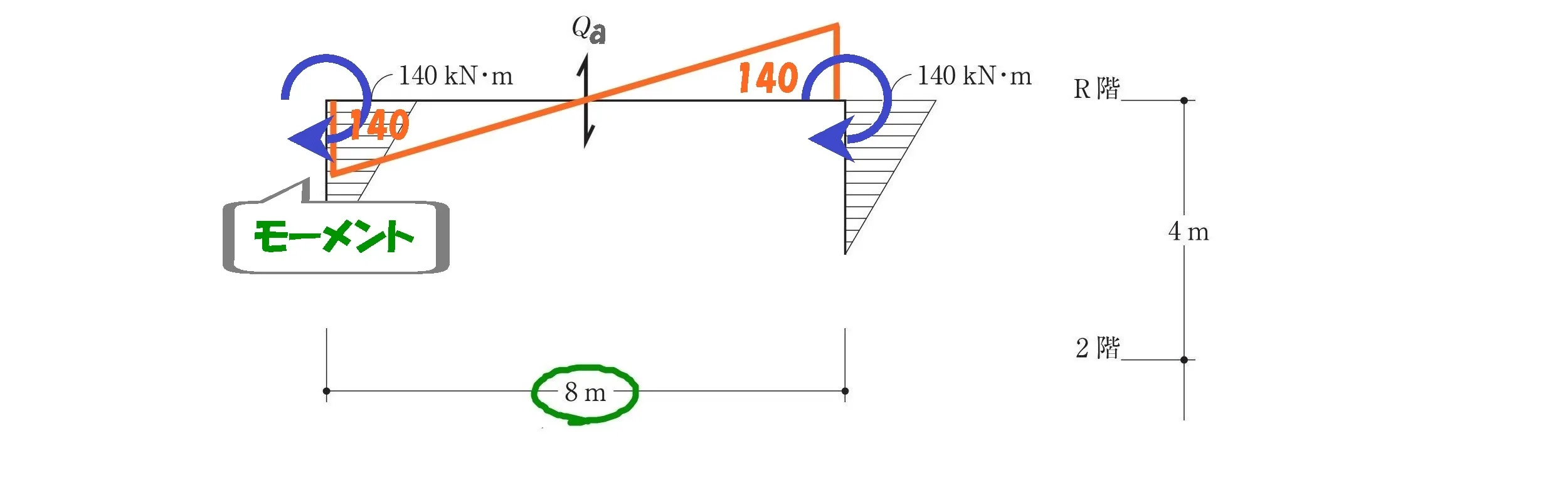

$$モーメント=力×距離$$$$モーメント=(140kN+140kN)$$$$力=Qa・距離=8m$$
3.梁(最上部)のせん断力を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
せん断力Qaを求める
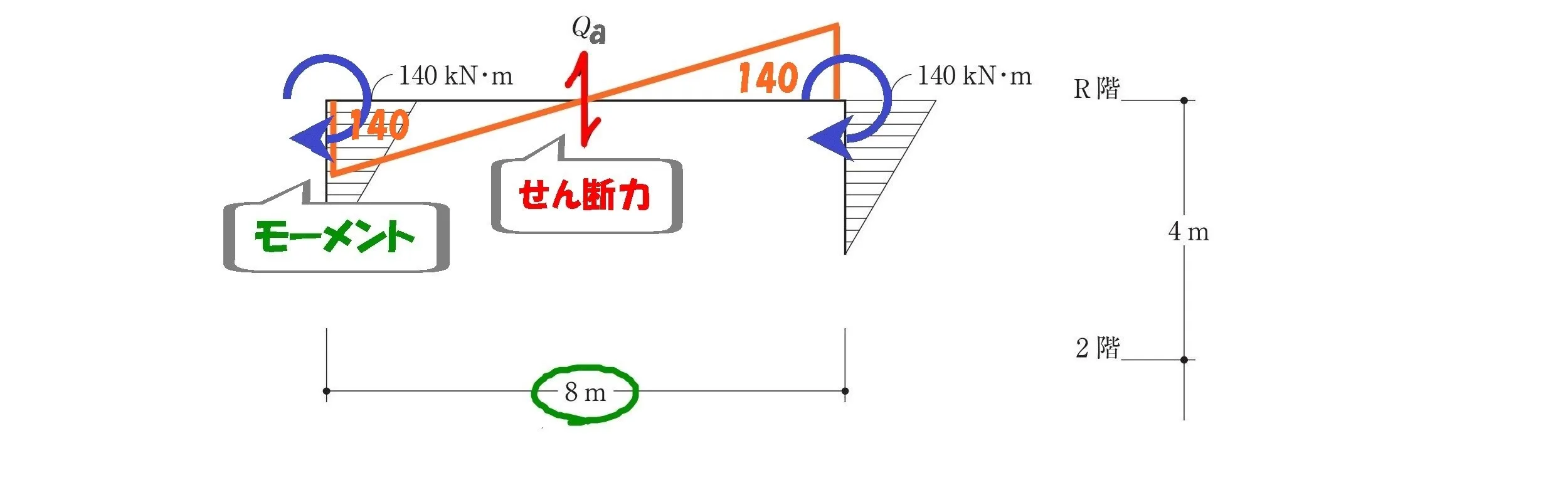

モーメント図の傾き
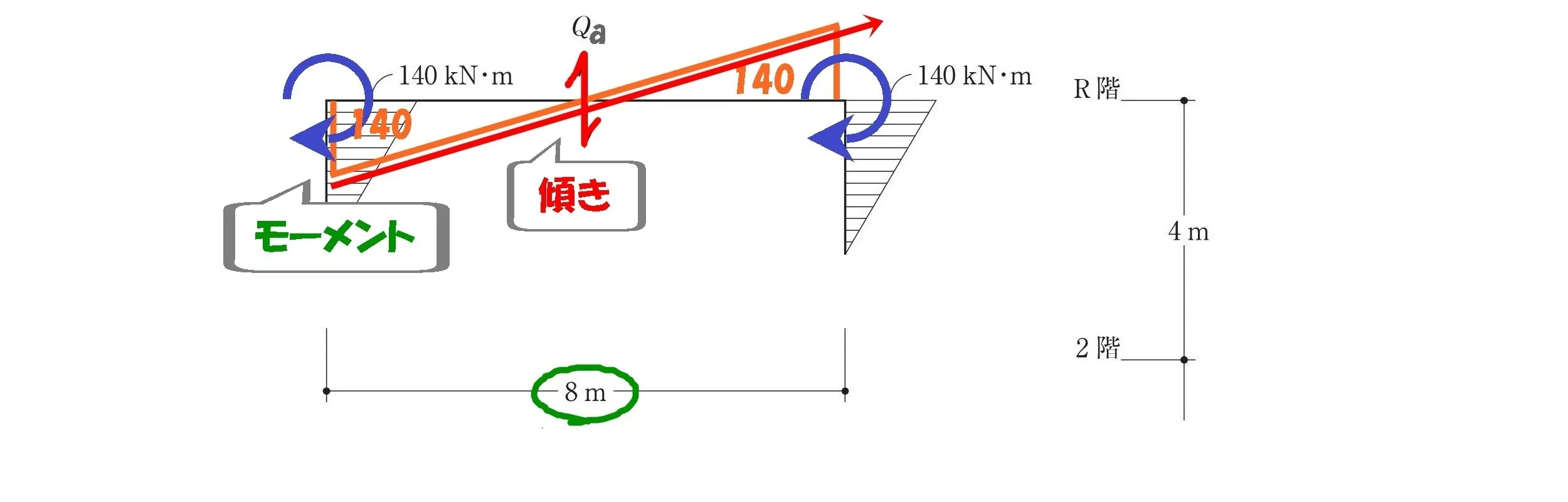

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
せん断力Qaを求める
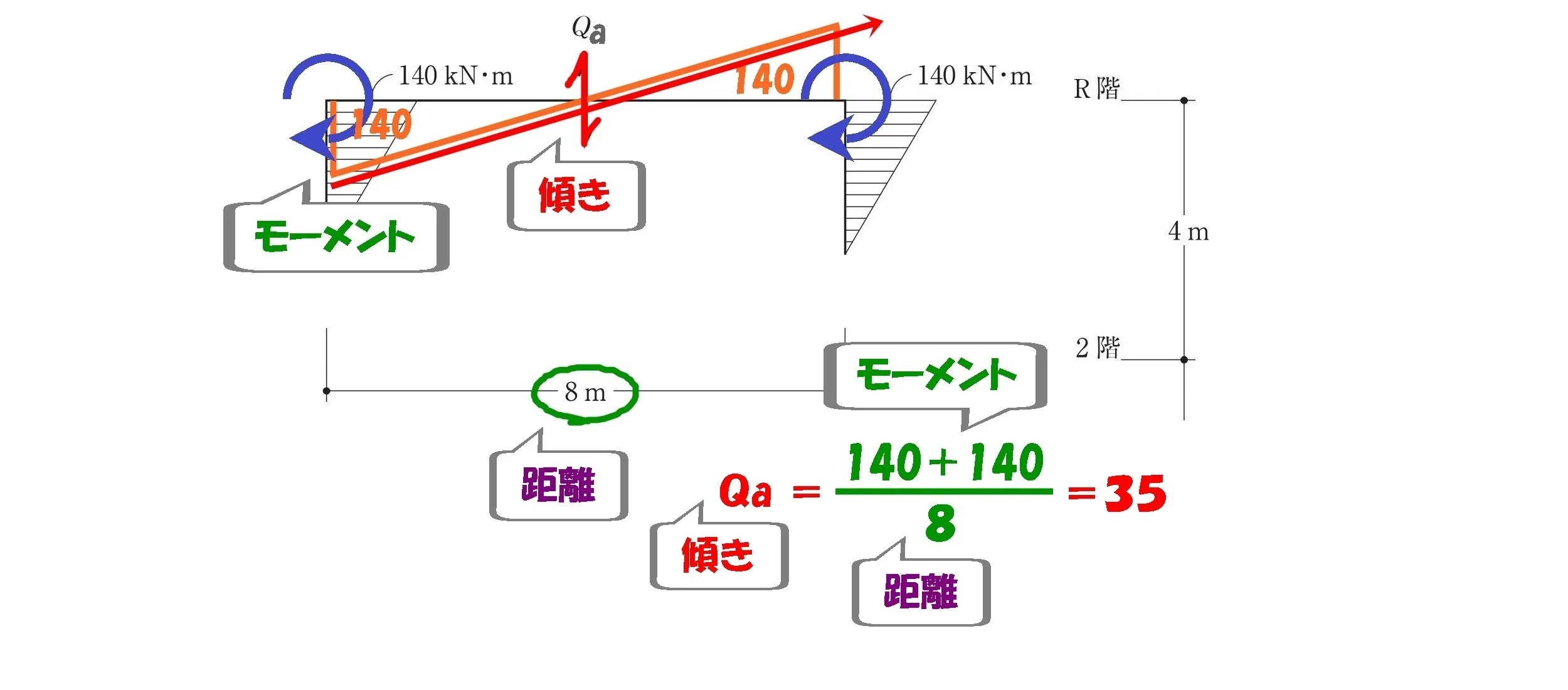

$$せん断力:Qa=\frac{ 140+140 }{ 8 }=35kN$$
2.モーメント図を描く
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
モーメント図を描く
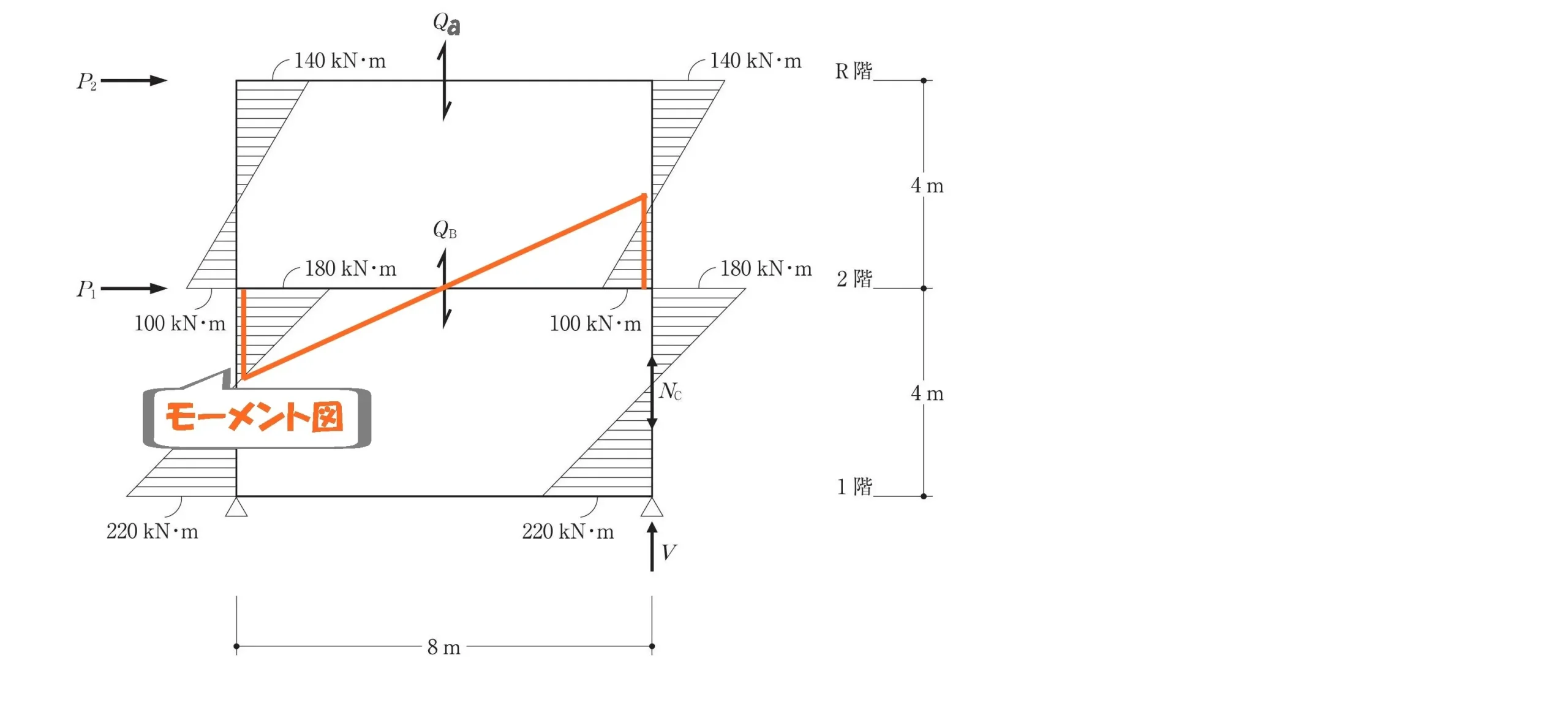

モーメント=力×距離

$$モーメント=力×距離$$$$モーメント=(100kN+180kN)$$$$力=Qb・距離=8m$$
3.梁(2層目)のせん断力を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
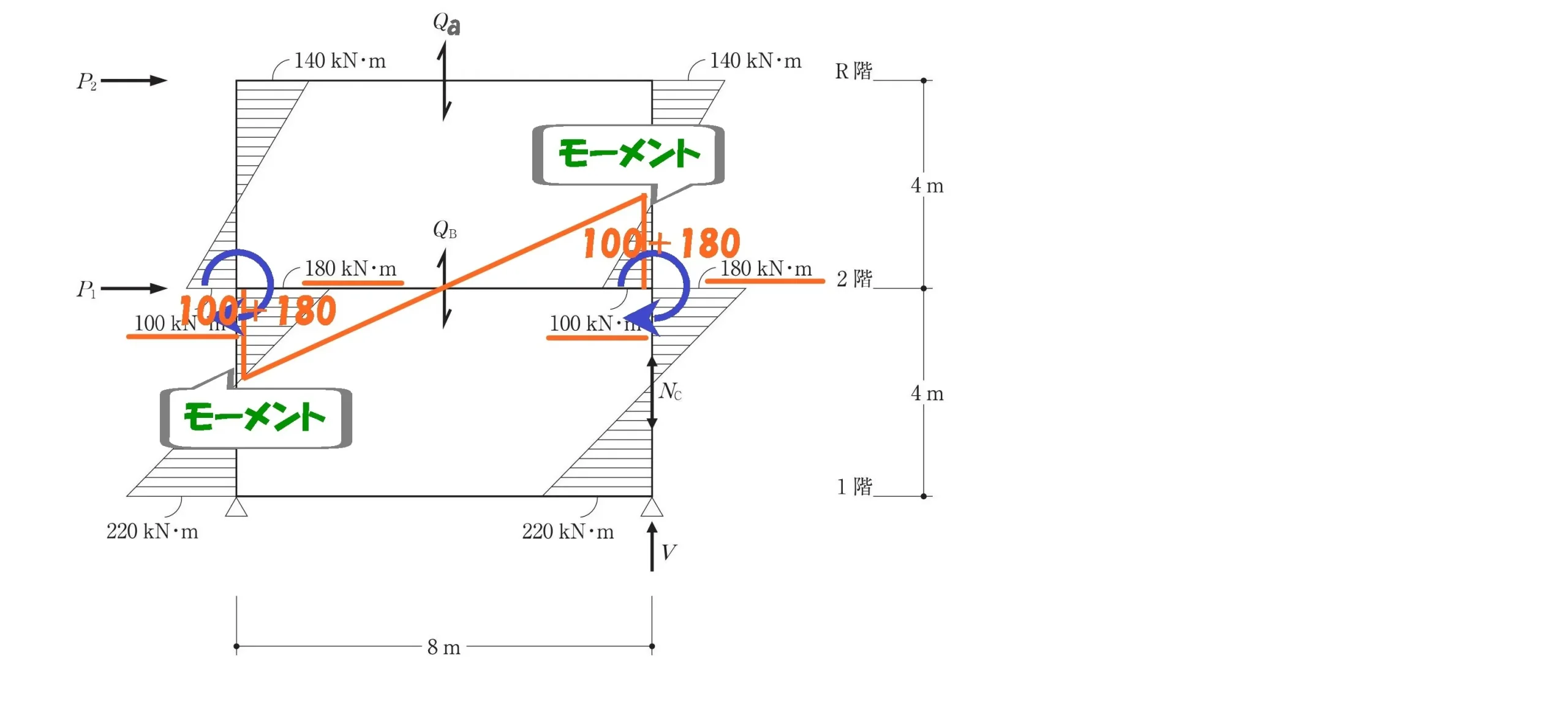
モーメント図の傾き

$$柱・梁の接続部のモーメント=100kN+180kN=280kN$$
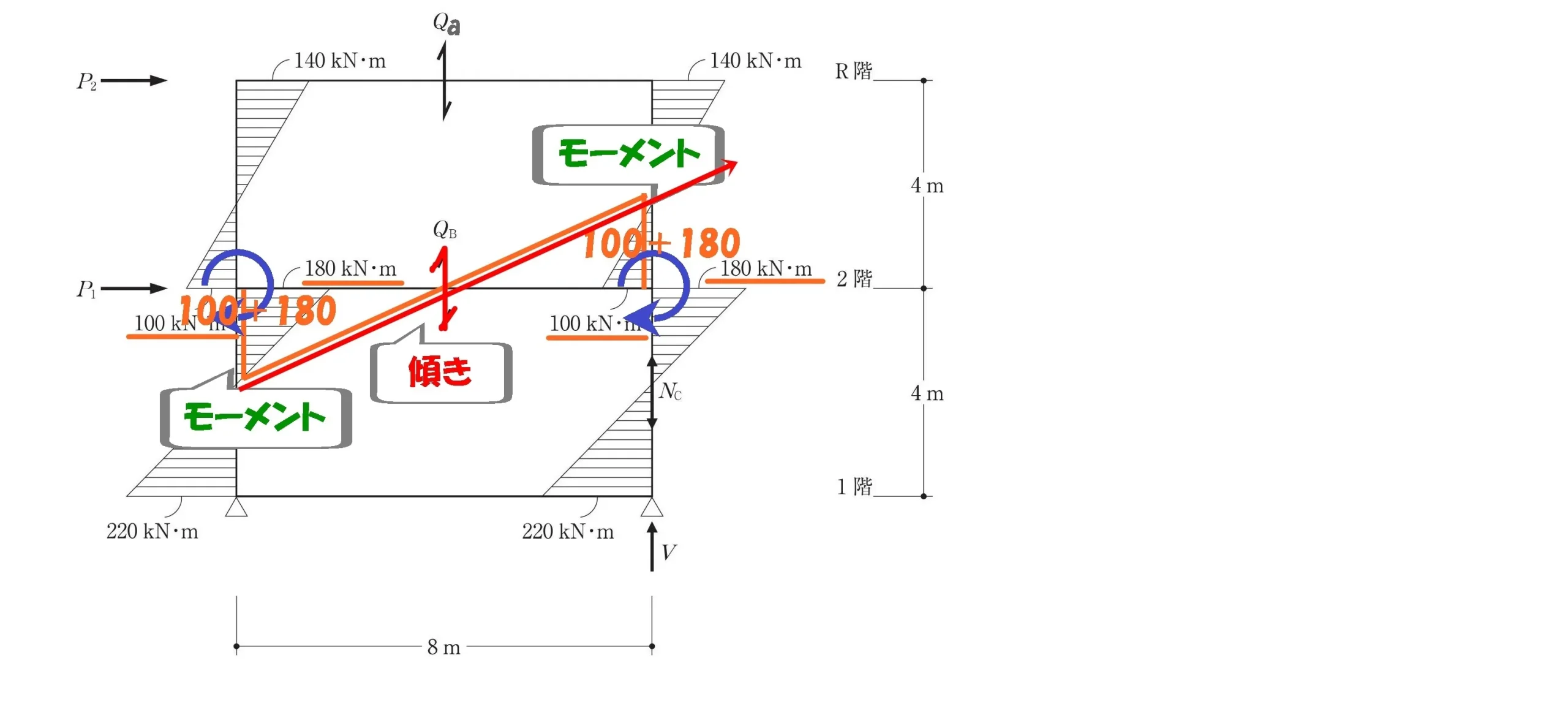
せん断力Qbを求める
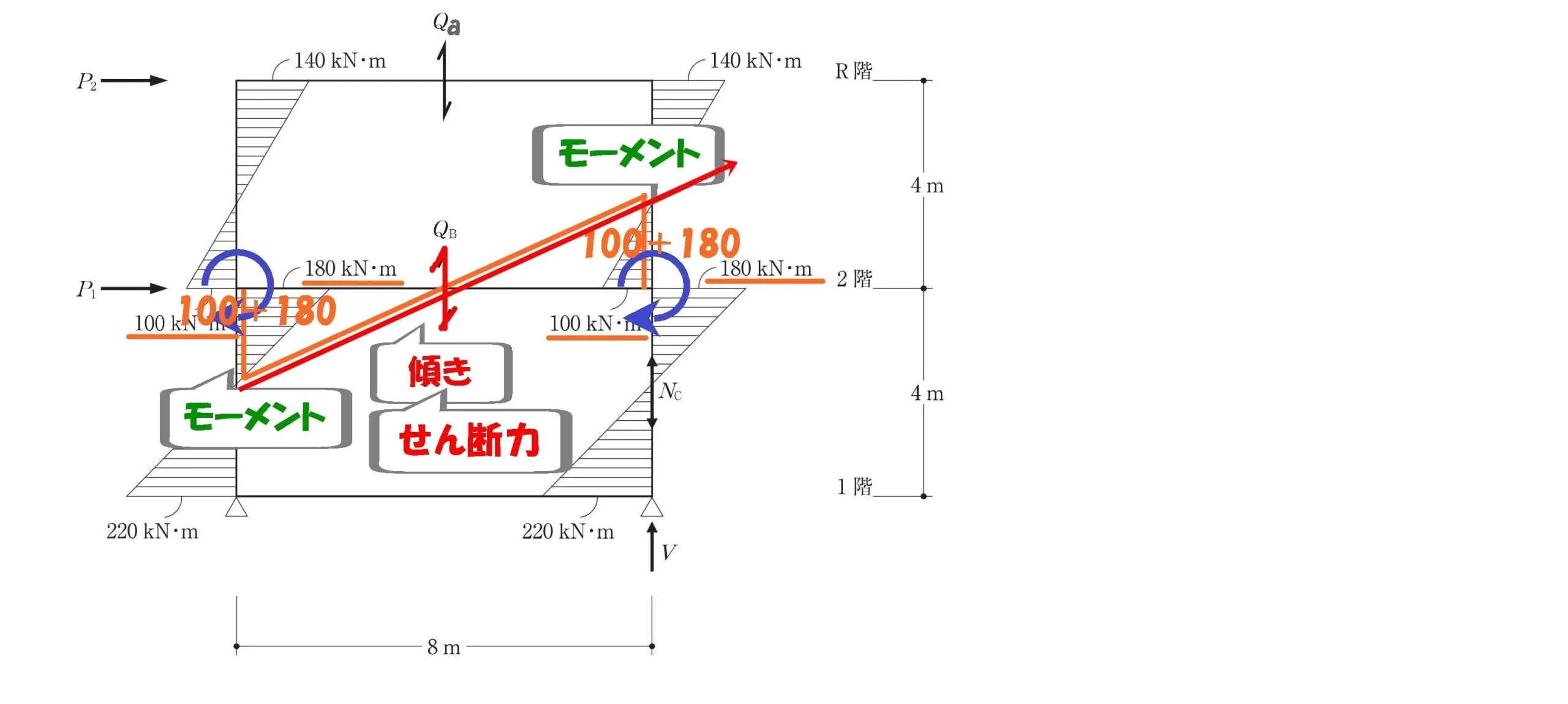

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
せん断力Qbを求める
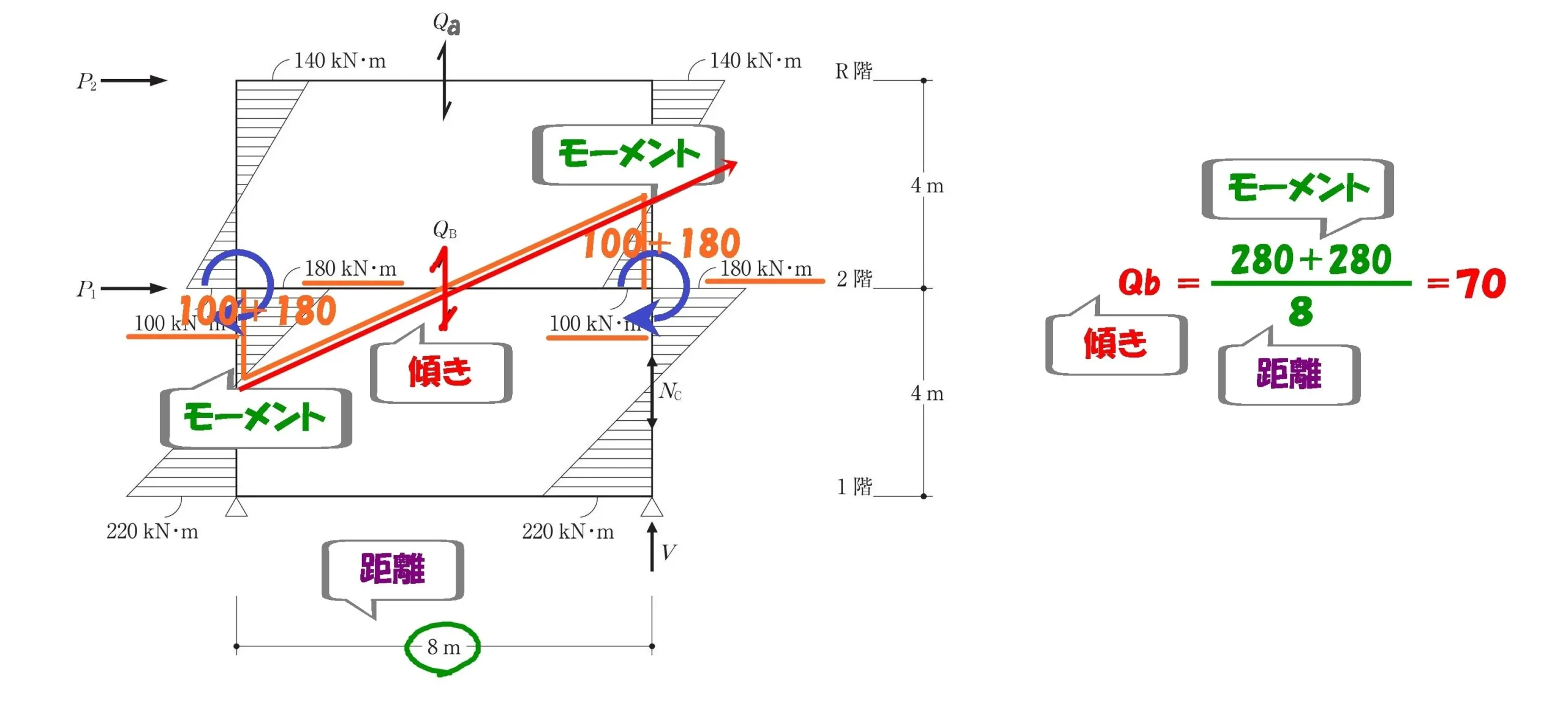

$$せん断力:Qb=\frac{ 280+280 }{ 8 }=70$$$$梁せん断力Qb=70kN$$



せん断力は
モーメントの傾き。


この動画を YouTube で視聴
枝.3


$$3.[1階右側の柱の軸方向圧縮力Ncは、105kNである。]$$
1.部材を切断して取り出す
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
Ncを含む位置で部材を切断する
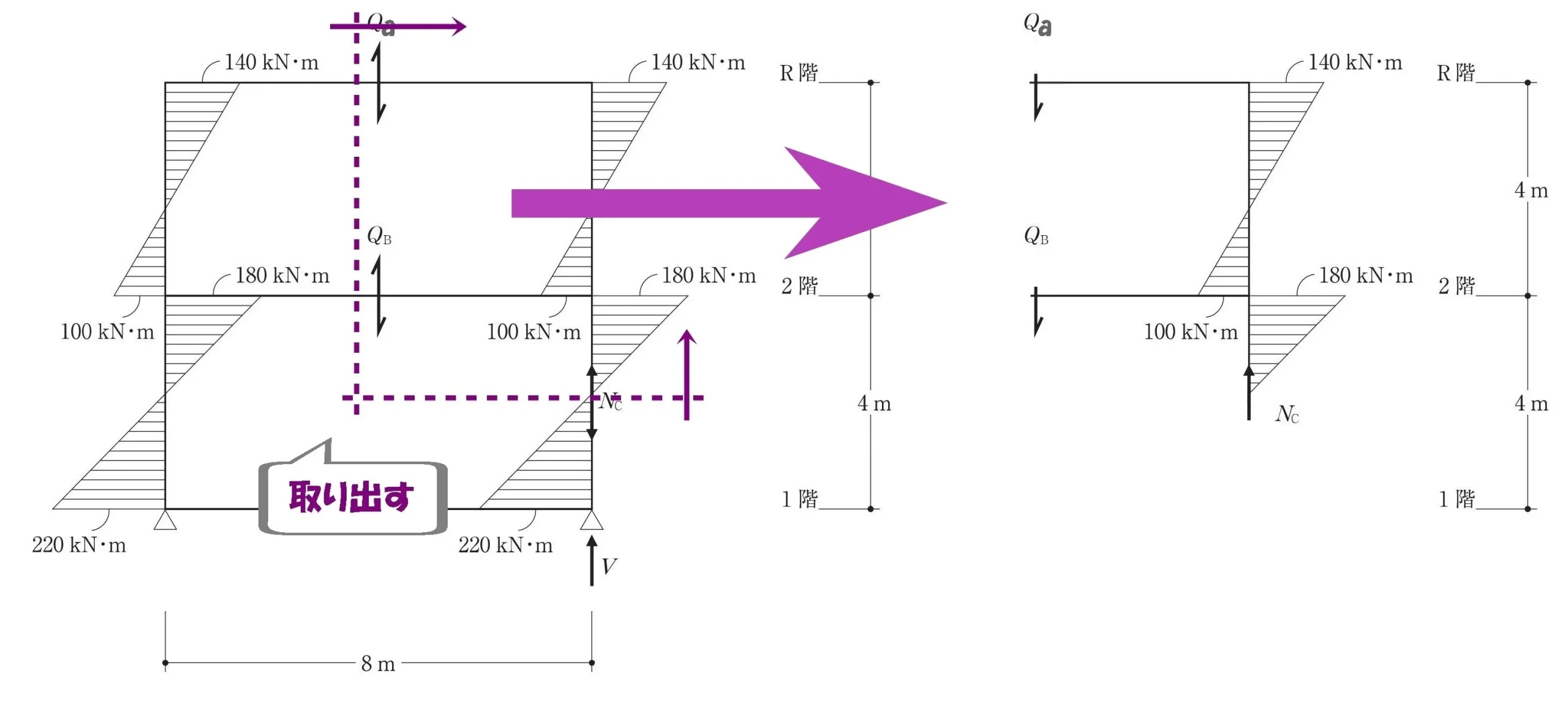

Nc(柱)を含む位置で部材を切断し、力の吊り合いが分かるように取り出します。



伝家の宝刀、部材斬り!



え!?そんな
取り出し方ってアリ?
4.ΣY=0から未知数を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
吊り合い式ΣY=0
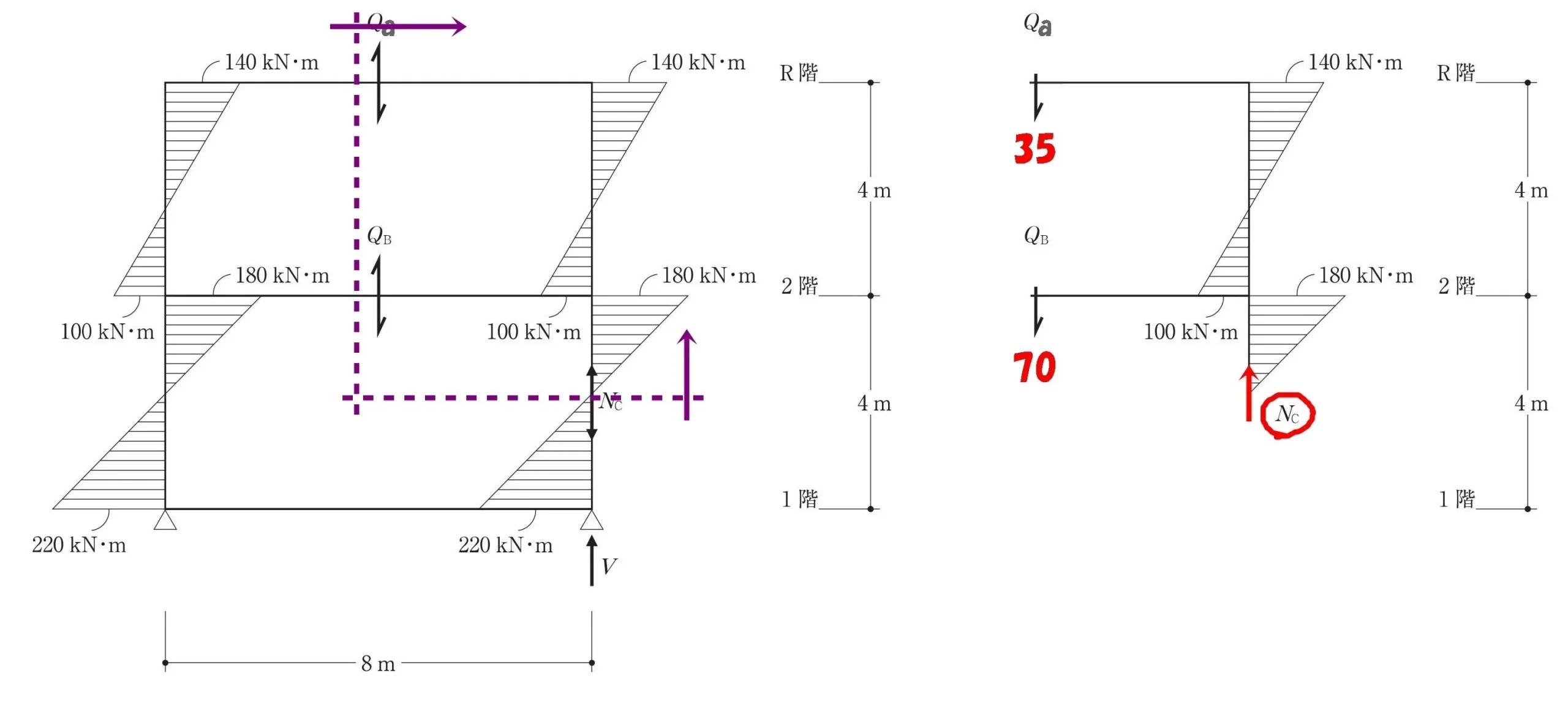

$$\Sigma Y=0より,$$$$Qa+Qb-Nc=0が成り立つ$$
軸力Ncを求める
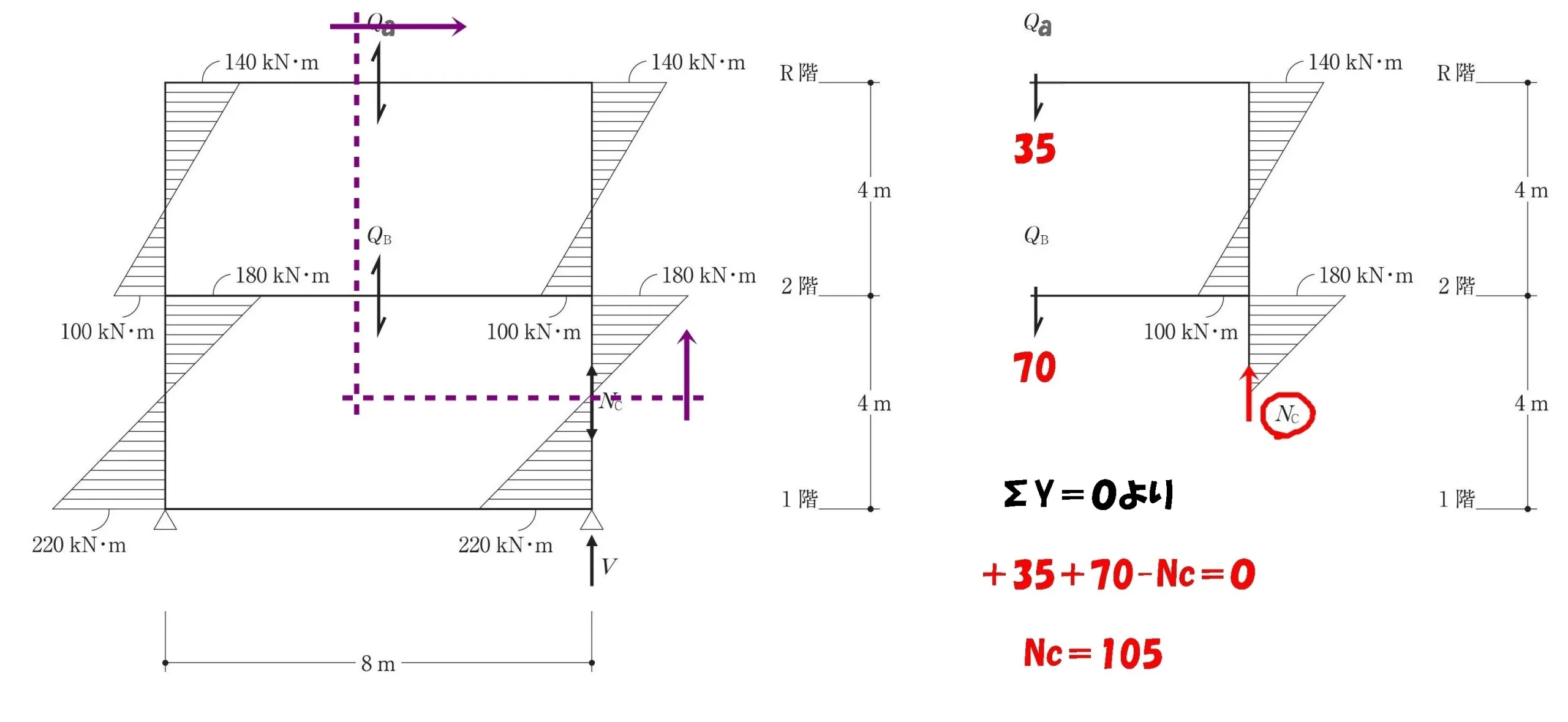

$$Qa+Qb-Nc=0より,$$
$$Nc=Qa+Qb=35+70=105kN$$$$軸力Nc=105kN$$
公式
$$\Sigma Y=0$$



Σワイ!
枝.4


$$4.[右側の支点の鉛直反力Vは、120kNである。]$$
2.モーメント図を描く
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
鉛直反力Vを求める
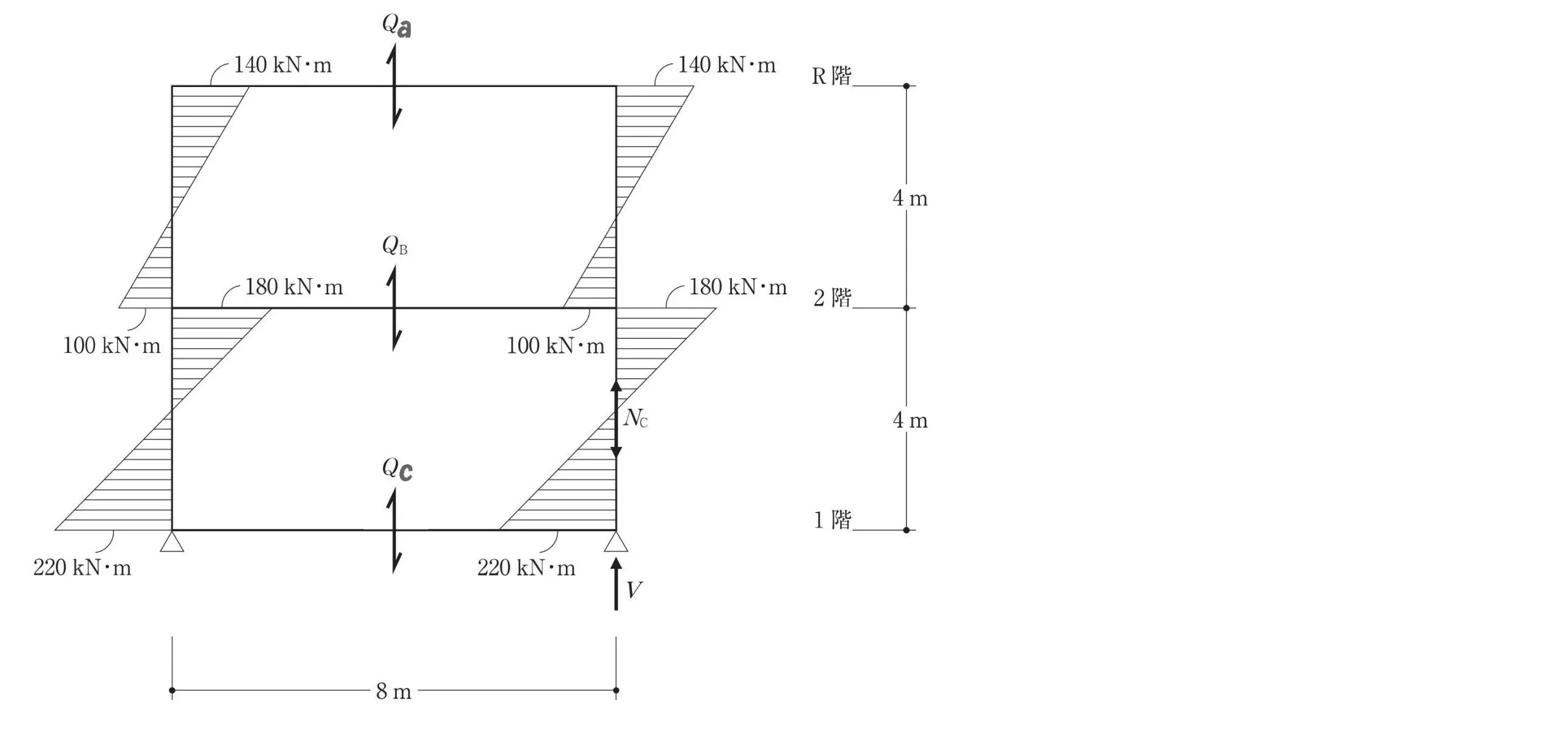

モーメント図を描く
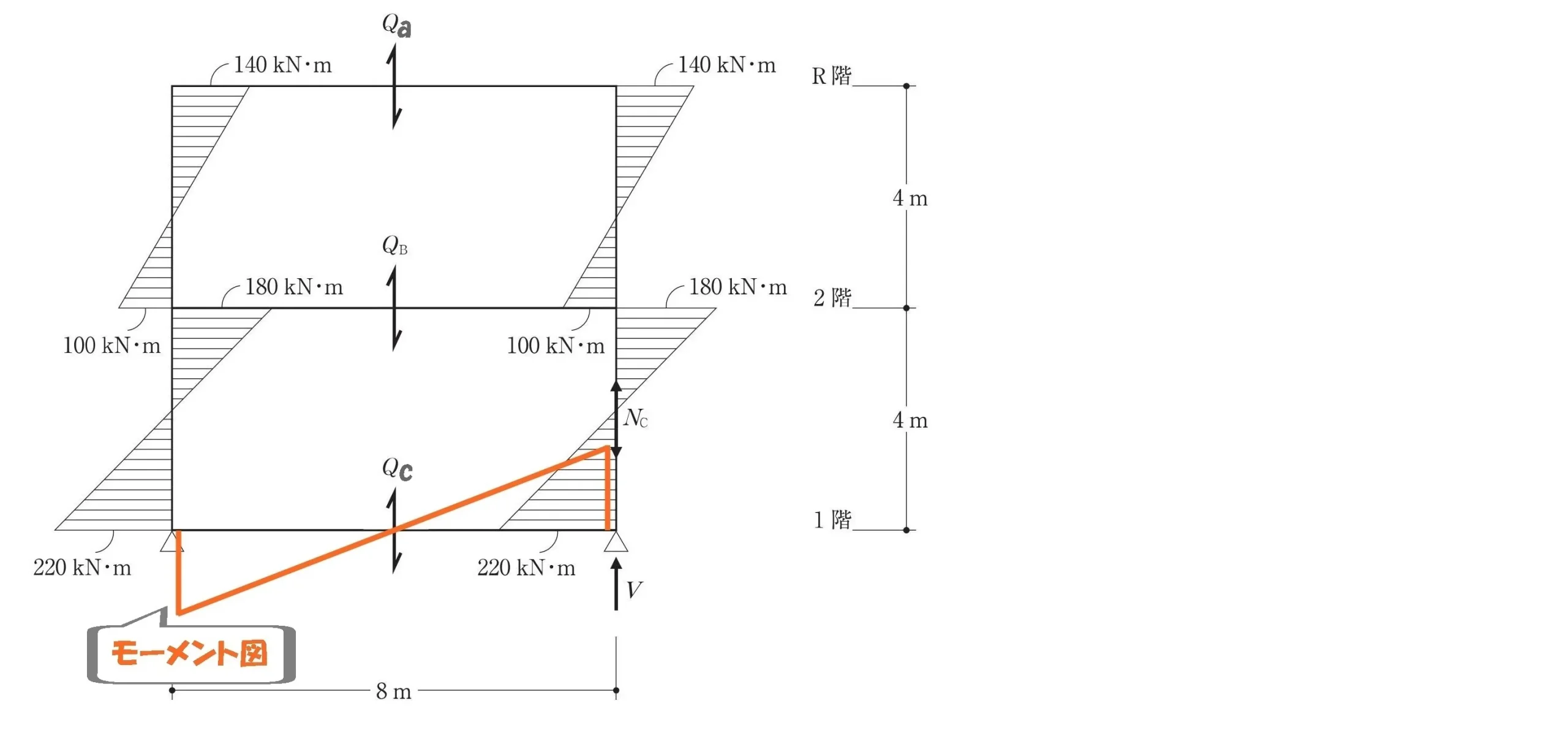

モーメント=力×距離
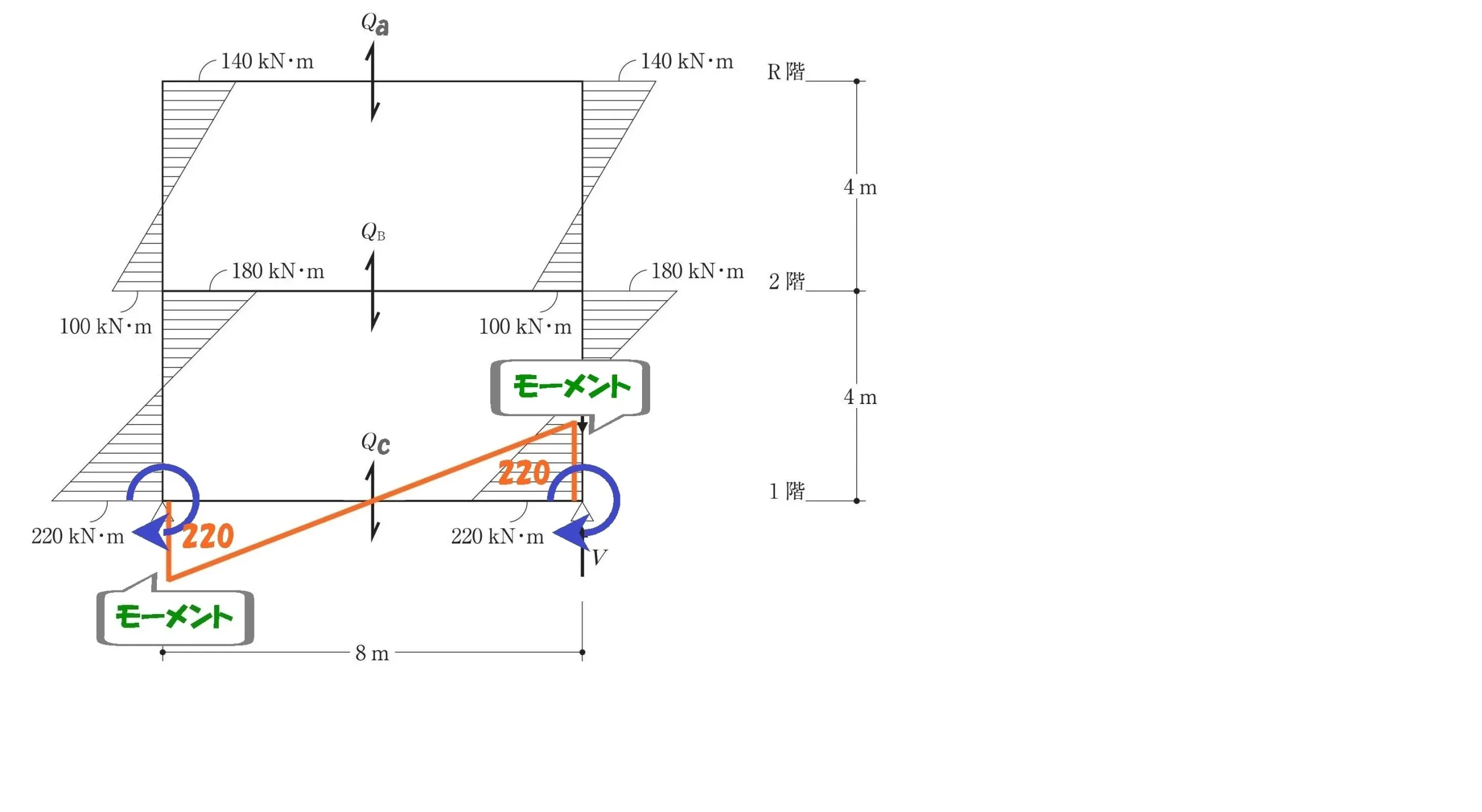

$$モーメント=力×距離$$$$モーメント=220kN$$$$力=Qc・距離=8m$$
3.梁(1層目)のせん断力を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
せん断力Qcを求める
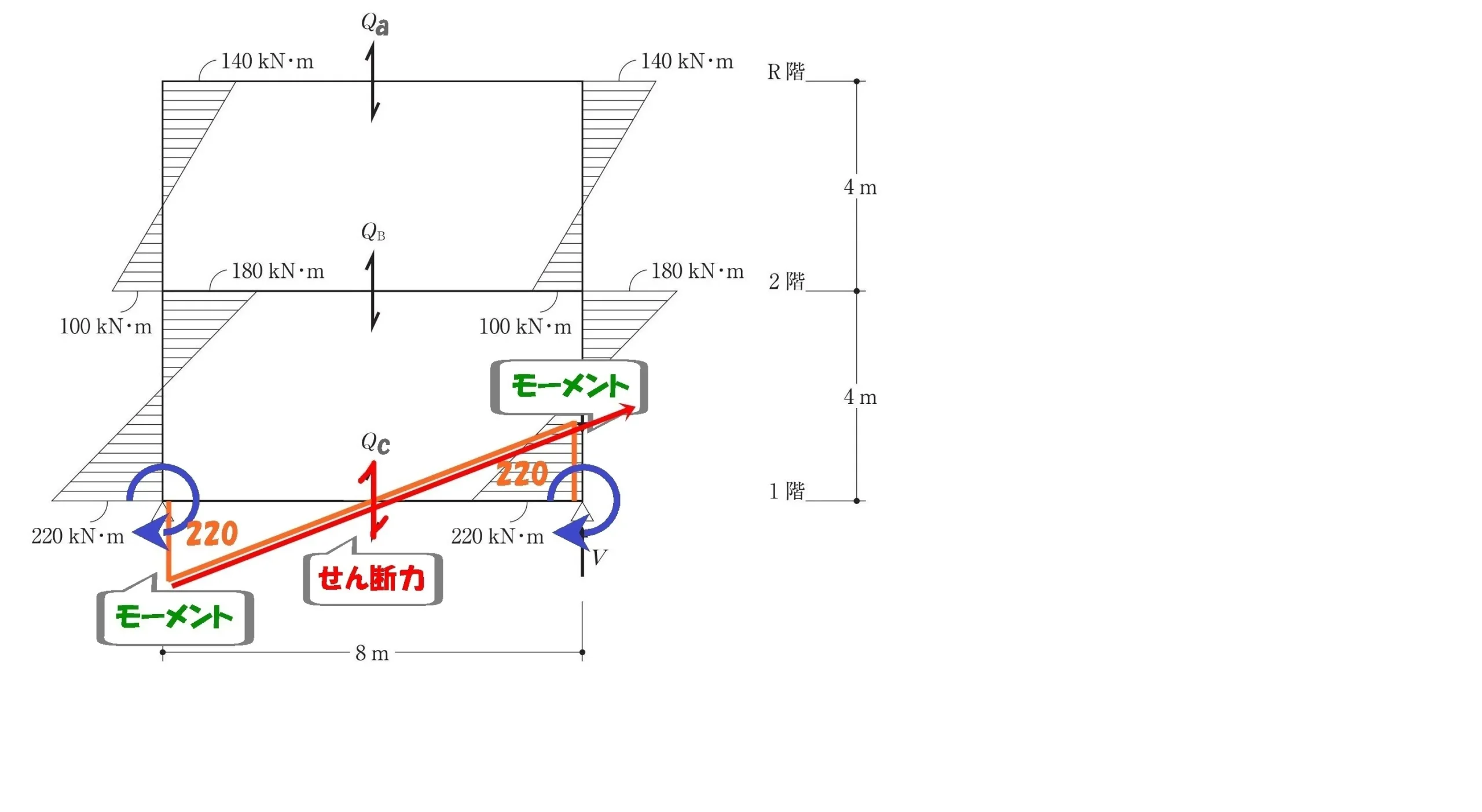

$$1層目の梁せん断力Qcを求める$$



せん断力は
モーメントの傾き。
考え方
せん断力は「モーメント図の傾き」として捉える。
モーメント図の傾き
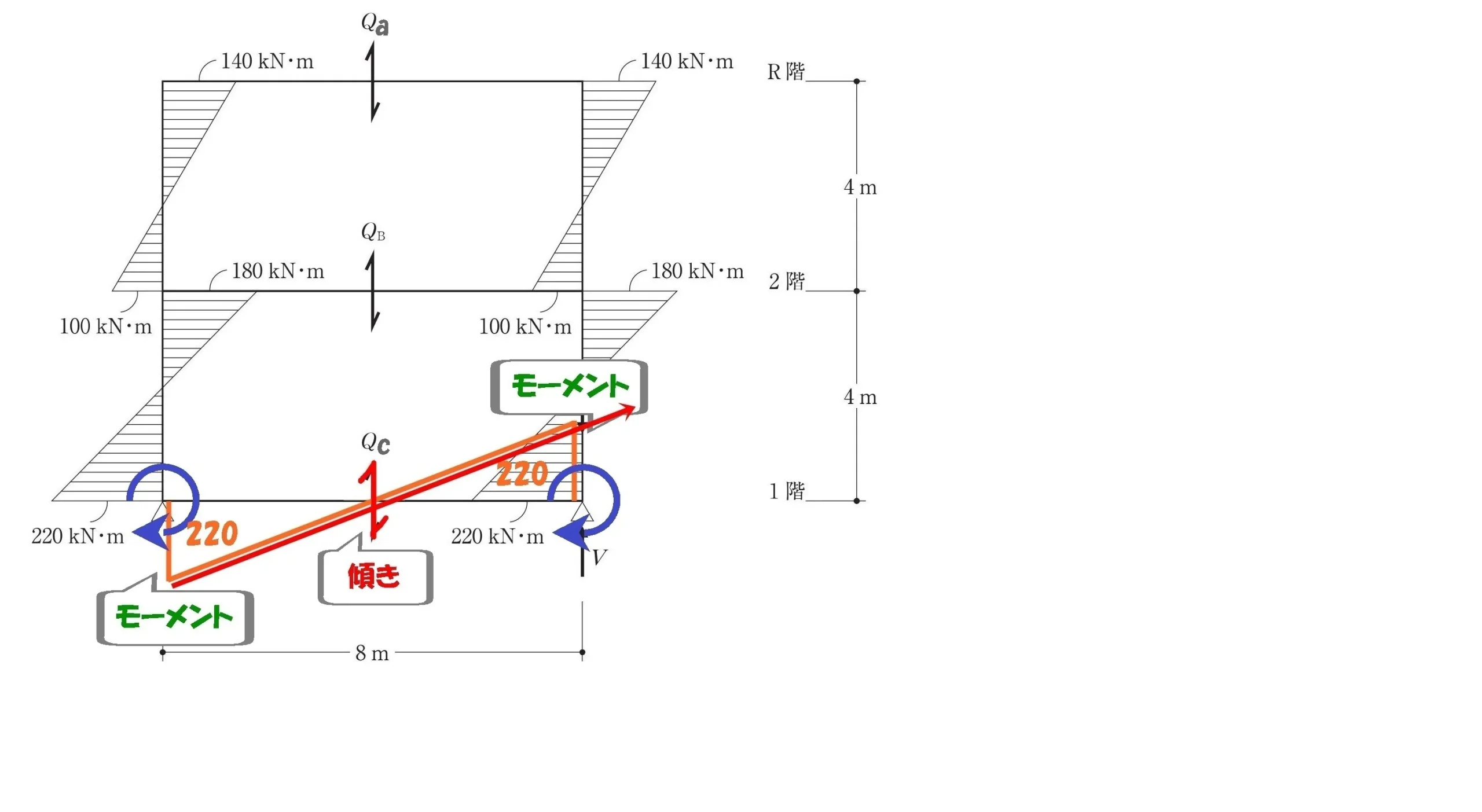

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
せん断力Qcを求める
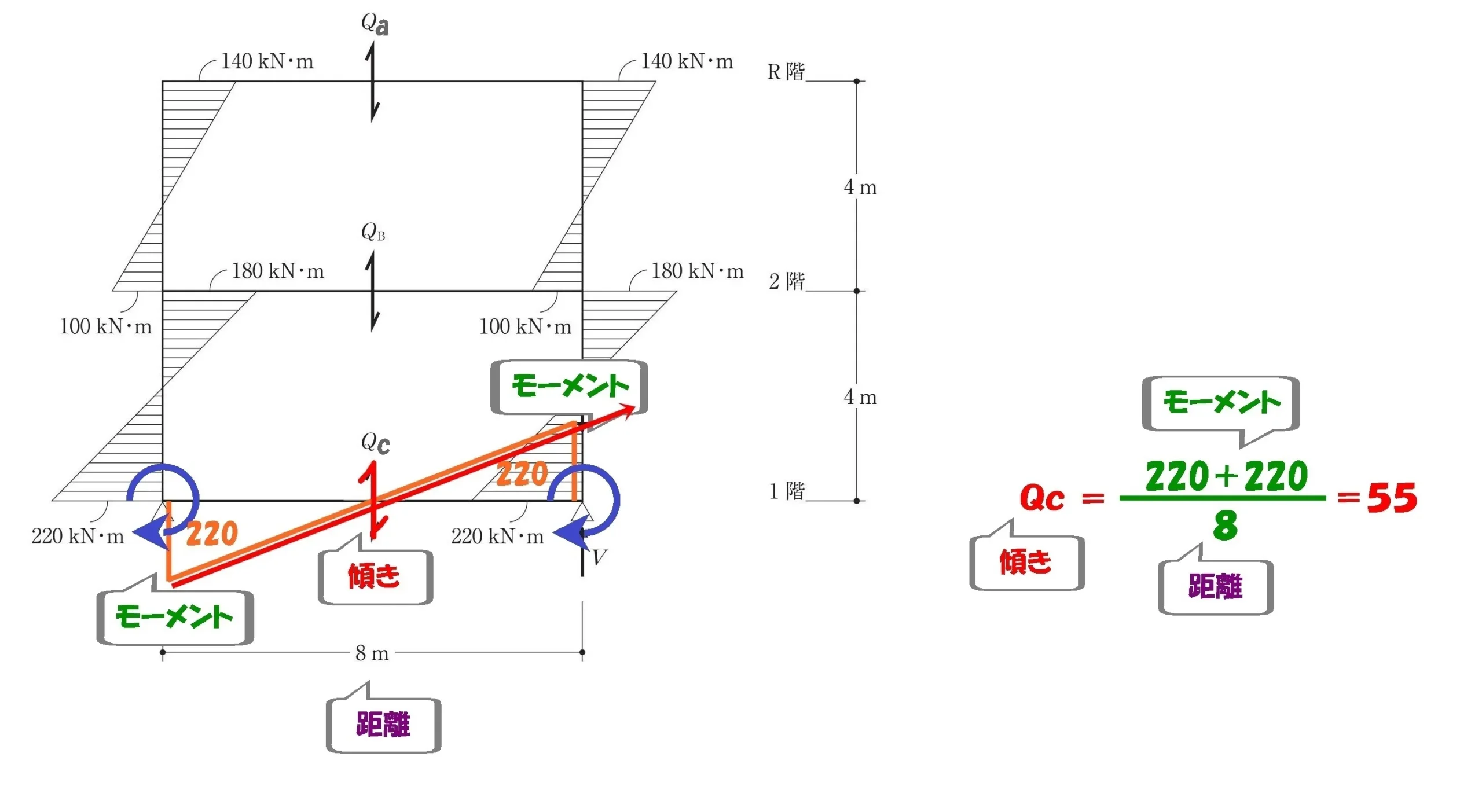

$$せん断力:Qc=\frac{ 220+220 }{ 8 }=55$$$$梁せん断力Qc=55kN$$
4.ΣY=0から未知数を求める
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める
吊り合い式ΣY=0
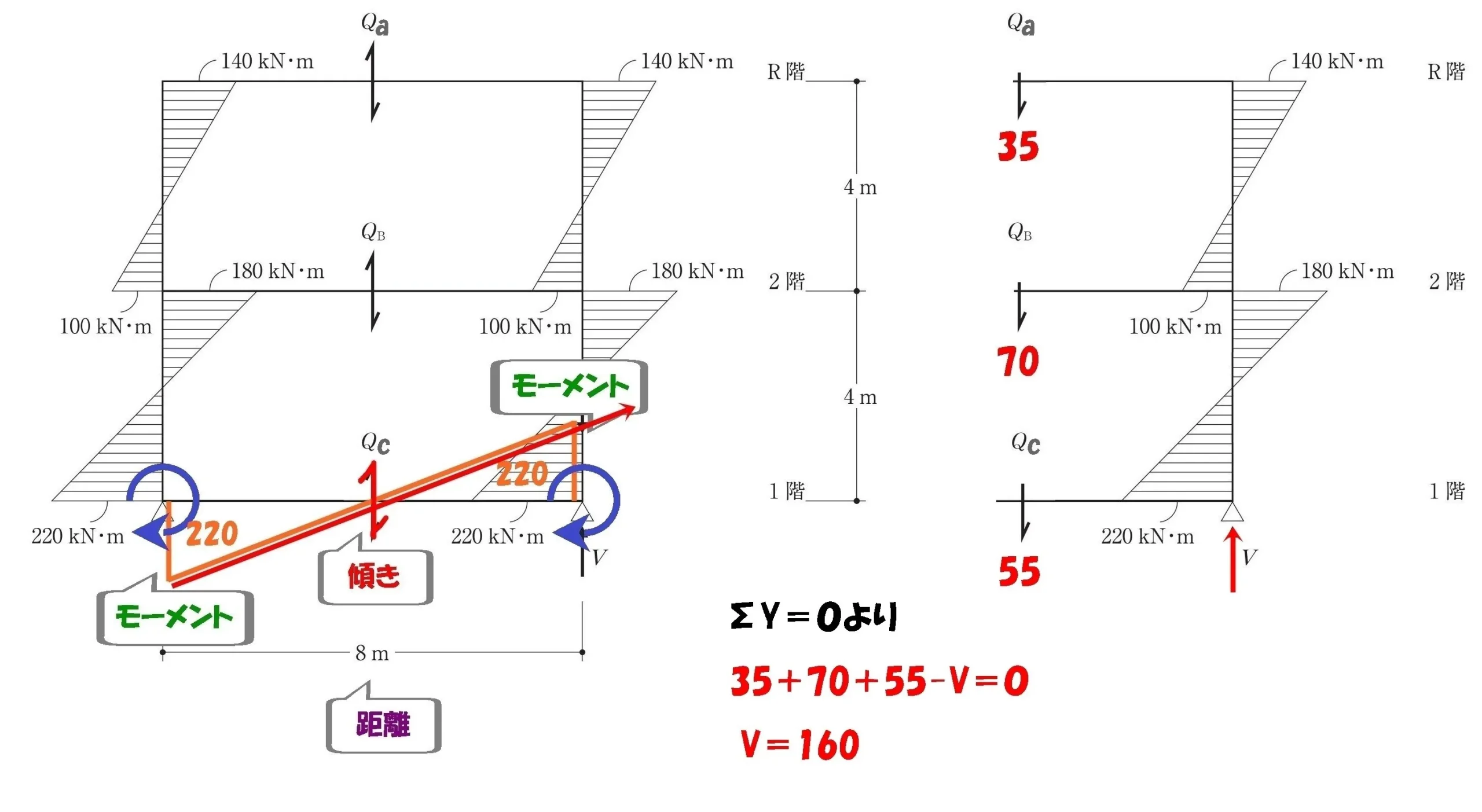

$$\Sigma Y=0より,$$$$Qa+Qb+Qc-V=0が成り立つ$$
$$V=Qa+Qb+Qc=35+70+55=160kN$$$$反力V=160kN(\neq120kN)$$
公式
$$\Sigma Y=0$$



Σワイ!
答え.4(誤り)





成仏するのだ。
攻略ポイント
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める


この動画を YouTube で視聴
崩壊メカニズム-1
難易度:★★★☆☆
ここがポイント
「外力による仕事」と「内力による仕事」は吊り合う。
攻略ポイント
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める
問題
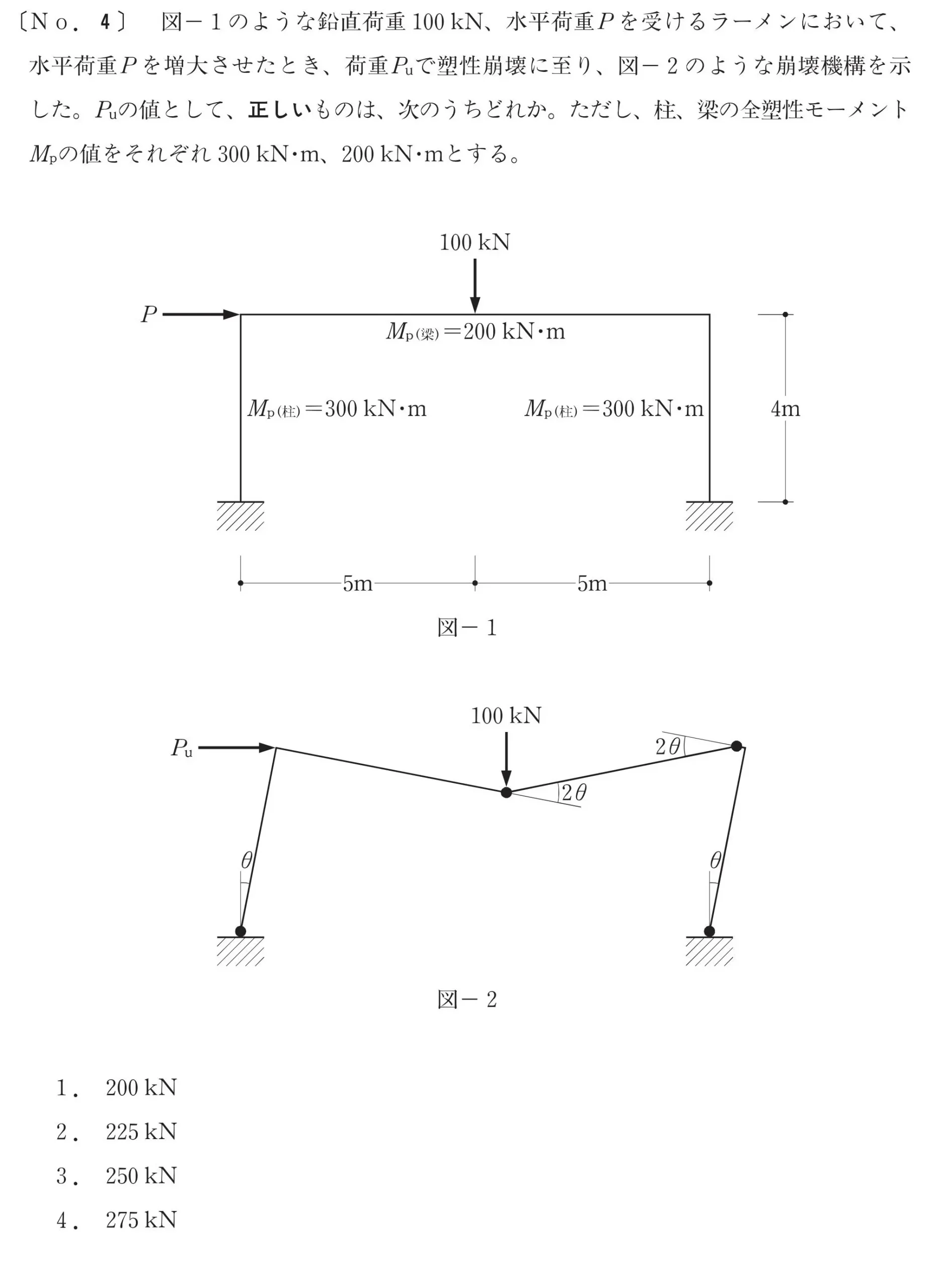

「外力による仕事」と「内力による仕事」は吊り合う。
外力の仕事=内力の仕事
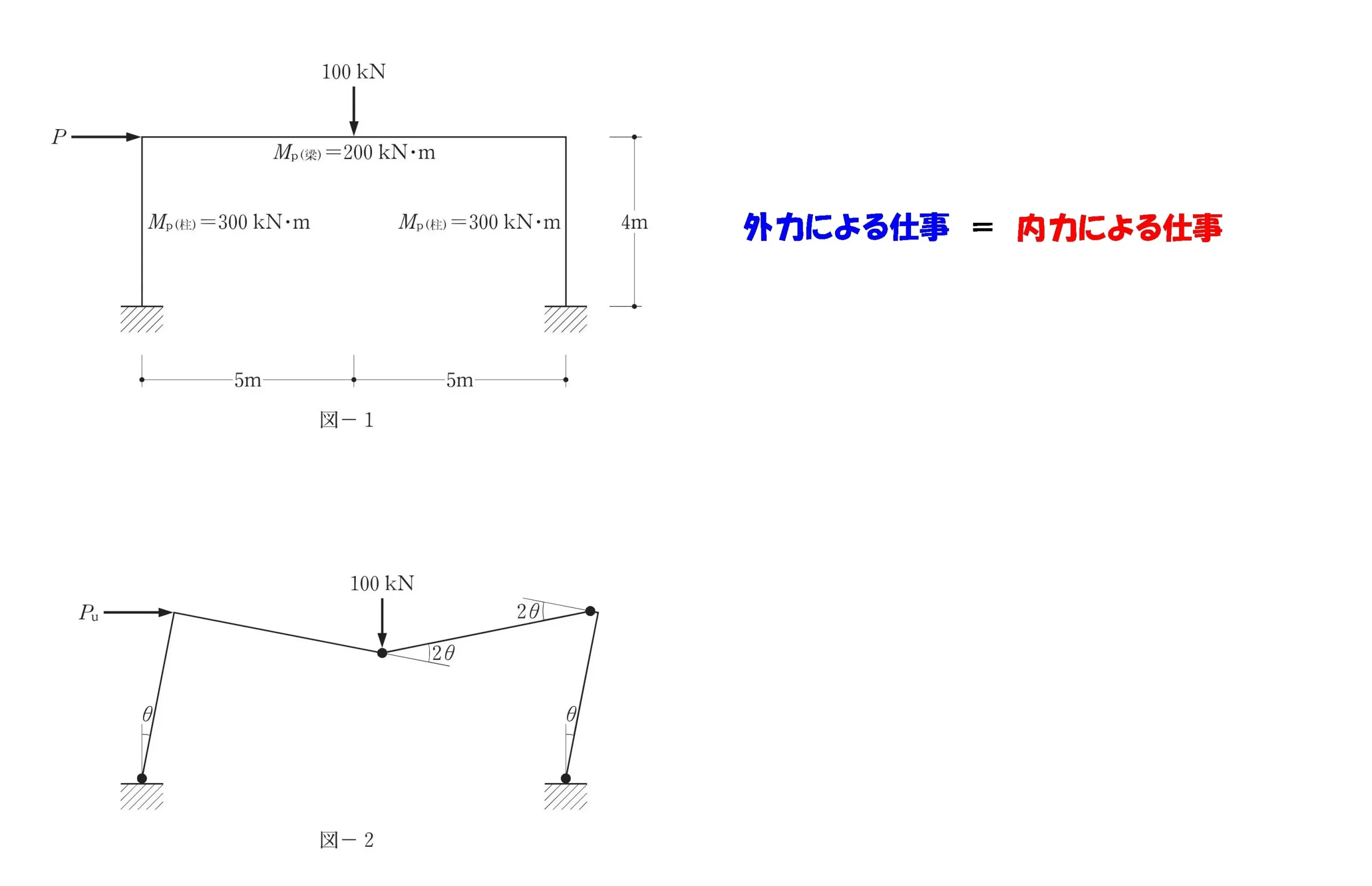

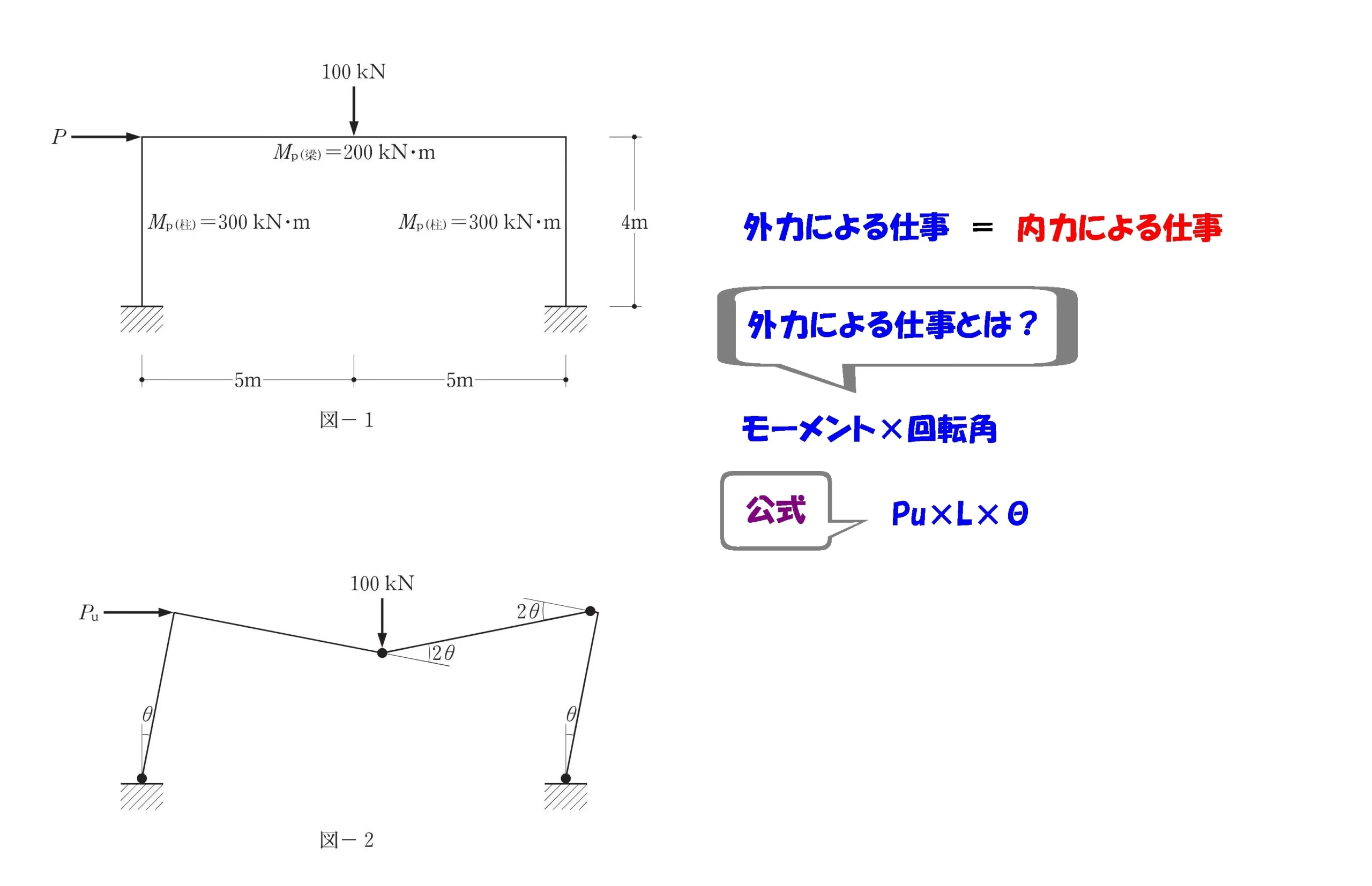
外力による仕事とは?

公式
外力による仕事=モーメント×回転角

「仕事=物を押す力×物が動いた距離」というのは、物理の学習で習ったことがありますよね?
原理は同じ
- 「物を押す力」→「回転する力」
- 「物が動いた距離」→「回転角」
公式
外力による仕事=力×距離×回転角
内力による仕事とは?
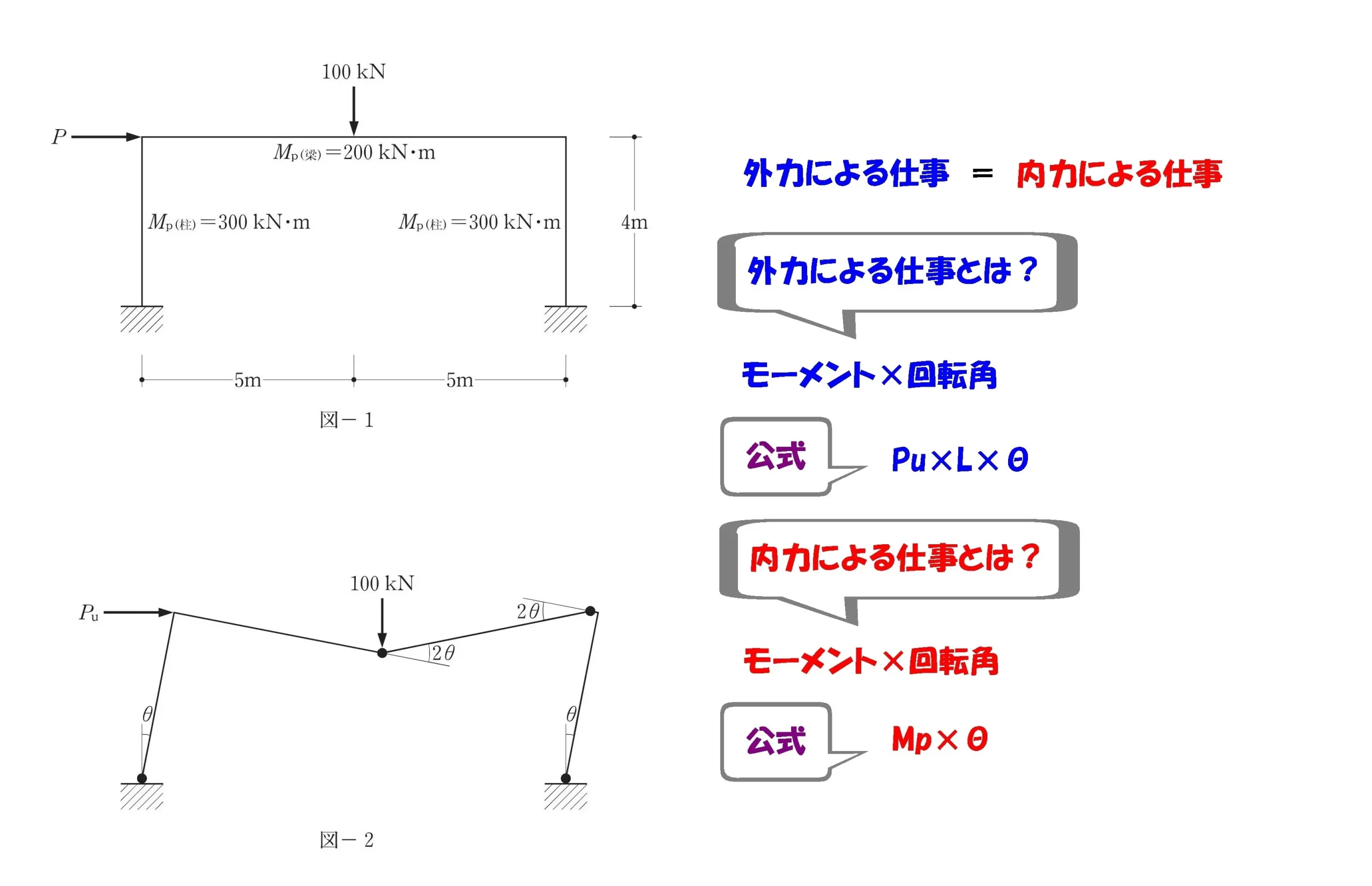

公式
内力による仕事=モーメント×回転角
1.外力による仕事:力×距離×θをすべて足す
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める
外力による仕事
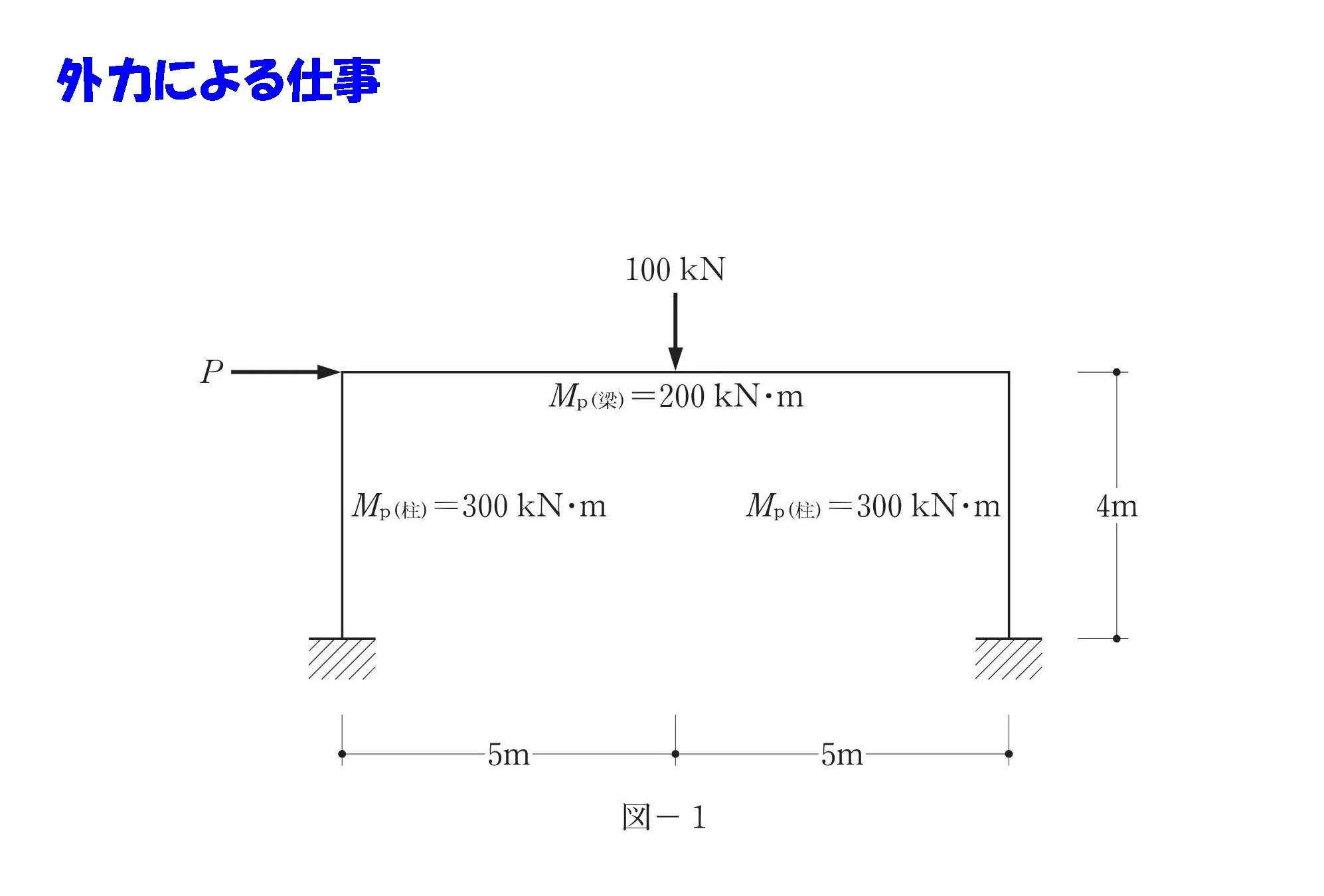

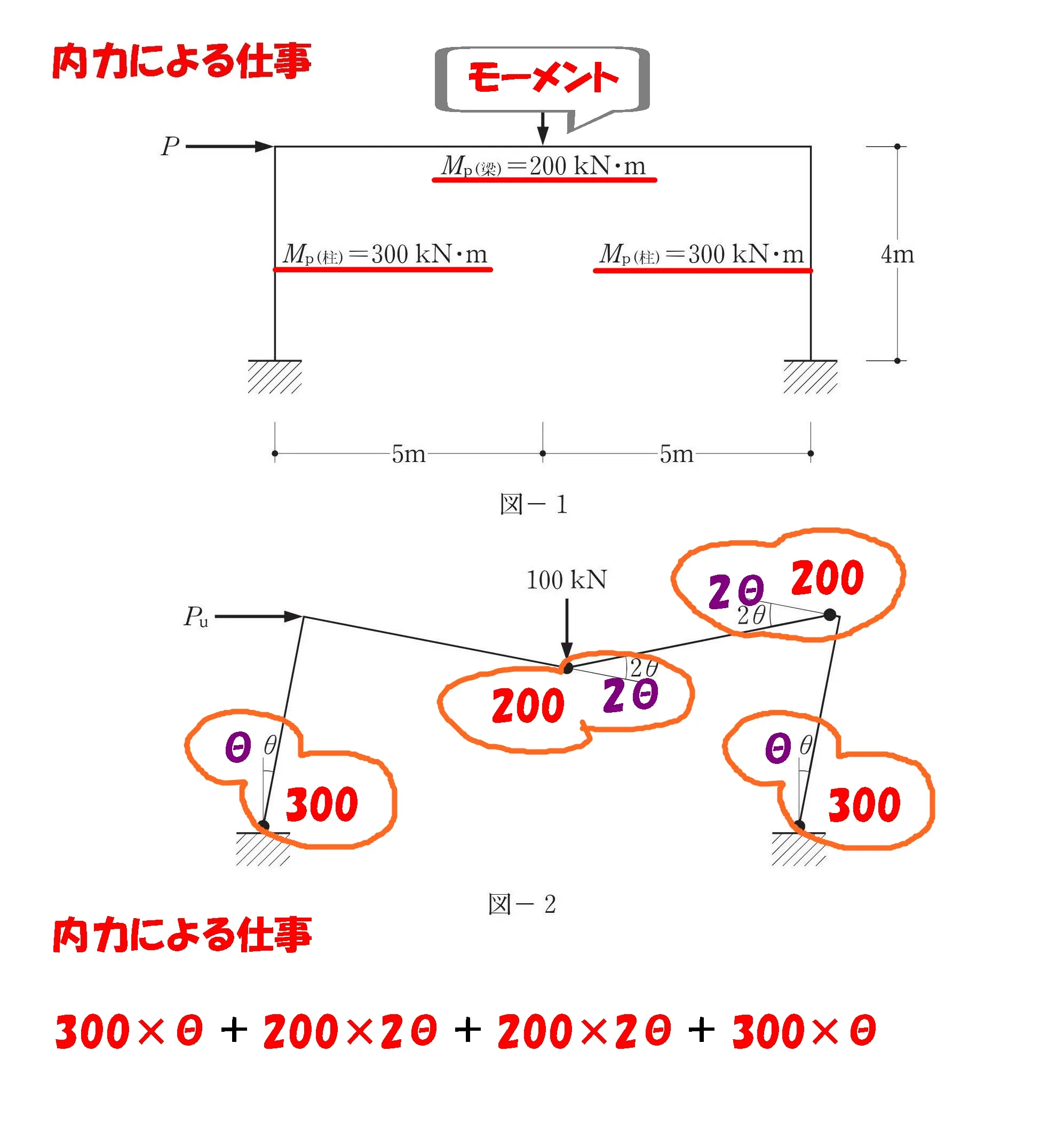
力と距離にマークする
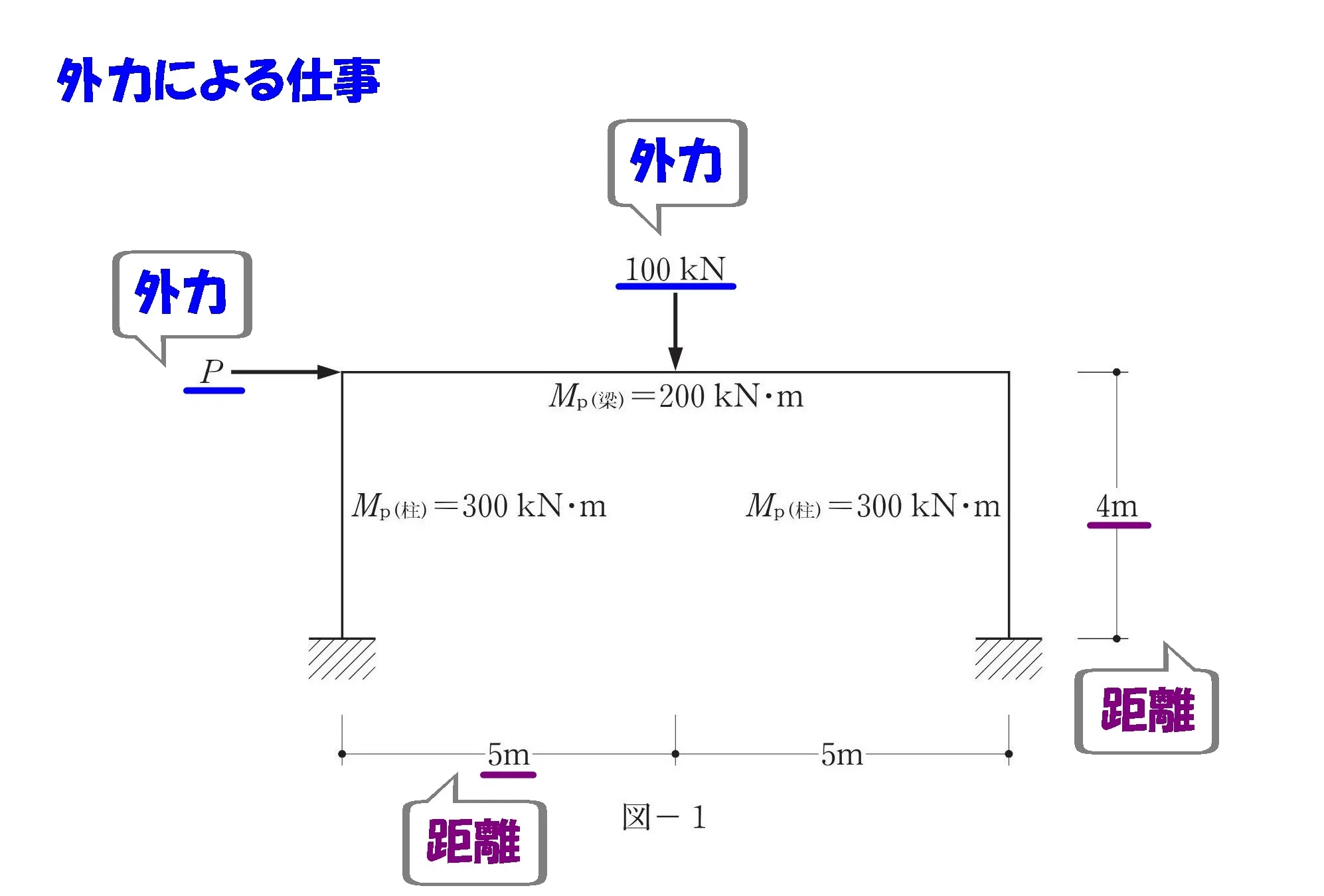

マークする
- 図-1:作用する外力(回転力)
- 図-1:柱脚から外力の延長ラインまでの距離
外力による仕事を求める準備として、必要な数値にマークしておきましょう。
回転角θを書き込む
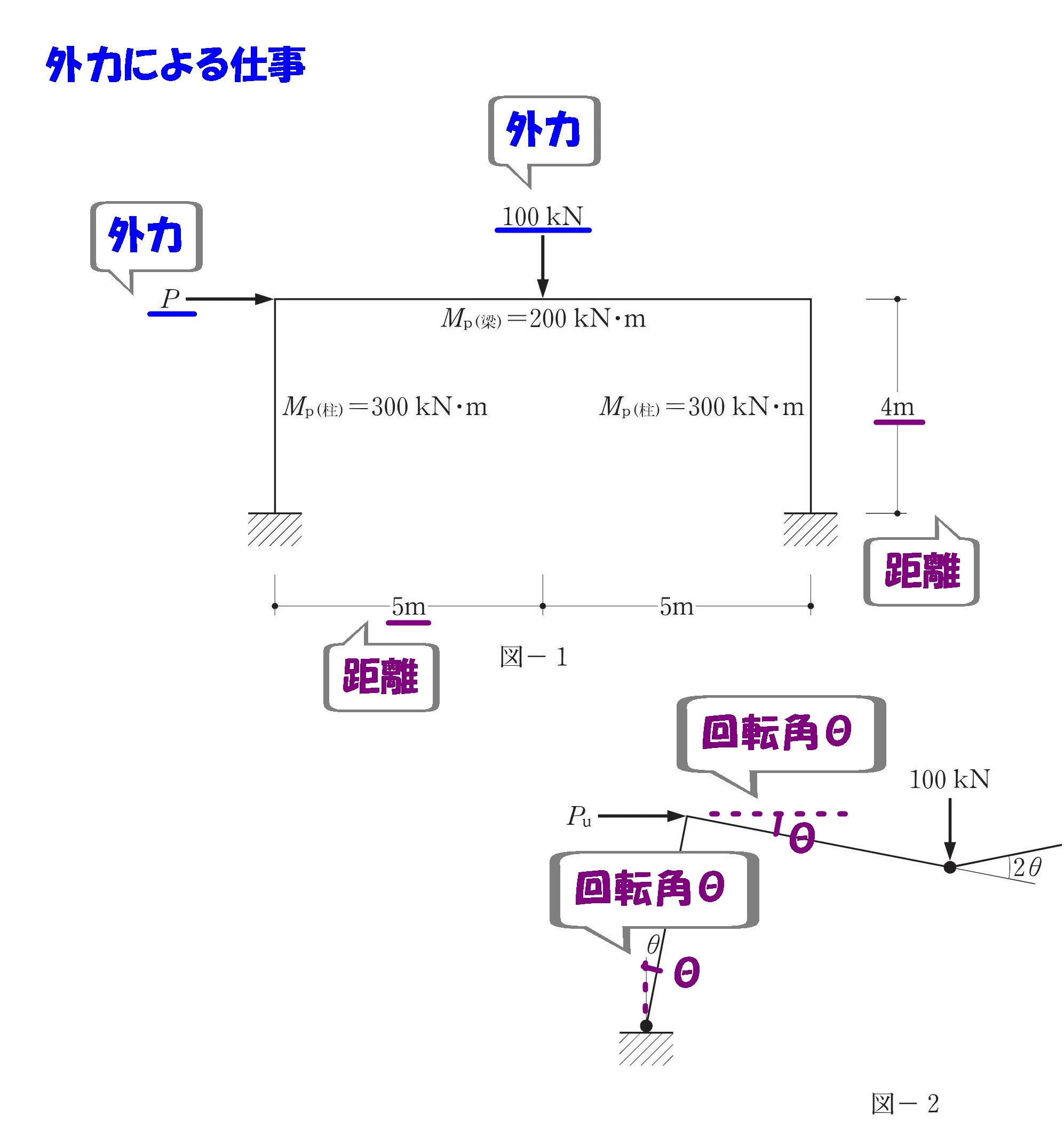

θを書き込む
- 図-2:外力によって回転が生じる位置に「θ」を書き込む。
外力によって生じる部材の回転角θは「すべて同じ角度」ということを押さえておきましょう。



θの書き込みをすると
崩壊のイメージが膨らむ。
モーメント=力×距離
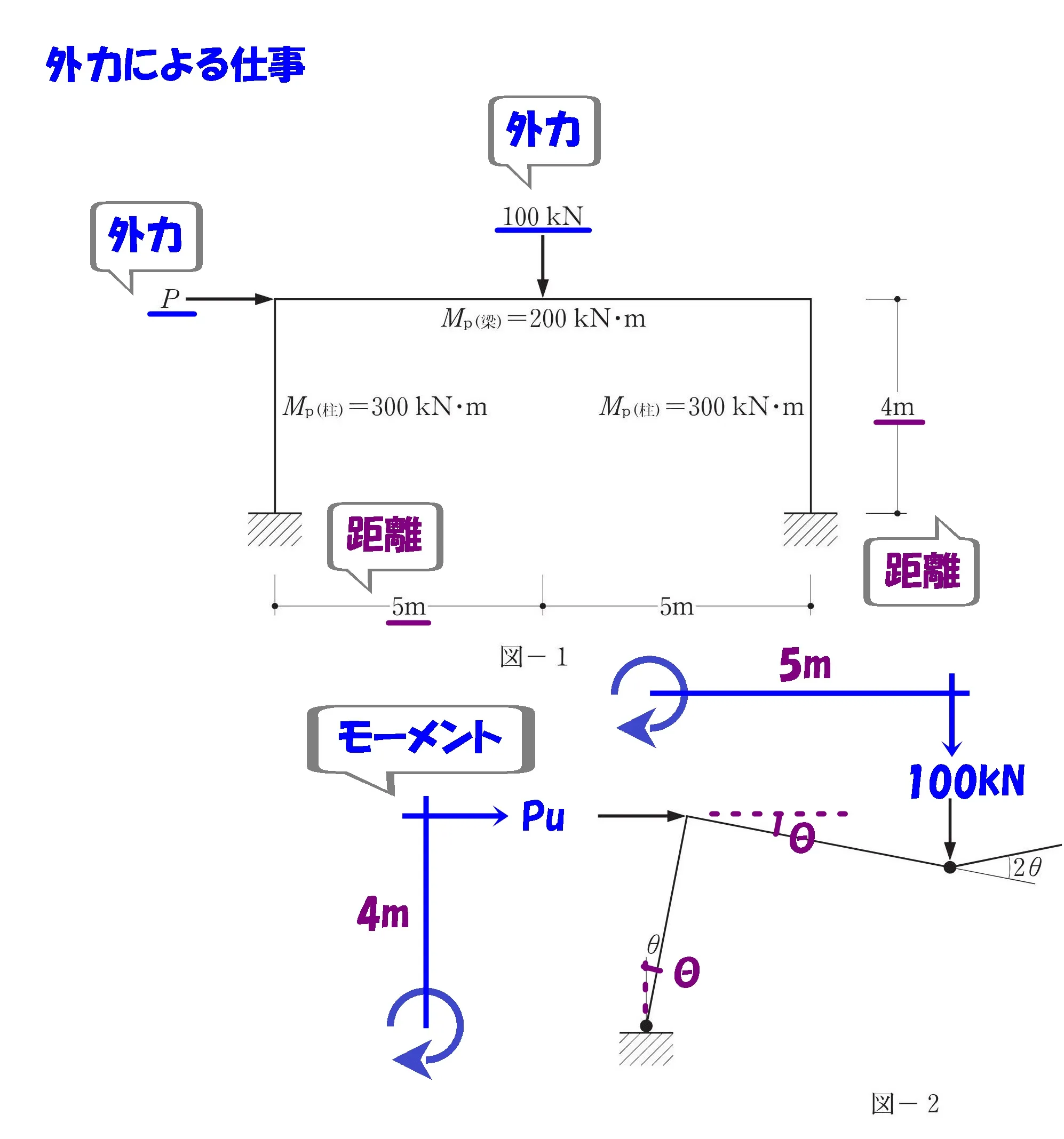

$$モーメント=力×距離より,$$
$$100kN*5m+Pu*4m$$
モーメント=力×距離
外力による仕事を求める
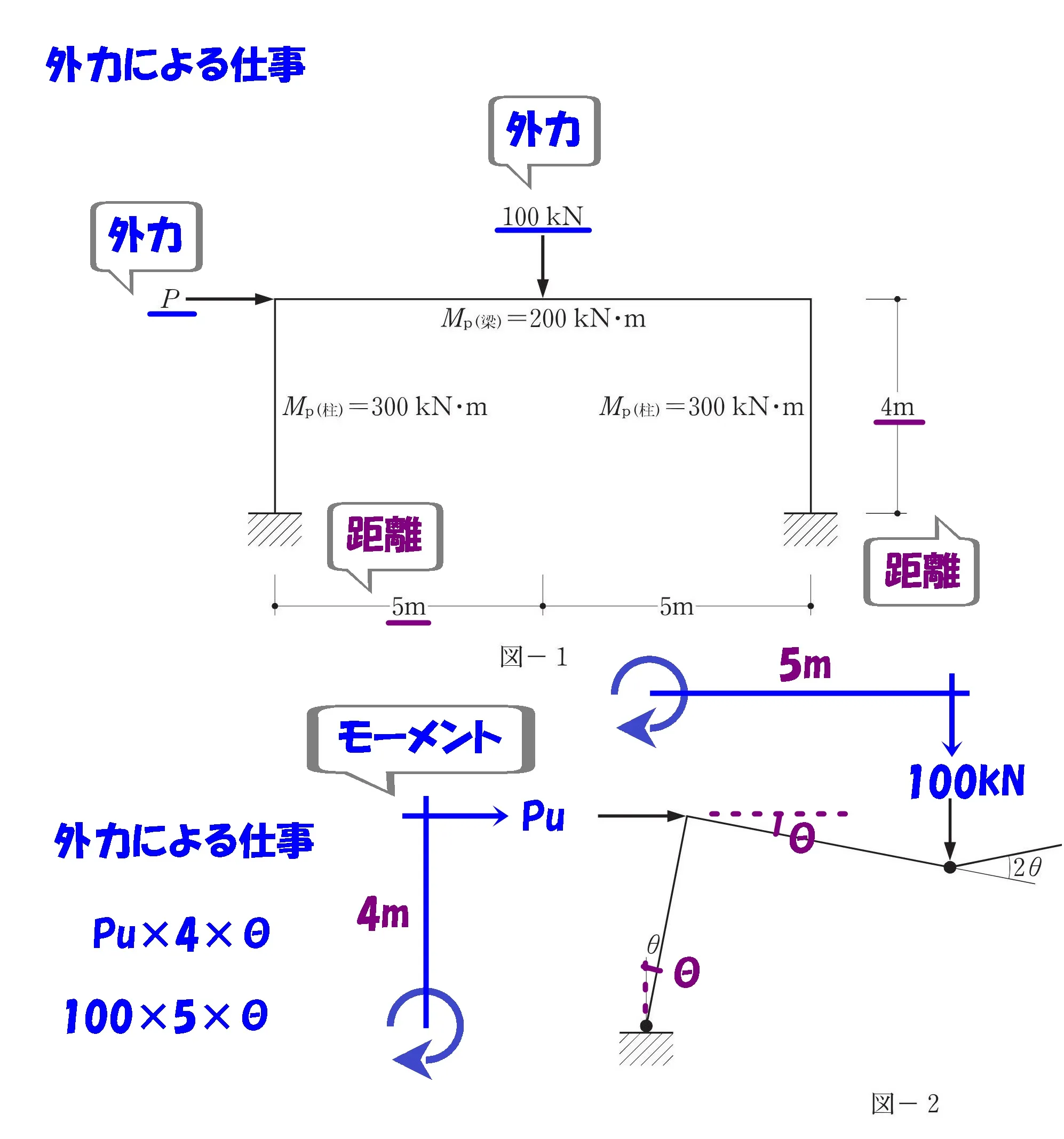

$$外力による仕事=モーメント×回転角より,$$
$$\{Pu*4*\theta+100*5*\theta\}$$
公式
外力による仕事=力×距離×回転角
2.内力による仕事:モーメント×θをすべて足す
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める
内力による仕事
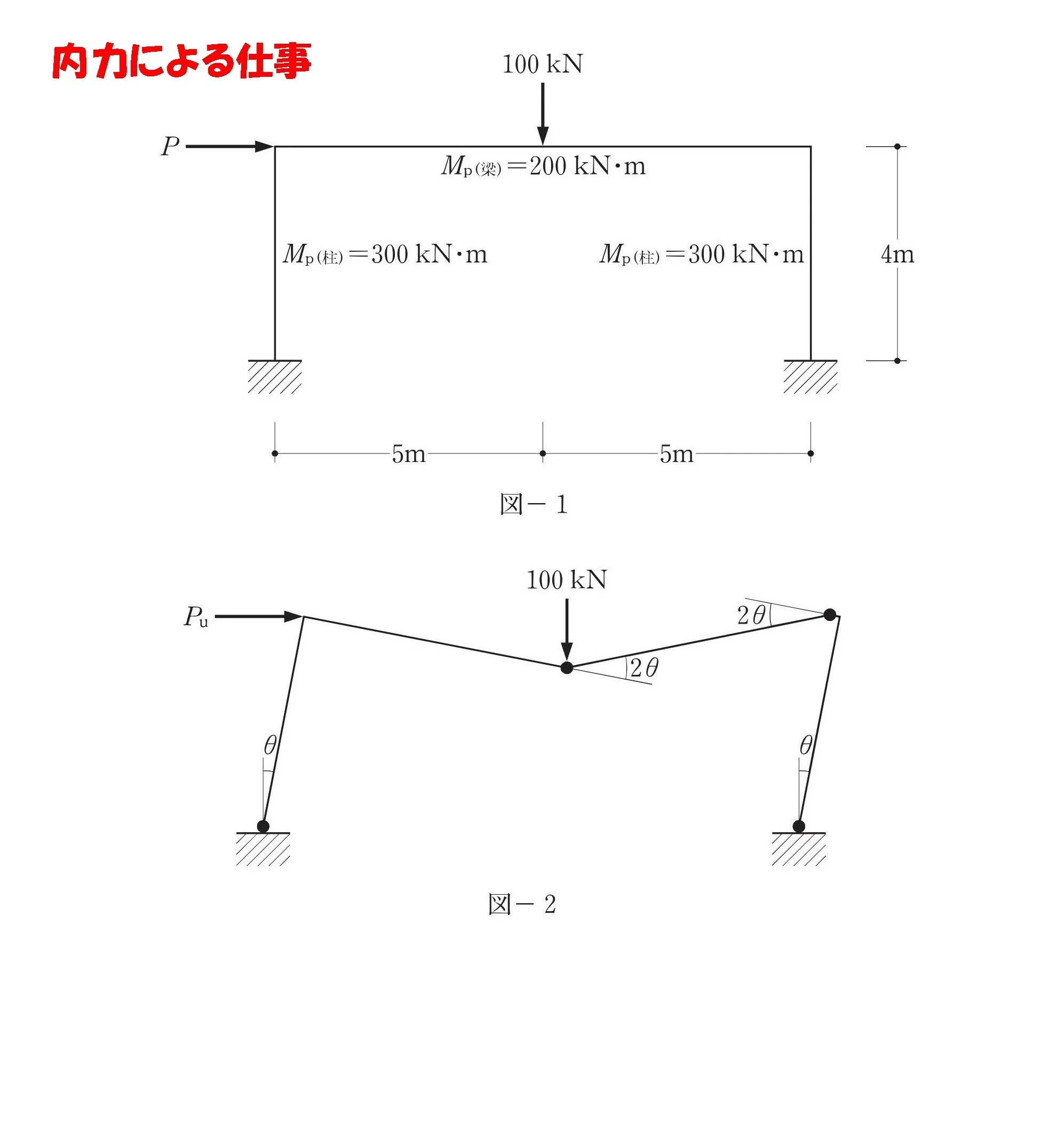

図-1:モーメントMp
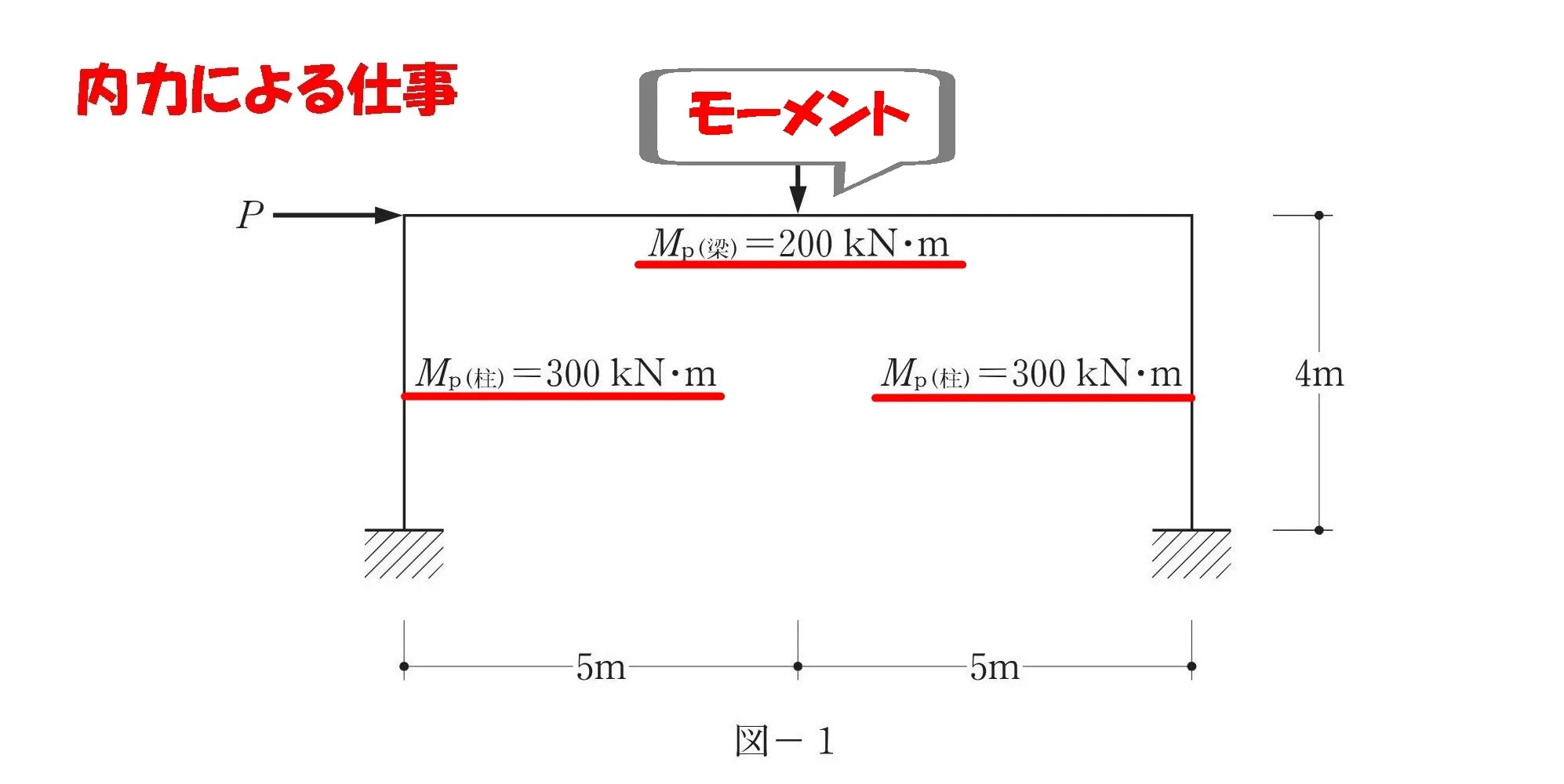

図-2:回転角θ
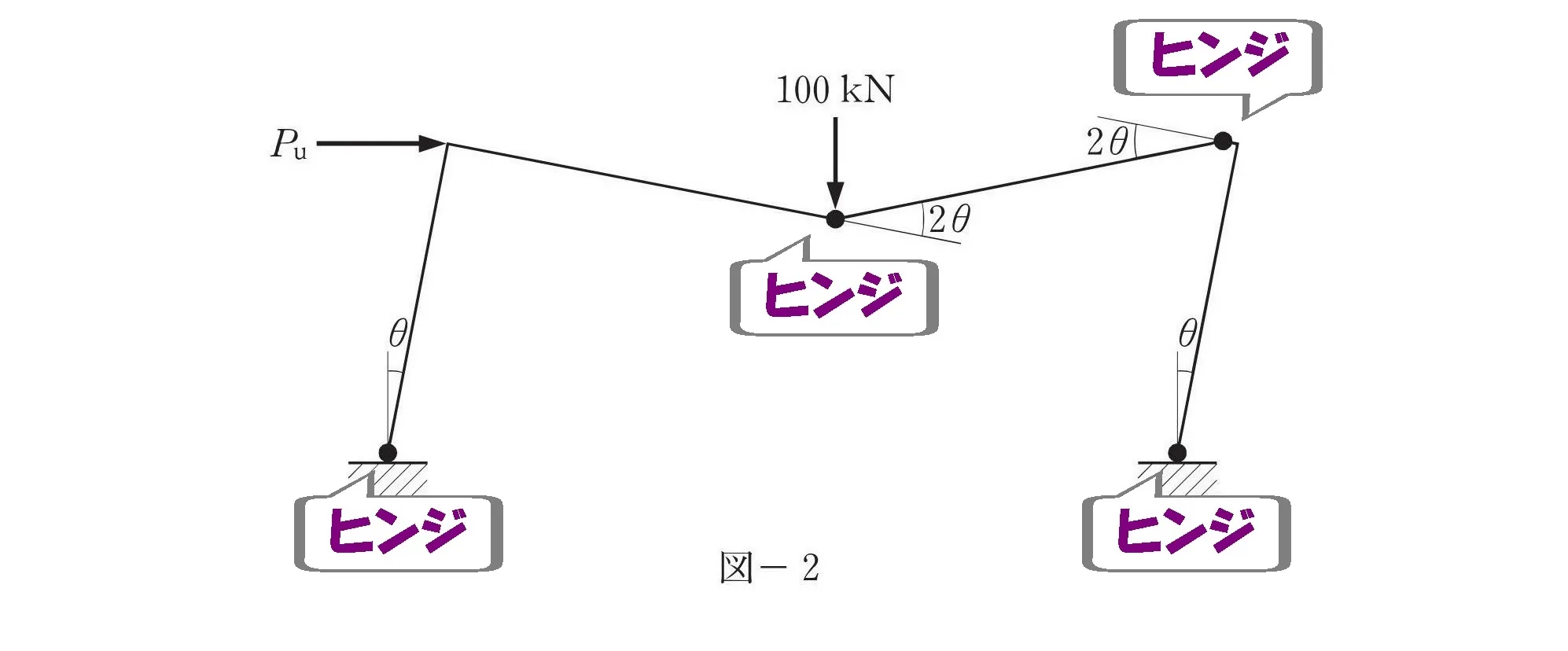

マークする
- 図-1:モーメントMp
- 図-2:回転角θ、2θ
内力による仕事を求めるうえで、必要な数値となります。
図-1から図-2に数値を転記する
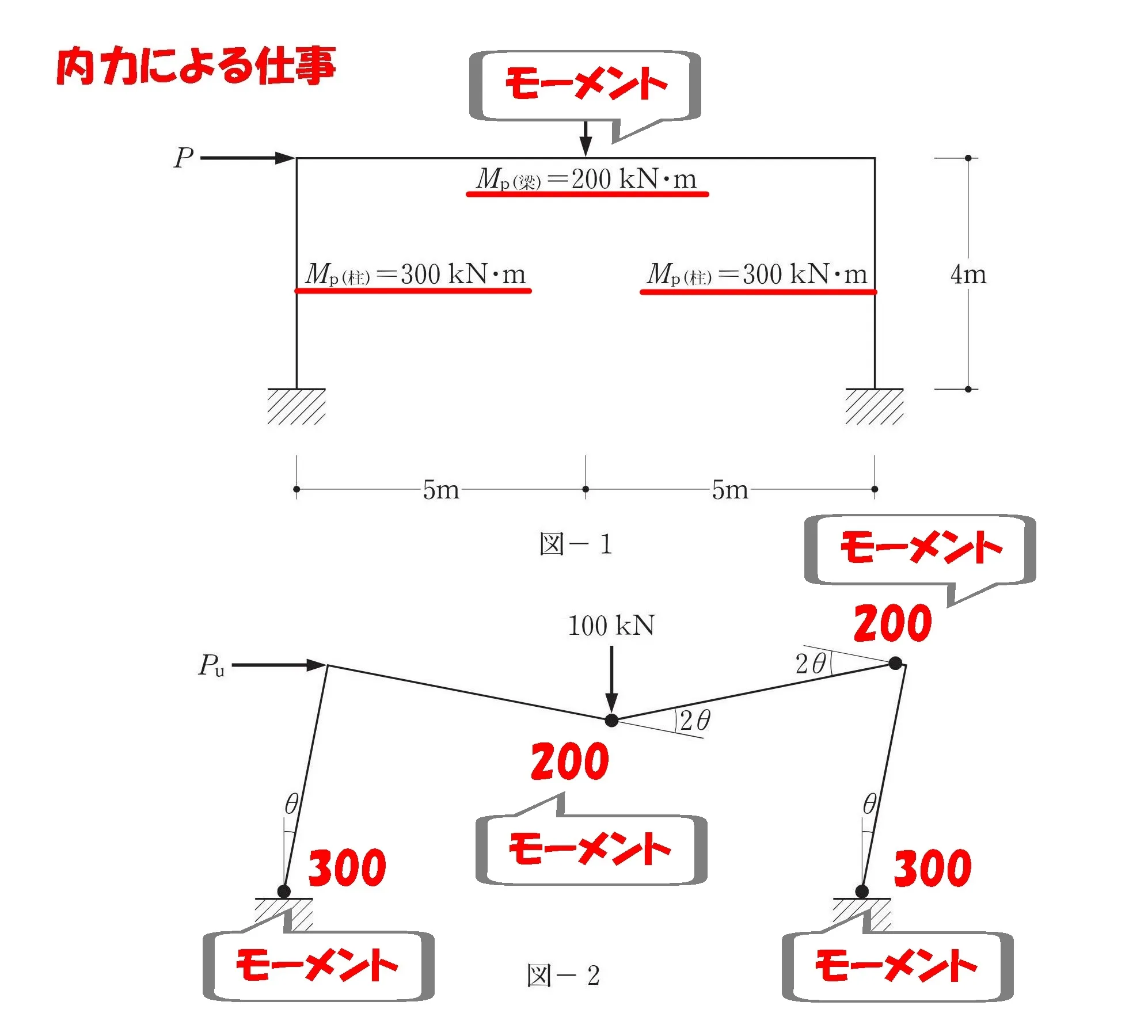

図-1の「モーメントMpの数値」を、図-2の「塑性ヒンジ」にすべて転記しましょう。



必要な数値を
図-2に書き写しておく。
Mpの数値×回転角
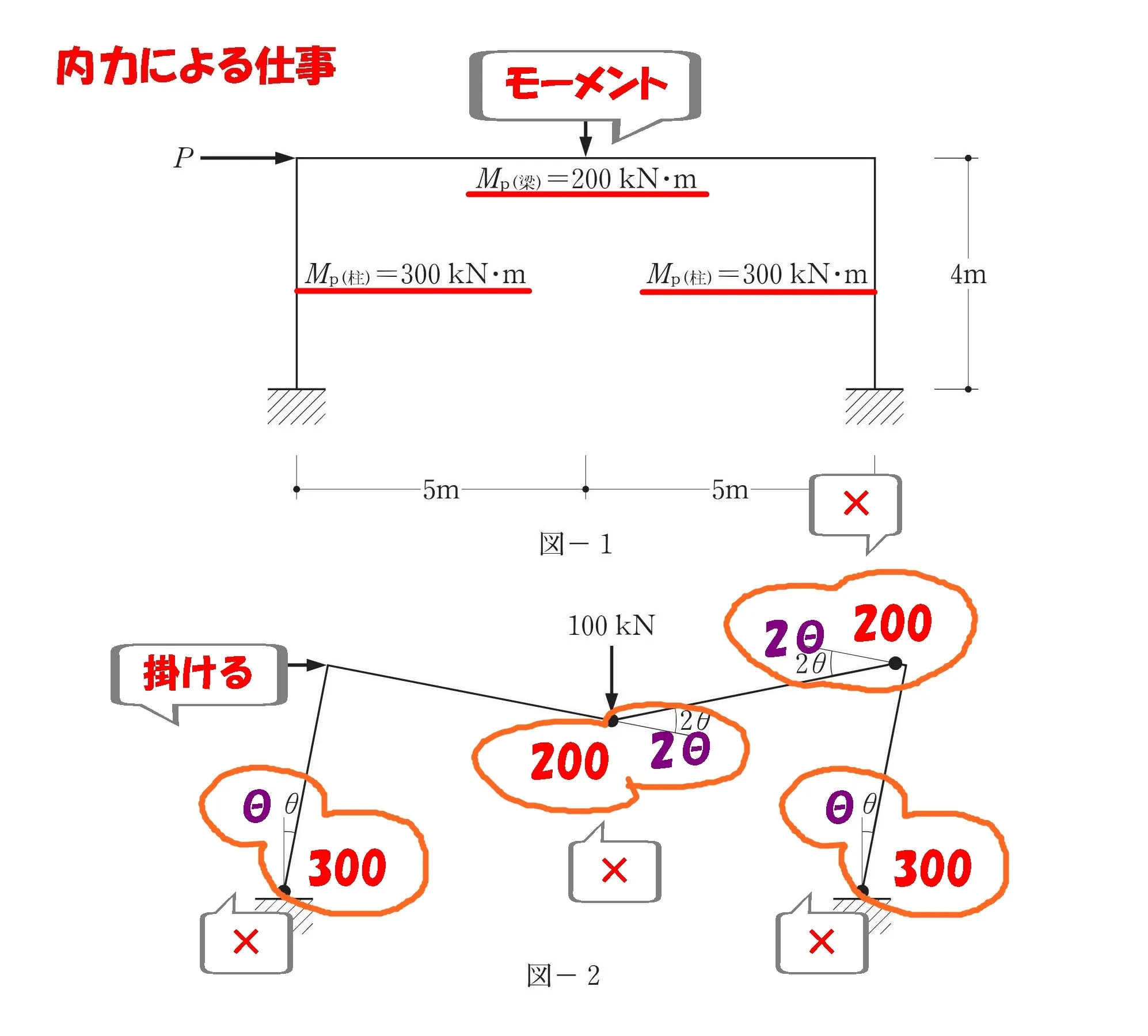

モーメントの「Mpの数値」×塑性ヒンジの「回転角θ」をすべて足した式をつくる。
内力による仕事を求める


$$内力による仕事=モーメント×回転角より,$$
$$\{300*\theta+200*2\theta+200*2\theta+300*\theta\}$$



〇囲みした数値を
掛けて足すだけで良い!
公式
内力による仕事=モーメント×回転角
3.外力による仕事=内力による仕事 ⇨ Puを求める
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める
イコールで結ぶ
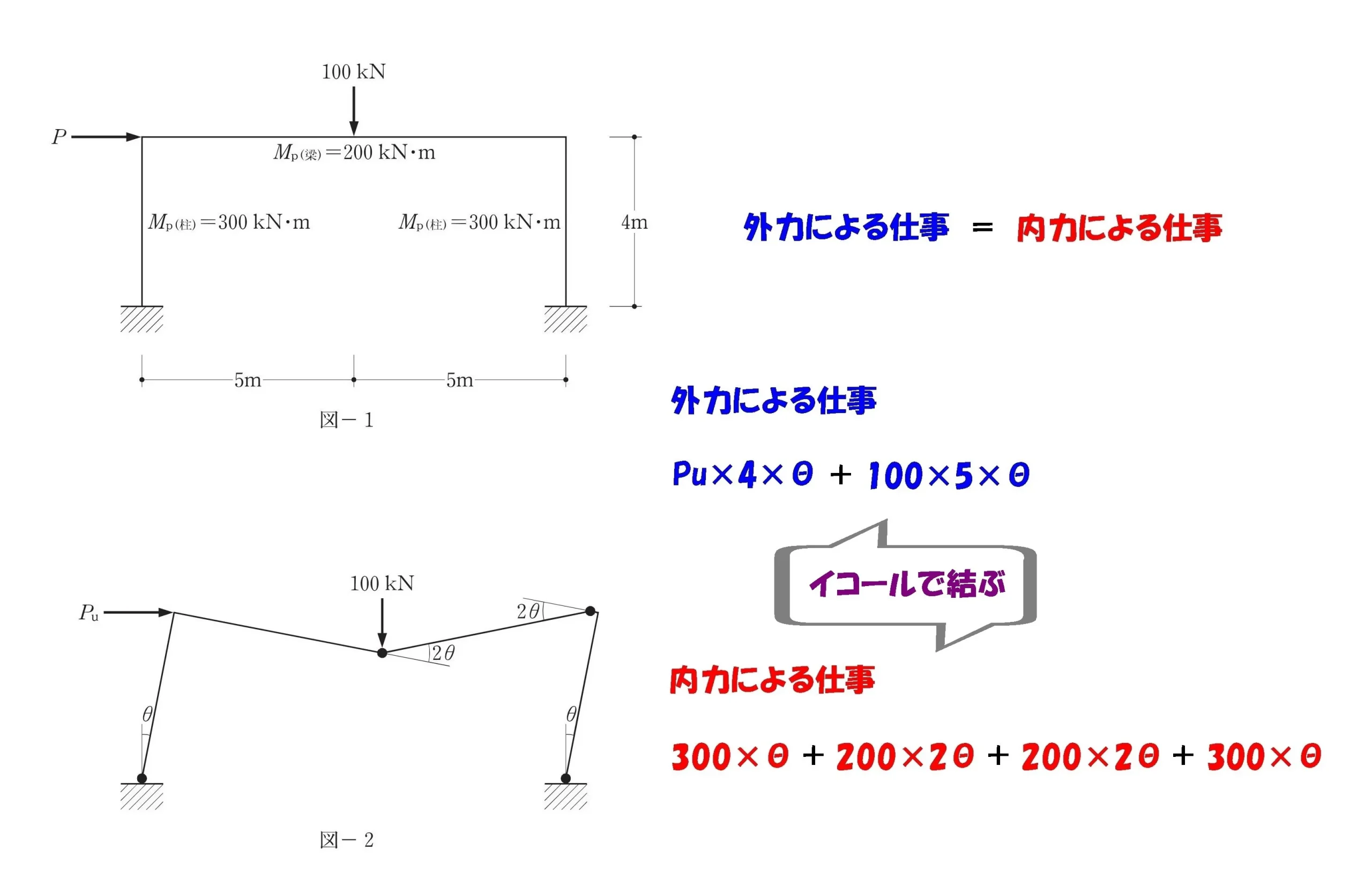

$$「外力による仕事」=「内力による仕事」より,$$
$$\{Pu*\underline{4*\theta}+\underline{100}*5*\underline{\theta}\}=\{\underline{300*\theta}+200*\underline{2\theta}+200*\underline{2\theta}+\underline{300*\theta}\}$$
$$\underline{2*\theta}*\{Pu*2+50*5\}=\underline{2*\theta}*\{300+200+200\}$$
$$Pu*2+50*5=300+200+200$$$$Pu*2=700-50*5$$$$Pu*2=450⇨Pu=225kN$$



これは簡単に解ける!
答え.2

攻略ポイント
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める
崩壊メカニズム-2
難易度:★★★★★
ラーメン架構における力学の「集大成」となる問題です。



ラーメンの集大成となる
全部盛りでございます。



お主、ラーメンをすするな。
腹が減ってくるではないか。


この動画を YouTube で視聴
考え方
せん断力は「モーメント図の傾き」として捉える。
攻略ポイント
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
問題
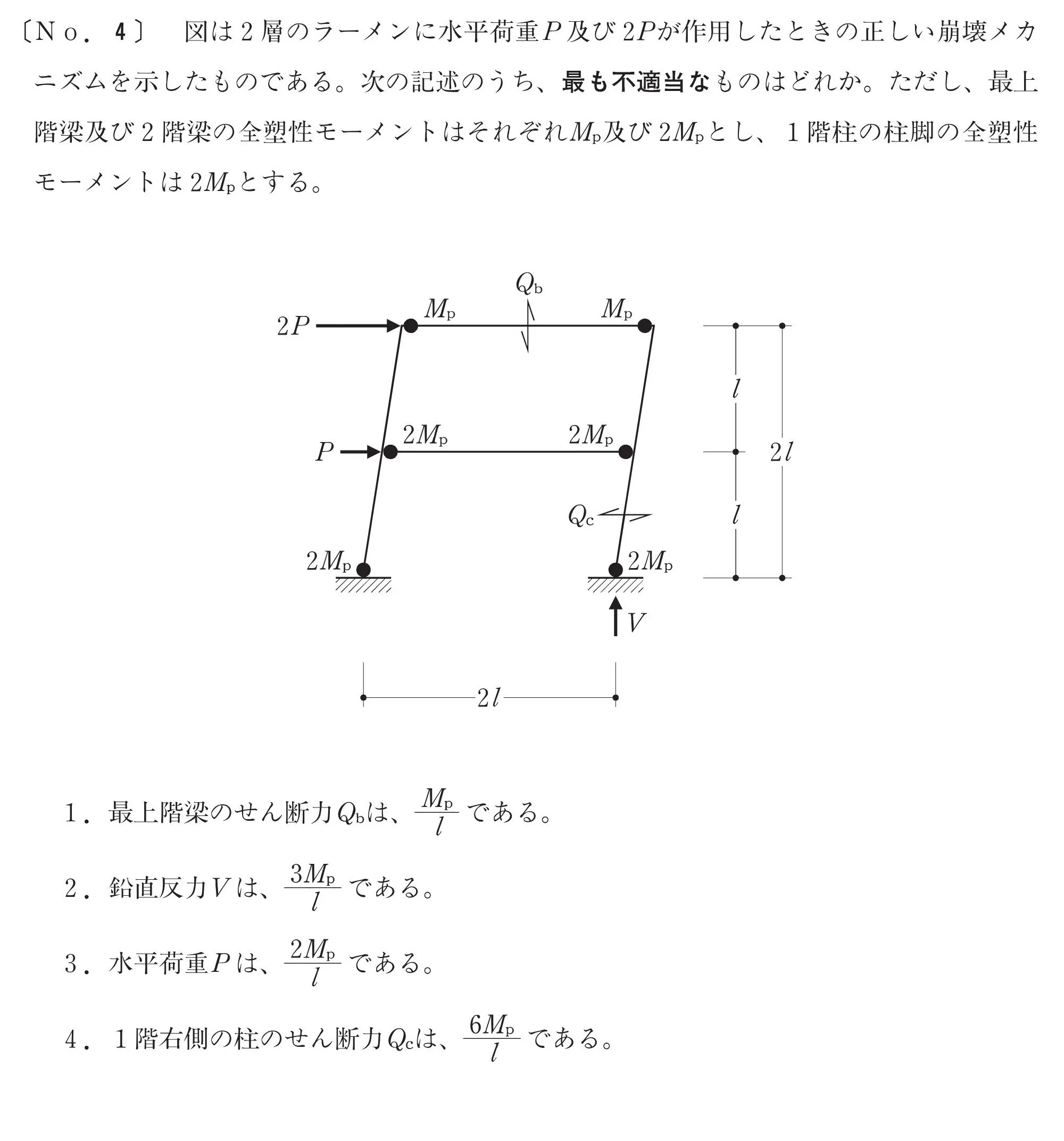

1.モーメント図の傾きより、せん断力を求める
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
枝.1


$$1.[最上階梁のせん断力Qbは、\frac{ Mp }{ L }である。]$$
梁のせん断力Qbを求める
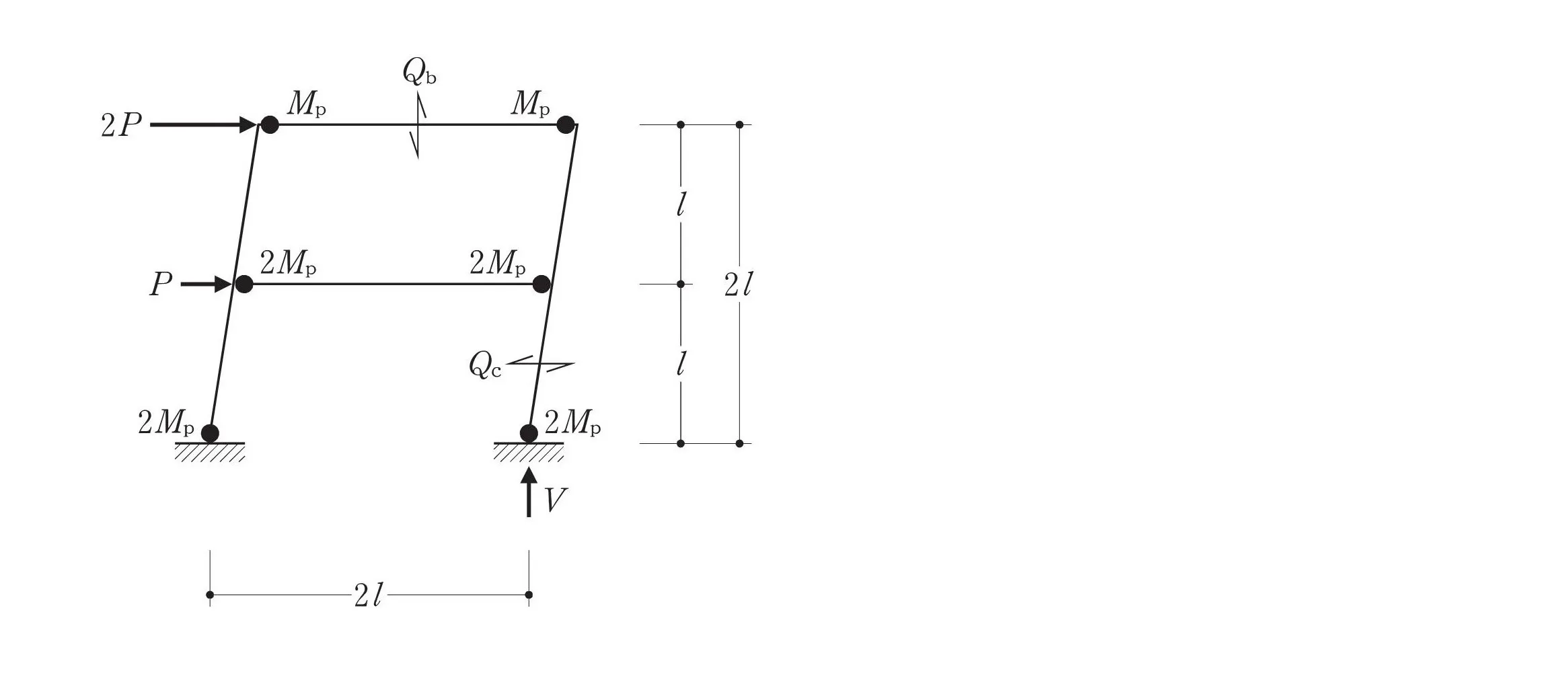

モーメント図を描く
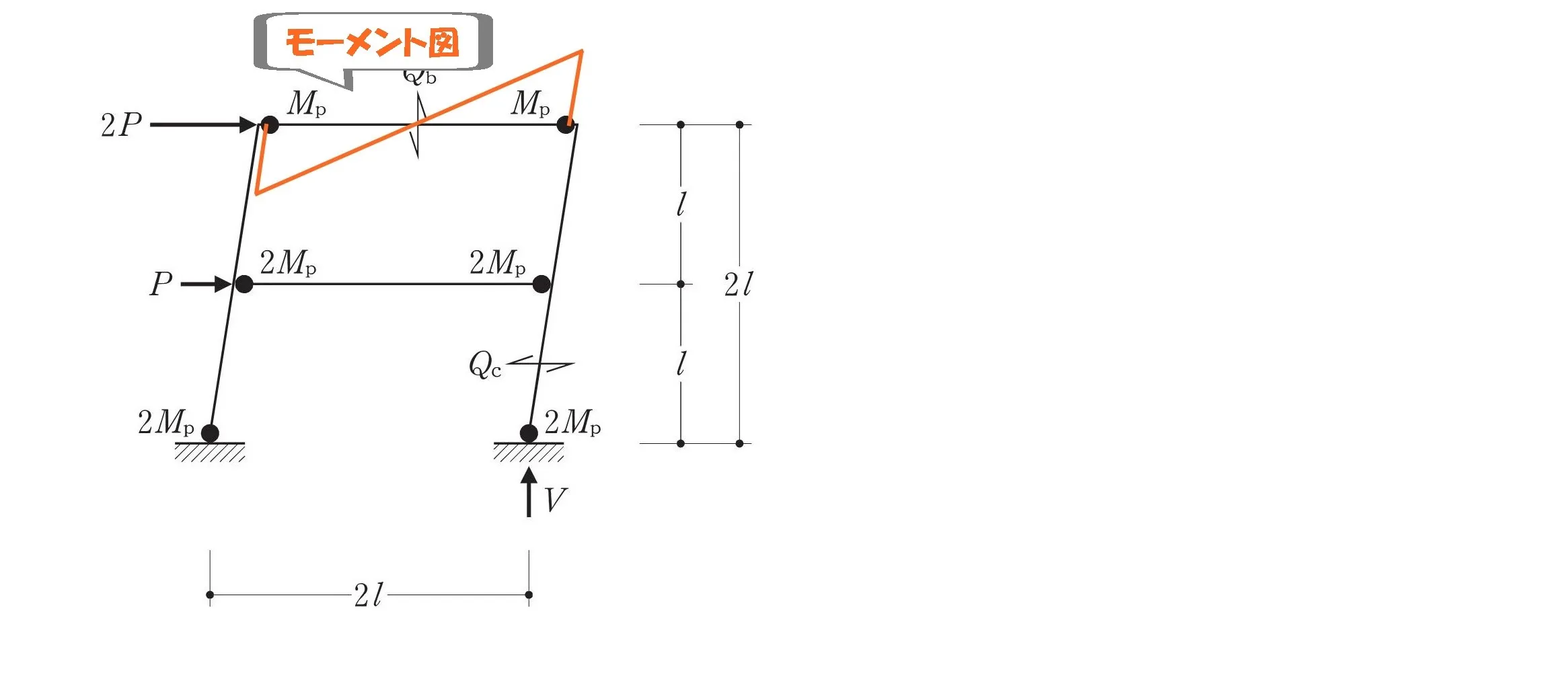

モーメント=力×距離
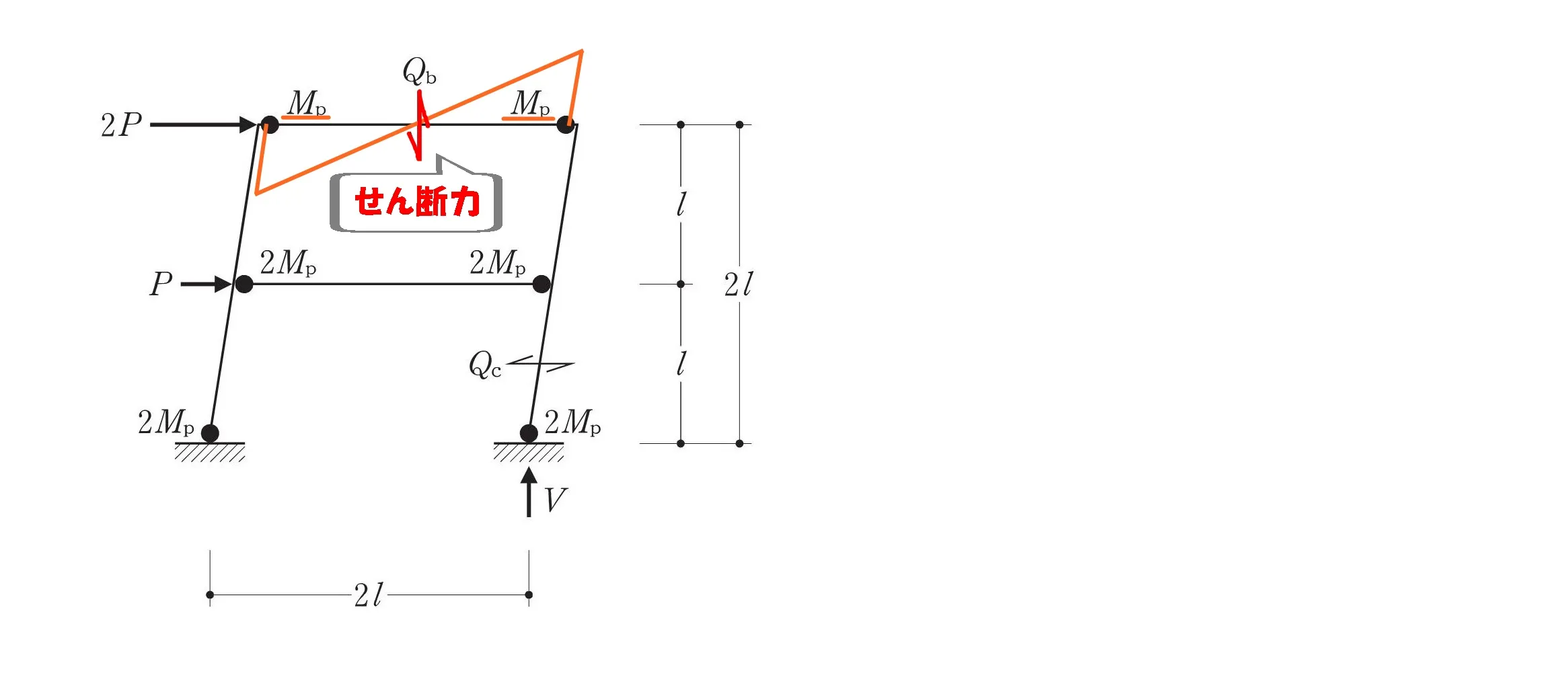

$$モーメント=力×距離$$$$モーメント=(Mp+Mp)$$$$力=Qb・距離=2L$$
モーメント図の傾き
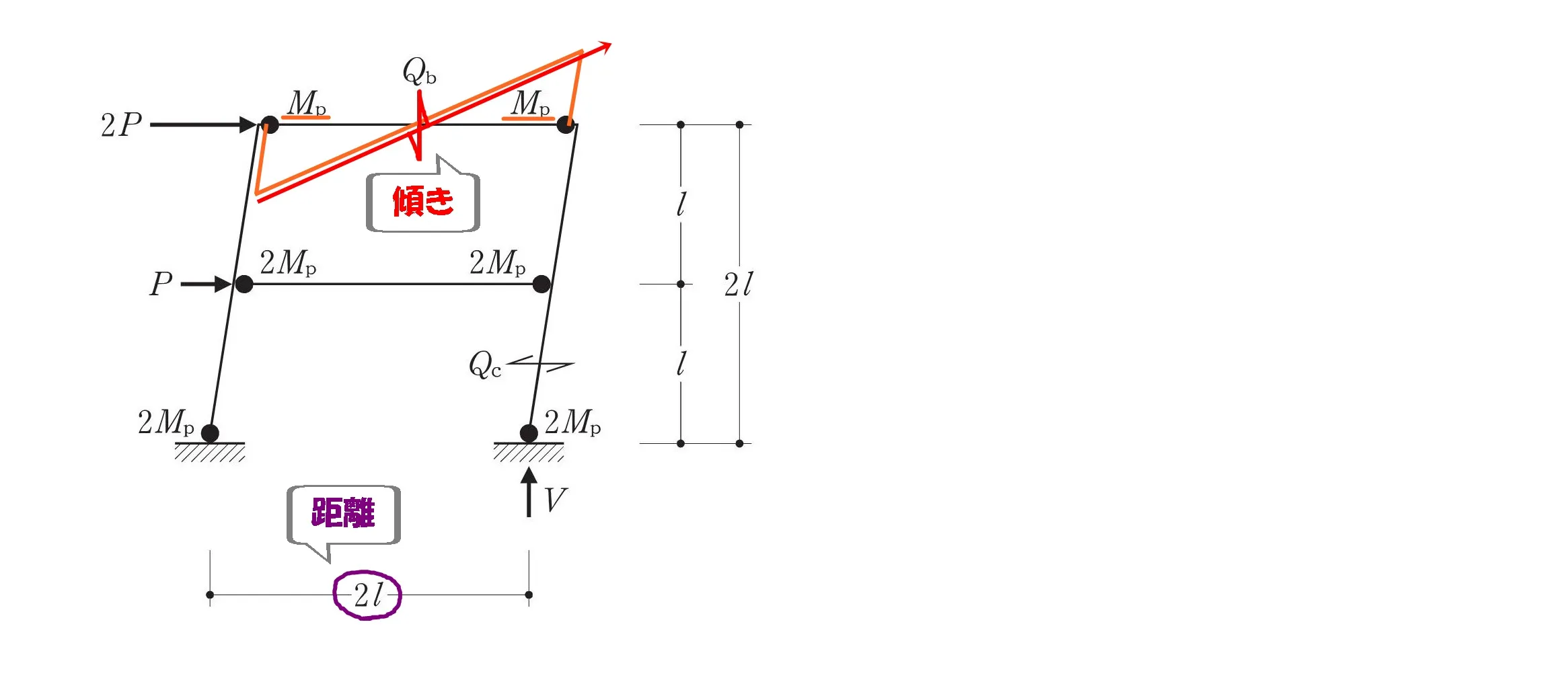

$$せん断力=モーメントの傾き$$$$モーメントの傾き=\frac{ モーメントの大きさ }{ 距離 }$$
せん断力Qbを求める
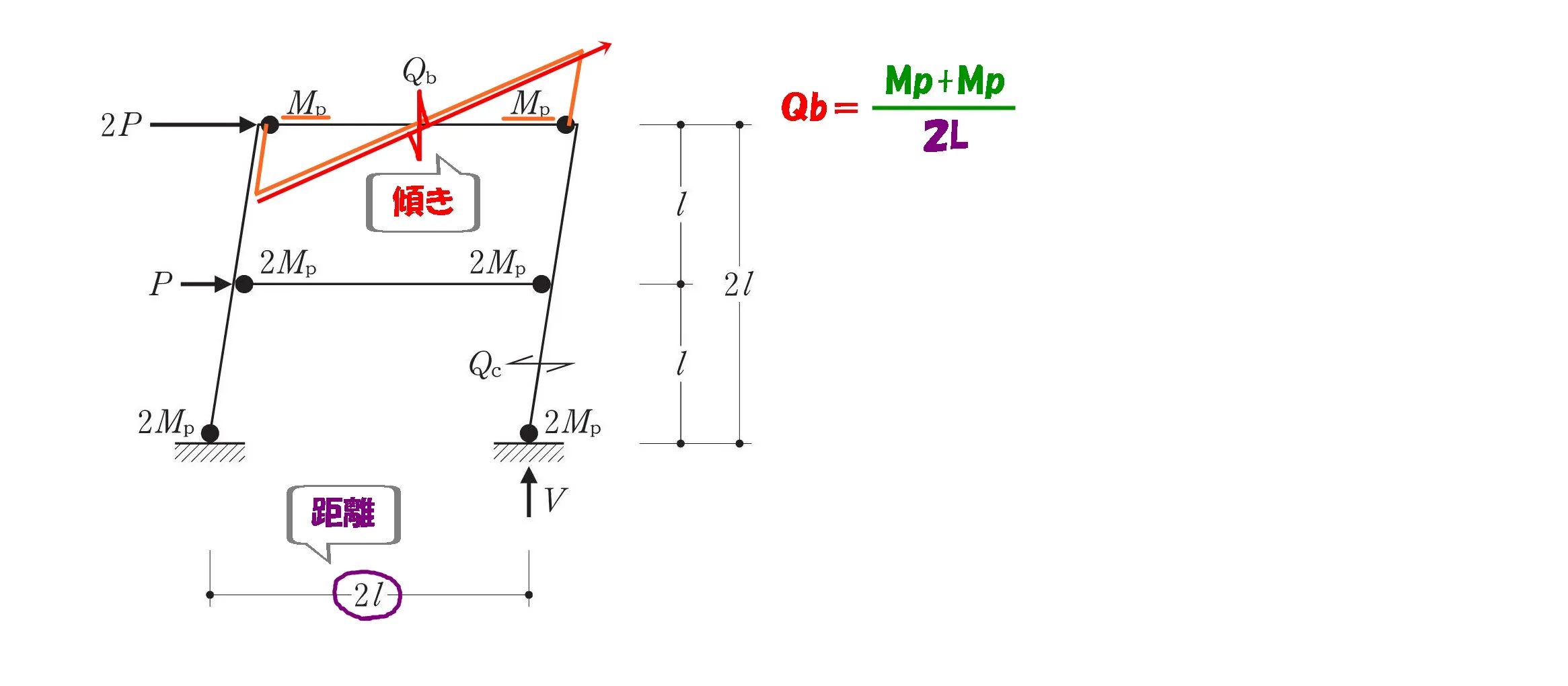

$$せん断力:Qb=\frac{ Mp+Mp }{ 2L }=\frac{ Mp }{ L }$$
せん断力Qeを求める
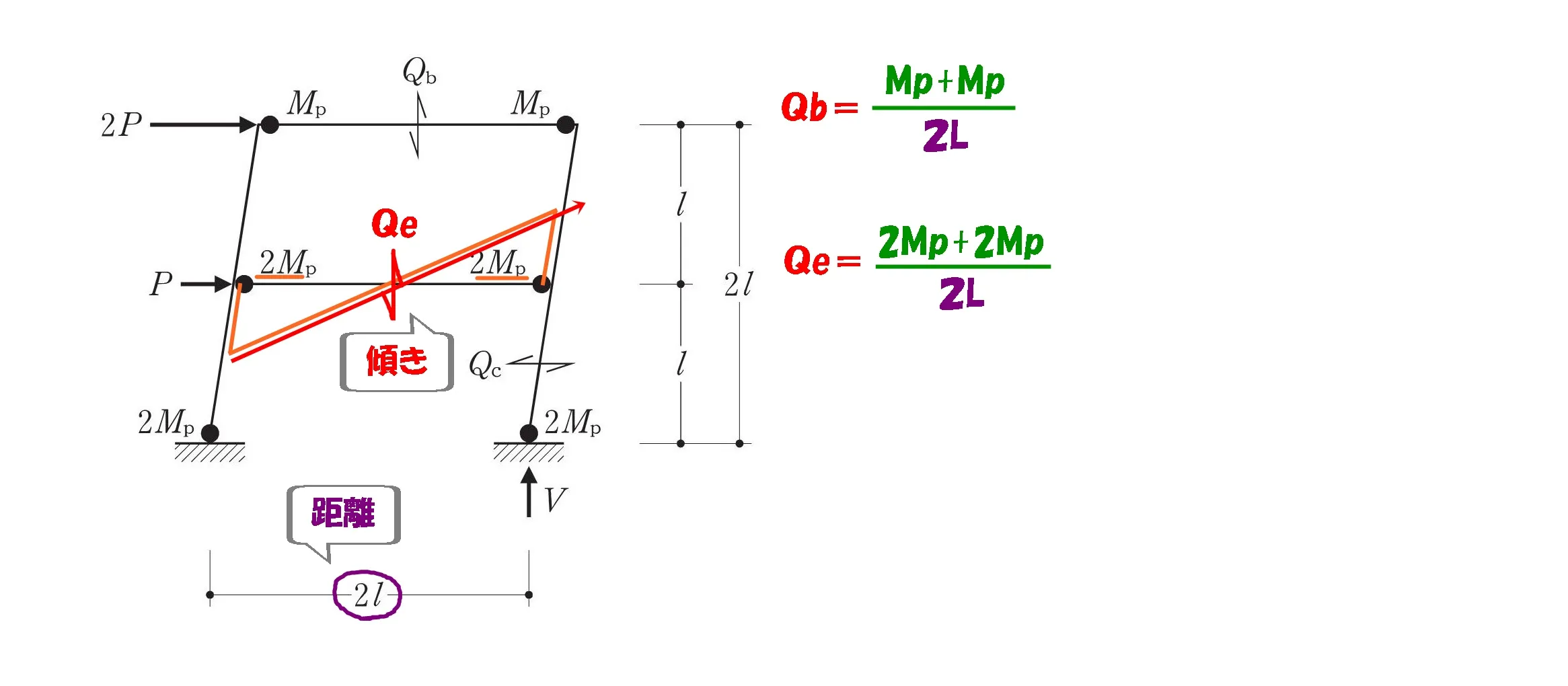

$$せん断力:Qe=\frac{ 2Mp+2Mp }{ 2L }=\frac{ 2Mp }{ L }$$
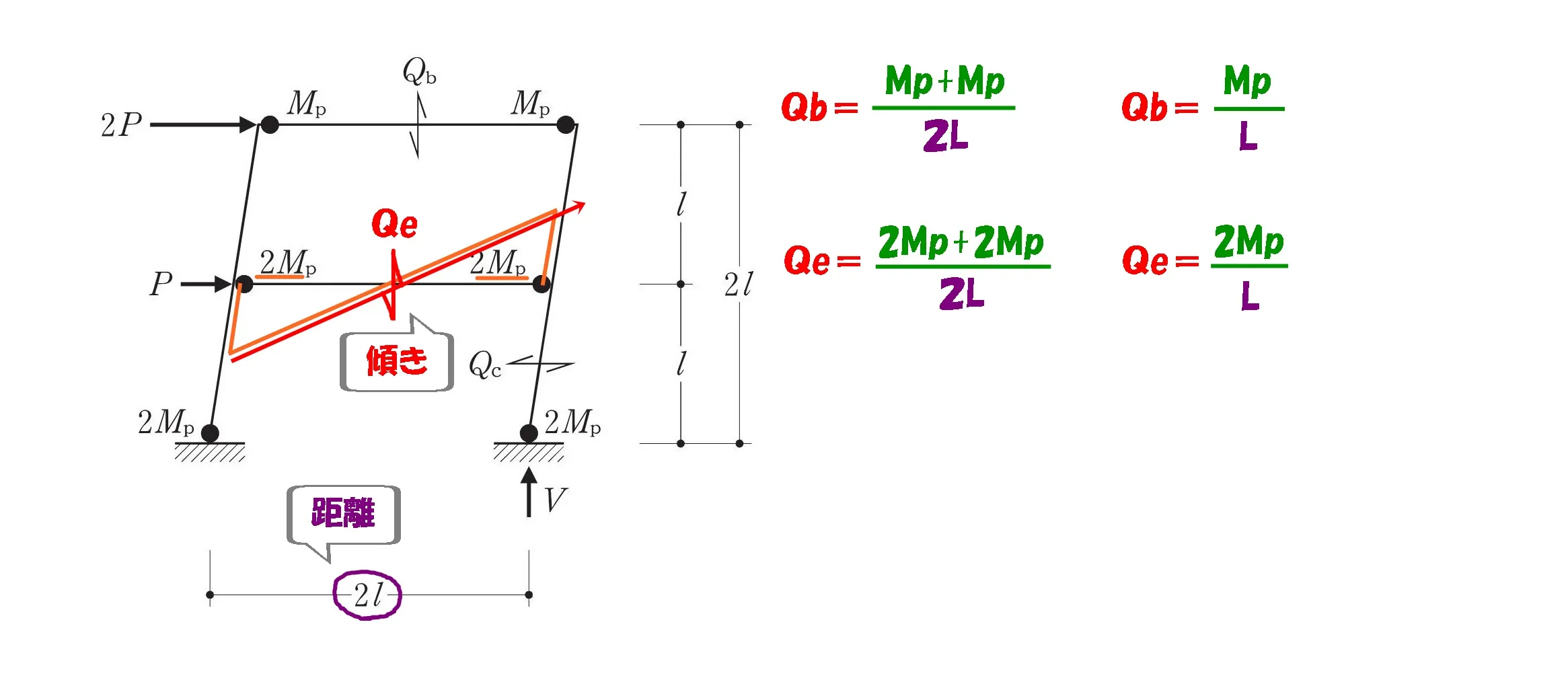

$$最上階梁のせん断力:Qb=\frac{ Mp }{ L }$$$$2階梁のせん断力:Qe=\frac{ 2Mp }{ L }$$



せん断力は
モーメントの傾き。
せん断力は「モーメント図の傾き」として捉える。
2.部材を切断して取り出し、ΣY=0より鉛直反力を求める
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
枝.2


$$2.[鉛直反力Vは、\frac{ 3Mp }{ L }である。]$$
鉛直反力Vを求める
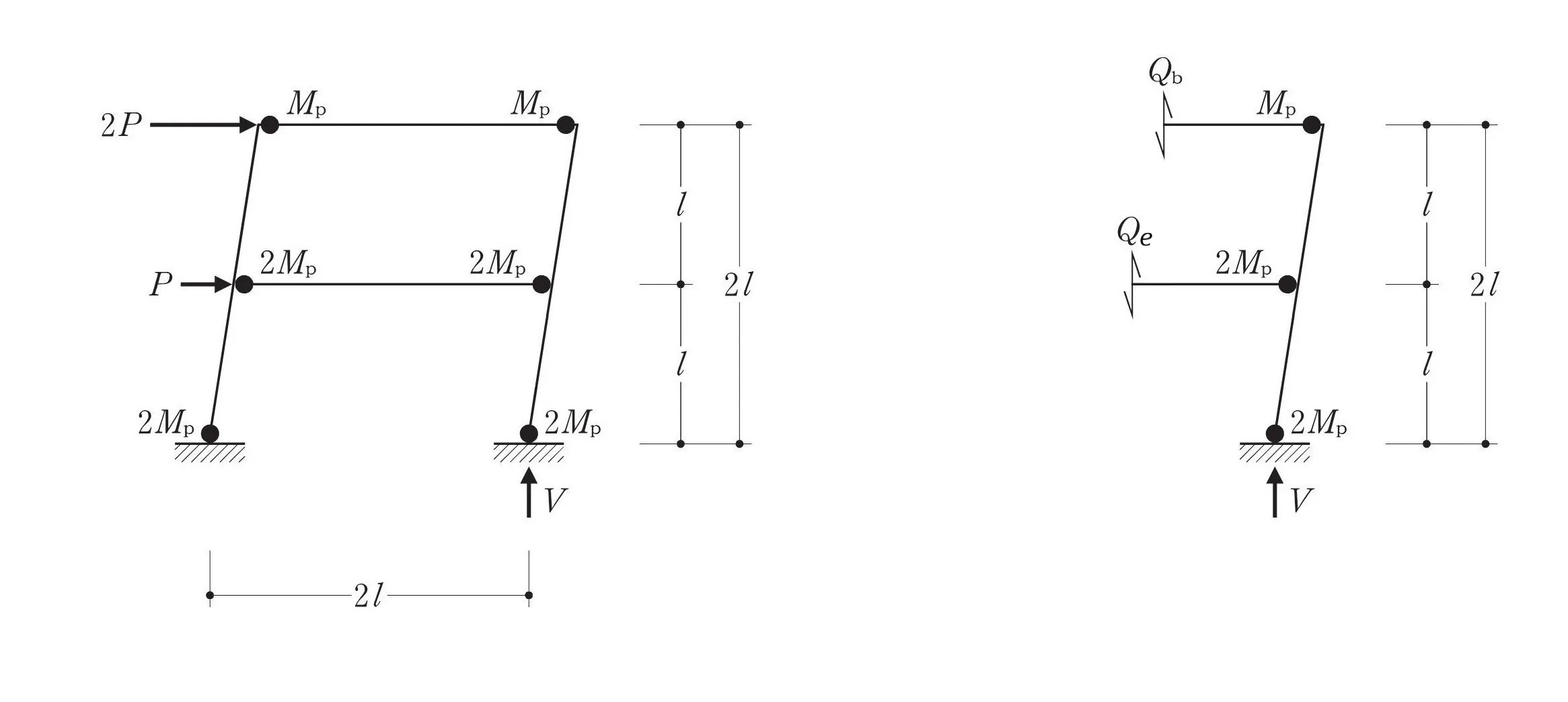




準備は良いか?
部材を切断して取り出す
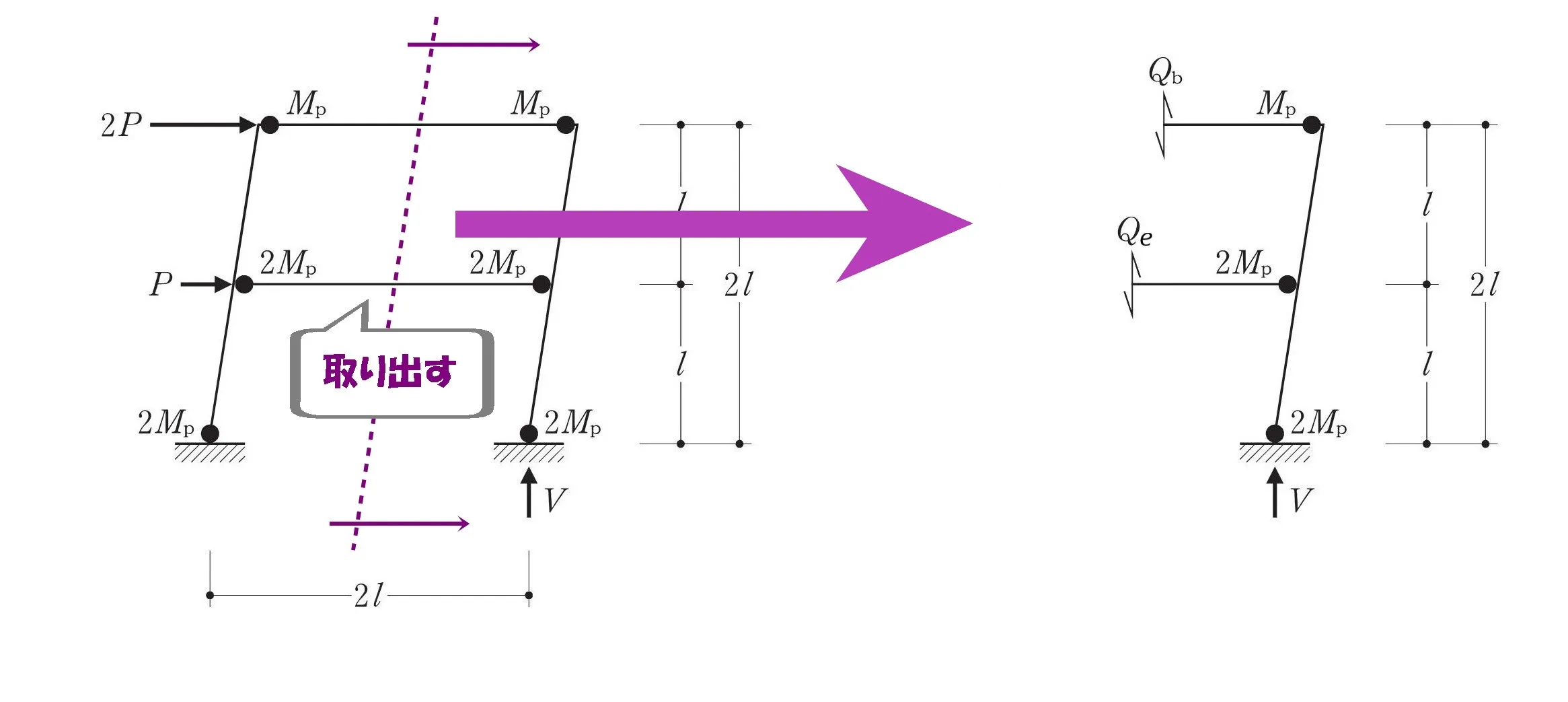

各階の梁を中央から切断して、鉛直反力Vのある方を取り出します。



伝家の宝刀、部材斬り!
梁せん断力を書き込む
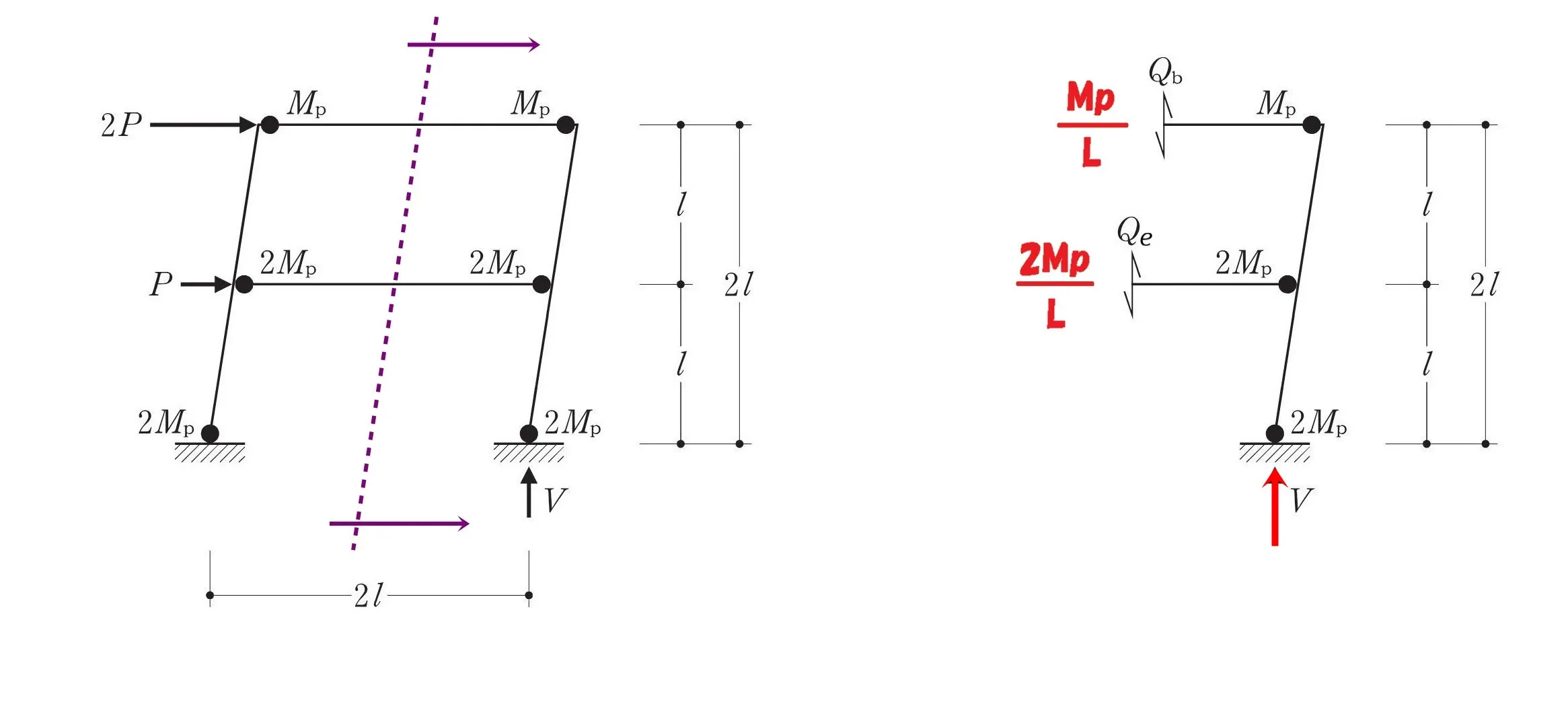

$$最上階梁のせん断力:Qb=\frac{ Mp }{ L }$$$$2階梁のせん断力:Qe=\frac{ 2Mp }{ L }$$
先ほど求めた梁せん断力Qb、Qeを書き込みます。
吊り合い式ΣY=0
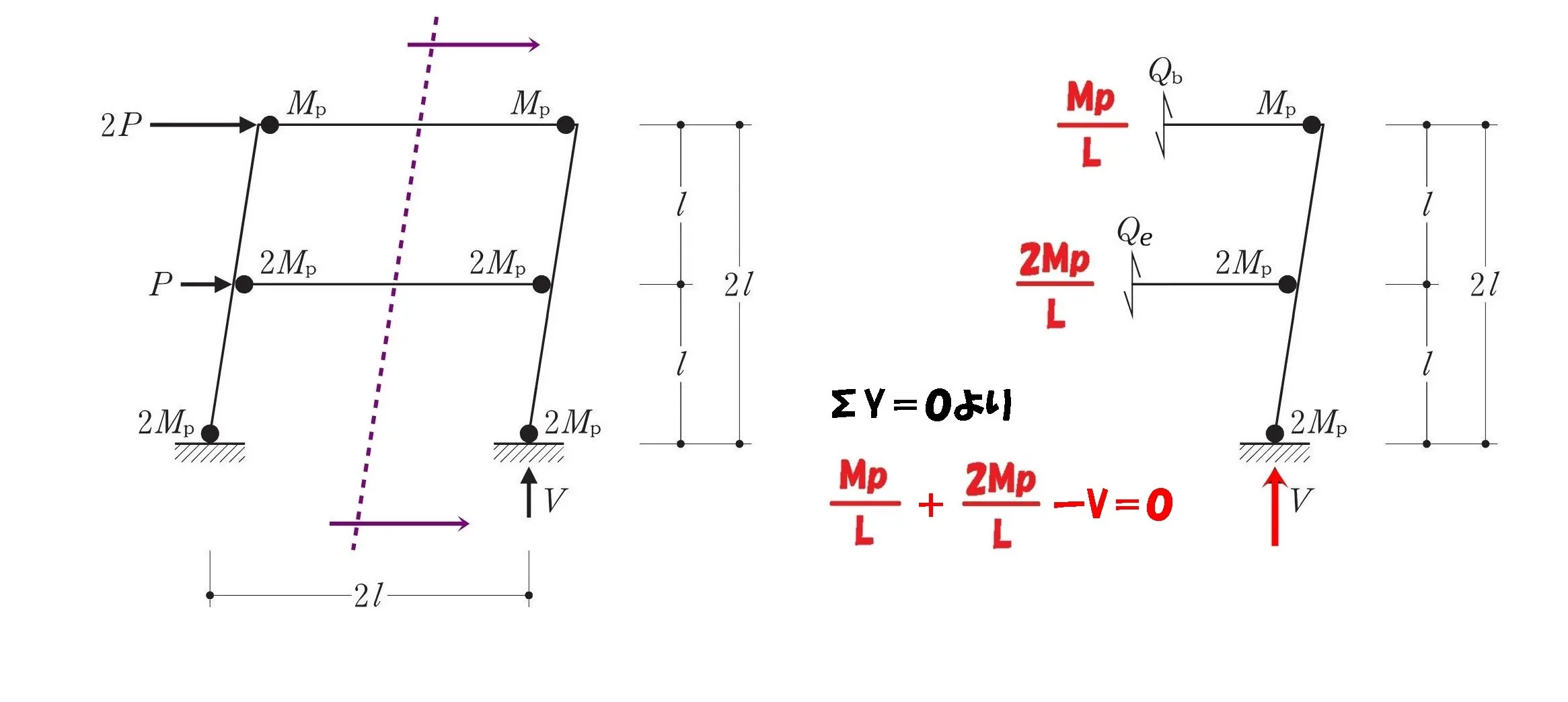

$$\Sigma Y=0より,$$$$Qb+Qe-V=0が成り立つ$$
鉛直反力Vを求める
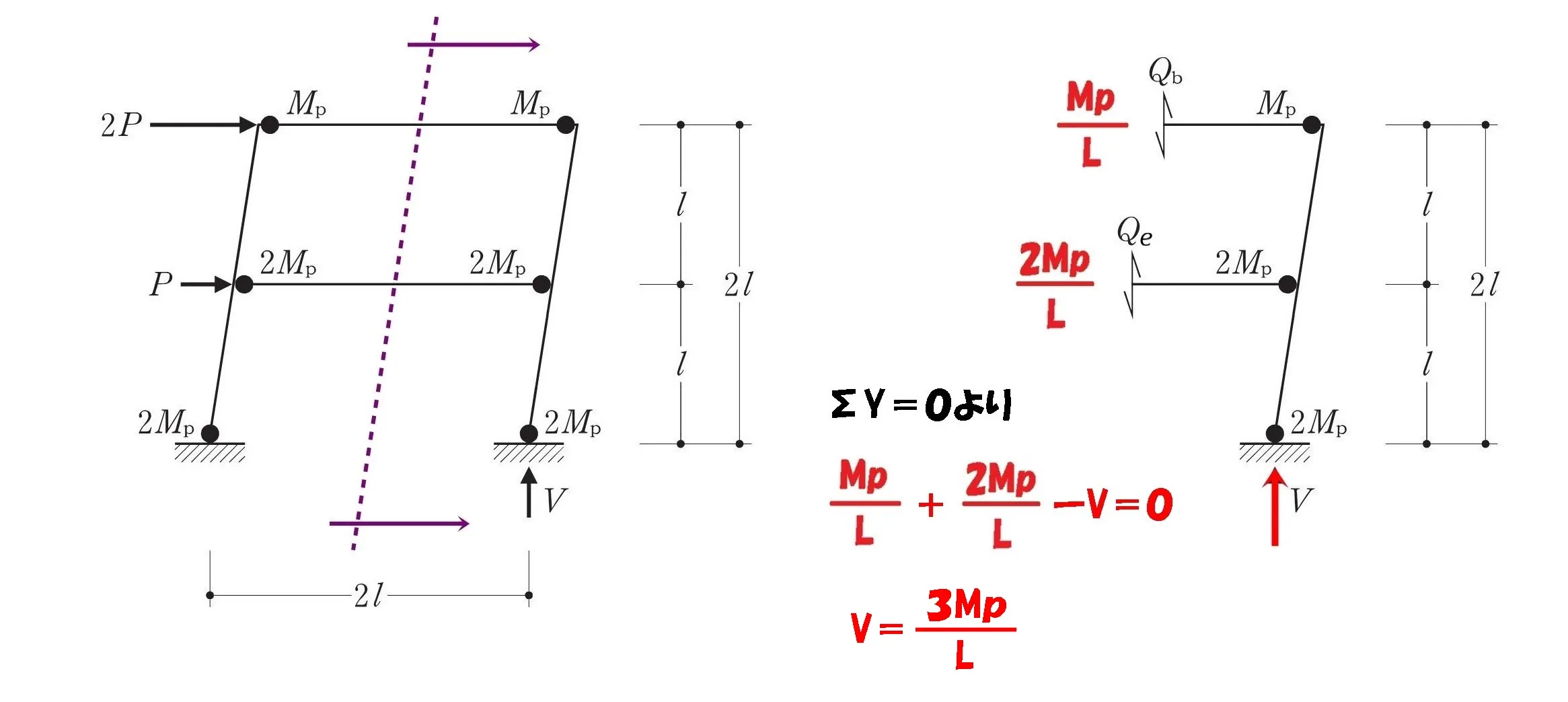

$$\frac{ Mp }{ L }+\frac{ 2Mp }{ L }-V=0より,$$
$$V=\frac{ Mp }{ L }+\frac{ 2Mp }{ L }=\frac{ 3Mp }{ L }$$$$反力V=\frac{ 3Mp }{ L }$$
公式
$$\Sigma Y=0$$



Σワイ!
3.外力による仕事=内力による仕事から、水平荷重を求める
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
枝.3


$$3.[水平荷重Pは、\frac{ 2Mp }{ L }である。]$$
仕事の吊り合い式
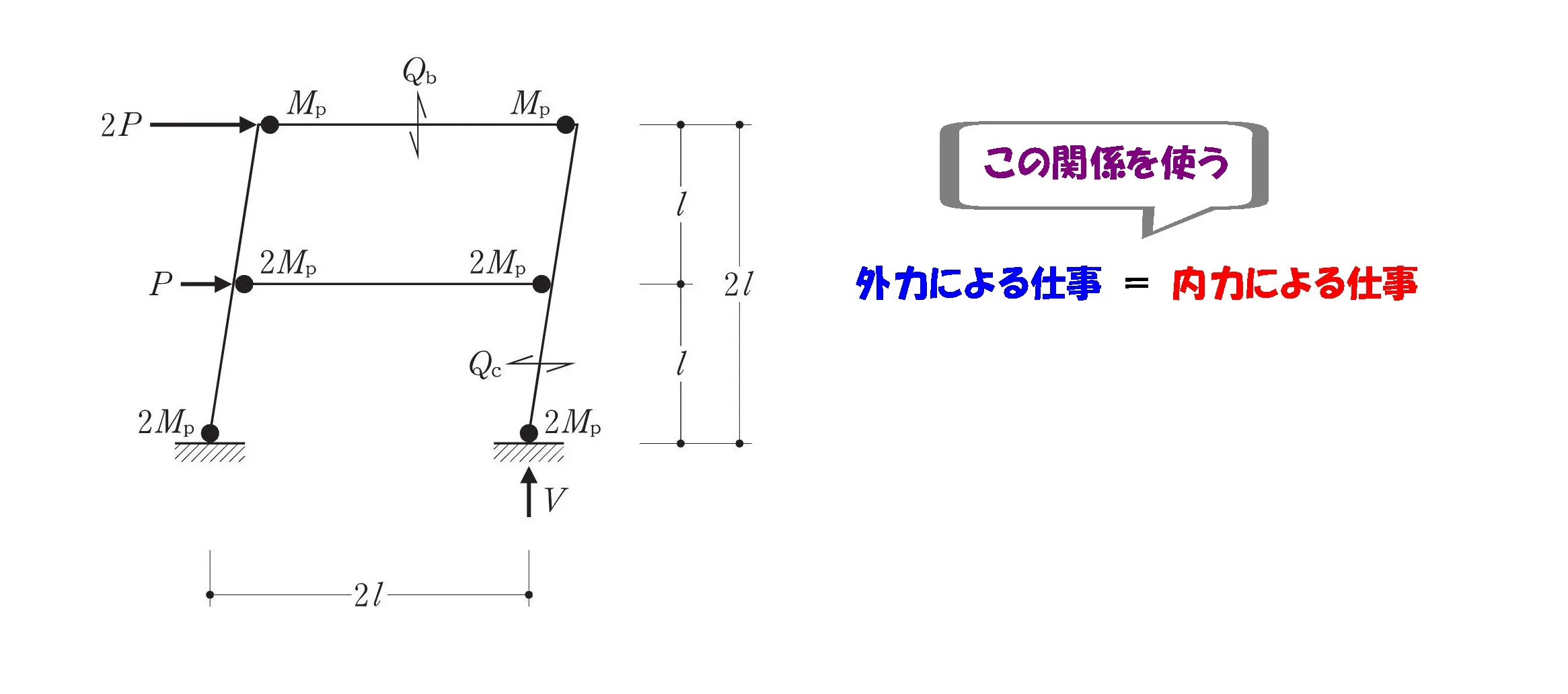

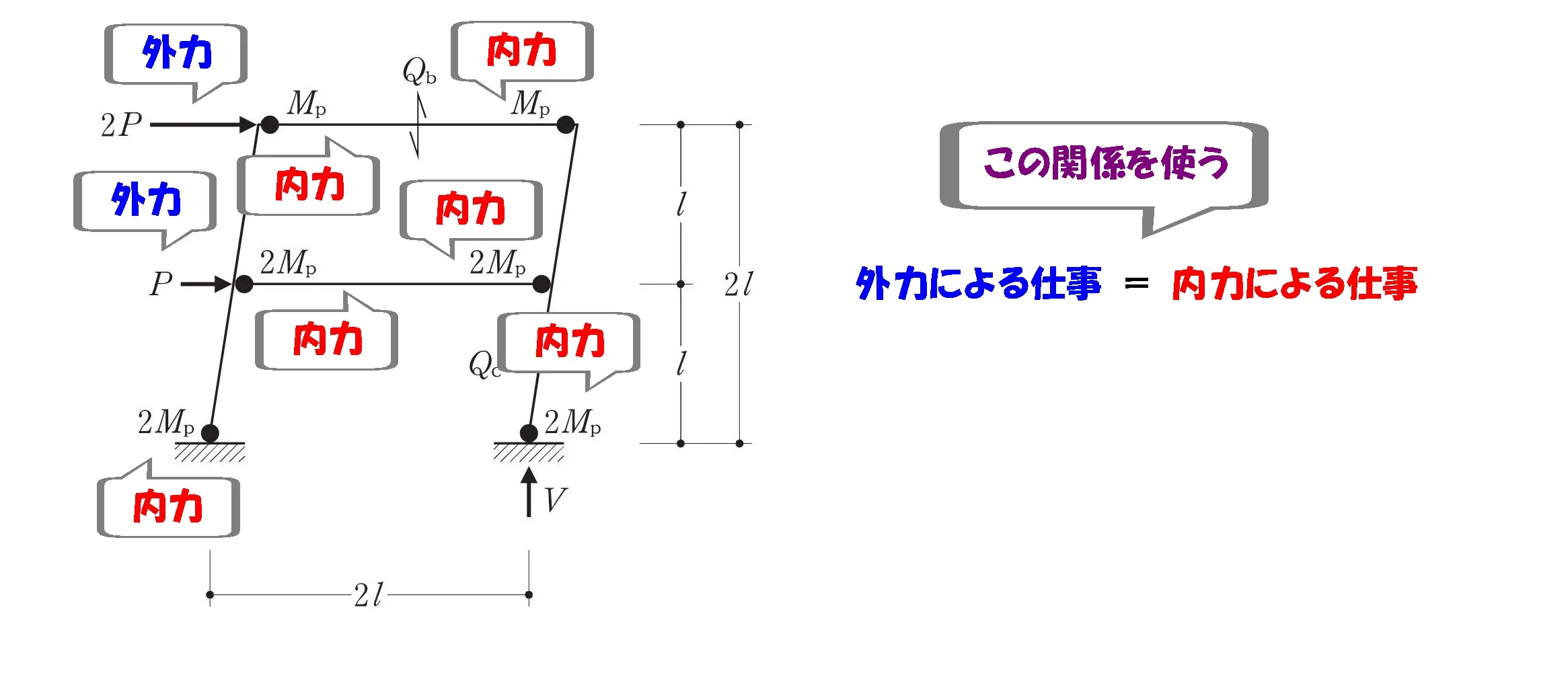
外力による仕事=内力による仕事

モーメント=力×距離
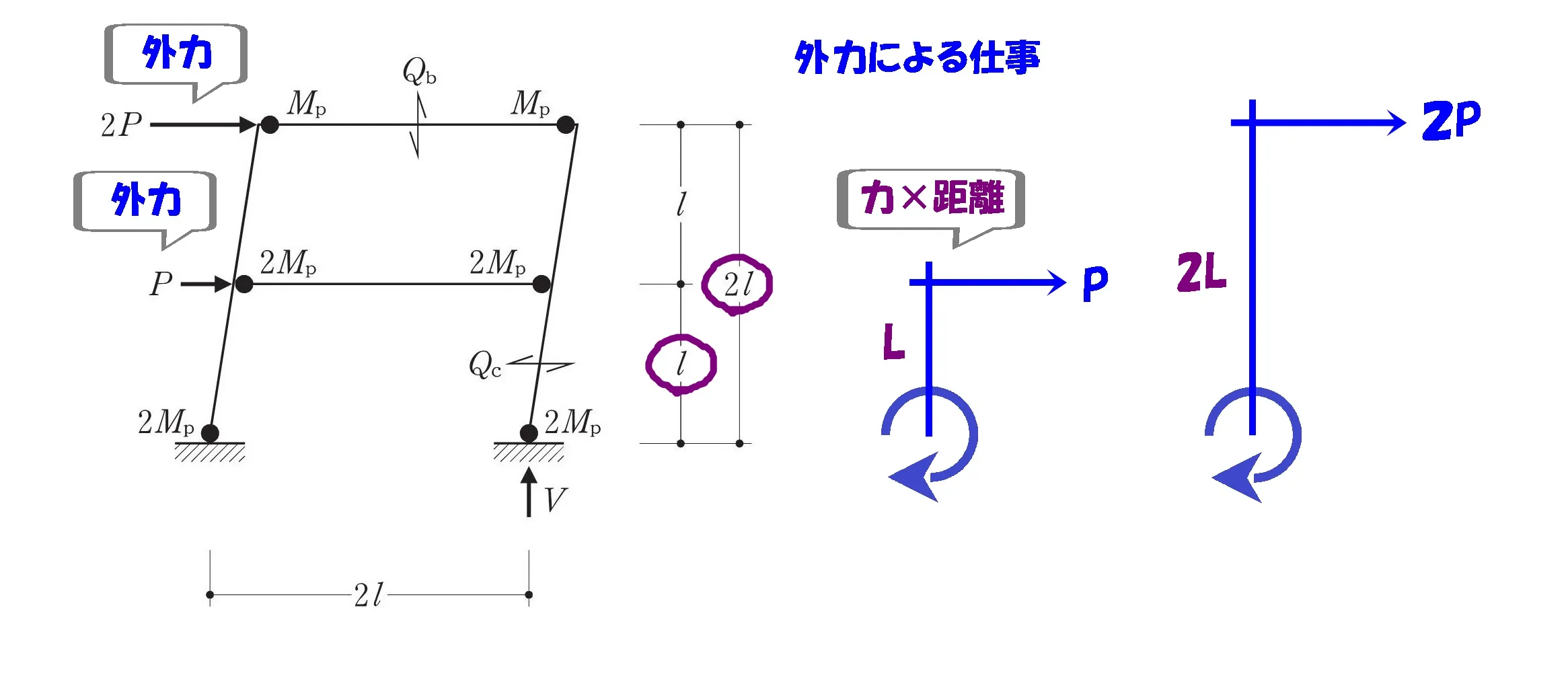

$$モーメント=力×距離より,$$$$2P*2L+P*L$$
外力による仕事
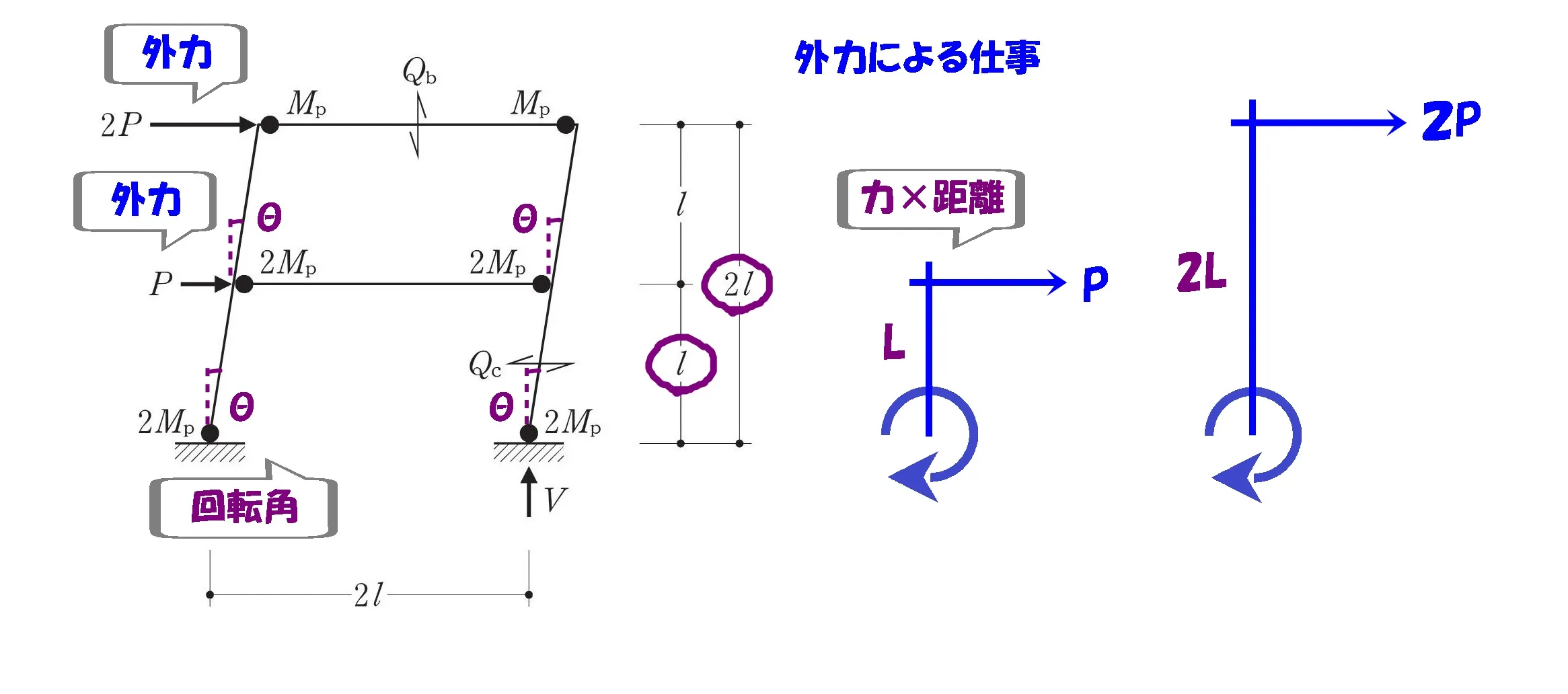

ラーメン図に、外力によって回転が生じる位置に「θ」を書き込む。



必要な要素は
すべて書き込む。
公式
外力による仕事=力×距離×回転角
外力による仕事を求める
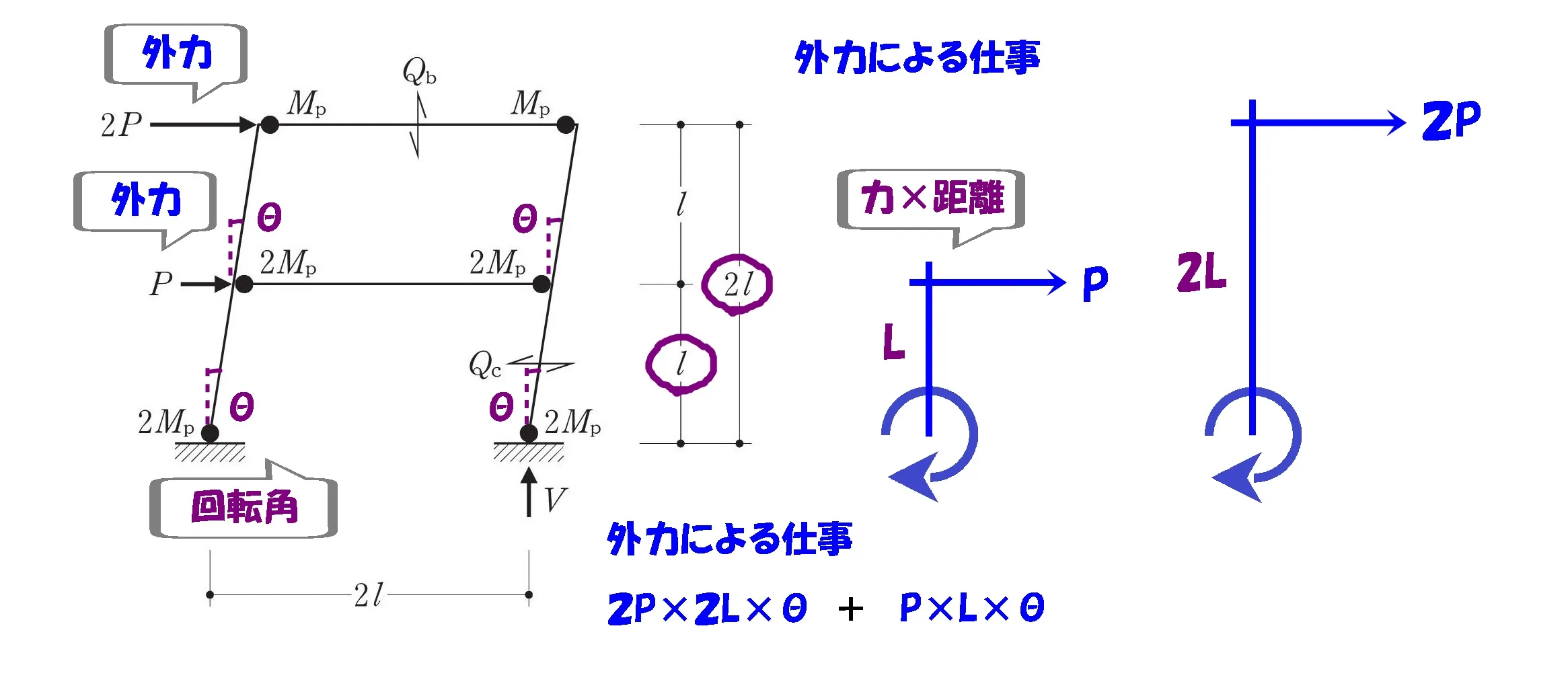

$$外力による仕事=モーメント×回転角より,$$
$$\{{2P*2L*\theta+P*L*\theta}\}$$
内力による仕事を求める
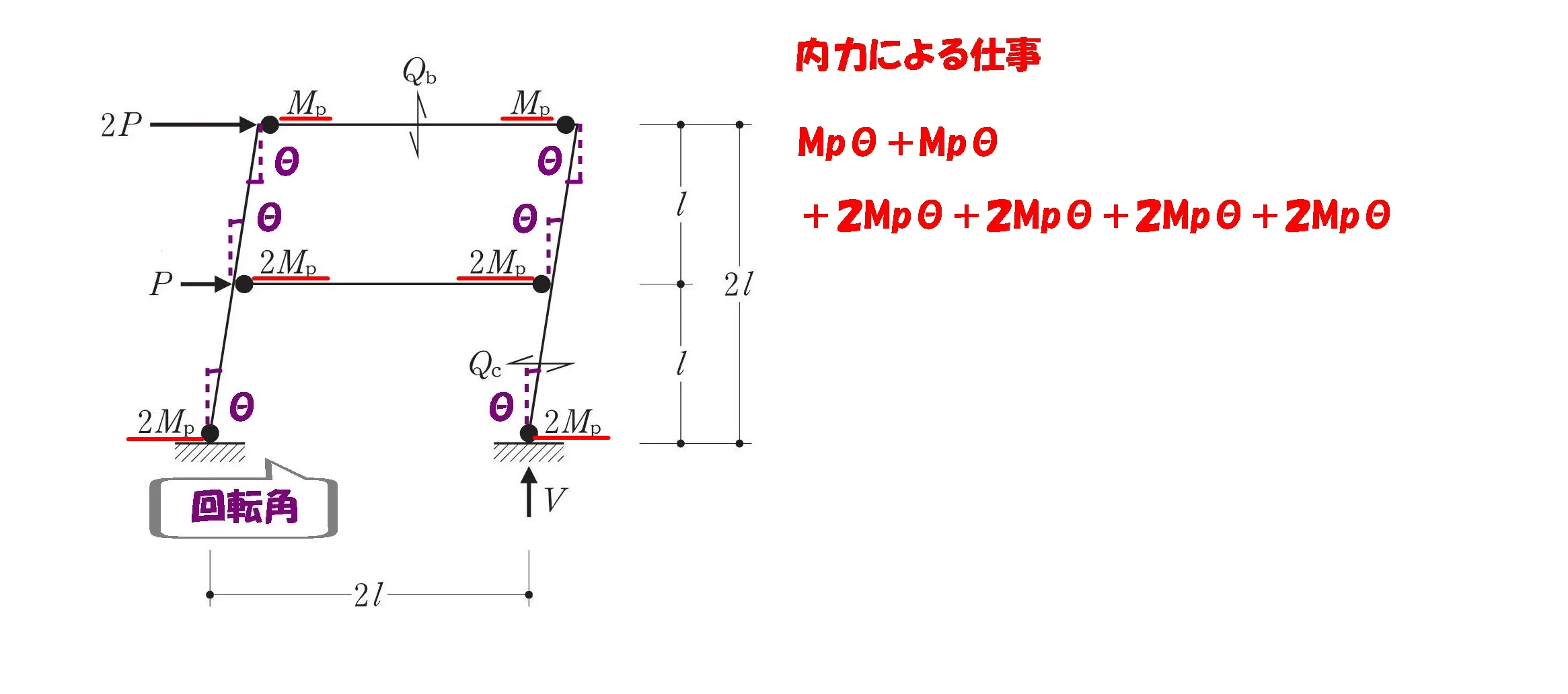

$$内力による仕事=モーメント×回転角より,$$
$$\{{Mp*\theta+Mp*\theta+2Mp*\theta+2Mp*\theta+2Mp*\theta+2Mp*\theta}\}$$



掛けて足す!
掛けて足すだけ!
イコールで結ぶ
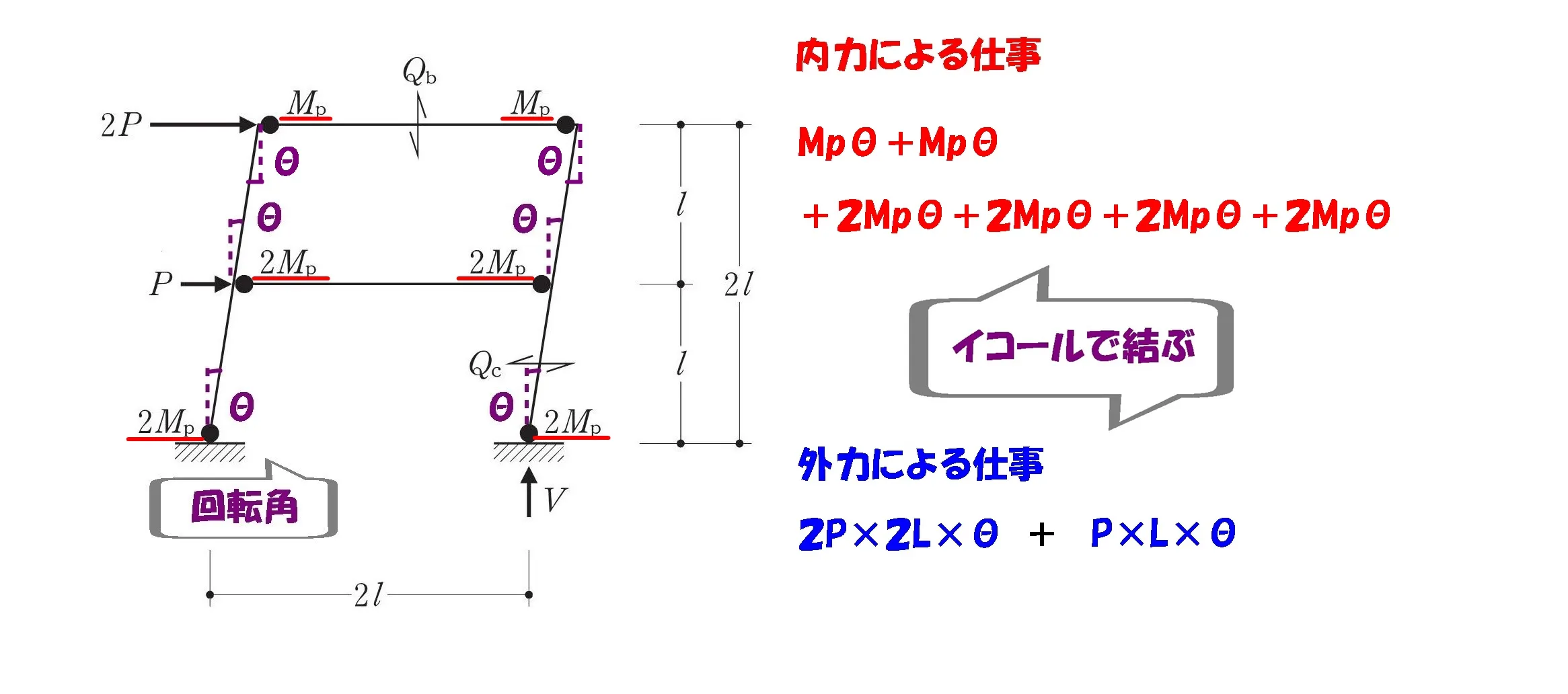

$$「外力による仕事」=「内力による仕事」より,$$
$$\{2P*2L*\theta+P*L*\theta\}$$$$=\{Mp*\theta+Mp*\theta+2Mp*\theta+2Mp*\theta+2Mp*\theta+2Mp*\theta\}$$
$$\{5*\theta*P*L\}$$$$=\{Mp*\theta+2Mp*\theta+2Mp*\theta\}+\{Mp*\theta+2Mp*\theta+2Mp*\theta\}$$
$$5*\theta*PL=5*\theta*\{Mp+Mp\}⇨PL=\{Mp+Mp\}$$
$$P=\frac{ Mp+Mp }{ L },水平荷重:P=\frac{ 2Mp }{ L }$$
4.部材を切断して取り出し、ΣX=0よりせん断力を求める
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
枝.4


$$4.[1階右側の柱のせん断力Qcは\frac{ 6Mp }{ L }である。]$$
部材を切断して上部を取り出す
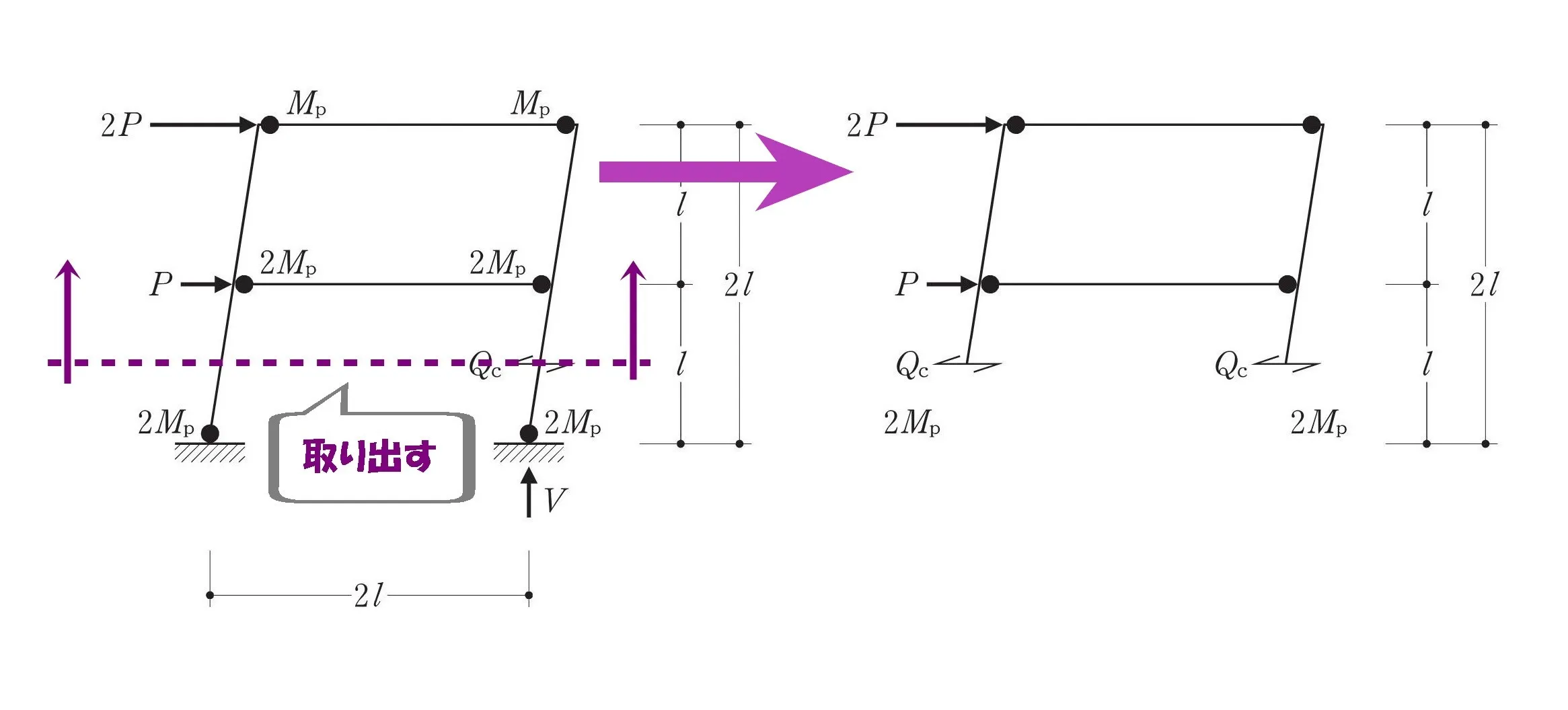

1階の柱を切断して上部を取り出す。



部材斬り!
上部を取り出すのだ。
せん断力Qcを求める
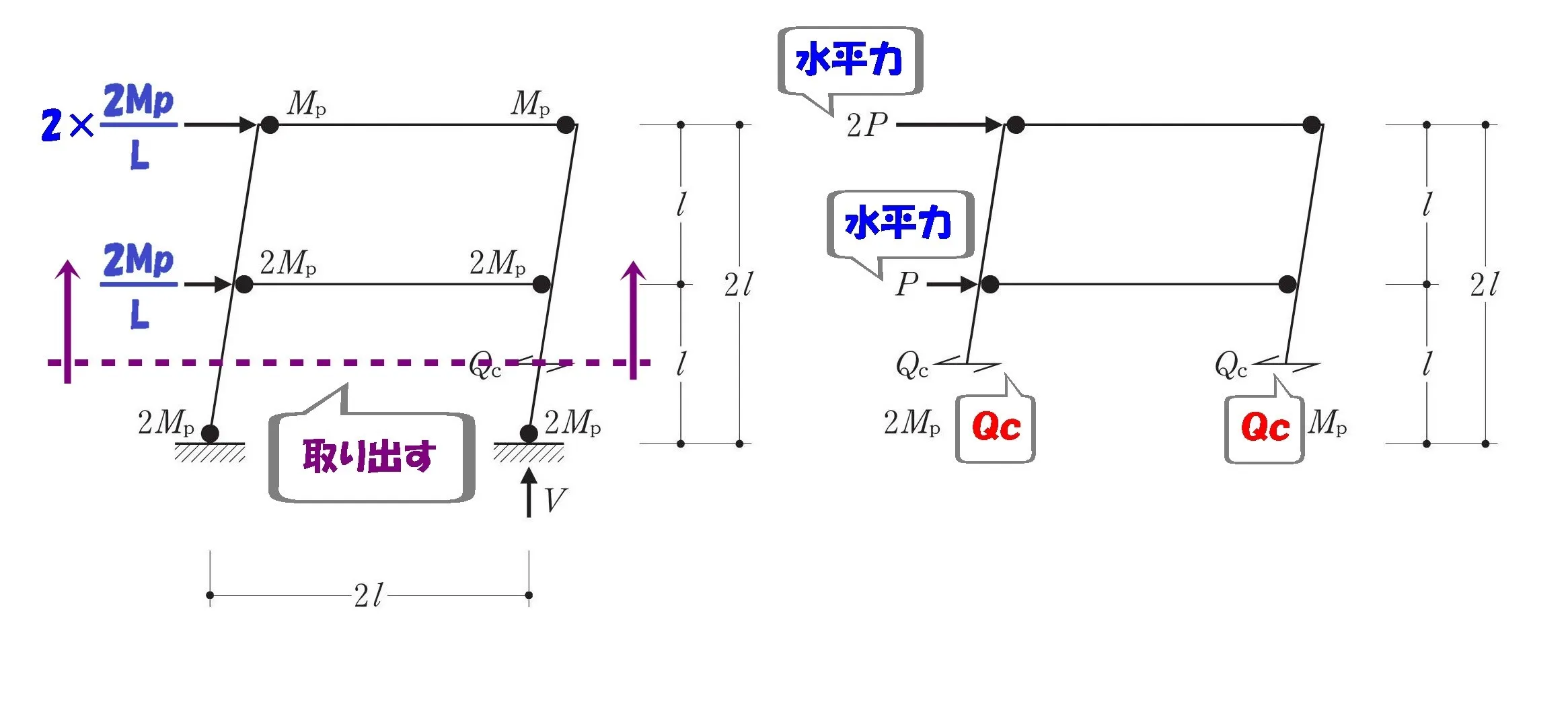

公式
$$\Sigma X=0$$



Σエックス!
水平力との吊り合いを取る
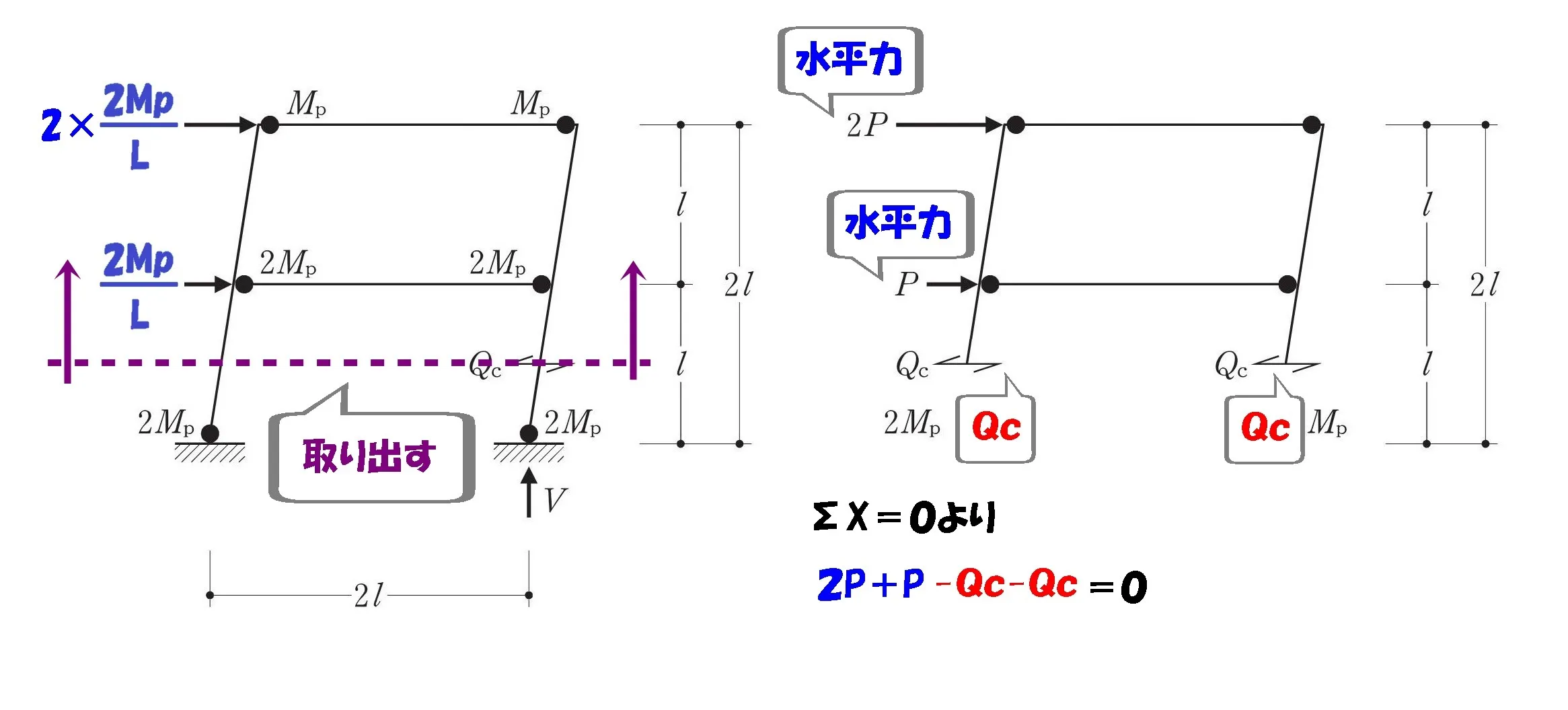

$$\Sigma X=0より,$$$$2P+P-Qc-Qc=0$$$$⇨Qc+Qc=3Pより,Qc=\frac{ 3 }{ 2 }*P$$
$$(水平力との吊り合い式が成立する)$$
$$P=\frac{ 2Mp }{ L }を代入する。$$
$$Qc=\frac{ 3 }{ 2 }*\frac{ 2Mp }{ L }⇨Qc=\frac{ 3Mp }{ L }(\neq\frac{ 6Mp }{ L })$$
答え.4(誤り)
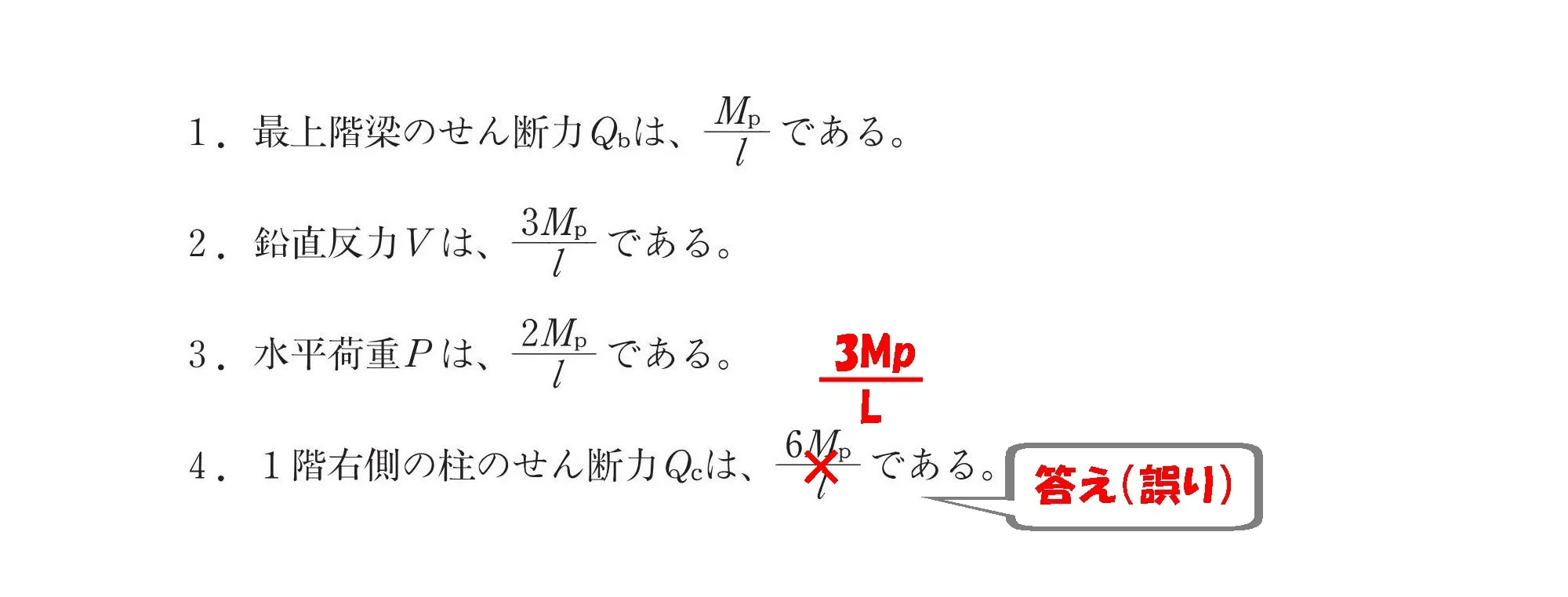




また斬ってしまった。
拙者の出番は終わりでござる。
攻略ポイント
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める
固有周期
難易度:★★★☆☆
固有周期とせん断力との関係を読み解く問題です。
ここは計算問題だけでなく、文章問題でもよく出題されます。
公式と記述をセットにして押さえておきましょう。
振り子のイメージ

固有周期とは、地震時による建物の揺れが「一往復する」までの時間をいいます。
(一往復:建物が一方に揺れて反対側に戻ってくるまでの時間のこと。)
この固有周期は、建物の高さ・形状・頂部の重さによって左右されるもので、その動きを解析するためのモデルとして振り子が使われるのです。



専門用語が
たくさんあるね。
揺れ方の違い
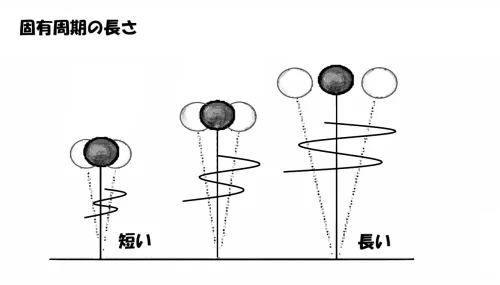

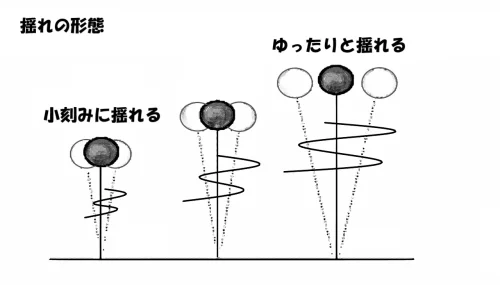

固有周期が短い
小さく小刻みに速く揺れる。
揺れが加速して、せん断力が大きくなる。
固有周期が長い
大きくゆったりと揺れる。
揺れが安定して、せん断力は小さくなる。



固有周期は
せん断力と関わりがある。


この動画を YouTube で視聴
攻略ポイント
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める
問題
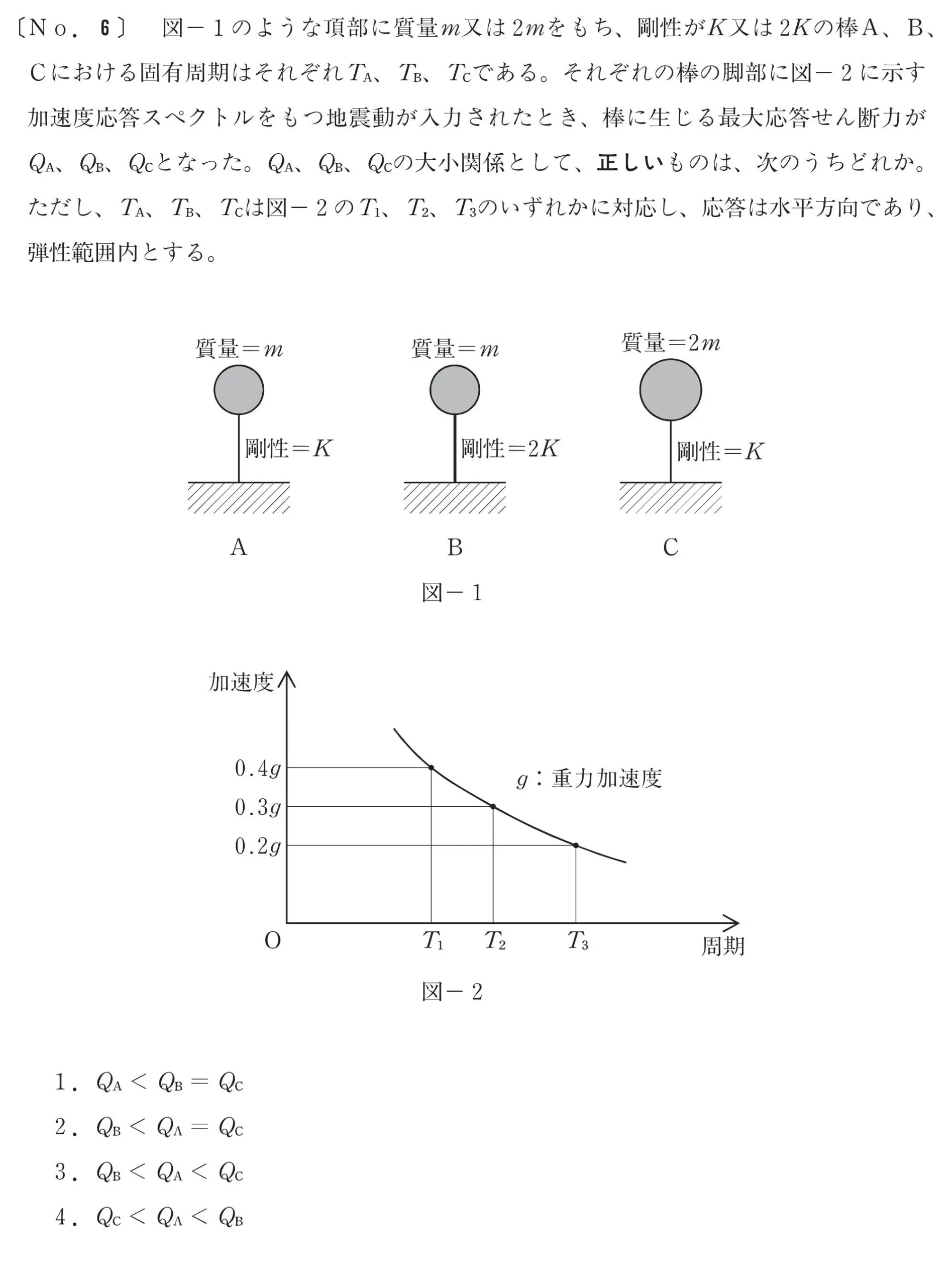

ここを読み解く
- 求めるものは、せん断力Qの大小関係であること。
- せん断力Qを求めるには固有周期Tの数値が必要となる。
- 固有周期Tを求めるには質量mと剛性Kの数値が必要となる。
せん断力の大小関係


せん断力:Qa・Qb・Qcを比較する問題
1.求めるものは、せん断力Qの大小関係であること。
図-2の読み方


図-1のA・B・Cの固有周期:Ta・Tb・Tcは、図-2のT1・T2・T3のいずれかに対応している
2.せん断力Qを求めるには固有周期Tの数値が必要となる。
質量と剛性が異なる


図-1のA・B・Cは質量と剛性が、それぞれ2種類で異なる
3.固有周期Tを求めるには質量mと剛性Kの数値が必要となる。
ここを読み解く
- 求めるものは、せん断力Qの大小関係であること。
- せん断力Qを求めるには固有周期Tの数値が必要となる。
- 固有周期Tを求めるには質量mと剛性Kの数値が必要となる。
必要な公式は2つ
$$せん断力:Q=m*a$$
$$固有周期:T=2\pi\sqrt{\frac{ m }{ K }}$$
水平剛性の式(参考)
$$水平剛性:K=\frac{ 3EI }{ h^3 }$$
図-1、図-2
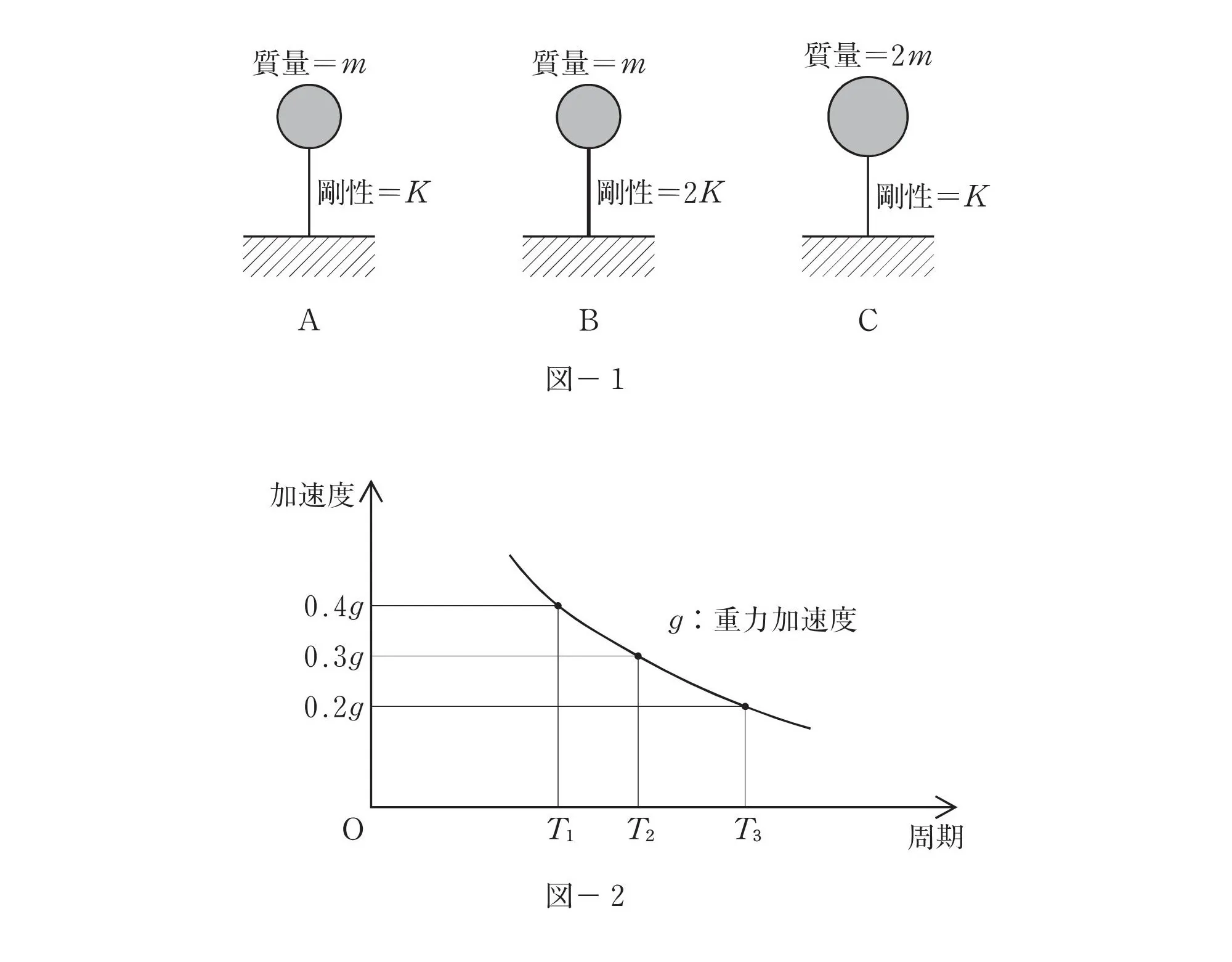

図-2の読み方
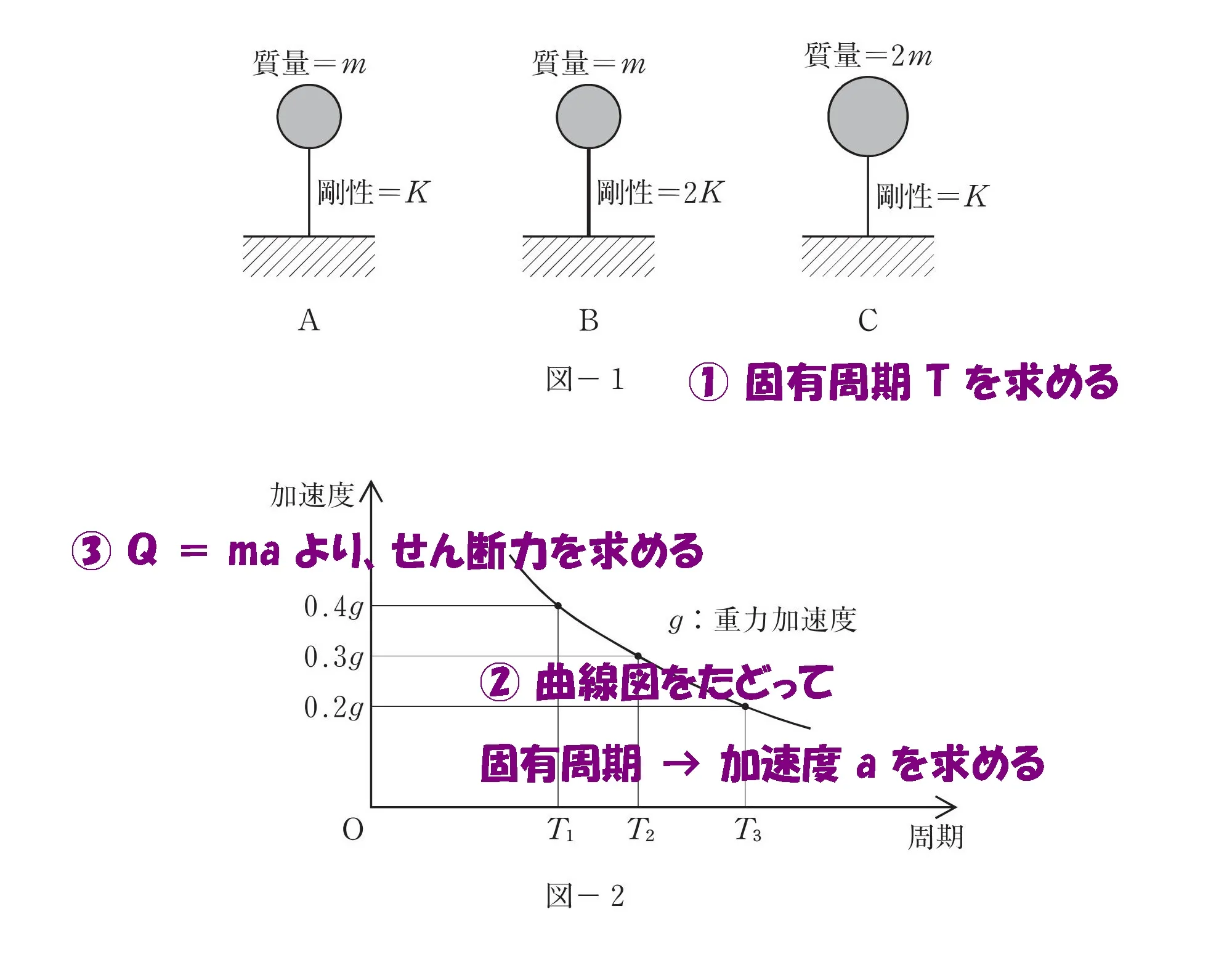




固有周期、加速度、
せん断力の順に求める。
図-2の読み方
- 固有周期を求めて、T1・T2・T3に置き換える。
- 固有周期から曲線図をたどって、加速度aを求める。
- 公式「Q=ma」質量×加速より、せん断力を求める。
1.m/Kを図-1に書き込む
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める
固有周期の公式
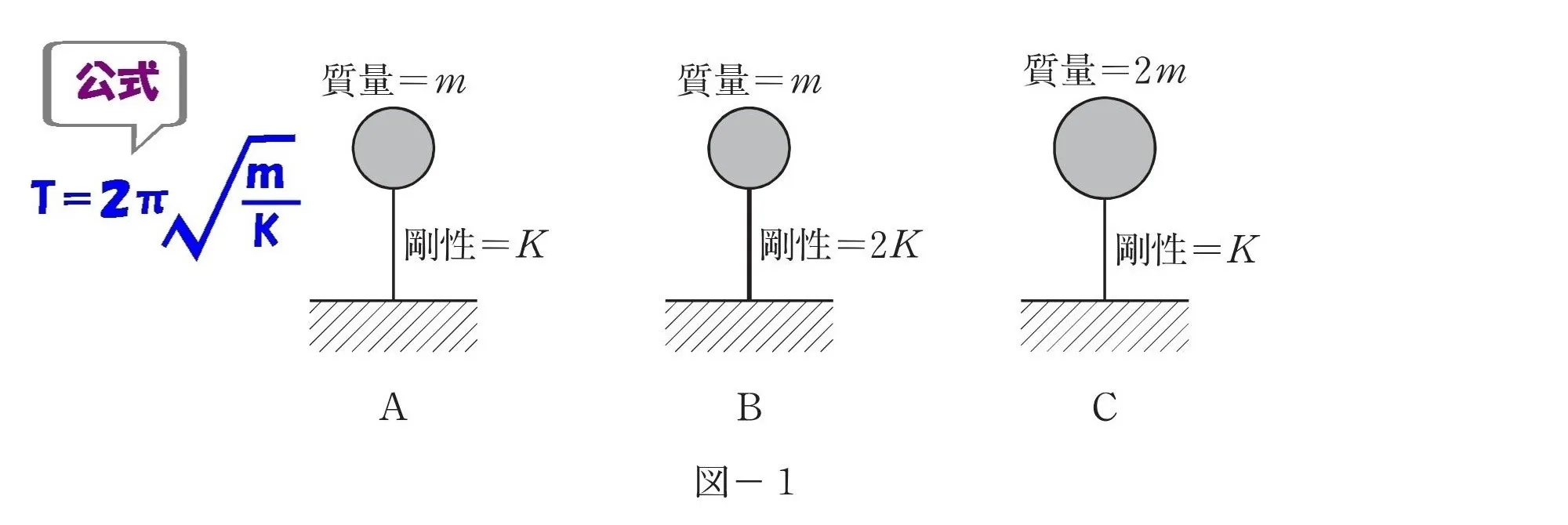

公式
$$固有周期:T=2\pi\sqrt{\frac{ m }{ K }}$$
固有周期の比較
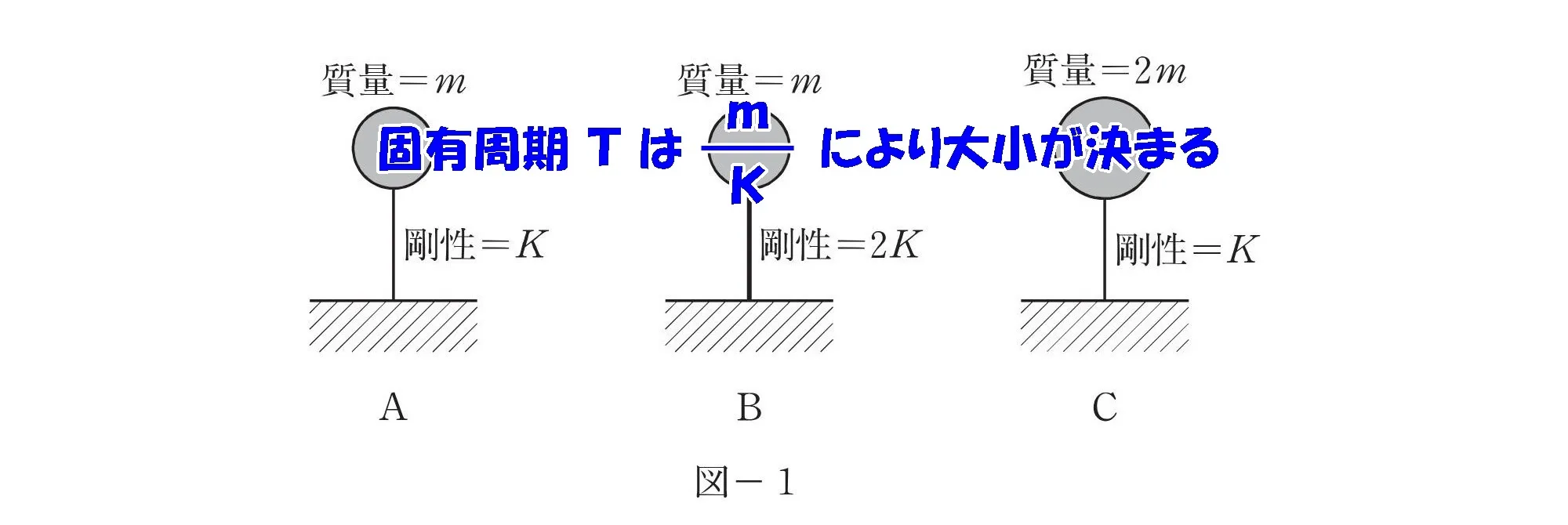

$$固有周期:T=2\pi\sqrt{\frac{ m }{ K }}より$$
$$固有周期の大小関係は,\frac{ m }{ K }によって決まる$$



2πは定数なので
同じ数値は省いて比較する。
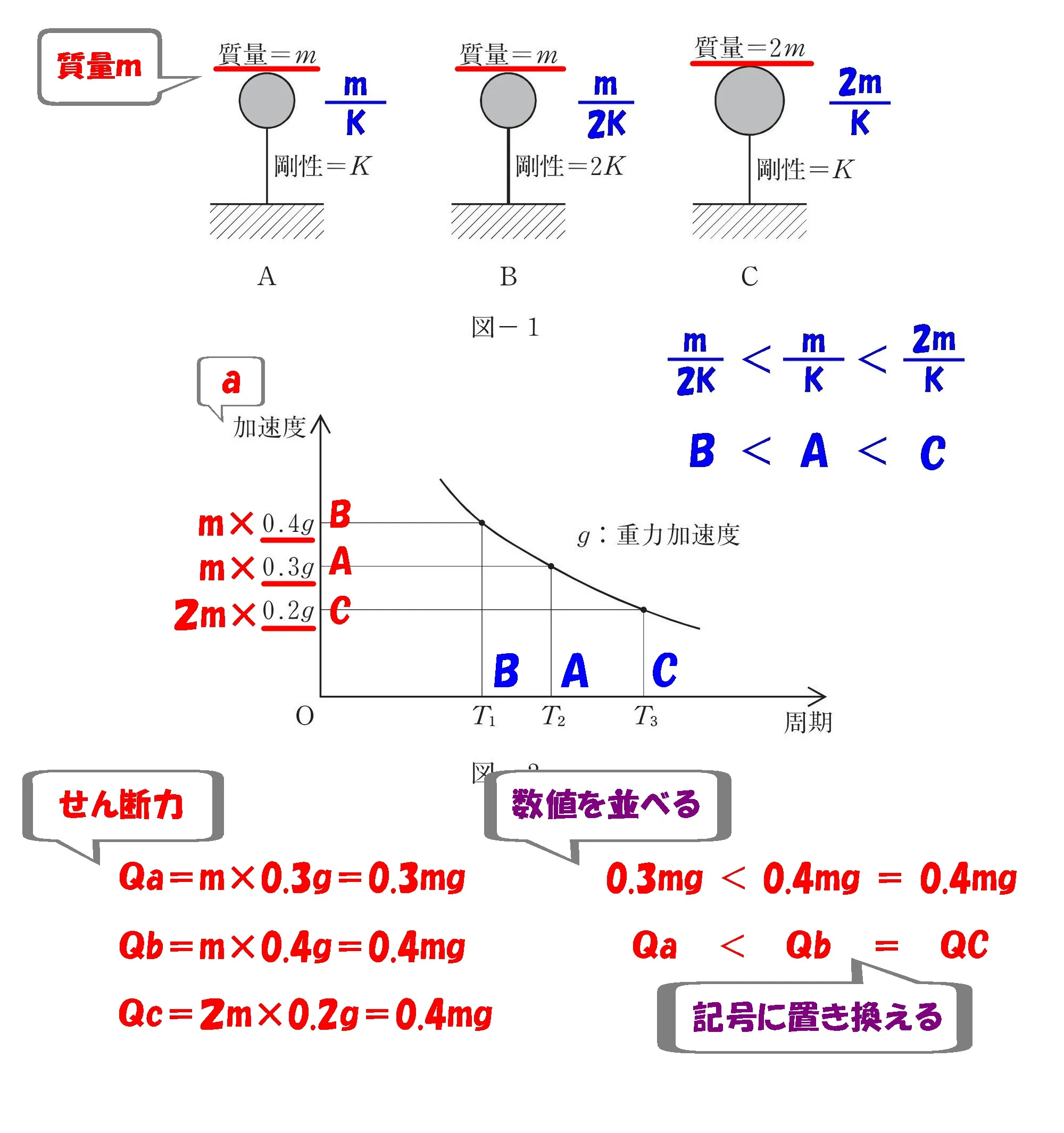
m/Kを書き込む
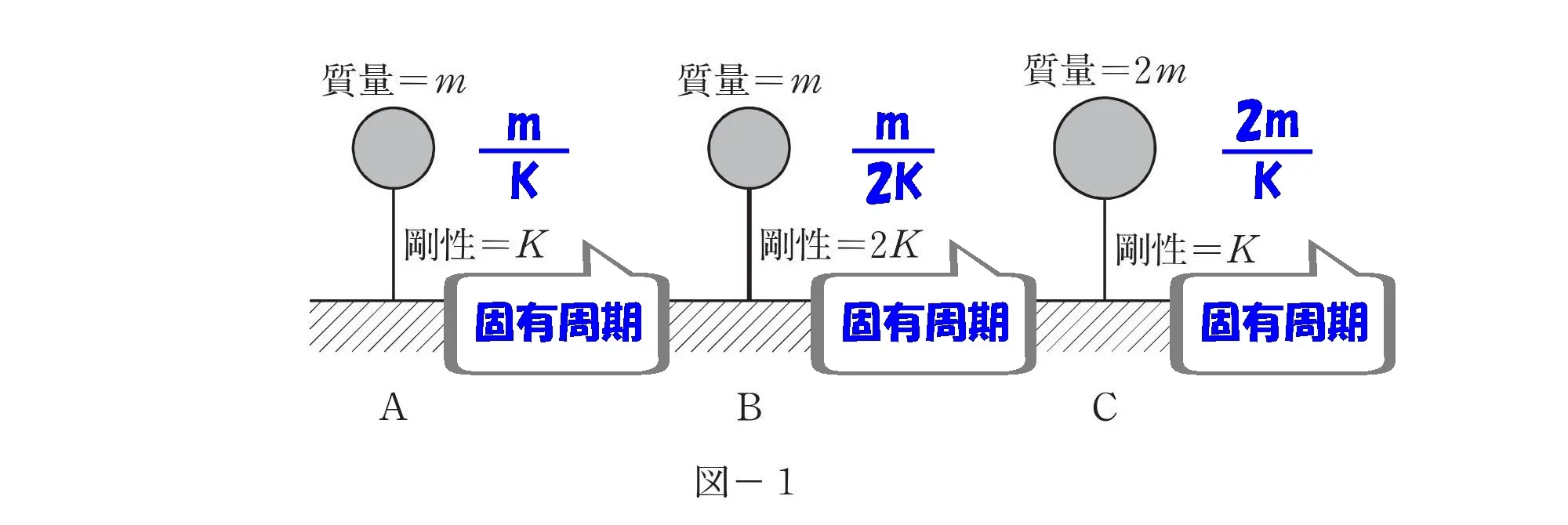

$$A:\frac{ m }{ K }$$
$$B:\frac{ m }{ 2K }$$
$$C:\frac{ 2m }{ K }$$
$$固有周期の大きさは\frac{ m }{ K }で比較する。$$
2.m/Kの並びから、T1・T2・T3(図-2)に置き換える
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める
数値の小さい順に並べる
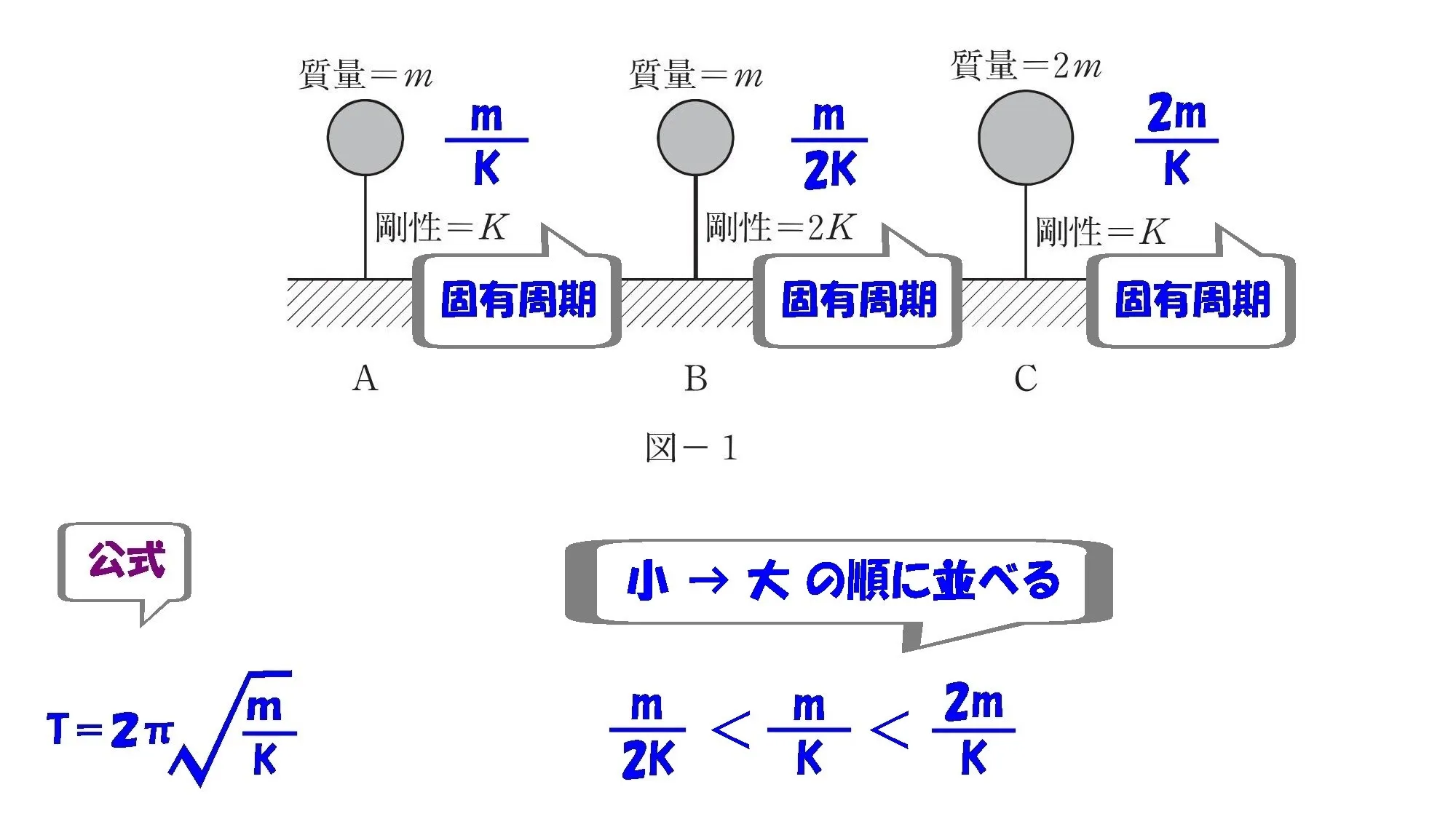

$$\frac{ m }{ 2K }<\frac{ m }{ K }<\frac{ 2m }{ K }$$
$$固有周期の大きさは\frac{ m }{ K }で比較する。$$
対応するアルファベットを書く
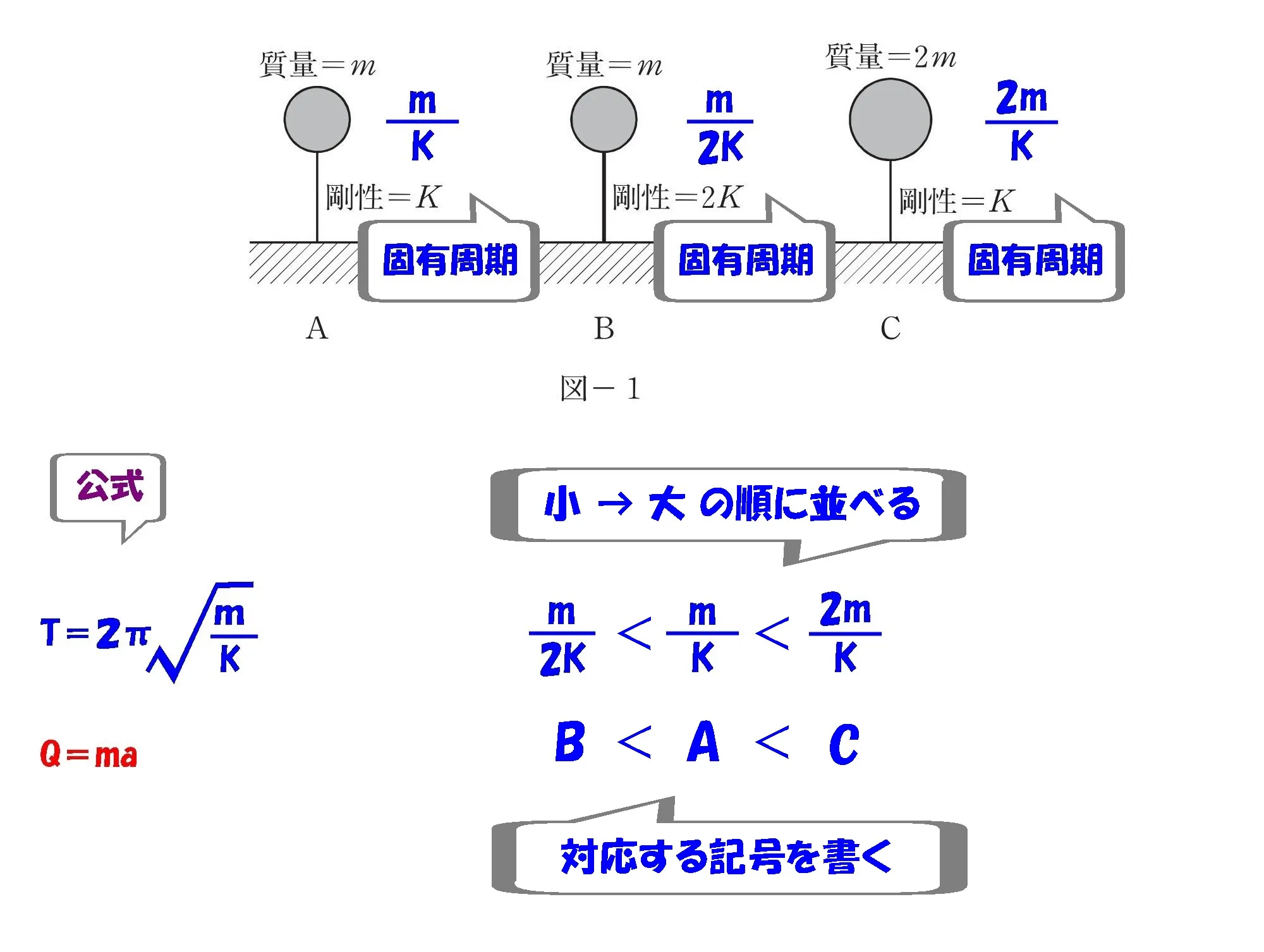

B < A < C
$$B:\frac{ m }{ 2K }$$
$$A:\frac{ m }{ K }$$
$$C:\frac{ 2m }{ K }$$
数値を並べた後に対応するアルファベットを記入します。



数値を並べて記号を書く
これが間違いのない手法。
図-1から図-2へ転記する
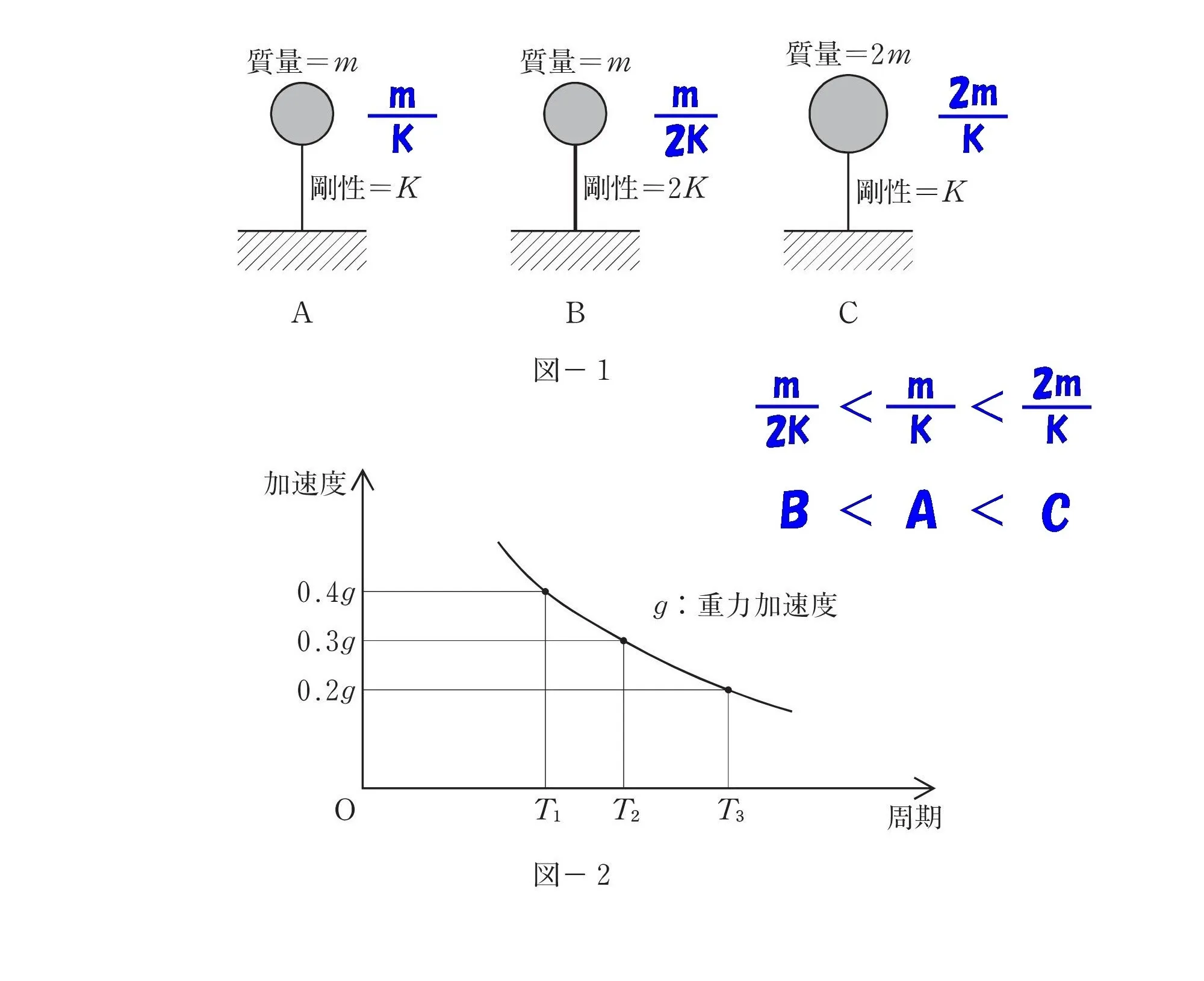

置き換える
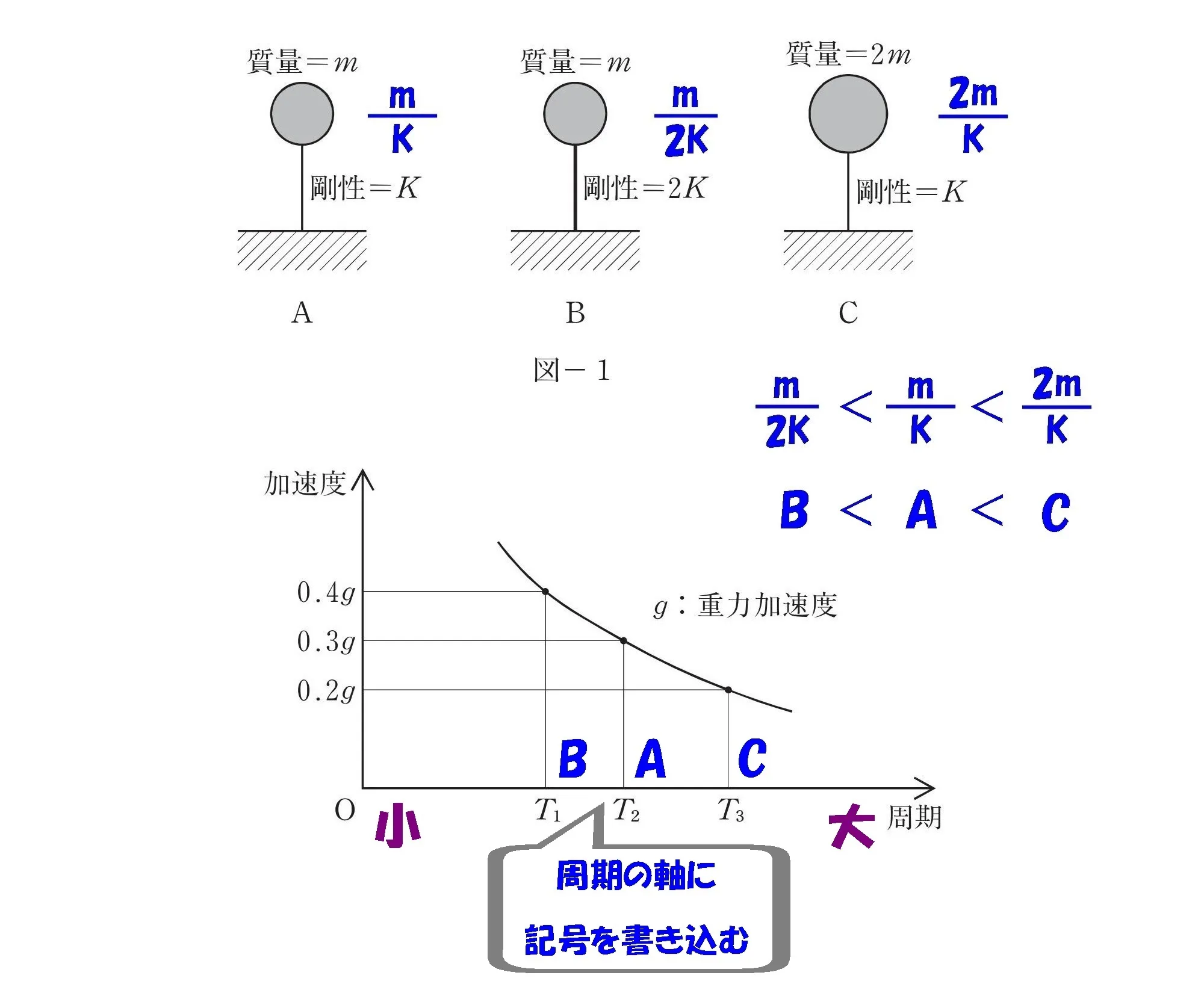

固有周期の軸にB・A・C
T1 ⇨ B
T2 ⇨ A
T3 ⇨ C
「B<A<C」をそれぞれ小さい順に「T1<T2<T3」と置き換える。
このとき、周期の軸「T1・T2・T3」に「B・A・C」を書き込みましょう。
3.固有周期から曲線図をたどって、加速度aに置き換える
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める
加速度の軸にB・A・C
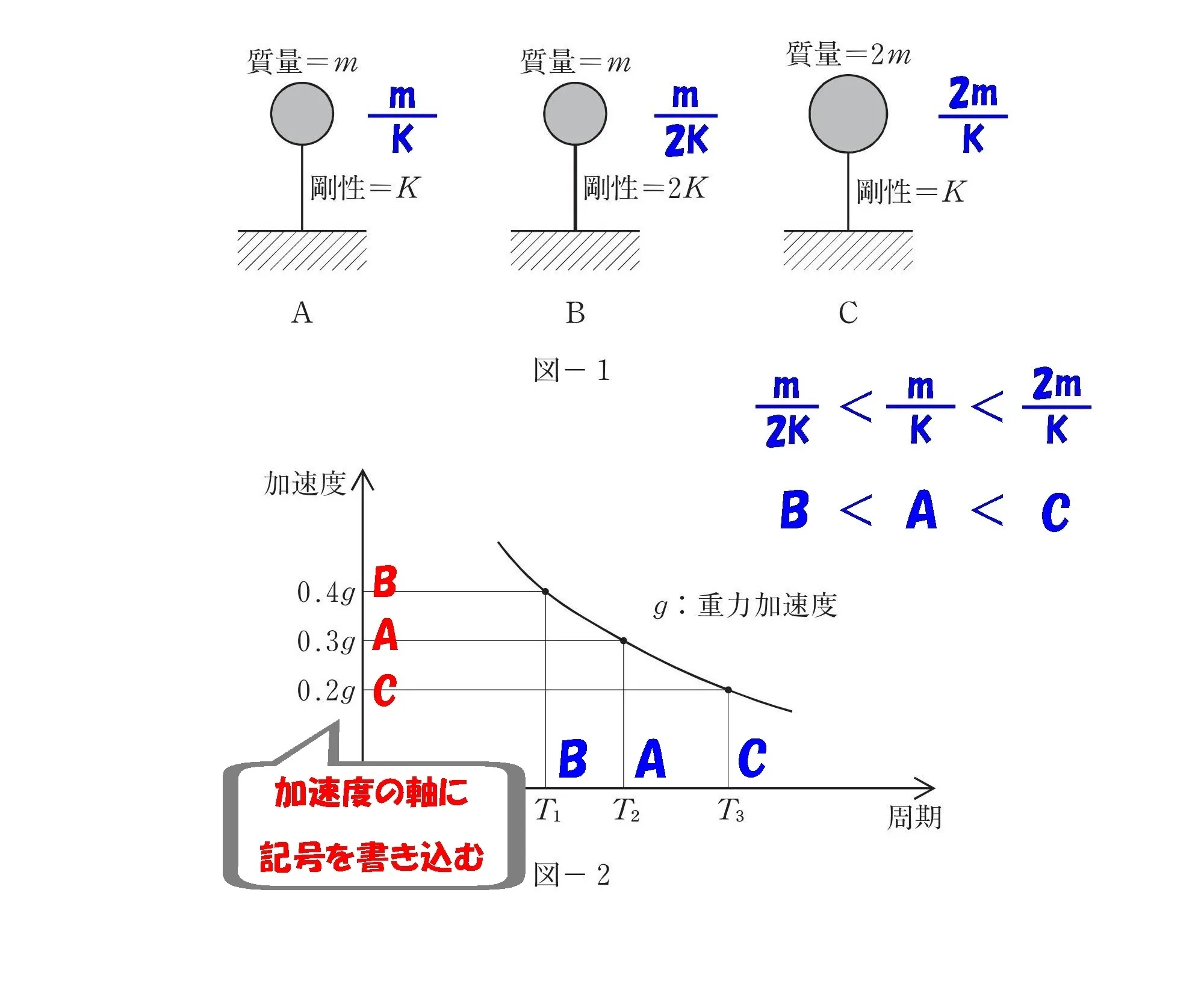

加速度の軸にB・A・C
- 0.4g ⇨ B
- 0.3g ⇨ A
- 0.2g ⇨ C
固有周期から曲線図をたどって、加速度にも「B・A・C」を書き込む。
Q=m×a
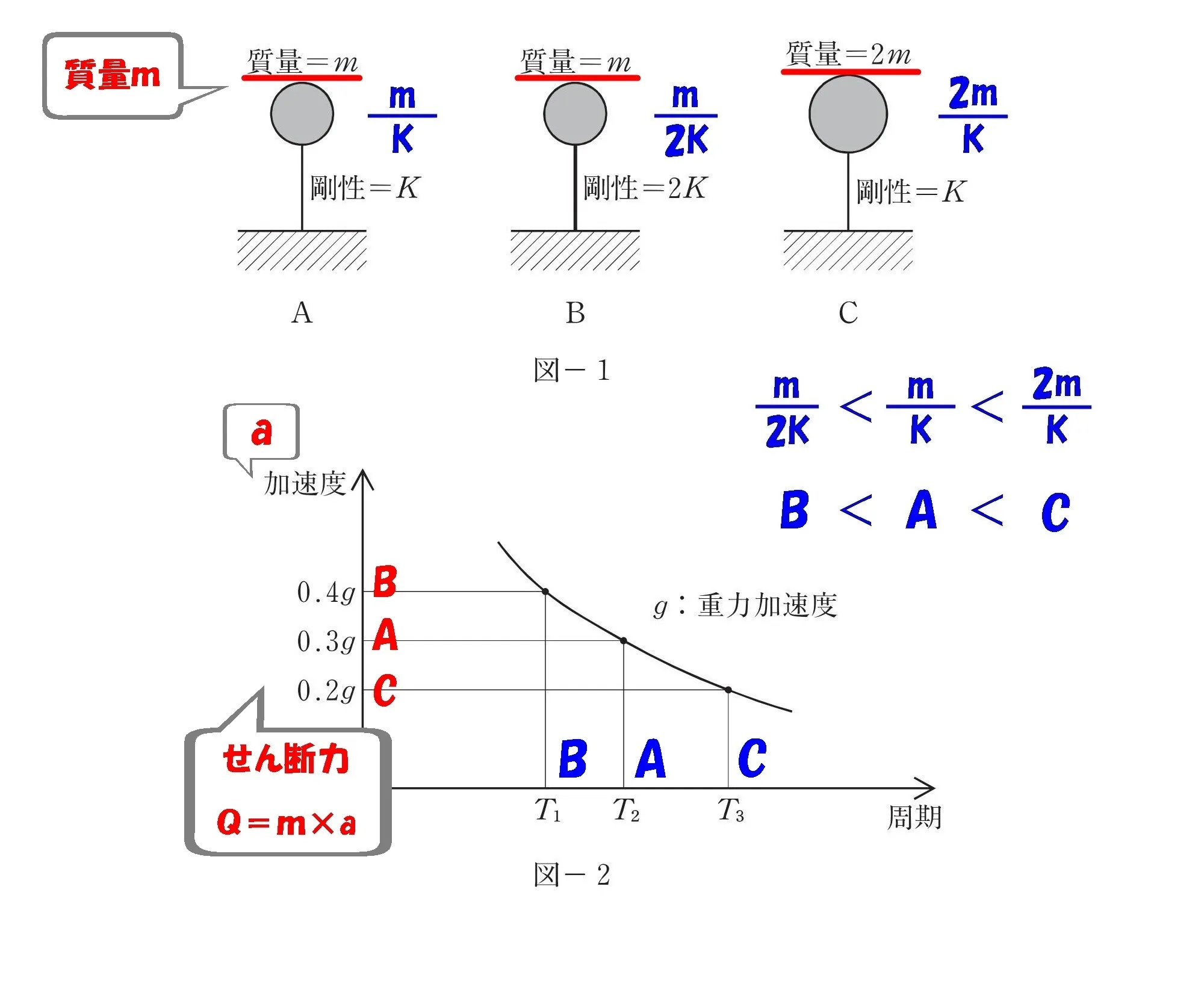

×質量m
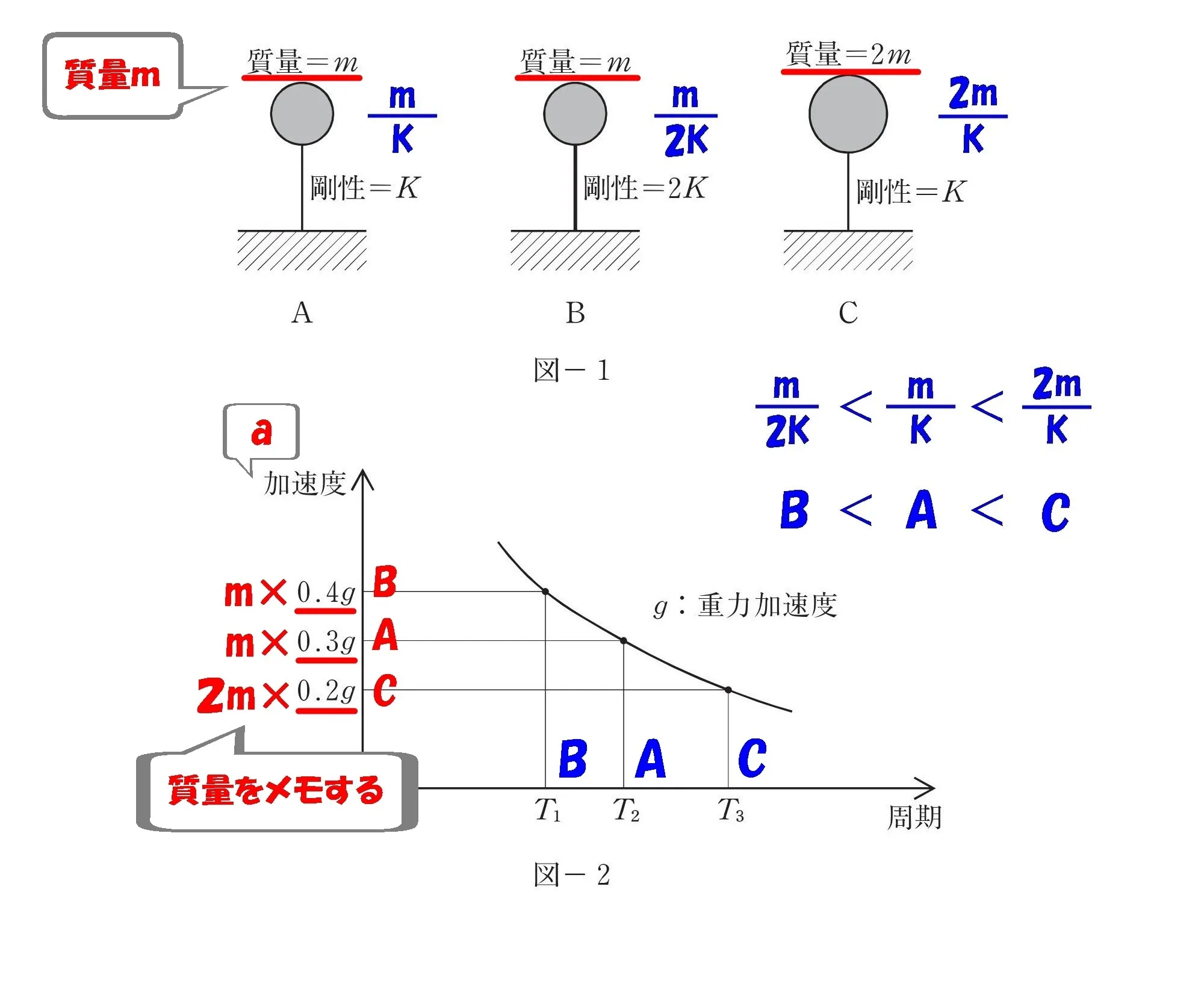

加速度の軸に、A・B・Cのそれぞれの質量(×m、×2m)を書き込む。
×質量
- B(×m)
- A(×m)
- C(×2m)



加速度に質量を掛ける。
「×m」「×2m」!
4.公式「Q=ma」質量×加速より、せん断力を求める
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める
せん断力を求める
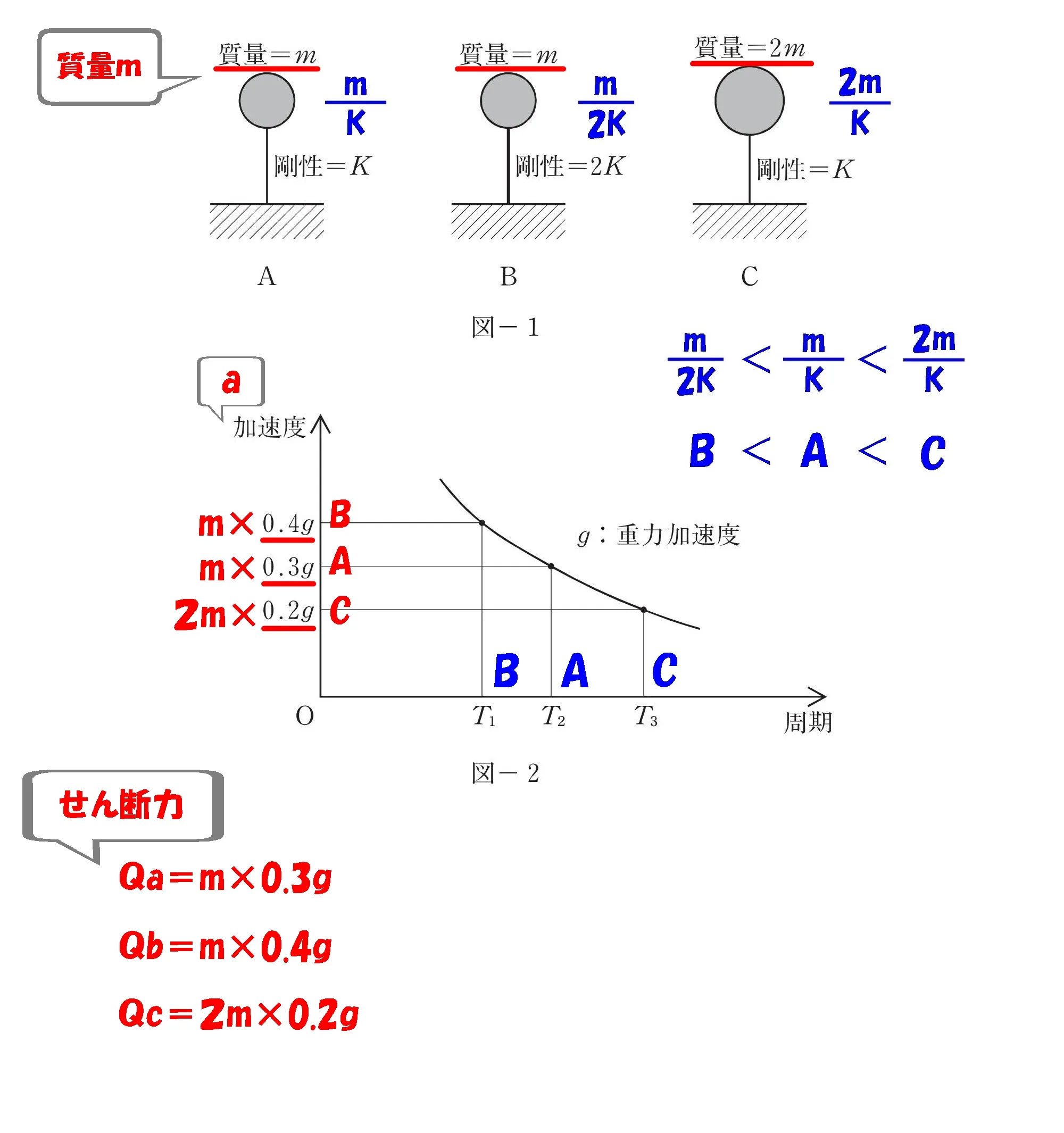

$$Qa=m*0.3g=0.3mg$$
$$Qb=m*0.4g=0.4mg$$
$$Qc=2m*0.2g=0.4mg$$
公式
$$せん断力:Q=m*a$$
数値を小さい順に並べる
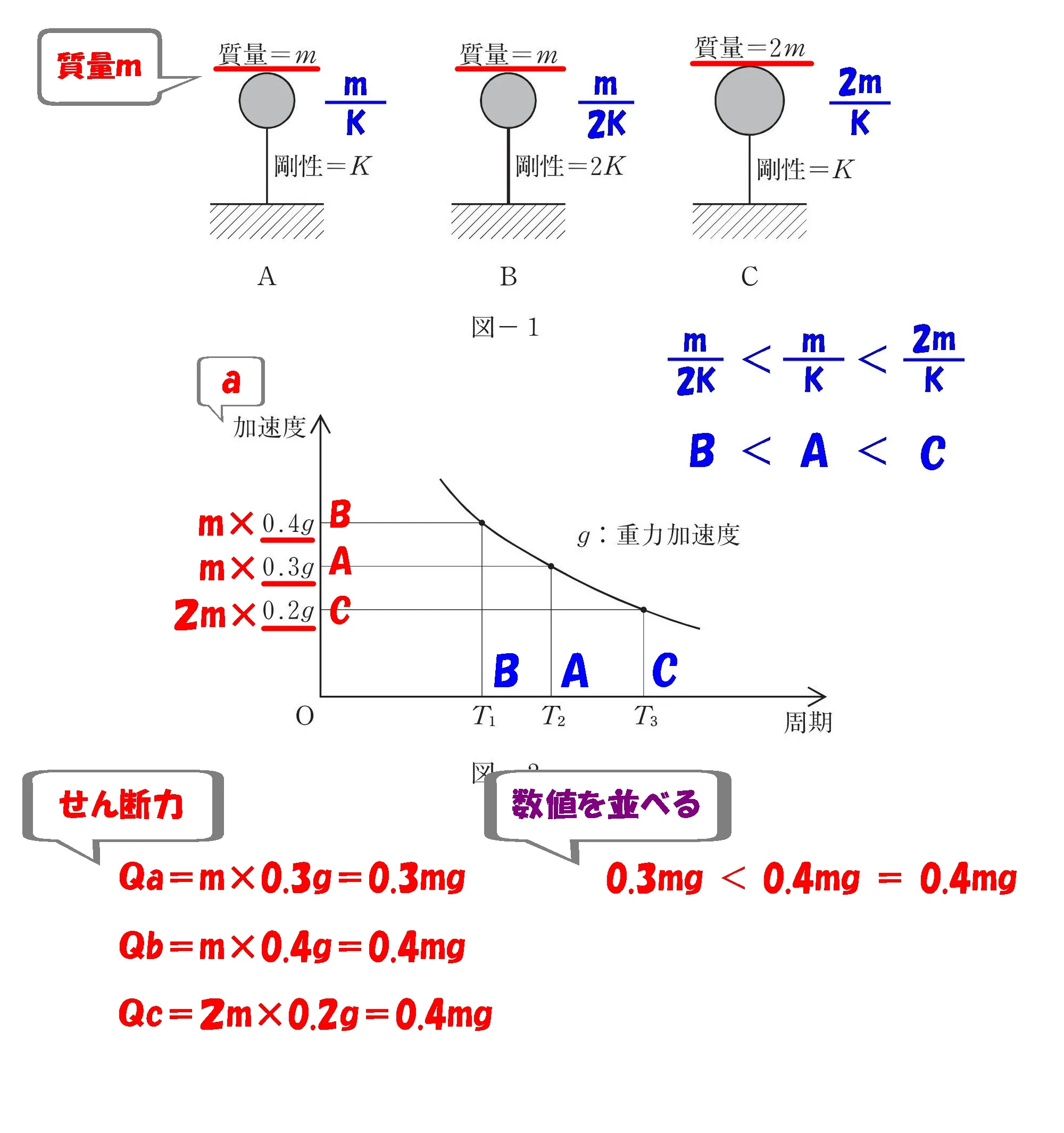

数値を小さい順に並べる
$$0.3mg<0.4mg=0.4mg$$
対応するアルファベットを書く





数値を並べて記号を書く
これが間違いのない手法。
$$0.3mg<0.4mg=0.4mg$$$$Qa<Qb=Qc$$
答え.1
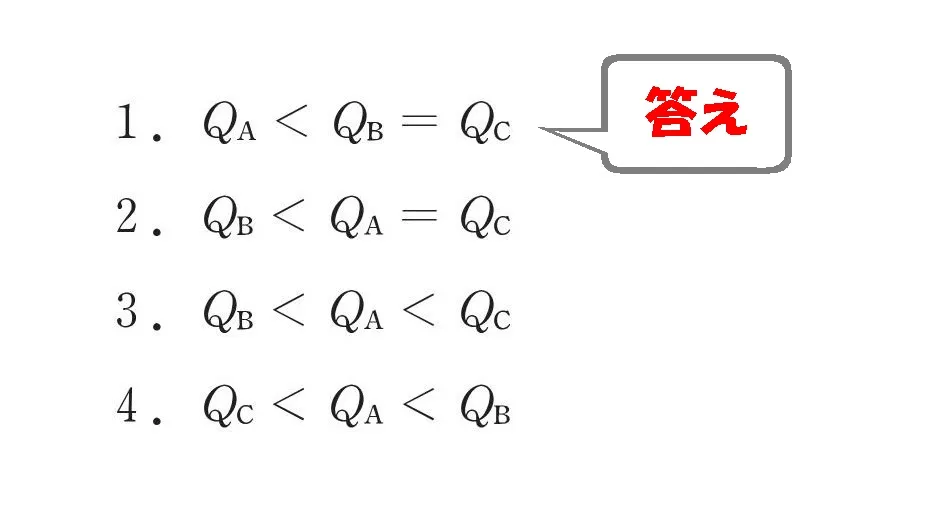

攻略ポイント
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める




この動画を YouTube で視聴
お疲れ様でした、まとめに入ります。

一級建築士(構造)計算問題に挑戦して攻略ポイントを解説
(まとめ)



おさらいでござる。
独学で構造を勉強する方はこちら
一級建築士試験|独学で合格を目指すには過去問から!(問題集の仕込み方)


(平成29年度出題:No.3)
攻略ポイント
- 支点反力を求める
- 片持ち梁の絵を描く
- モーメント図を描く


(令和元年度出題:No.3)
攻略ポイント
- 力×距離よりモーメント図を描く
- モーメントの大きさを「部材の剛比」で振り分ける
- 柱と梁それぞれのモーメントは2:1で分布される


(平成30年度出題:No.3)
攻略ポイント
- 答えに繋がる反力を見定める
- 支点に作用する反力を書き込む
- ヒンジを起点にΣM=0
- 力の吊り合い式ΣX=0、ΣY=0
- 答えに繋がる反力を定めて連立方程式を組む


(平成29年度出題:No.1)
攻略ポイント
- 軸力と曲げ力を求める
- 軸力による応力度:N/Aを求める
- 断面係数:bh²/6の式をつくる
- 曲げ力による応力度:M/Zを求める
- 応力度を合成する(ーN/A±M/Z)


(平成28年度出題:No.1)
攻略ポイント
- モーメント=力×距離
- 断面形状を軸力と曲げ力に分ける
- 応力度に作用する断面積を求める
- 応力度分布を軸力と曲げ力に分ける
- 軸力=面積×σより、鉛直荷重Pを求める
- モーメント=力(面積)×距離×σより、水平荷重Qを求める


(平成27年度出題:No.1)
攻略ポイント
- 選択肢の共通部分に注目する
- 共通部分を除き、残り2つを比較する
- 部材を成形なパーツに分解し、比較しやすくする
- 計算式は共通項を(・)で束ねて計算式から省く


(平成30年度出題:No.2)
攻略ポイント
- 梁の形状と荷重の受ける範囲を読み取る
- 問題用紙の余白に必要な公式をメモする
- 公式をイコールで結び、Pa:Pbの比を求める


(平成27年度出題:No.2)
攻略ポイント
- 文章を読み取る
- 部材を切断してパーツを取り出す
- w×Lを集中荷重に置き換える
- それぞれのモーメントを合成する


(平成29年度出題:No.5)
攻略ポイント
- 支点反力を求める
- 斜め部材を切断する(切断法)
- ΣY=0の吊り合い式より軸力を求める


(平成28年度出題:No.5)
攻略ポイント
- 支点反力を求める
- 対象となる部材を切断する
- 斜材の延長ラインの交点に注目する
- 三角形の辺の比を使って距離を求める
- ΣM=0の吊り合い式より軸力を求める


(平成28年度出題:No.3)
攻略ポイント
- 問題文を読み取り、求める物を定める
- ブレースを含む部材を切断して取り出す
- ΣX=0により、2つのせん断力を求める
- せん断力×距離により、モーメントを求める


(平成29年度出題:No.6)
攻略ポイント
- 弾性座屈荷重に比例するもの、反比例するものを把握する
- 柱・梁の支持条件の違いを読み取り、座屈長さを求める
- 柱の座屈長さより、弾性座屈荷重の大小関係を求める


(令和2年度出題:No.3)
攻略ポイント
- せん断力に比例するもの、反比例するものを把握する
- 柱脚の支持条件の違いを読み取り、剛比を求める
- 柱の剛比から、せん断力の大小関係を求める


(平成元年度出題:No.4)
攻略ポイント
- 層間変位に比例するもの、反比例するものを把握する
- 柱脚のラインで部材を切断して、上部の架構を取り出す
- 水平方向の吊り合い式ΣX=0より、層せん断力を求める
- 層せん断力Q / 水平剛性Kの比から、層間変位の比を求める


(平成30年度出題:No.4)
攻略ポイント
- 部材を切断して取り出す
- モーメント図を描き出す
- 柱・梁のせん断力を求める
- 力の吊り合い式から未知数を求める


(平成28年度出題:No.4)
攻略ポイント
- 外力による仕事:力×距離×θをすべて足す
- 内力による仕事:モーメント×θをすべて足す
- 外力による仕事=内力による仕事 ⇨ Puを求める


(平成29年度出題:No.4)
攻略ポイント
- モーメント図の傾きより、せん断力を求める
- 部材を切断して取り出し、ΣY=0より鉛直反力を求める
- 外力による仕事=内力による仕事から、水平荷重を求める
- 部材を切断して取り出し、ΣX=0よりせん断力を求める


(平成28年度出題:No.6)
攻略ポイント
- m/Kを図-1に書き込む
- m/Kの並びから、T1・T2・T3(図-2)に置き換える
- 固有周期から曲線図をたどって、加速度aに置き換える
- 公式「Q=ma」質量×加速より、せん断力を求める





構造を斬る!
構造力学の計算問題18問を立て続けに斬ってきました。
数多くの画像を挿入したイラスト解説で、攻略法をお伝えしてきました。
「構造なんて大嫌い!計算式を見るだけでアレルギーが出る」から、少しは解放されたでしょうか?



エネルギーが
みなぎって来るぞ!
計算問題に取り組むときのポイントは、数値や公式よりも「解く手順」を覚えること。
苦手意識を克服するためには、理論よりも「イメージ」から組み立てる習慣をつけましょう。
この記事が、構造力学の計算問題に取り組むきっかけになれば幸いです。
最後まで記事を読んでいただき、本当にありがとうございます!



修行に励むのだ!



構造マスターの称号を
お主に授けよう。
トラスの力学を完全攻略






法規の計算問題を攻略!




-300x197.webp)



.webp)

