一級建築士受験生の方、構造力学で行き詰ってはいませんか?
計算問題を解くうえで、必要不可欠となるものは「公式を覚える」こと。
その中でも”梁のたわみ”の公式は、似たような数値が多くていつも迷いますよね?
迷いがちな公式
- 梁のたわみとたわみ角
- 断面一次モーメントと断面二次モーメント
それぞれの公式は、なるべくコンパクトにまとめて覚えておきたいもの。
この記事では「公式を覚える」ことに焦点を当てて、情報をまとめています。
覚えるだけでなく、思い出すためのヒントもお伝えするので、心配は要りません。
この機会に一度覚えてしまえば、「あの公式を覚える」ことから解放されるでしょう。
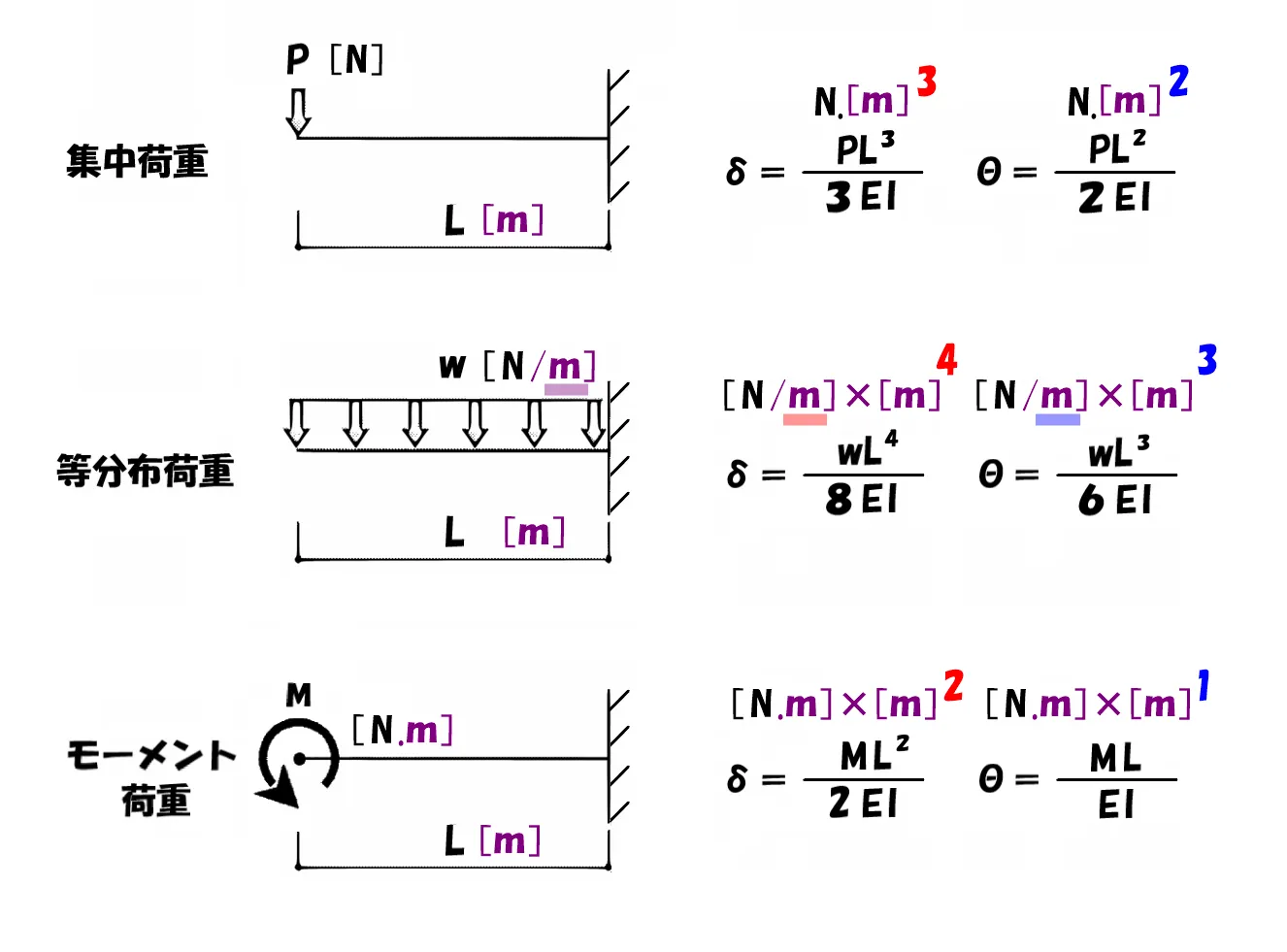

梁のたわみ


公式を覚えるヒント
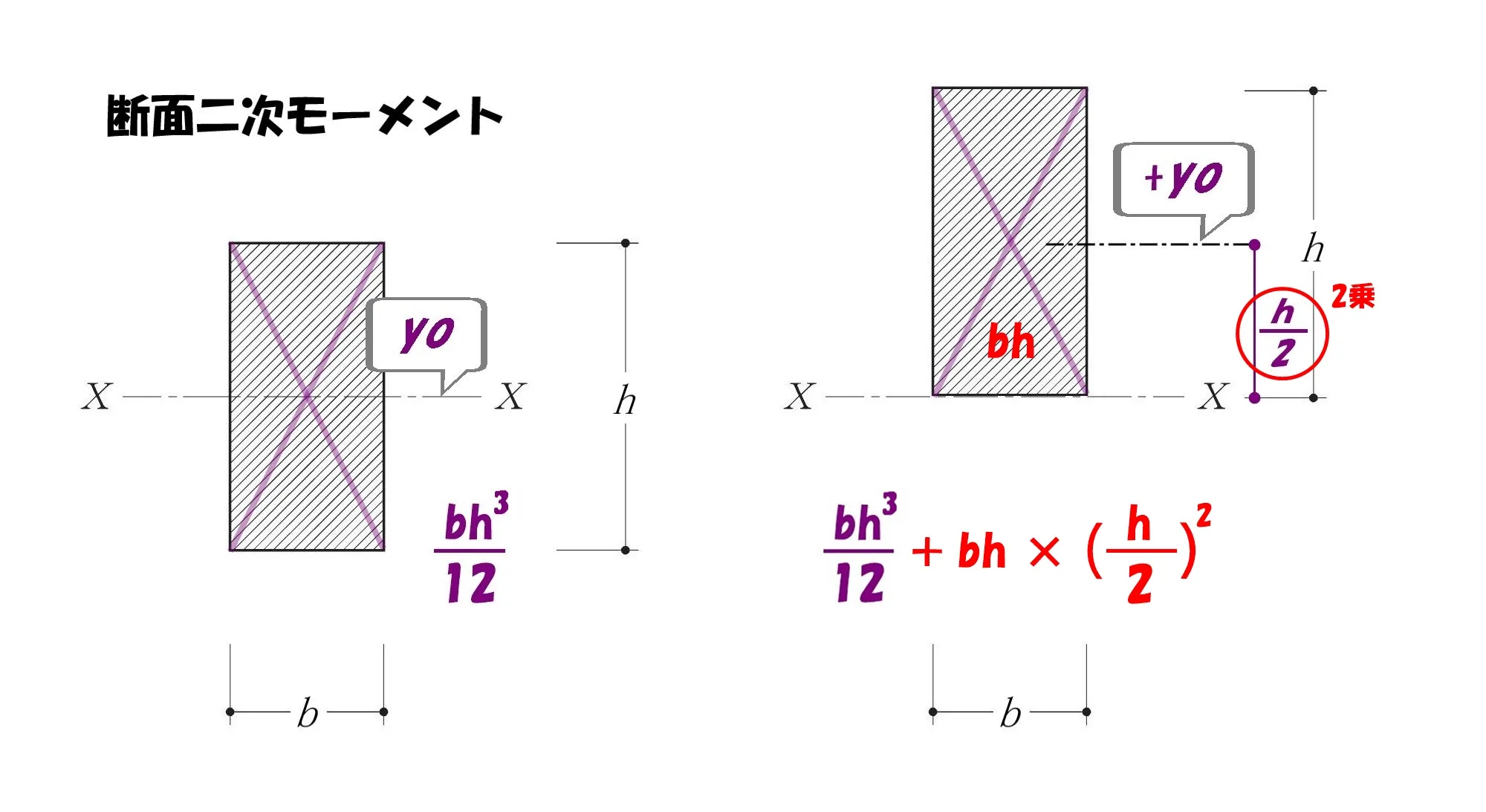

断面※※モーメント
こんな人におすすめ!
- 梁のたわみの公式が覚えられない。
- 公式を覚える語呂が多すぎて持て余している。
- それぞれの公式を単純な法則で、意味づけして覚えたい。


この動画を YouTube で視聴



独学の方にオススメ!


一級建築士|構造力学の「たわみ」の公式の覚え方


迷いがちな公式
- 梁のたわみとたわみ角
- 断面一次モーメントと断面二次モーメント
「とりあえず公式を覚えなければ・・」と思っていませんか?
公式というのは、過去問を繰り返し解きながら自然に覚えていくものです。
しかし、似たような公式が至るところで登場して来ると、つい意識してしまいがち。
「公式をどうやって覚えるの!」といった方でも心配は要りません。
その中身を少しだけ読み解くことで、覚えるためのヒントが得られるでしょう。
たわみとたわみ角の公式
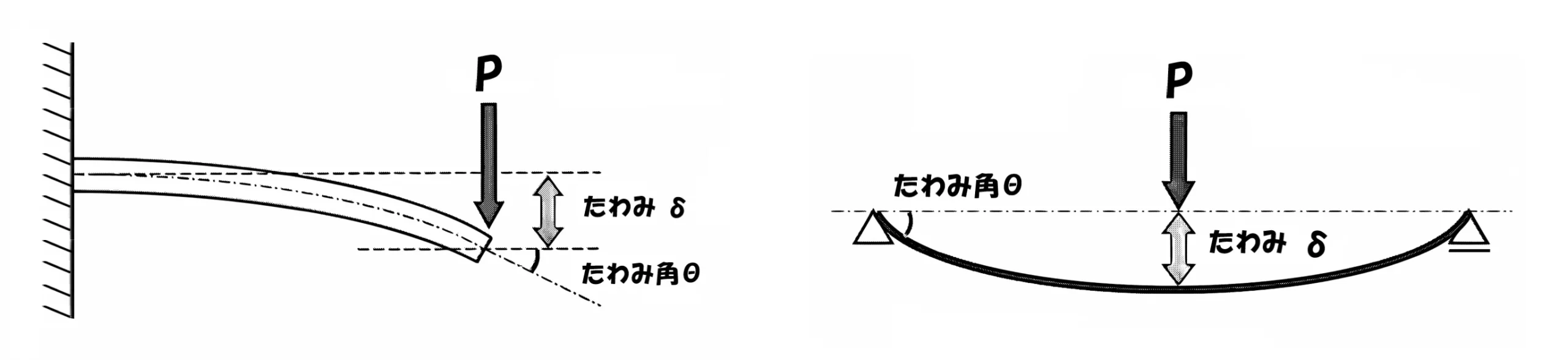

片持ち梁(左)と単純梁(右)とでは公式が違います。
さらに、「たわみ」と「たわみ角」でも、使い分けが要りますよね?
しかし、公式を読み解くうえでの原理や捉え方は統一させるので、心配は要りません。
片持ち梁のたわみ
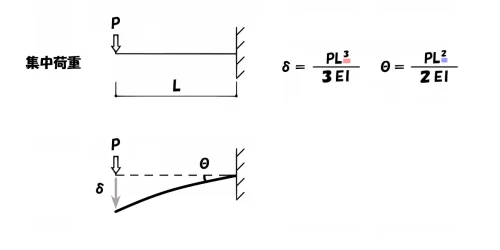

$$たわみ:\delta=\frac{ PL^3 }{ 3EI }, たわみ角:\theta=\frac{ PL^2 }{ 2EI }$$
たわみの原理
- 外力Pが大きくなるほど、たわみは比例して大きくなる。
- たわみはLの3乗に比例し、たわみ角はLの2乗に比例する。
- たわみは部材の曲げ剛性EIが大きくなるほど、小さくなる。
公式の「分子⇧にあるものは比例する」「分母⇩にあるものは反比例する」要素となります。
たわみに「比例するもの、反比例するもの」を想像できると、公式のかたちが見えて来ますよね?
そして、たわみの公式で押さえるべきところは、分子「L」の”乗数の違い”です。
変位の大・小
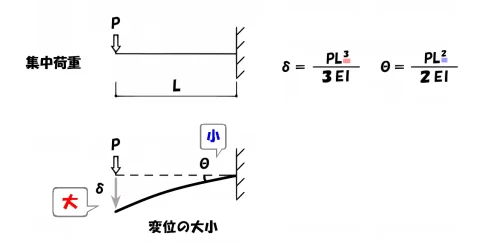

「どっちが2乗で、どっちが3乗だったかな?」
たわみとたわみ角の公式で、そんなことに引っかかったことはありませんか?
そのときは、梁のたわみのスケッチを描きだして、その変位の大小から記憶に結び付けましょう。
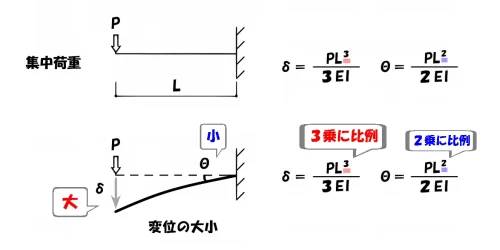

Lの乗数の見分け方
- 梁の先端に生じる「たわみδ」は振れが大きいので、Lの3乗に比例する。
- 梁の接合部に生じる「たわみ角θ」は振れが小さいので、Lの2乗に比例する。
外力の大きさに応じて「変位の大きい方が、比例の度合いも大きくなる」
たわみのスケッチを描き出してみると、その原理がイメージが出来ますよね?
「乗数の違い」については、このような視点で正しく見分けられるかと思います。
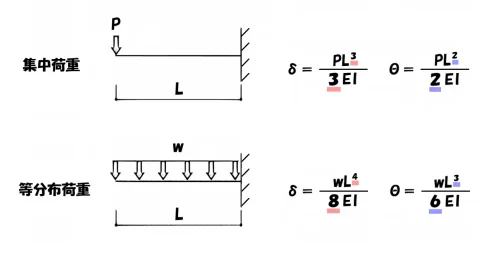

ここでひとつ、やっかいなテーマにぶつかります。
それは「集中荷重」と「等分布荷重」とでは、乗数の扱いが変わるということです。
乗数がひとつ増える
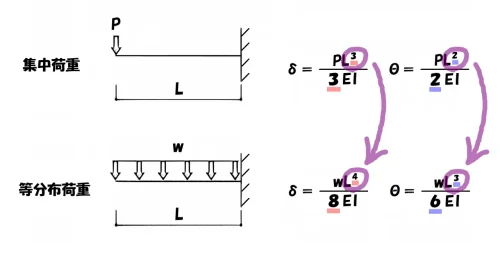

等分布荷重は集中荷重よりも「Lの乗数がひとつずつ増える」という感覚ではないでしょうか?
ここの”謎の仕様”についても、公式の原理を読み解き、その意味を紐解いていきましょう。
片持ち梁の集中荷重
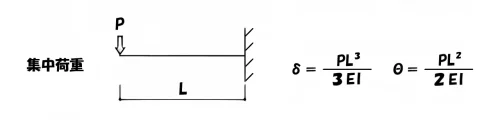

$$たわみ:\delta=\frac{ PL^3 }{ 3EI }, たわみ角:\theta=\frac{ PL^2 }{ 2EI }$$
外力の種別によって異なるたわみ公式にも、共通するものがひとつだけあります。
ここがポイント!
それぞれの異なる梁のたわみ公式は、分子の「単位」に注目すること。


分子の単位は[m]3乗、[m]2乗
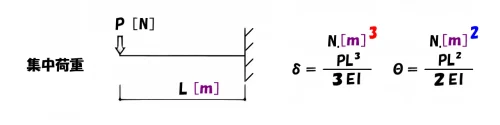

共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
異なる数値の覚え方は、ここの「単位」だけを押えておくと良いでしょう。
片持ち梁の等分布荷重
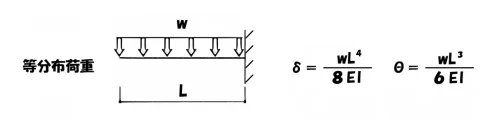

$$たわみ:\delta=\frac{ wL^4 }{ 8EI }, たわみ角:\theta=\frac{ wL^3 }{ 6EI }$$
分子の単位は[m]3乗、[m]2乗
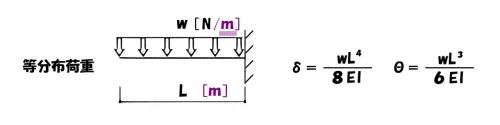

共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
まず始めに、等分布荷重の単位は[N/m]であることに注目しましょう。
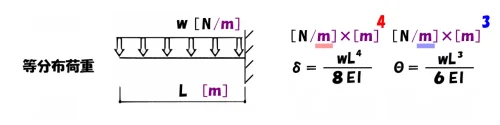

”w”の単位の分母に[N/m]がある以上、このmを打ち消して”共通の単位”にする必要があります。
$$たわみδの単位:\frac{ N }{ m}*\underline{m^4}=\frac{ N*m }{ m}*m^3=N.m^3$$
$$たわみ角θの単位:\frac{ N }{ m}*\underline{m^3}=\frac{ N*m }{ m}*m^2=N.m^2$$
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
それぞれを”共通の単位”にするには、[×m⁴]と[×m³]を掛けることになりますよね?
Lの単位は[m]であることから、単位計算より「Lの何乗を掛けるのか?」が見えて来るはずです。
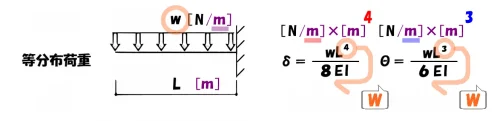
「w」に注目!
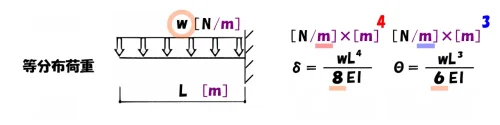

ここで、等分布荷重のシンボル「w」と公式の「係数」の関係に注目です。
「w」⇨「×2倍」
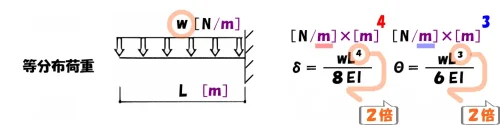

「w(ダブル)=2倍」と語呂合わせで、覚えておきましょう。
- たわみの係数:4乗×w(2倍)=8
- たわみ角の係数:3乗×w(2倍)=6
等分布荷重の係数に至っては、「w=2倍」と紐づけて記憶に刻みます。
片持ち梁のモーメント荷重
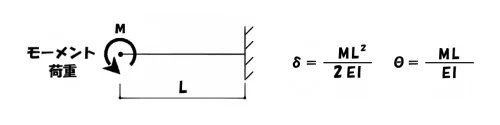

最後にひとつ、モーメント荷重によるたわみの登場です。
モーメント荷重においても「集中荷重」とは少しだけ、乗数の扱いが変わります。
分子の単位は[m]3乗、[m]2乗
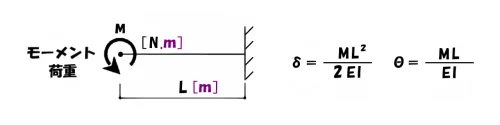

$$たわみ:\delta=\frac{ ML^2 }{ 2EI }, たわみ角:\theta=\frac{ ML }{ EI }$$
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
まず始めに、モーメント荷重の単位は[N*m]であることに注目しましょう。
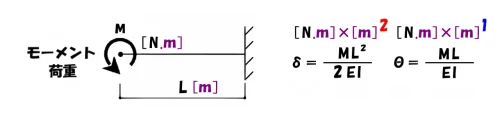

モーメント荷重の単位に[*m]があるので、このmを数えて”共通の単位”にする必要があります。
$$たわみδの単位:N*m*\underline{m^2}=N.m^3$$
$$たわみ角θの単位:N*m*\underline{m}=N.m^2$$
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
それぞれを”共通の単位”にするには、[×m²]と[×m]を掛けることになりますよね?
Lの単位は[m]であることから、単位計算より「Lの何乗を掛けるのか?」が見えて来るはずです。
片持ち梁の公式の覚え方
分子の単位は[m]3乗、[m]2乗
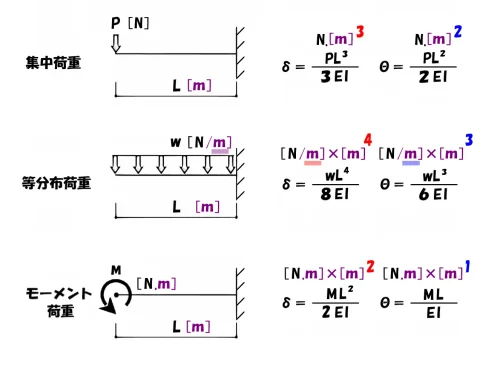

「w」⇨「×2倍」

共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
ここがポイント!
それぞれの異なる梁のたわみ公式は、分子の「単位」に注目すること。


この動画を YouTube で視聴


単純梁のたわみ
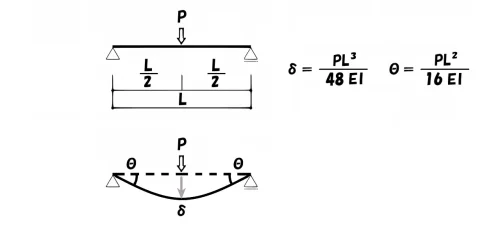

ここからは、梁の構造が変わって「単純梁」の公式に移ります。
しかし、公式を読み解くうえでの考え方は同じなので、繰り返し解説していきましょう。
変位の大・小
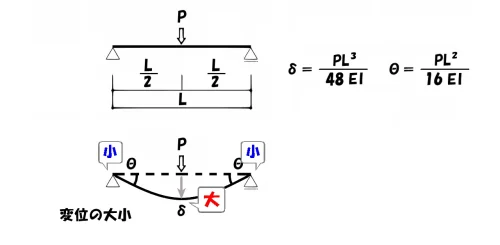

「どっちが2乗で、どっちが3乗だったかな?」
そのときは、梁のたわみのスケッチを描きだして、その変位の大小から記憶に結び付けましょう。
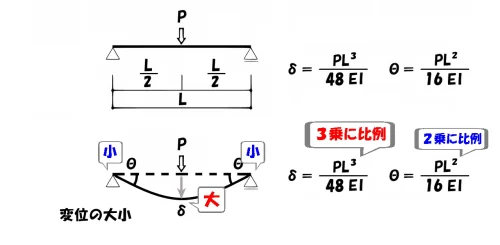

異なる乗数の見分け方
- 梁の中央に生じる「たわみδ」は振れが大きいので、Lの3乗に比例する。
- 梁の接合部に生じる「たわみ角θ」は振れが小さいので、Lの2乗に比例する。
「変位の大きい方が、比例の度合いも大きくなる」
片持ち梁であっても単純梁であっても、ここの捉え方は同じです。
「乗数の違い」は、イメージで正しく見分けられるように、覚えておきましょう。
単純梁の係数の覚え方
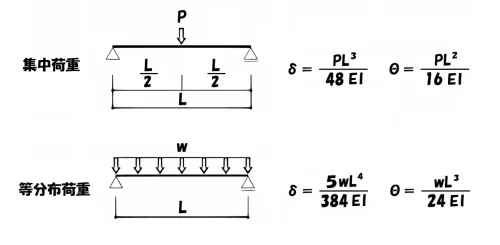

係数は、「48」「16」「384」「24」と色々な数字が登場して来ますが、コンパクトにまとめます。
桟橋へ Go!
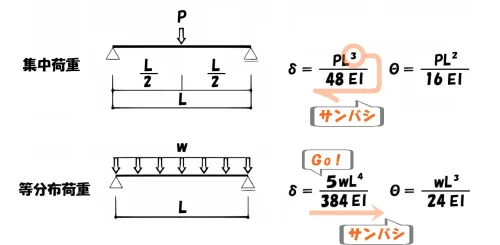

係数の語呂合わせ
- 集中荷重のたわみの係数は、左 ⇦ 右へ「サンバシ」
- 等分布荷重のたわみの係数は、左 ⇨ 右へ「サンバシ」へ「Go!」
「桟橋へGo!」覚えやすく知られている語呂ワードなので、2つセットで覚えておきましょう。
単純梁の公式の覚え方
ここがポイント!
それぞれの異なる梁のたわみ公式は、分子の「単位」に注目すること。


分子の単位は[m]3乗、[m]2乗
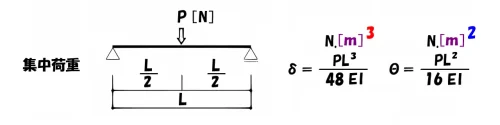

$$たわみ:\delta=\frac{ PL^3 }{ 48EI }, たわみ角:\theta=\frac{ PL^2 }{ 16EI }$$
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
異なる数値の覚え方は、ここの「単位」だけを押えておくと良いでしょう。
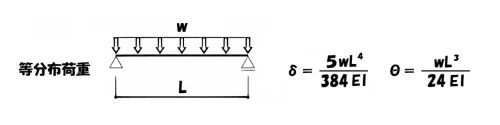

$$たわみ:\delta=\frac{ 5wL^4 }{ 384EI }, たわみ角:\theta=\frac{ wL^3 }{ 24EI }$$
分子の単位は[m]3乗、[m]2乗
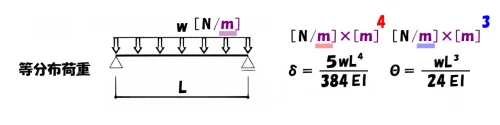

まず始めに、等分布荷重の単位は[N/m]であることに注目しましょう。
”w”の単位の分母に[N/m]がある以上、このmを打ち消して”共通の単位”にする必要があります。
$$たわみδの単位:\frac{ N }{ m }*\underline{m^4}=\frac{ N*m }{ m }*m^3=N.m^3$$
$$たわみ角θの単位:\frac{ N }{ m }*\underline{m^3}=\frac{ N*m }{ m }*m^2=N.m^2$$
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
それぞれを”共通の単位”にするには、[×m⁴]と[×m³]を掛けることになりますよね?
Lの単位は[m]であることから、単位計算より「Lの何乗を掛けるのか?」が見えて来るはずです。
桟橋へ Go!
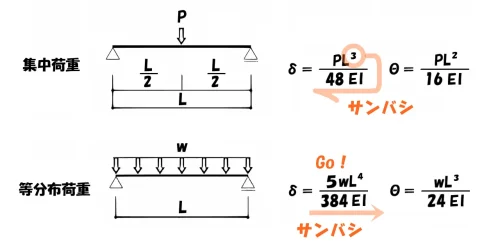

係数の語呂合わせ
- 集中荷重のたわみの係数は、左 ⇦ 右へ「サンバシ」
- 等分布荷重のたわみの係数は、左 ⇨ 右へ「サンバシ」へ「Go!」
×8
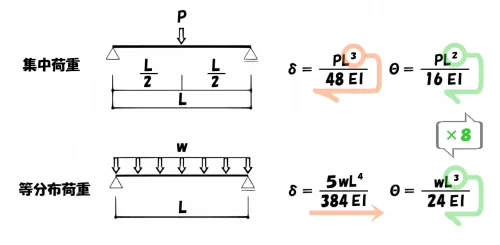

たわみ角の係数は×8倍
- 集中荷重のたわみ角の係数:2乗×8=16(係数)
- 等分布荷重のたわみ角の係数:3乗×8=24(係数)
「×8」に至っては、たわみ角θのシンボルが「8」に似ていることに、紐付けても良いでしょう。
4つの係数に対して、覚える語呂ワードは「桟橋へGo!」と「×8」の2つだけです。
共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
ここがポイント!
それぞれの異なる梁のたわみ公式は、分子の「単位」に注目すること。


この動画を YouTube で視聴
断面一次モーメントの公式
断面一次モーメントは、主に2級建築士の構造力学で出題されるもの。
しかし、1級建築士の問題でも稀に姿を現すことがあるため、簡単に押さえておきます。
ここを丁ねいに理解しておくことで、断面二次モーメントの公式を覚える”手助け”にもなるでしょう。
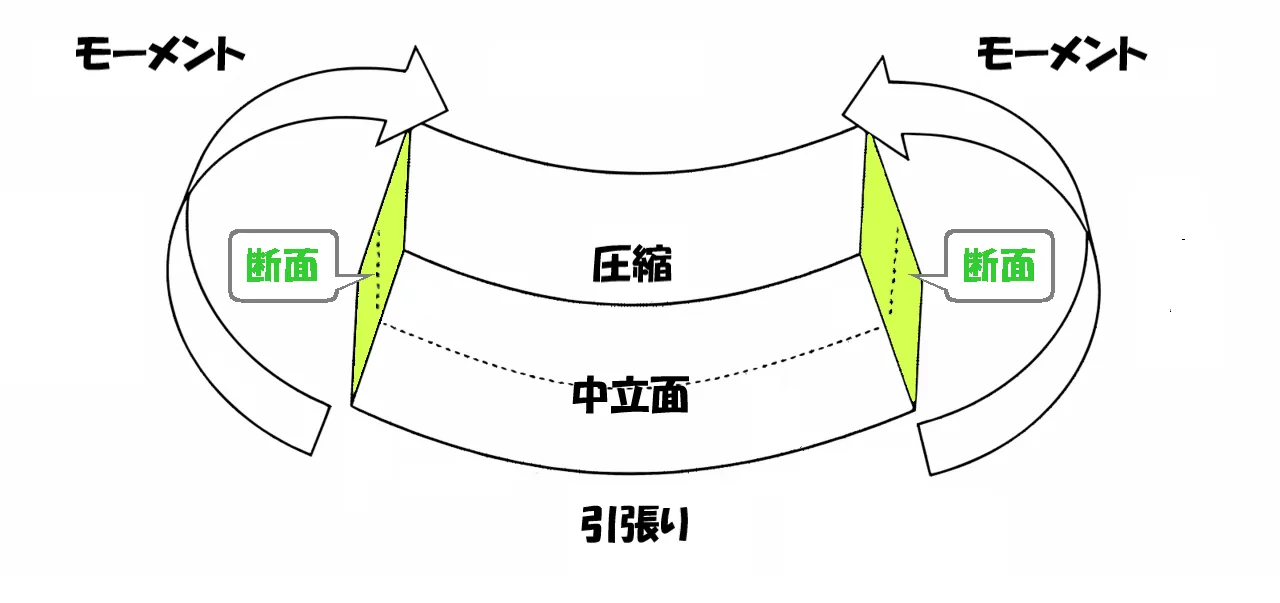
モーメントとは?
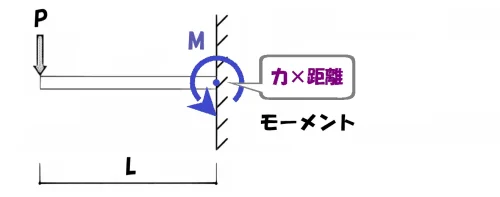

構造力学の視点で、モーメントを簡単に言い表すと「力×距離」のこと。
それは、モーメントの単位「N.m」が、公式の意味を表していると言えるでしょう。
断面積(力)×距離
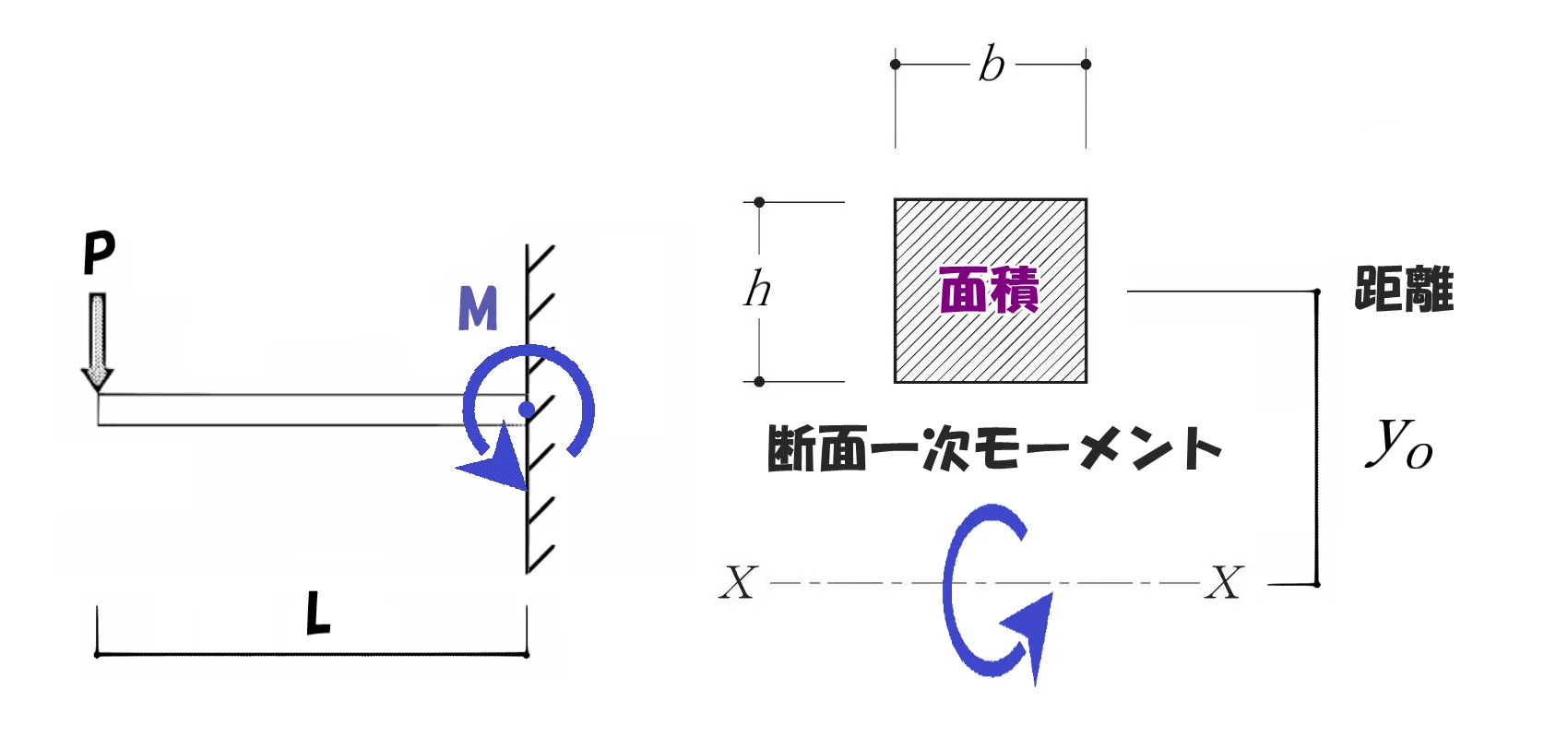

断面一次モーメントのおいても、その捉え方は同じこと。
「力×距離」の「力」が、「力」→「断面積」に変わるだけです。
断面一次モーメント
断面一次モーメント=「断面積」×「距離」
断面積(力)×距離の2乗
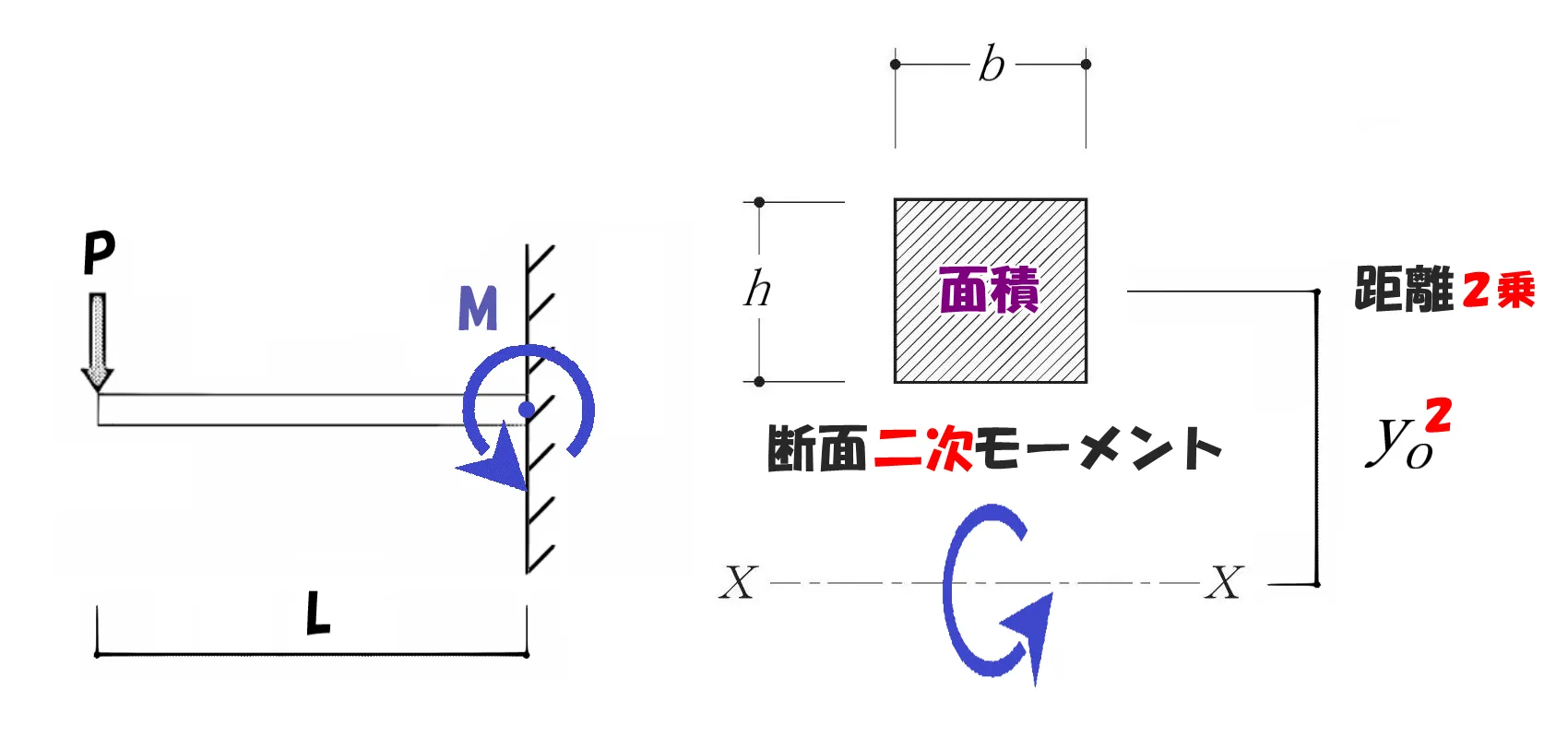

断面二次モーメントのおいても、その考え方は同じこと。
「力×距離」の「力」が「断面積」に、「距離」が「距離の2乗」に置き換わるのです。
断面二次モーメント
断面二次モーメント=「断面積」×「距離」の2乗
力×距離の関係
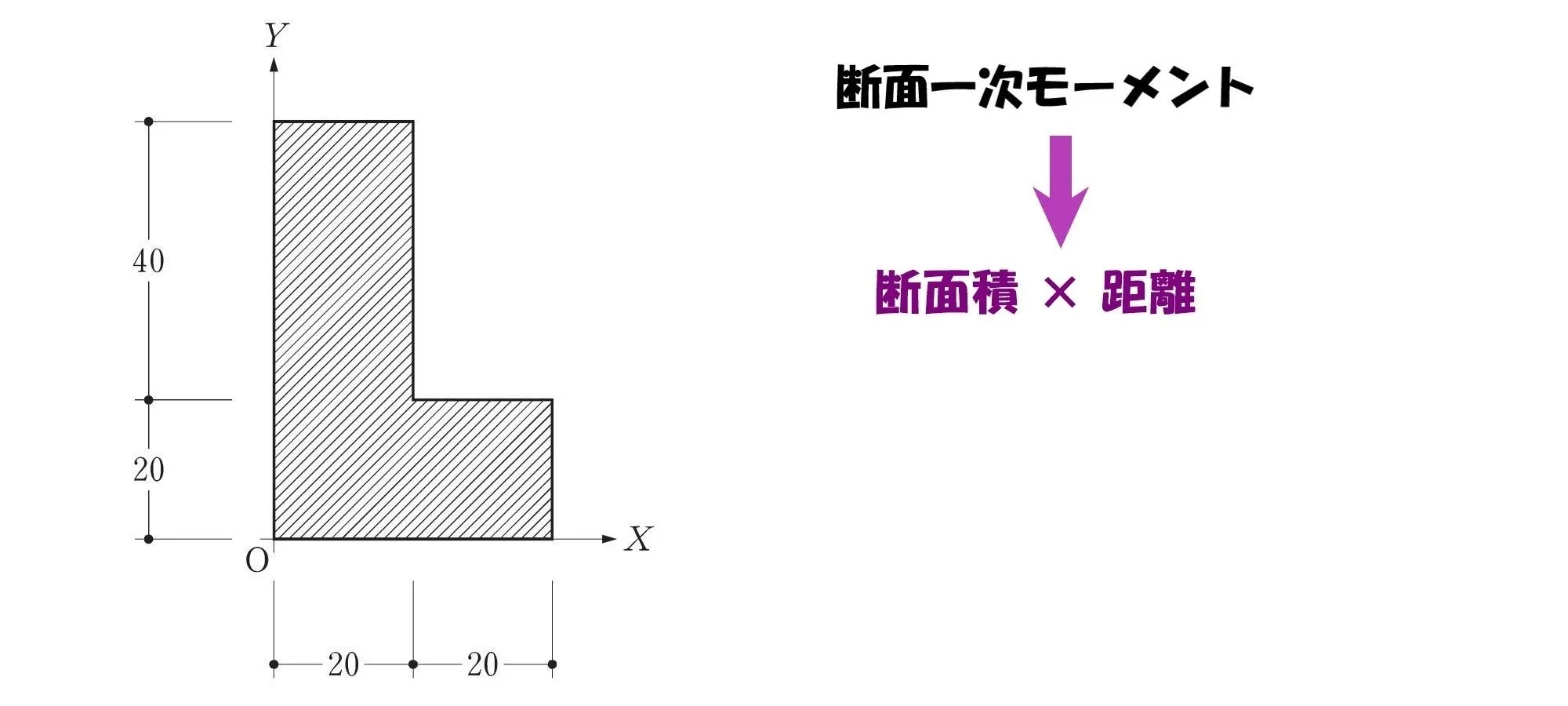

ここでひとつ、「断面一次モーメント」のサンプル課題で、解説していきましょう。
断面積(力)×距離
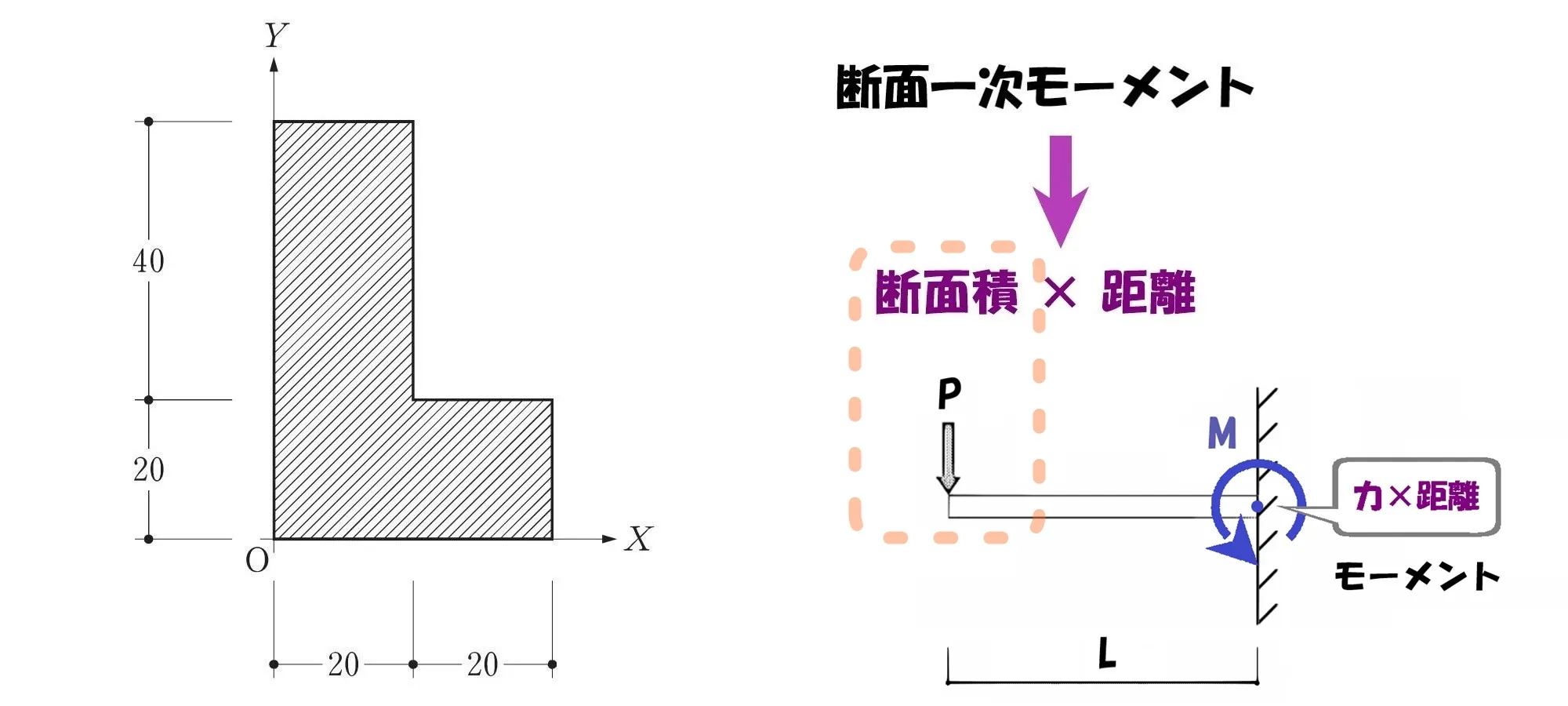

$$断面一次モーメント=断面積×距離$$
断面積×距離
- 断面積:部材の矩形部分の断面積
- 距離:基準軸からその図芯までの距離
断面積(力)×距離
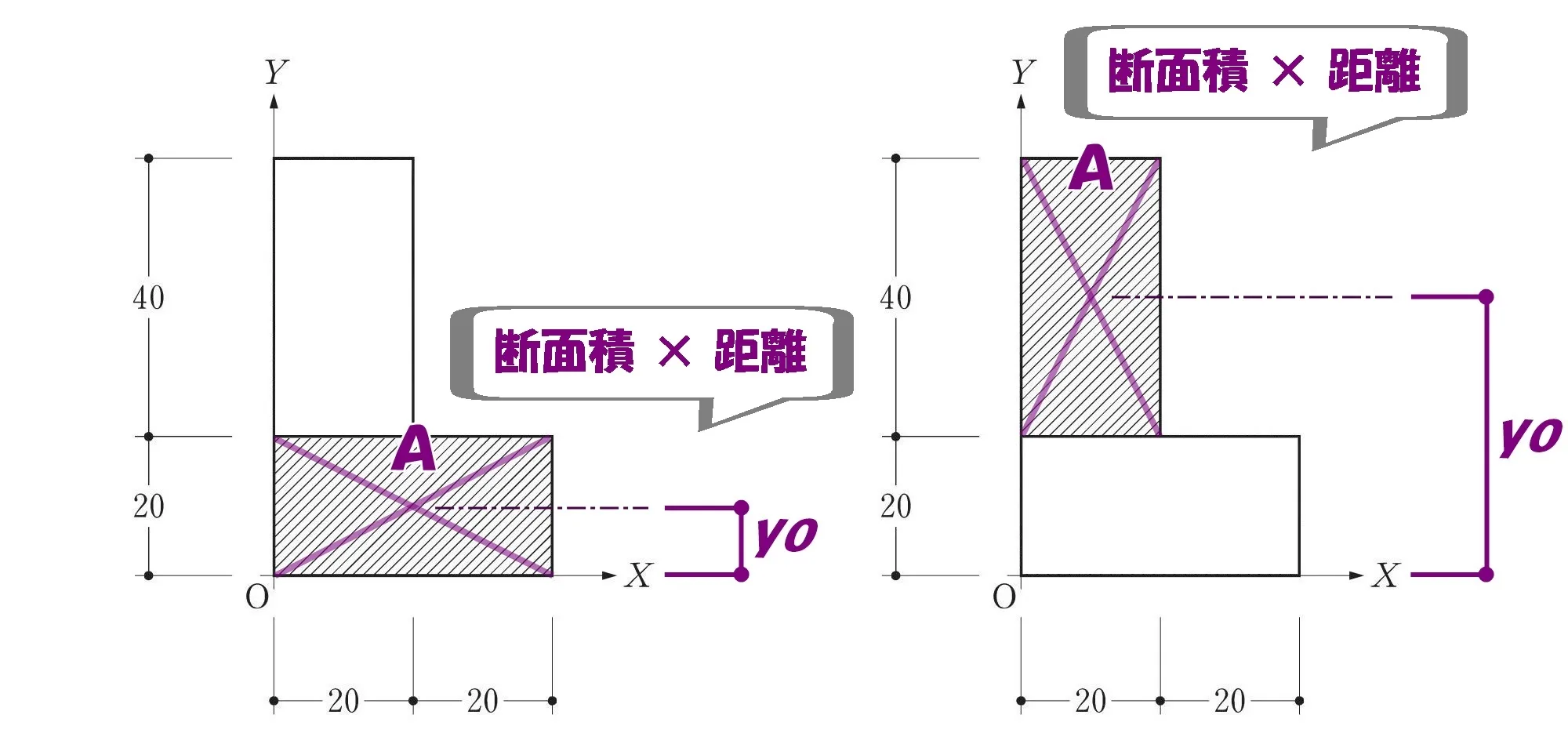

$$断面一次モーメント=A*yo+A*yo$$,$$=(20+20)*20*10+20*40*(20+20)$$
断面積×距離
- A:部材の矩形部分の断面積
- Yo:基準軸からその図芯までの距離
断面一次モーメント
断面一次モーメント=「断面積」×「距離」
一次二次とは?
そもそも「断面一次、二次とは何のこと?」
疑問をここで解消して、後の説明に繋げていきます。
一次二次とは、関数の呼び名
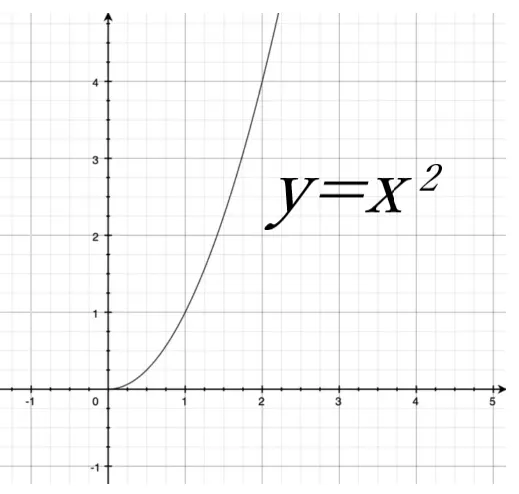

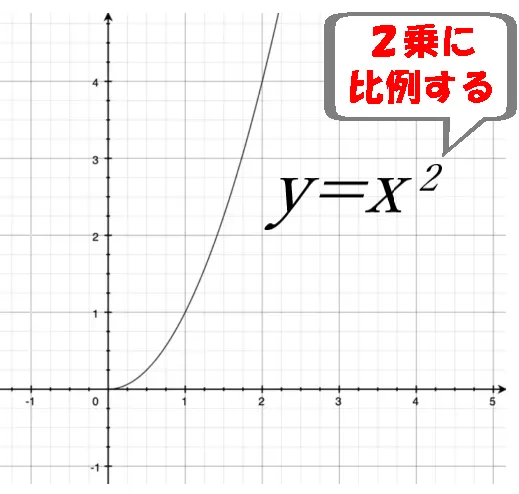

断面二次モーメントの「二次」とは、「二次関数」のこと。
二次関数は「y=x²」の曲線図のことで、「yはxの2乗に比例する」ことを表しています。
その原理から、断面二次モーメントは「距離の2乗に比例する」という意味に繋がるのです。
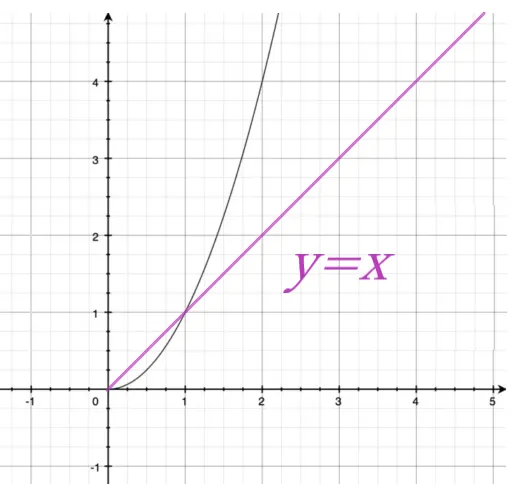

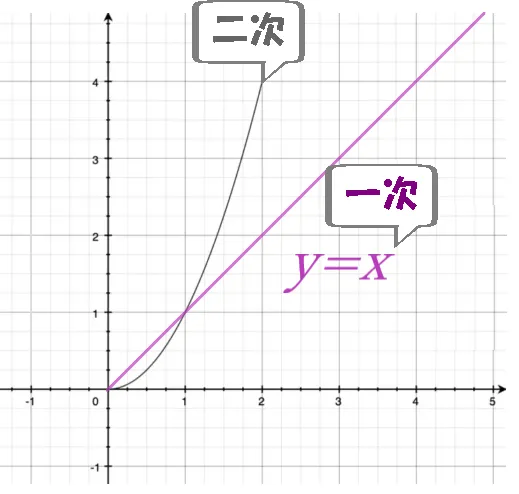

断面一次モーメントの「一次」とは、「一次関数」のこと。
その関数は「y=x」の直線図となり、「yはxに正比例する」関係となります。
断面「一次、二次」についてはそれぞれ「距離に比例」「距離の2乗に比例」という理解で十分です。


この動画を YouTube で視聴
断面二次モーメントの公式

断面一次モーメントの公式について、ここまで丁ねいに解説してきました。
断面二次モーメントについても”公式を覚える”という視点で、サクッと解説していきます。
先ほどの考え方を理解していただくことで、断面二次モーメントの公式の本質が見えてくるでしょう。
断面二次モーメント
断面二次モーメント=「断面積」×「距離」の2乗
断面積(力)×距離の2乗
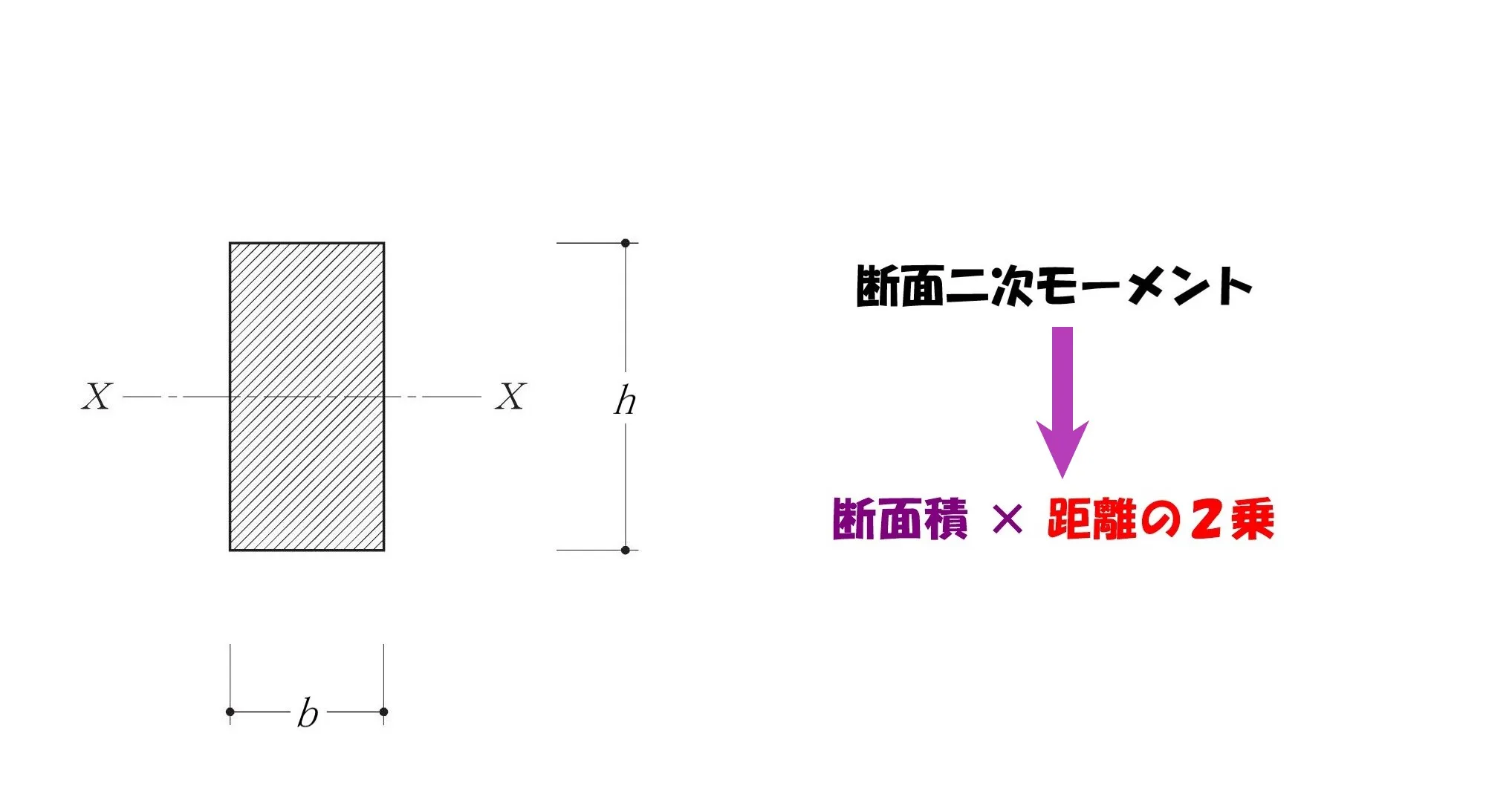

断面二次モーメント=断面積×距離の2乗
断面積×距離の2乗
- 断面積:部材の矩形部分の断面積
- 距離:基準軸からその図芯までの距離
断面二次モーメントの本質
断面二次モーメント=断面積bh×距離yoの2乗
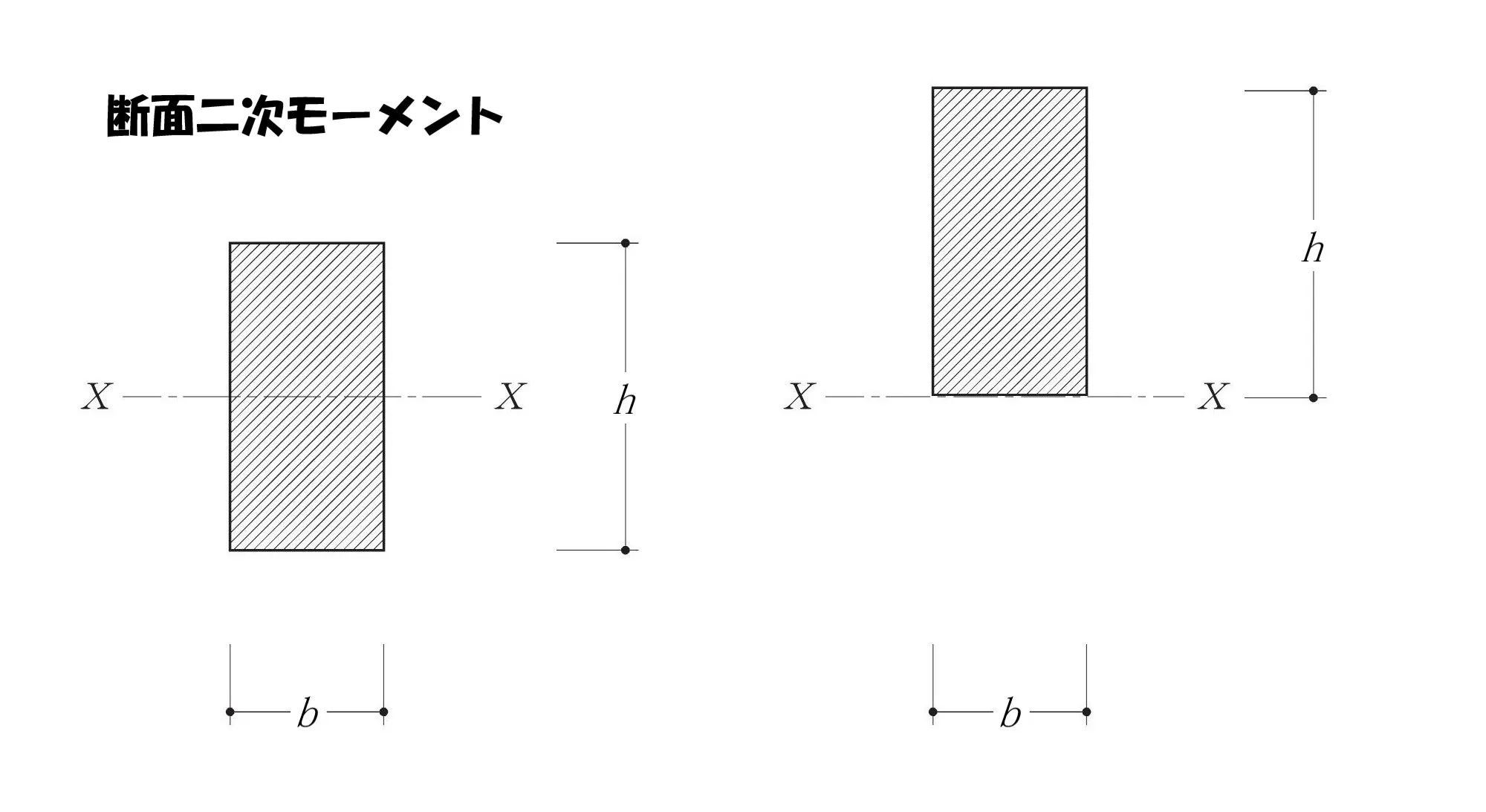

ここからは、「断面二次モーメント」のサンプル課題で、実践していきましょう。
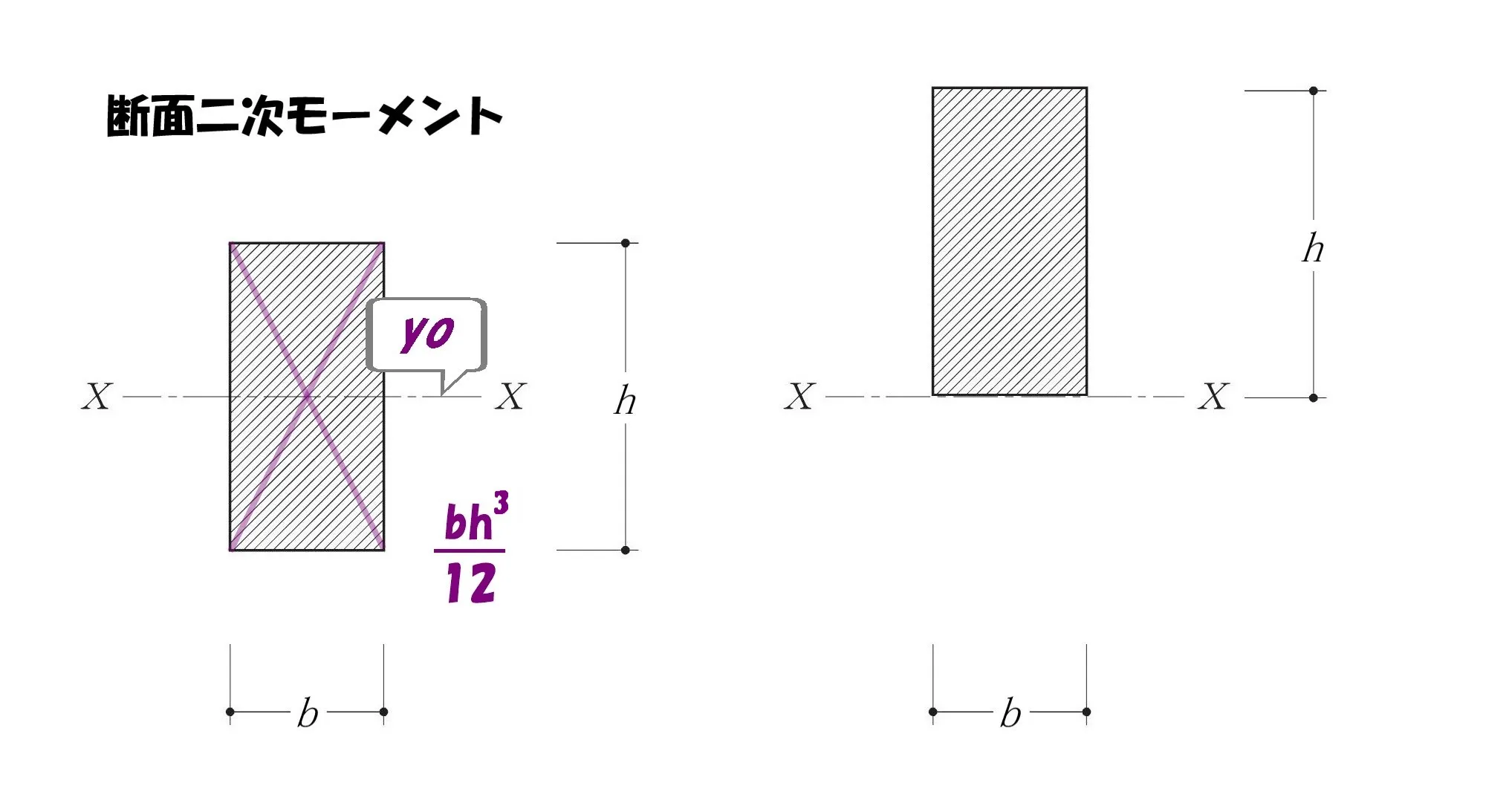

$$断面二次モーメント=\frac{ bh^3 }{ 12 }$$
$$※公式はあくまでも、基準軸から図芯までの距離がゼロの場合です。$$
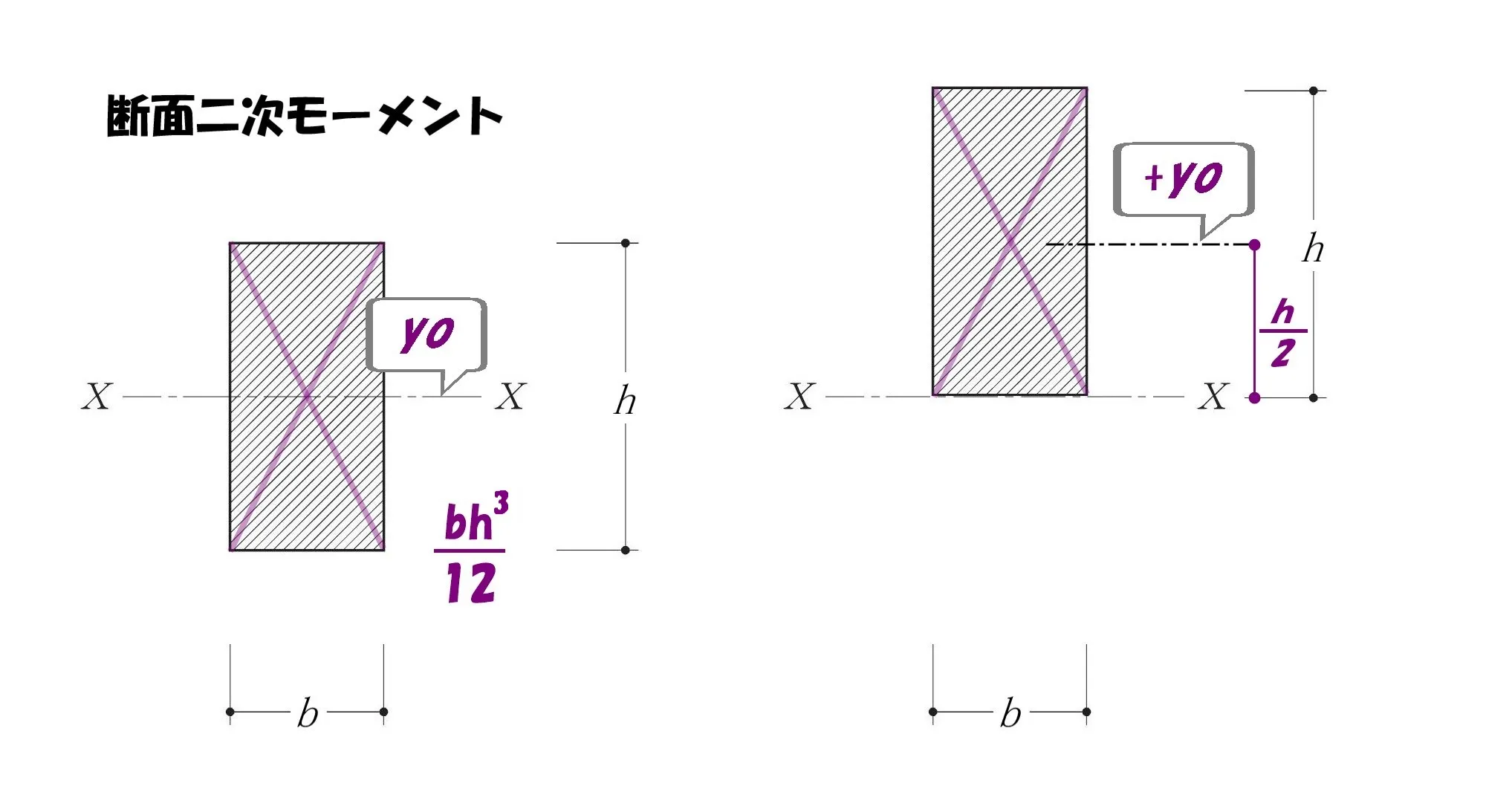

ここでひとつ、断面二次モーメントの本質を発揮しましょう。
矩形断面の図芯が基準軸のうえに乗っていないケースは、どうなるかご存知ですか?
モーメントは大きくなる
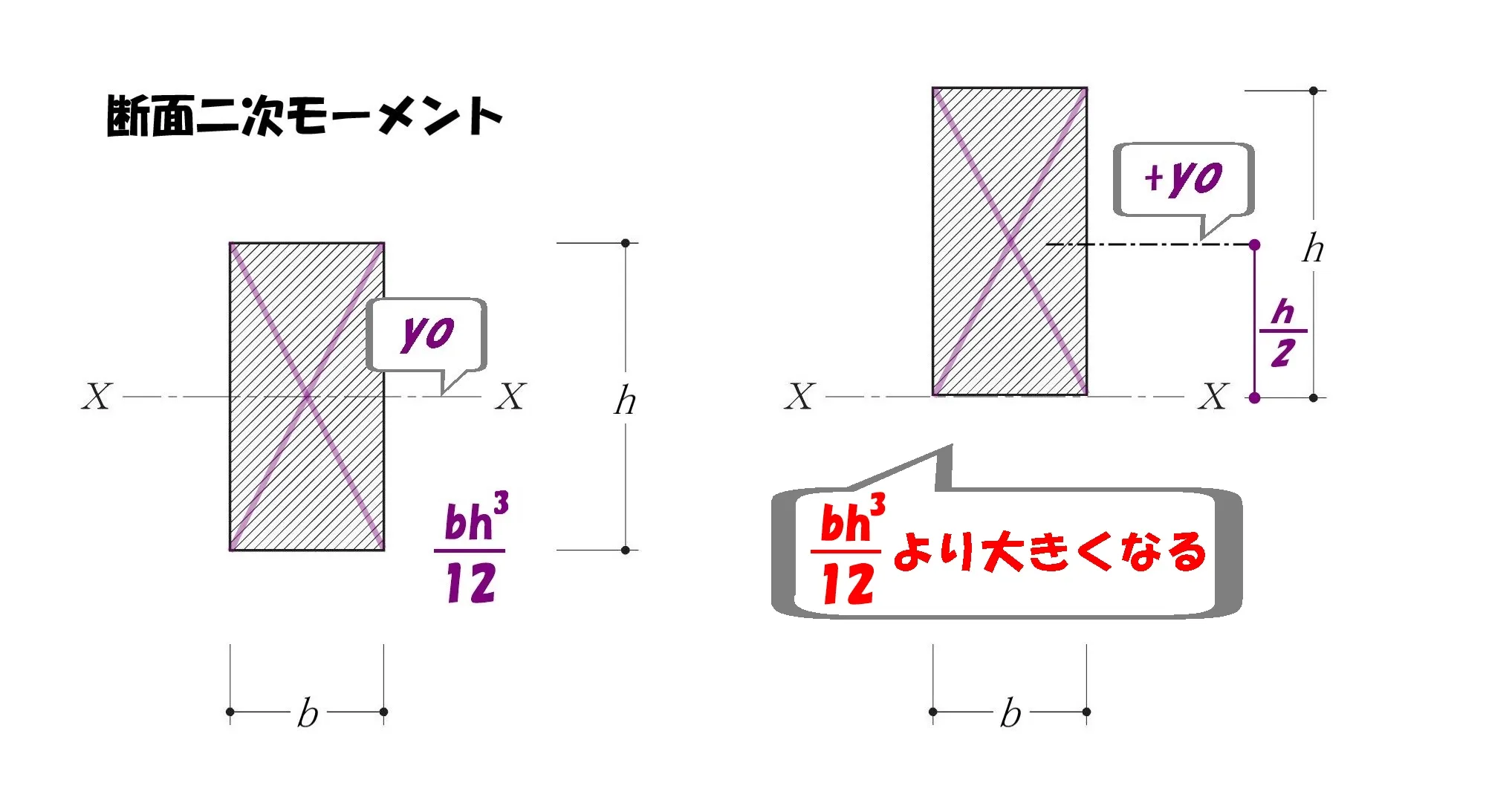

断面二次モーメント=断面積×距離の2乗
公式により、断面二次モーメントは「図芯からの距離の2乗に比例する」
つまり、図芯からの距離がゼロより大きくなるため、断面二次モーメントも大きくなります。
少なくとも「bh³/12」より大きくなるということは、想像できますよね?
断面積(力)×距離の2乗
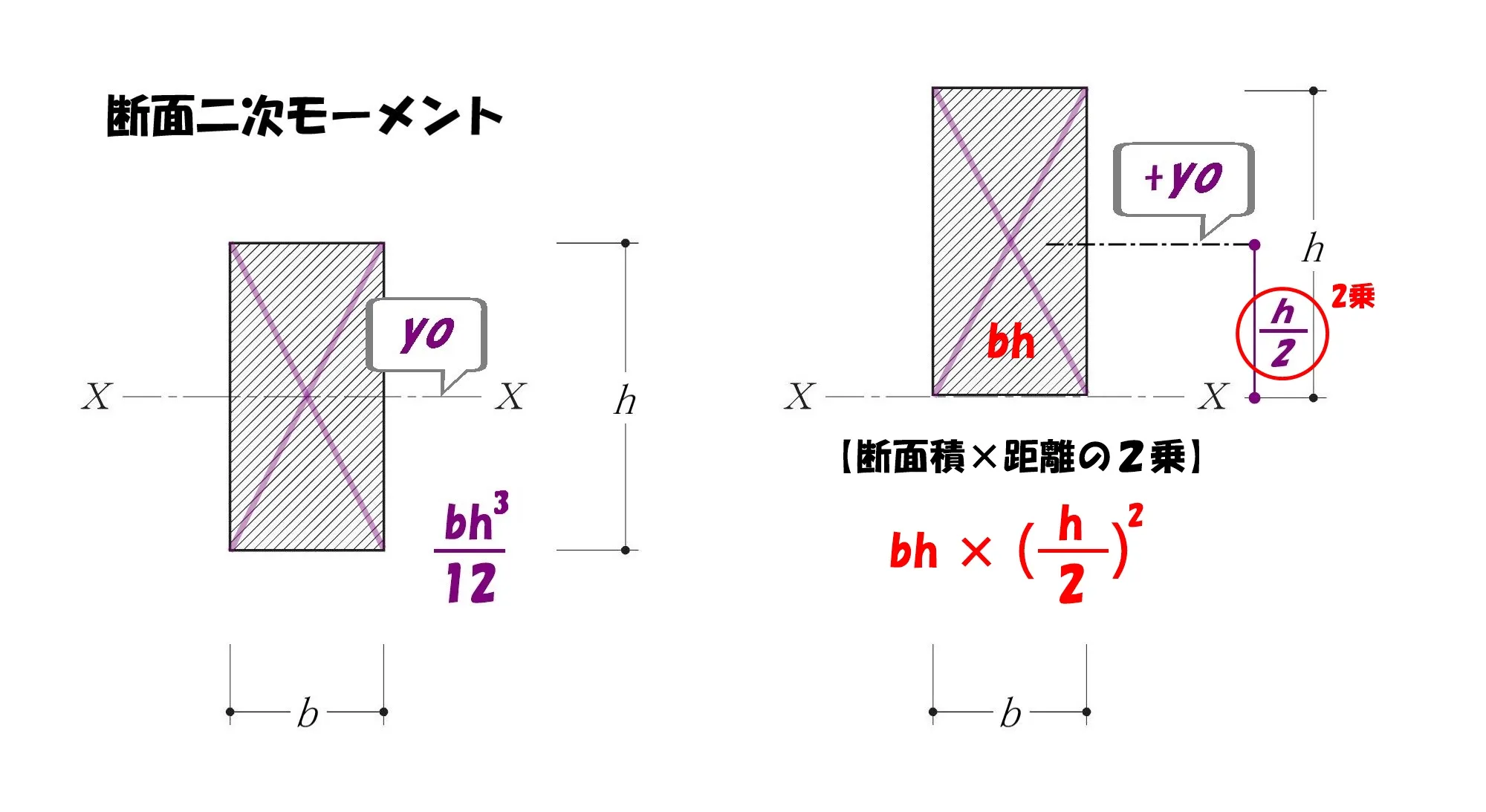

$$断面二次モーメント=断面積*(距離)^2$$
$$図芯:+yo=\frac{ h}{ 2 }の断面二次モーメント=bh*(\frac{ h}{ 2 })^2$$
断面二次モーメント
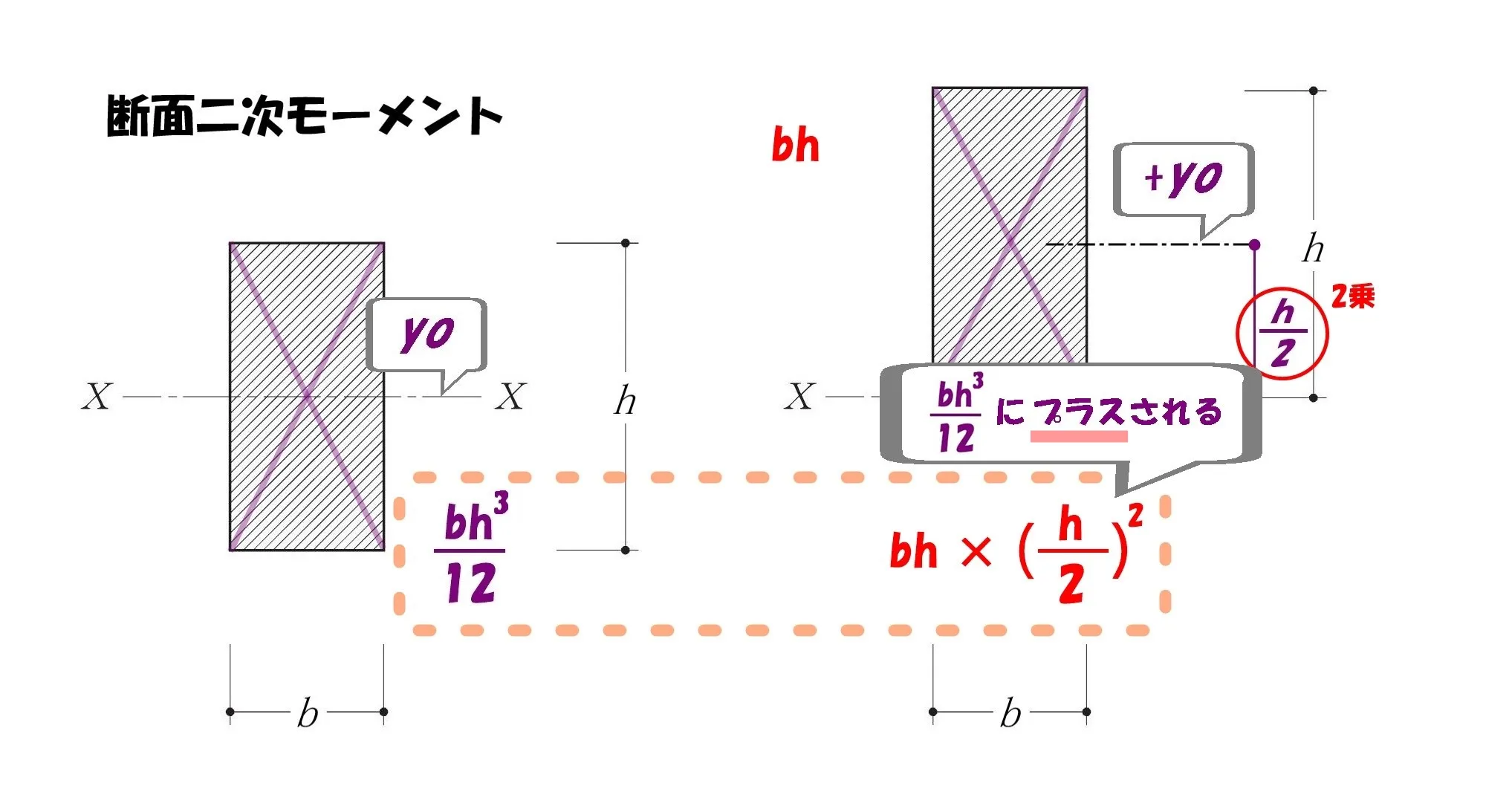

$$断面二次モーメント=\frac{ bh^3 }{ 12 }+bh*(\frac{ h}{ 2 })^2$$


$$\frac{ bh^3 }{ 12 }+bh*(\frac{ h}{ 2 })^2=\frac{ bh^3 }{ 12 }+\frac{ bh^3 }{ 4 }$$
$$=\frac{ bh^3 }{ 12 }+\frac{ 3*bh^3 }{ 12 }=\frac{ (1+3)*bh^3 }{ 12 }=\frac{ 4*bh^3 }{ 4*3 }=\frac{ bh^3 }{ 3 }$$
断面二次モーメントの本質
断面二次モーメント=断面積bh×距離yoの2乗
お疲れ様でした、まとめに入ります。

一級建築士|構造力学の「たわみ」の公式の覚え方(まとめ)


梁のたわみ
- 梁の先端に生じる「たわみ」は振れが大きいので、Lの3乗に比例する。
- 梁の接合部に生じる「たわみ角」は振れが小さいので、Lの2乗に比例する。


共通の単位
- たわみδの公式:分子の単位は、N*[m]3乗になる。
- たわみ角θの公式:分子の単位は、N*[m]2乗になる。
ここがポイント!
それぞれの異なる梁のたわみ公式は、分子の「単位」に注目すること。


断面一次モーメント
断面一次モーメント=「断面積」×「距離」


断面二次モーメント
断面二次モーメント=「断面積」×「距離」の2乗


断面二次モーメントの本質
断面二次モーメント=断面積bh×距離yoの2乗




計算問題を攻略するうえで、「公式を覚える」ことは必須です。
そのためのヒントや公式の捉え方について、ひとつずつ解説して来ました。
迷いがちな公式
- 梁のたわみとたわみ角
- 断面一次モーメントと断面二次モーメント
それぞれの「公式を覚える」ための情報をコンパクトにまとめましょう。
記事の”まとめ”文を何度も読み返し、思い出すためのきっかけを作っておくのです。
そうすることで、公式に対する記憶力がより強くなって、ミスを減らせるはず。
この記事をきっかけにして、「公式を覚える」ことから解放されましょう。




.webp)
.webp)




-300x197.webp)





