一級建築士受験生の皆さん、構造力学の勉強に苦労していませんか?
「構造力学に多くの時間を浪費してしまい、構造以外の対策に手が回らない」
そういった方のために、一級建築士になった私が効果的な勉強方法を紹介しましょう。
才能や学歴は要りません。独学でも出来る3ステップをコツコツと繰り返すだけ。
この記事を通してあなたの苦手意識を取り除き、その不安も自信に変わることでしょう。

勉強方法3ステップ


苦手な人の戦い方


勉強を楽にするコツ
こんな人におすすめ!
- 構造力学の勉強に手がつけられない
- 構造力学の効果的な勉強方法を知りたい
- 構造力学の計算問題に時間を取られてしまう
.webp)
.webp)



もう限界・・・
構造力学は超えらない。


この動画を YouTube で視聴


一級建築士:構造力学の勉強方法に悩む方へ
構造力学の勉強には、集中力が必要です。
計算問題に至っては「何から手をつけて良いのか?」と気が滅入ってしまい、なかなか踏み切れないこともありますよね?


構造力学の悩み
- 問題文を目のまえにして手が進まない。
- 解説文を読むと数字ばかりでめまいがしそう。
- 計算問題に時間を浪費して他の対策に手が回らない。
構造力学の問題は図の読み取り、方程式を作るところから始まります。
計算式にボリュームがあると時間を浪費させられてしまうこともありますよね?
そして、答え合わせをする際の”自分の解答が間違っていた”ときの喪失感は何とも言い切れません。



何故だ・・・
「あれだけの労力を掛けて答えを絞り出した、あの時間は何だったのか?」
・・・という虚しさから、次の問題へ進む気力すら奪われてしまいます。



俺の時間を返してくれ。
構造力学の勉強に手が出せずに「絶望感を感じている」人であっても心配は要りません。
そういった計算問題が苦手な人に向けて、私が実践していた勉強方法をお伝えしましょう。
お伝えする勉強方法
誰でも確実に点が取れるシンプルで「再現性の高い」勉強方法。
気合を入れるぞ!
一級建築士:構造力学の勉強方法との向き合い方
- 構造力学の勉強の悩み
- 構造力学の難しさの正体とは?
- 始めから理論と向き合い過ぎないこと
伝えたいこと
勉強が苦手な人には「苦手な人なり」の取り組み方がある。
構造力学の勉強の悩み


構造力学の勉強の悩み
- 公式が覚えられない。
- 問題の解き方が見えない。
- 計算問題の解答に時間が掛かる。
初受験生にとっては、構造力学は大きな壁となり「すごく難しい学問」のように見えるもの。
独学で始める人にとっては「何が分からないのか」も分からない状況ですよね?
構造力学を苦手とする主な原因として、以下の4つが挙げられます。
苦手な人によくある傾向
- 構造力学は難しいと思っている。
- 公式は暗記するものと思っている。
- 解き方や求める順番を覚えていない。
- 言葉や理屈だけで覚えようとしている。
そのひとつひとつは、それほど大きな問題ではないように思えるかもしれません。
しかし、これらの悩みは同時に抱え込んでしまうと重くなり、苦手意識へと変えてしまうのです。


ラーメン構造って
食べれるの?



そこからかよ!
構造力学の難しさの正体とは?
構造が苦手な方は想像してみてください。
一級建築士試験の構造力学は果たして、どれほど難しいのか?
ずばり答えは?
構造力学を苦手とする人が、想像するほど難しくない。


一般的な感覚より、どちらかと言うと「難しい」学問であることには間違いありません。
その一方で、押さえどころさえ分かれば「確実に点の取れる分野」であることも事実です。
そこで、構造力学の難しさについて具体的にすると以下の3つになります。
- 図を描くスキルが必要
- 簡単な物理の知識が必要
- 高校生レベルの数学力が必要
そのひとつひとつを切り出してみると、いかがでしょうか?
社会人にとっては、人並みの勉強をすれば克服できるものばかりですよね?
それでは、構造力学の「何がそこまで難しくしているのか」について明らかにします。
構造力学の難しさの正体
- 図を描くスキル
- 簡単な物理の知識
- 高校生レベルの数学力
この3つの力を組み合わせること。



これが鬼の正体、
おのれ悪魔よ・・・
「3つのスキルを複合的に組み合わせる」、これが構造力学に苦しめられる要因です。
構造力学を苦手とする人は、この要因を理解しておくことで「難しさと向き合える」ようになります。
始めから理論と向き合い過ぎないこと


- 固有周期とは?
- 全塑性モーメントとは?
- 弾性座屈荷重って一体なに?
構造力学には難しい専門用語がたくさん登場してきますよね?
その度に真っ向勝負で「理論と向き合おう」とすると、メンタルが擦り減ってしまいます。
構造力学が苦手な人ほど「理論を突き詰めて克服しようとして、さらに嫌いになる」
そして、「もう限界・・・」という自信喪失のパタンに陥ってはいませんか?



もう限界・・・


理論的な内容を読み解くには、それなりの予備知識が必要となります。
構造初心者の方は、始めに過去問題の回数をこなして予備知識を身につけていくこと。
過去問を解いていく中で、「知りたいと思ったときに知る」くらいのスタンスが丁度よいでしょう。
過去問を解いていく中で、理論を追求することはひとまず置いておく。


この動画を YouTube で視聴
構造力学が苦手な人の戦い方


「理論と真っ向勝負で向き合う」
この姿勢は、構造力学が得意な人たちの取り組み方です。
そういった思考が苦手な人たちが、必ずしも得意な人たちと同じやり方をする必要はありません。



理論・全開!
私は構造の鉄人です。



ありえない。
信じられない。



応力!トラス!せん断!
座屈!軸力!モーメント!
つまり、構造力学が苦手な人には「苦手な人なりの取り組み方」があるということ。
ここでは、苦手な人が始める「勉強の取り組み方」を3つ紹介します。


苦手な人の取り組み方
難しい理論は、単純な「絵」や「手の動き」に置き換え、理論は小さくまとめる。
「どういうこと?」と思われるかもしれません。
難しそうな表現をしましたが、決して難しいことではありません。
いわゆる「手を動かして覚える」という古くからある伝統のやり方です。



結局、それかよ!


理論をすべて言葉で処理すると、どうしても情報量が増えてしまい脳に負荷が掛かかります。
そこで、言葉による情報は絵に描き出し、その動作と合わせて読み解くことを習慣にしましょう。
「絵」や「手の動き」に情報を持たせることによって「言葉による情報量をスリム化」するのです。



言葉や理屈は
絵にして吐き出そう!
構造が苦手な人の戦い方
- 言葉とイメージをセットにする。
- 問題用紙をコピーして図に書き込む。
- 部材を切断して一部のパーツを取り出す。
1.言葉とイメージをセットにする


「1つの言葉に対して1つのイメージ図」
理論が苦手な人は、「言葉」と「イメージ」とセットにする習慣をつけましょう。
言葉だけでなく視覚的な要素を加えて「情報を見える化する」ことで、記憶も定着します。



言葉とイメージは
セットにして覚える。
参考例
2.問題用紙をコピーして図に書き込む


構造力学と向き合うには、問題用紙に積極的に書き込みするクセをつけましょう。
過去問題集の場合は問題図のコピーを取ることで、何度でも書き込みが出来るようになります。



書いて書いて書きまくる!
問題用紙に図や計算式など積極的に書き込みが出来る体勢をととのえる。
その紙代がもったいない!
コンビニのコピー機で白黒印刷すれば1枚10円で出来ますよね?
5年度分の計算問題のみを印刷しても350円くらいしか出費が掛かりません。
さらに、コピーにメモ書きした用紙はファイリングすることでノートにもなります。
そのノートの値段が350円と考えれば、決して高くないといえるでしょう。



紙代がもったいないよ!



バカモン!
コピー代で手に入れるのは紙ではなく、「情報」と「時間」の2つです。
書き込み例
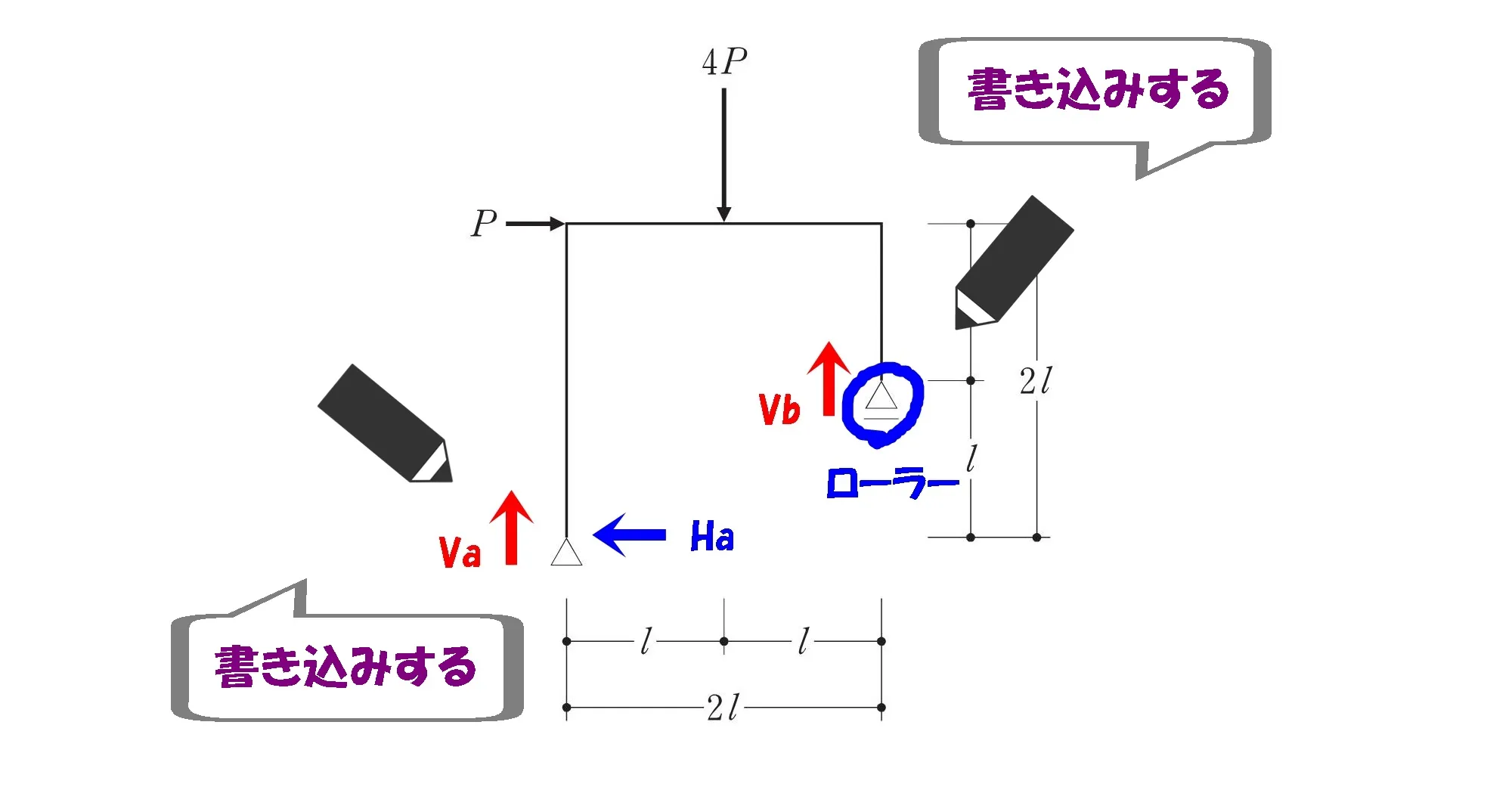

問題図に書き込みをすることで、イメージから展開して身体に覚えさせましょう。
書き込みにより情報を視覚化することで、答えに向けてのアプローチも見えて来るようになります。



かかってきなさい。
問題図に積極的に書き込みして、理論よりもイメージから展開する。
3.部材を切断して一部のパーツを取り出す


構造力学の戦い方の極めつきは、構造物の部材を斬って取り出すことです。
計算問題においてこの手法は、どんなものにも使える「万能テクニック」といえるでしょう。



構造の鬼に制裁を下す!
最終奥義
部材をパーツごとに切り離し、考え方を小さくまとめる。
部材斬りの図


問題図に書き込みをすることで、イメージから展開して身体に覚えさせる。
さきほど、そのように伝えました。
しかし、ひとつの図形に多くの書き込みをしていくと情報量が増えてしまうこともあります。
その情報量をコントロールするためには「部材斬り」を取り入れること。
必要最小限の部材を取り出すことで、コンパクトな情報にまとめることが出来るのです。



伝家の宝刀、部材斬り!
部材斬りの活用例
一級建築士【構造力学】計算問題に挑戦して攻略ポイントを紹介!
部材を切断する目的
- 部材のパーツごとに考え方を小さくまとめる。
- 思考するうえで、不要な部分をマスキングする。
- バリエーションのある過去問に対して応用が利く。
部材をパーツごとに切り離し、考え方を小さくまとめる。


この動画を YouTube で視聴
一級建築士:構造力学の勉強方法(独学)の3ステップ!


勉強方法3ステップでは、過去問題集を活用します。
人によっては構造力学の勉強を「独学で始める」という方もいるかもしれません。
しかし心配は要りません。紹介するのは「独学で始める人のための勉強法」でもあるからです。
タイトルにもある「誰でも確実に点が取れるシンプルな勉強方法」というテーマで紹介します。



構造を斬る!
使用する教材の紹介
一級建築士試験|独学で合格を目指すには過去問から!(オススメの問題集)
勉強が苦手な人には「苦手な人なり」の取り組み方がある。
勉強法3ステップ
| ステップ① | 問題を解くための手順や公式をまとめる。 |
| ステップ② | 手順や公式を問題文の余白に箇条書きする。 |
| ステップ③ | 箇条書きしたメモに習って繰り返し問題を解く。 |
ステップ①:問題を解くための手順や公式をまとめる


ステップ①
- 問題文を丁ねいに読み、図に書き込みする。
- 解説文を丁ねいに読み、必要な言葉をチョイスする。
- 問題を解くための手順や公式を小さくまとめる。
1.問題文を丁ねいに読み、図に書き込みする
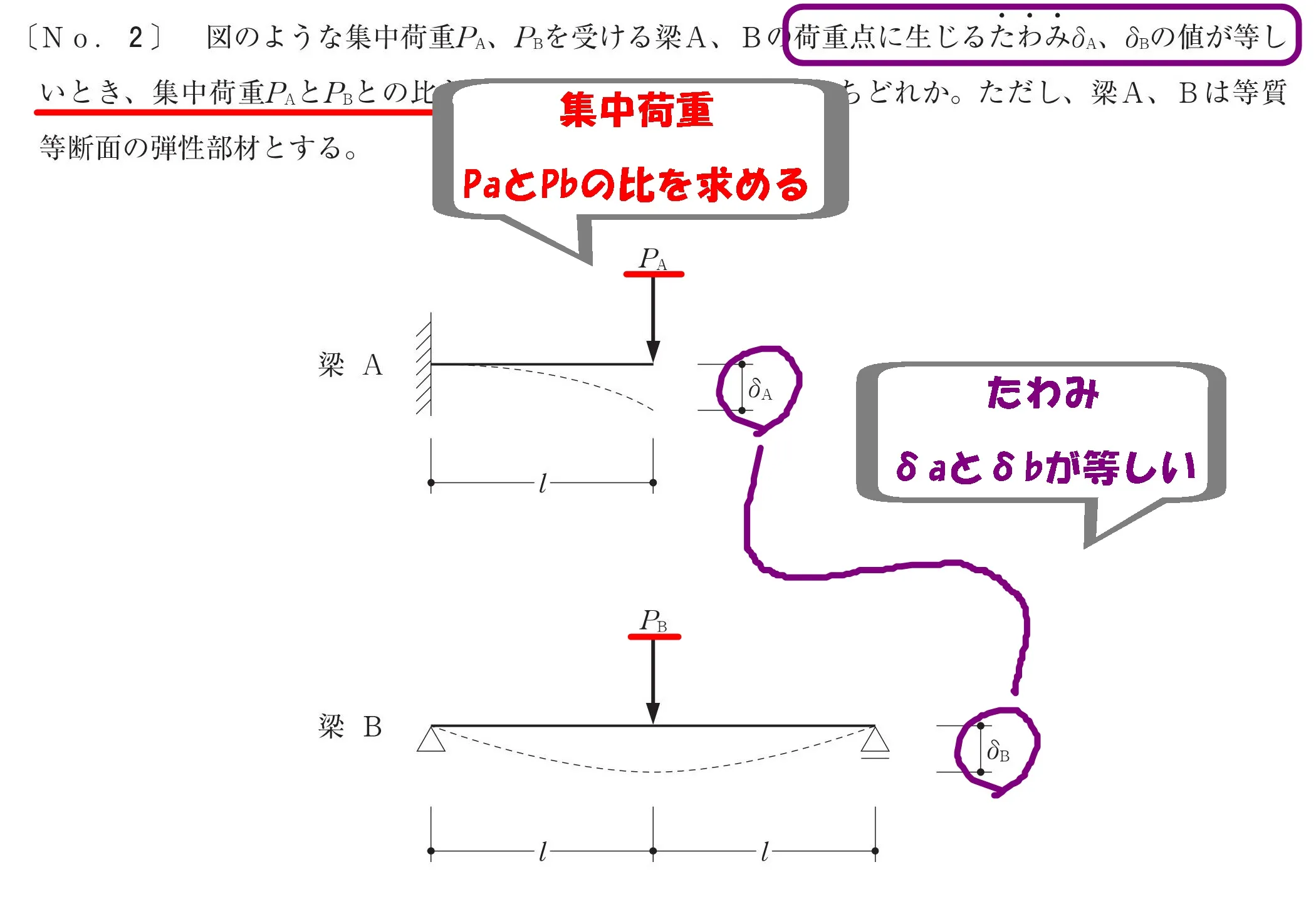

過去問題集を使われている方は、まず始めに問題図のコピーを取ります。
問題文を読みながら、コピーした紙のほうに積極的に書き込みをしていきましょう。
「何を求めるのか?」「何から求めればよいか?」などを考えながら手を動かしいくのです。
その手が止まった段階で、読み取りは一旦ストップしましょう。



そこまで!止め!
構造が苦手な人の戦い方
問題図に積極的に書き込みして、理論よりもイメージから展開する。
2.解説文を丁ねいに読み、必要な言葉をチョイスする
答えではなく解説を読む!


問題文と”にらみ合う”のは5分まで。
5分経った後は、次に解説文を読んでいきましょう。
その際に、図に書き込んだスケッチと照らし合わせると解説を読みやすくなります。


必要な言葉をチョイスする
- 必要な公式
- 必要な考え方
- 必要な図の取り出し
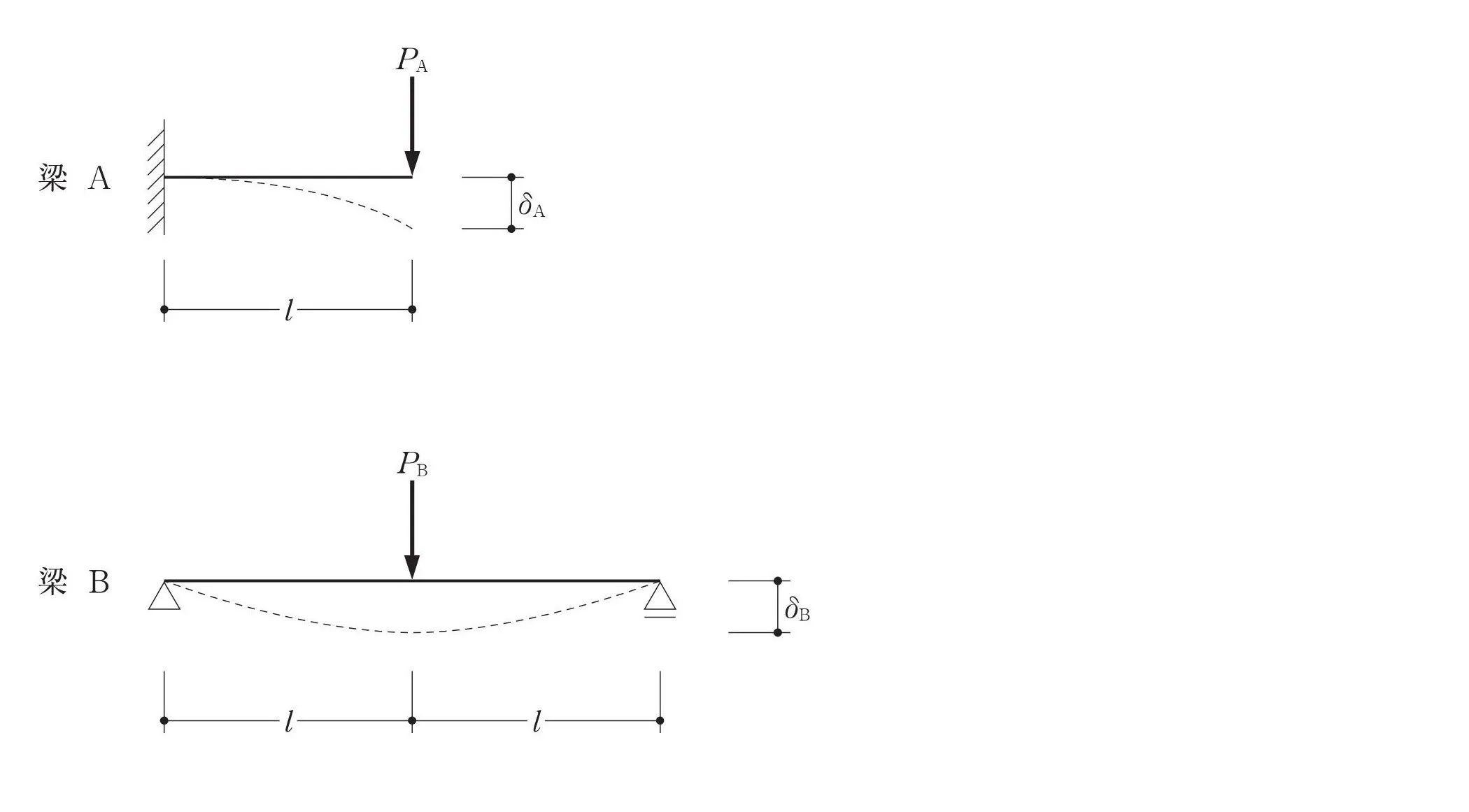

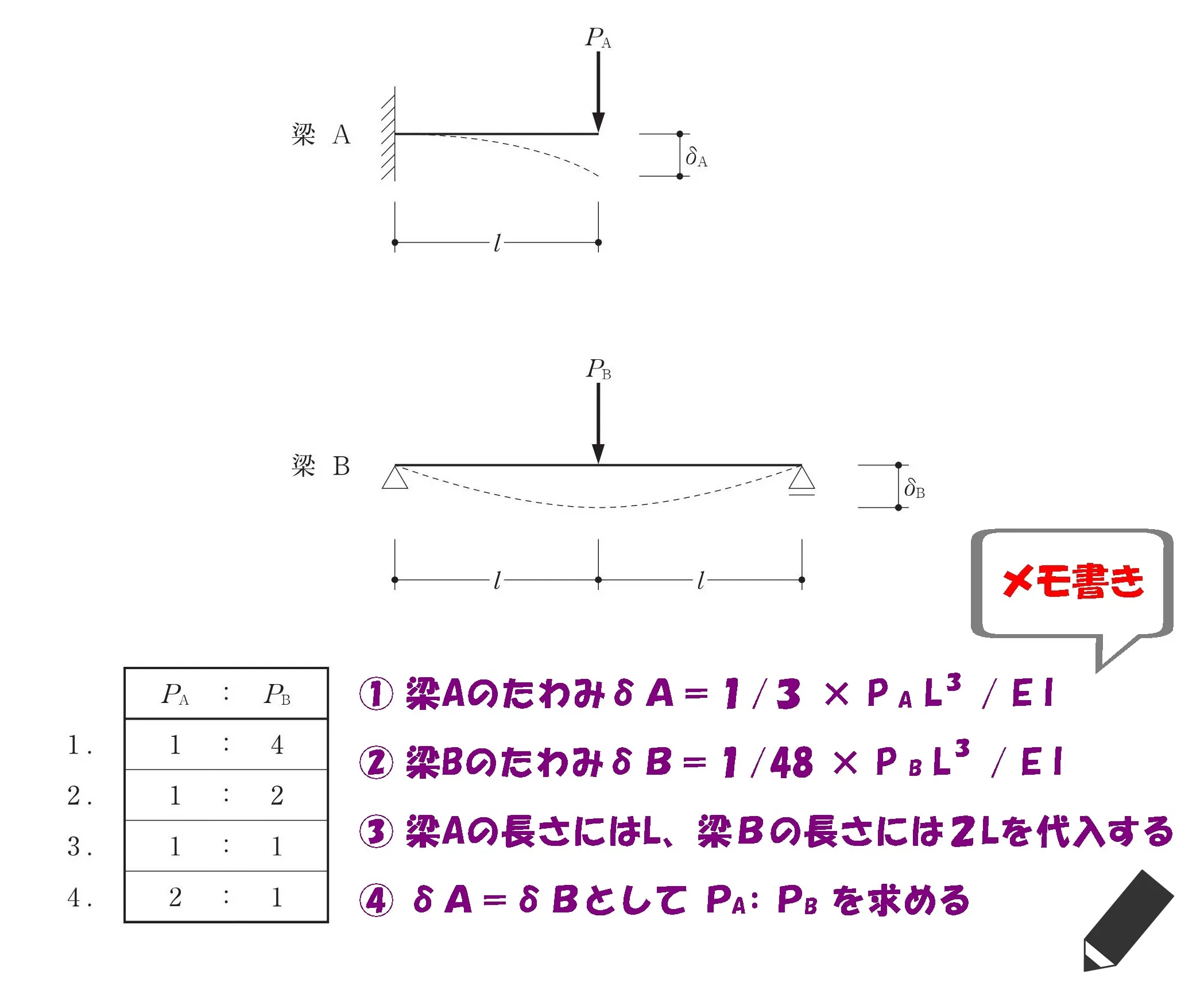
$$δa=\frac{ PaL^3 }{ 3EI },δb=\frac{ Pb(2L)^3 }{ 48EI }$$
$$問題文より,たわみ:δa=δb(イコールで結ぶ)$$
解説文の中から要点を洗い出しましょう。
ここでは「解き方・解く手順」に集中して、計算過程などは読み飛ばしても大丈夫です。
過去問題を攻略するための武器や材料をそろえる。
3.問題を解くための手順や公式を小さくまとめる




(解き方の手順は箇条書きにする。)
解説文の要点をまとめて、箇条書きにしてまとめます。
情報が大きくなり過ぎないように内容をコンパクトに収めることもトレーニングです。
言葉を厳選して、”自分だけが分かる表現”でも良いので小さくまとめましょう。



理論は小さくまとめる。
過去問題を攻略するための武器や材料をそろえる。
ステップ②:手順や公式を問題文の余白に箇条書きする
メモは余白に書き込む
ここからは、「問題集の仕込み」となる作業に移っていきます。
過去問題集を開く


過去問題集は、「メモを書き込める余白のあるもの」を選んで準備しましょう。
問題文の余白にメモする
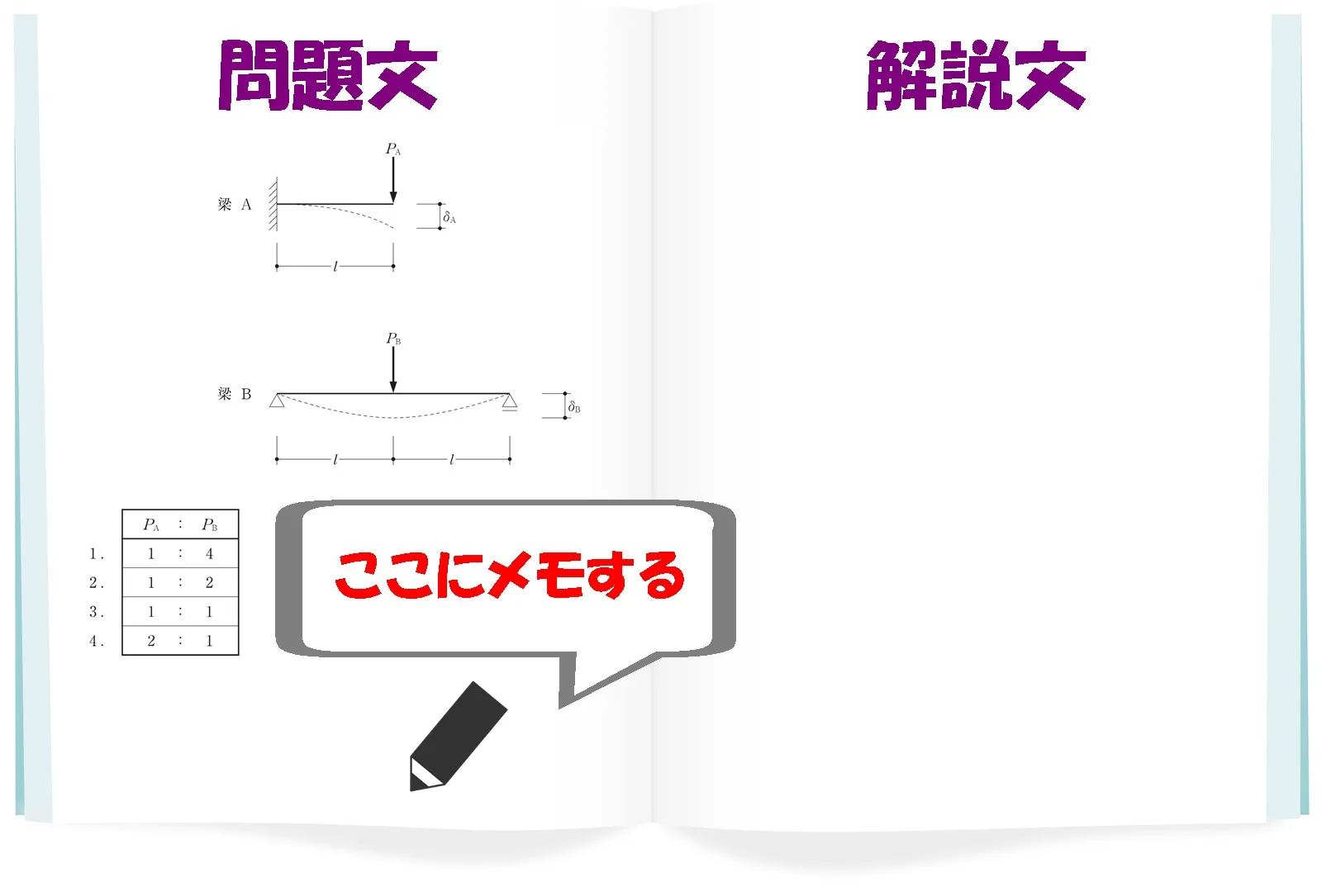

ステップ①でまとめた「問題を解くための手順や公式」を余白に書き込む。
箇条書きにしてメモする


ステップ①でまとめた「問題を解くための手順や公式」を余白に書き込む。
(メモ書きスペースがない場合は、付箋で対応する⇩)
メモのスペースがない場合




メモを書くスペースがない場合は、付箋「Post-it」を貼って余白の代わりにします。
付箋は解説のページに、「解答番号に被せる」ように貼ると良いでしょう。



答えが先に見えてしまうと
やる気と情熱が冷めるよね?
メモは「自分の言葉」で書き込む


解説文に記載されてあるマニュアル的な定型文は、何度読んでも覚えられないもの。
その点、自分の言葉で書き残した文字は「自分なりの感覚がある」ため、記憶に残りやすくなります。



余白にメモを書き込む。
「自分の言葉で書いた手書きの文字」は記憶に残りやすい。
ステップ③:箇条書きしたメモに習って繰り返し問題を解く


メモをもとに、いざ攻略といきましょう。
攻略のための必要な材料はすでにそろっていますよね?
問題を解くための手順や公式を頼りに、過去問と向き合っていきましょう。
メモに習って攻略する
- 問題文を丁ねいに読む。
- 余白に書き残したメモを読む。
- メモに習って問題を解いてみる。
1.問題文を丁ねいに読む
問題文
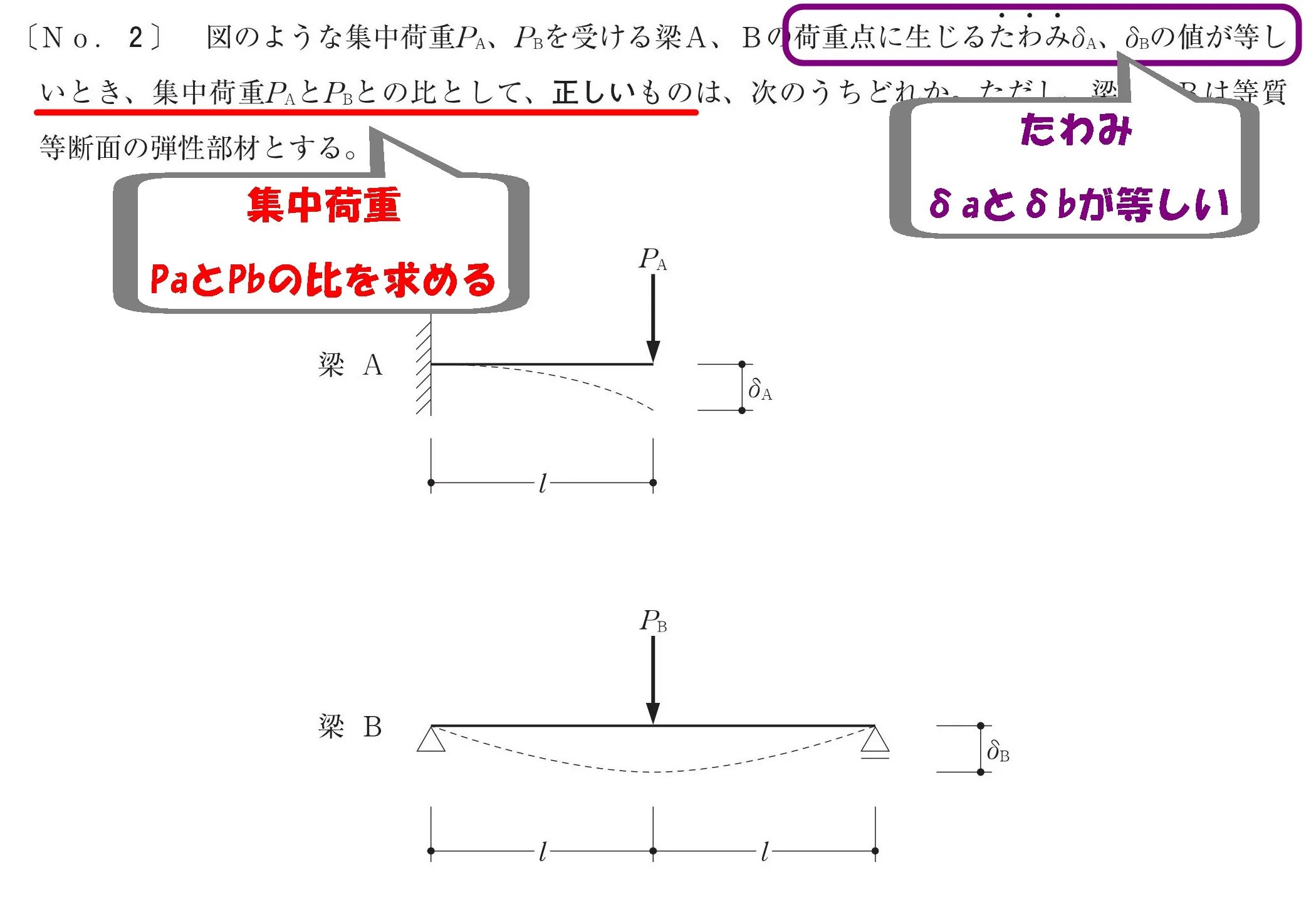

構造が苦手な人の戦い方
問題図に積極的に書き込みして、理論よりもイメージから展開する。
2.余白に書き残したメモを読む
メモを読み返す




書き残したメモを読み返して、解く手順を再確認しましょう。



メモを確認しよう。
3.メモに習って問題を解いてみる
メモに習って問題を解く


メモを頼りに問題を解くことで、「攻略のための必要な知識や考え方」を効率良く学べます。
この方法は、勉強を苦手とする人が自力でまえに進むための「アシストをする」役割といえます。
勉強法の目的
書き残したメモは、自力で攻略法を身につけるためのアシストになる。
知識は自分の言葉でモノにする
- 自分の言葉で解説をまとめる。
- 自分の言葉で攻略法を書き込む。
- 自分の言葉で思考して問題を解く。
勉強方法3ステップを通してやり遂げたことは、以上の3つになります。
「自分の言葉で・・」そのひとつひとつは、手間のかかる作業かもしれません。
しかし「自分の言葉」でまとめた情報というのは、自分にとって”生きた知識”となるのです。
”生きた知識”として定着させることで、その記憶は長期にわたって保存されるため、確かな学習効果が得られるでしょう。



生きた知識、それは財産。
勉強ステップは継続することが大事
- メモに習って問題を解く。
- 解説文をもう一度、読み返す。
- 不足している内容をメモに書き足す。
何度も問題を解きながら、このルーティーンを繰り返します。
手書きのメモが増えていくにつれて蓄積されたものが、「知識の財産」となるのです。
このステップを繰り返しているうちに、理論的な知識も次第に身に付くでしょう。
「解く手順を読み、解き方を理解して、攻略法として覚える」
身体に染み込ませるように繰り返し問題を解くことで、不安も自信に変わるはずです。




解ける!解ける!
攻略法が見えてきたぞ!
解けない問題には時間を浪費しない
解説文を先に読んでも良いのだろうか?
そのように疑問に思われる方もいるかと思います。


自力で問題を解ける方であれば、自己完結するに越したことはありません。
しかし、戦う武器や材料がない人にとっては苦痛以外の何ものでもないですよね?
何も分からずに堂々巡りしている時間は、何も生み出せないので単純にもったいないことです。


構造を制すれば、
もう怖いものなどない。


構造を制する!
勉強が苦手な人には「苦手な人なり」の取り組み方がある。
勉強法3ステップ
| ステップ① | 問題を解くための手順や公式をまとめる。 |
| ステップ② | 手順や公式を問題文の余白に箇条書きする。 |
| ステップ③ | 箇条書きしたメモに習って繰り返し問題を解く。 |



目指せ!構造の猛者。
ラーメンをぶった斬る!



ゴリゴリの構造マニアは
ちょっと近寄りがたい。



公式!数学!物理!
力の分布!モーメント図!




この動画を YouTube で視聴
一級建築士:構造力学の勉強(独学)を楽にする5つのコツ


構造力学のシンプルな勉強法3ステップをお伝えしました。
しかし、どのような勉強法であっても「継続なしでは効果ゼロ」です。
この勉強法をより継続させるためには、負担になるものを取り除くことです。
ここからは「構造の勉強を楽にする」5つのコツを授けましょう。



お主よ・・・
これで終わりだと思うなよ。
公式は「単位」と合わせて覚える


(例)
$$速度(m/s)=\frac{ 距離(m) }{ 時間(s) }$$
ここでは誰もが知っている分かりやすい公式として、速度(m/s)を例に説明します。
速度を求める公式の場合、速度の単位が「m/s」であれば移動距離(m)÷時間の単位(s)も「m/s」になりますよね?
このときに速度の単位「m/s」さえ覚えていれば、その公式は単位の「m/s」から「距離(m)/時間(s)」と予測することが出来るのです。



単位に心を向けるのだ。
公式と単位はセット
求める数値の単位は、その公式を構成する単位でもある。
それでは、本題です。
「車の速度」と「移動距離」から「所要時間を求める公式」を作りなさい。
という問題が出題されたときに、すぐに反応できるでしょうか?
おそらく多くの人が、「あれあれ?」っと戸惑うのではないかと思います。
このときにそれぞれの”言葉と単位を紐づける”と公式を予測することが出来るのです。


公式と単位はセット
求める数値の単位は、その公式を構成する単位でもある。
速度の単位は「m/s」、距離の単位は「m」、そして時間の単位は「s」ですよね?
求める所要時間の単位は「s」なので、「s」の単位になるように公式を組み立てるのです。
$$所要時間(s)=\frac{ 距離(m) }{ 速度(m/s) }=単位:(s)$$
それぞれの単位に注目すると、求める時間の単位「s」になるような式が成り立ちますよね?
この”言葉と単位を紐づける”という考え方は、構造力学のすべての公式に当てはまります。



単位を極めれば
恐れることはない。
N/mの単位に注目!
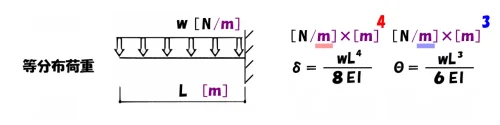

要チェック
一級建築士【構造力学】計算問題に挑戦して攻略ポイント(応力と応力度)
一級建築士|構造力学のよく間違える公式の覚え方、(単位で公式を覚える)
公式は比例・反比例の関係と合わせて覚える


要チェック
一級建築士【構造力学】計算問題に挑戦して攻略ポイント(比例・反比例)
構造力学では「条件の異なる構造物が A・B・C とあり、それぞれの求める数値の大小関係を求めなさい」という問題が、毎年のように出題されます。
このような出題に対応するには、公式の本質的な理解を必要とします。
【弾性座屈荷重Pの公式の例】
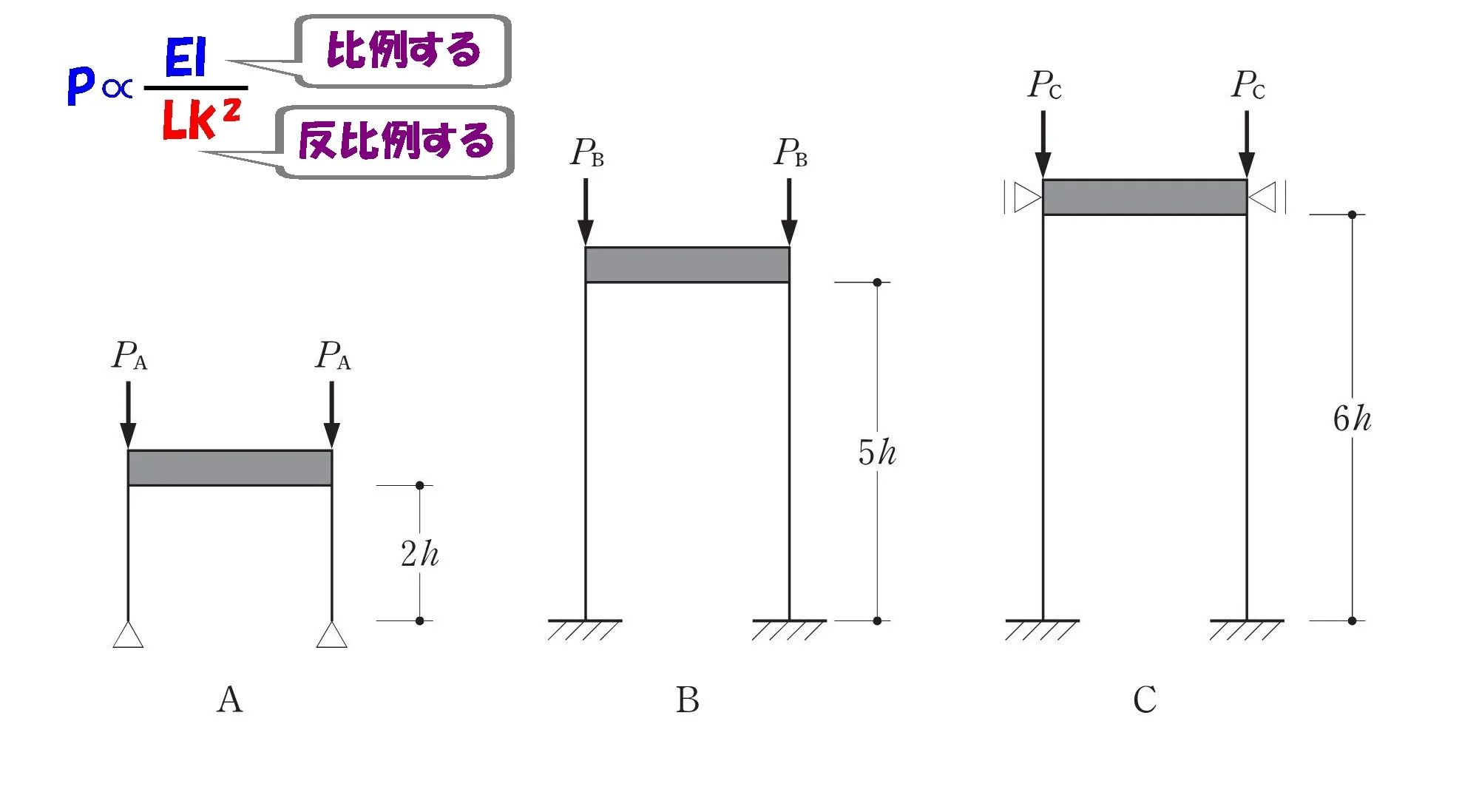

$$P=\frac{ \pi^2*EI }{ Lk^2 }⇨P\propto\frac{ EI }{ Lk^2 }$$
弾性座屈荷重Pは曲げ剛性EIに比例し、座屈長さLkの2乗に反比例する
このように、それぞれの言葉と関係性をセットにするで「公式の本質的な理解」が身に付くのです。
比例・反比例を読み解く
- 公式の本質的な理解
- 数値の比較問題への対応力
- 文章問題において公式を言葉で読み解く力
公式のそれぞれの比例・反比例の関係は、比較問題を攻略するための材料となる。
桁数の多い計算式は、かっこ(・)でくくる


構造問題では桁数の多い計算を余儀なくされることがありますよね?
こんなときに「電卓が使えれば・・・」と思うこともあるかもしれません。
しかし、電卓はいっさい必要ありません。
ここでは、中学生時代の数学で習った「かっこ(・)でくくる」手法が大活躍します。
計算式をかっこ(・)でくくることで、「暗算する」を「分解する」に置き換える。
「かっこ(・)でくくる?」

桁数の多い計算式をまえに、”暗算するのが苦痛”だという人は多いかと思います。
ところで、高校時代の数学で「因数分解」を習ったことは覚えていますでしょうか?
計算式を共通の数値でまとめて、かっこで(・)くくるという手法です。
かっこ(・)でくくる
- 数値を分解する。
- 計算式をスリム化する。
- 暗算処理を分解処理に置き換える。
計算処理テクニックの紹介
$$例1:6^3=(2*3)^3=2^3*3^3$$
$$例2:6000=6*10^3=2^3*3^3*10^3$$
(かっこでくくった後に共通部分の処理をする)



これは覚えておこう。




計算式をかっこ(・)でくくることで、「暗算する」を「分解する」に置き換える。
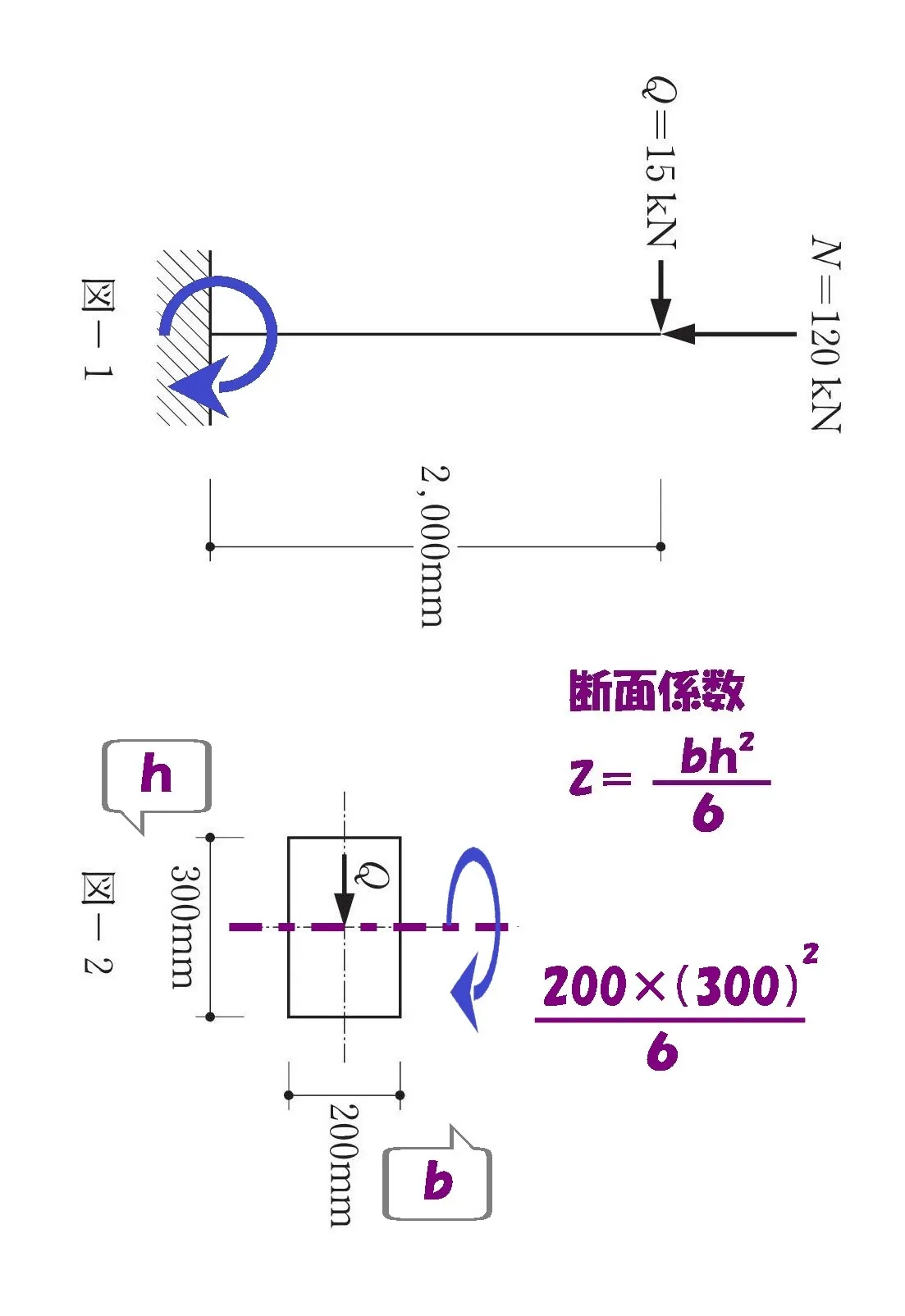
曲げ応力度の計算式の例
クリックすると開きます。
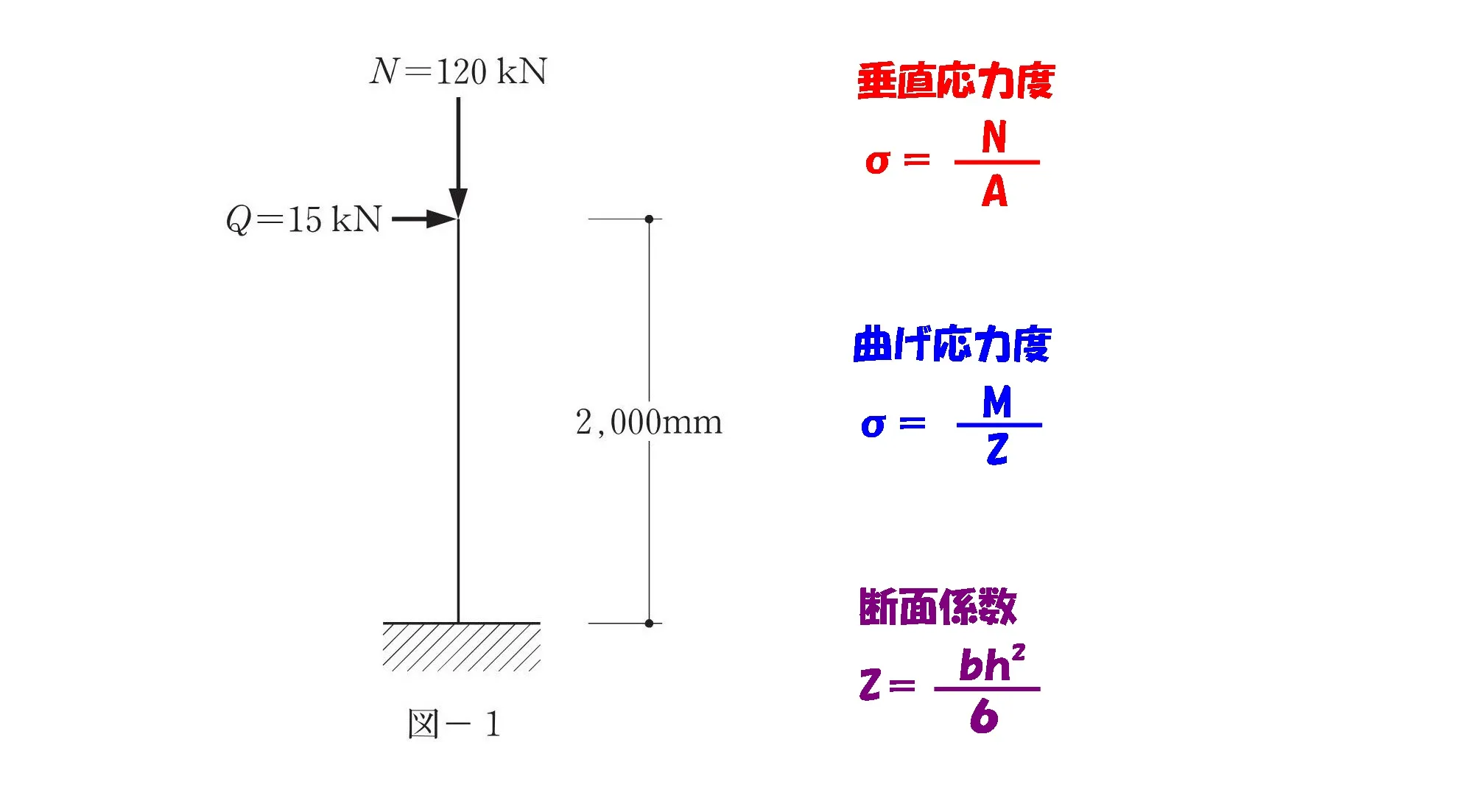

$$曲げ応力度:\sigma=\frac{ M }{ Z }より$$$$\frac{ 15000*2000 }{ 200*(300)^2/6 }=\frac{ 15*10^3*2*10^3 }{ 200*(300)^2/\underline{6} }=\frac{ 15*10^3*2*10^3*\underline{6} }{ 200*(300)^2 }$$$$(⇩かっこでくくる⇩)$$$$=\frac{ \underline{(15)}*10^3*2*10^3*\underline{(6)} }{ \underline{200*(300)^2} }=\frac{ \underline{(3*5)}*10^3*2*10^3*\underline{(2*3)} }{ \underline{200*300*300} }$$$$=\frac{ \underline{(3*5)}*2*\underline{(2*3)}*10^6 }{ \underline{(2*3*3)}*10^6 }=\frac{ \underline{(2*3*3)}*2*5*\underline{10^6} }{ \underline{(2*3*3)}*\underline{10^6} }=2*5=10[N/mm^2]$$



暗算処理を分解処理に、
計算式をかみ砕いてみる。
計算は頑張らなくて良い
- 数値を分解する。
- 計算式をスリム化する。
- 暗算処理を分解処理に置き換える。
計算式をかっこ(・)でくくることで、「暗算する」を「分解する」に置き換える。
勉強期間中は、計算する作業を省略してもよい


一級建築士学科試験Ⅳ・Ⅴの所要時間はご存知でしょうか?
構造と施工の2科目合わせて「2時間45分」
模擬試験を受けたことのある方は分かると思いますが、この科目はとにかく時間を持て余します。



構造問題を制ばい
全力で斬りまくる!



残り時間は
まだ1時間あるよ~。



時間が余り過ぎ。
もうやることがない。
構造の勉強スタイル
解き方の手順と方程式を確立できれば、次の問題へと進む。


タイムマネジメント
- 構造30問
- 計算問題7問(5分/問)
- 文章問題23問(90秒/問)
- 施工25問
- 計算問題1問(5分/問)
- 文章問題24問(90秒/問)
2科目の解答時間の合計を試算します。
5分×7問+1.5分(90秒)×23問+5分×1問+1.5分(90秒)×24問=1時間50分30秒。
2時間45分-1時間50分30秒=余り時間”54分30秒”となります。
1時間弱というのは余り過ぎですよね?



え?もう終わり?



燃え尽きた・・・
余韻にひたるしかない。


つまり、構造と施工の2科目においては「時間が足りない」ということはあり得ません。
試験問題の解答を終えて、計算問題のチェックを済ませて、時間を持て余して寝ている受験生が多くいるような状況です。
このような実態であることから、構造力学の計算問題には「時間を十分に使える」ということです。


それ必要?
計算の練習はしなくても良い。
計算が苦手な人であっても制限時間内に必ず解答できます。
そのような環境であるので「計算力を鍛える必要性」はありません。
つまり、勉強期間中における構造力学の勉強法は「解き方の手順を確立する」こと。
「攻略法の確立」に時間を使いつつ、計算処理という作業は省略してもOKといえるでしょう。



解き方を整理して
力学を完全武装しよう。
「解き方の手順と方程式を確立できれば、次の問題へと進む」
そのテンポで勉強を進めることで、攻略に必要な力を効率良く習得できるようになります。
解き方の手順と方程式を確立できれば、次の問題へと進む。
比較問題は2つずつ比較して消去法で攻める


構造力学では「条件の異なる構造物が A・B・C とあり、それぞれの求める数値の大小関係を求めなさい」という問題が、毎年のように出題されます。
このような出題において「A・B・C のすべてを計算」した後に、その計算結果を比較するという作業はやりたくないですよね?
比較問題であっても、ゴールは変わりなく「4択の中から正しい答え」を導くことになります。
2つずつ比較する


【A・B・Cを比較する方法】
- AとBを比較する
- BとCを比較する
- A・B・Cの大小関係が決まる
比較問題においては、3つの数値を同時に比較するよりも、2つずつ比較して答えを絞り込むほうが、圧倒的に楽になります。



2つずつ選んで比較する。


比較対象が少なくなる。



消去法で答えは絞られる。
ここが狙い!
比較問題は2つずつ比較することで、大小関係を判断するための計算過程を省略できる。
断面二次モーメントの比較例
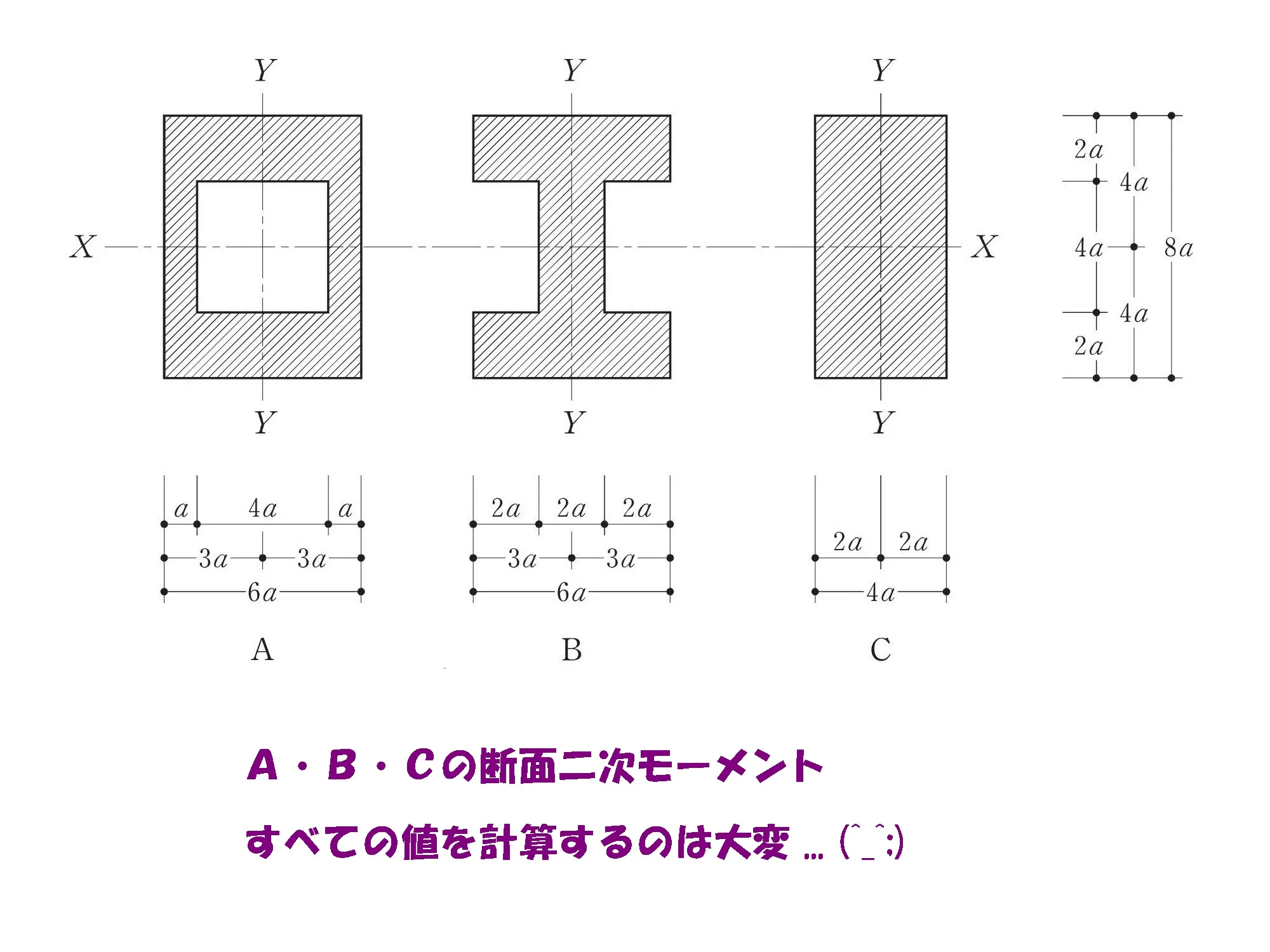

$$断面二次モーメント:I=\frac{ bh^3 }{ 12 }$$
断面 A・B・C すべての部材に公式を当てはめて計算するのはとても大変な作業になります。



嫌な予感が・・・
ノイローゼになりそう。
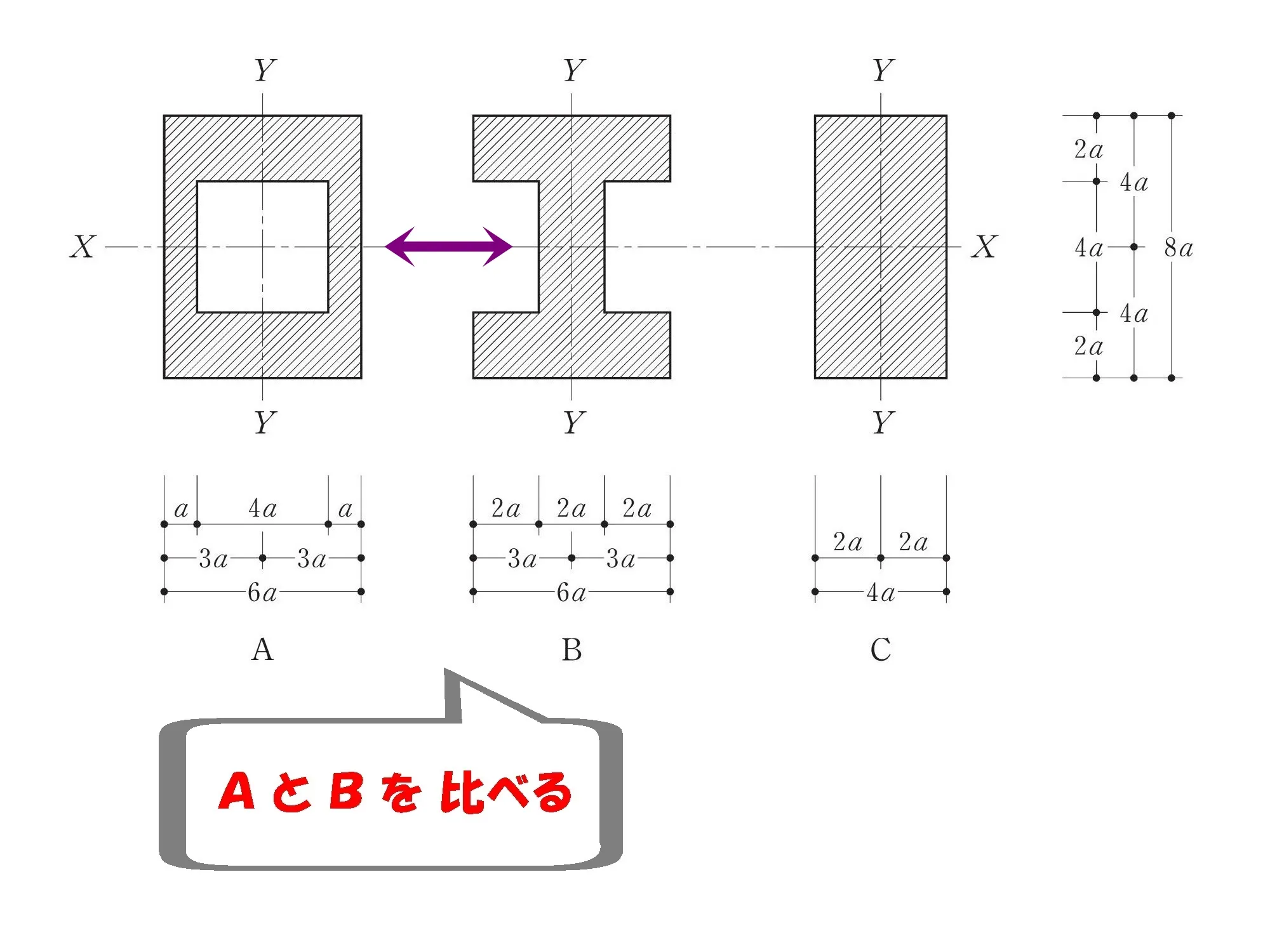




AとBを比べる。





BとCを比べる。
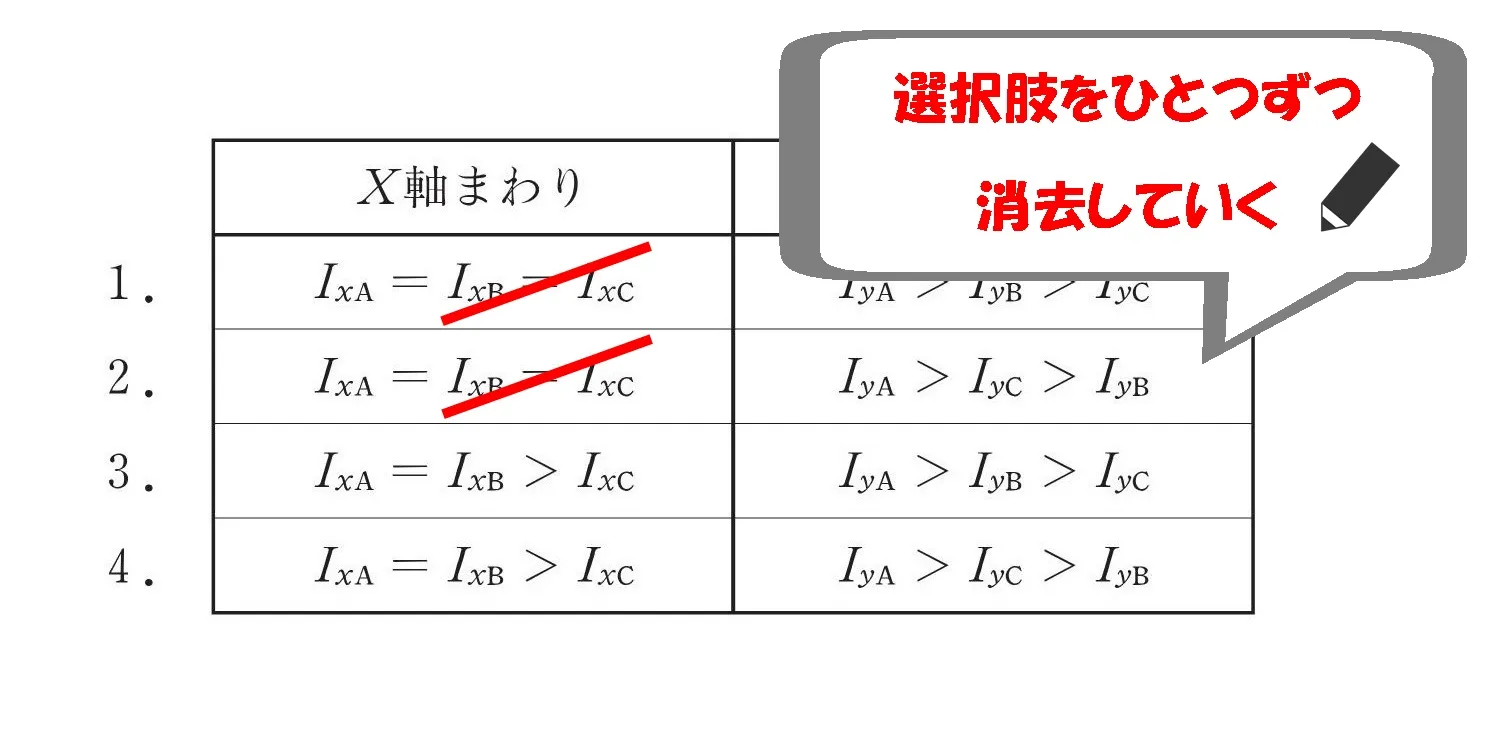

4択の中から選択肢を消去していくと、このようなイメージになります。
紹介した「2つずつ比較して消去する」メリットについて、おさらいしましょう。
比較問題の攻略法
- AとBを比較する
- 選択肢を消去する
- BとCを比較する
- 選択肢を消去する
- 答えを1つに絞り込む
2ずつ比較するメリット
- AとBの共通部分が増える
- 共通部分を除外して比較する
- AとBの比較対象となるのは一部のみ
- 比較対象の部分を最小限にする
- 計算のボリュームが減り、時短になる
比較問題は2つずつ比較することで、大小関係を判断するための計算過程を省略できる。
断面二次モーメントの比較
クリックすると開きます。


$$断面二次モーメント:I=\frac{ bh^3 }{ 12 }より$$
$$Ixa:Ixb(比較する)$$$$\frac{ 1 }{ 12 }*\{6a*8a^3-\underline{4a}*4a^3\}:\frac{ 1 }{ 12 }*\{6a*8a^3-\underline{2*2a}*4a^3\}$$$$\frac{ 1 }{ 12 }*\{6a*8a^3-4a*4a^3\}:\frac{ 1 }{ 12 }*\{6a*8a^3-4a*4a^3\}$$$$1:1(左右で同じ数値の式になる)⇨Ixa=Ixb$$


$$断面二次モーメント:I=\frac{ bh^3 }{ 12 }より$$
$$Ixb:Ixc(比較する)$$$$\underline{\frac{ 1 }{ 12 }}*\{6*8^3-2*2*4^3\}:\underline{\frac{ 1 }{ 12 }}* 4*8^3$$
$$(6*\underline{8^3}-2*2*4^3):4*\underline{8^3}$$
$$(6*\underline{2^3*4^3}-4*\underline{4^3}):4*\underline{2^3*4^3}$$
$$\underline{4^3}*(6*2^3-4):\underline{4^3}*4*2^3$$
$$(6*2^3-4):4*2^3⇨(6*2*\underline{2^2}-\underline{2^2}):4*2*\underline{2^2}$$
$$\underline{2^2}*(6*2-1):\underline{2^2}*4*2⇨(6*2-1):4*2$$
$$(6*2-1):4*2⇨11:8=Ixb>Ixc$$
$$Ixa=Ixb及びIxb>Ixcより,Ixa=Ixb>Ixc$$



計算式を並べないで、
ノイローゼになりそうです。
比較問題は2つずつ比較することで、大小関係を判断するための計算過程を省略できる。


この動画を YouTube で視聴
a =1、L =1、h=1を代入する


これは、公式を使って計算処理するうえで「アルファベット」を省いて式を簡略化する方法です。
計算式は、「答えとなる未知数以外のアルファベット」を省いて簡略化できる。
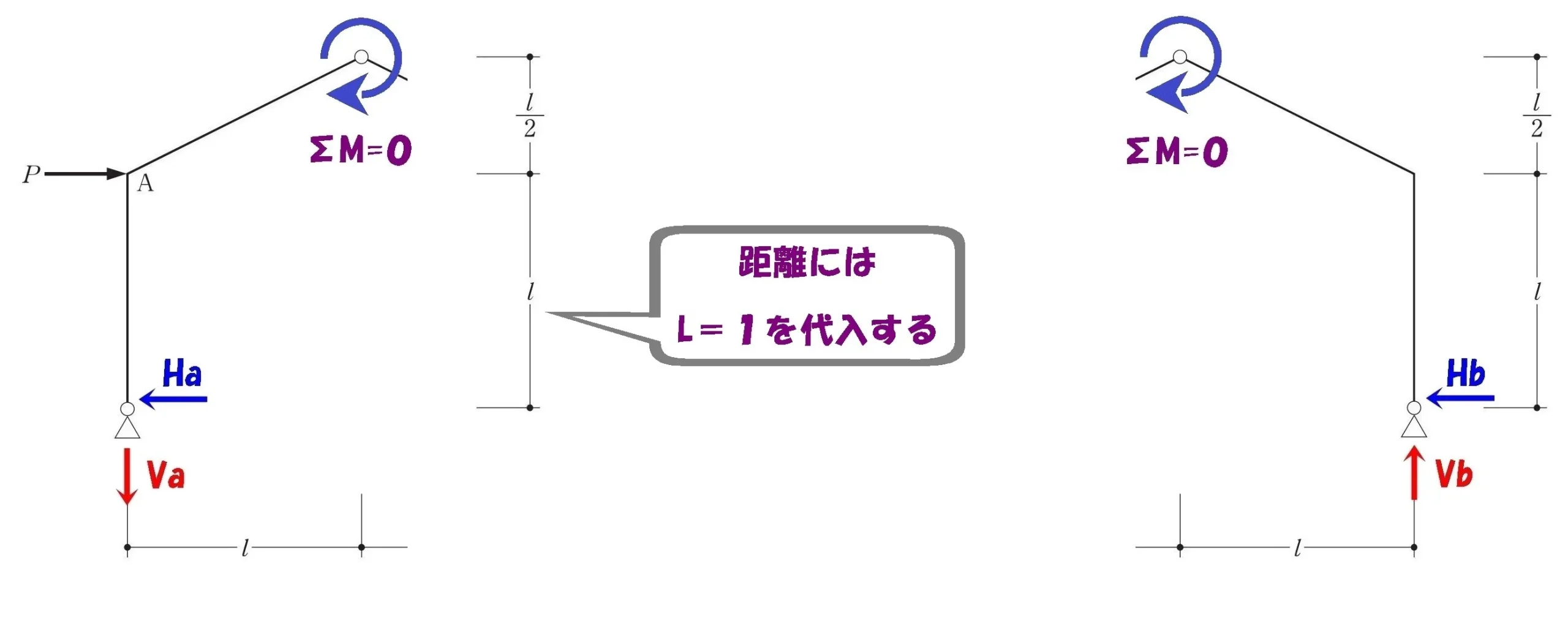

1を代入できるもの
- L:3ヒンジラーメンの部材の長さ
- a:断面二次モーメントを求める部材の寸法
- h:弾性座屈荷重の比較問題における柱の長さ
これらの記号には「1」を代入できることは、ご存知でしょうか?
構造力学の勉強では、計算に費やす時間と労力をできるだけ減らしたいもの。
答えとなる未知数以外の「L」「a」「h」に1を代入することも有効な手段です。
要チェック
一級建築士【構造力学】計算問題に挑戦して攻略ポイント(3ヒンジラーメン)



これは使える!
記号に1を代入できないもの
- 問題文より答えとなる未知数
- ラーメン架構の柱脚に発生する反力
- ラーメン架構やトラスなどに発生する軸力
計算式は、「答えとなる未知数以外のアルファベット」を省いて簡略化できる。
大小関係において失敗しない答えの並べ方


構造力学では「条件の異なる構造物が A・B・C とあり、それぞれの求める数値の大小関係を求めなさい」という問題が、毎年のように出題されます。
- 問題文より大小関係を求める
- 答え合わせで、何故か間違えている
- 解説文を読み、間違いを探してみる
- 方程式は合っているのに理由が見つからない
- 結局は「大小関係の並びをミスっている」というオチ
間違い探しに堂々巡りした「あの無駄な時間」にガックリ来ることもありますよね?
大小関係を求める問題で意外にもやってしまいがちな、並べ間違いによる失敗の話です。



これは恥ずかしい・・
穴があったら入りたい。



疲れているときに
意外にあるあるだよね。
構造Ⅳの試験はその日の終盤になるため、疲労のピークを迎えたときにミスは起こりがち。
せっかく正しい答えを導いたのに、最後の詰めの甘さでこれをやってしまうと悔やみ切れません。



こころの乱れ・・・
まだまだ修行が足りぬ。
答え並べに失敗しがちな問題3選


大小関係を求める出題
- 座屈荷重
- 水平剛性
- 固有周期
A・B・Cの数値を並べる出題の多い3項目です。
この中でも特に間違いが起こりやすいのは”座屈荷重”、これを例に「失敗しない答えの並べ方」をお伝えしましょう。
【座屈荷重の並べ方が間違えやすい理由】
$$P\propto\frac{ 1 }{ Lk^2 }$$
座屈荷重Pは、座屈長さLkの2乗に反比例することになります。
公式から「Pの大小関係とLkの大小関係は逆になる」という理由から間違えやすいわけです。



その通り!あるある!


失敗しない答え並べ方


【失敗しない答えの並べ方】
- 選択肢に習って不等号を先に書いておく。
- 数値を並べたあとに対応する記号を並べる。
- 並べた記号をそのまま選択肢と対比させる。
注意点
※座屈荷重の問題でPを並べる場合は、注意が必要。
大小関係は、数値を並べたあとに対応する記号を並べる。
弾性座屈荷重の並べ方の例



心を静かに・・・
身構えるのだ。


求めたABCのそれぞれの座屈長さの”数値”(3h・4h・5h)を不等号「<」に習って並べる。
$$P\propto\frac{ 1 }{ Lk^2 }$$
注意点
Pの大小関係とLkの大小関係は逆になる。
これを踏まえて、選択肢の不等号「>」とは逆の「<」方向の不等号を書いておく。


問題図を確認しながら、数値に対応したアルファベット「Lka・Lkb・Lkc」を書き込む。


「Lka・Lkb・Lkc」に対応したアルファベット「Pa・Pb・Pc」を書き込む。
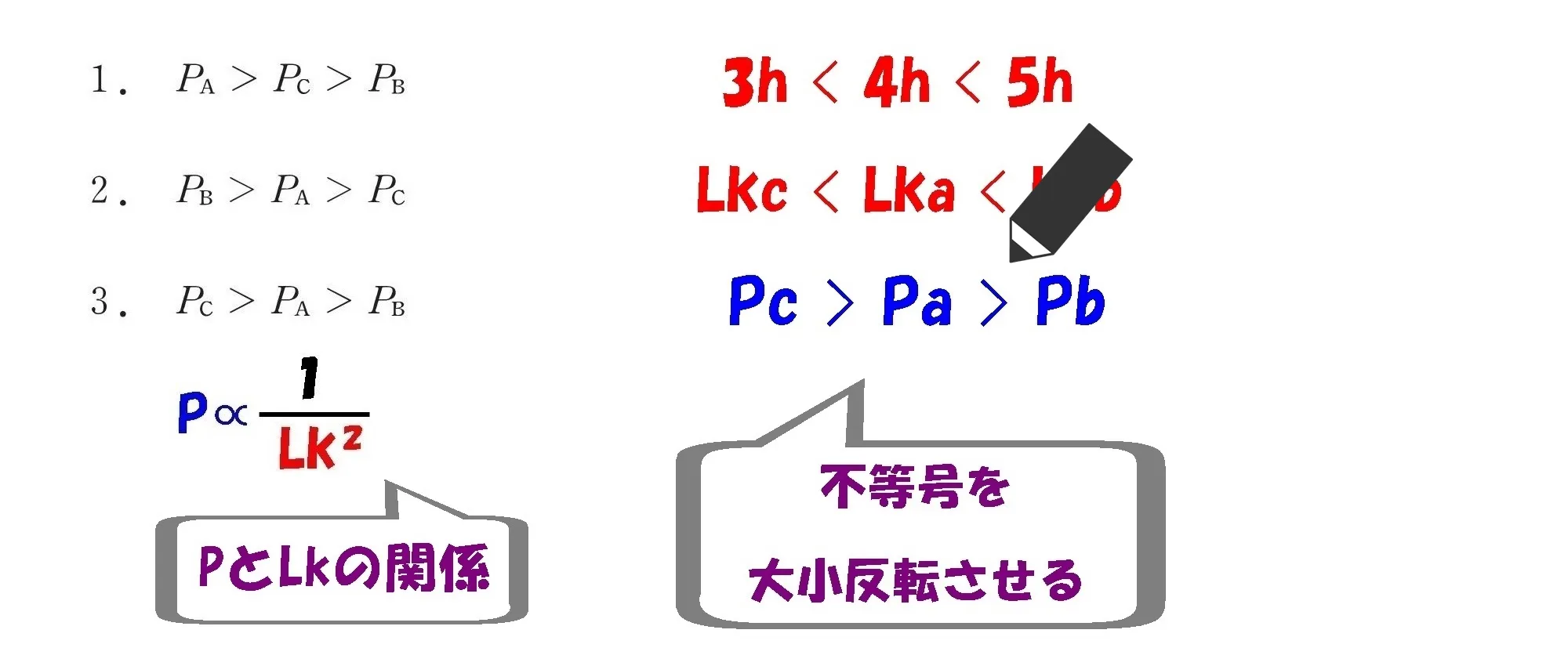

$$P\propto\frac{ 1 }{ Lk^2 }$$
注意点
Pの大小関係とLkの大小関係は逆になる。
これを踏まえて、Lkの「<」の不等号とは逆向きの「>」の不等号を書き込む。
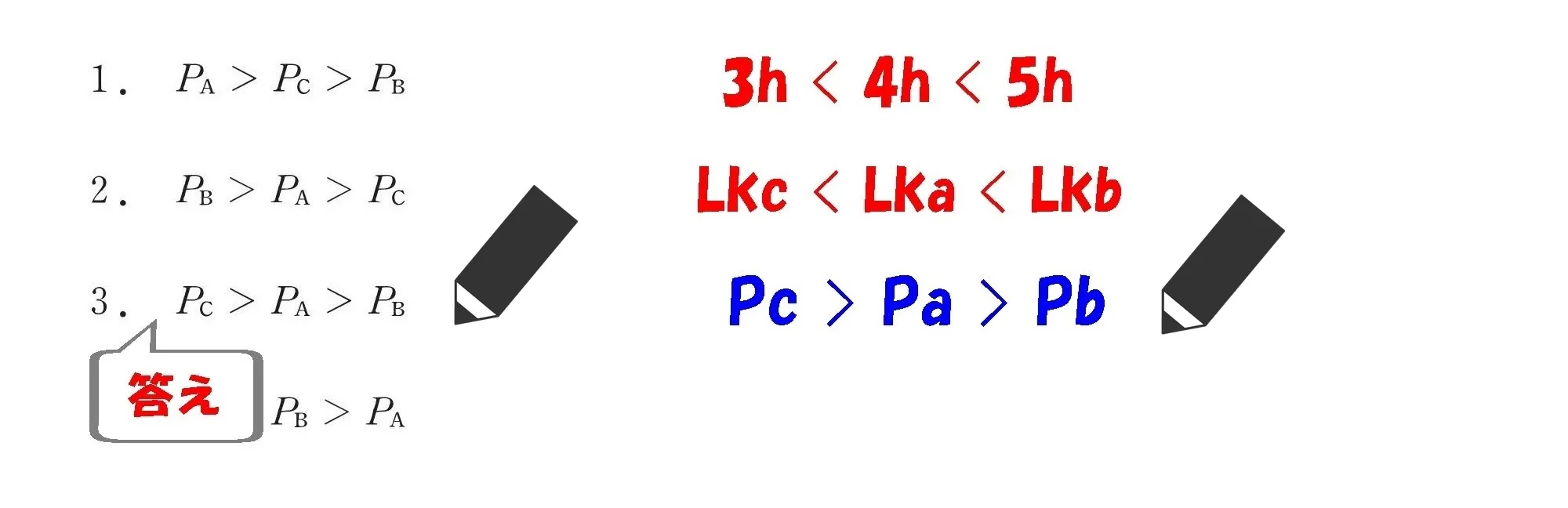

並べた記号「Pc>Pa>Pb」が、そのまま選択肢の答えになる。
「数値を並べたあとに対応する記号を並べる」
この手順によって、答えの並べ替えによるヒューマンエラーを防ぐことが出来るでしょう。
要チェック
一級建築士【構造力学】計算問題に挑戦して攻略ポイント(弾性座屈荷重)



ありがたい・・・
私の努力が報われます。
大小関係は、数値を並べたあとに対応する記号を並べる。


この動画を YouTube で視聴
実践1:比較問題は2つずつ比較して答えを求める
Mission1


勉強を継続させるために「負担になる要素を取り除く」のは重要なこと。
ここからは「構造力学の勉強を楽にするコツ」の3つを使って問題を解いてみます。
「問題がよく分からない?」という方も、今後の為に知っておくときっと役に立つでしょう。



AとBを比べる



BとCを比べる
力学の勉強を楽にするコツ
- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。
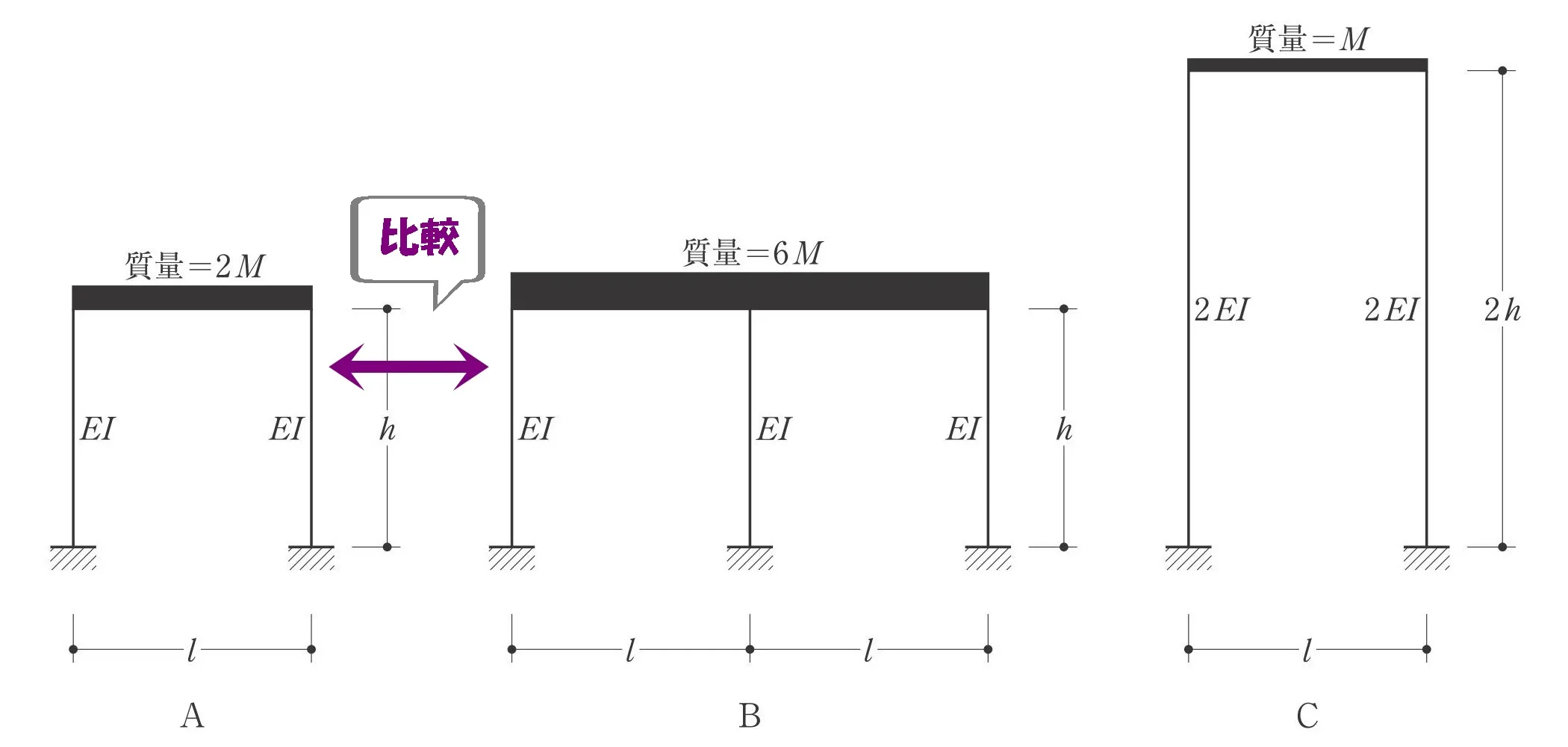
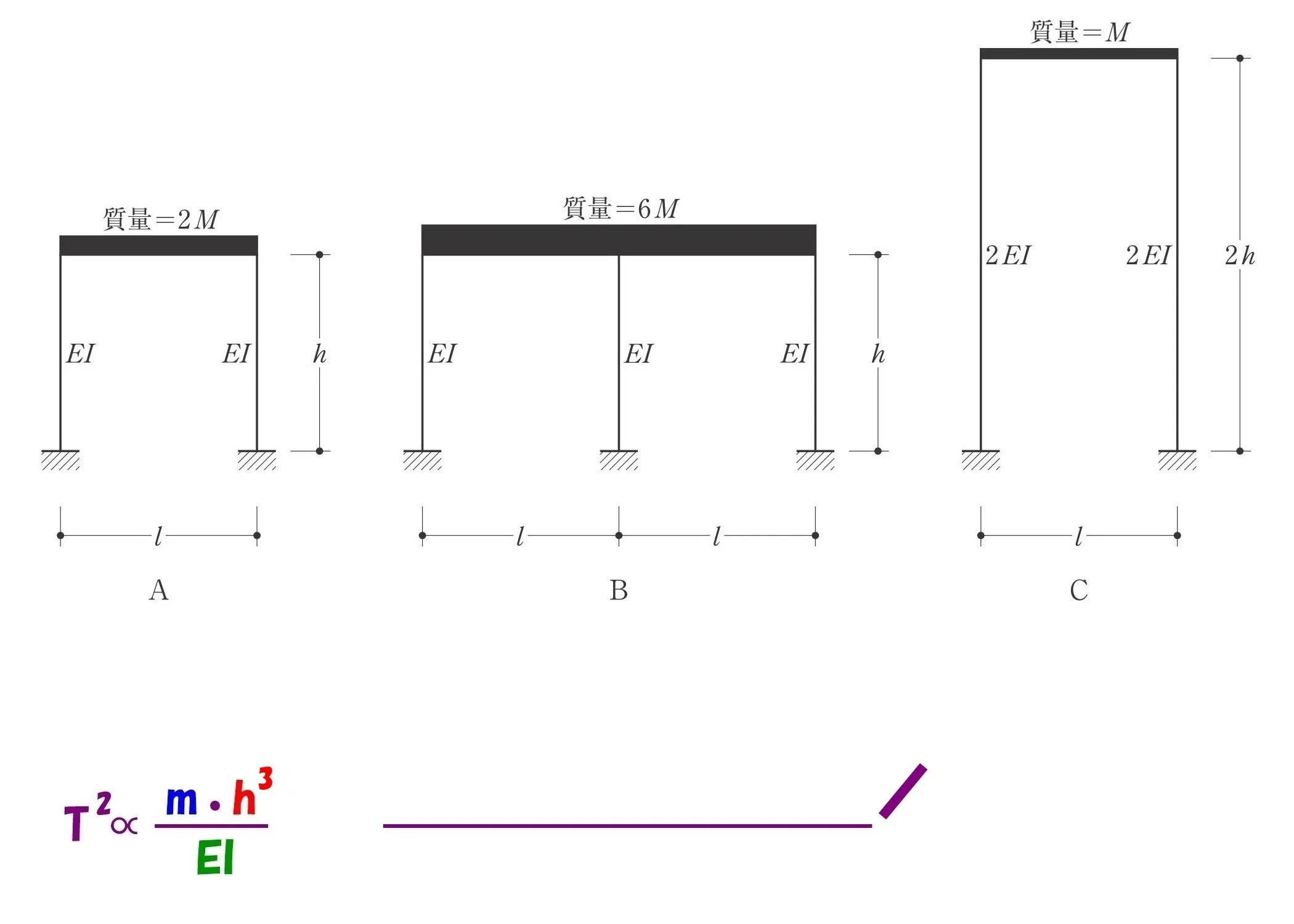
固有周期の比較
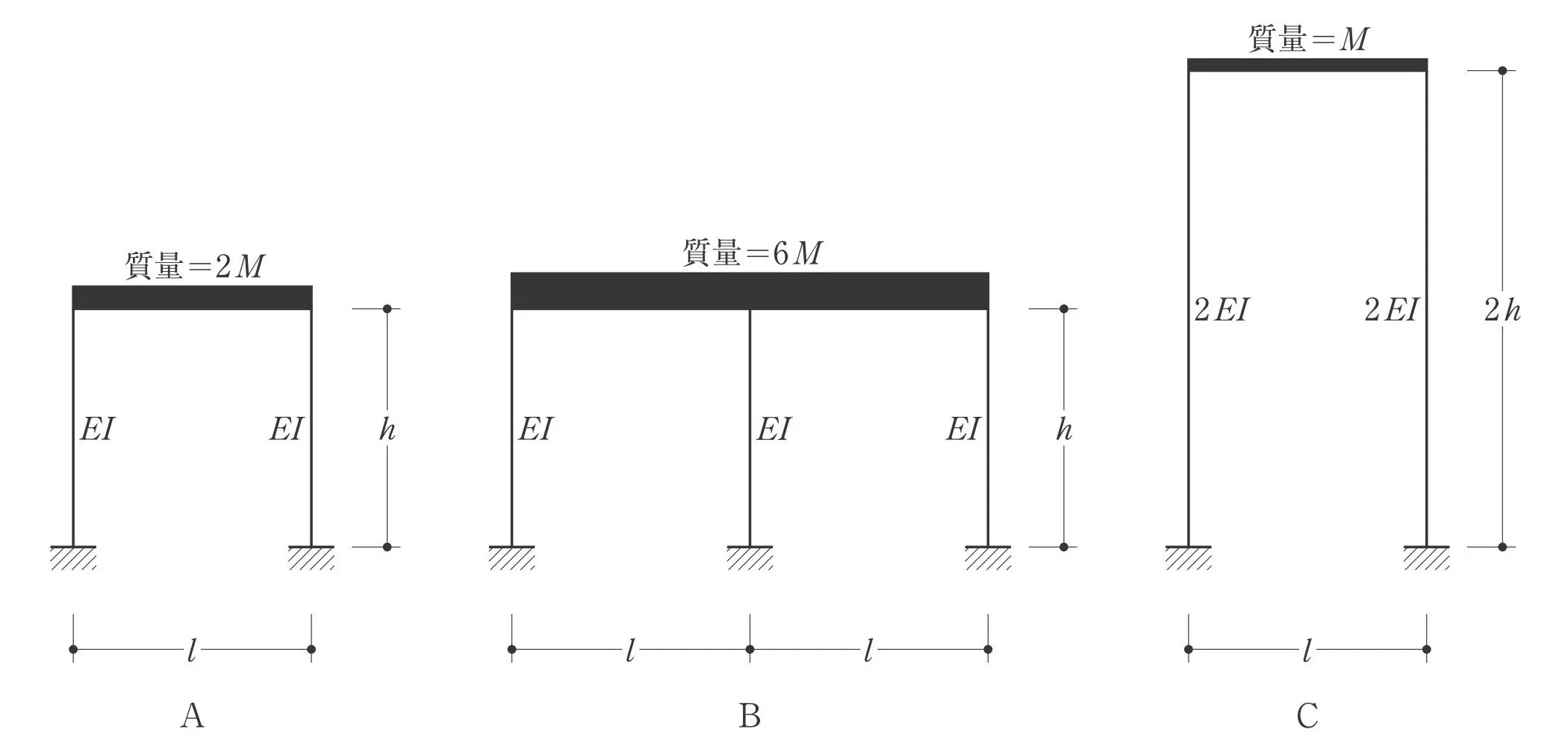

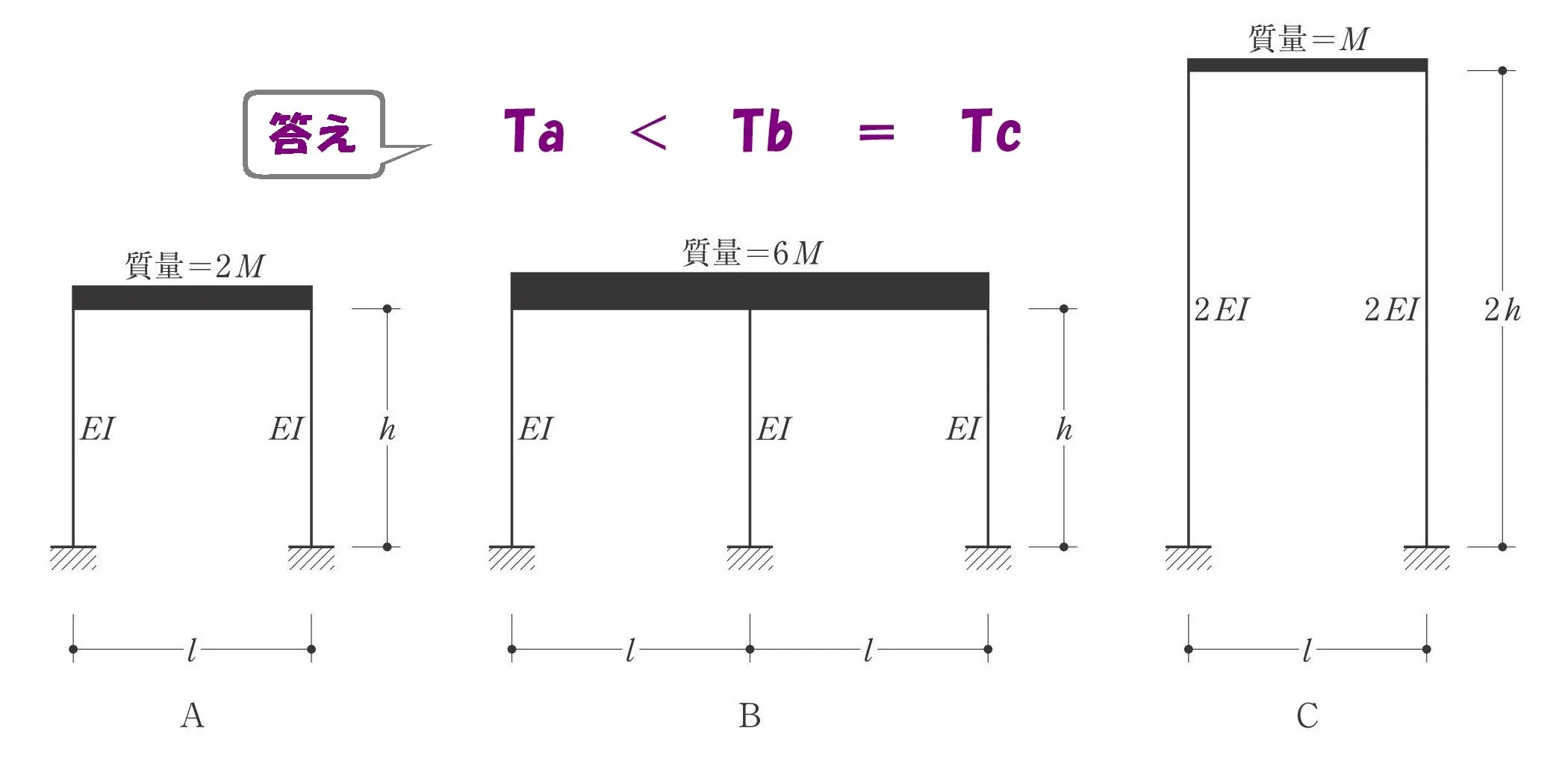
固有周期Ta、Tb、Tcの大小関係を求める問題です。
参考までに、ラーメン架構の固有周期を求める公式を以下に記載しておきます。
$$①水平剛性:k=\frac{ 12EI }{ h^3 }$$
$$②固有周期:T=2\pi\sqrt{\frac{ m }{ k }}$$
$$②←kに①を代入して,T=2\pi\sqrt{m*\frac{ h^3 }{ 12EI }}=2\pi\sqrt{\frac{ m*h^3 }{ 12EI }}$$



パイルート3乗!?
ひええ!力学の拒絶反応が・・




AとBを比べる
$$Ta=2\pi\sqrt{\frac{ \underline{2m}*h^3 }{ \underline{2}*12EI }}$$
$$(柱が2本あるので2を掛ける)$$
$$Tb=2\pi\sqrt{\frac{ \underline{6m}*h^3 }{ \underline{3}*12EI }}$$
$$(柱が3本あるので3を掛ける)$$
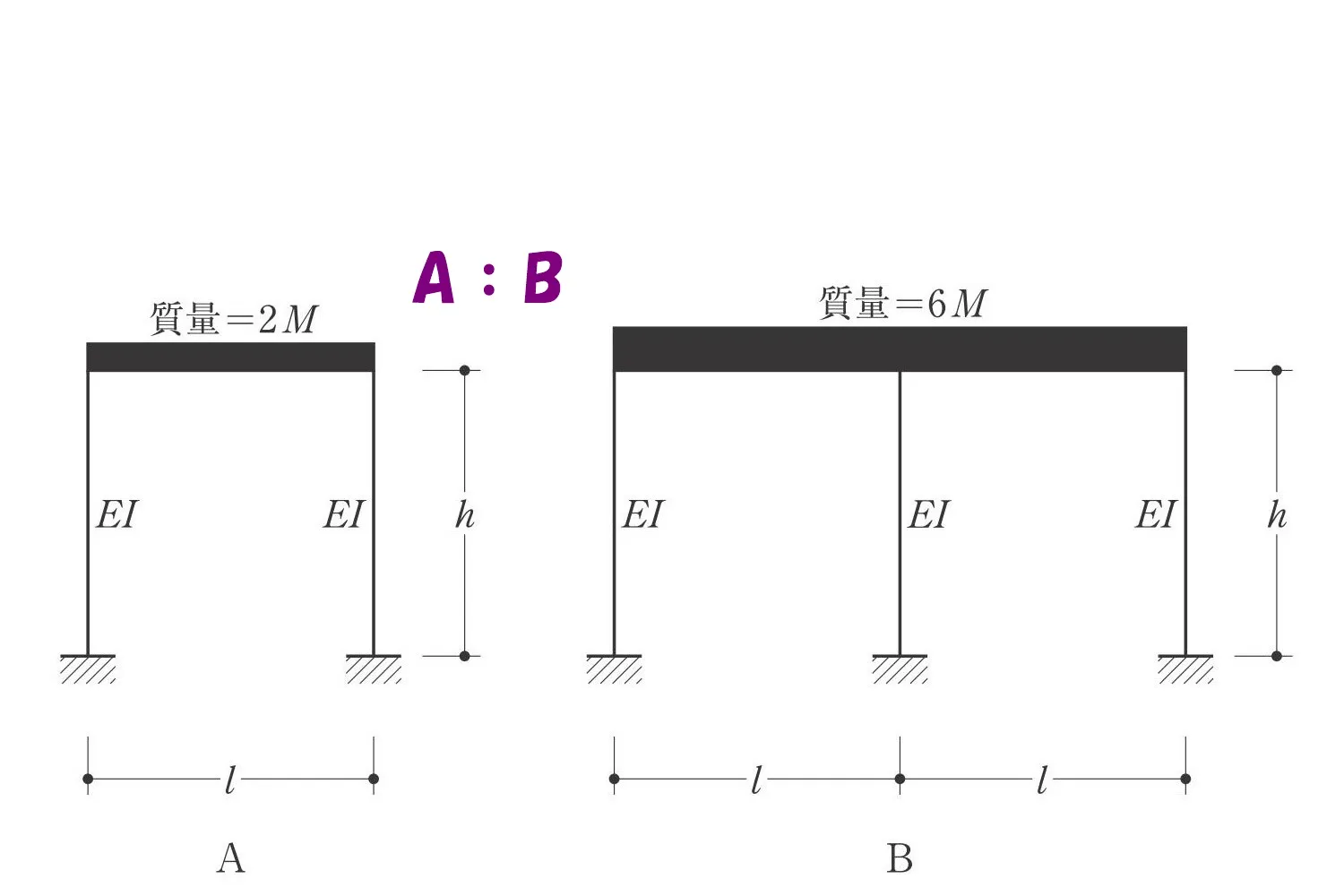

$$Ta:Tb=\underline{2\pi}\sqrt{\frac{ 2*\underline{m*h^3} }{ 2*\underline{12EI}}}:\underline{2\pi}\sqrt{\frac{ 6*\underline{m*h^3}}{3*\underline{12EI}}}$$
$$\underline{2\pi}\sqrt{\frac{ \underline{m*h^3} }{ \underline{12EI}}}の共通項を除外し,Ta^2:Tb^2=\frac{ 2 }{ 2}:\frac{ 6 }{ 3 }=1:2$$



A:Bの比を求める形にして
共通項を除外するのがポイント!
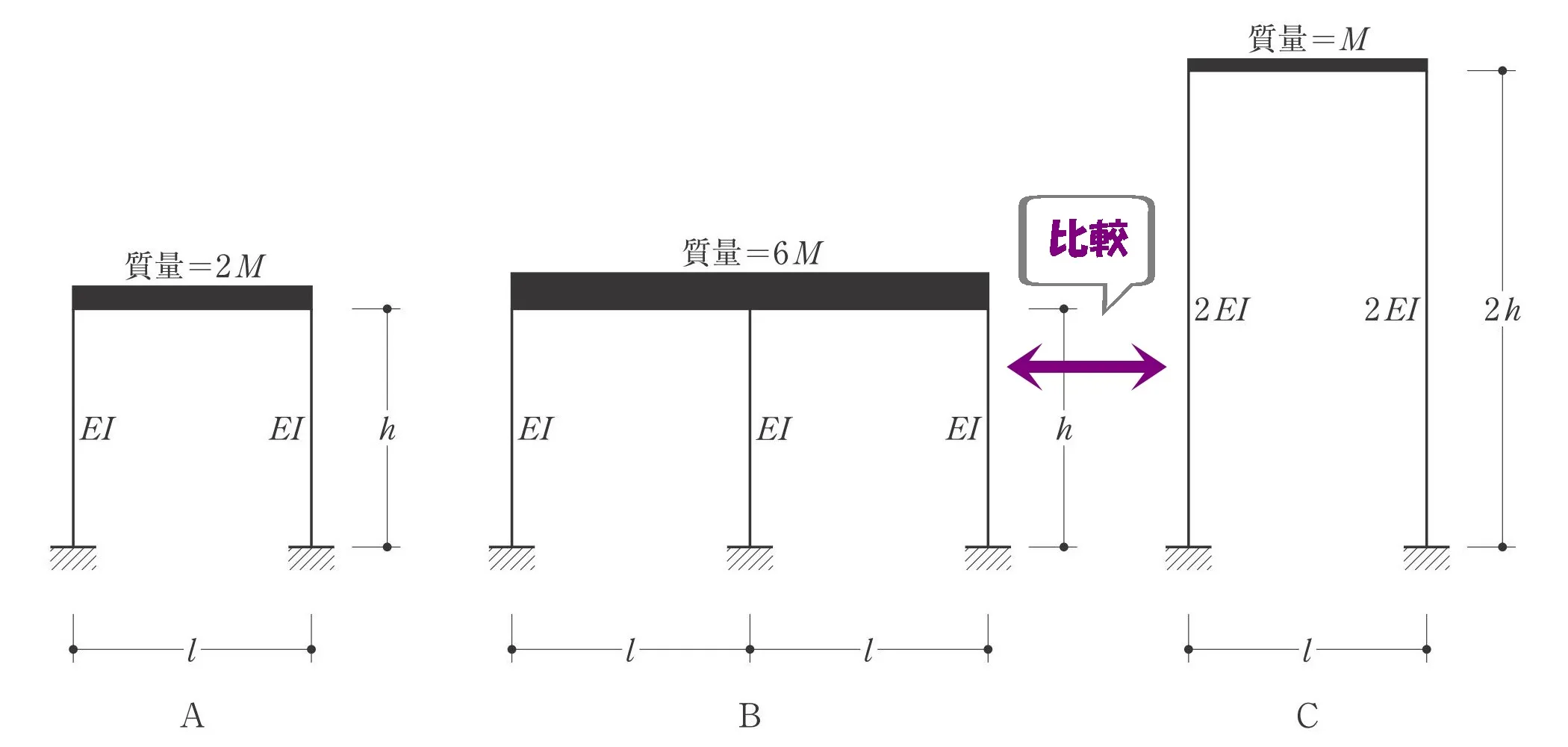




BとCを比べる
$$Tb=2\pi\sqrt{\frac{ \underline{6m}*h^3 }{ \underline{3}*12EI }}$$
$$(柱が3本あるので3を掛ける)$$
$$Tc=2\pi\sqrt{\frac{ \underline{m} *\underline{(2h)}^3 }{ \underline{2}*\underline{2}*12EI }}$$
$$(柱が2本あるので2を掛ける)$$$$(水平剛性が2*EIなので*2)$$
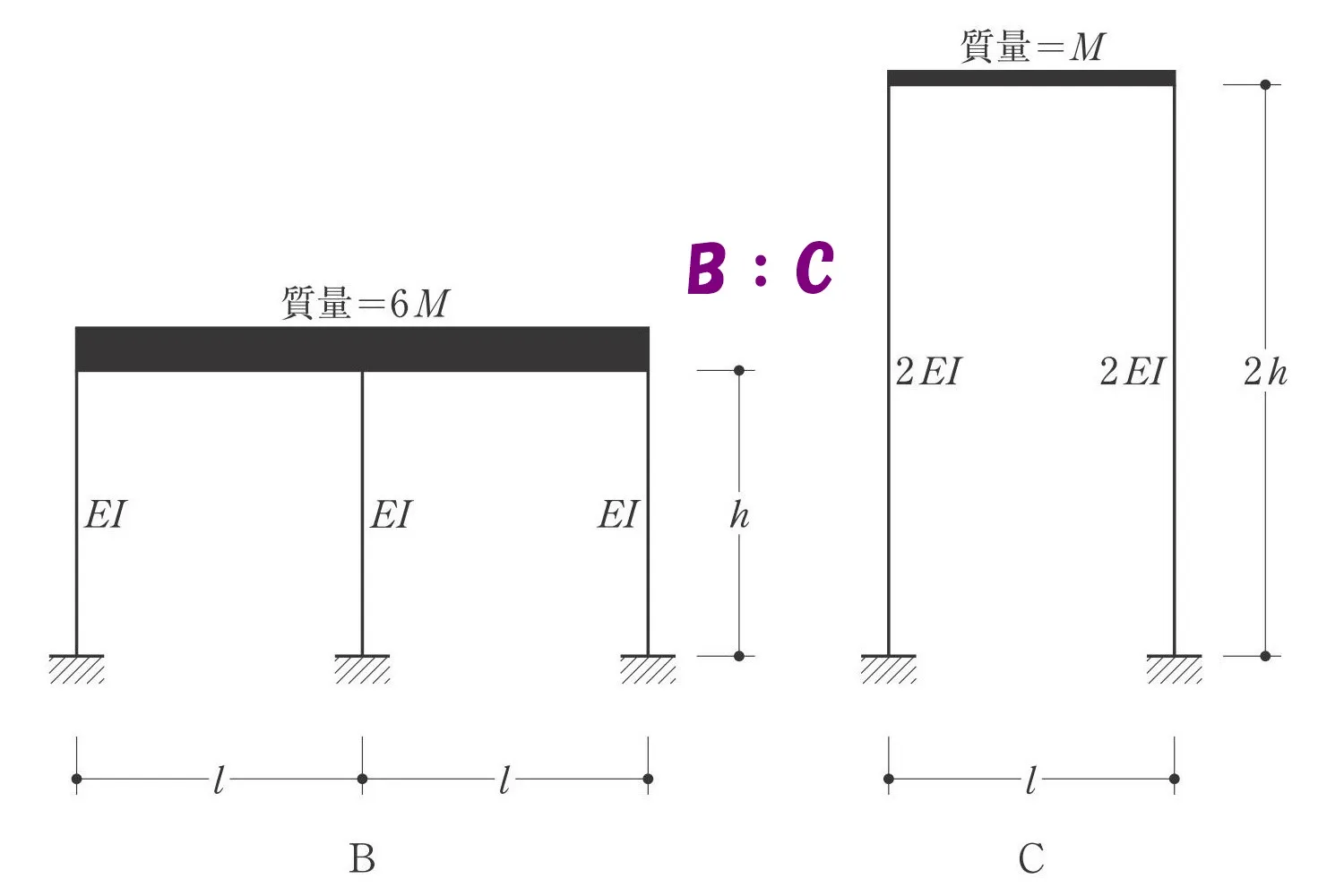

$$Tb:Tc=\underline{2\pi}\sqrt{\frac{ 6*\underline{m*h^3}}{3*\underline{12EI}}}:\underline{2\pi}\sqrt{\frac{ \underline{m}*2^3*\underline{h^3} }{ 2*2*\underline{12EI}}}$$
$$\underline{2\pi}\sqrt{\frac{ \underline{m*h^3} }{ \underline{12EI}}}の共通項を除外し,Tb^2:Tc^2=\frac{ 6 }{ 3 }:\frac{ 2^3 }{2*2 }$$$$ → \frac{ \underline{3}*2 }{ \underline{3} }:\frac{ \underline{2*2}*2 }{\underline{2*2} }=2:2=1:1$$



B:Cの比を求める形にして、
共通項を除外するのがポイントです!
$$A:B=1:2より,Ta<Tb$$$$B:C=1:1より,Tb=Tc$$
$$\underline{Ta<Tb=Tc}$$

- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。


実践2:公式は比例・反比例の関係を使って比較表で解く
Mission2


3つの選択肢を2つずつ比較し、式を簡略化して問題を解きました。
さらに計算の手間を省くため、簡易的な比較表を書き出し、問題を解いてみます。
「問題がよく分からない?」という方も、今後の為に知っておくときっと役に立つでしょう。



さらに未知の世界へ!
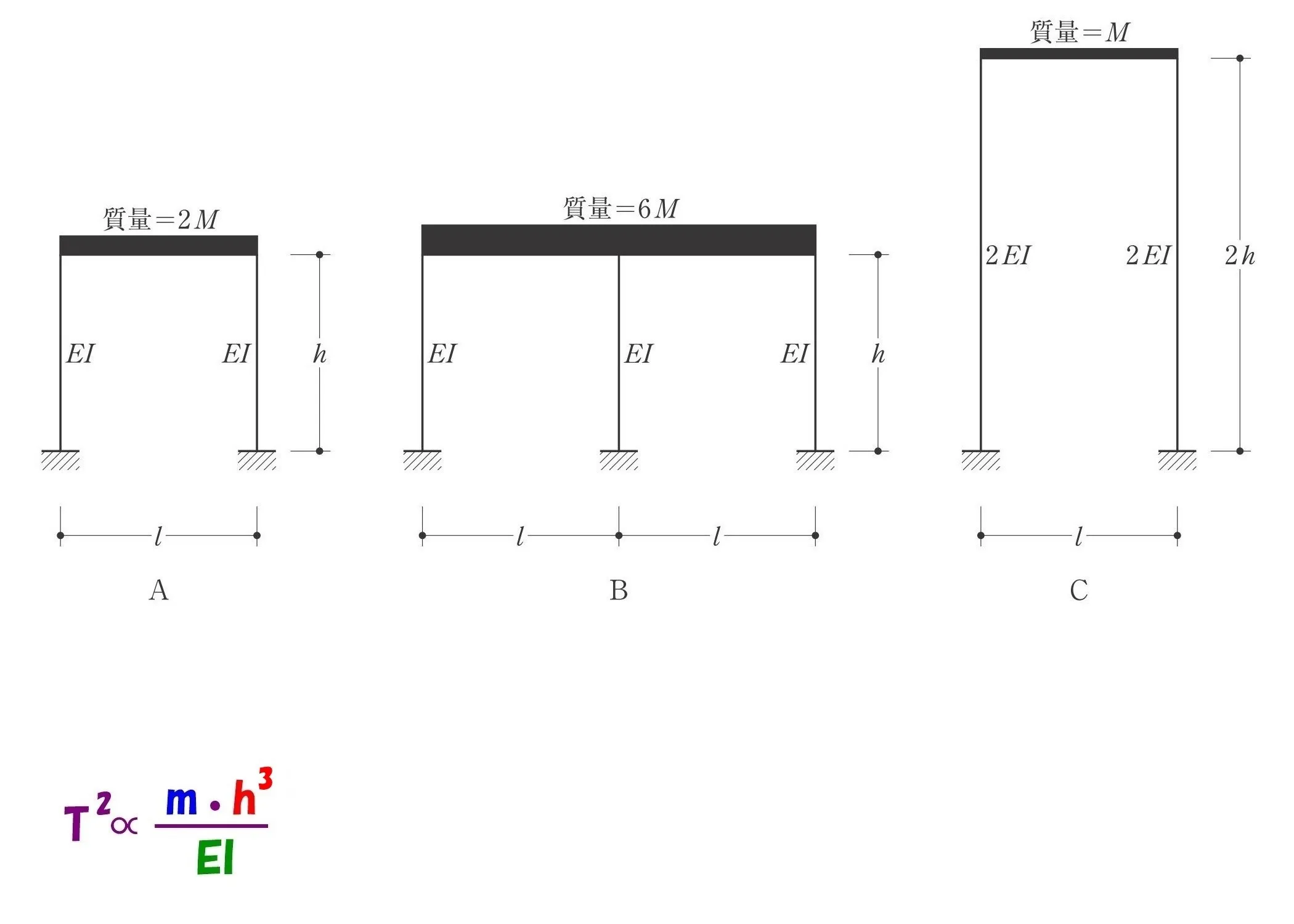

$$①水平剛性:k=\frac{ 12EI }{ h^3 }$$
$$②固有周期:T=2\pi\sqrt{\frac{ m }{ k }}$$
$$②←kに①を代入して,T=2\pi\sqrt{m*\frac{ h^3 }{ 12EI }}=\underline{2\pi}\sqrt{\frac{ m*h^3 }{ \underline{12}EI }}$$
$$\underline{2\pi}を除外し,両辺を2乗してルートを消して,係数の12を除外すると,$$$$T^2\propto{\frac{ m*h^3 }{ EI }} → (T^2はmとh^3に比例し、EIに反比例する)$$



この比例・反比例を使って
固有周期の大小関係を求めます。



・・というか、
固有周期が分かんないだよね。
- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。
実践!

ヨコ線を長く引きます。
このラインは「分数のヨコ線」だと思って下さい。
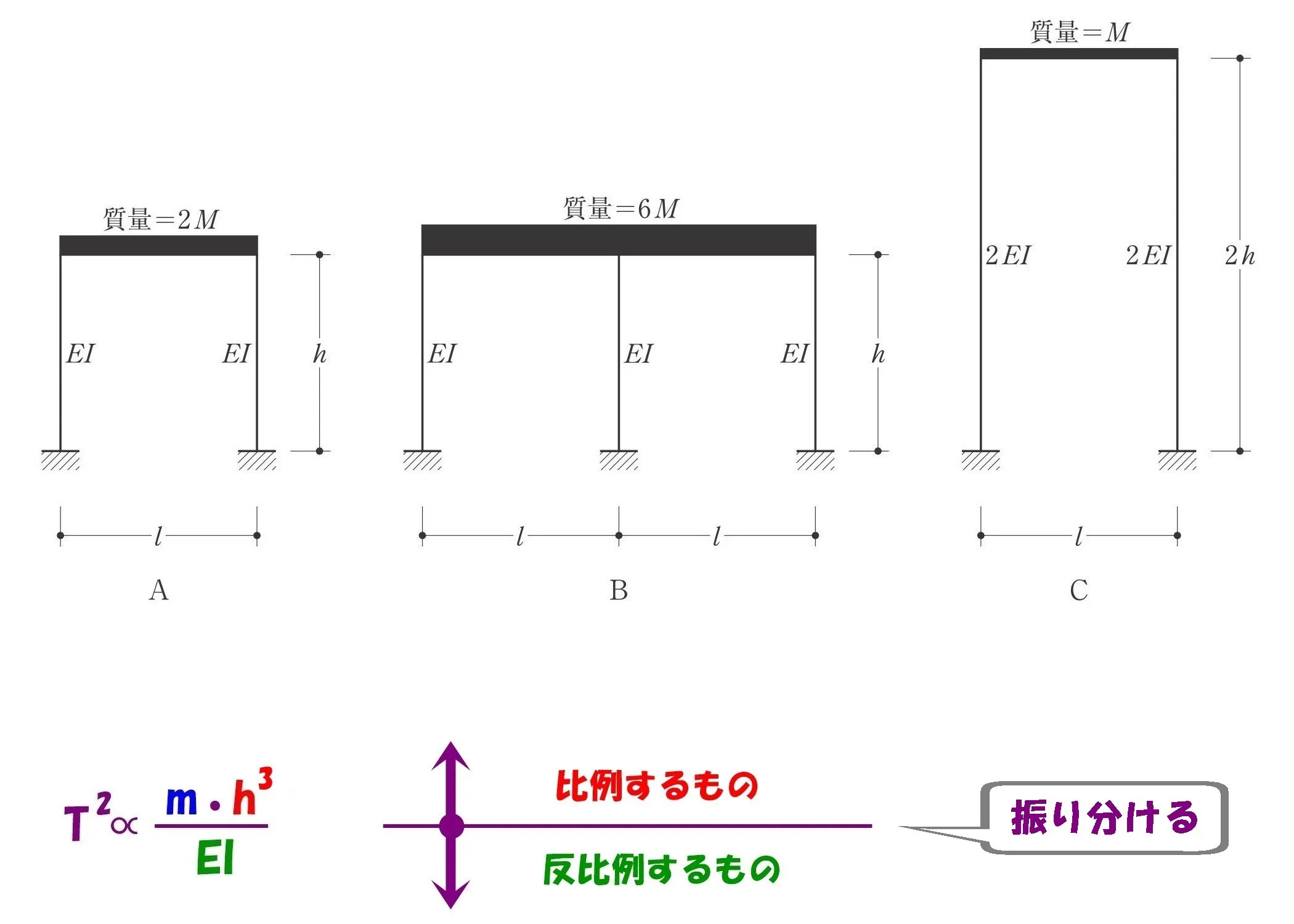

長いヨコ線を境に、分子のエリアに「比例するもの」、分母のエリアに「反比例するもの」を振り分ける。
$$\frac{ 分子 }{ 分母 }=\frac{ 比例するもの }{ 反比例するもの }$$
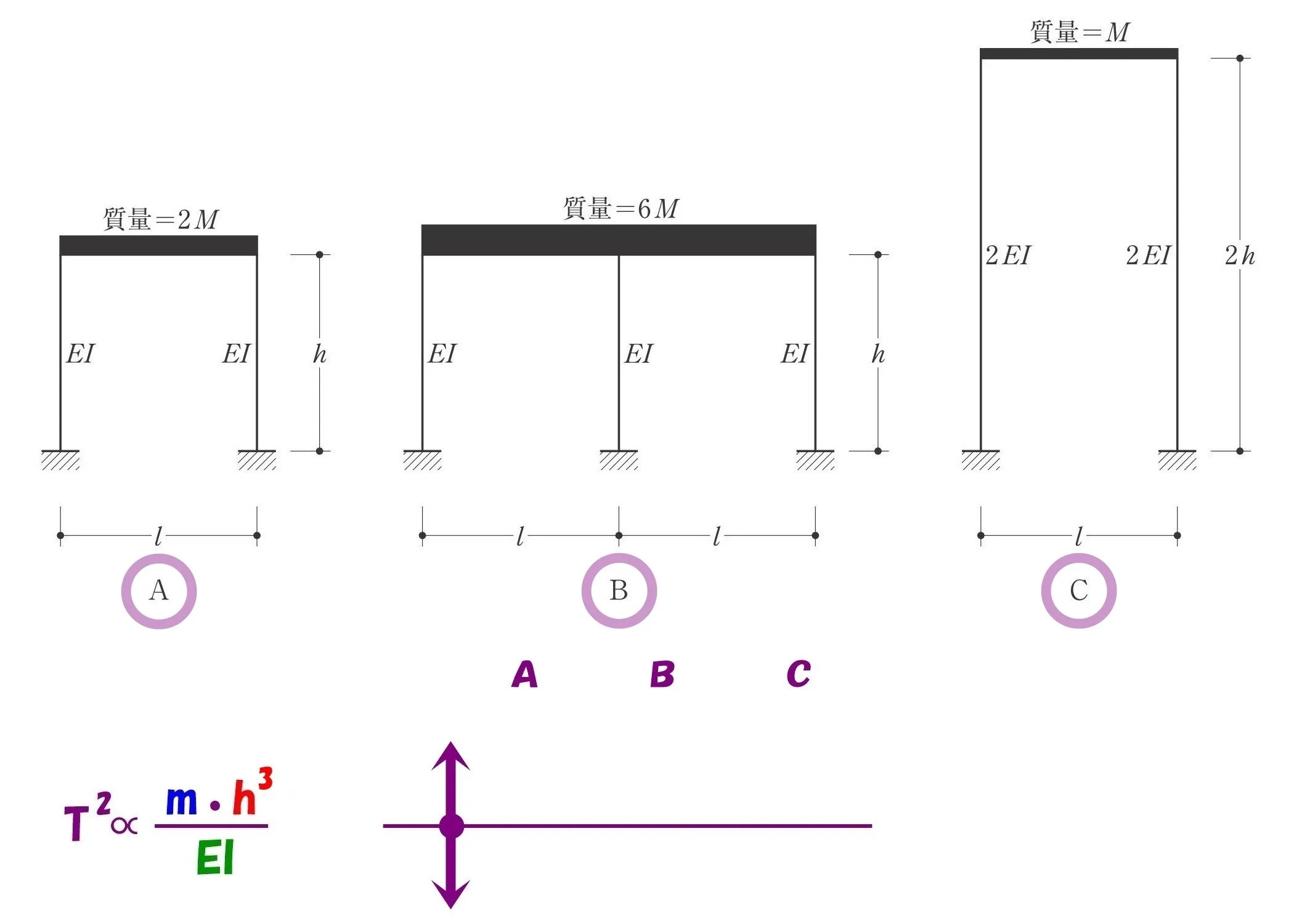

ヨコ線の分子エリアの最上部に「A・B・C」を書きましょう。
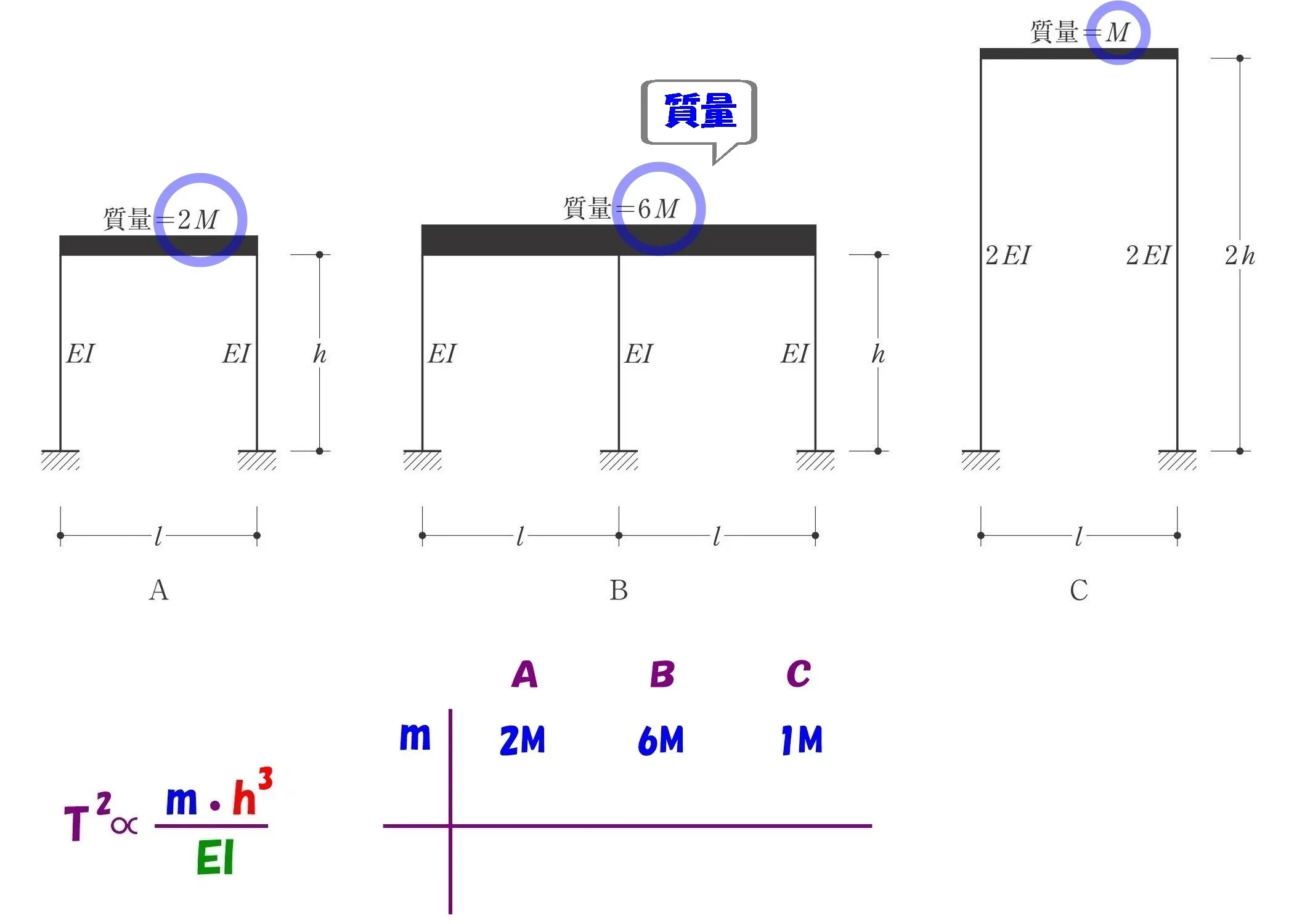

$$比例するもの「m」=A:B:C=2m:6m:1m$$
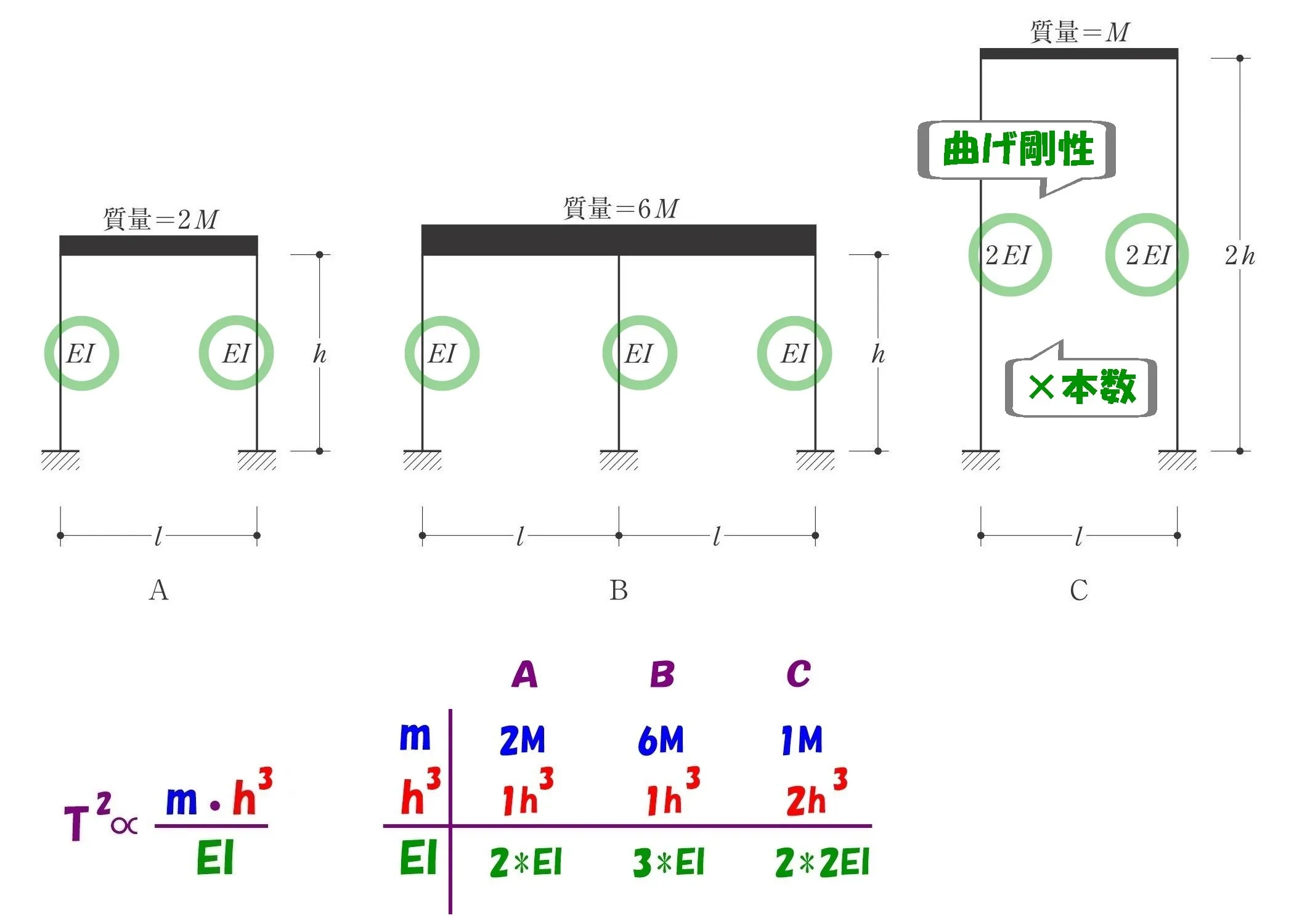

$$比例するもの「h^3」=A:B:C=1h^3:1h^3:2h^3$$$$反比例するもの「EI」=A:B:C=2EI:3EI:2*2EI$$$$柱の本数に応じて,2*EI,3*EI,Cの曲げ剛性は2EIなので,2本*2EI$$
- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。



ここから本気を出すでござる
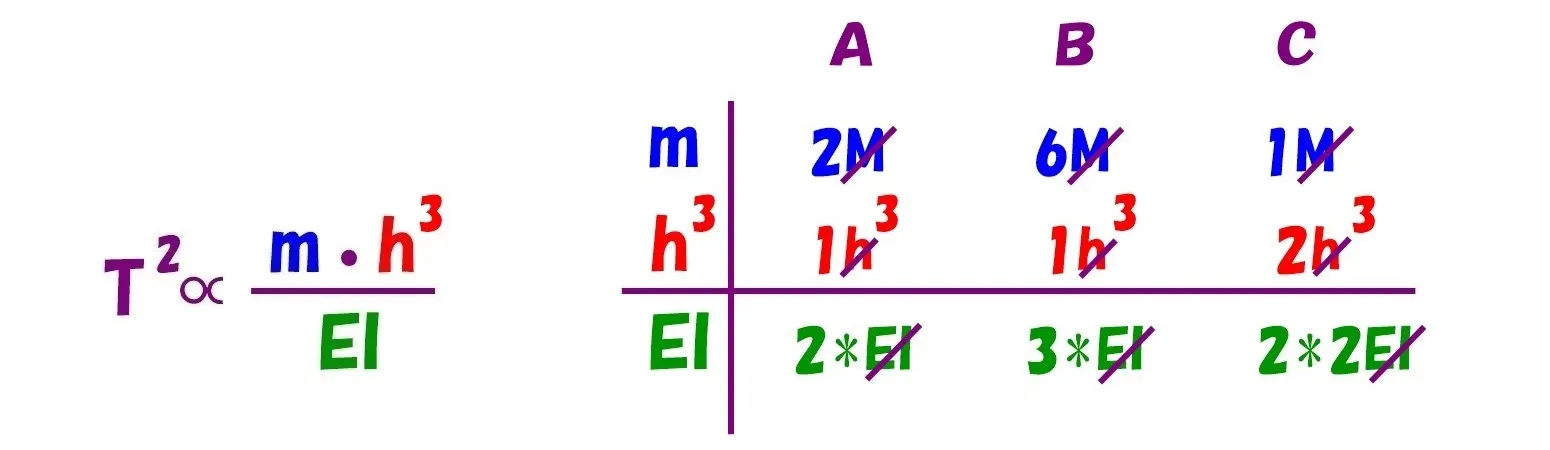

$$共通項となる「m」「h」「EI」にそれぞれ,m=1,h=1,EI=1を代入すると,$$$$「m」「h」「EI」が消滅して,比較対象だけが残る。$$



まとめて、せいや!うおりゃ!
「m」「h」「EI」斬り!
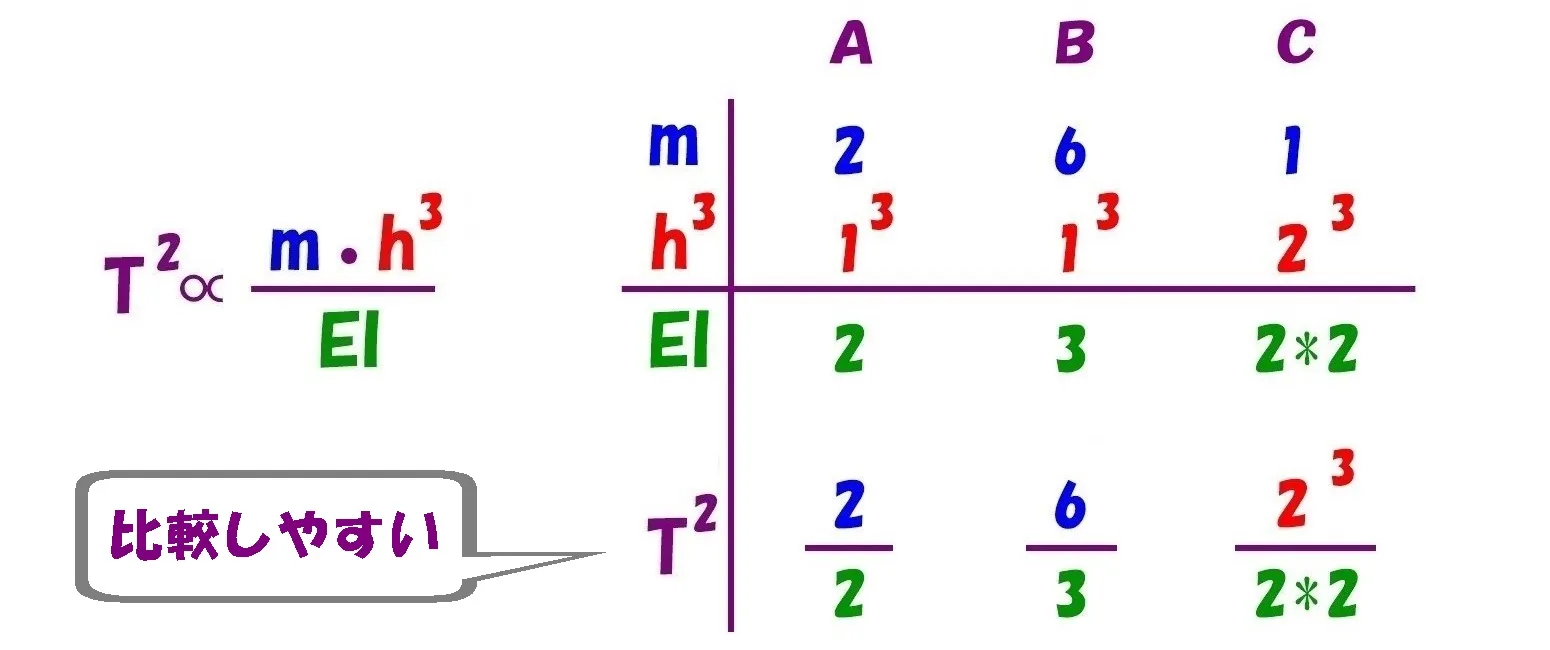

$$\frac{ 分子 }{ 分母 }=\frac{ 比例するもの }{ 反比例するもの }として,T^2を比較する$$$$A:B:C=\frac{ 2 }{ 2 }:\frac{ 6 }{ 3 }:\frac{ 2^3 }{ 2*2 } → 1:2:2=\underline{Ta<Tb=Tc}$$



つまらぬものを斬ってしまった。





なんか勢いと掛け声だけで
倒したような気がする!?



すべて打ち取ったり!
力学の勉強を楽にするコツ
- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。
「構造力学の勉強を楽にする」3つのコツを使って問題を解きました。
これらの知恵の引き出しは、難解な計算作業を省力化し、学習を継続させる手助けとなるでしょう。



これから力学の克服のために、
知恵をしっかりと仕込んでおこう。


仕込むだけでなくて使って下さい。
知恵は使わないと腐ってしまいます。



力学は実に興味深い!
- 比較問題は2つずつ比較する。
- 公式は比例・反比例と合わせる。
- m=1,h=1, EI =1を代入する。






お疲れ様でした、まとめに入ります。

一級建築士:構造力学の勉強方法(独学)の3ステップ!
(まとめ)
勉強が苦手な人には「苦手な人なり」の取り組み方がある。
勉強法3ステップ
| ステップ① | 問題を解くための手順や公式をまとめる。 |
| ステップ② | 手順や公式を問題文の余白に箇条書きする。 |
| ステップ③ | 箇条書きしたメモに習って繰り返し問題を解く。 |



おさらいでござる!
| ステップ① | 問題を解くための手順や公式をまとめる。 |
ステップ①
- 問題文を丁ねいに読み、図に書き込みする。
- 解説文を丁ねいに読み、必要な言葉をチョイスする。
- 問題を解くための手順や公式を小さくまとめる。
図に書き込みする


問題図に積極的に書き込みして、理論よりもイメージから展開する。


必要な言葉をチョイスする
- 必要な公式
- 必要な考え方
- 必要な図の取り出し
過去問題を攻略するための武器や材料をそろえる。
手順や公式を小さくまとめる




(解き方の手順は箇条書きにする。)
| ステップ② | 手順や公式を問題文の余白に箇条書きする。 |
ステップ②




ステップ①でまとめた要点を問題文の余白に書き込む。


メモ書きスペースがない場合


「自分の言葉で書いた手書きの文字」は記憶に残りやすい。
| ステップ③ | 箇条書きしたメモに習って繰り返し問題を解く。 |
ステップ③
- 問題文を丁ねいに読む。
- 余白に書き残したメモを読む。
- メモに習って問題を解いてみる。
問題文を丁ねいに読む。


余白に書き残したメモを読み、メモに習って問題を解いてみる。




書き残したメモは、自力で攻略法を身につけるためのアシストになる。
勉強を楽にする5つのコツ
- 公式は「単位」と合わせて覚える。
- 公式は比例・反比例の関係と合わせて覚える。
- 比較問題は2つずつ比較して消去法で攻める。
- 桁数の多い計算式は、かっこ(・)でくくる。
- 大小関係において失敗しない”答えの並べ方”がある。



コツも押さえておくのだ。
1.公式は「単位」と合わせて覚える。
$$速度(m/s)=\frac{ 距離(m) }{ 時間(s) }$$
求める数値の単位は、その公式を構成する単位でもある。
2.公式は比例・反比例の関係と合わせて覚える。
$$P=\frac{ \pi^2*EI }{ Lk^2 }⇨P\propto\frac{ EI }{ Lk^2 }$$
弾性座屈荷重Pは曲げ剛性EIに比例し、座屈長さLkの2乗に反比例する
公式のそれぞれの比例・反比例の関係は、比較問題を攻略するための材料となる。
4.桁数の多い計算式は、かっこ(・)でくくる。
$$例1:6^3=(2*3)^3=2^3*3^3$$
$$例2:6000=6*10^3=2^3*3^3*10^3$$
(かっこでくくった後に共通部分の処理をする)




計算式をかっこ(・)でくくることで、「暗算する」を「分解する」に置き換える。
3.比較問題は2つずつ比較して消去法で攻める。




比較問題は2つずつ比較することで、大小関係を判断するための計算過程を省略できる。
5.大小関係において失敗しない”答えの並べ方”がある。
失敗しない答えの並べ方
- 選択肢に習って不等号を先に書いておく
- 数値を並べたあとに対応する記号を並べる
- 並べた記号をそのまま選択肢と対比させる










大小関係は、数値を並べたあとに対応する記号を並べる。








構造力学が苦手な人であっても戦い方はあります。
苦手意識を克服するためには、理論よりも「イメージから組み立てる」こと。
あらゆる問題に対して「解く手順」を確立することで、再現性の高い学習効果が得られます。


お伝えした「勉強方法3ステップ」を取り入れることで、あなたの勉強が今日から変わるはず。
一級建築士試験を目指す方にとって、一歩踏み出せるきっかけとなれば幸いです。
最後まで記事を読んでいただき、本当にありがとうございます!






.webp)
.webp)
法規の勉強法を線引き解説




-300x197.webp)







