一級建築士の試験に向けて、最初にぶつかる壁は「構造力学」
力学の中でも「トラス」は奥が深く、苦手意識を持っている受験生も多いかと思います。
トラスの沼は深い!
- 何から手を付ければ良いのか分からない?
- トラスの軸力を求めるまでの手掛かりが分からない?
- ベクトルが色々あって何と何を釣り合わせればよいか分からない?
もしこれらの悩みに当てはまるなら、この記事は奇跡的なめぐり合わせかも!?
ここではトラスの過去問に挑戦し、節点法・図解法・切断法の3つの方法で解説します。
一級建築士の構造力学のトラスを克服したい人は必見、さっそく始めていきましょう!
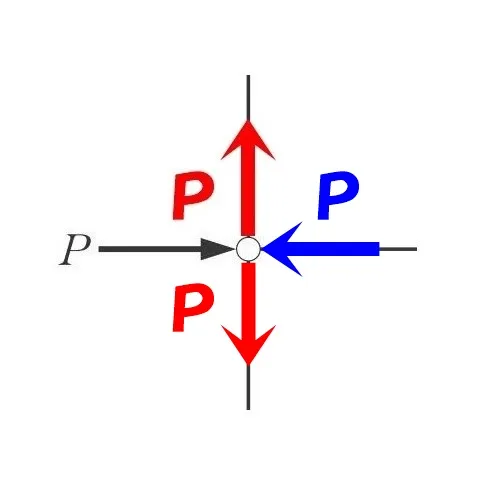

「節点法」
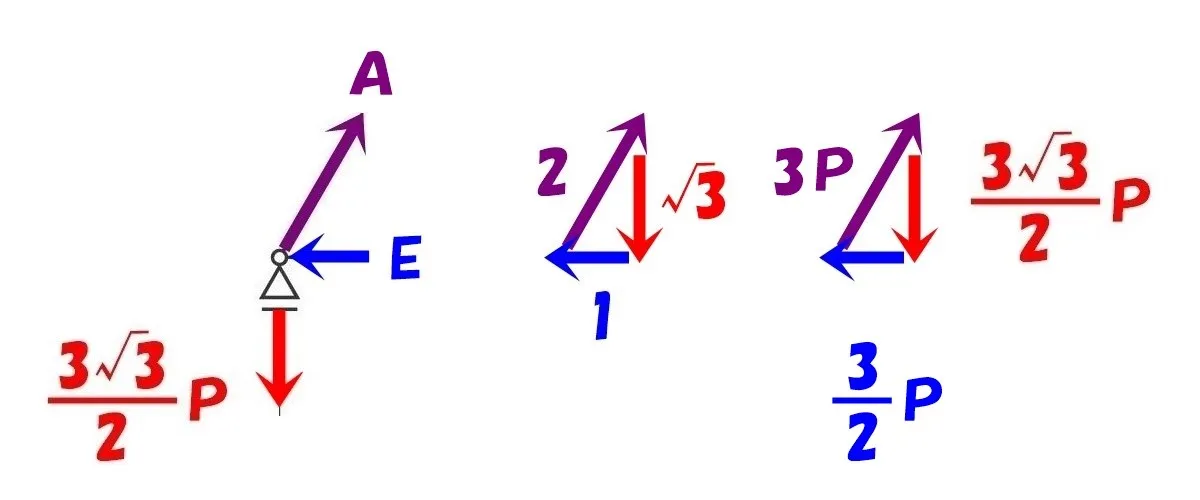

「図解法」
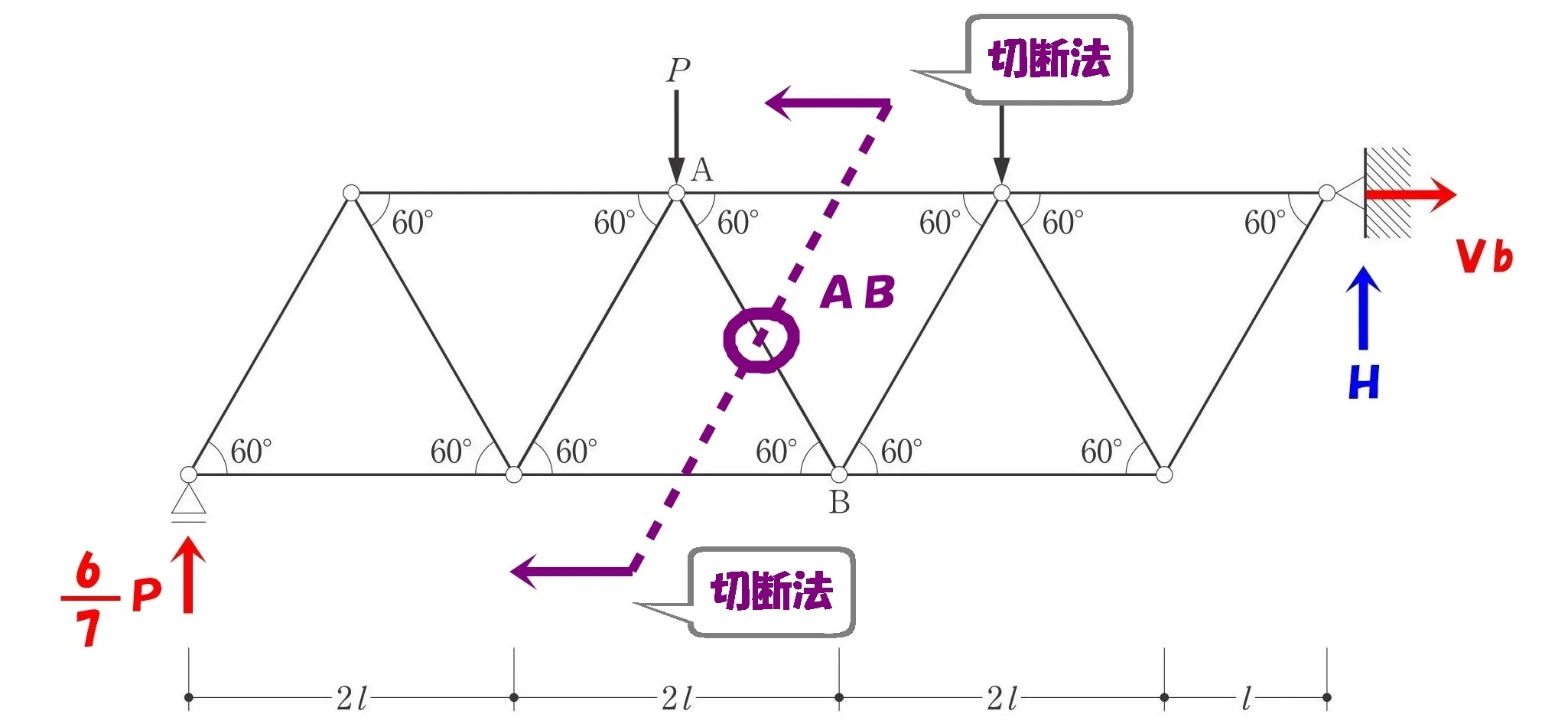

「切断法」
こんな人におすすめ!
- トラスの軸力の求め方が分からない。
- ゼロメンバー?の見分け方が分からない。
- 節点法と図解法、切断法の判断が分からない。



トラス・マジック!


この動画を YouTube で視聴
この記事のテーマは「トラス」です。
力学の勉強を始めると、河川で鉄橋を見たときに「あ!トラスだ」と反応しますよね?
何ごとも身近なものに興味を持つことから、探求心が生まれるもの。
過去問をやるときは、山奥に建つ送電線の鉄塔を頭に浮かべながら取り組むとイメージが膨らみます。
力学の攻略ポイントを集結!
.webp)
.webp)


トラスの時間が始まります。
一級建築士|構造力学「トラス」の3つの攻略法を解説!


「トラスの沼から抜け出せない!?」
そのような、構造力学の洗礼を受けた人もいるかもしれません。
トラスの沼で気力を削がれて力学が嫌いになる人には、次のような傾向があるといえるでしょう。



底が見えない・・
トラスの沼は深すぎる。
トラスの沼
- 何から手を付ければ良いのか分からない?
- トラスの軸力を求めるまでの手掛かりが分からない?
- ベクトルが色々あって何と何を釣り合わせればよいか分からない?



う~ん、そろそろ
トラスを克服しなきゃね。
「今さらトラスって何?」という話は、今日で終わり。
この記事では、オリジナルのイラストを使って丁ねいに解説していきます。
少しでも気を抜くと取り残されてしまいますので、気合を入れて突き進んでいきましょう!


気合を入れるぞ。
トラスの3つの攻略法について
まず始めに、トラスの3つの解き方について、簡単に紹介します。
「トラスの3つの心得」についても、しっかりと胸に刻んでおきましょう!



トラスの心得?
トラスの3つの攻略法
- 節点法
- 図解法
- 切断法
トラスの3つの心得!
- 反力を求めなければ何も始まらない。
- トラスの軸力は力の釣り合いを追いかける。
- トラスの一部を切り出して、方程式を組み立てる。



胸に刻むことにした。
・節点法
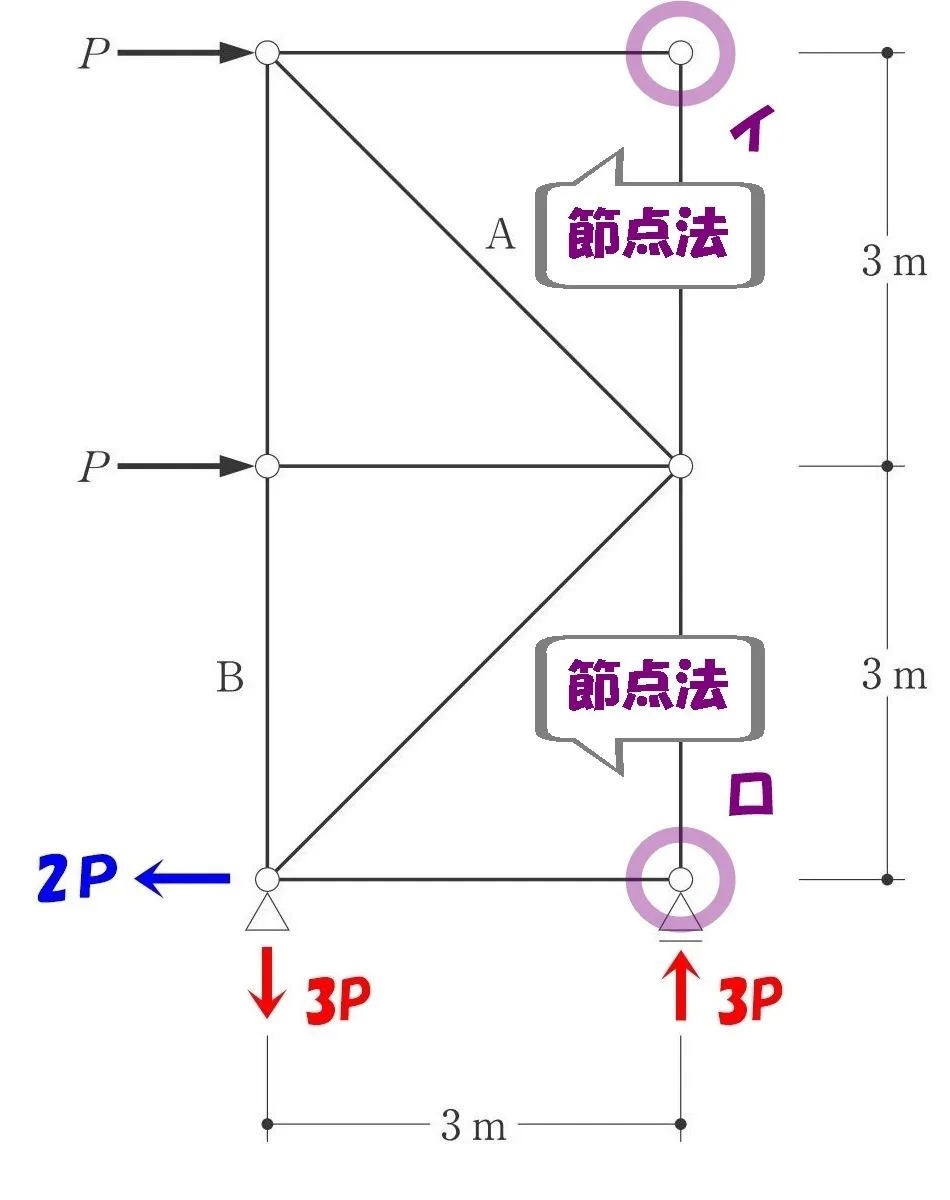

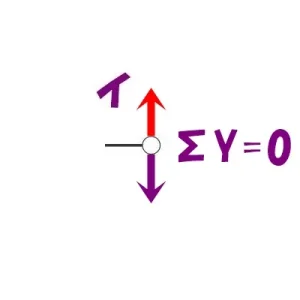

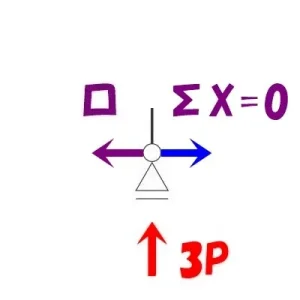

節点法の使い方
外力や反力との釣り合いから、軸力を持たない「ゼロメンバー」を見つけます。
軸力のつり合いを考えるうえで、部材の数を減らしたいときに使える手法といえるでしょう。
トラスの節点に働く力を釣り合わせ、部材の軸力を求める方法
・図解法
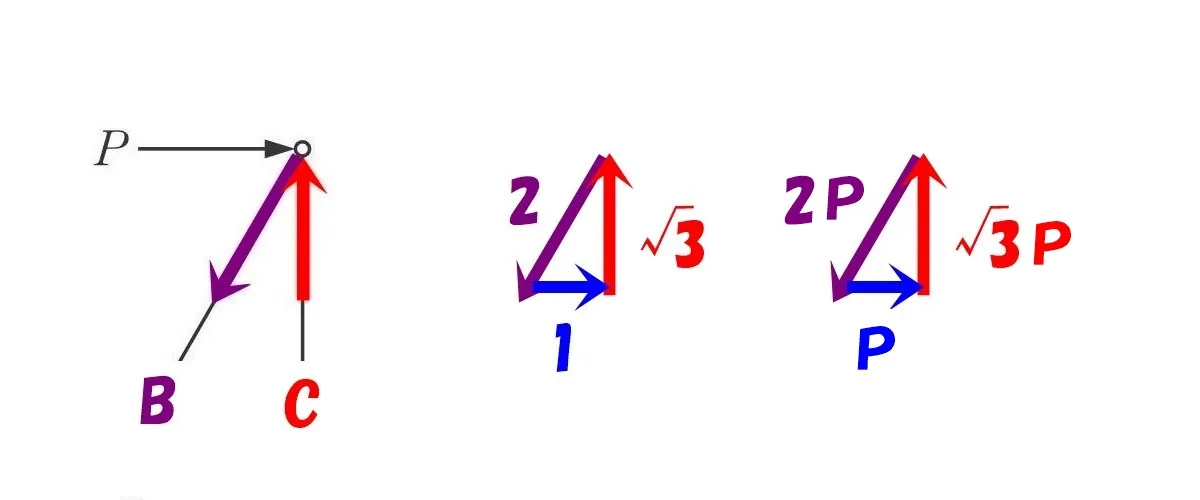
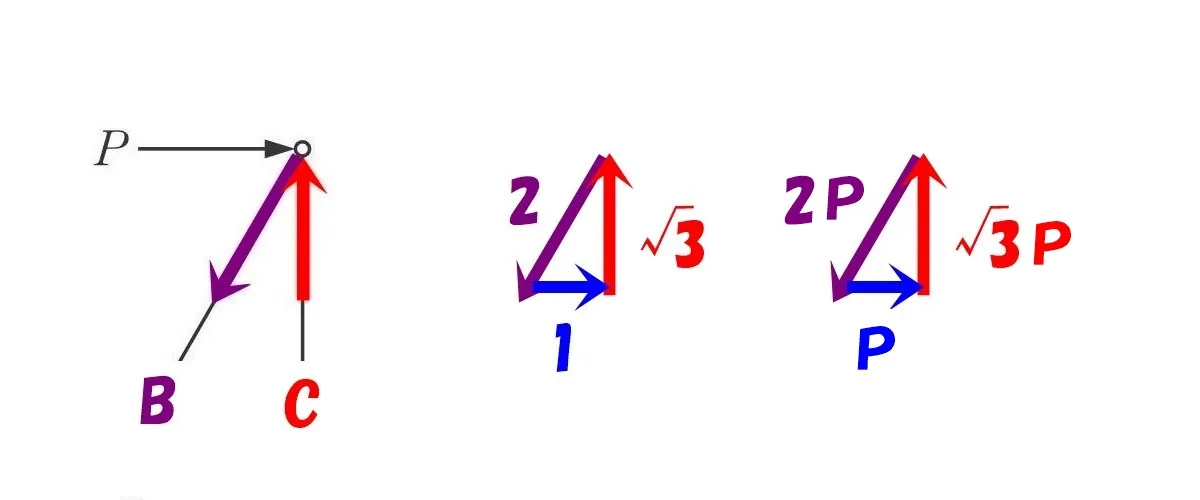
図解法の使い方
X方向とY方向、斜め方向の3つのベクトルで三角形をつくり、辺の長さの比より軸力を求める。
外力または反力があれば、三角比から「残り2つの軸力」を一度に求めることが出来ます。
トラスの部材の軸力をベクトルとして図示して、三角比で求める方法
・切断法
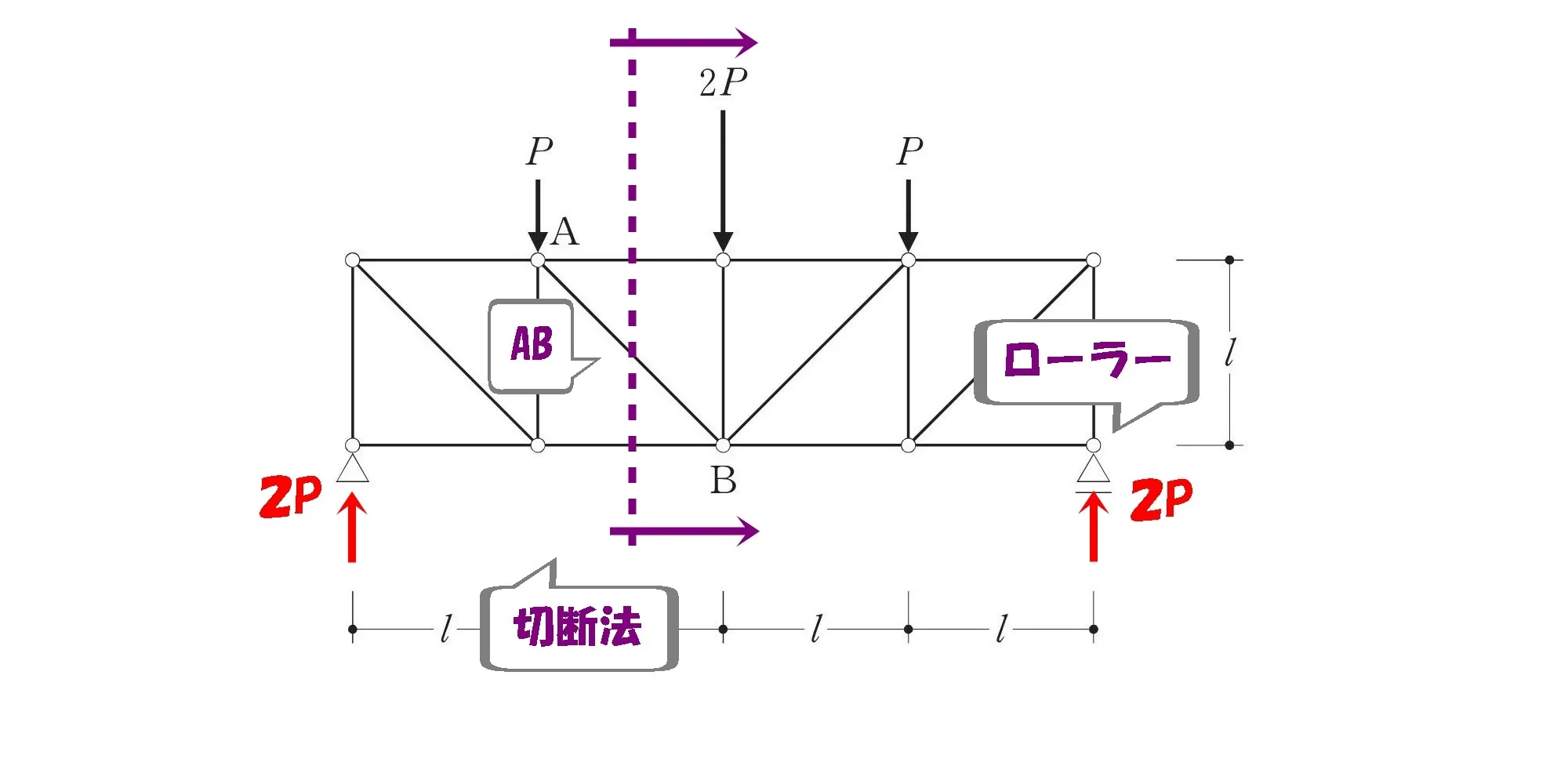

切断法の使い方
トラスの問題で万能的に使える攻略法といえば、これですよね?
X方向やY方向だけでなく、「モーメントの釣り合い式」が使えることが特徴といえるでしょう。
トラスを切断して片側を取り出し、力の釣り合いにより部材の軸力を求める方法
トラスの3つの方程式
$$\Sigma X=0$$
$$\Sigma Y=0$$
$$\Sigma M=0$$
- 水平力との力の釣り合い
- 鉛直反力との力の釣り合い
- 支点のモーメントの釣り合い
それでは本題ともなる過去問を通して、実践していきます。
節点法と図解法と切断法がすべて登場するので、必ずモノにして下さい。
「トラスの沼の渦」へ突撃!3つの攻略法を駆使して、何としても生還しましょう。



集中力を高めよ・・
トラスの3本ノック!
トラスの過去問に挑戦!(No.1-節点法)


節点法とは?
トラスの節点に働く力を釣り合わせ、部材の軸力を求める方法
節点法の攻略ポイント
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。


この動画を YouTube で視聴



No.1
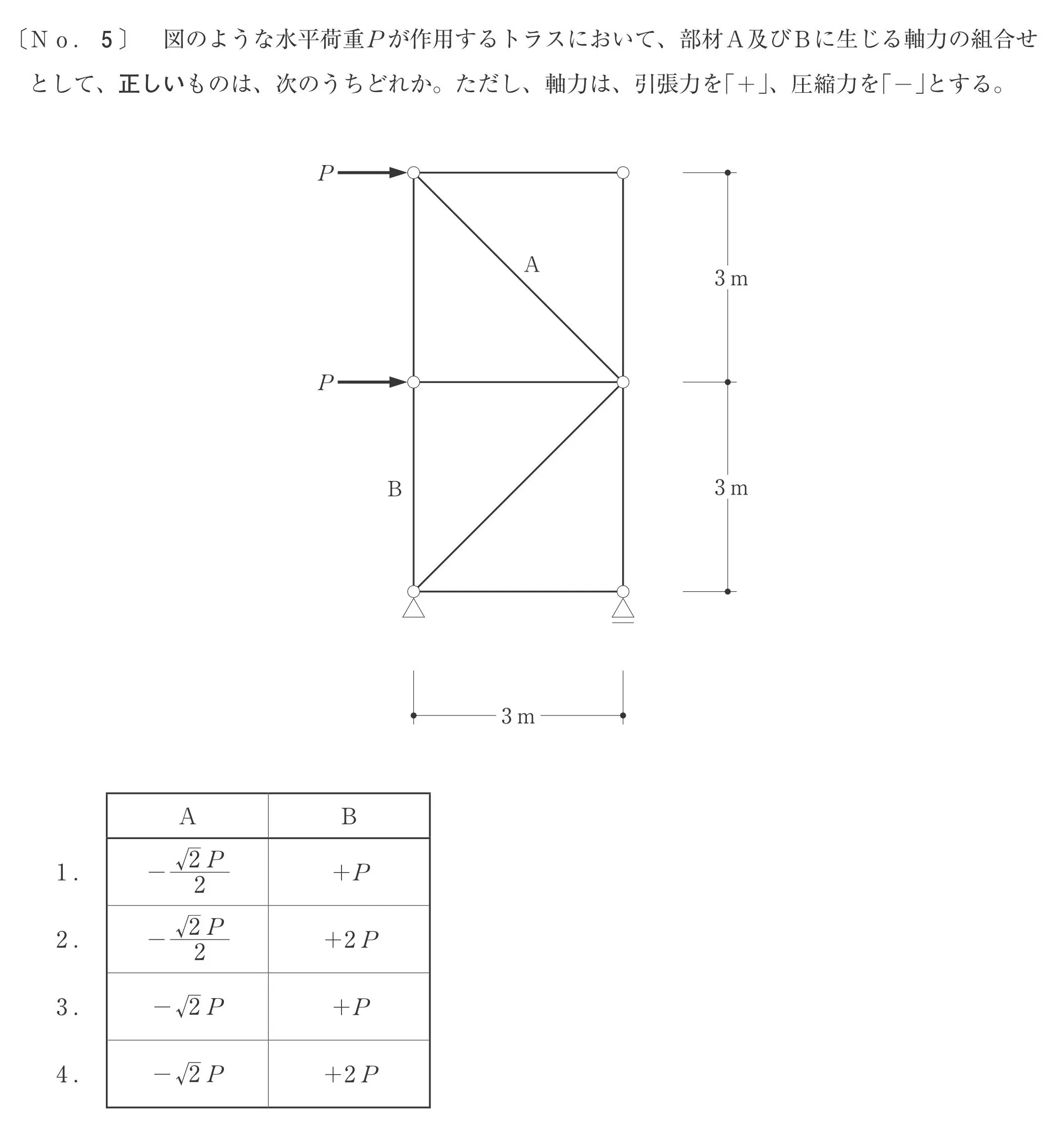

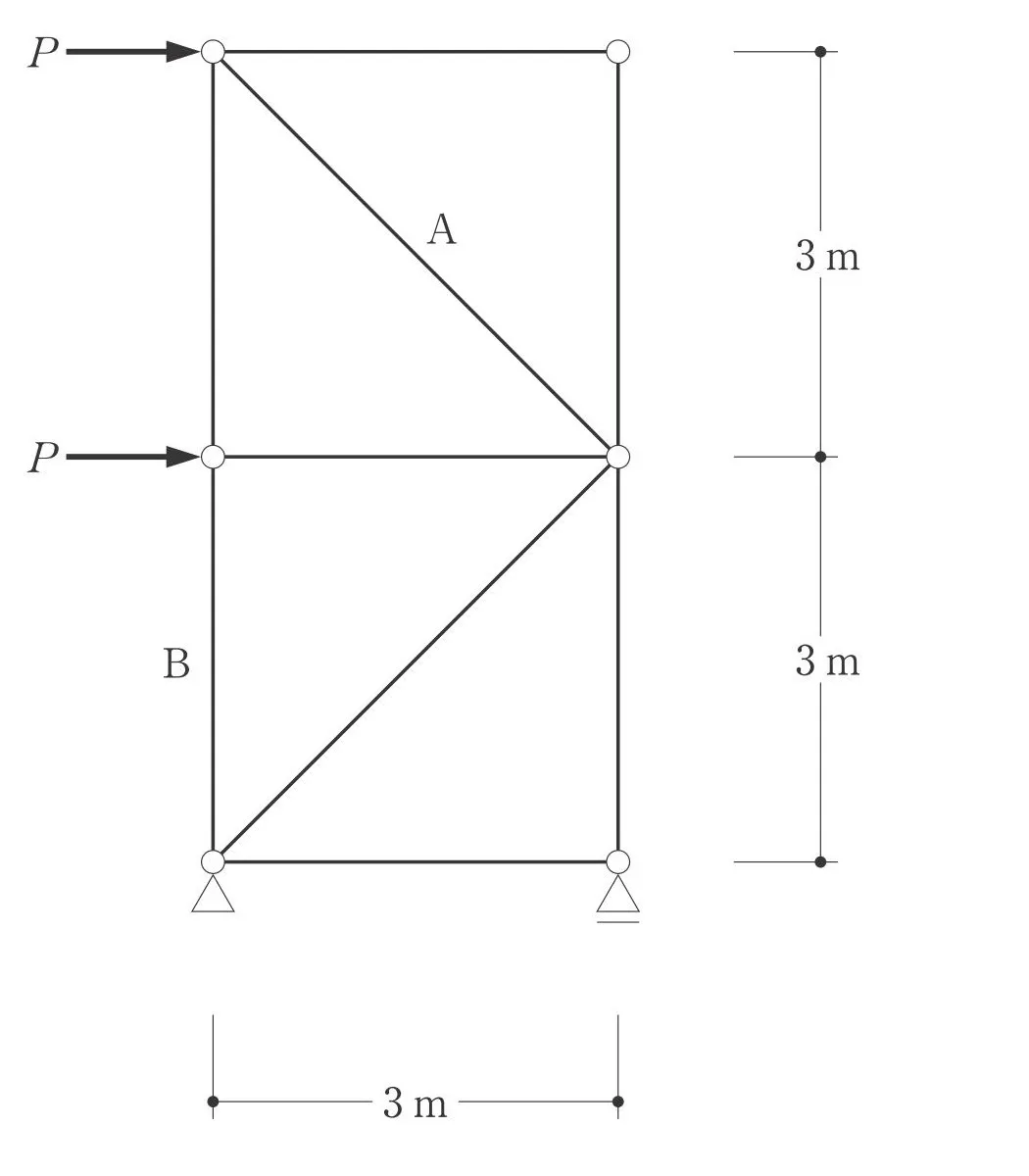

左:ピン支点
右:ローラー支点
1.支点反力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
反力を求める
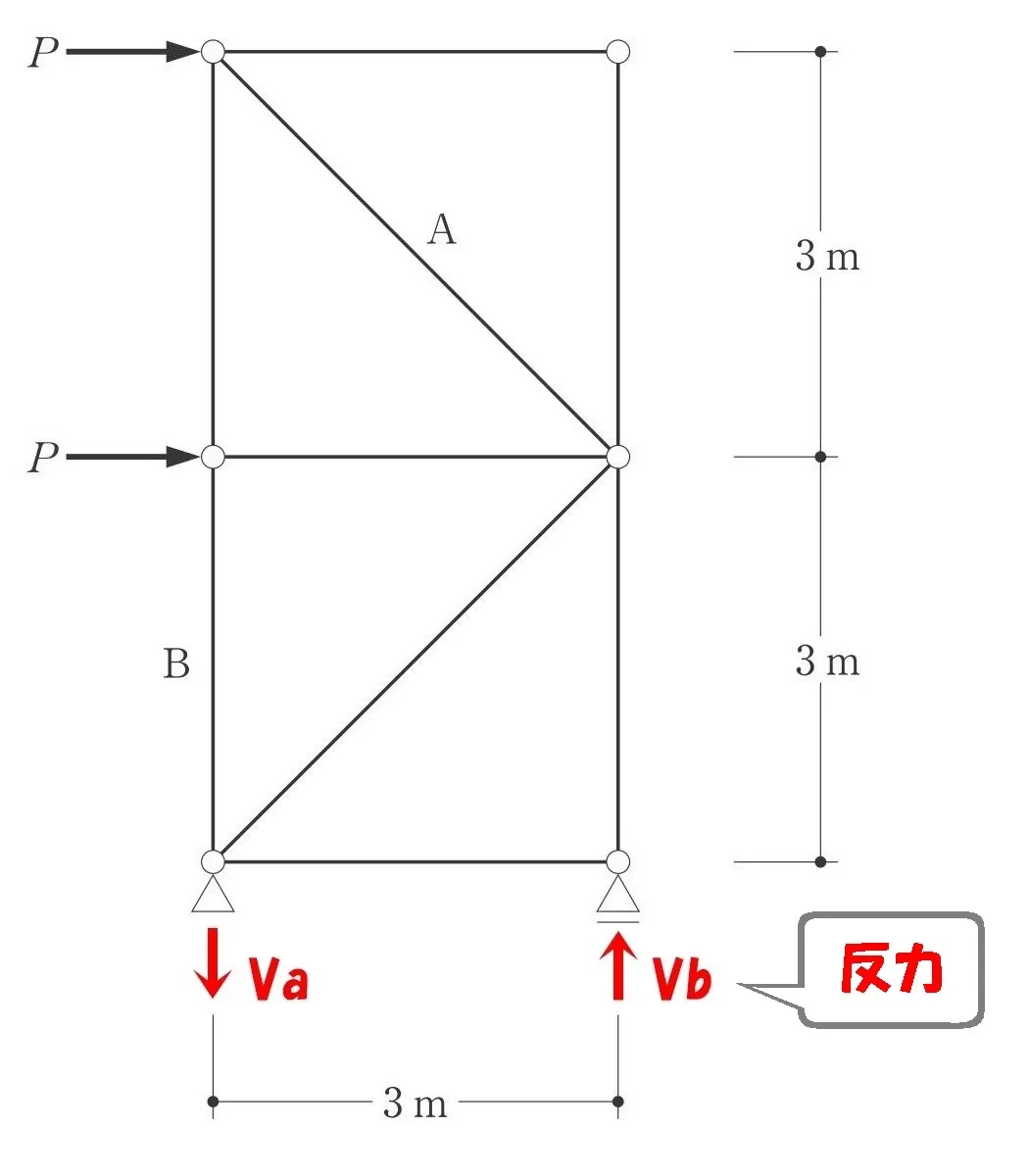

ピン支点とローラー支点にそれぞれ、鉛直反力Va、Vbを書き込む。



支点反力を求める。
ΣM=0
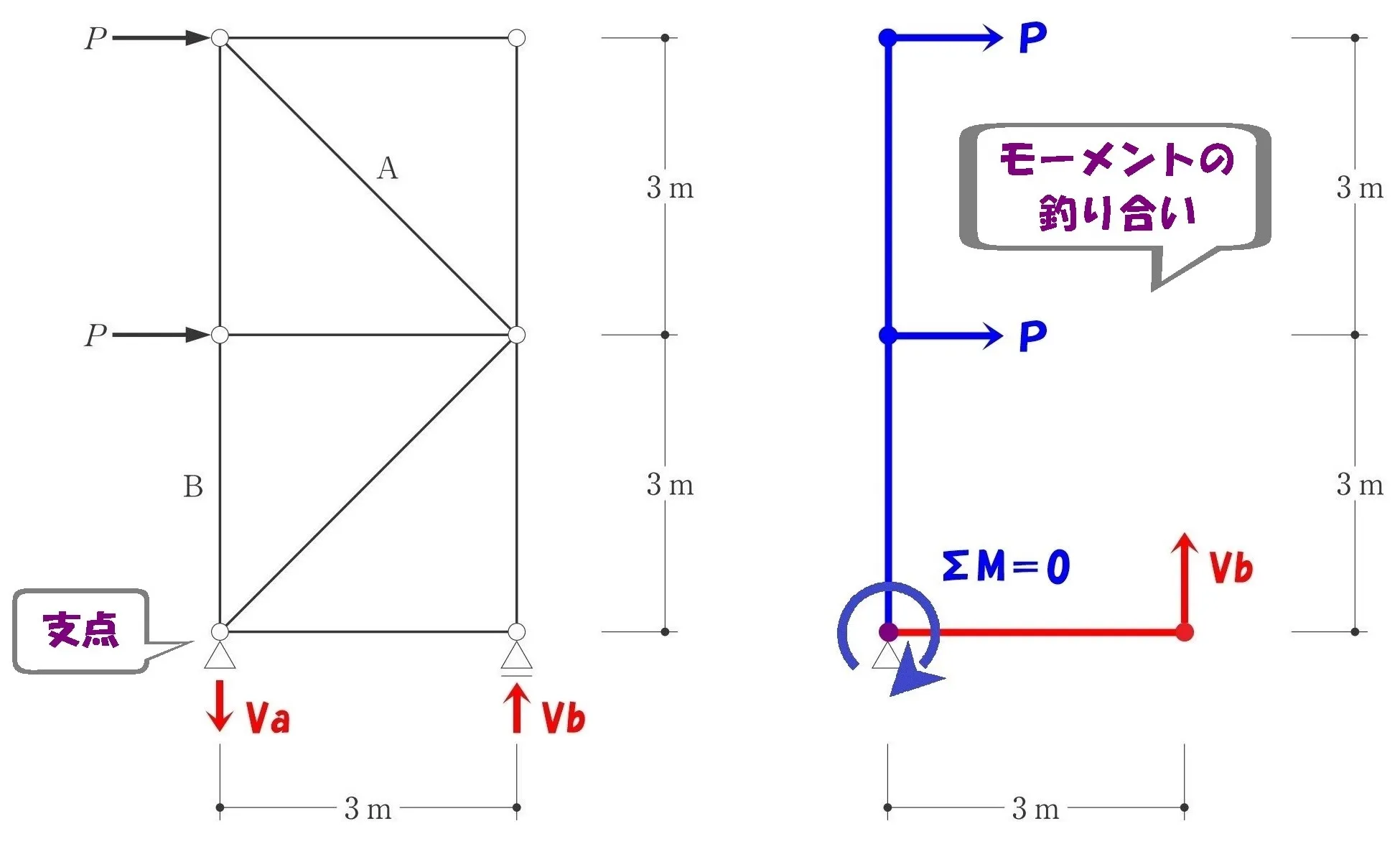

$$\Sigma M=0より$$$$P*6+P*3-Vb*3=0$$$$3Vb=9Pより,Vb=3P(上向き)$$
$$\Sigma Y=0より$$$$Va+Vb=0$$$$Va+3P=0より,Va=-3P(下向き)$$



シグマ・M
反力を求める
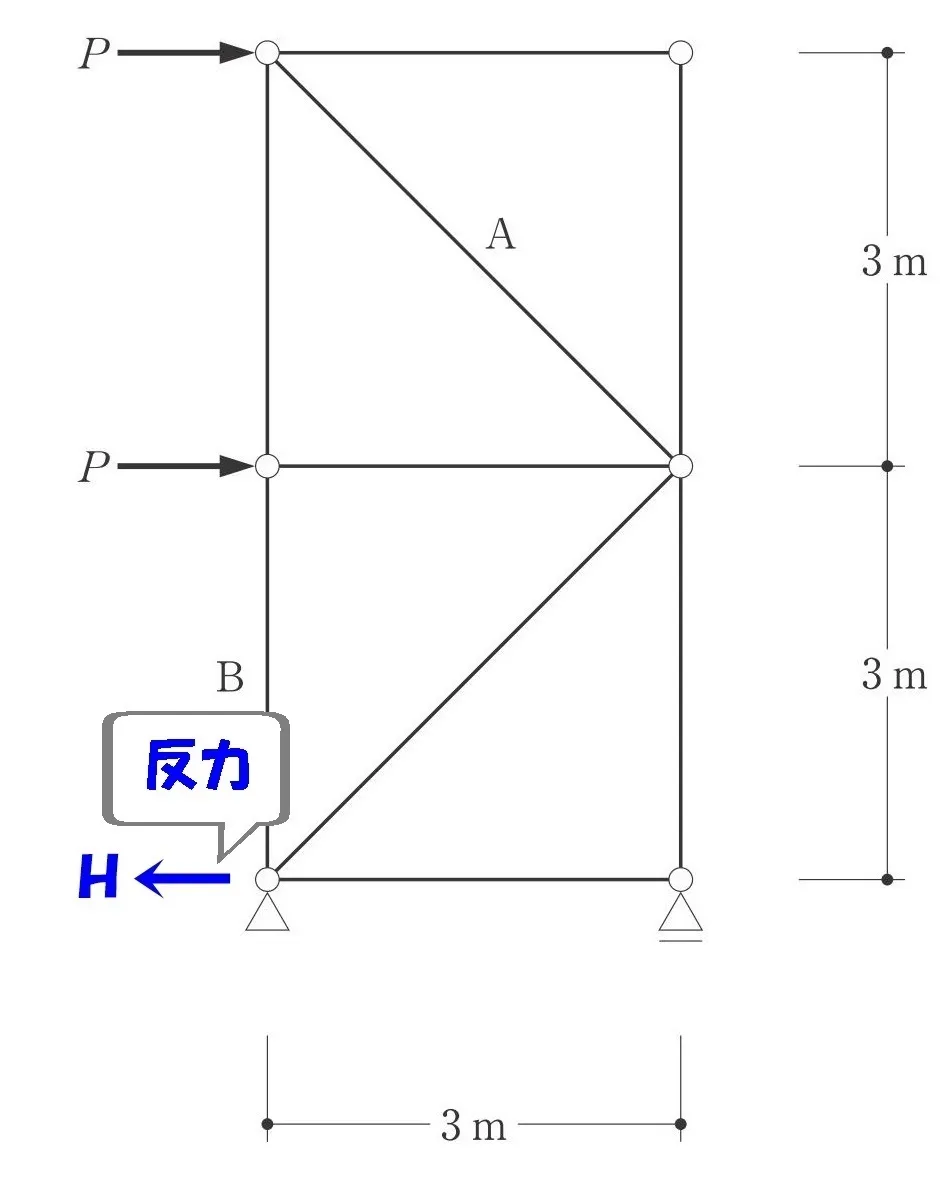

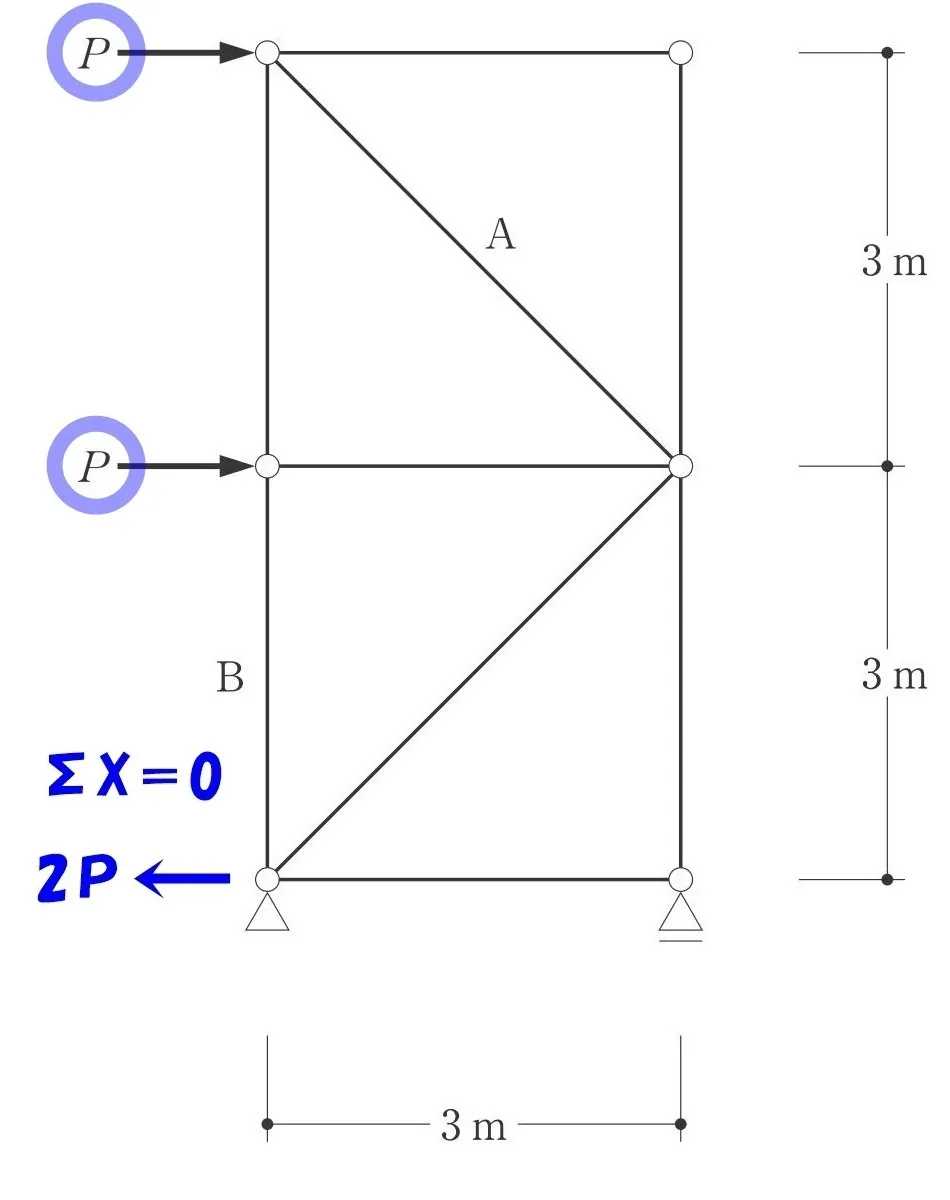

ピン支点(左)に働く水平反力Hを求める。
$$\Sigma X=0より$$$$P+P-H=0 → H=2P$$
3つの公式
$$\Sigma X=0$$$$\Sigma Y=0$$$$\Sigma M=0$$



Σコンボ!
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
トラスの節点を取り出す
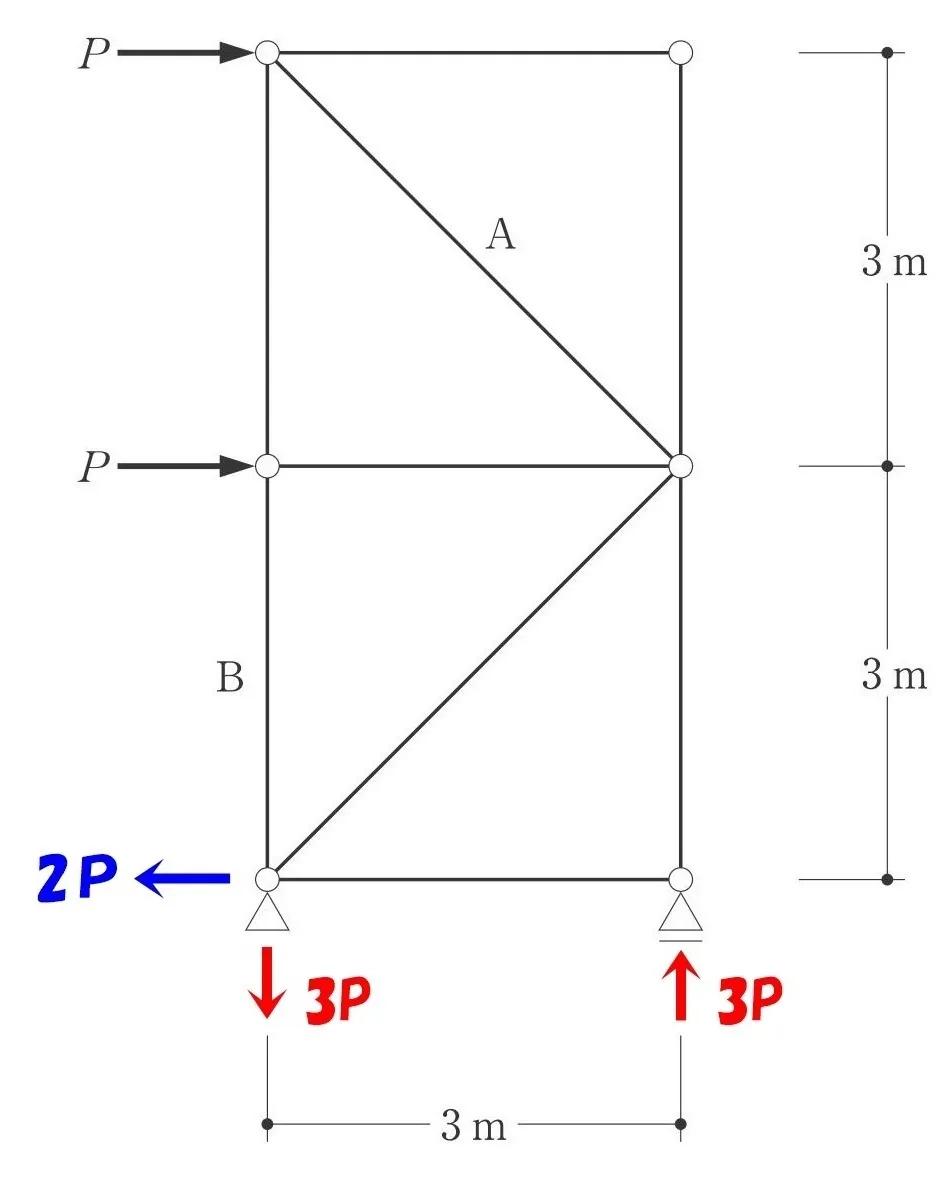





節点法:「イ」と「ロ」の接合部から、それぞれ部材を切り出す。



節点にフォーカス!
節点法とは?
トラスの節点に働く力を釣り合わせ、部材の軸力を求める方法
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
節点法「イ」


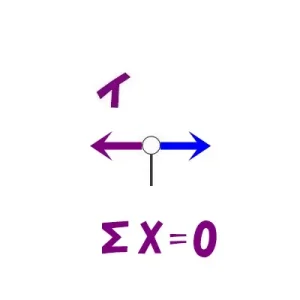

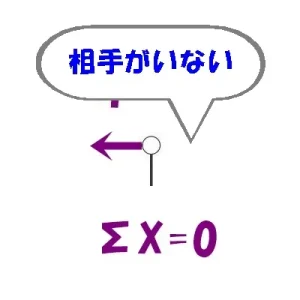

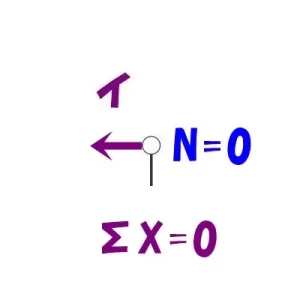

$$\Sigma X=0より$$$$N+(釣り合う相手がいない)=0なので,N=0となる$$




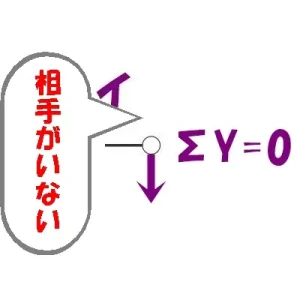

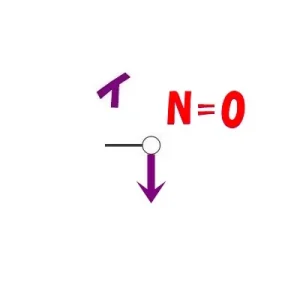

$$\Sigma Y=0より$$$$N+(釣り合う相手がいない)=0なので,N=0となる$$



相手がいない?
つまり、節点「イ」には軸力が存在しないことが分かりますよね?
このような、無くても良い部材のことを「ゼロメンバー」と呼ぶのです。



ゼロメンバーは、
幽霊部材みたいなもの。
節点法「ロ」




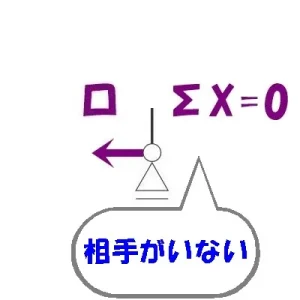

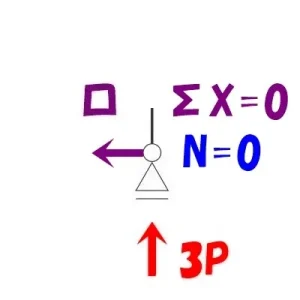

$$\Sigma X=0より$$$$N+(釣り合う相手がいない)=0なので,N=0となる$$
そもそもローラー支点は水平反力を負担しないため、当然といえるでしょう。
Y方向の釣り合い


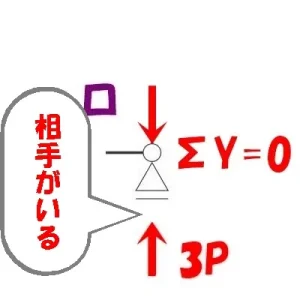

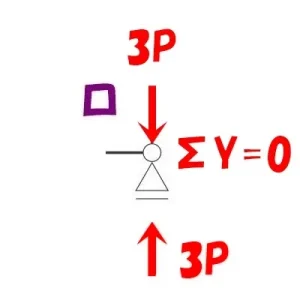

公式
ΣX=0
ΣY=0
$$\Sigma Y=0より$$$$軸力+3P(鉛直反力)=0→軸力=-3P(圧縮力)となる$$



釣り合う相手に
やっとめぐり会えた。
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
トラスの節点を取り出す
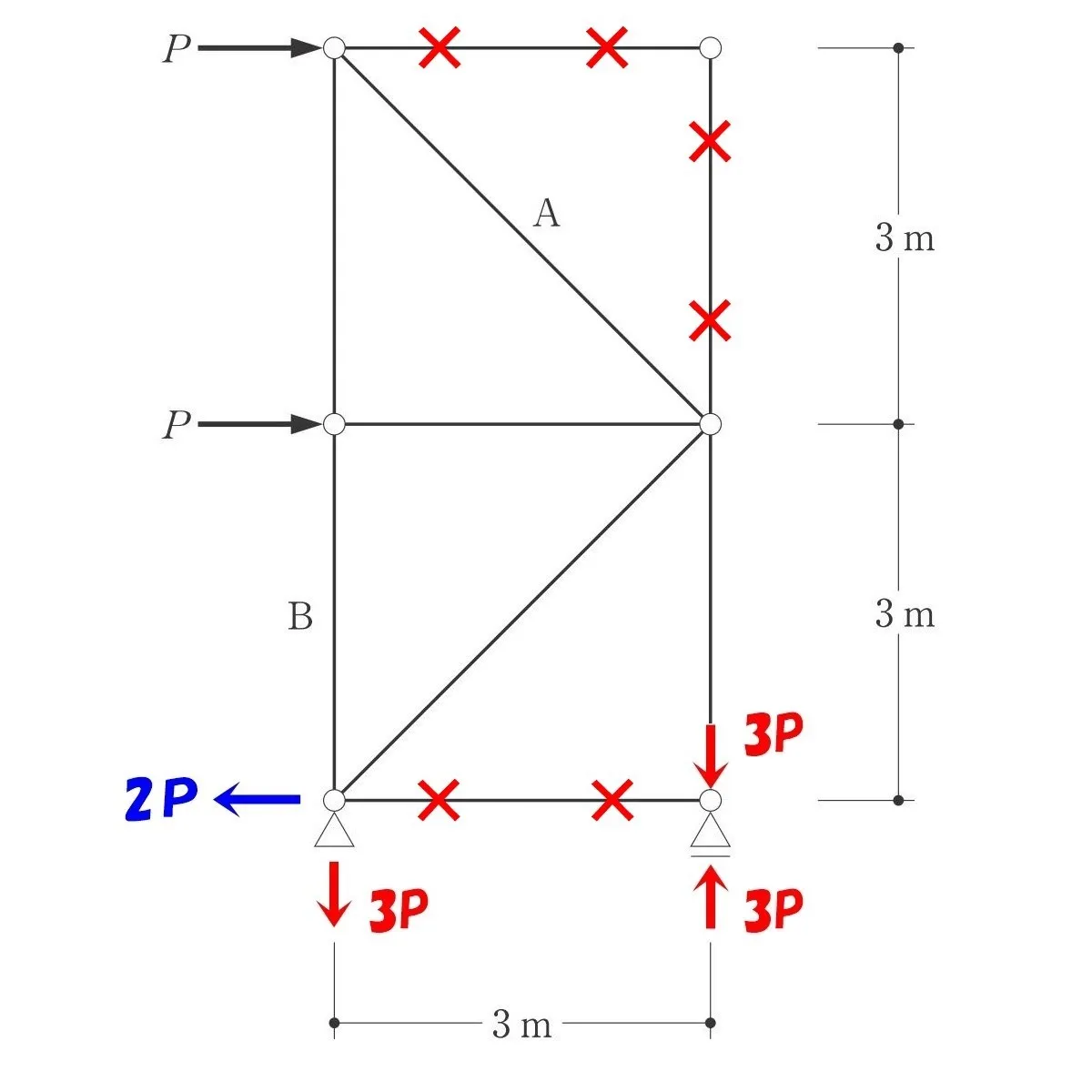

軸力を負担しないゼロメンバーには×印をする。
(釣り合い式において、扱わなくても良い)
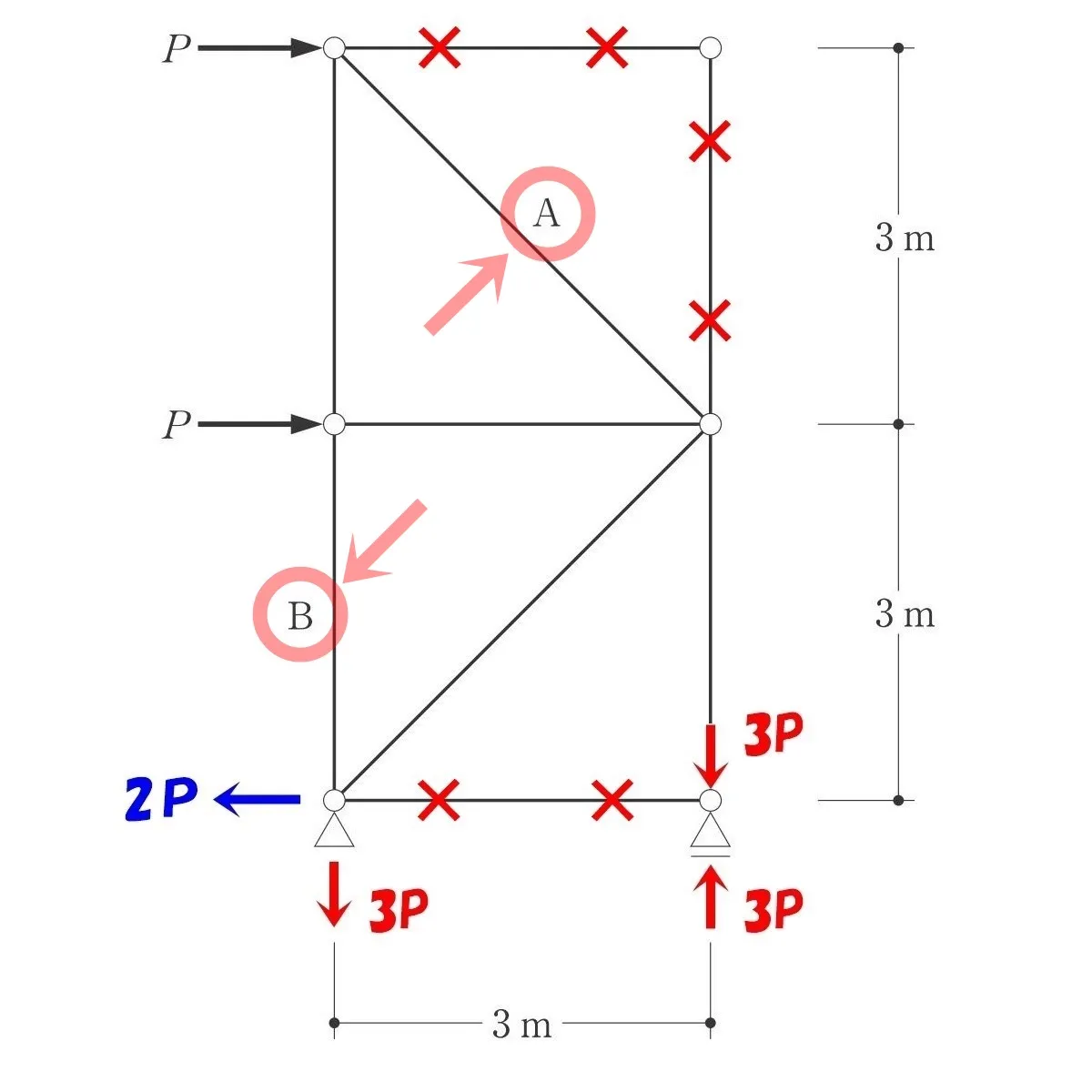

求める部材:AとBには〇印を付ける。



何を求めるのか?を
見失わないようにマークする。


節点「ハ」を切り出し、釣り合いを取る。
(ゼロメンバー✕✕は無視する)



節点にフォーカス!
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
ベクトルを分解する
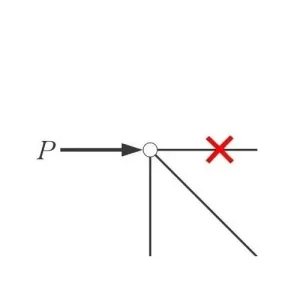

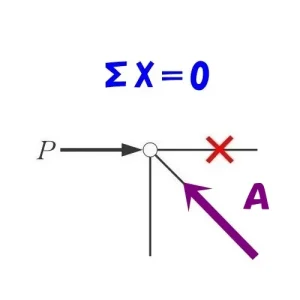

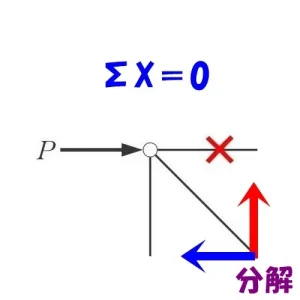

ゼロメンバー✕は無視する。
ななめ部材の軸力AをX方向とY方向のベクトルに分解する。



ベクトルを分解する。
節点法「ハ」
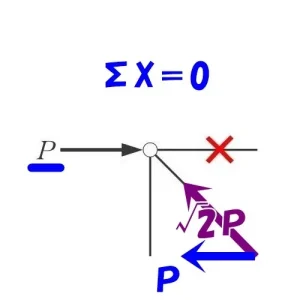

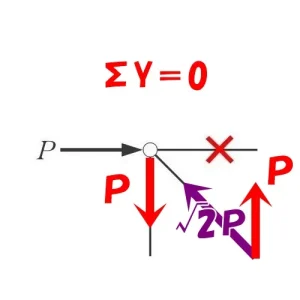

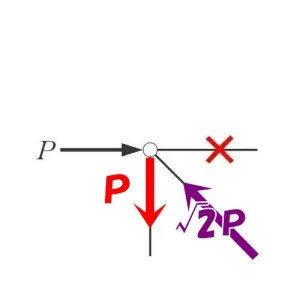

$$\Sigma X=0より$$$$P(水平力)+A*\frac{ 1 }{ \sqrt{2} }=0$$$$A=-{ \sqrt{2} }*P=-{ \sqrt{2} }P(圧縮力)$$
$$\Sigma Y=0より$$$$-{ \sqrt{2} }P*\frac{ 1 }{ \sqrt{2} }+軸力=0$$$$タテ部材の軸力=+P(引張り力)$$
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
トラスの節点を取り出す
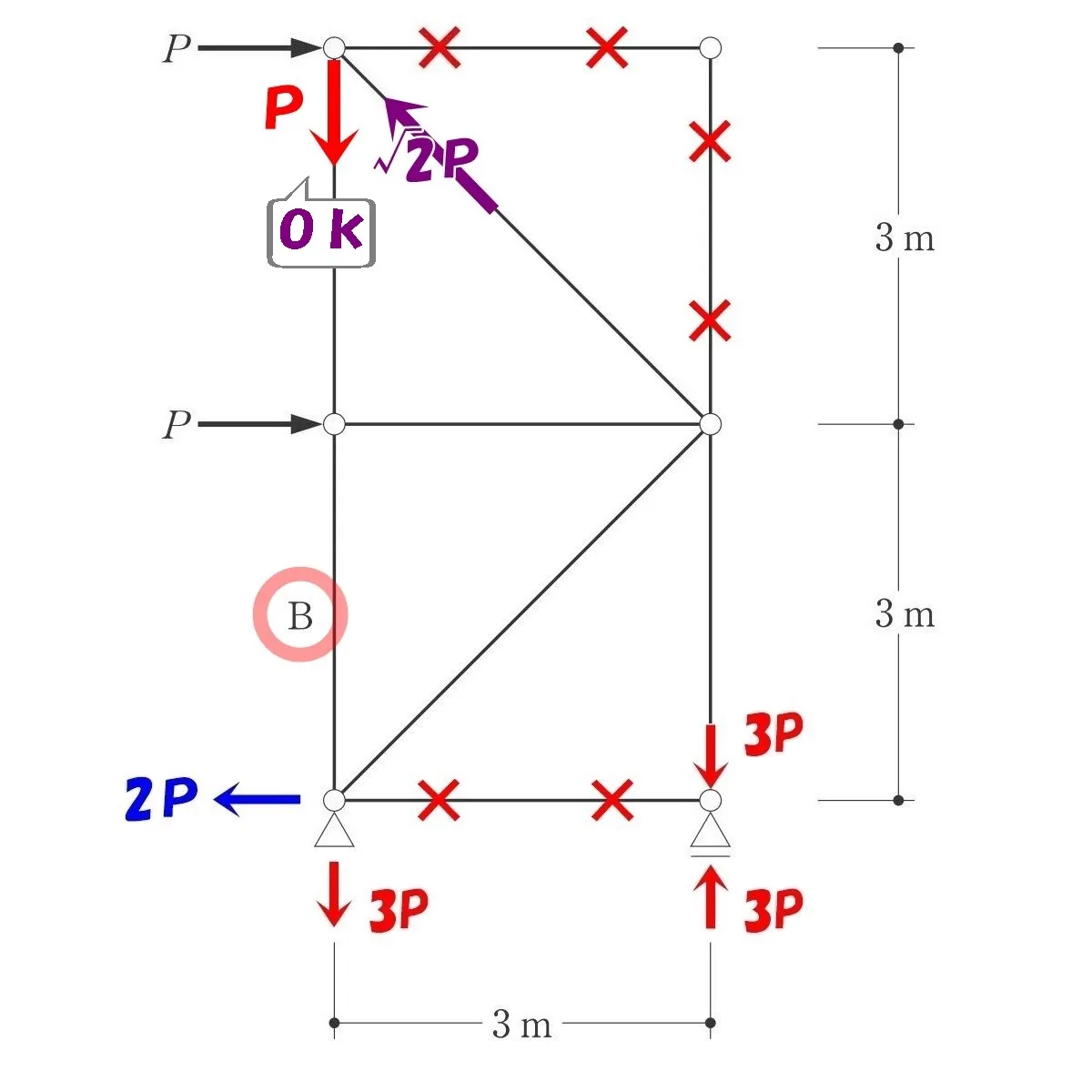

節点法より、ななめ部材の軸力=√2P、タテ部材の軸力=Pとなる。
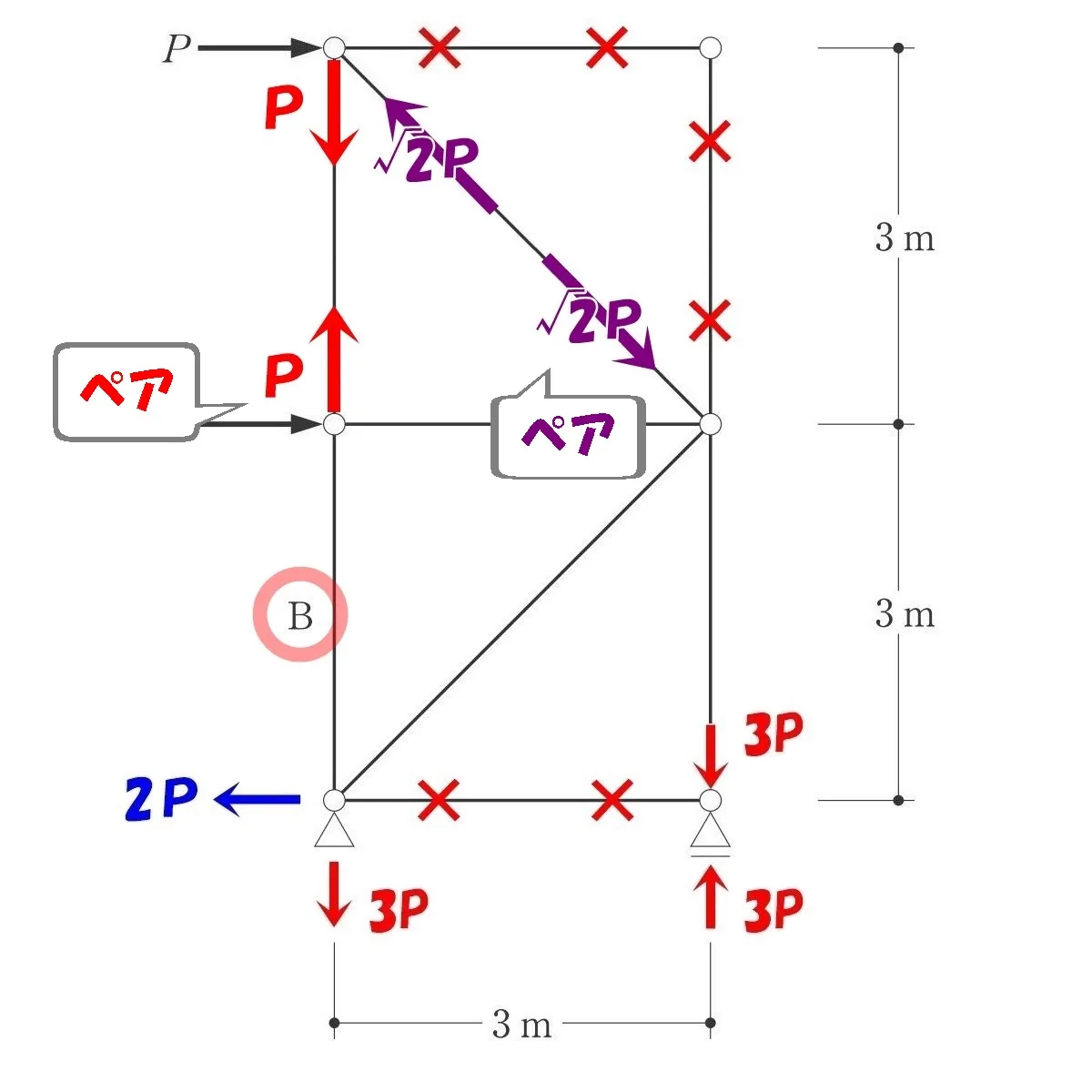

ななめ部材の軸力=√2Pとタテ部材の軸力=Pは、両端でペアとなる。
つまり、反対側の軸力もそれぞれ√2PとPになる。
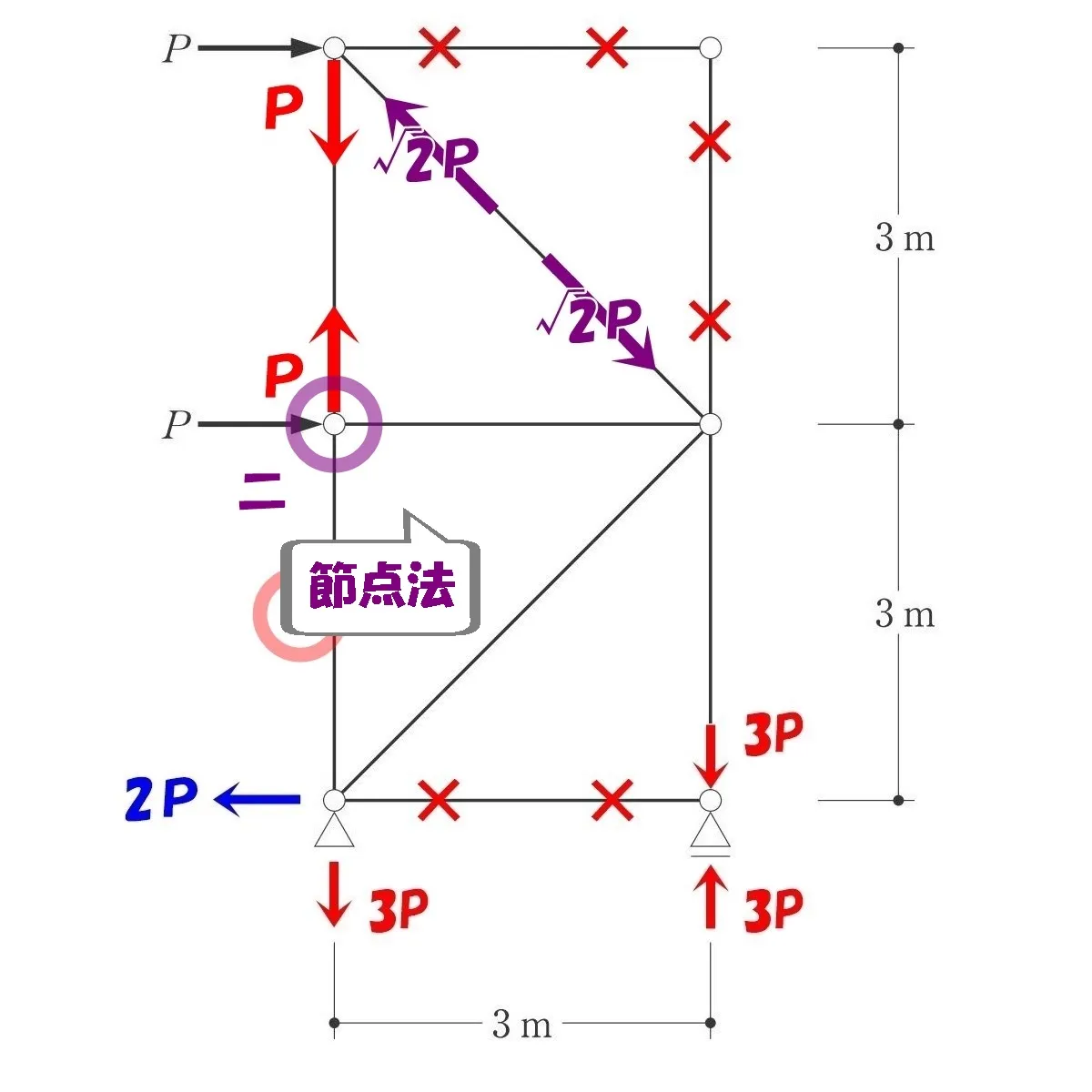

節点「二」を切り出し、力の釣り合いを取る。



節点にフォーカス!
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
節点法「二」
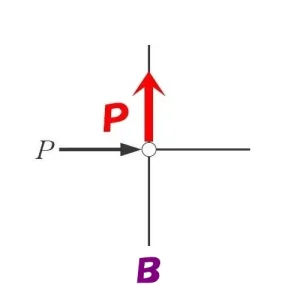

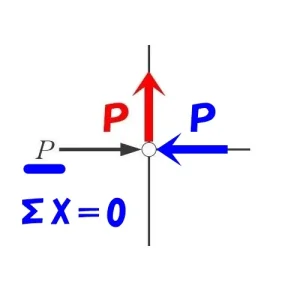


$$\Sigma X=0より$$$$-P(水平力)+軸力=0$$$$ヨコ部材の軸力=P(圧縮力)$$
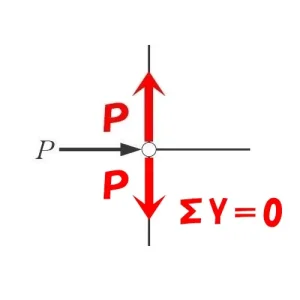
$$\Sigma Y=0より$$$$+P-軸力=0$$$$タテ部材の軸力=P(引張り力)$$
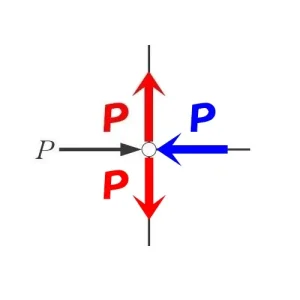

節点法
$$トラスの軸力は,\Sigma X=0,\Sigma Y=0で釣り合う$$


トラス・マジック!
トラスの軸力を書き込む
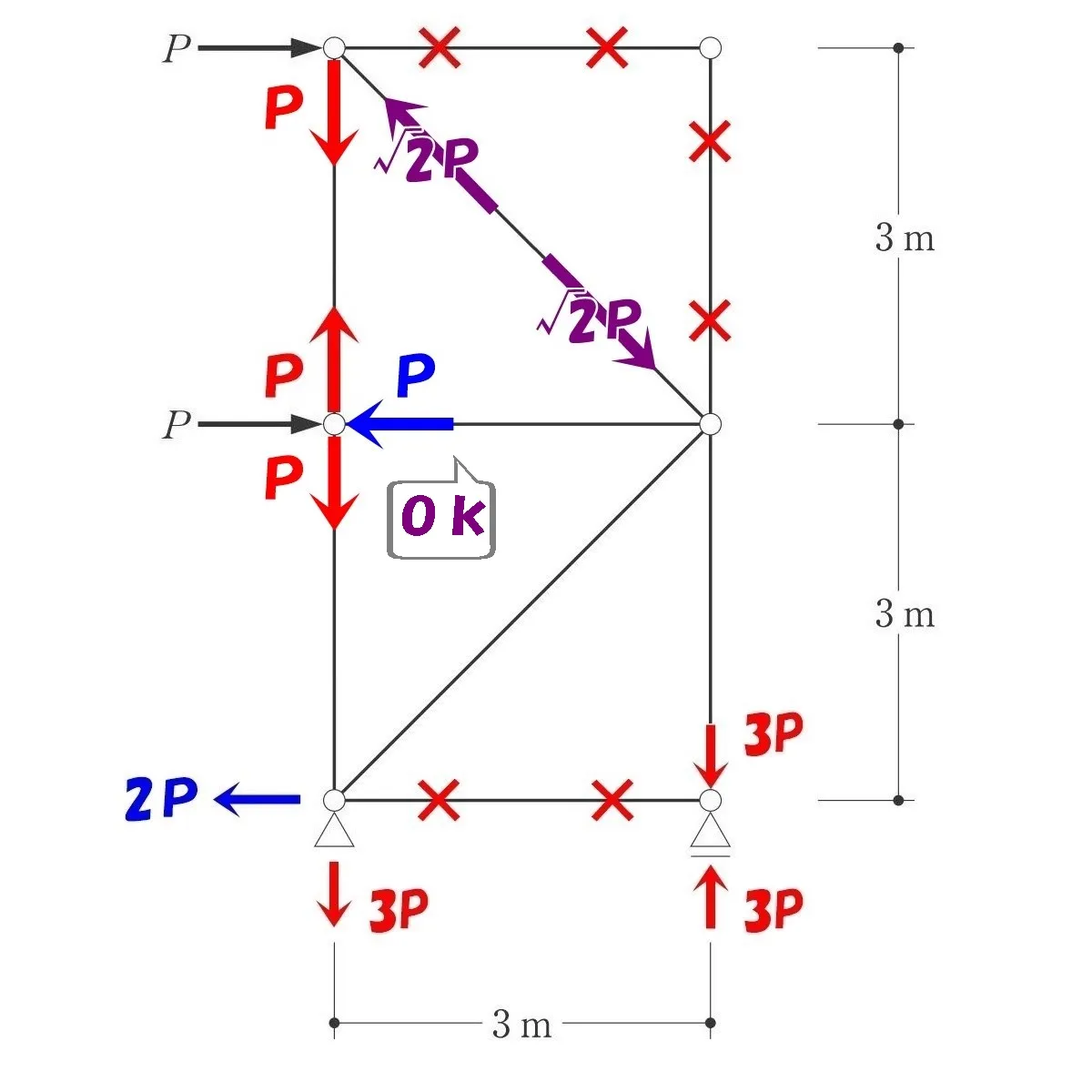

節点法より、ヨコ部材の軸力=P、タテ部材の軸力=Pとなる。
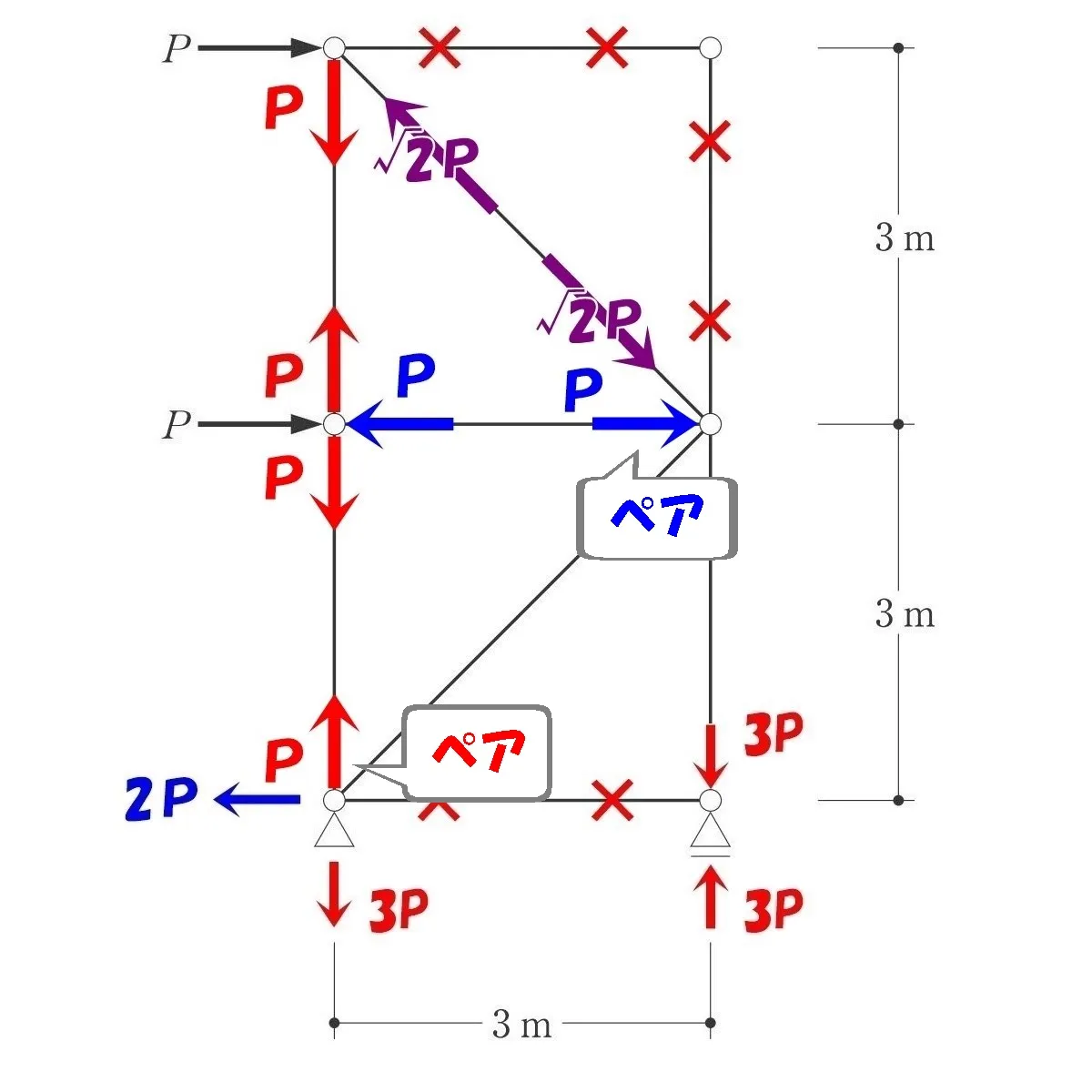

ヨコ部材とタテ部材の軸力=PとPは、両端でペアとなる。
つまり、反対側の軸力もそれぞれP(圧縮)とP(引張り)になる。
ここで、柱脚のピン支点(左)を取り出し、力の釣り合いを取りましょう。



ピン支点にフォーカス!
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
軸力と反力を差し引きする
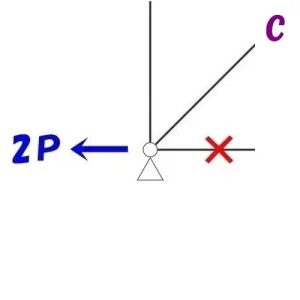

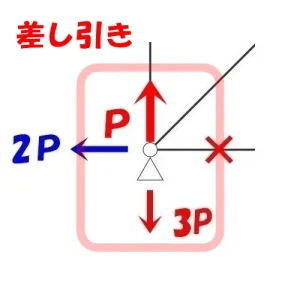

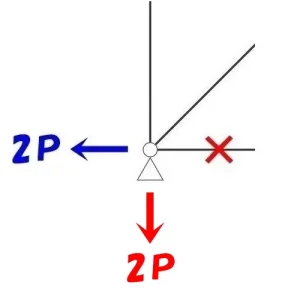

$$Y方向の力=P-3P=-2P$$
タテ部材の軸力Pとピン支点の反力3Pを差し引きすると、X方向の力は2P(下向き)となる。



軸力は相殺できるの!?



ゼロメンバーは無視ね。
節点法「ピン支点」
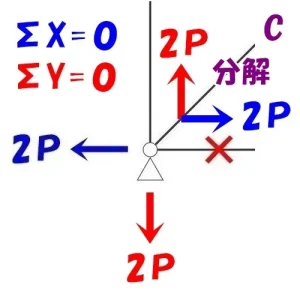


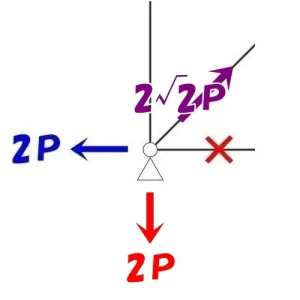

$$\Sigma X=0より$$$$2P(水平力)-軸力*\frac{ 1 }{ \sqrt{2} }=0$$$$軸力={ \sqrt{2} }*2P=2{ \sqrt{2} }P(引張り力)$$
$$\Sigma Y=0より$$$$2P(鉛直反力)-軸力*\frac{ 1 }{ \sqrt{2} }=0$$$$軸力={ \sqrt{2} }*2P=2{ \sqrt{2} }P(引張り力)$$



何とか食らいつく!


この動画を YouTube で視聴
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
トラスの節点を取り出す
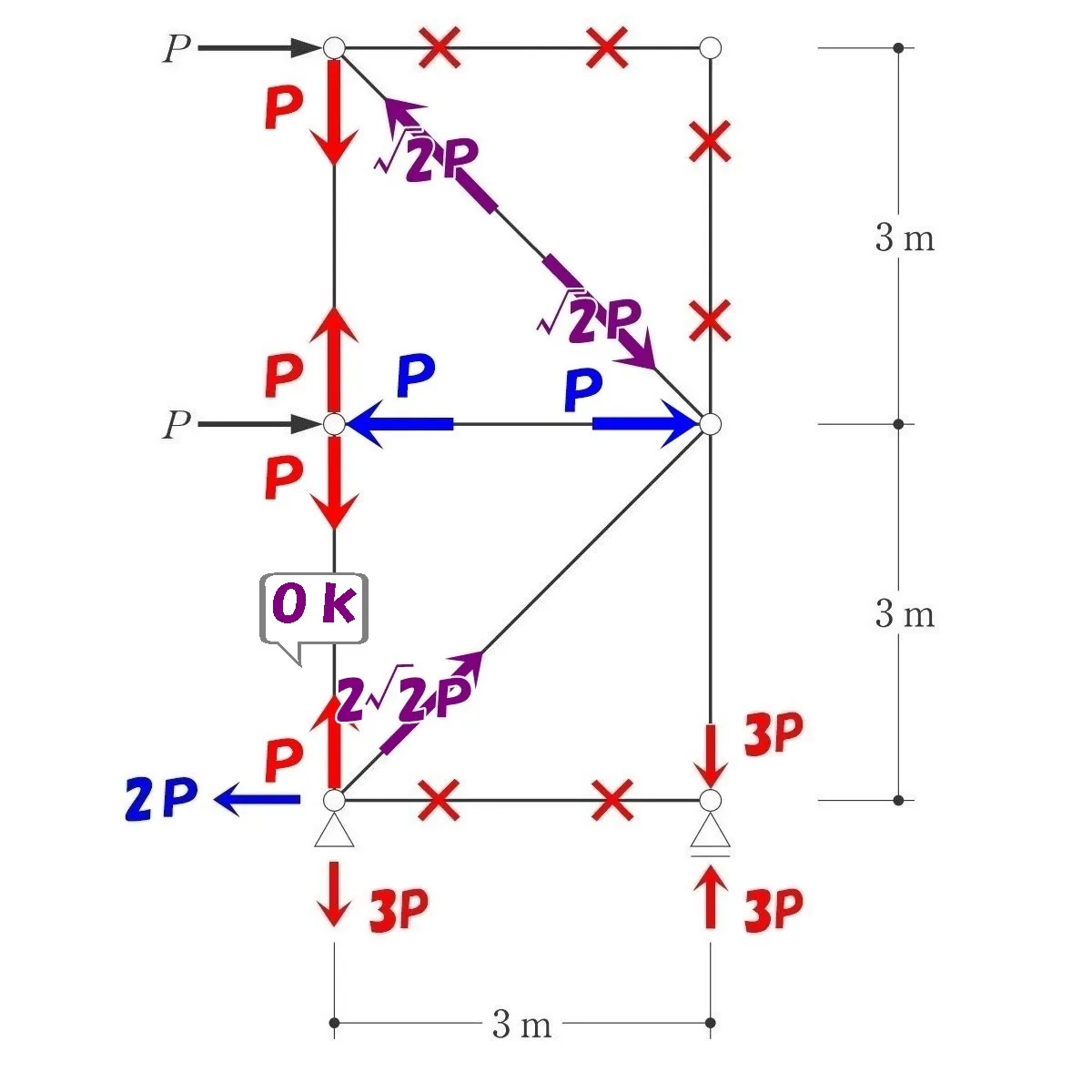

節点法より、ななめ部材の軸力=2√2Pとなる。
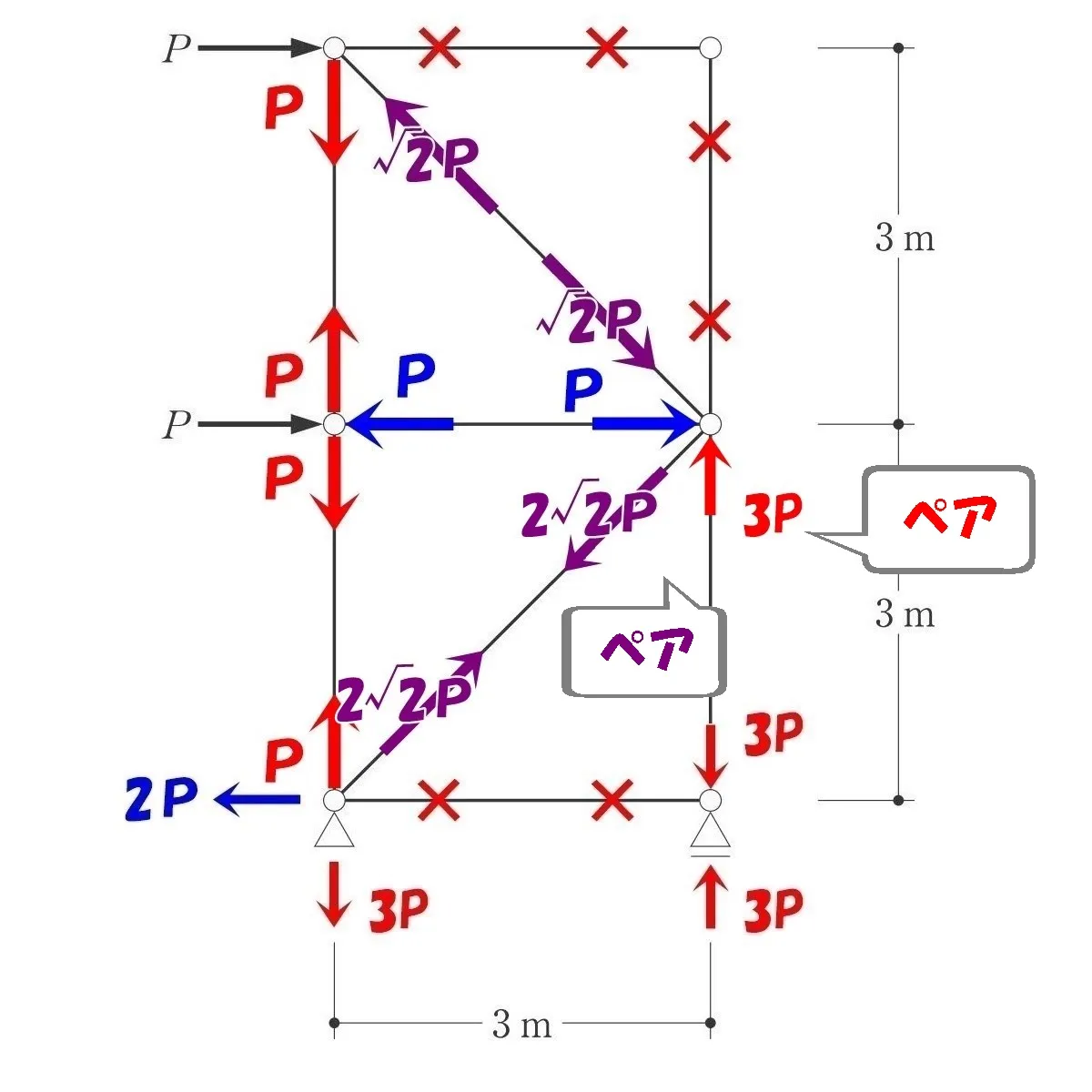

ななめ部材の軸力=2√2Pは両端でペアとなるため、反対側の軸力も2√2Pとなる。
ローラー支点(右)の力の釣り合いより、タテ部材の軸力=3Pの反対側も3Pとなる。
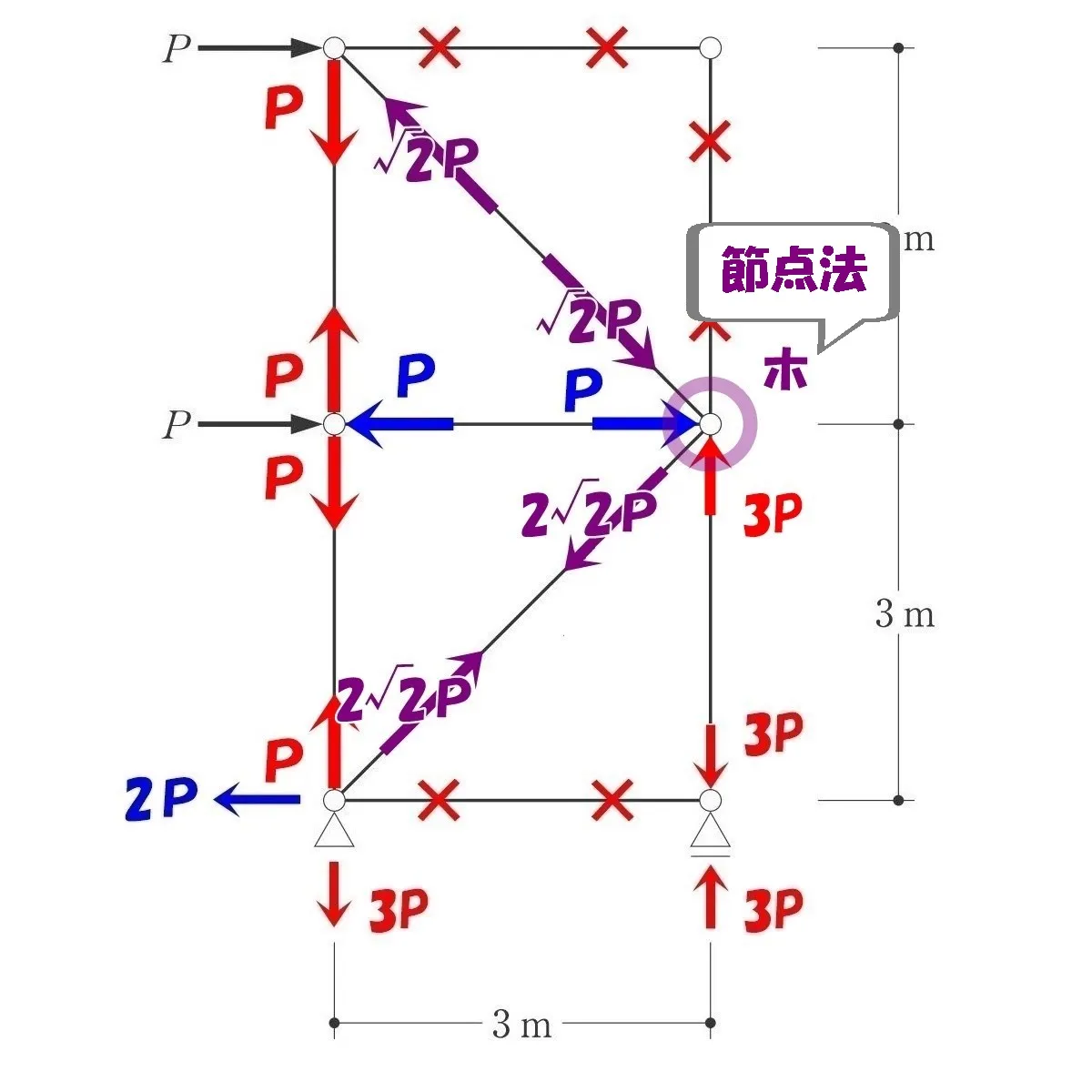

節点「ホ」を切り出し、力の釣り合いを取る。



節点にフォーカス!
節点法「ホ」
最後に節点「ホ」を取り出し、力の釣り合いを確認しましょう。
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
X方向の釣り合い
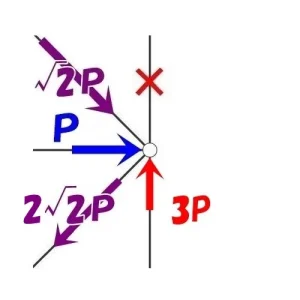

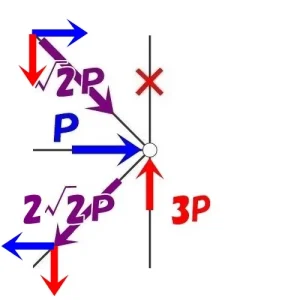

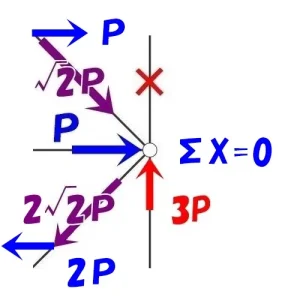

$$-P(ヨコ部材)-{ \sqrt{2} }P*\frac{ 1 }{ \sqrt{2} }+2{ \sqrt{2} }P*\frac{ 1 }{ \sqrt{2} })$$
$$-P-P+2P=0となり,\Sigma X=0が成り立つ。$$



シグマ・X
Y方向の釣り合い


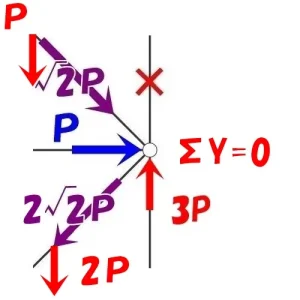

$$\Sigma Y=0$$$$+上向き$$$$-下向き$$
$$+3P(タテ部材)-{ \sqrt{2} }P*\frac{ 1 }{ \sqrt{2} }-2{ \sqrt{2} }P*\frac{ 1 }{ \sqrt{2} })$$
$$+3P-P-2P=0となり,\Sigma Y=0が成り立つ。$$



シグマ・Y
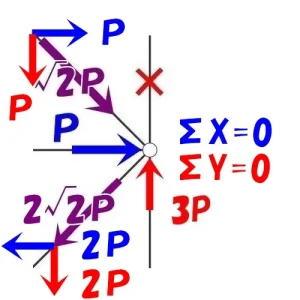

節点法
$$トラスの軸力は,\Sigma X=0,\Sigma Y=0で釣り合う$$



トラス・マジック!
求める軸力AとBの答えは?
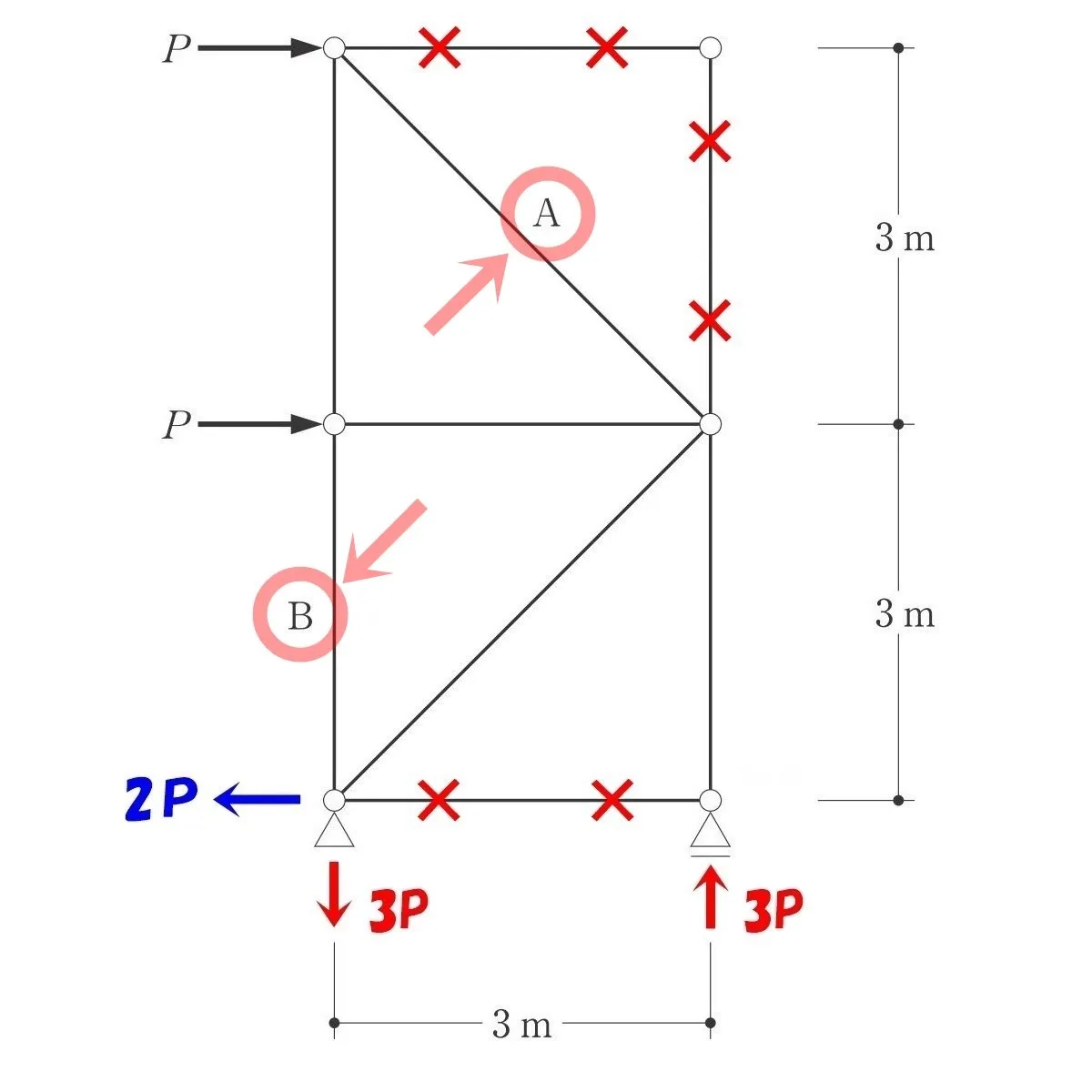

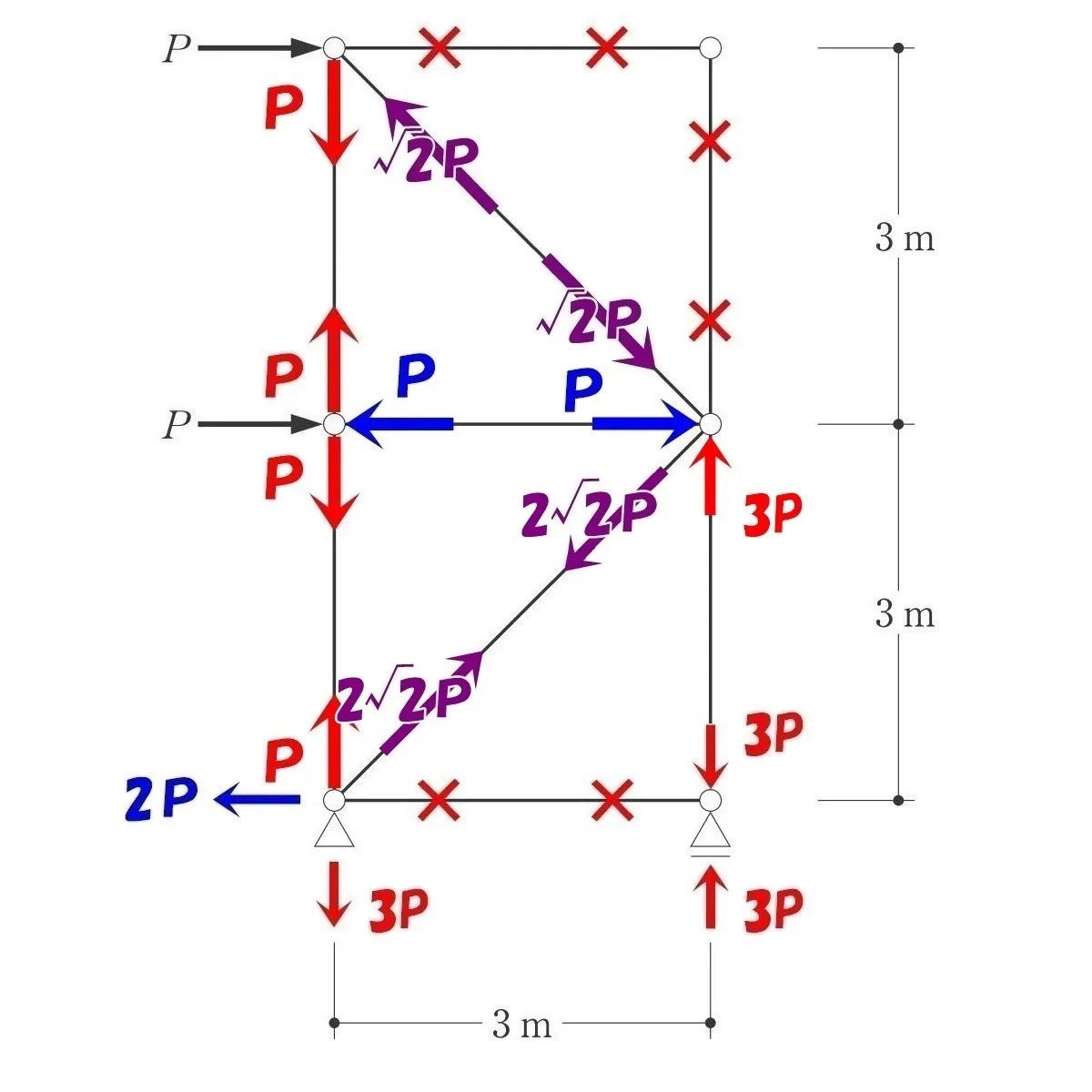

$$ななめ部材の軸力A=-{ \sqrt{2} }P(圧縮力)$$$$タテ部材の軸力B=+P(引張り力)となる。$$



恐れ入りました。
注意点
圧縮力や引張り力は、部材そのものに働く力ではありません。
節点に向かって来るベクトルを圧縮力、節点を引っ張るベクトルを引張り力と呼ぶのです。
4.切断法で求める(別解)



斬る?
No.1-切断法(別解)
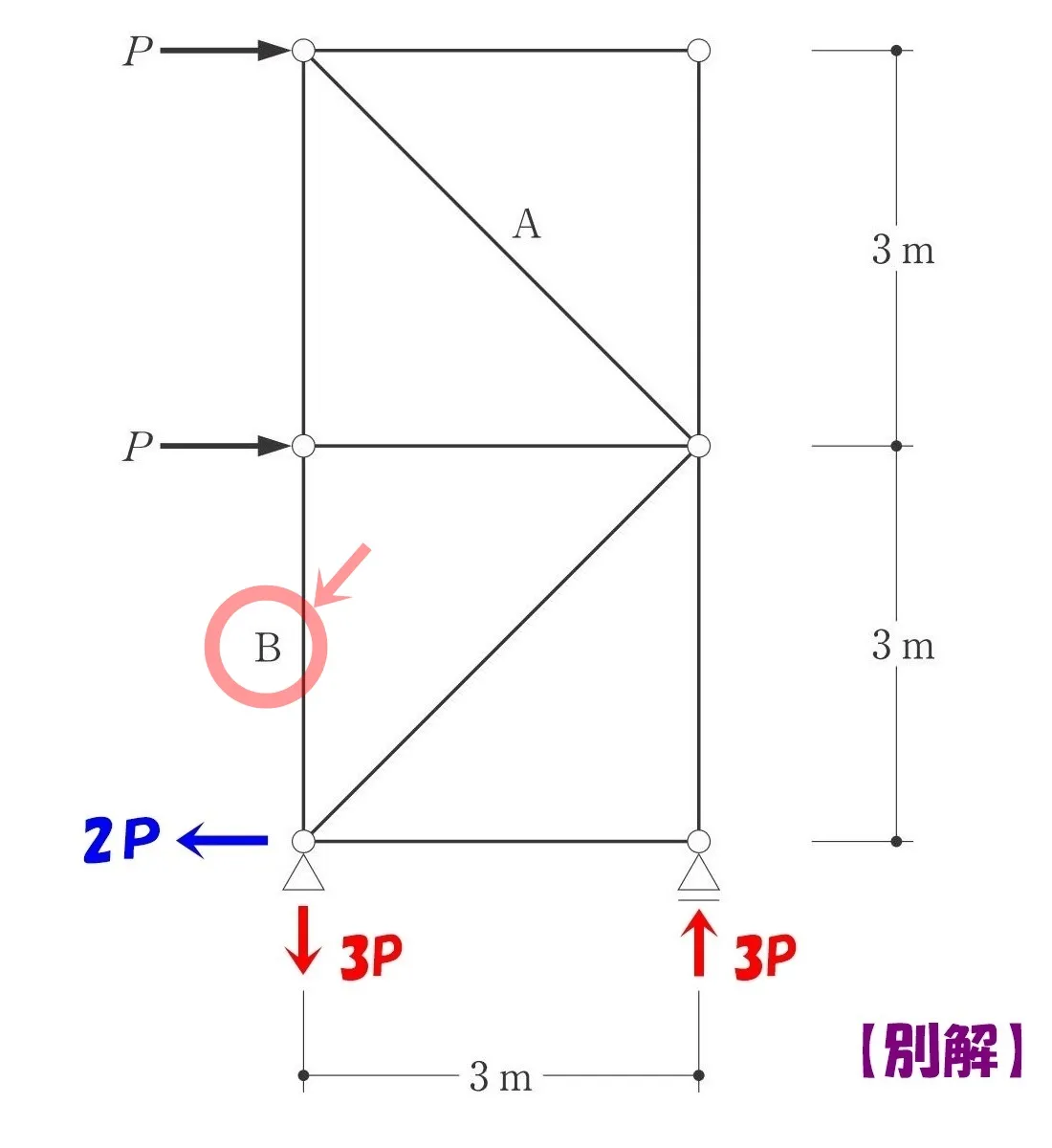

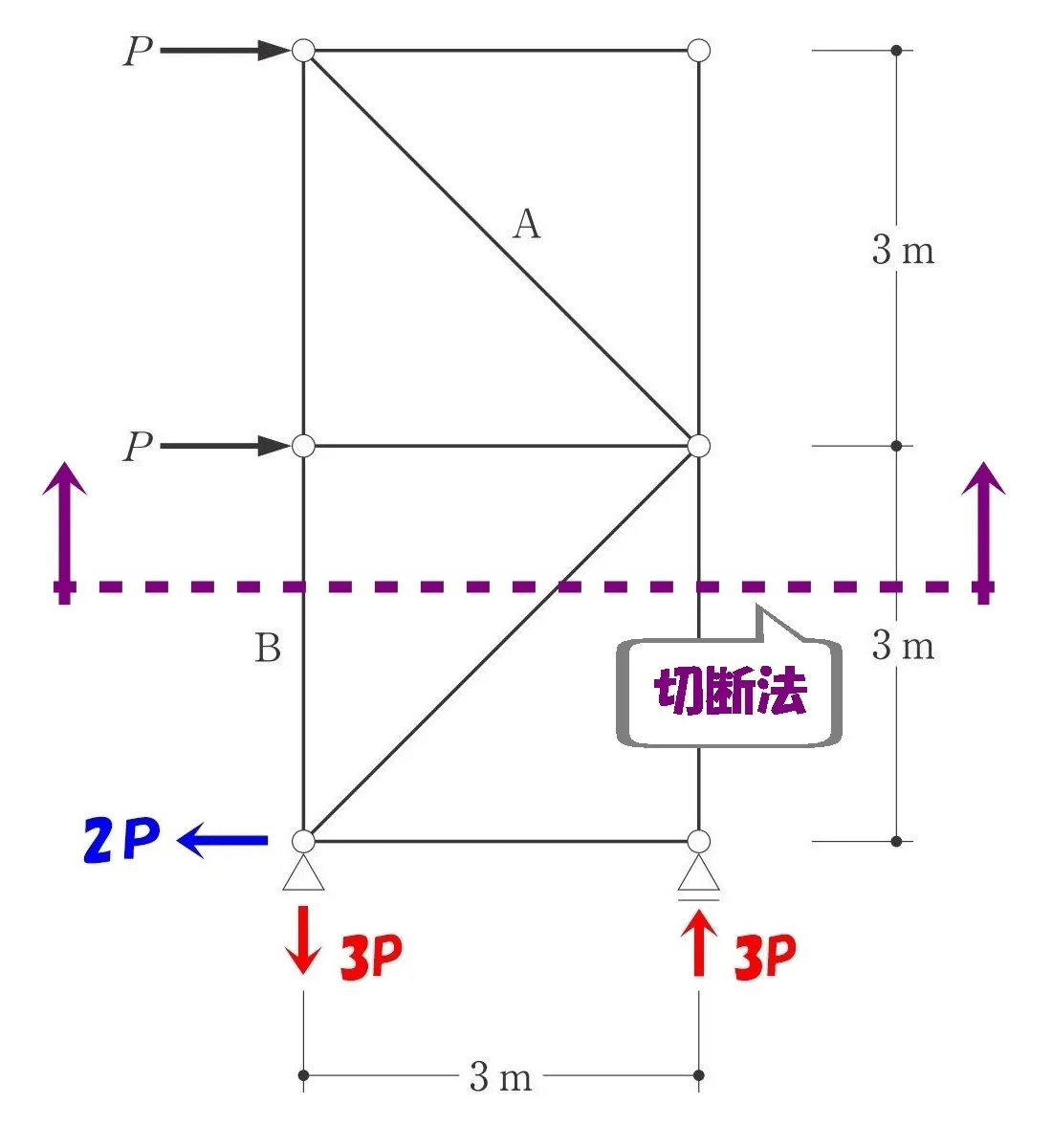

部材「B」を含む部分を切断して、上部のみを取り出す。
力の釣り合いを使って、タテ部材の軸力「B」を求めて見ましょう。



部材斬り!
モーメントの釣り合いを取る
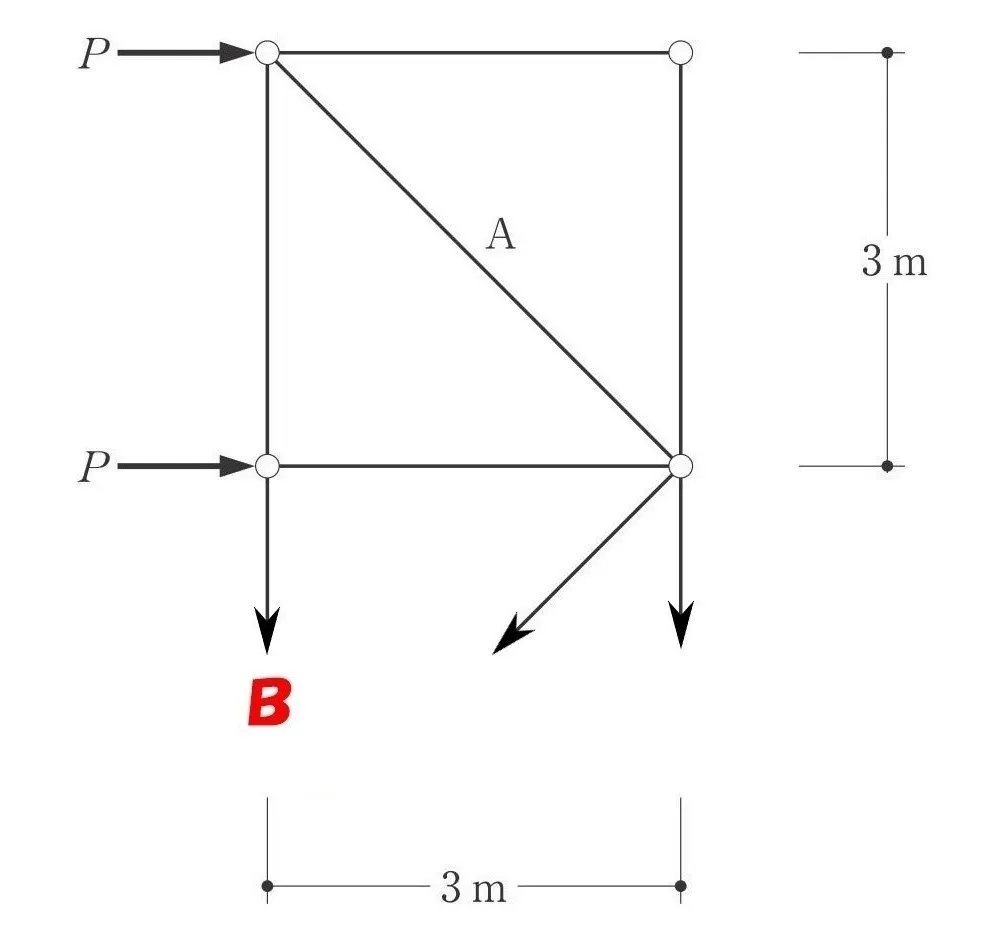

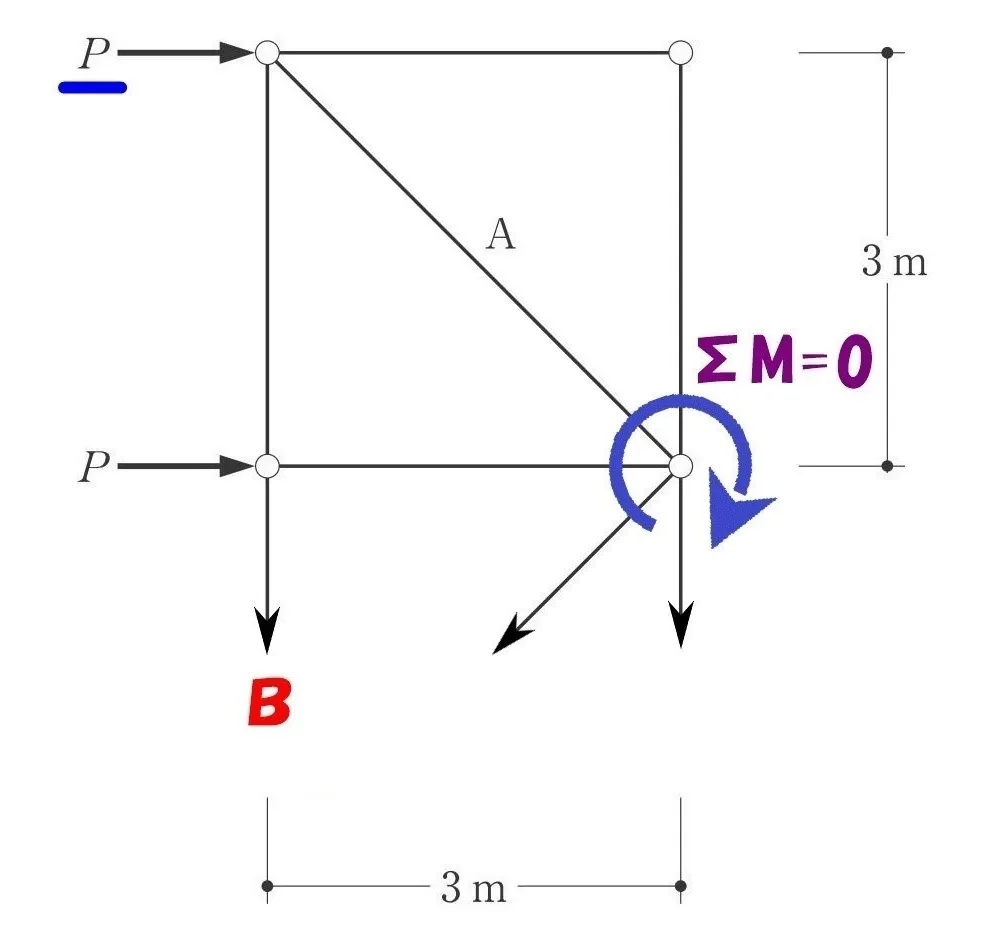

多くの部材の力が集中する節点(右)に注目してみましょう。
ここに回転軸の起点を取ることで、モーメント=力×距離のうちの「距離」がゼロとなります。



シグマ・M
モーメントの釣り合い
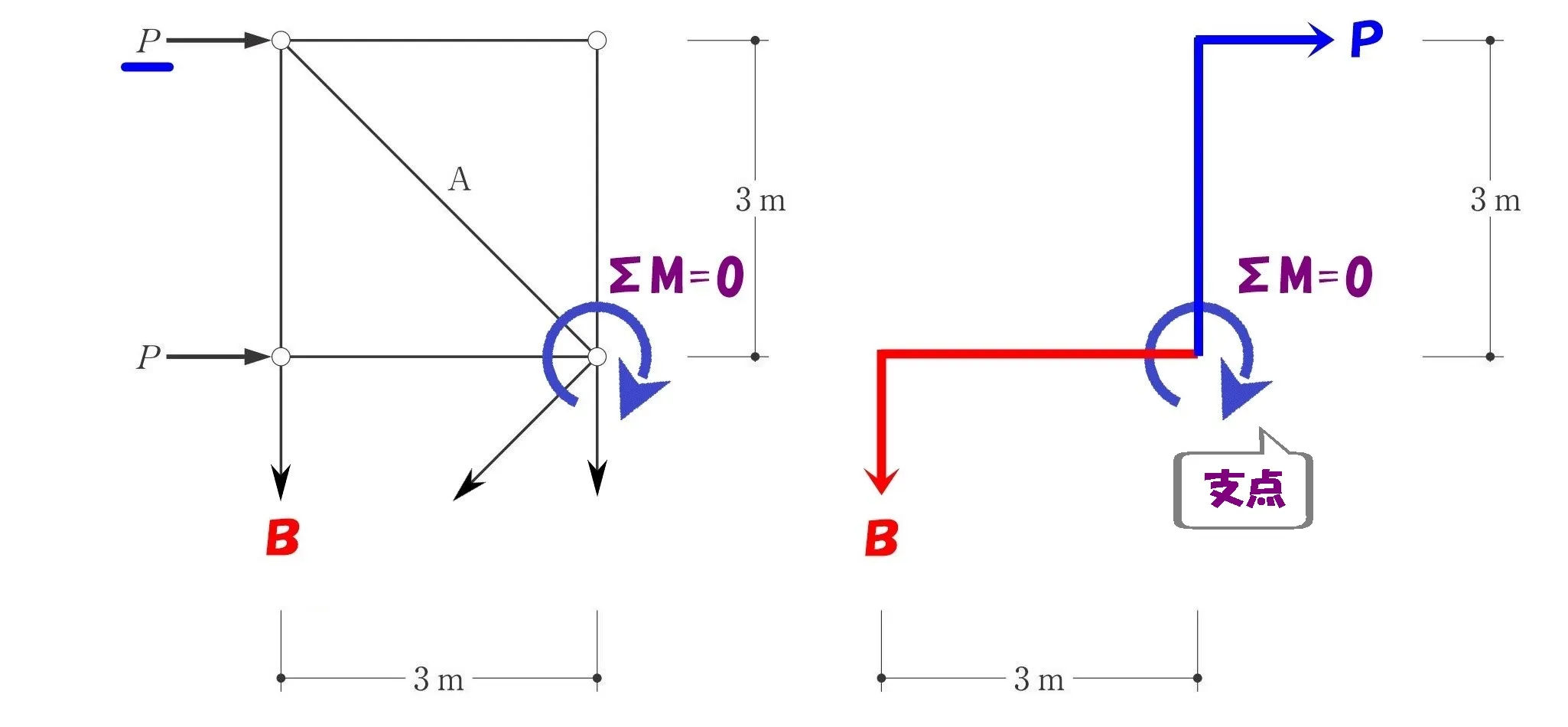

$$\Sigma M=0より,$$$$+P*3-B*3=0→タテ部材の軸力B=+P(引張り力)$$



つまらぬモノを
斬ってしまった。
答え.3
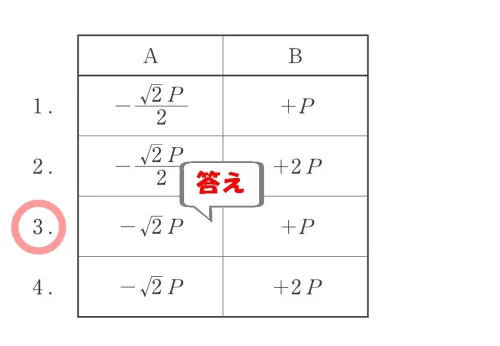

節点法の攻略ポイント
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。


この動画を YouTube で視聴
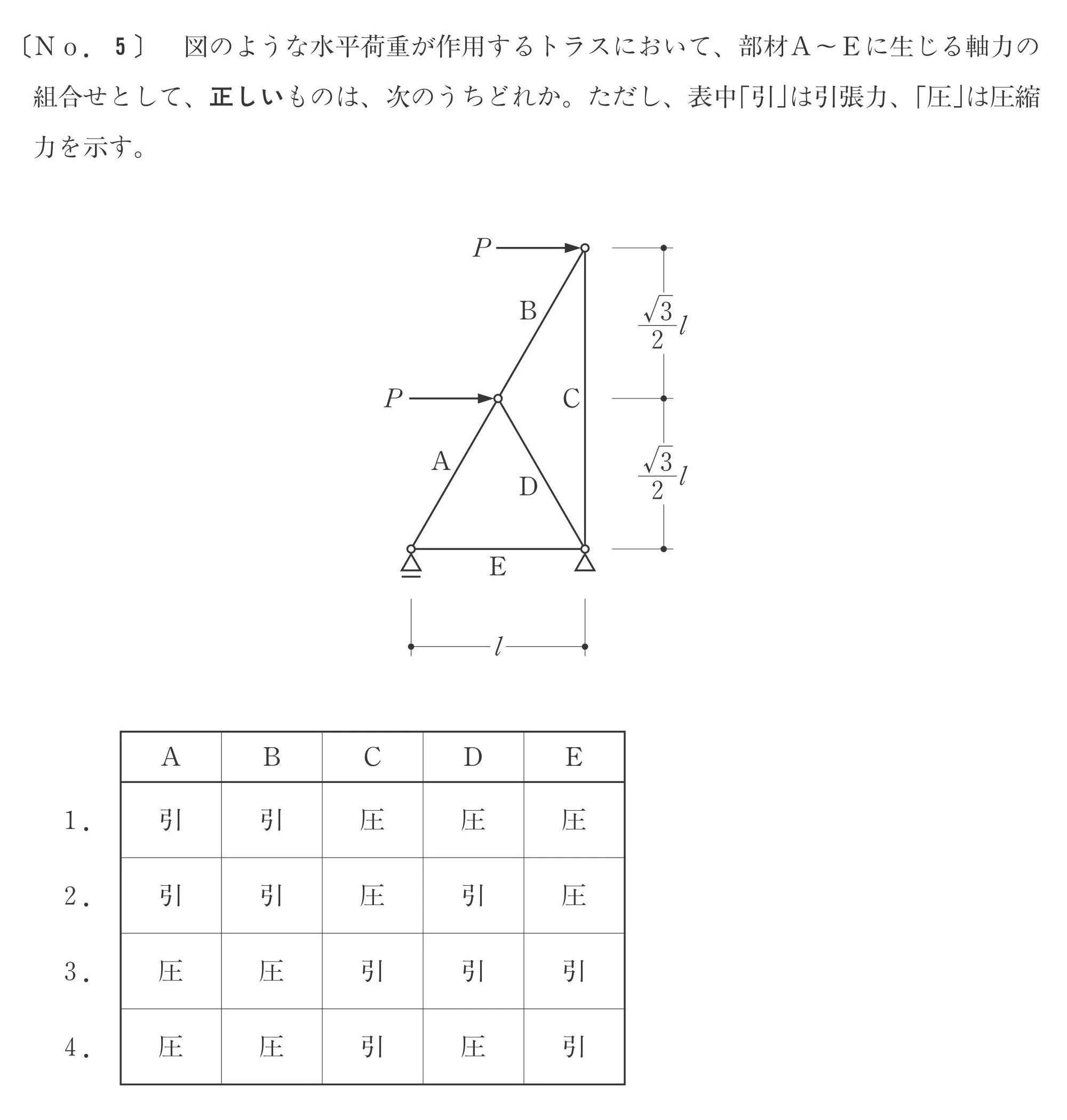
トラスの過去問に挑戦!(No.2-図解法)


図解法とは?
トラスの部材の軸力をベクトルとして図示して、三角比で求める方法
図解法の攻略ポイント
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。


この動画を YouTube で視聴



No.2

引張り力と圧縮力の考え方



考えてみよう。
図を90度回転させる
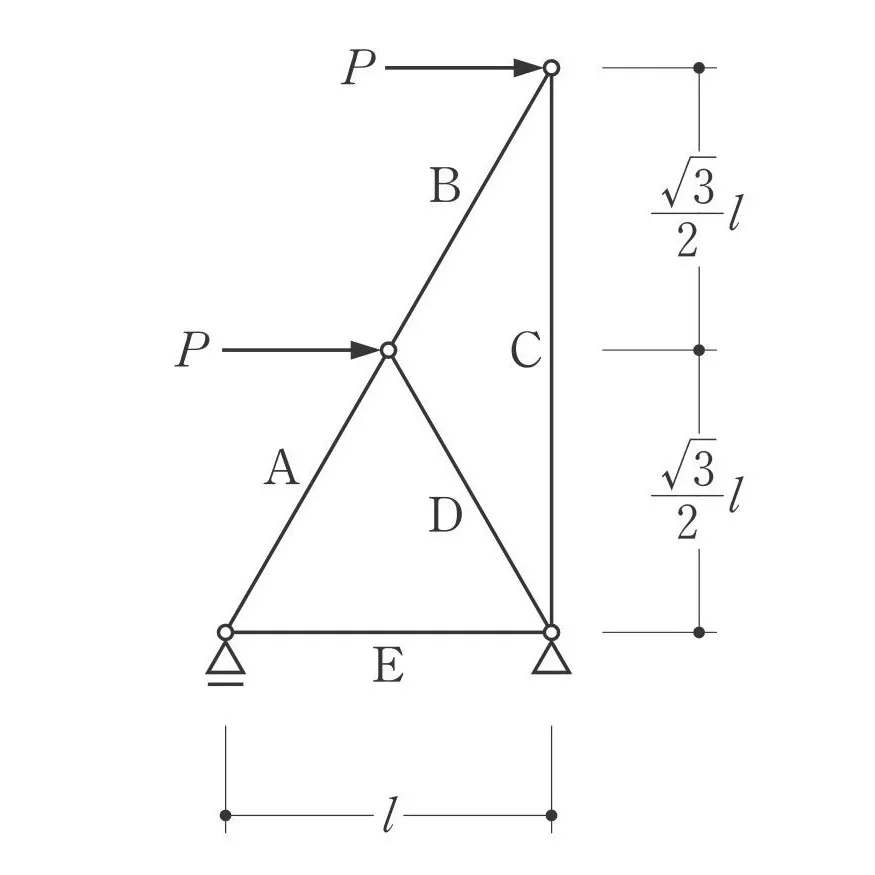



トラスを90度回転させてみる。
そうすると部材はヨコ向きになり、外力は下向き⇩となって、あるモノに見えて来ませんか?



何に見える?
片持ち梁と同じかたち
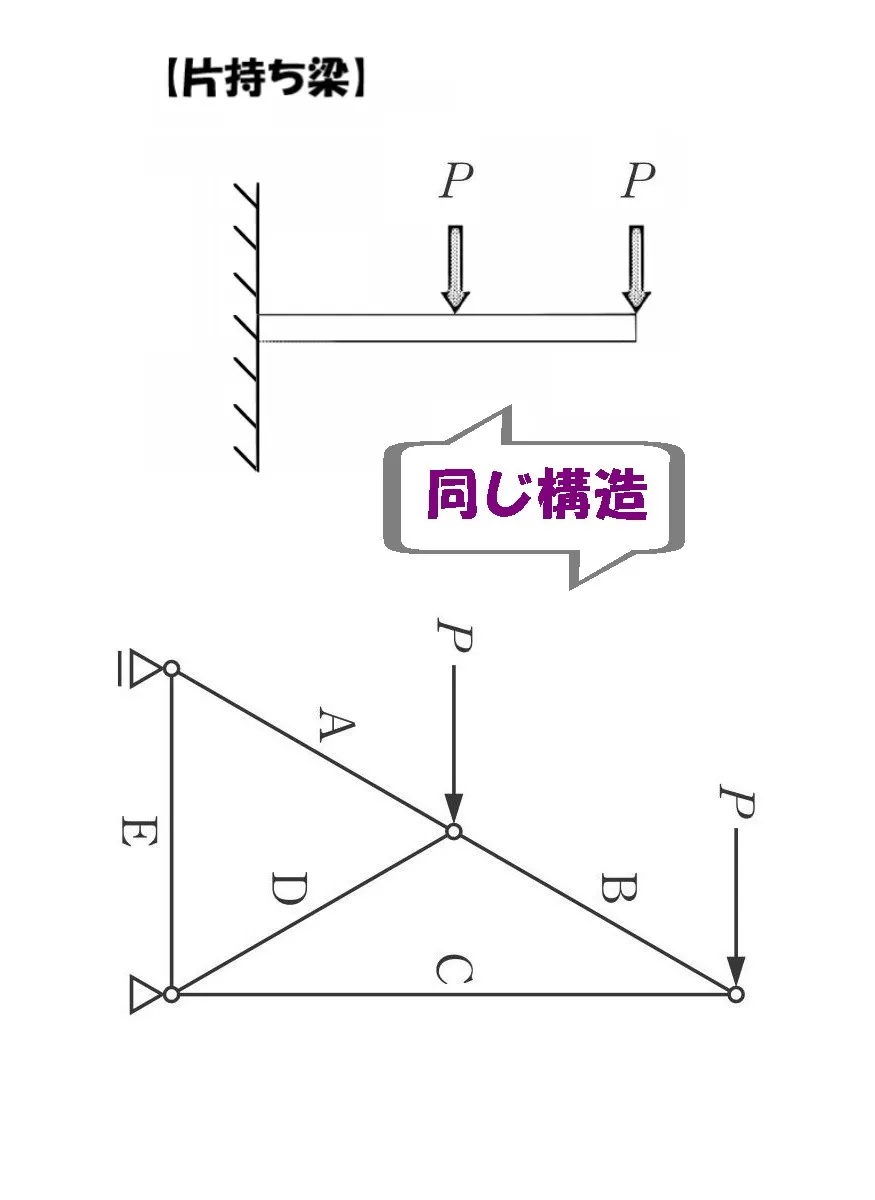

そうです!
片持ち梁と同じかたちになるのが分かりますよね?
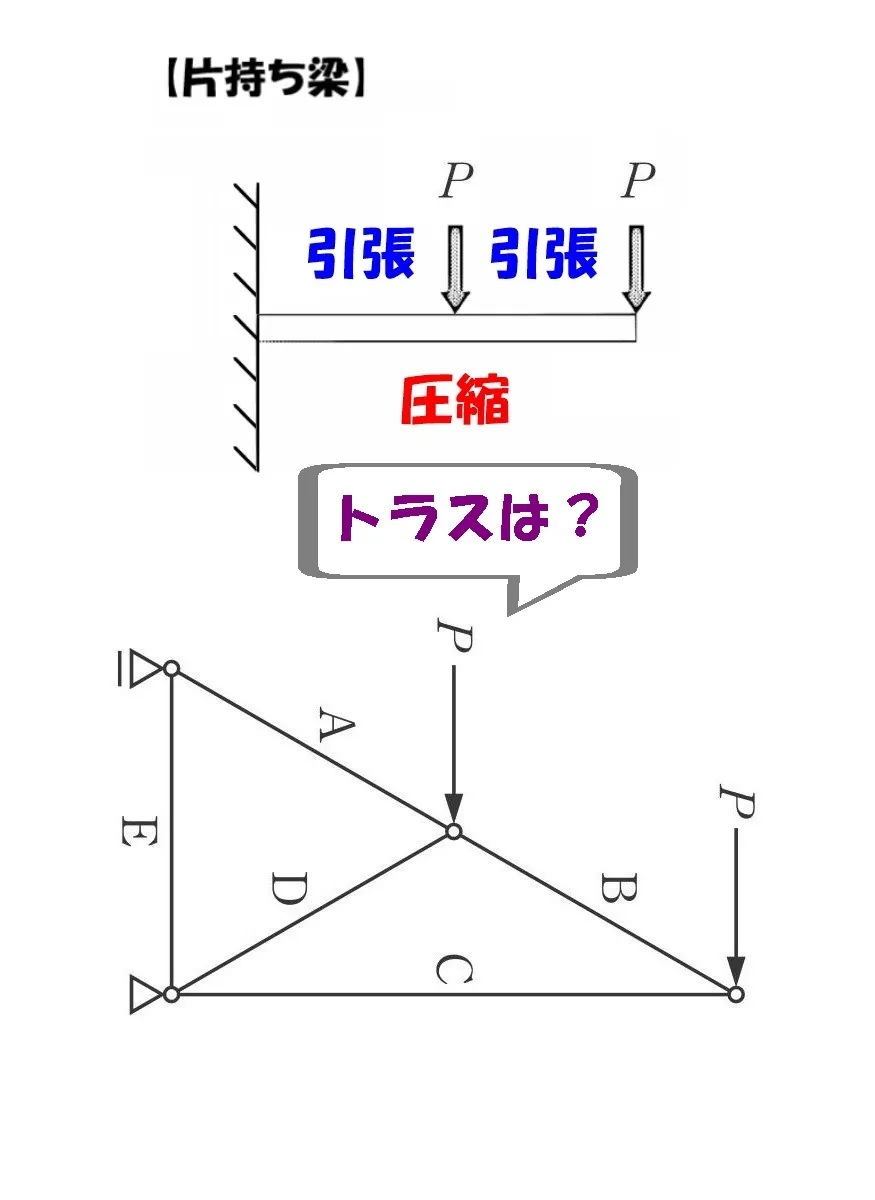

片持ち梁に下向き⇩の力が加わると、梁の上面には引張り力、底面には圧縮力が作用します。
・・・ということは、トラスの場合はどうなる?
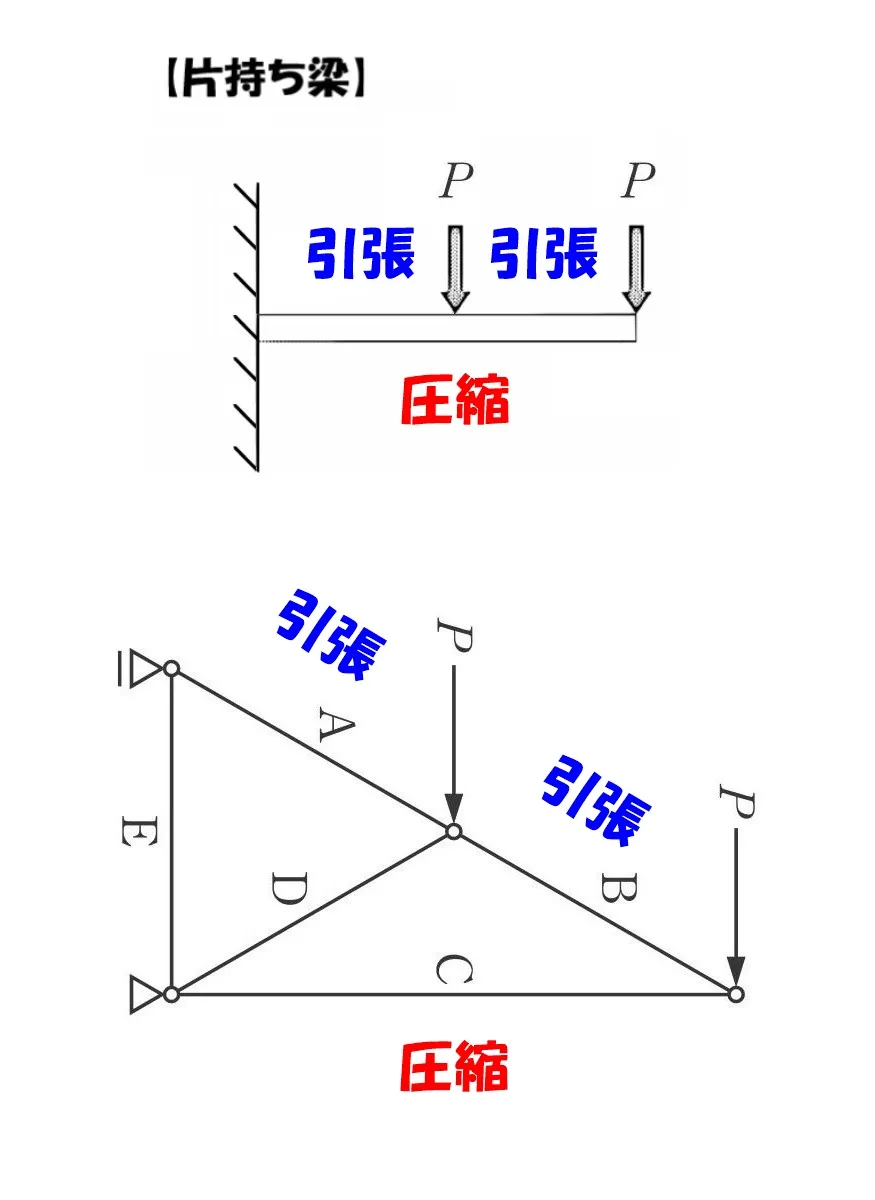

トラスの場合でも原理は同じこと。
部材に下向き⇩の力が加わると、上の部材には引張り力、下の部材には圧縮力が作用するのです。



よくよく見ると、
力学の原理は同じこと。
トラスにベクトルを書き込む
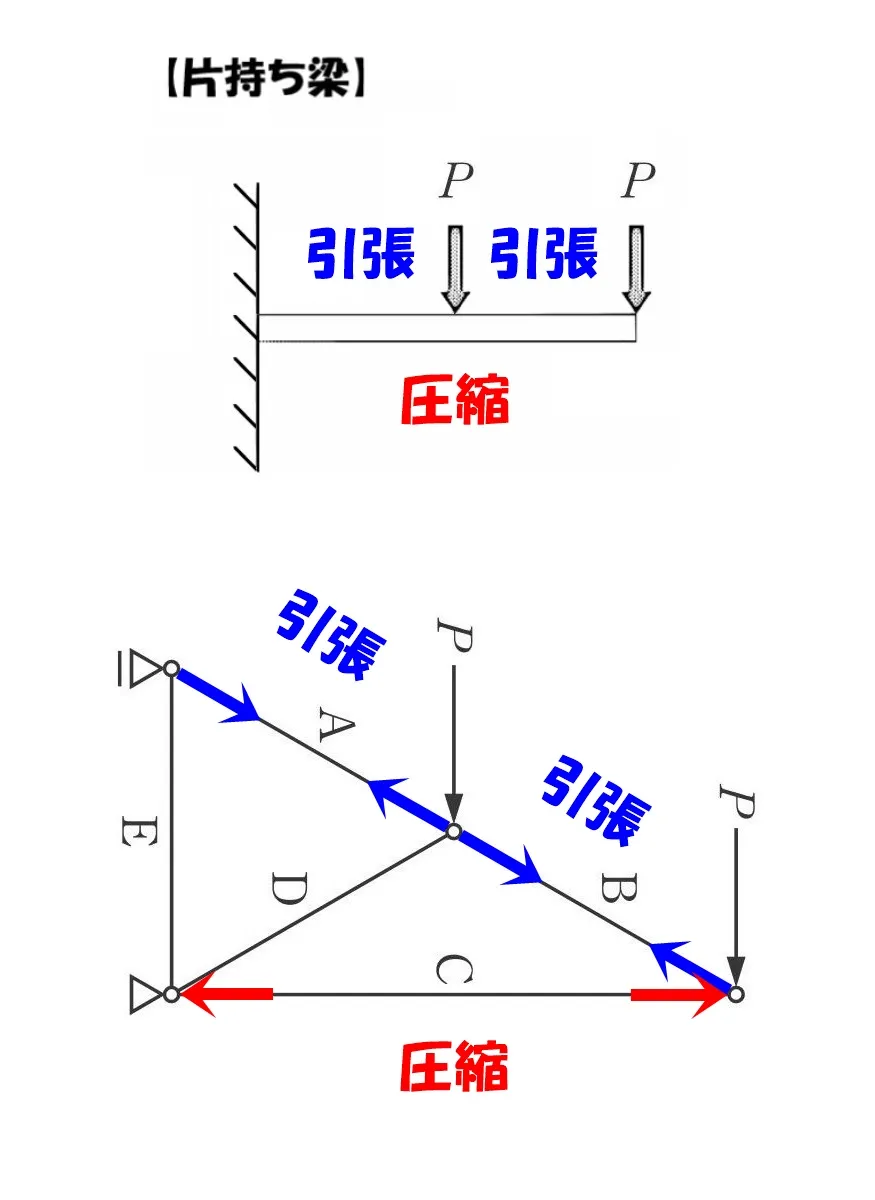

注意点
圧縮力や引張り力は、部材そのものに働く力ではありません。
トラスの応力は「節点に作用する」ため、どちらの力も「節点」から見たベクトルの方向を指します。



ここは要注意です!
トラスの向きを元に戻す。


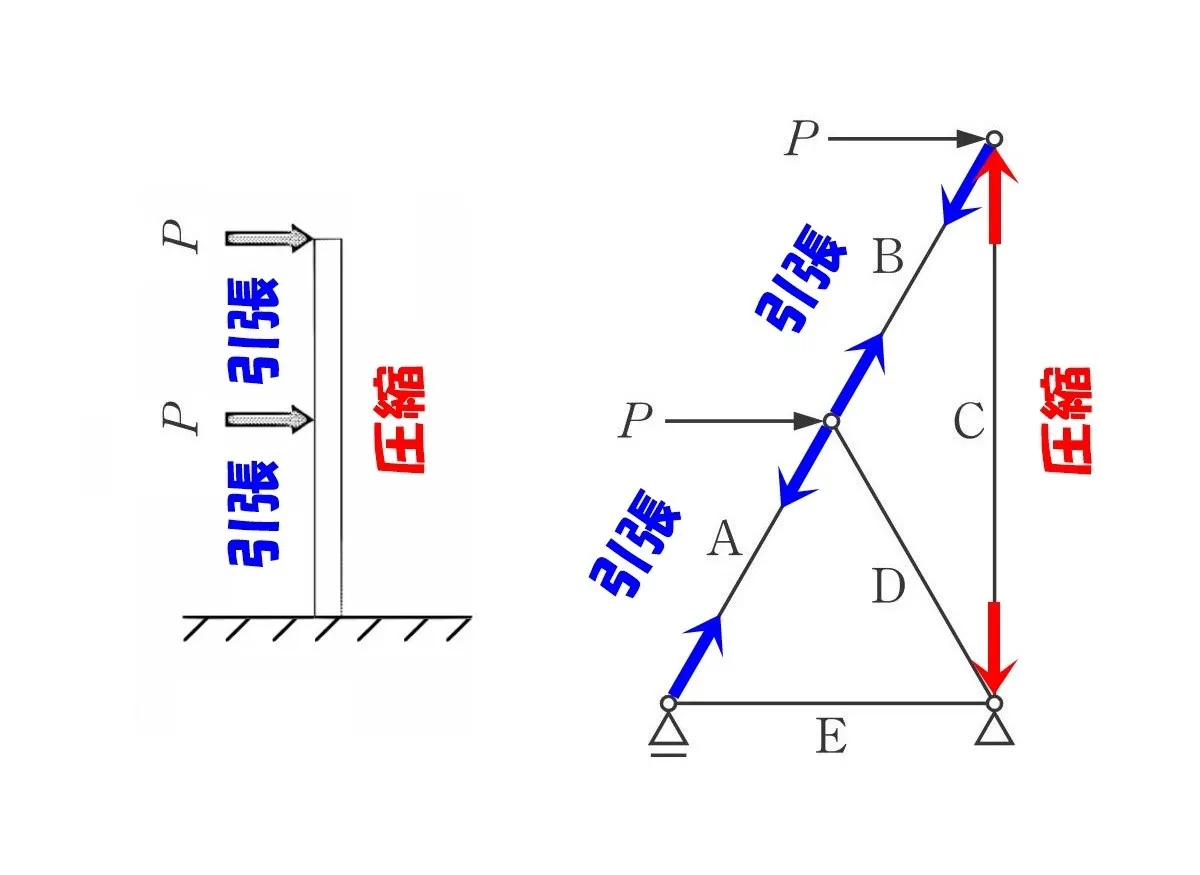

「節点」に作用する力の引張りと圧縮が分かったところで、トラスの向きを戻しましょう。



エネルギーが
みなぎってきたぞ!
ベクトルを書き込む
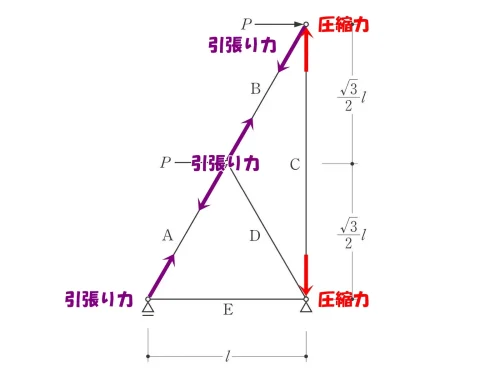

圧縮力と引張り力のベクトルを書き込む。
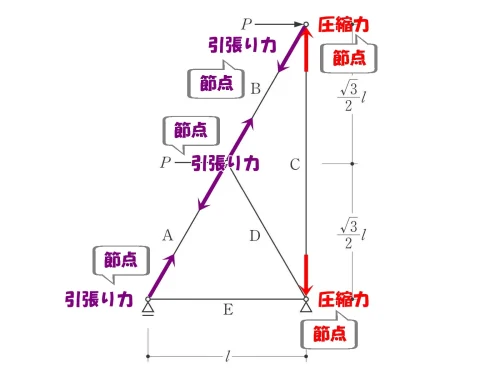

応力は「節点に作用する」ため、ベクトルは「節点」から書き込む。
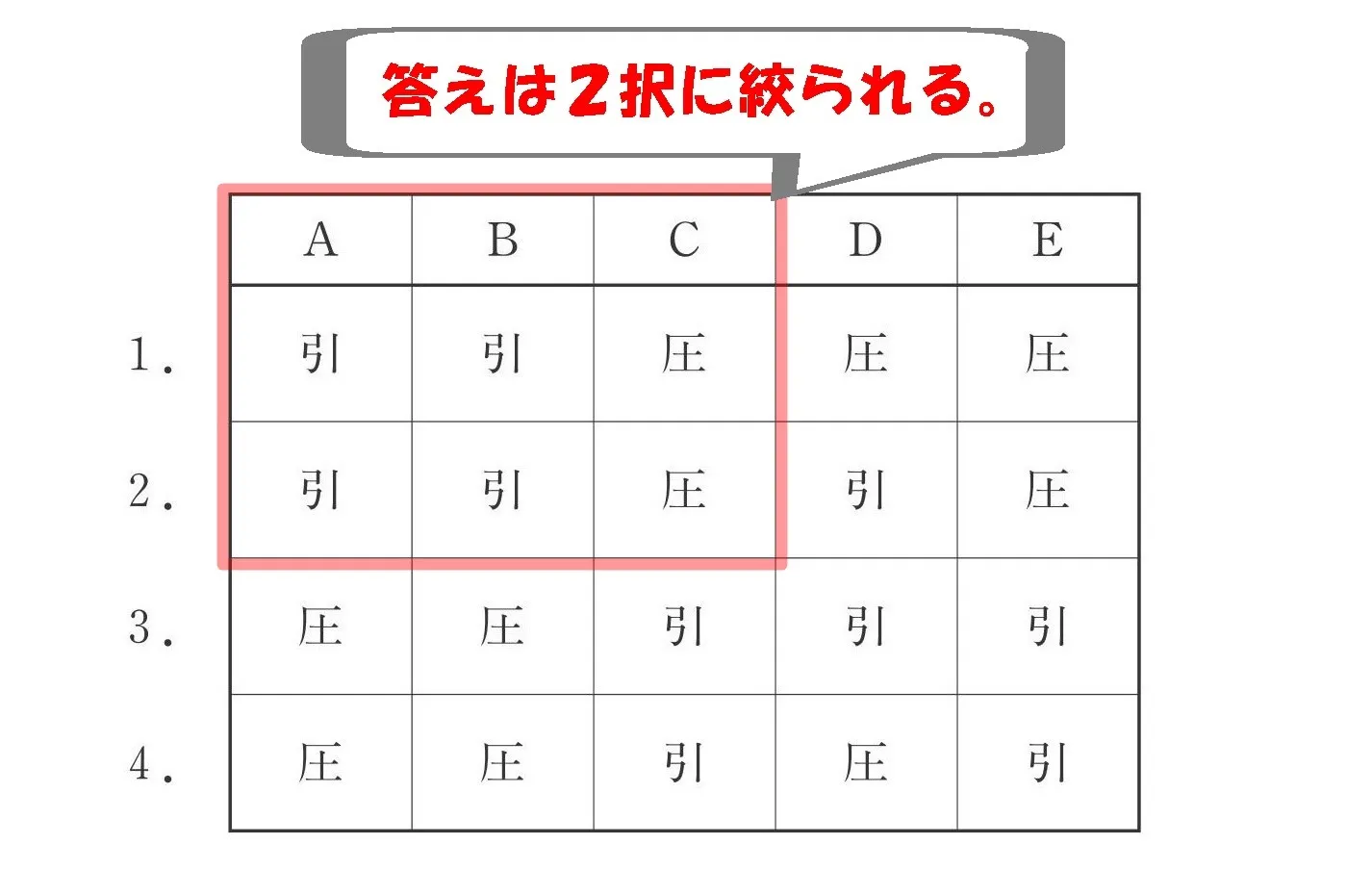




ホントに要注意!
圧縮力や引張り力は、部材そのものではなく節点に作用するベクトルを指す。
1.支点反力を求める
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
支点反力を求める
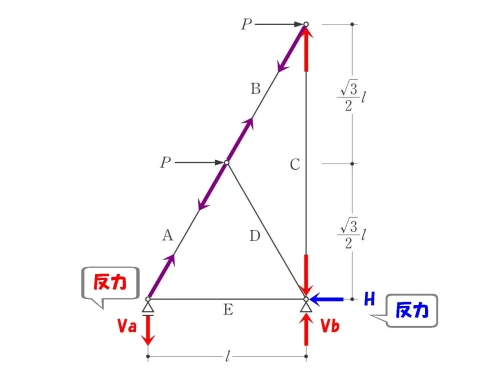

支点を確認する
- 左:ローラー支点
- 鉛直反力Vaのみ作用する。
- 右:ピン支点
- 水平反力Hと鉛直反力Vbが働く。
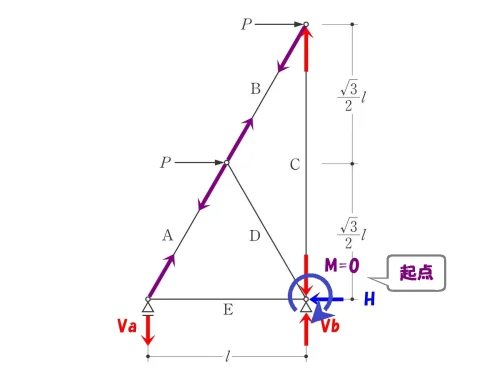

モーメントの釣り合い
作用する力の多いピン支点を回転軸にする。
ここに起点を取ることで、モーメント=力×距離のうちの「距離」がゼロとなる。



支点反力を求める。
モーメントの釣り合い式
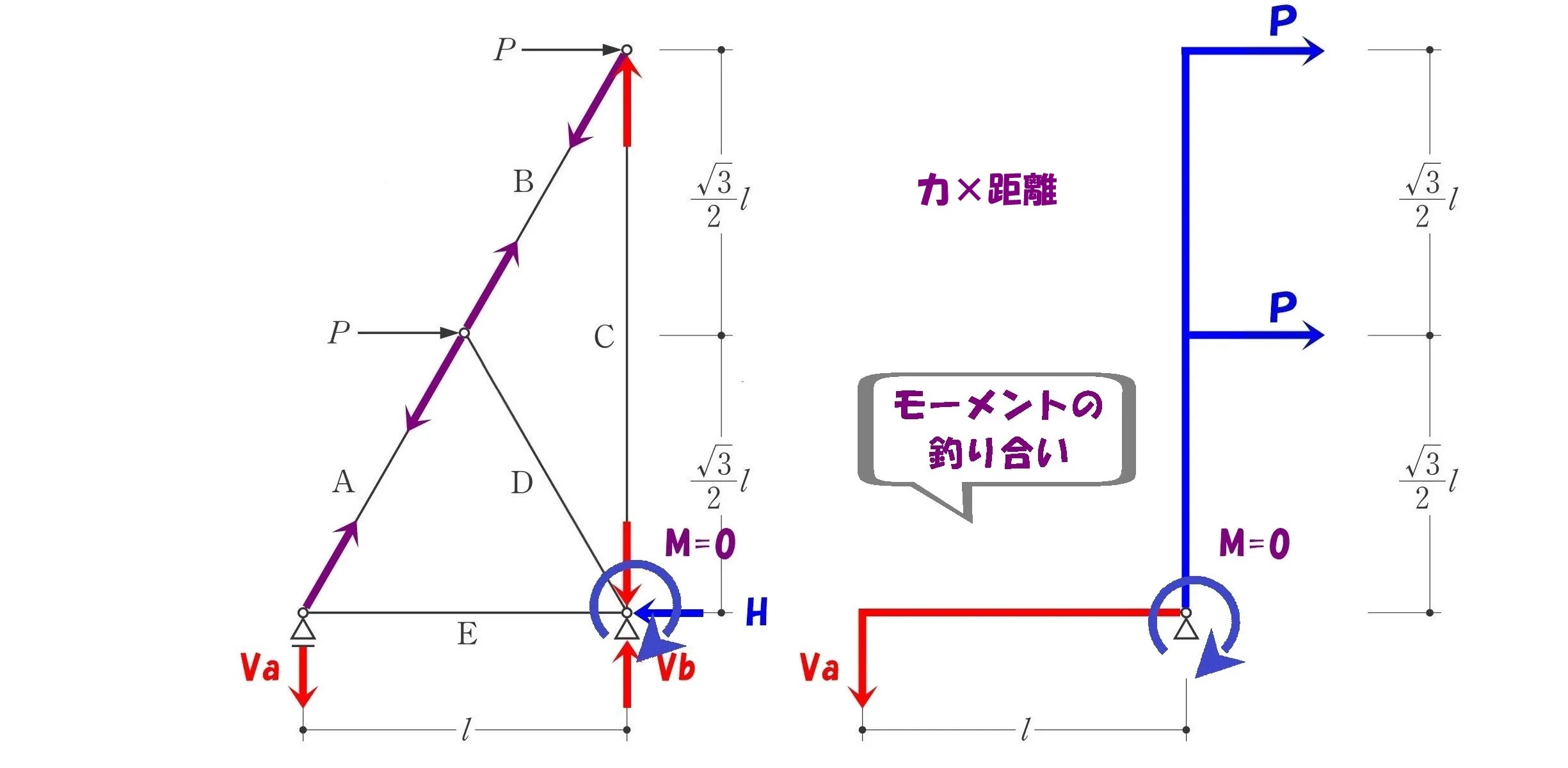

公式
$$\Sigma M=0$$



Σエム!
L=1を代入する
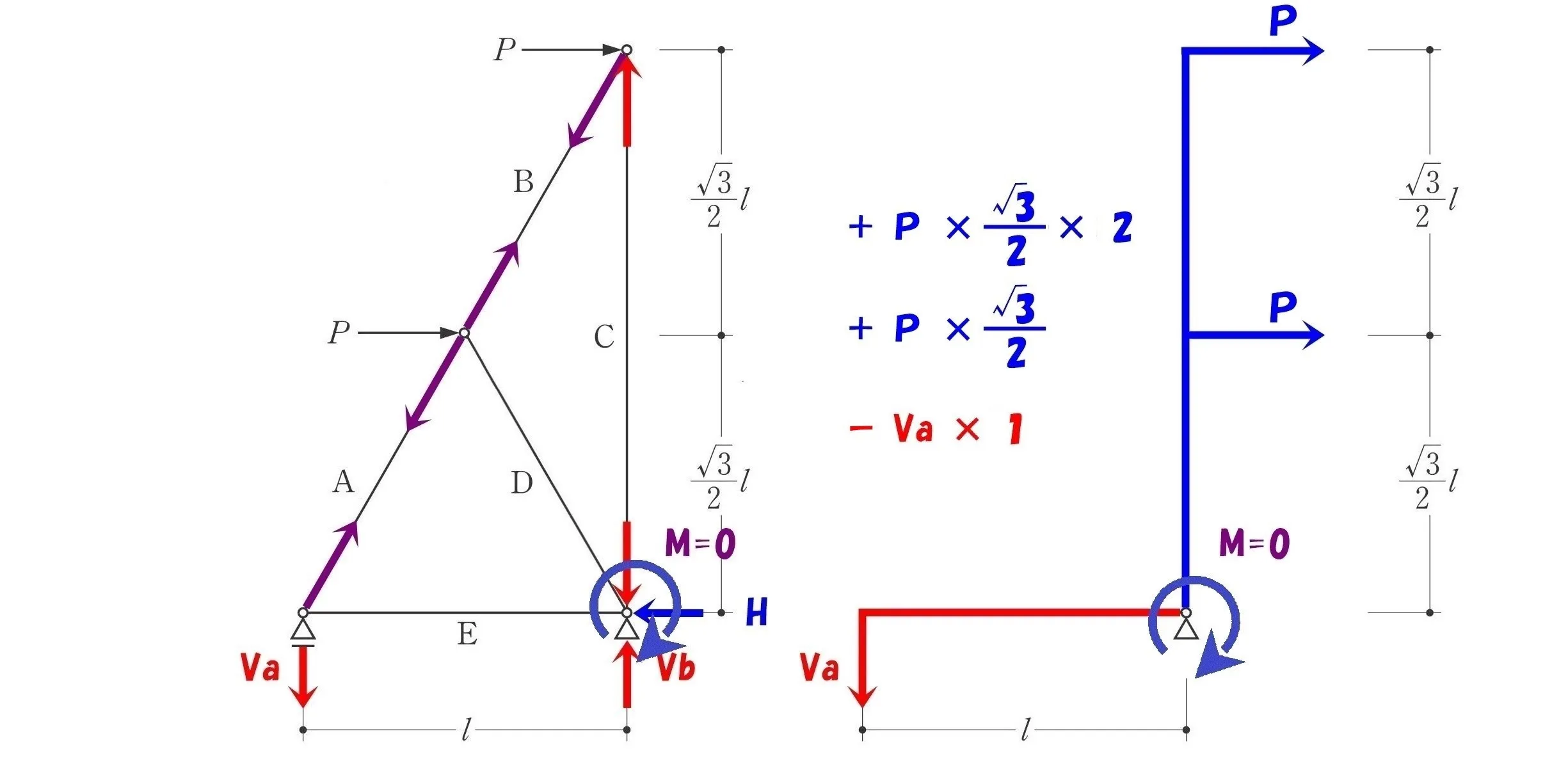

$$\Sigma M=0より$$
$$+P*\frac{ \sqrt{3} }{ 2 }*2+P*\frac{ \sqrt{3} }{ 2 }-Va*1=0$$
$$Va=P*\frac{ \sqrt{3} }{ 2 }*3=\frac{ 3\sqrt{3} }{ 2 }P (↓下向き)$$
2.ベクトルを三角形に組み合わせる
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
ローラー支点を切り出す
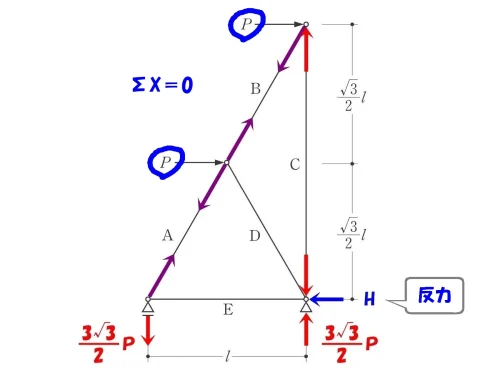

$$\Sigma X=0より$$
$$+P+P-H=0$$$$→H=2P$$
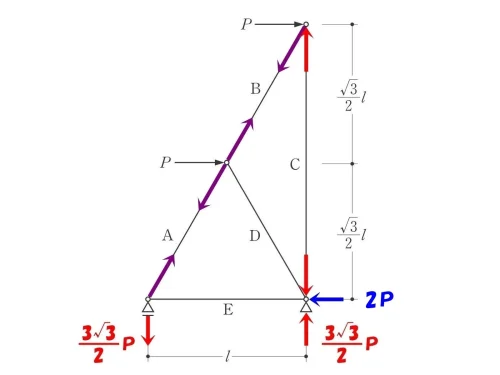

$$水平反力H=2P$$
$$鉛直反力V=\frac{ 3\sqrt{3} }{ 2 }P$$
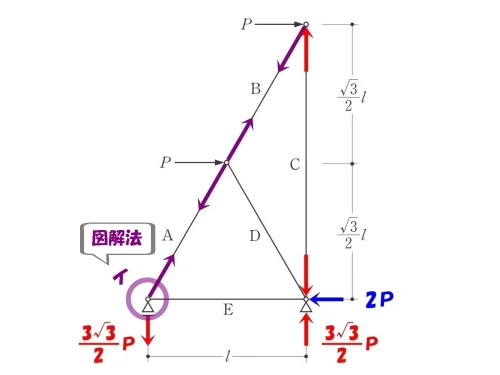

ローラー支点「イ」を切り出す。



ローラー支点を
クローズアップ!
図解法「イ」


図解法を使って、ななめ部材の軸力Aとヨコ部材の軸力Eを求める。
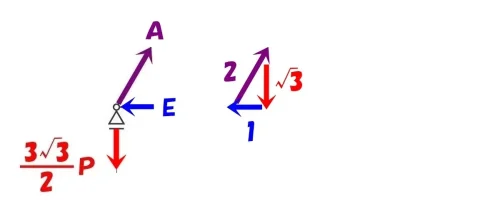

それぞれのベクトルを繋ぎ合わせると、60度の直角三角形が形成される。
$$※ベクトルの比=2:1:\sqrt{3}$$



何とか食らいつく。
3.三角比の辺の比率から、2つの軸力を求める
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
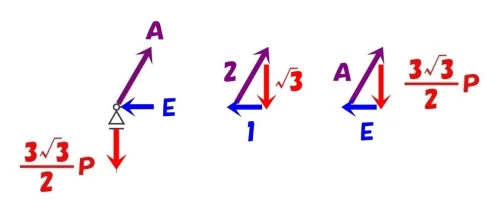

ベクトルの比は、それぞれの部材の軸力の比と相似になる。
$$2:1:\sqrt{3}=A:E:\frac{ 3\sqrt{3} }{ 2 }P$$
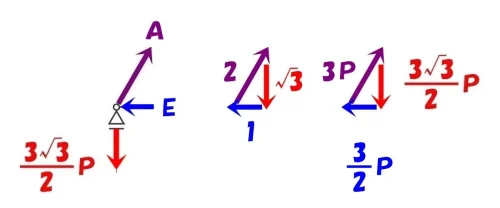

$$比率=\frac{ 1 }{ \sqrt{3} }*\frac{ 3\sqrt{3} }{ 2 }P=\frac{ 3 }{ 2 }P$$
$$A=2*\frac{ 3 }{ 2 }P=3P , E=1*\frac{ 3 }{ 2 }P=\frac{ 3 }{ 2 }P$$
$$2:1:\sqrt{3}=A:E:\frac{ 3\sqrt{3} }{ 2 }P=3P:\frac{ 3 }{ 2 }P:\frac{ 3\sqrt{3} }{ 2 }P$$
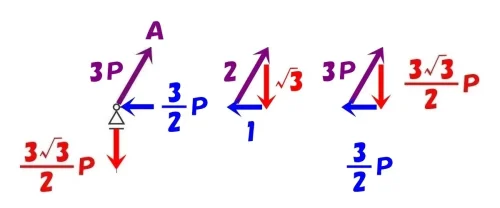

$$軸力A=3P(引張り) , 軸力E=\frac{ 3 }{ 2 }P(圧縮) , 鉛直反力Va=\frac{ 3\sqrt{3} }{ 2 }P$$
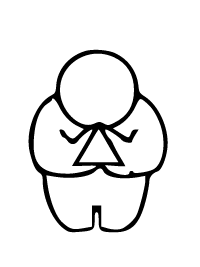


トラス・マジック!
図解法とは?
トラスの部材の軸力をベクトルとして図示して、三角比で求める方法


この動画を YouTube で視聴
ピン支点を切り出す
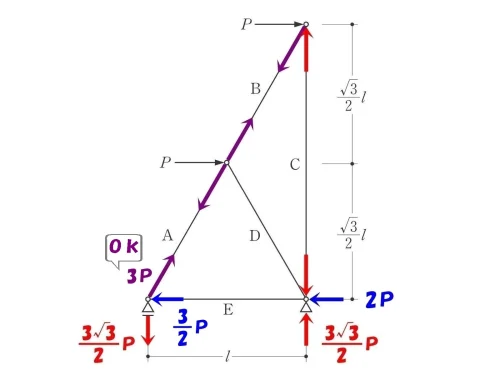

図解法より、軸力E=3/2P(圧縮)、軸力A=3P(引張り)が求まる。
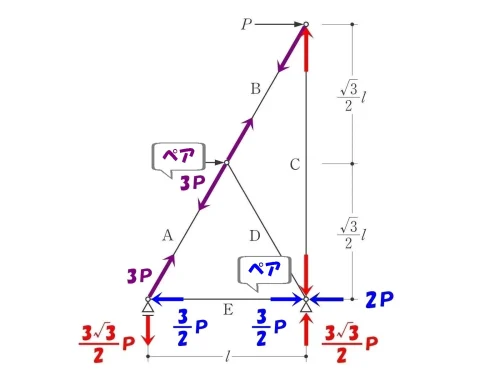

トラスの軸力の大きさは両端でペアになるため、反対側にも同じ数値をメモする。
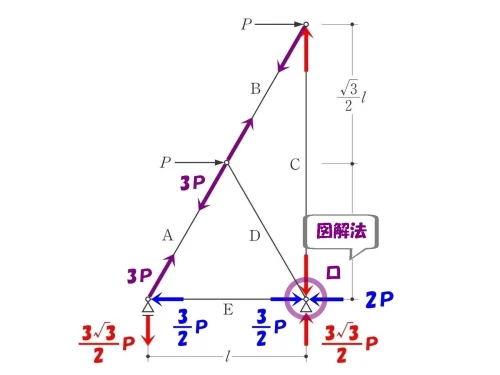

ピン支点「ロ」を切り出す。



ピン支点を
クローズアップ!
図解法「ロ」?


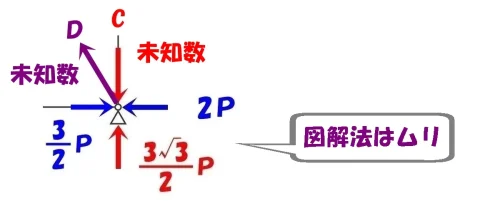

軸力を求めたいが、タテ部材の軸力Cとななめ部材の軸力Dと未知数が2つある。
複数のベクトルが集中していて図解法では計算式が複雑となるため、とりあえず保留にしておく。
2.ベクトルを三角形に組み合わせる
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
図解法の視点を変える
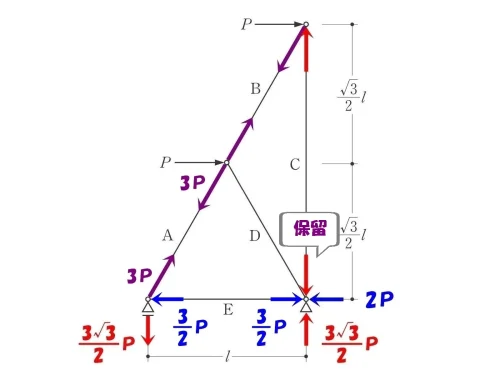

ピン支点での図解法は一旦保留にしておく。



一時撤退?
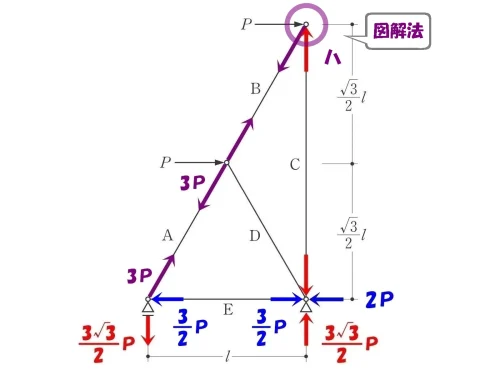

節点「ハ」を切り出す。



節点にフォーカス!
図解法「ハ」


図解法を使って、ななめ部材の軸力Bとタテ部材の軸力Cを求める。
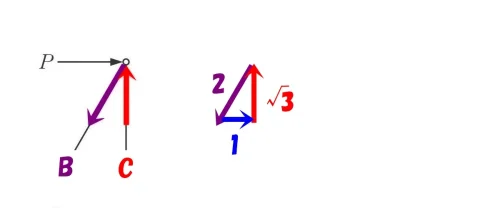

それぞれのベクトルを繋ぎ合わせると、30度の直角三角形が形成される。
$$※ベクトルの比=2:1:\sqrt{3}$$
3.三角比の辺の比率から、2つの軸力を求める
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
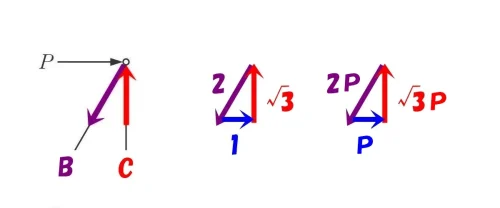
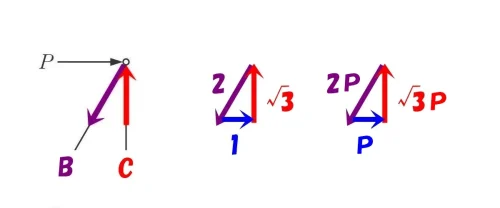
ベクトルの比は、それぞれの部材の軸力の比と相似になる。
$$2:1:\sqrt{3}=2P(軸力B):P(水平力):\sqrt{3}P(軸力C)$$
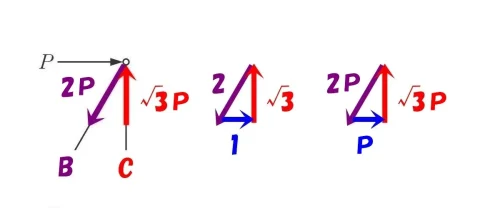
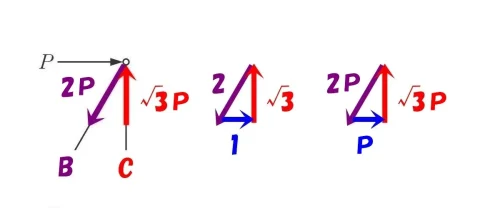
$$2:1:\sqrt{3}=2P:P(水平力):\sqrt{3}P$$
$$軸力B=2P(引張り) , 水平力=P , 軸力C=\sqrt{3}P(圧縮)$$



トラス・マジック!
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
節点を切り出す
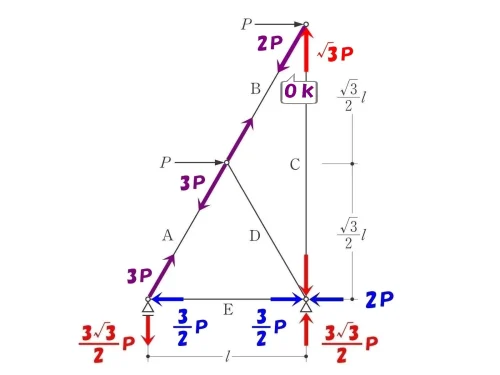

図解法より、軸力B=2P(引張り)、軸力C=√3P(圧縮)が求まる。
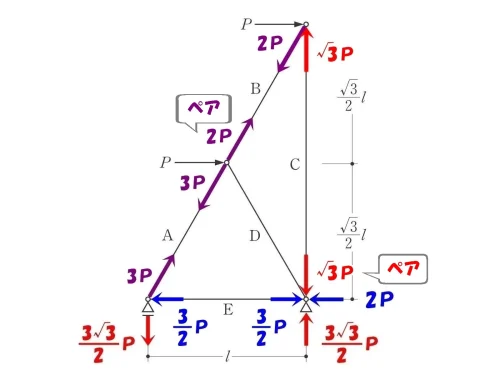

トラスの軸力の大きさは両端でペアになるため、反対側にも同じ数値をメモする。

節点「二」を切り出す。



節点にフォーカス!
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
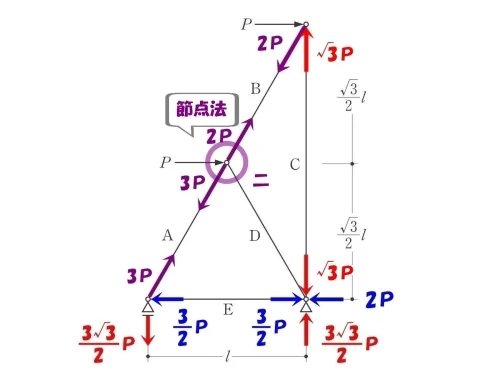
節点法「二」
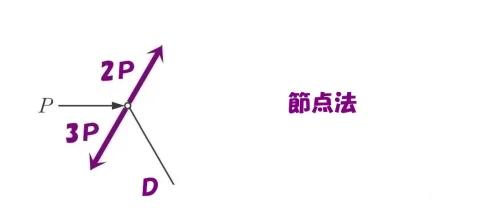

同じライン上の2つの軸力(引張り)、2Pと3Pに注目する。
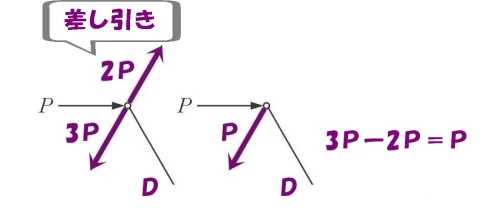

差し引きすると、3P-2P=「P」となる。
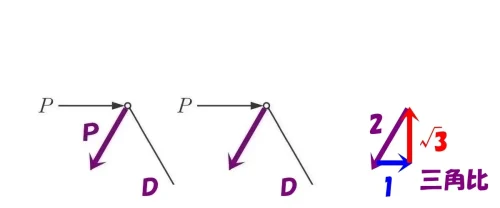

ベクトルの比は、それぞれの部材の軸力の比と相似になる。
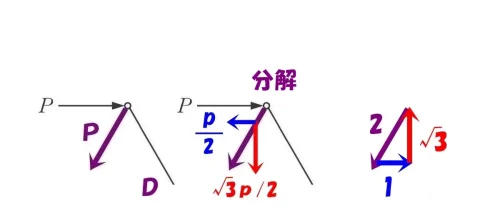

軸力Pのベクトルを分解する。
$$2:1:\sqrt{3}=P(軸力):\frac{ P }{ 2 }(←X方向):\frac{ \sqrt{3} }{ 2 }P(↓Y方向)$$



ベクトルを分解する。
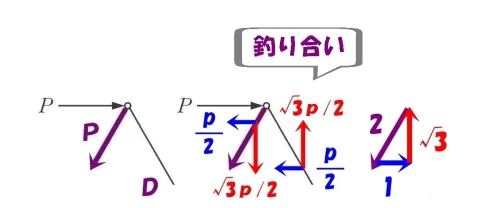

$$\Sigma X=0より , 水平力P-\frac{ P }{ 2 }(X方向)-\frac{ P }{ 2 }(X方向)=0$$
$$\Sigma Y=0より, -\frac{ \sqrt{3} }{ 2 }P(↓下向き)+\frac{ \sqrt{3} }{ 2 }P(↑上向き)=0$$
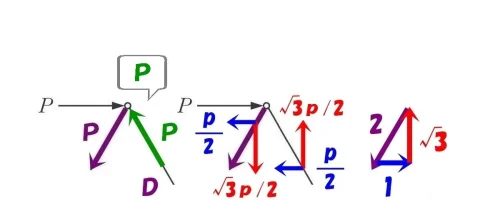

$$\frac{ P }{ 2 }(X方向)と\frac{ \sqrt{3} }{ 2 }P(Y方向)で,水平力Pと釣り合う$$
三角比より、ななめ部材の軸力=P(圧縮)ということが分かる。



トラス・マジック!


この動画を YouTube で視聴
2.トラスの節点を取り出す
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
ピン支点を切り出す。
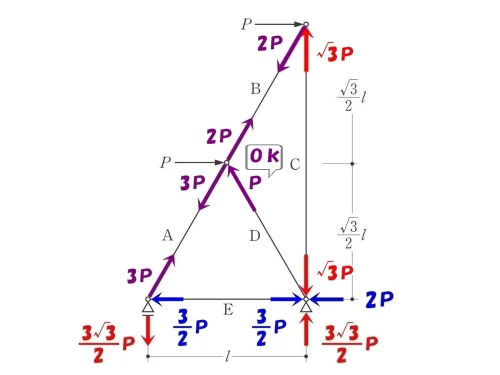

節点法より、軸力D=P(圧縮)が求まる。
※ななめ部材の両端ともP(圧縮)となる。
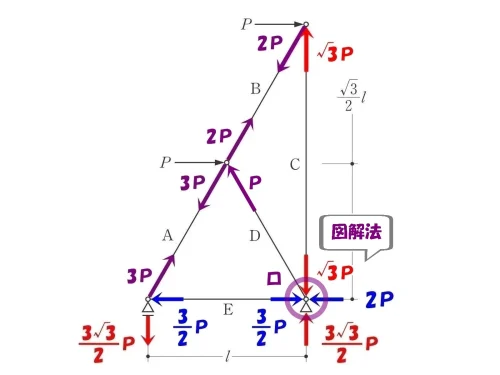

ピン支点「ロ」をもう一度切り出す。



ピン支点を
クローズアップ!
3.ΣX=0ΣY=0で軸力を求める
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。
節点法「ロ」


節点法と図解法により、2つあった未知数が1つになったため、力の釣り合いを確認する。
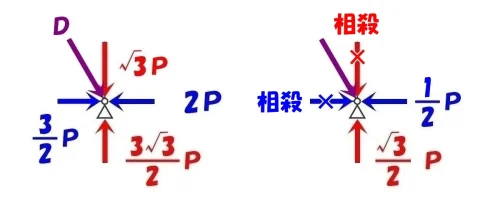

軸力の差し引き
$$X方向:-\frac{ 3 }{ 2 }P+2P=-\frac{ 3 }{ 2 }P+\frac{ 4 }{ 2 }P=\frac{ 1 }{ 2 }P$$
$$Y方向:+\frac{3\sqrt{3} }{ 2 }P-\sqrt{3}P=\frac{3\sqrt{3} }{ 2 }P-\frac{2\sqrt{3} }{ 2 }P=\frac{\sqrt{3} }{ 2 }P$$
$$X方向=\frac{ 1 }{ 2 }P , Y方向=\frac{\sqrt{3} }{ 2 }P$$



頭が痛い・・・
図解法「ロ」
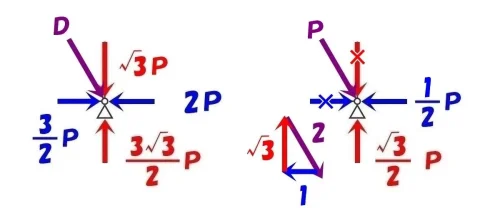

$$2:1:\sqrt{3}=P(ななめ部材):\frac{ 1 }{ 2 }P(←X方向):\frac{\sqrt{3} }{ 2 }P(↑Y方向)$$
$$ななめ部材の軸力D=P(圧縮力)$$



トラス・マジック!


さきほどの節点法「二」で求めた通り、ななめ部材の軸力D=P(圧縮力)となる。



答えがつながった!
全ての軸力が釣り合う
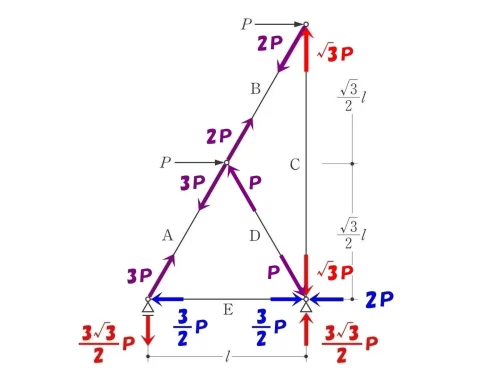

トラスの軸力の大きさは両端でペアになるため、反対側にも同じ力が作用する。



トラス・マジック!
答え.1
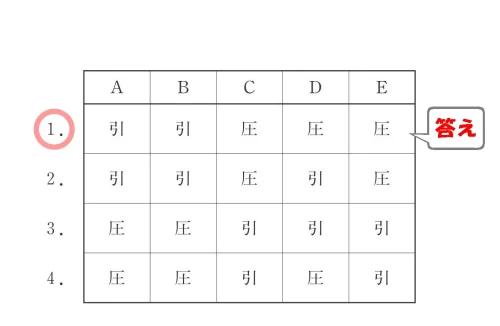

図解法の攻略ポイント
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。
トラスの過去問に挑戦!(No.3-切断法)


切断法とは?
トラスを切断して片側を取り出し、力の釣り合いにより部材の軸力を求める方法
切断法の攻略ポイント
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。


この動画を YouTube で視聴



No.3
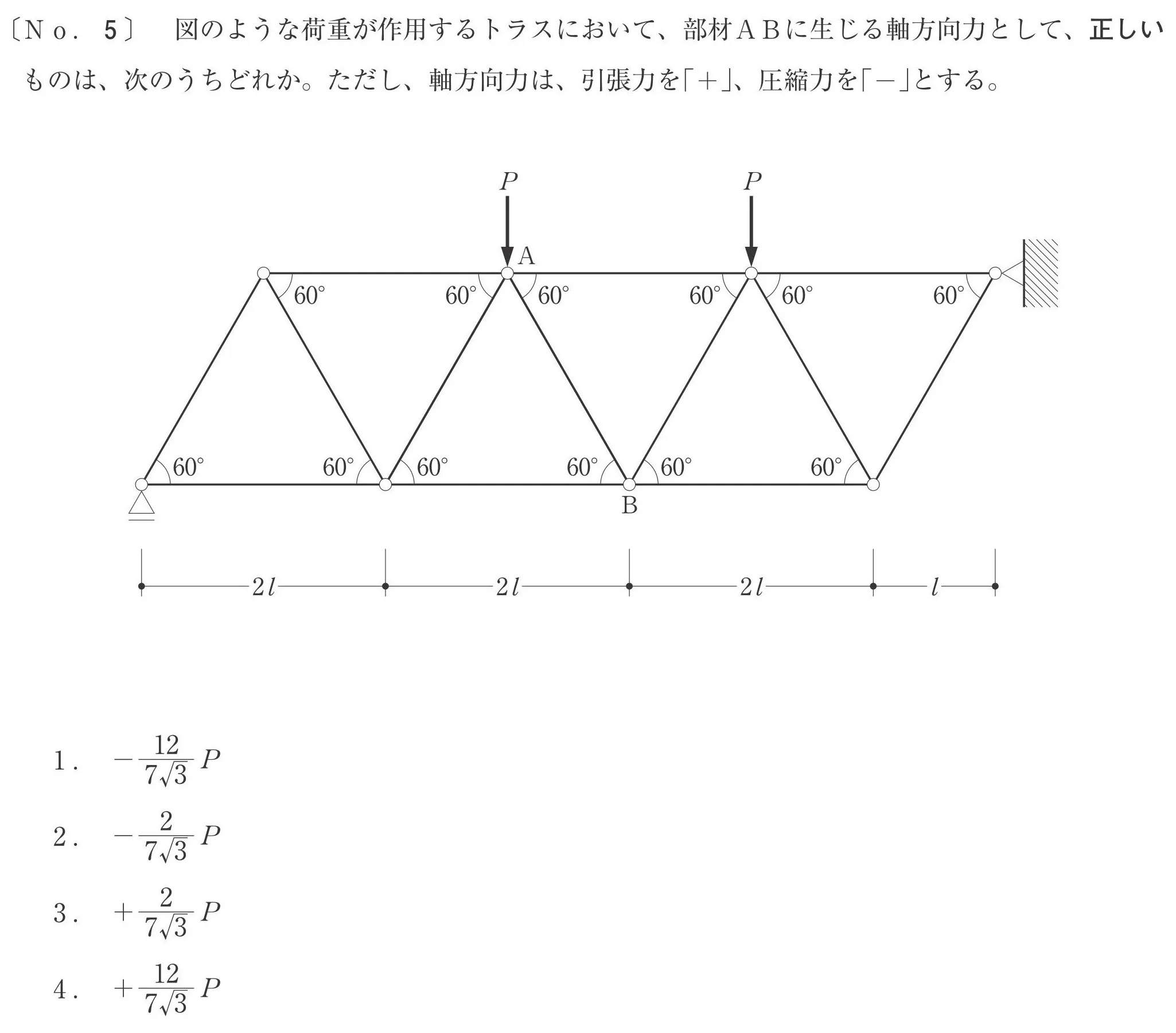

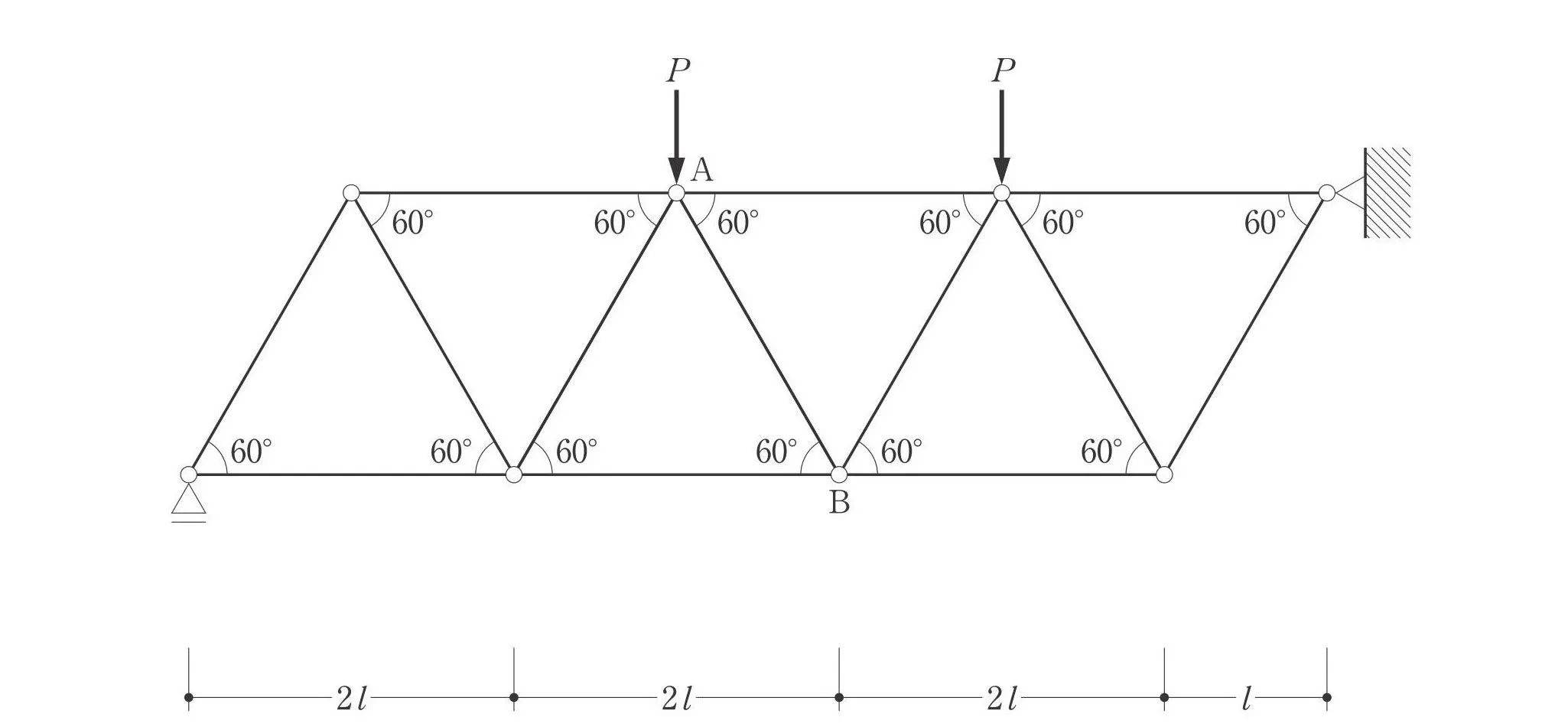

左:ローラー支点
右:ピン支点
1.支点反力を求める
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。



支点反力を求める。
支点反力を書き込む
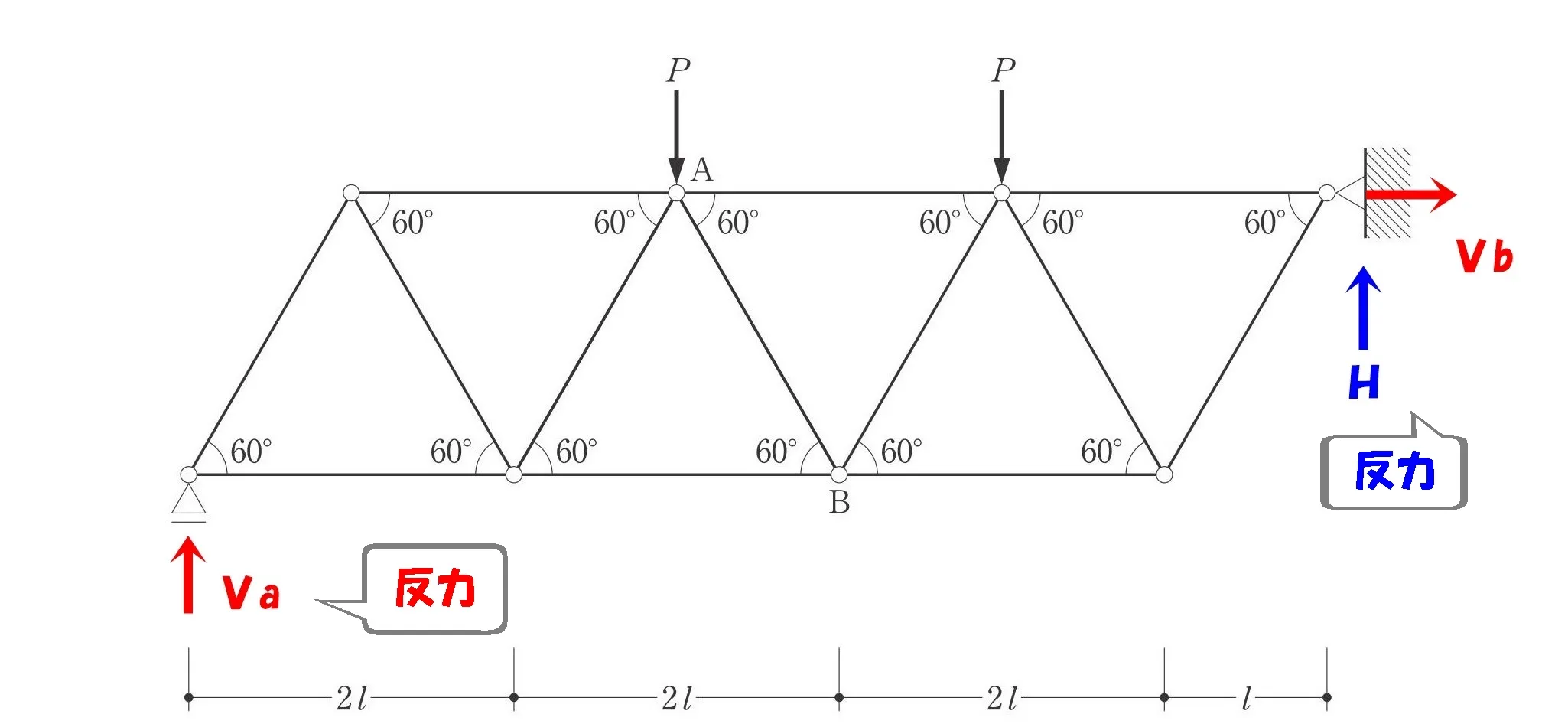

支点反力
左:ローラー支点
鉛直反力Vaのみ
右:ピン支点
水平反力Hと鉛直反力Vb
モーメントの釣り合い
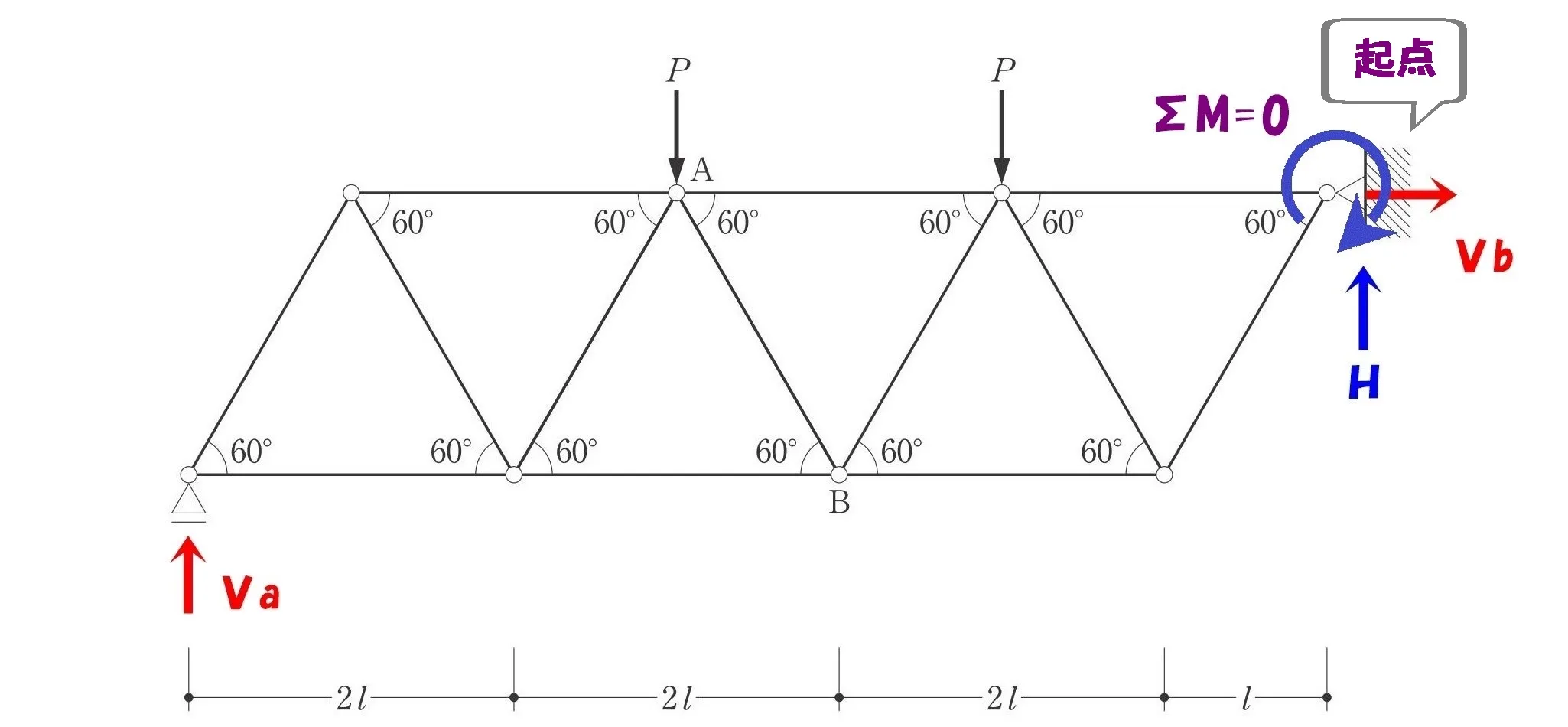

反力VbとHが交差するピン支点(右)に注目してみましょう。
ここに回転軸の起点を取ることで、モーメント=力×距離のうちの「距離」がゼロとなるのです。



シグマ・M
ΣM=0
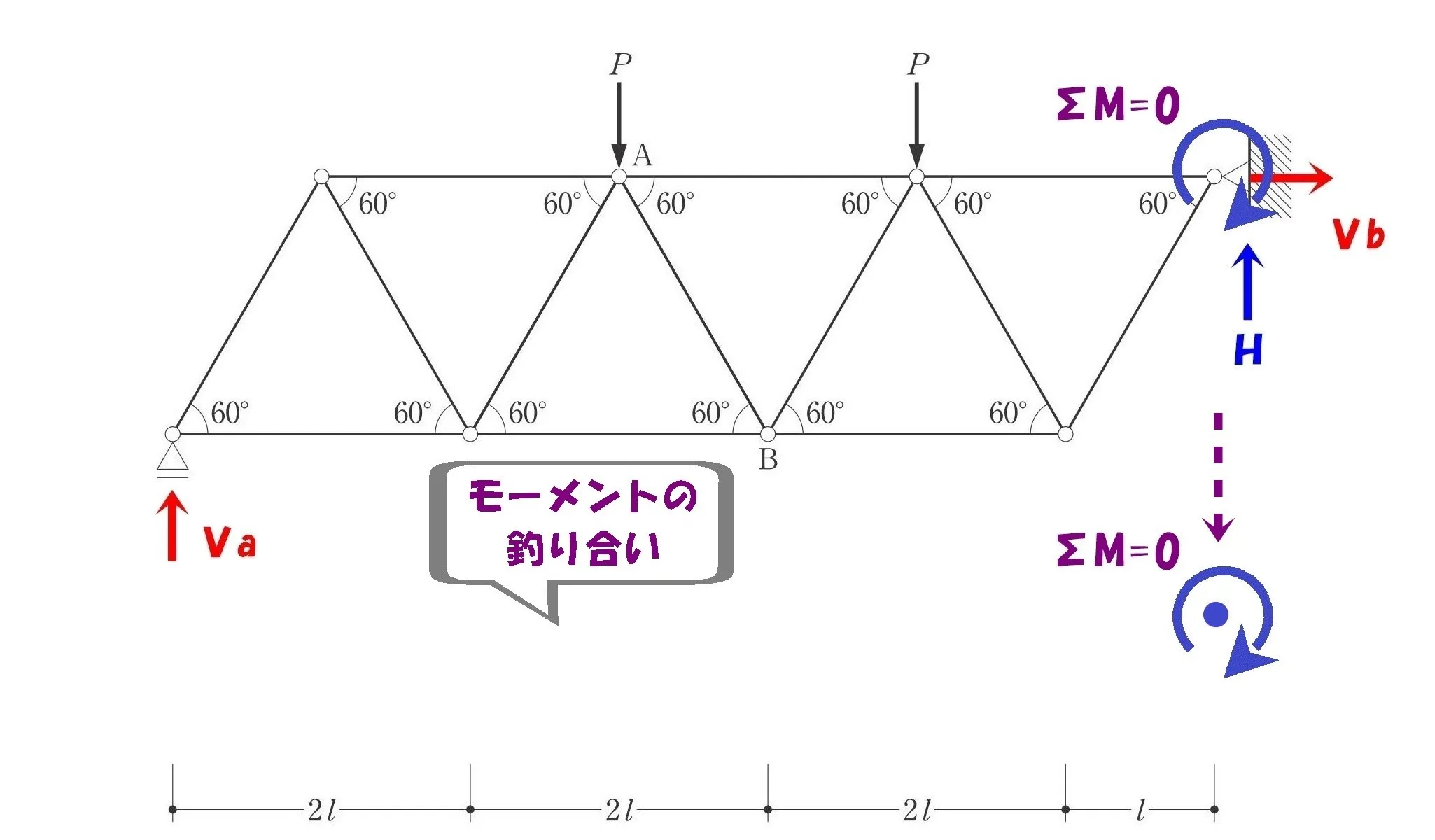

モーメントの回転軸を下の余白部分に書き込む。



下の余白を使って
ベクトルを書き出してみよう。
ベクトルVaを書き込む
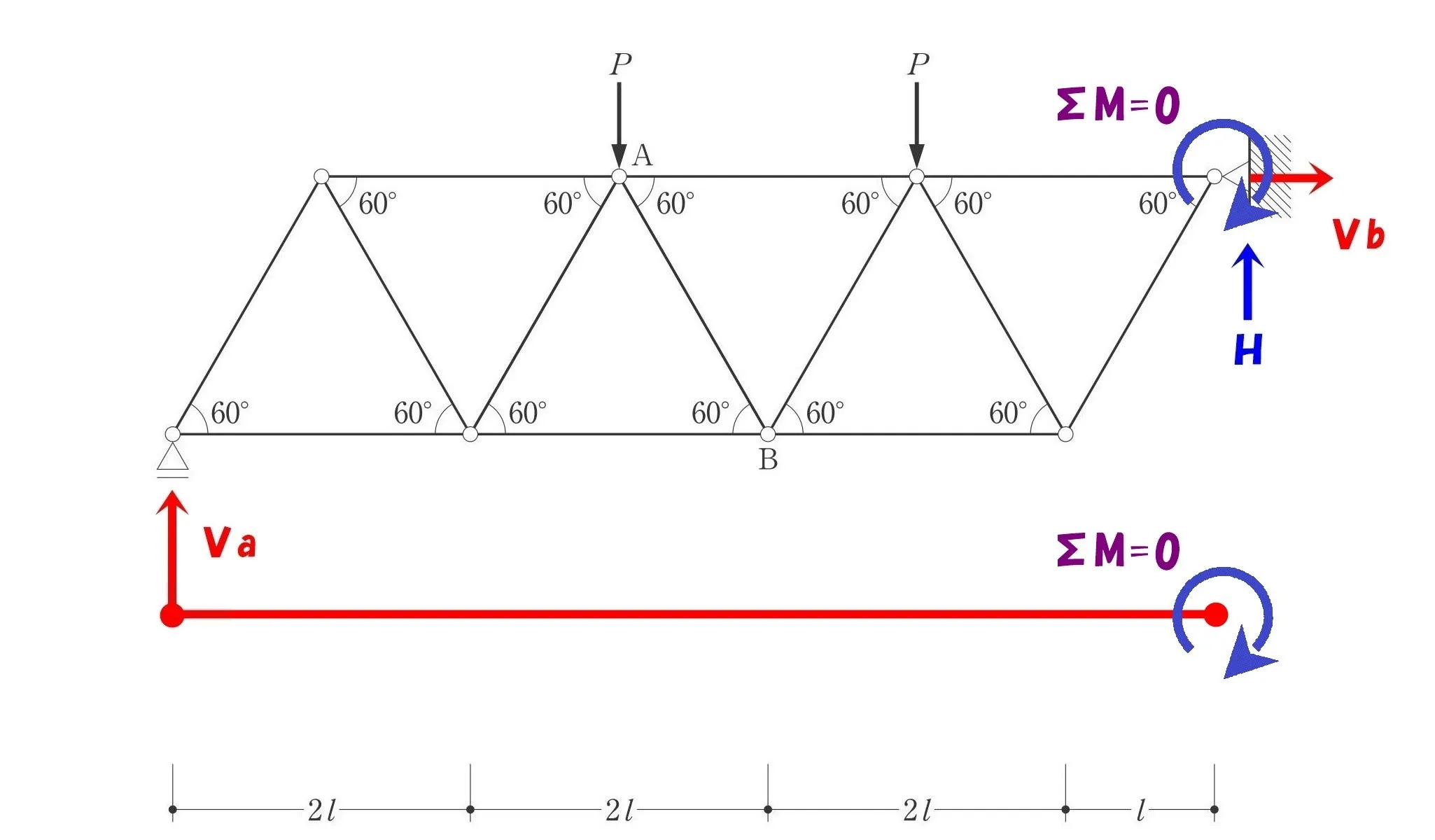

ローラー支点の鉛直反力Vaを書き込む。
ベクトルPを書き込む
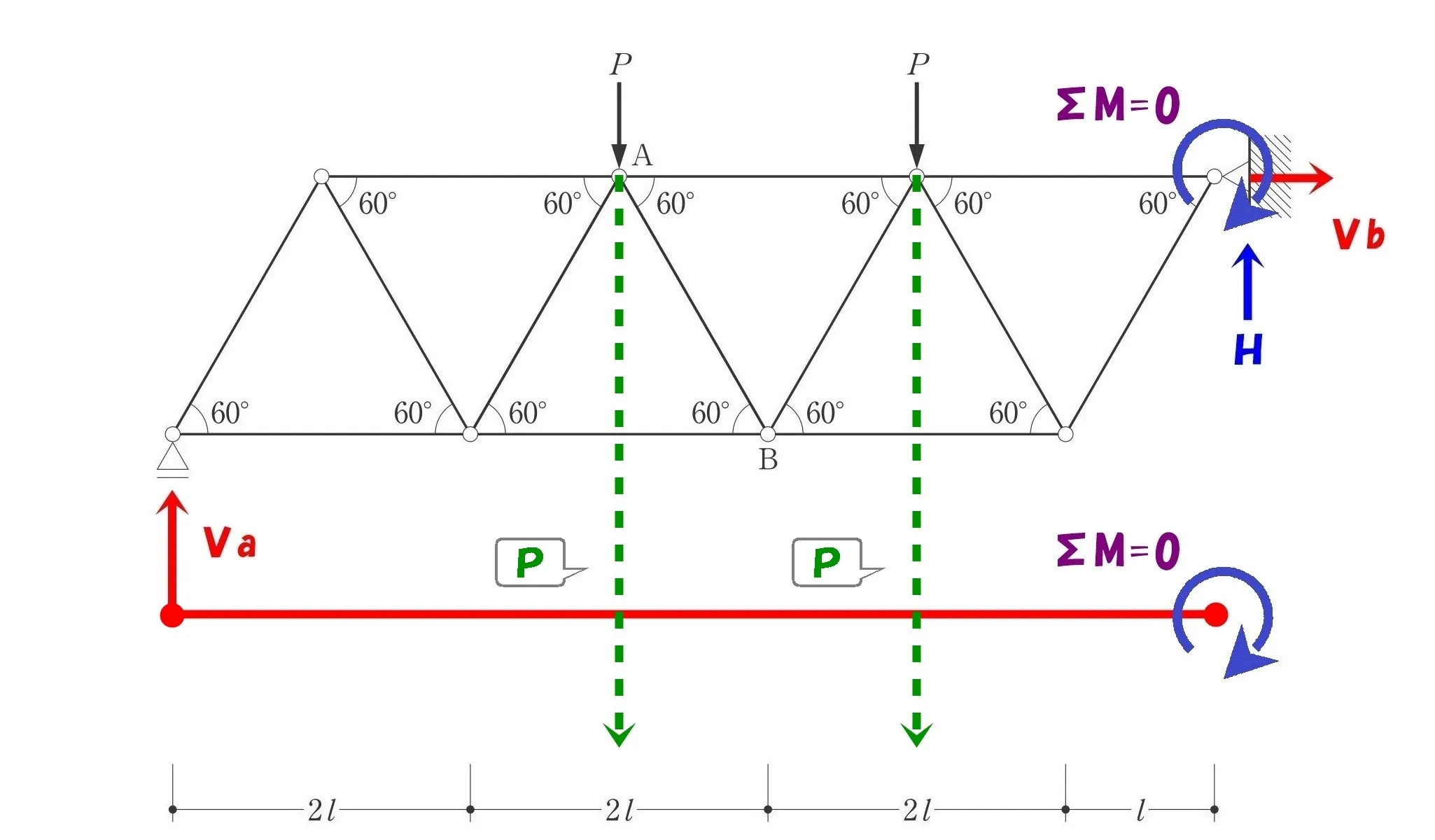

荷重「P」をそのまま回転軸からの赤ラインまで下ろす。



まずはライン出しから。
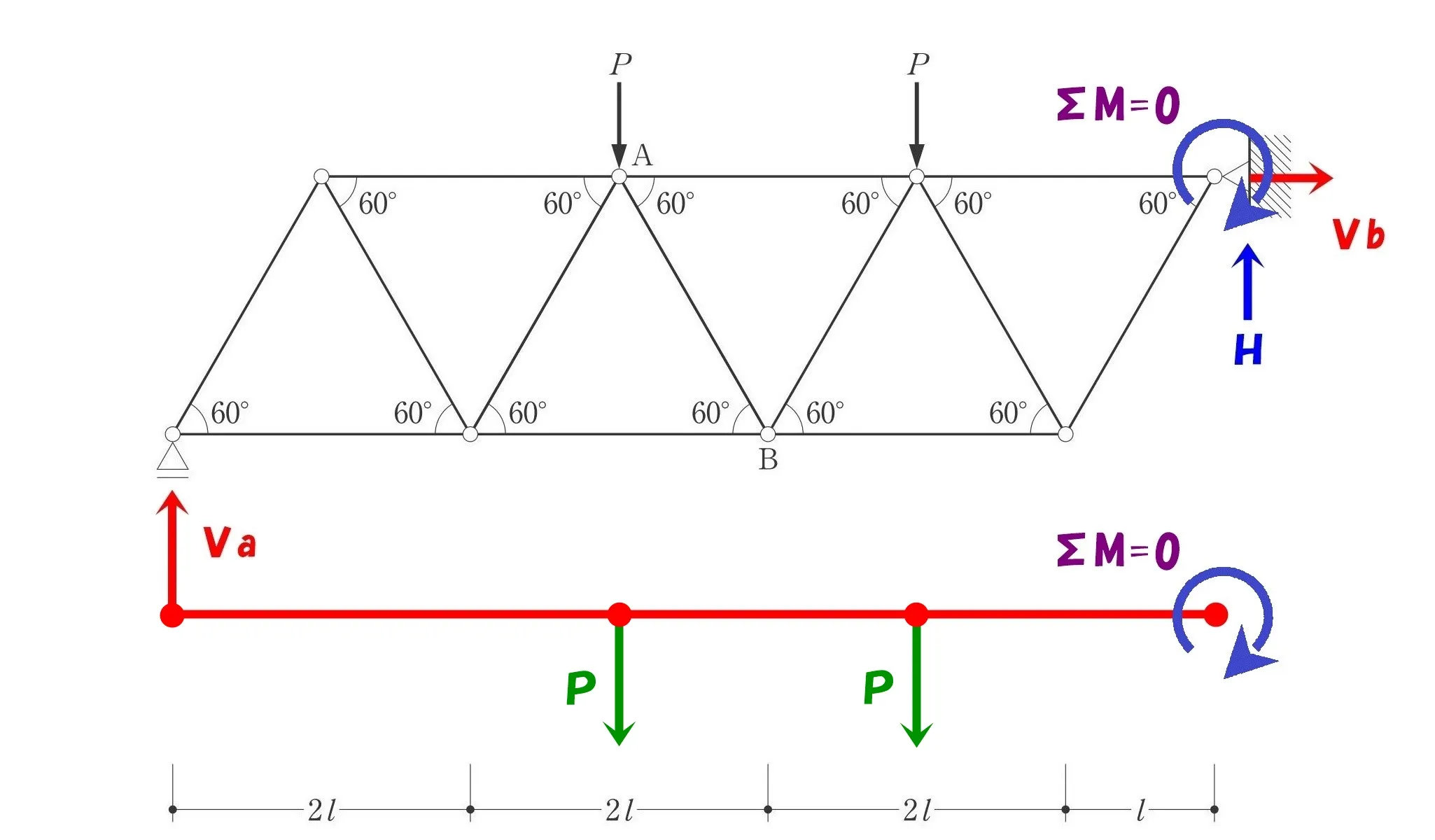

荷重「P」のベクトルをそれぞれ赤ラインのうえに書き込む。
位置を押さえる
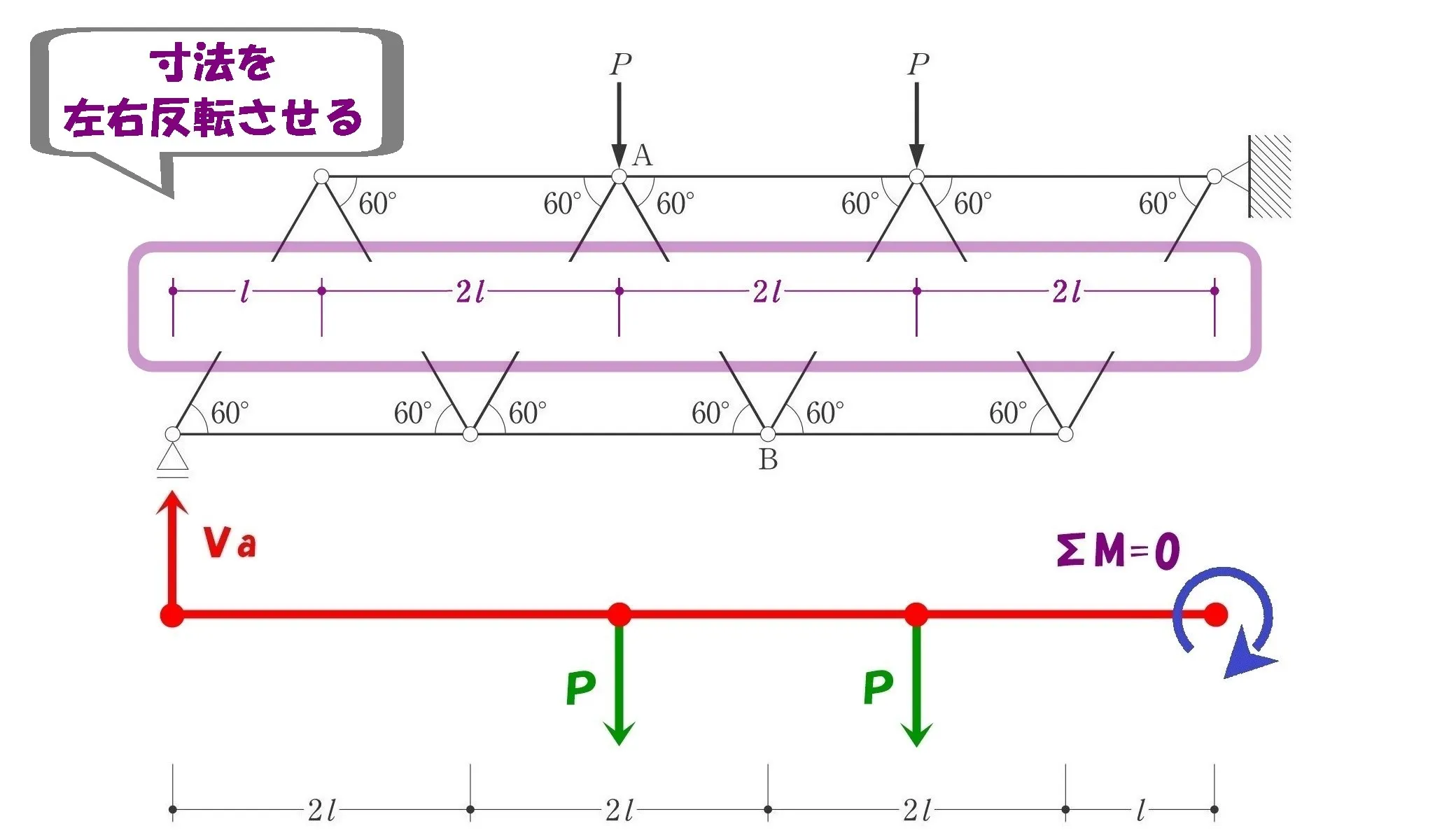

図示してある寸法線を左右反転させると、VaとPの位置を押さえられる。



準備OK?
距離を求める
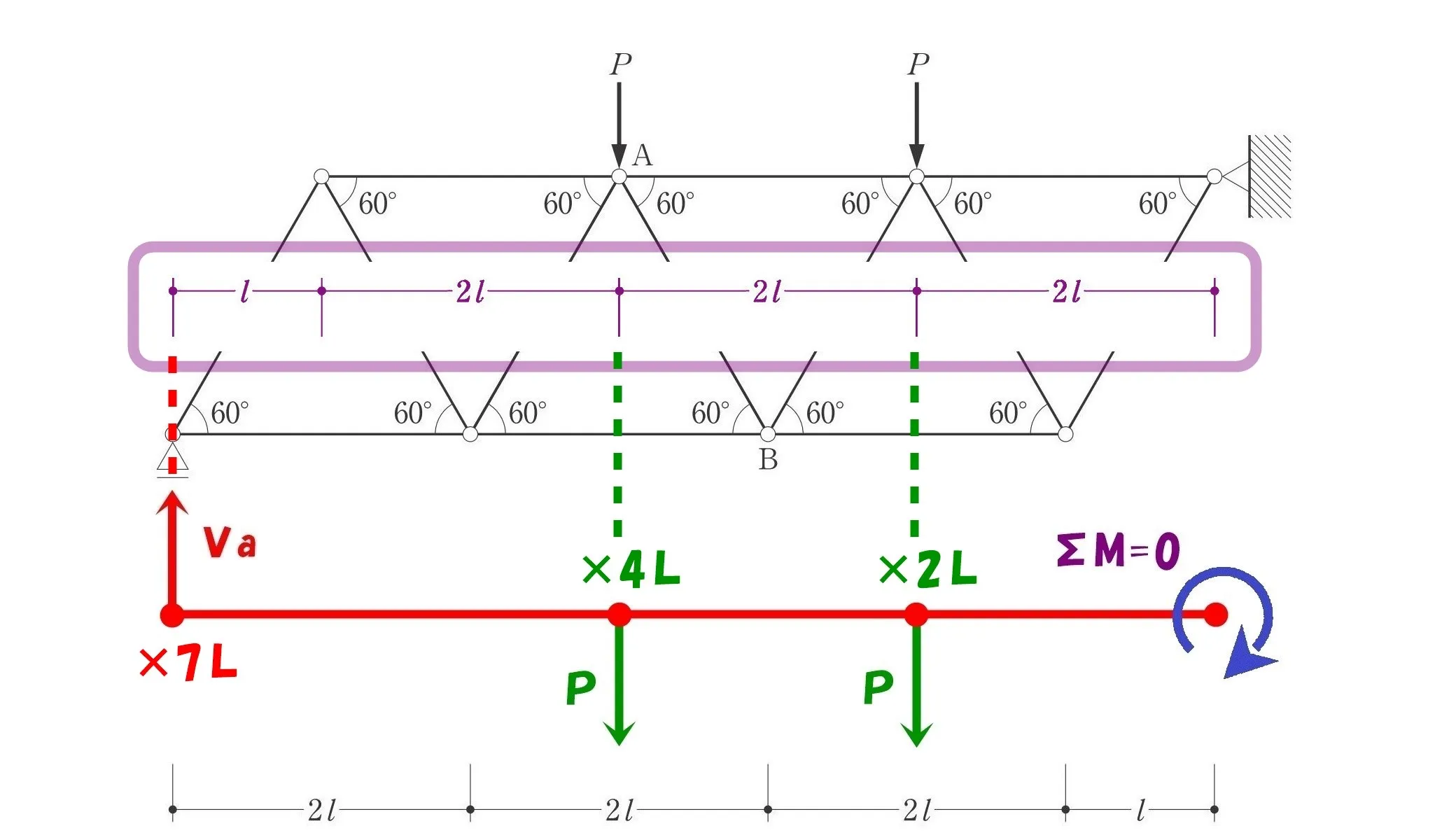

寸法線より、回転軸からVaまでの距離=7L、Pまでの距離=4Lと2Lを読み取る。



寸法から長さを読みとる。
モーメント=力×距離
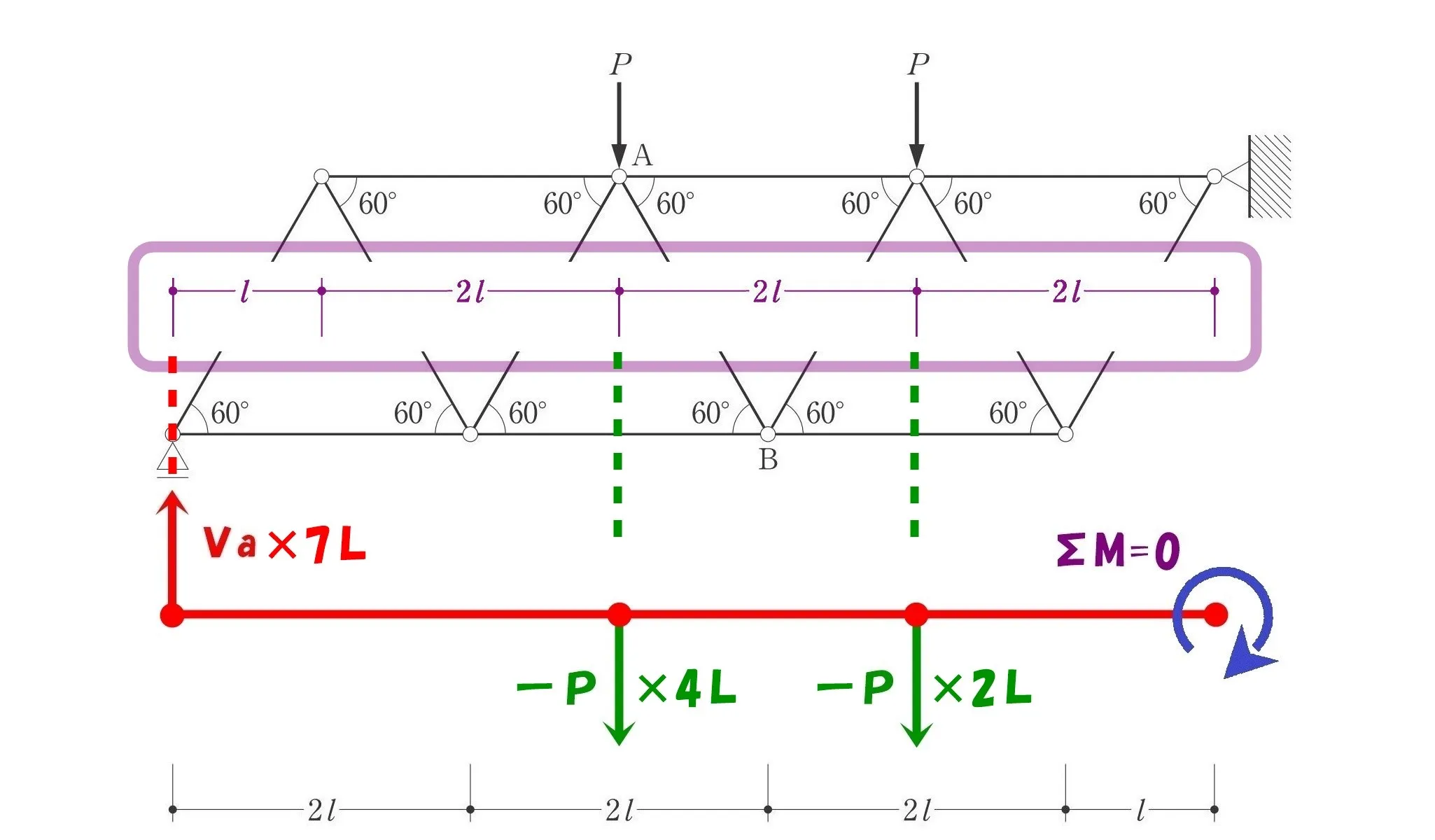

$$\Sigma M=0より,$$$$+Va*7-P*4-P*2=0$$$$7Va=6P→Va=\frac{ 6 }{ 7 }P$$
公式
$$\Sigma M=0$$



Σエム!
支点反力Va
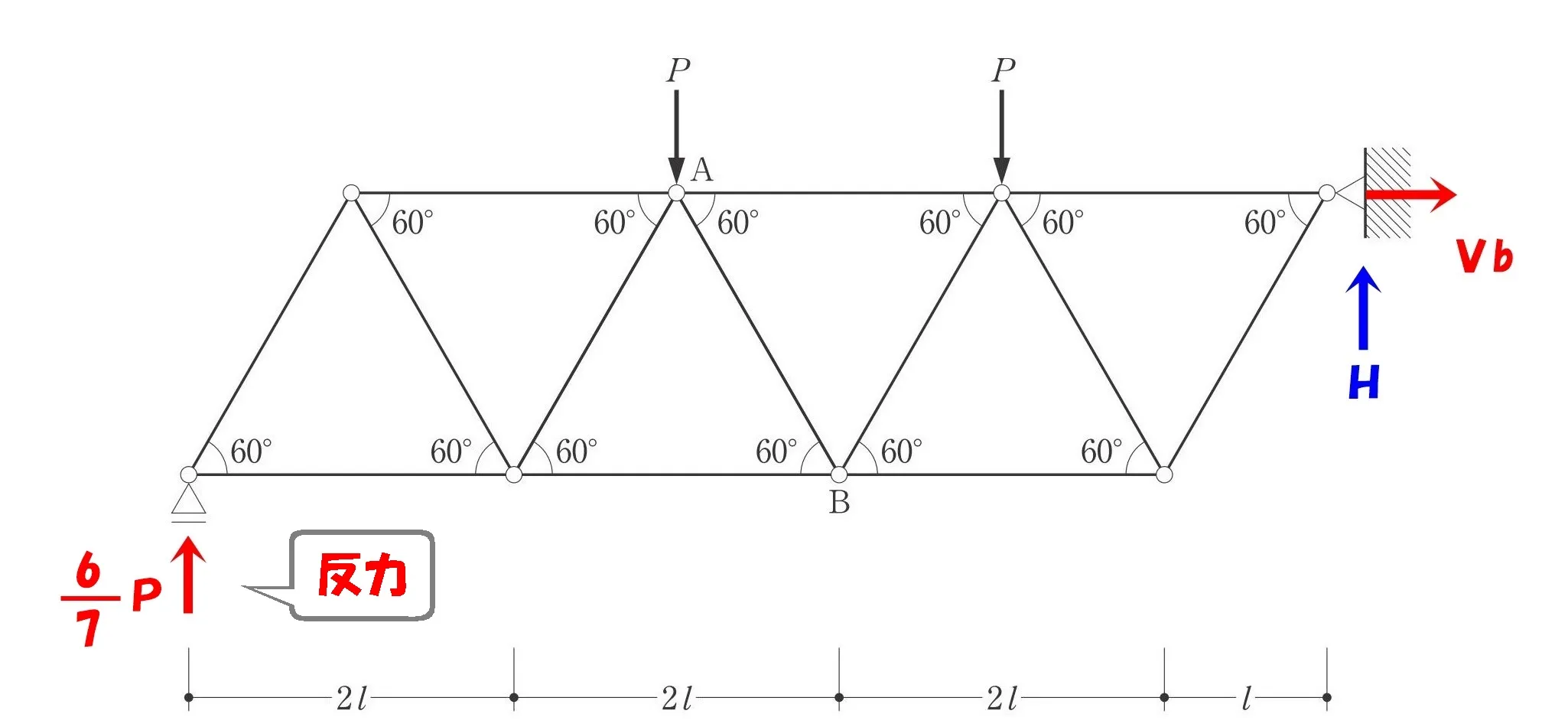

$$鉛直反力Va=\frac{ 6 }{ 7 }P$$
水平反力Hと鉛直反力Vbについては、ΣX=0とΣY=0で求められる。
(切断法で解答するため、ここでは省略します。)



めんどくさそう。
2.求める部材を切断し、片側を取り出す
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。
求める部材に印する
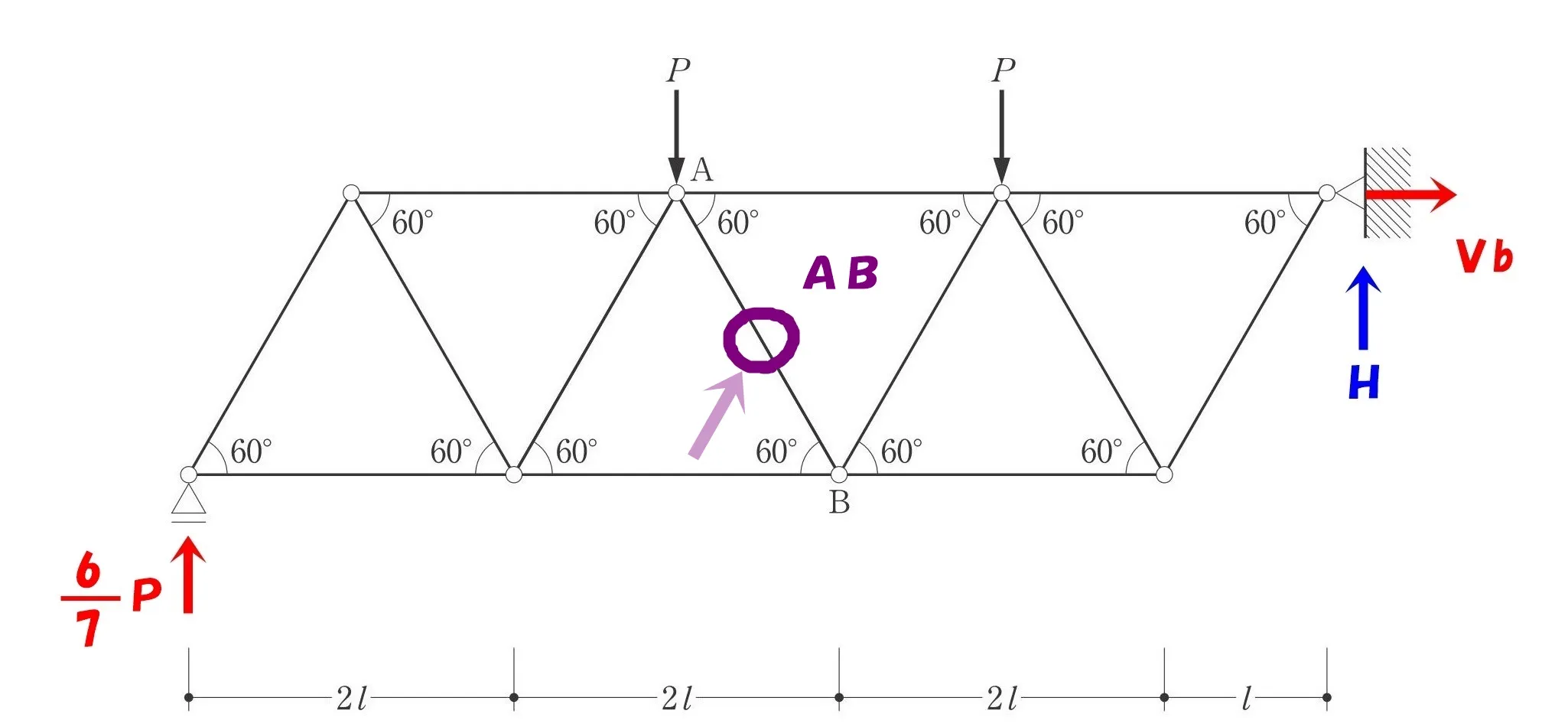

設問で問われている部材「AB」の位置に印を付けておく。



ターゲットを確認!
節点法を使うと?
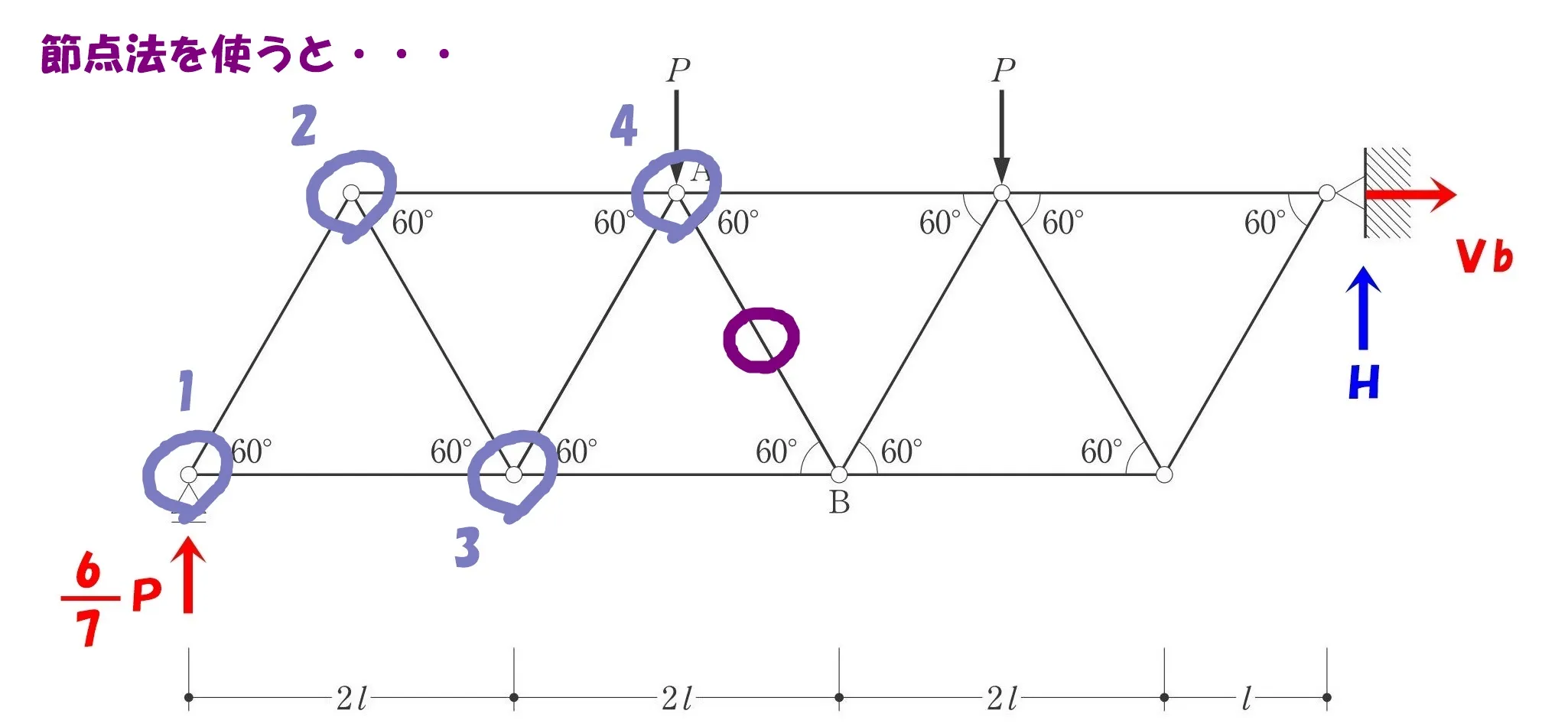

1.図解法(三角比)→ 2.節点法(釣り合い)→ 3.節点法(釣り合い)→ 4.節点法(釣り合い)



・・・
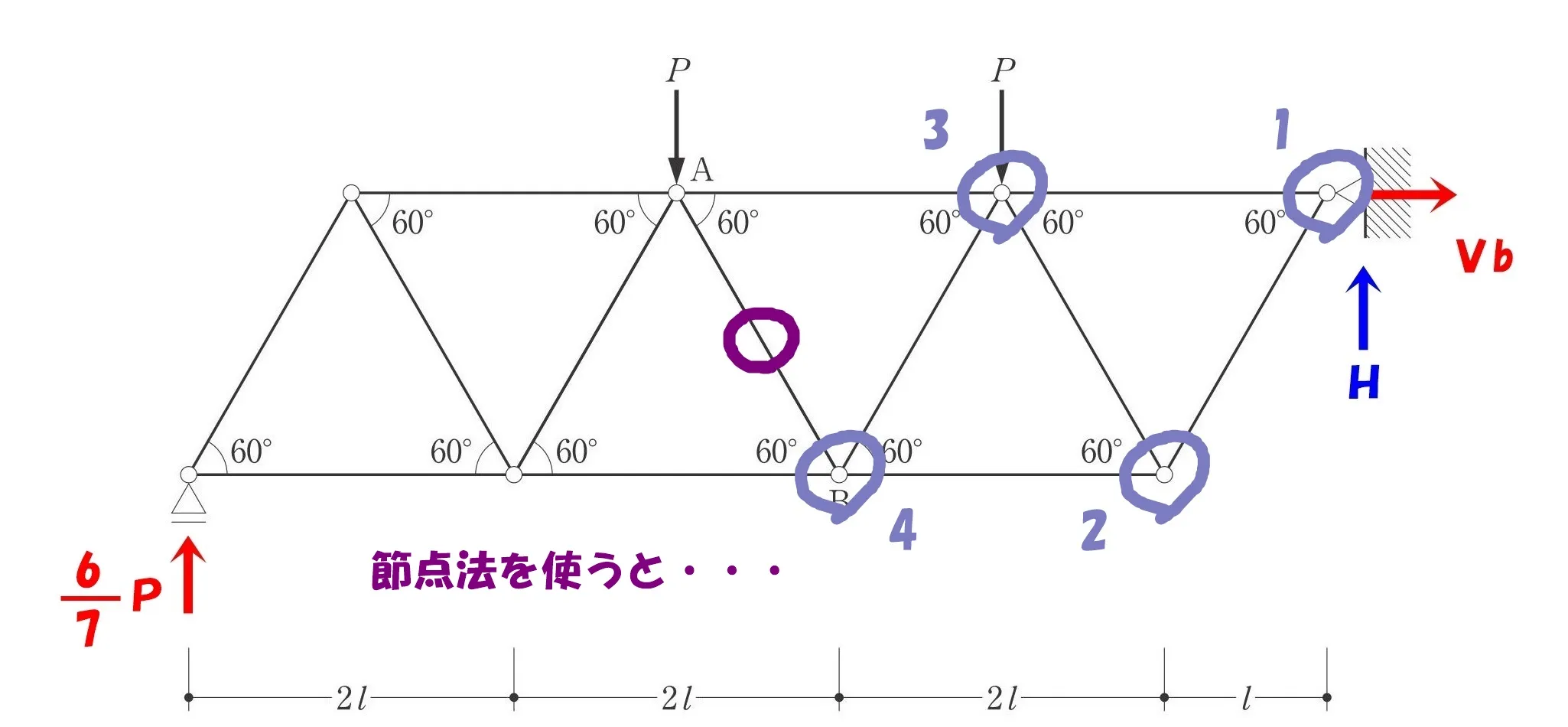

1.図解法(三角比)→ 2.節点法(釣り合い)→ 3.節点法(釣り合い)→ 4.節点法(釣り合い)



・・・
切断法ABで解く


部材ABを切断して、ローラー支点(左)側を取り出す。
ピン支点(右)の反力HとVbを釣り合い式に含めないため、対象部から外しておく。



斬ってしまえ!
部材を取り出す
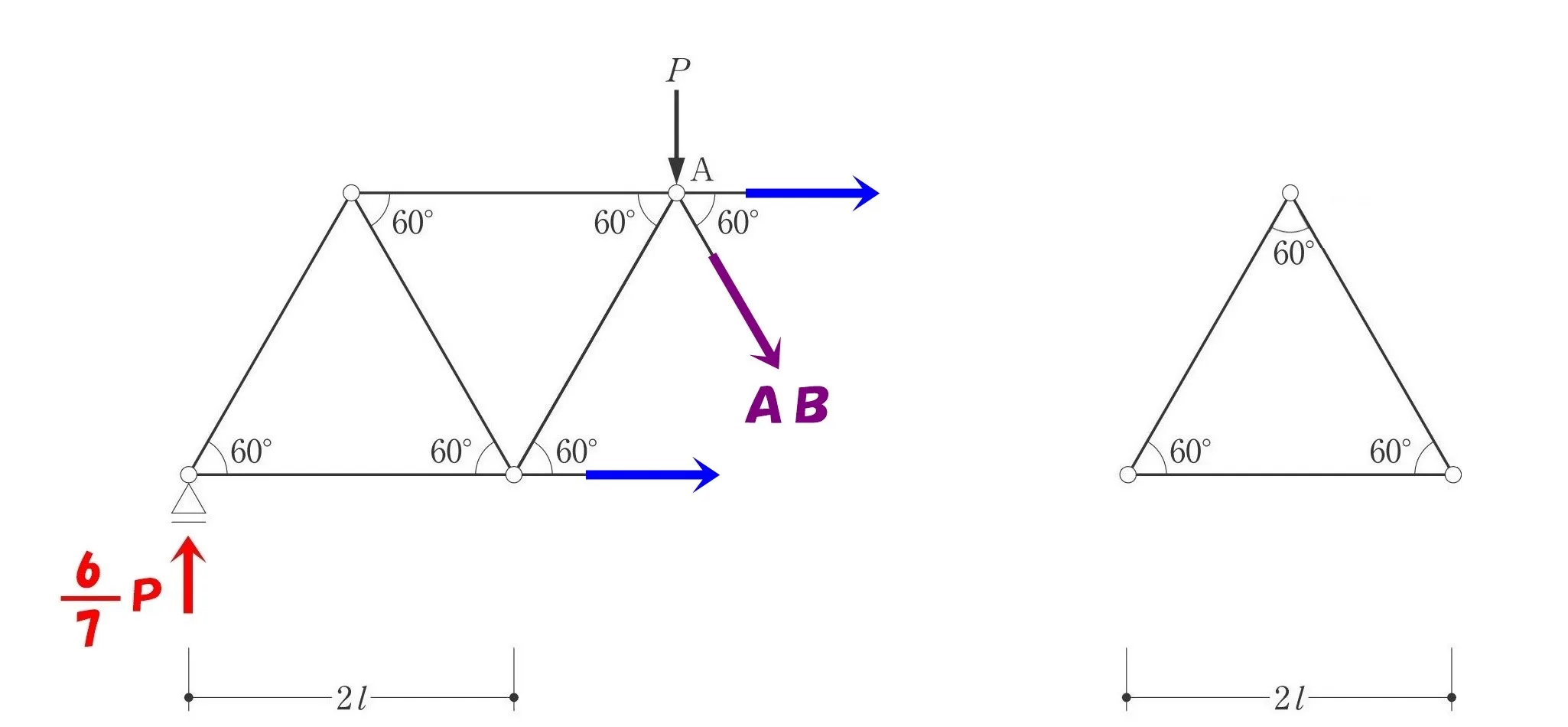

切断した部材ABの断面から、「引っ張る方向」にベクトルを書き出す。



ABをズバッと!
3.単純梁のトラスは、ΣY=0で軸力を求める
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。





つまらぬモノを
斬ってしまった。
ΣY=0
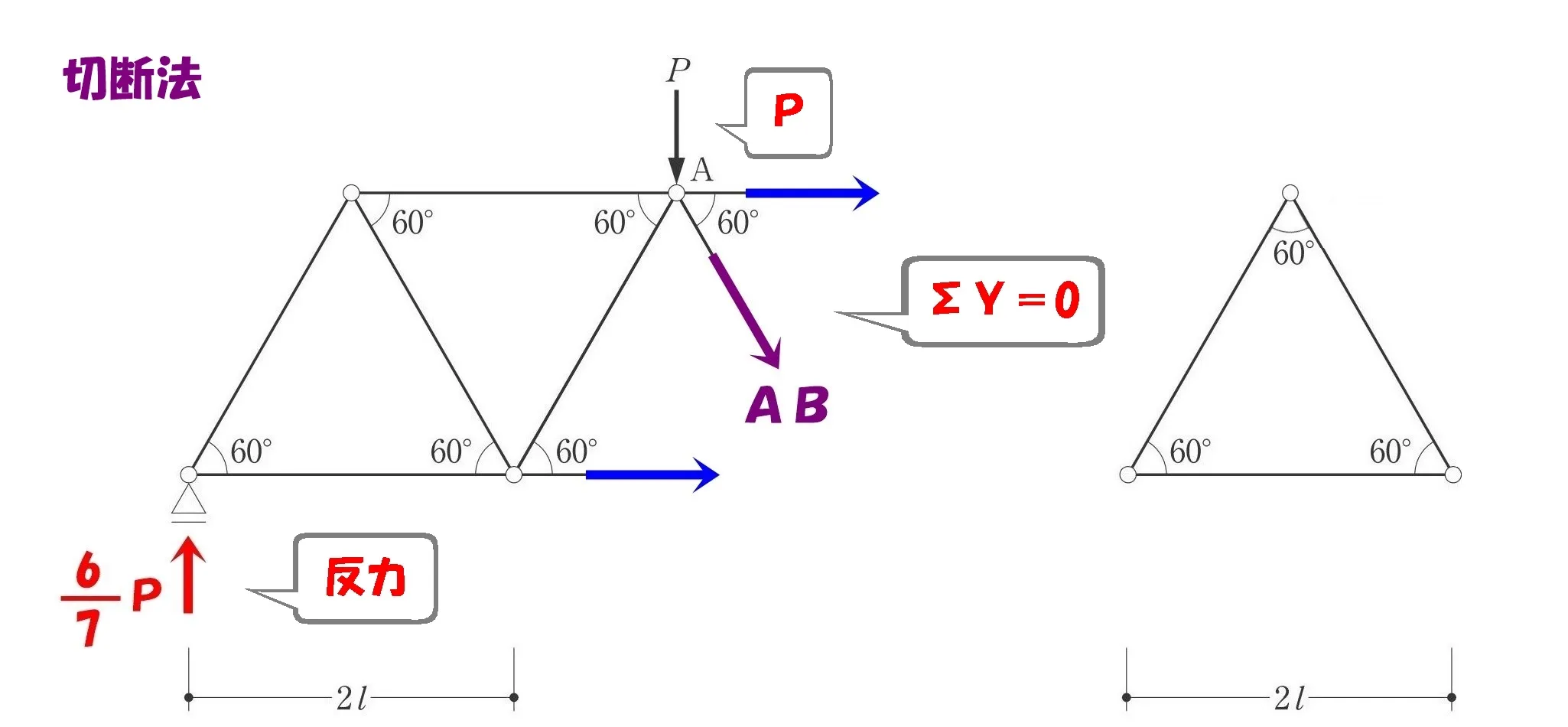

トラスは単純梁なので、「ΣY=0」の釣り合い式から軸力ABを求める。



シグマ・Y
ベクトルABの分解
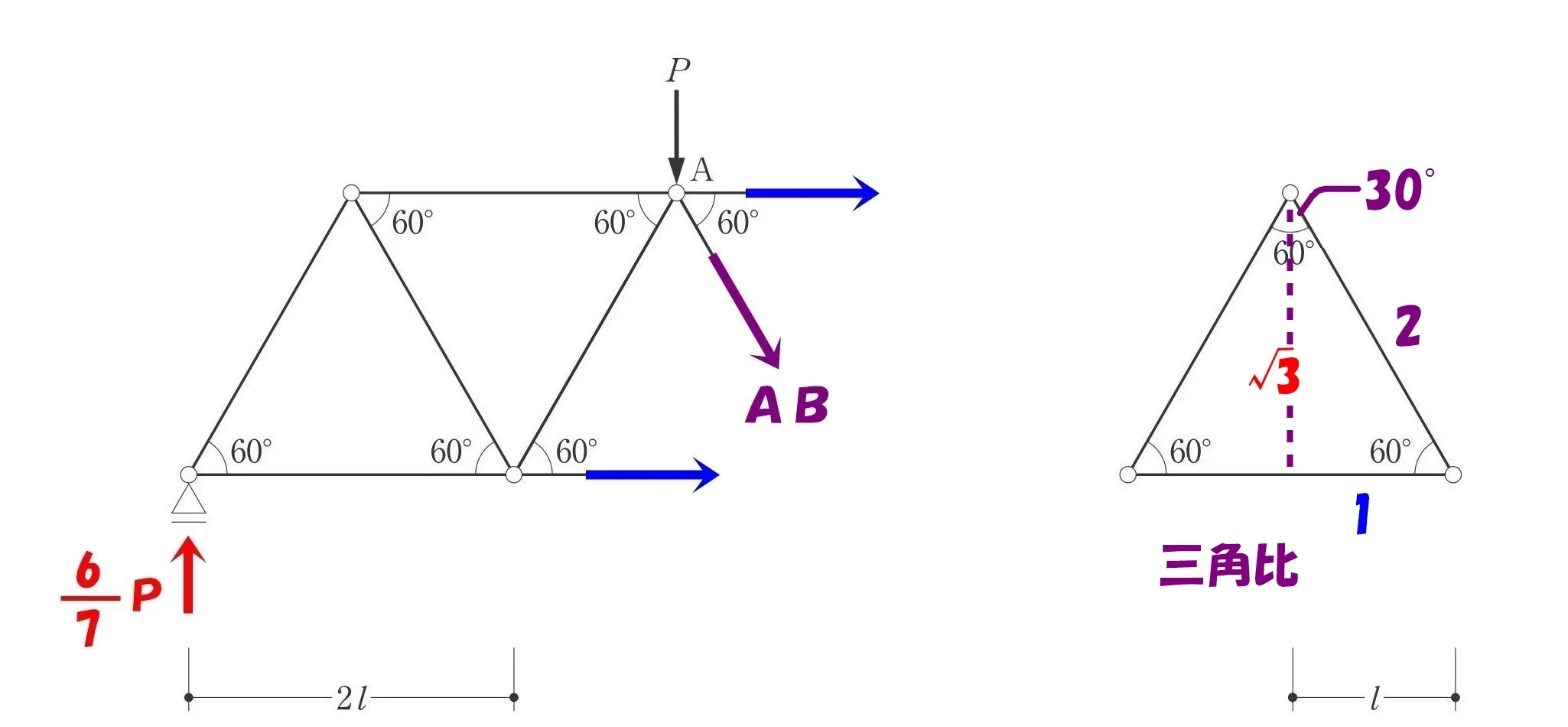

$$30°の直角三角形の比=2:1:\sqrt{3}$$
三角比を使ってベクトルABをX方向とY方向に分解する。



ベクトルを分解する。
ABのY方向を取り出す
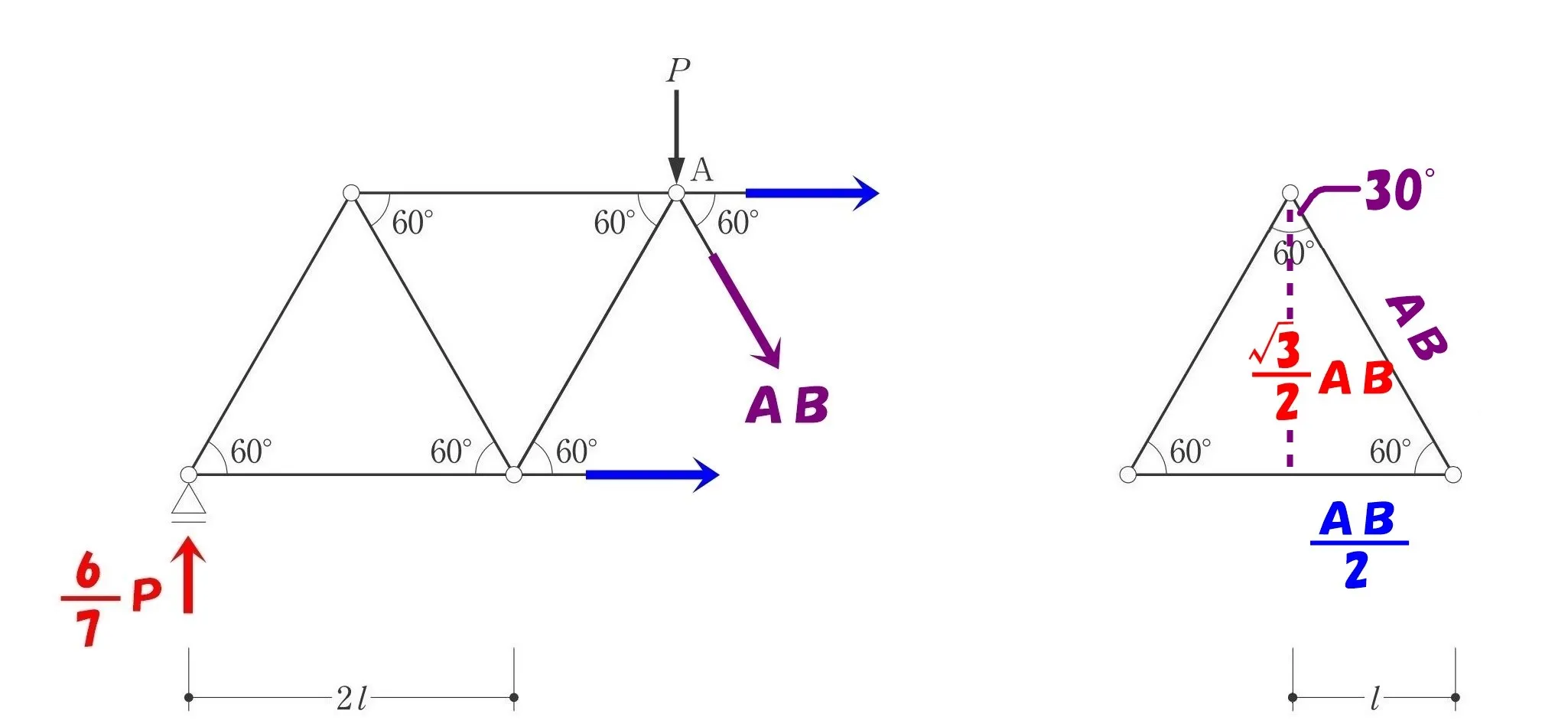

ベクトルの比は、それぞれの部材の軸力の比と相似になる。
$$2:1:\sqrt{3}=AB:\frac{ AB }{ 2 }:\frac{ \sqrt{3} }{ 2 }AB$$
$$ベクトルABのY方向=\frac{ \sqrt{3} }{ 2 }AB$$



トラス・マジック!
ΣY=0
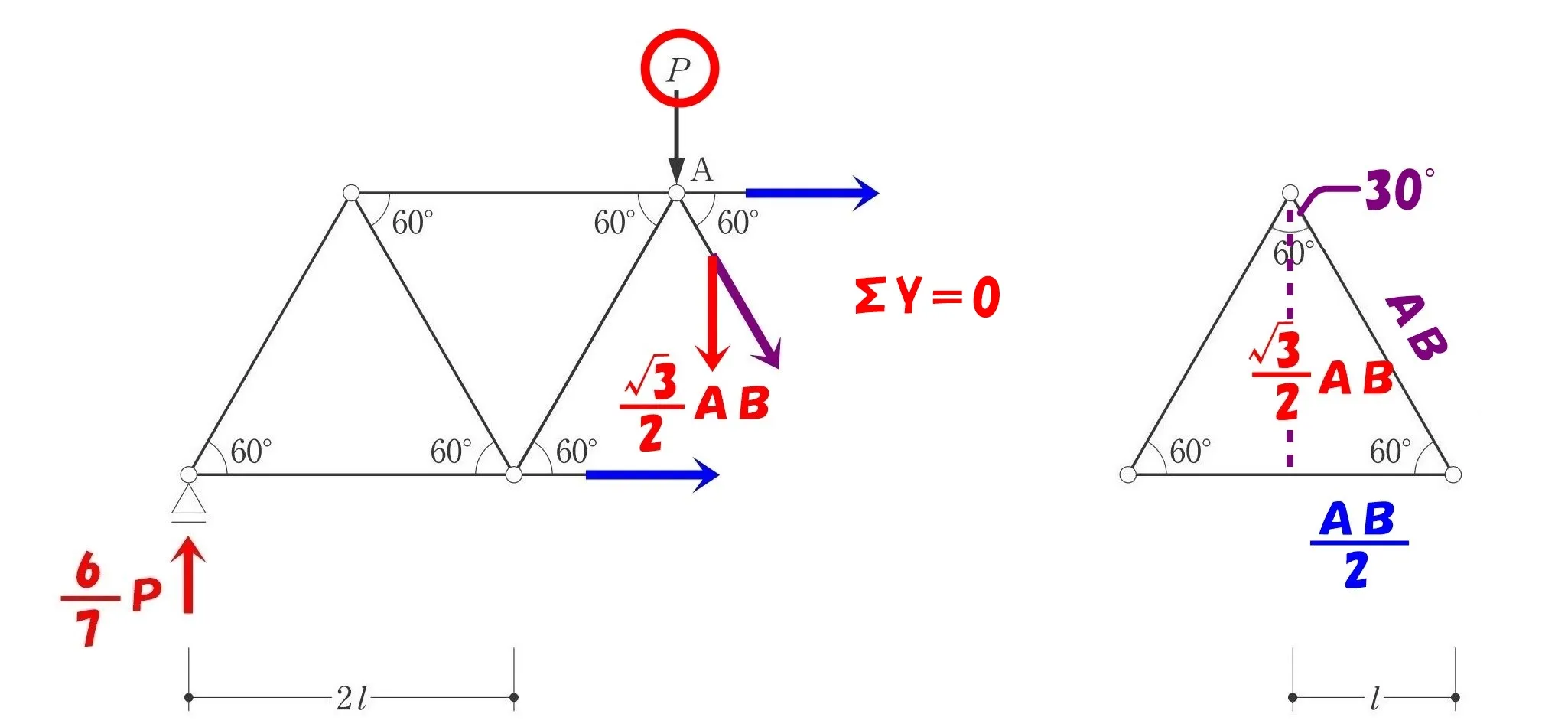

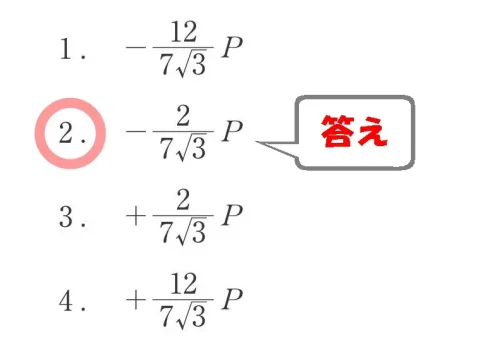
$$\Sigma Y=0より,+\frac{ 6 }{ 7 }P-P(荷重)-\frac{ \sqrt{3} }{ 2 }AB(↓下向き)=0$$$$+\frac{ 6 }{ 7 }P-\frac{ 7 }{ 7 }P(荷重)-\frac{ \sqrt{3} }{ 2 }AB=0→-\frac{ 1 }{ 7 }P-\frac{ \sqrt{3} }{ 2 }AB=0$$$$-\frac{ \sqrt{3} }{ 2 }AB=+\frac{ 1 }{ 7 }P→AB=+\frac{ 1 }{ 7 }P*-\frac{ 2 }{ \sqrt{3} }=-\frac{ 2 }{ 7\sqrt{3} }P(圧縮力)$$



めまいがしてくる。



終わった・・・
公式
$$\Sigma Y=0$$



Σワイ!
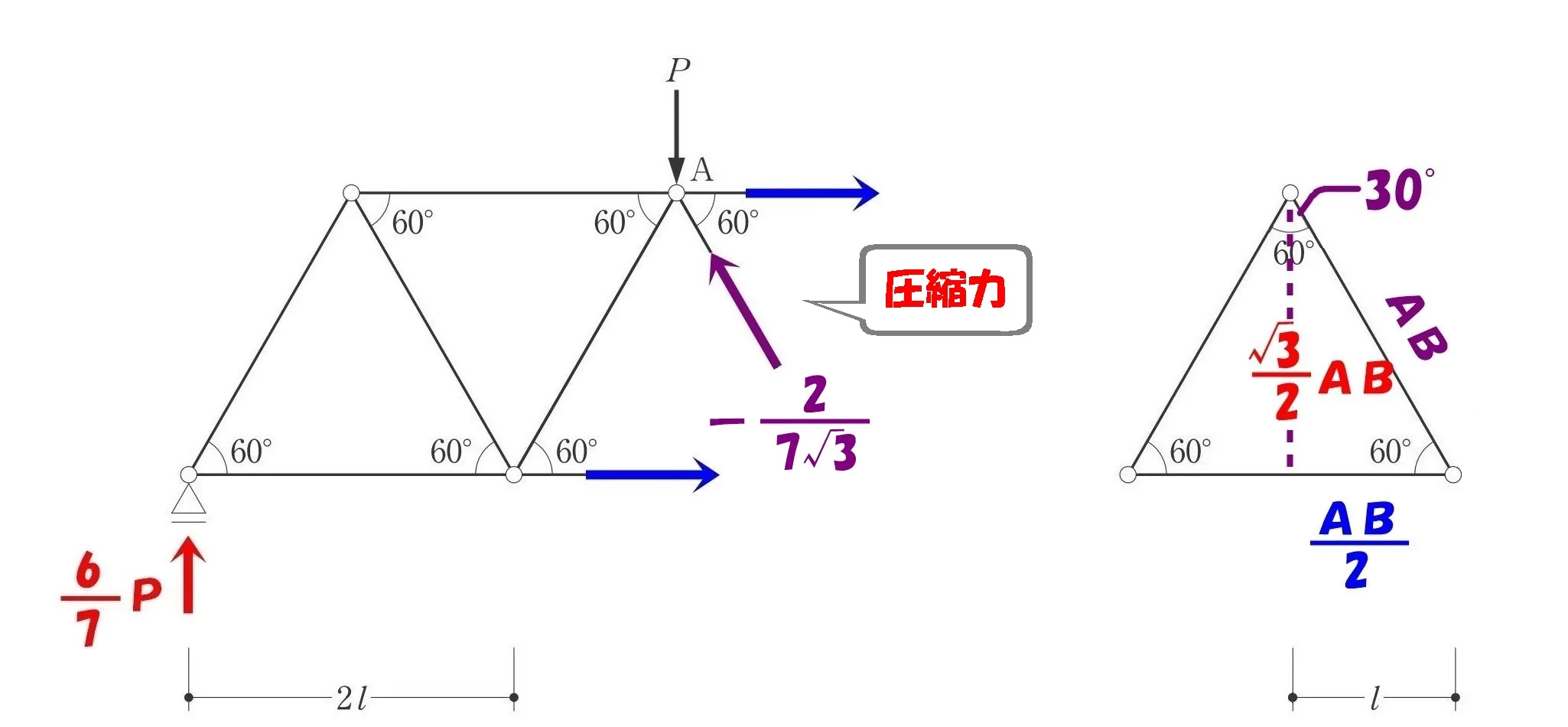

$$\Sigma Y=0より,AB=-\frac{ 2 }{ 7\sqrt{3} }P(圧縮力)$$



トラス・マジック!
答え.2

切断法とは?
トラスを切断して片側を取り出し、力の釣り合いにより部材の軸力を求める方法
切断法の攻略ポイント
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。


この動画を YouTube で視聴
お疲れ様でした、まとめに入ります。

一級建築士|構造力学「トラス」の3つの攻略法(まとめ)



トラスの心得!
トラスの3つの攻略法
- 節点法
- 図解法
- 切断法
トラスの3つの心得!
- 反力を求めなければ何も始まらない。
- トラスの軸力は力の釣り合いを追いかける。
- トラスの一部を切り出して、方程式を組み立てる。


節点法の攻略ポイント
- 支点反力を求める。
- トラスの節点を取り出す。
- ΣX=0ΣY=0で軸力を求める。


図解法の攻略ポイント
- 支点反力を求める。
- ベクトルを三角形に組み合わせる。
- 三角比の辺の比率から、2つの軸力を求める。


切断法の攻略ポイント
- 支点反力を求める。
- 求める部材を切断し、片側を取り出す。
- 単純梁のトラスは、ΣY=0で軸力を求める。
引張り力と圧縮力の考え方


注意点
圧縮力や引張り力は、部材そのものに働く力ではありません。
トラスの応力は「節点に作用する」ため、どちらの力も「節点」から見たベクトルの方向を指します。


「トラスの沼」から生還できましたでしょうか?
途中で何度か、意識がふっ飛んだかもしれませんね・・・。(^_^;)
節点法・図解法・切断法、いずれも知っておくことでトラスの知識が深まります。
トラスは解き方にバリエーションのあるため、攻略しやすいカテゴリーです。
そのため、「どう合理的に解くか?」を追求することで、楽しめる分野とも言えるでしょう。



トラス・マジック!
トラスの突破口!
- 反力を求めなければ何も始まらない。
- トラスの軸力は力の釣り合いを追いかける。
- トラスの一部を切り出して、方程式を組み立てる。
トラスが苦手だった人にとっては、この記事は運命的なめぐり合わせといえるでしょう。
これが刺激となり、力学の奥深さに目覚めるきっかけになるかもしれません。
最後まで記事を読んでいただき、本当にありがとうございました。


毎日、1トラス!
今日から始めるぞ~!
力学の攻略ポイントを集結!
.webp)
.webp)




法規の計算問題を完全攻略




-300x197.webp)






